Un método de muestreo para predecir la edad de ramas de primer orden

INTRODUCCIÓN

La evaluación de prescripciones silvícolas para especies de alto valor comercial destinadas a uso estructural requiere conocer atributos de ramas como su posición, tamaño, longevidad, mantención y persistencia a lo largo del fuste. Las ramas incluidas en el fuste se convierten en nudos que desde una perspectiva de calidad de madera se consideran como defectos internos (Trincado y Burkhart, 2008; Osborne y Maguire, 2015). Decisiones silvícolas tales como: densidad inicial de plantación y espaciamiento (Amateis, Radtke y Hansen, 2004), raleo (Baldwin et al., 2000), poda (Clark, Saucier, Baldwin y Bower, 1994) y fertilización (Yu, Chambers, Tang y Barnett, 2003) tienen un efecto en el tamaño de las ramas y consecuentemente en la dimensión de los nudos. A su vez, el estudio de la persistencia o tiempo de permanencia de ramas muertas en el fuste resulta fundamental en la producción de madera de alta calidad para decidir si podar artificialmente o dejar que ésta se produzca en forma natural. Las ramas que persisten mucho tiempo muertas antes de caer generan una pérdida de volumen de alta calidad importante en la troza basal, ya sea porque el pedúnculo de la rama es muy largo o muy grueso (Maguire y Hann, 1987; Mäkinen, 2002; Hein, 2008). Por lo tanto, para el desarrollo de una silvicultura orientada a la producción de madera de alta calidad es fundamental disponer de técnicas eficientes de medición de longevidad y persistencia de ramas que permitan la construcción de modelos de formación, desarrollo y recesión de copa (Weiskittel, Seymour, Hofmeyer y Kershaw, 2010; Wang et al., 2015).

El problema fundamental es que la medición de la dinámica de formación y crecimiento de las ramas, que está bajo fuerte control genético y es modificado por la competencia y el sitio, es difícil y costosa de realizar, especialmente a medida que los árboles aumentan su tamaño. Esto limita el estudio de la dinámica y estructura de la copa de los árboles. Para estimar la edad de las ramas se ha aplicado el método de disección de ramas y conteo de anillos de crecimiento descritos por Maguire y Hann (1987), sin embargo, no ha mostrado tener una alta exactitud. Uno de los mayores problemas de esta técnica es la pérdida de anillos anuales de crecimiento de las ramas cuando éstas empiezan a morir. Reukema (1959) comparó el número de anillos en la base de ramas vivas y en el fuste en su punto de inserción y encontró diferencias de 9 a 10 años en la medición de la edad de ramas en Pseudotsuga menziesii (Mirb.) Franco, atribuyéndolo a que las ramas no necesariamente forman anillos anuales en su base, siendo aún vitales. Este autor señala que probablemente se deba a la cercanía de la muerte de la rama, aun cuando su follaje era abundante y aparentemente sano. Coincidentemente, Kershaw, Maguire y Hann (1990) encontraron, en la misma especie que los anillos anuales de ramas perdidos en promedio fueron de 8 años, con un rango entre 0 y 49 años y que en términos de la longevidad de la rama resulta en promedio 34% con un rango entre 0% y 93%. Sprugel, Hinckley y Schaap (1991) señalan que en general las ramas más bajas resultan neutrales en el balance de carbono del árbol, fijan lo que necesitan para sus requerimientos, pero sin agregar nuevos tejidos. Este fenómeno de falta de formación de anillos anuales en las ramas ocurre con mayor intensidad en la zona baja del árbol, donde precisamente se encuentra el volumen comercial más interesante y que es hacia donde se dirigen los esfuerzos de la silvicultura, como lo señalan Andrews y Gill (1939). Reukema (1959) señala que la falla en la formación de anillos anuales de crecimiento en las ramas se debe a que la formación de células cesa en los últimos años de vida o a que la actividad cambial es tan débil que sólo forma una o dos corridas de células indiferenciadas entre primavera y verano. Estos antecedentes motivan a desarrollar un método alternativo que combine técnicas de análisis de tallo y estimación del punto de inserción en altura de la rama en el fuste para estimar la edad y año de formación de las ramas y el período de permanencia de ramas en la copa viva y muerta de los árboles. Se espera que el método propuesto facilite la medición y modelación de la dinámica de formación de las ramas vivas y muertas. Siendo un método de estimación de la edad de las ramas alternativo a la técnica de disección que evite la omisión de conteo de anillos anuales de crecimiento.

Protocolo de muestreo

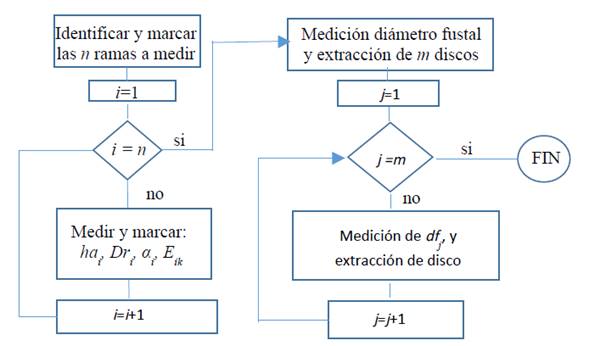
Antes de proceder al volteo y extracción de discos para el conteo de años, debe verificar que el árbol presente anillos anuales de crecimiento. Esto se puede corroborar extrayendo un tarugo del fuste y observando la diferenciación de anillos. Tiene que considerar que no todas las especies ni climas donde crecen los árboles forman anillos anuales de crecimiento, lo cual es de amplio conocimiento en la dendrocronología. Para cada uno de los árboles seleccionados se debe realizar la medición y marcación del diámetro normal (DAP). Posteriormente, se debe ejecutar el apeo de los árboles y medir la altura de tocón (T) y el largo fustal (L) desde la base hasta el ápice del árbol. La medición de ramas y extracciones de rodajas o discos requeridas para el análisis de tallo debe seguir la secuencia de actividades de la figura 1.

Figura 1: Protocolo utilizado para la medición de ramas y extracción de discos a lo largo del fuste.

Donde:

• i rama número i=1, …, n

• j rodaja número j=1, …, m

• ^_hai altura de emergencia de la rama i en el fuste (m)

• ^_Dri diámetro de la rama i (mm)

• ^_αi ángulo de inserción superior de la rama i (grados)

• ^_Ei estado de la rama i (viva o muerta)

• ^_dfj diámetro fustal de la rodaja j

Para cada árbol muestra se debe identificar y marcar a lo largo del fuste una submuestra de n ramas a las cuales se les medirá su altura de emergencia en el fuste, diámetro fustal, ángulo de inserción superior y estado de la rama. Finalmente, se procederá a la extracción de una submuestra de m rodajas a lo largo del fuste y se medirá en cada posición el diámetro fustal ^_dfj (cm). La secuencia de cortes idealmente deberá generar una diferencia constante de años entre rodajas sucesivas a fin de mantener errores de interpolación de baja magnitud, para lo cual se debe disponer curvas de índice de sitio (Corvalán, Araya, Blanco y Cox, 1987). El trozado del árbol para la obtención de discos fustales deberá considerar adicionalmente la ubicación de las ramas que han sido medidas de tal manera que la interpolación de la altura de formación de la rama en el fuste sea realizada en un intervalo de altura breve, para disminuir errores propios de interpolación.

Algoritmos de estimación

El método requiere reconstruir para cada edad la altura total del árbol seleccionado. Esto se realiza aplicando técnicas de análisis de tallo que requieren del conteo y medición de los anillos contenidos en cada una de las secciones transversales obtenidas a lo largo del fuste (Cancino, Acuña y Espinosa, 2012).

Estimación del año de formación de las ramas

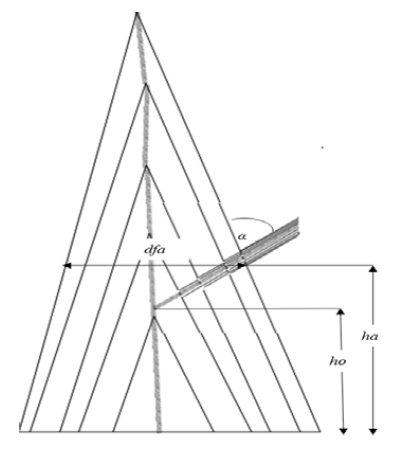
Para estimar la edad de formación de la rama es necesario estimar previamente la altura de origen de la rama ^_ho (m) en el fuste. Esta se estima corrigiendo la altura de emergencia o aparición de la rama ^_ha en el fuste (m) por el ángulo de inserción superior α (grados) y el diámetro fustal a la altura de aparición de la rama ^_dfa (m) al aplicar la siguiente fórmula (figura 2):

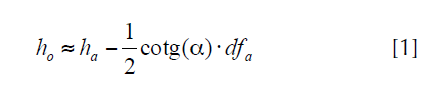
Figura 2: Representación esquemática de formación de ramas de primer orden en el fuste.

El procedimiento asume que no existe excentricidad de los anillos de crecimiento en la sección transversal del fuste, lo cual puede ser observado en las rodajas. Para determinar la edad de formación de la rama se compara la altura de origen de la rama con la altura total del árbol reconstruida para las distintas edades ( ^_he ). La rama medida tendrá la edad de formación ^_ef cuando _{^he- 1} < ^_ho < ^_he . Por lo tanto, el año de formación ( ^_af ) se obtendrá restando del año de la medición ( ^_am ) la edad de formación estimada de la rama ( ^_ef ).

Estimación de la edad de las ramas

Una vez estimado el año de formación de la rama se requiere clasificar la condición de la rama. Si la rama está viva entonces la diferencia entre el año de medición ( ^_am ) y el año de formación ( ^_af ) de la rama corresponderá a la edad actual de la rama (E _r). En caso contrario, si la rama está muerta, solo se podrá determinar la edad y año cuando se produjo su formación. Determinar la edad de la rama importa solamente si ella está viva o muerta. Otros estados de vitalidad no afectan su edad.

Estimación del período de mantención de la copa viva

El período de tiempo de mantención de la copa viva puede ser estimado como la diferencia entre el año de medición del árbol y el año de formación de la rama viva más baja en altura en la base de la copa viva.

Estimación del período de persistencia de las ramas muertas

La persistencia de ramas muertas corresponde al máximo número de años estimado en que las ramas inferiores de la copa permanecen muertas sin caer. Esto se puede estimar como la diferencia entre el año de formación de la rama más baja de la copa muerta ( ^_AFrm ) y la rama viva más baja de la copa viva ( ^_AFrv ).

Medición de ramas a lo largo del fuste

El fuste del árbol fue dividido en 10 secciones relativas (deciles). En cada sección se seleccionaron las ramas de mayor diámetro siguiendo los protocolos de medición descritos en Corvalán (2015). En este caso, 7 de las 10 secciones relativas tenían presencia de ramas vivas o muertas (tabla 1). Este procedimiento de reconstrucción no considera la selección de ramas de origen epicórmico que se pudieran presentar a lo largo del fuste. Las variables medidas en cada rama seleccionada fueron: estado de la rama (viva o muerta), diámetro de la rama ^_Dr en mm, altura de emergencia de la rama en el fuste ^_ha en m, ángulo de inserción superior de la rama α en grados y diámetro fustal a la altura de emergencia de la rama ^_dfa en cm. El ángulo de la rama y su diámetro fueron medidos con transportador y pie de metro, respectivamente.

Tabla 1: Variables de estado de ramas medidas a distintos rangos de alturas relativas (HR) y reconstrucción de altura de origen, edad y año de formación y edad estimada de cada rama.

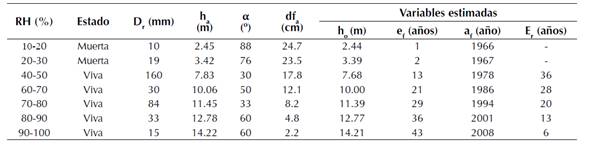
Donde:

• Dr diámetro de la rama (mm)

• ha altura de emergencia de la rama (m)

• α ángulo de inserción superior de la rama (grados)

• dfa diámetro fustal a la altura de emergencia de la rama (cm)

• ho altura de origen de la rama (m)

• ef edad del árbol a la que se formó la rama (años)

• af año de formación de la rama

• Er años de vida de la rama

Reconstrucción de ramas

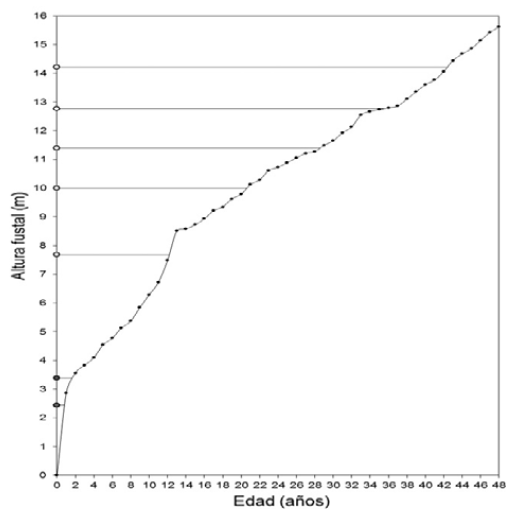
Aplicando la fórmula [1] es posible estimar la altura de origen ^_ho (m) de cada una de las ramas en el fuste (tabla 1 ). Posteriormente, para estimar la edad de formación ^_ef se debe comparar la altura estimada de origen ^_ho con la altura del árbol a las distintas edades ^_he . La figura 3 presenta el desarrollo en altura del árbol para las distintas edades con la intersección de las alturas de origen estimadas para cada una de las ramas.

Figura 3: Desarrollo en altura total con la intersección de la altura de origen de las ramas muertas (●) y vivas (○).

Los datos señalados en la tabla 1 permiten determinar que el período de permanencia de ramas en la copa viva alcanza 36 años, esto corresponde a la rama viva medida en la parte más baja de la copa a los 7.83 m. Finalmente, el período de persistencia de ramas muertas se podría estimar como la diferencia entre el año de formación de la rama medida más baja de la copa viva (1978) y el año de formación de la rama muerta más baja de la copa muerta (1966) siendo en este caso de 12 años.

DISCUSIÓN

La aplicación del método permite estimar el año de formación de ramas, edad de las ramas, período de mantención de ramas dentro de la copa viva y período de persistencia de ramas muertas alrededor del fuste. Un claro limitante del método es que puede ser aplicable únicamente a especies forestales en las cuales se puedan diferenciar verdaderos anillos anuales de crecimiento y no presenten excentricidad exagerada.

La aplicación del método asume que las ramas muestreadas tienen un origen axial y no corresponden a brotes epicórnicos originados en el fuste Shigo, 1986; Weiskittel et al., 2010; Lowell et al. (2014); Ishii y Wilson (2001) describen las principales características que diferencian las ramas epicórnicas de las originales: textura de la corteza más suave y blanquecina, ángulo de inserción tangencial al fuste, vecindad de alguna rama original muerta o moribunda, crecer en grupo en forma de abanico y diámetro más pequeño. Sin duda, estas características observadas en conjunto difícilmente confundirán a un observador experimentado, incluso cuando la única forma de saber con certeza es muestreando destructivamente la unión de las médulas (Kozlowski, 1971).

Otro supuesto involucrado en el cálculo de la altura de inserción de la rama es la invariabilidad de su ángulo de inserción desde la médula hasta el punto de emergencia en el fuste. De acuerdo con Rautiainen y Stenberg (2005), este supuesto resulta bastante razonable, al menos en ramas juveniles. Para ramas adultas es probable que el ángulo de inserción aumente como lo señalan Colin y Houllier (1992), Lemieux, Samson y Usenius (1997), Vestøl y Høibø (2001), Trincado y Burkhart (2008) y Osborne y Maguire (2015). El tamaño y peso de las ramas modifica el ángulo de inserción como se deduce de los estudios de Shigo (1986) y Lemieux et al. (1997). Consecuentemente, el error de sobreestimación de la altura de inserción de la rama conduciría a una probable subestimación de la edad de la rama. Sin embargo, la magnitud del error resulta despreciable comparado con el incremento en altura que se produce de año en año.

Otra limitante de la aplicación del método propuesto y difícil de verificar, es asumir que la médula del fuste del árbol se encuentre exactamente en su centro geométrico. Knapic et al. (2014) al estudiar la excentricidad de la médula en Pino marítimo establecieron que esta es homogénea y baja para el fuste con un valor promedio de 20%, aun cuando señalan que para el duramen alcanza un 50%. Vestøl y Høibø (2000) indican que la excentricidad del fuste en Picea abies ocurre en sitios con altas pendientes debido a la madera de reacción que se forma en esas condiciones. Kellogg y Barber (1981) encontraron alta excentricidad del fuste en árboles de segundo crecimiento de Tsuga heterophylla, mas no encontraron correlaciones con el diámetro normal, edad y altura total, algo que dificulta de esta manera su predicción. Para el método propuesto, es recomendable realizar las lecturas de anillos en el análisis de tallo sobre el radio geométrico de las rodajas. Ya que esto minimiza el error de localización del punto de nacimiento de la rama sin afectar la estimación de su edad, dado que la edad registrada en las rodelas no depende de la excentricidad del árbol.

La estimación del año de formación de la rama estará determinada por la exactitud en la estimación de altura del árbol para las distintas edades. En este aspecto, una posible causa de error se deberá a la longitud de los cortes transversales para la obtención de rodajas para realizar el análisis de tallo. Se recomienda realizar los cortes al menos cada 2 m (Anuchin, 1970; Trincado, Kiviste y von Gadow, 2002). Otra fuente de variabilidad podría deberse al algoritmo utilizado para la estimación de alturas totales (Kariuki, 2002; Cancino et al., 2012). A futuro sería recomendable poder realizar estudios comparativos que determinen el efecto de utilizar diversos algoritmos de interpolación de alturas sobre la posición del origen de las ramas y hacer comparaciones con el método de disección de ramas.

En los últimos años se está utilizando con mayor frecuencia tomografía computacional de rayos X (CT) en la medición detallada de nudos en la madera. CT es la técnica de medición no destructiva más promisoria para la medición de la edad de las ramas, sin embargo, su uso es de alto costo por lo que no será discutida aquí (Hailey y Morris, 1987; Chang, 1992; Schad, Schmoldt y Ross, 1996).

A pesar de las limitantes y supuestos del método propuesto, no parece existir una alternativa más eficiente y exenta de errores para la estimación de la edad de formación y persistencia de las ramas vivas en la copa del árbol. Ello permite estudiar la caracterización de la estructura de las ramas y la dinámica de persistencia tanto de la copa viva como la copa muerta (Corvalán, 2017). Este método es utilizable en estudios de dinámica de la copa en especies que presenten anillos anuales de crecimiento.

CONCLUSIONES

La metodología combinada de análisis de tallo con medición del diámetro fustal, estado y ángulo de inserción a la altura de emergencia de las ramas permite extraer valiosa información sobre la dinámica de desarrollo, muerte y caída de ramas de primer orden en el perfil fustal. Puede constituirse en una herramienta alternativa al método de disección para el estudio de la dinámica de la copa, como se muestra en el caso de un árbol de roble.