DOI:
https://doi.org/10.14483/2256201X.19392Publicado:
01-01-2023Número:
Vol. 26 Núm. 1 (2023): Enero-junioSección:
Artículos de investigación científica y tecnológicaAplicación de diferentes tipos de datos en el modelado de la distribución de especies arbóreas en México
Application of Different Types of Data in the Distribution Modeling of Tree Species in Mexico
Palabras clave:
Altitud, clima, encinos, pinos, precipitación, temperatura (es).Palabras clave:
Altitude, climate, oaks, pines, precipitation, temperature (en).Descargas
Referencias
Allouche, O., Tsoar, A. & Kadmon, R. (2006). Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). Journal of Applied Ecology, 43(6), 1223-1232. https://doi.org/10.1111/j.1365-2664.2006.01214.x DOI: https://doi.org/10.1111/j.1365-2664.2006.01214.x
Anderson, R., & Gonzalez, I. (2011). Species-specific tuning increases robustness to sampling bias in models of species distributions: An implementation with Maxent. Ecological Modelling, 222(15), 2796-2811. https://doi.org/10.1016/j.ecolmodel.2011.04.011 DOI: https://doi.org/10.1016/j.ecolmodel.2011.04.011
Araújo, M., & Peterson, A. (2012). Uses and misuses of bioclimatic envelope modeling. Ecology, 93(7), 1527-1539. https://doi.org/10.1890/11-1930.1 DOI: https://doi.org/10.1890/11-1930.1
Araújo, M., Thuiller, W., Williams, P., & Reginster, I. (2005). Downscaling European species atlas distributions to a finer resolution: Implications for conservation planning. Global Ecology and Biogeography, 14(1), 17-30. https://doi.org/10.1111/j.1466-822X.2004.00128.x DOI: https://doi.org/10.1111/j.1466-822X.2004.00128.x
Ashcroft, M., French, K., & Chisholm, L. (2012). A simple post-hoc method to add spatial context to predictive species distribution models. Ecological Modelling, 228, 17-26. https://doi.org/10.1016/j.ecolmodel.2011.12.020 DOI: https://doi.org/10.1016/j.ecolmodel.2011.12.020
Austin, M. (2007). Species distribution models and ecological theory: A critical assessment and some possible new approaches. Ecological Modelling, 200(1-2), 1-19. https://doi.org/10.1016/j.ecolmodel.2006.07.005 DOI: https://doi.org/10.1016/j.ecolmodel.2006.07.005
Barve, N., Barve, V., Jiménez-Valverde, A., Lira-Noriega, A., Maher, S., Peterson, A., Soberón, J., & Villalobos, F. (2011). The crucial role of the accessible area in ecological niche modeling and species distribution modeling. Ecological Modelling, 222(11), 1810-1819. https://doi.org/10.1016/j.ecolmodel.2011.02.011 DOI: https://doi.org/10.1016/j.ecolmodel.2011.02.011
Bewley, J., & Krochko, J. (1982). Desiccation-tolerance. En O. Lange, S. Nobel, C. Osmond & H. Ziegler (Eds.), Physiological Plant Ecology II (pp. 325-378). Springer. https://doi.org/10.1007/978-3-642-68150-9_11 DOI: https://doi.org/10.1007/978-3-642-68150-9_11
Bonte, D., van Dyck, H., Bullock, J., Coulon, A., Delgado, M., Gibbs, M., Lehouck, V., Matthysen, E., Mustin, K., Saastamoinen, M., Schtickzelle, N., Stevens, V., Vandewoestijne, S., Baguette, M., Barton, K., Benton, T., Chaput-Bardy, A., Clobert, J., Dytham, C., … & Travis, J. (2012). Costs of dispersal. Biological Reviews, 87(2), 290-312. https://doi.org/10.1111/j.1469-185X.2011.00201.x DOI: https://doi.org/10.1111/j.1469-185X.2011.00201.x
Boria, R., Olson, L., Goodman, S., & Anderson, R. (2014). Spatial filtering to reduce sampling bias can improve the performance of ecological niche models. Ecological Modelling, 275, 73-77. https://doi.org/10.1016/j.ecolmodel.2013.12.012 DOI: https://doi.org/10.1016/j.ecolmodel.2013.12.012
Buckland, S., & Elston, D. (1993). Empirical models for the spatial distribution of wildlife. Journal of Applied Ecology, 478-495. https://doi.org/10.2307/2404188 DOI: https://doi.org/10.2307/2404188
Comisión Nacional para el Conocimiento y Uso de la Biodiversidad (CONABIO) (2022). Sistema Nacional de Información sobre Biodiversidad. https://www.snib.mx/ejemplares/descarga/
Dirección General de Repositorios Universitarios. (2022). Portal de Datos Abiertos UNAM. https://datosabiertos.unam.mx/biodiversidad/
Elith, J., Phillips, S., Hastie, T., Dudík, M., Chee, Y., & Yates, C. (2011). A statistical explanation of MaxEnt for ecologists. Diversity and distributions, 17(1), 43-57. https://doi.org/10.1111/j.1472-4642.2010.00725.x DOI: https://doi.org/10.1111/j.1472-4642.2010.00725.x
Feng, X., Park, D., Walker, C., Peterson, A., Merow, C., & Papeş, M. (2019). A checklist for maximizing reproducibility of ecological niche models. Nature Ecology & Evolution, 3(10), 1382-1395. https://doi.org/10.1038/s41559-019-0972-5 DOI: https://doi.org/10.1038/s41559-019-0972-5
Fernández-Eguiarte, A., Zavala-Hidalgo, J., & Romero-Centeno, R. (2012). Atlas climático digital de México (versión 2.0). Centro de Ciencias de la Atmósfera, Universidad Nacional Autónoma de México y Servicio Meteorológico Nacional, Comisión Nacional del Agua.
Fielding, A., & Bell, J. (1997). A review of methods for the assessment of prediction errors in conservation presence/absence models. Environmental Conservation, 24(1), 38-49. https://doi.org/10.1017/S0376892997000088 DOI: https://doi.org/10.1017/S0376892997000088
Forbes, A. (1995). Classification-algorithm evaluation: Five performance measures based on confusion matrices. Journal of Clinical Monitoring, 11(3), 189-206. https://doi.org/10.1007/BF01617722 DOI: https://doi.org/10.1007/BF01617722
García-Mendoza, A., & Meave, J. (2012). Diversidad florística de O-axaca: de musgos a angiospermas (colecciones y lista de especies). Instituto de Biología Universidad Nacional Autónoma de México.
García, E. (2004). Modificaciones al sistema de clasificación climática de Köpen. UNAM.
Global Biodiversity Information Facility (GBIF) (2022). Datos de ocurrencias de las especies. https://www.gbif.org/occurrence/search?occurrence_status=present&q=
Hao, T., Elith, J., Lahoz‐Monfort, J., & Guillera‐Arroita, G. (2020). Testing whether ensemble modelling is advantageous for maximising predictive performance of species distribution models. Ecography, 43(4), 549-558. https://doi.org/10.1111/ecog.04890 DOI: https://doi.org/10.1111/ecog.04890
Hernndez, P., Graham, C., Master, L., & Albert, D. (2006). The effect of sample size and species characteristics on performance of different species distribution modeling methods. Ecography, 29(5), 773-785. https://doi.org/10.1111/j.0906-7590.2006.04700.x DOI: https://doi.org/10.1111/j.0906-7590.2006.04700.x
Instituto Nacional de Estadística y Geografía (2013). Conjunto de datos de Perfiles de suelos. Escala 1:250 000. Serie II (Continuo Nacional). https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=702825266707
Inventario Nacional Forestal y de Suelos (INFyS) (2022). Datos del inventario. https://snmf.cnf.gob.mx/datos-del-inventario/
Lee‐Yaw, J., McCune, J., Pironon, S., & Sheth, S. (2022). Species distribution models rarely predict the biology of real populations. Ecography, 2022(6), e05877. https://doi.org/10.1111/ecog.05877 DOI: https://doi.org/10.1111/ecog.05877
Liu, C., Berry, P., Dawson, T., & Pearson, R. (2005). Selecting thresholds of occurrence in the prediction of species distributions. Ecography, 28(3), 385-393. https://doi.org/10.1111/j.0906-7590.2005.03957.x DOI: https://doi.org/10.1111/j.0906-7590.2005.03957.x
Martínez-Meyer, E., Peterson, A., Servín, J., & Kiff, L. (2006). Ecological niche modelling and prioritizing areas for species reintroductions. Oryx, 40(4), 411-418. https://doi.org/10.1017/S0030605306001360 DOI: https://doi.org/10.1017/S0030605306001360
Meineri, E., Skarpaas, O., & Vandvik, V. (2012). Modeling alpine plant distributions at the landscape scale: Do biotic interactions matter? Ecological Modelling, 231, 1-10. https://doi.org/10.1016/j.ecolmodel.2012.01.021 DOI: https://doi.org/10.1016/j.ecolmodel.2012.01.021
Merow, C., Smith, M., Edwards, T., Guisan, A., McMahon, S., Normand, S., Thuiller, W., Wüest, R., Niklaus, E., & Elith, J. (2014). What do we gain from simplicity versus complexity in species distribution models? Ecography, 37(12), 1267-1281. https://doi.org/10.1111/ecog.00845 DOI: https://doi.org/10.1111/ecog.00845
Mitchell, P., Monk, J., & Laurenson, L. (2017). Sensitivity of fine‐scale species distribution models to locational uncertainty in occurrence data across multiple sample sizes. Methods in Ecology and Evolution, 8(1), 12-21. https://doi.org/10.1111/2041-210X.12645 DOI: https://doi.org/10.1111/2041-210X.12645
Mouton, A., De Baets, B., & Goethals, P. (2010). Ecological relevance of performance criteria for species distribution models. Ecological Modelling, 221(16), 1995-2002. https://doi.org/10.1016/j.ecolmodel.2010.04.017 DOI: https://doi.org/10.1016/j.ecolmodel.2010.04.017
Nogués‐Bravo, D. (2009). Predicting the past distribution of species climatic niches. Global Ecology and Biogeography, 18(5), 521-531. https://doi.org/10.1111/j.1466-8238.2009.00476.x DOI: https://doi.org/10.1111/j.1466-8238.2009.00476.x
Padalia, H., Srivastava, V., & Kushwaha, S. (2014). Modeling potential invasion range of alien invasive species, Hyptis suaveolens (L.) Poit. in India: Comparison of MaxEnt and GARP. Ecological Informatics, 22, 36-43. https://doi.org/10.1016/j.ecoinf.2014.04.002 DOI: https://doi.org/10.1016/j.ecoinf.2014.04.002
Pearson, R., Raxworthy, C., Nakamura, M., & Peterson, A. (2007). Predicting species distributions from small numbers of occurrence records: A test case using cryptic geckos in Madagascar. Journal of Biogeography, 34(1), 102-117. https://doi.org/10.1111/j.1365-2699.2006.01594.x DOI: https://doi.org/10.1111/j.1365-2699.2006.01594.x
Peterson, A. (2001). Predicting species' geographic distributions based on ecological niche modeling. The Condor, 103(3), 599-605. https://doi.org/10.1093/condor/103.3.599 DOI: https://doi.org/10.1093/condor/103.3.599
Peterson, A. (2003). Predicting the geography of species’ invasions via ecological niche modeling. The Quarterly Review of Biology, 78(4), 419-433. https://doi.org/10.1086/378926 DOI: https://doi.org/10.1086/378926
Peterson, A. Ortega-Huerta, M., Bartley, J., Sánchez-Cordero, V., Soberón, J., Buddemeier, R., & Stockwell, D. (2002). Future projections for Mexican faunas under global climate change scenarios. Nature, 416(6881), 626-629. https://doi.org/10.1038/416626a DOI: https://doi.org/10.1038/416626a
Peterson, A., Sánchez-Cordero, V., Beard, C., & Ramsey, J. (2002). Ecologic niche modeling and potential reservoirs for Chagas disease, Mexico. Emerging Infectious Diseases, 8(7), 662. https://doi.org/10.3201/eid0807.010454 DOI: https://doi.org/10.3201/eid0807.010454
Phillips, S., Anderson, R., & Schapire, R. (2006). Maximum entropy modeling of species geographic distributions. Ecological Modelling, 190(3-4), 231-259. https://doi.org/10.1016/j.ecolmodel.2005.03.026 DOI: https://doi.org/10.1016/j.ecolmodel.2005.03.026
Saupe, E., Barve, V., Myers, C., Soberón, J., Barve, N., Hensz, C., Peterson, A., Owen, H., & Lira-Noriega, A. (2012). Variation in niche and distribution model performance: The need for a priori assessment of key causal factors. Ecological Modelling, 237, 11-22. https://doi.org/10.1016/j.ecolmodel.2012.04.001 DOI: https://doi.org/10.1016/j.ecolmodel.2012.04.001
Shabani, F., Kumar, L., & Ahmadi, M. (2016). A comparison of absolute performance of different correlative and mechanistic species distribution models in an independent area. Ecology and Evolution, 6(16), 5973-5986. https://doi.org/10.1002/ece3.2332 DOI: https://doi.org/10.1002/ece3.2332
Simmonds, E., Jarvis, S., Henrys, P., Isaac, N., & O'Hara, R. (2020). Is more data always better? A simulation study of benefits and limitations of integrated distribution models. Ecography, 43(10), 1413-1422. https://doi.org/10.1111/ecog.05146 DOI: https://doi.org/10.1111/ecog.05146
Smith, R., Smith, T., & Román, E. (2007). Ecología. Pearson Educación.
Smith, A., & Santos, M. (2020). Testing the ability of species distribution models to infer variable importance. Ecography, 43(12), 1801-1813. https://doi.org/10.1111/ecog.05317 DOI: https://doi.org/10.1111/ecog.05317
Soberón, J., & Peterson, A. (2005). Interpretation of models of fundamental ecological niches and species’ distributional areas. Biodiversity Informatics, 2, 1-10. https://doi.org/10.17161/bi.v2i0.4 DOI: https://doi.org/10.17161/bi.v2i0.4
Soberón, J. (2007). Grinnellian and Eltonian niches and geographic distributions of species. Ecology letters, 10(12), 1115-1123. https://doi.org/10.1111/j.1461-0248.2007.01107.x DOI: https://doi.org/10.1111/j.1461-0248.2007.01107.x
Soberón, J. (2010). Niche and area of distribution modeling: a population ecology perspective. Ecography, 33(1), 159-167. https://doi.org/10.1111/j.1600-0587.2009.06074.x DOI: https://doi.org/10.1111/j.1600-0587.2009.06074.x
Stankowski, P., & Parker, W. (2011). Future distribution modelling: A stitch in time is not enough. Ecological Modelling, 222(3), 567-572. https://doi.org/10.1016/j.ecolmodel.2010.10.018 DOI: https://doi.org/10.1016/j.ecolmodel.2010.10.018
Stanton-Geddes, J., Tiffin, P., & Shaw, R. (2012). Role of climate and competitors in limiting fitness across range edges of an annual plant. Ecology, 93(7), 1604-1613. https://doi.org/10.1890/11-1701.1 DOI: https://doi.org/10.1890/11-1701.1
Trejo, I. (2004). Clima. En A. García-Mendoza, M. Ordóñez & M. Briones-Salas (eds.). Biodiversidad de Oaxaca (Pp. 67-85). UNAM, Fondo Oaxaqueño para la Conservación de la Naturaleza, World Wildlife Fund.
Wisz, M., Hijmans, R., Li, J., Peterson, A., Graham, C., Guisan, A., & NCEAS Predicting Species Distributions Working Group (2008). Effects of sample size on the performance of species distribution models. Diversity and Distributions, 14(5), 763-773. https://doi.org/10.1111/j.1472-4642.2008.00482.x DOI: https://doi.org/10.1111/j.1472-4642.2008.00482.x
WorldClim. (2022). Variables bioclimáticas. https://www.worldclim.org/data/bioclim.html
Zaniewski, A., Lehmann, A., & Overton, J. (2002). Predicting species spatial distributions using presence-only data: A case study of native New Zealand ferns. Ecological Modelling, 157(2-3), 261-280. https://doi.org/10.1016/S0304-3800(02)00199-0 DOI: https://doi.org/10.1016/S0304-3800(02)00199-0
Zurell, D., Franklin, J., König, C., Bouchet, P., Dormann, C., Elith, J., Fandos, G., Feng, X., Guillera-Arroita, G., Guisan, A., Lahoz-Monfort, J., Leitão, P., Park, D., Peterson, A., Rapacciuolo, G., Schmatz, D., Schröder, B., Serra-Diaz, J., Thuiller, W., … & Merow, C. (2020). A standard protocol for reporting species distribution models. Ecography, 43(9), 1261-1277. https://doi.org/10.1111/ecog.04960 DOI: https://doi.org/10.1111/ecog.04960
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 14 de mayo de 2022; Aceptado: 28 de septiembre de 2022
Resumen
El objetivo de este estudio fue aplicar diferentes tipos de datos biológicos y climáticos en el modelado de la distribución de cinco especies arbóreas en México (Pinus ayacahuite, Pinus montezumae, Pinus oocarpa, Quercus calophylla y Quercus uxoris). Para el modelado se utilizaron dos tipos de capas climáticas (tipos de clima y variables bioclimáticas) y tres tipos de datos biológicos de colecta (datos de solo presencia, datos de abundancia, y datos de presencia/ausencia). Los resultados muestran que no hay un tipo de datos biológicos y climáticos que se ajuste a todas las especies. Este trabajo evidencia que el uso de un solo tipo de datos puede derivar en subestimación o sobrestimación en las áreas potenciales de distribución.
Palabras clave:
altitud, clima, encinos, pinos, precipitación, temperatura..Abstract
The objective of this study was to apply different types of biological and climatic data in the distribution modeling of tree species in Mexico (Pinus ayacahuite, Pinus montezumae, Pinus oocarpa, Quercus calophylla, and Quercus uxoris). Two types of climate layers (climate types and bioclimatic variables) and three types of biological collection data (presence only data, abundance data, and presence/absence data) were used for modeling. The results show that there is no one type of biological and climatic data that fits all species. This study evidences that the use of a single type of data may result in underestimation or overestimation in potential distribution areas.
Keywords:
altitude, climate, oaks, pines, precipitation, temperature..INTRODUCCIÓN
La distribución geográfica de una especie está determinada por tres grupos de factores que operan a diferentes escalas e intensidades: factores abióticos o ambientales, habilidades de colonización u ocupación de áreas (accesibilidad) y factores bióticos como las interacciones ecológicas (Soberón, 2007, 2010; Soberón & Peterson, 2005). De los factores ambientales, el clima, la altitud y el tipo de suelo están entre los más importantes para determinar la distribución de especies arbóreas. Esto se debe principalmente a que las especies vegetales responden a gradientes ambientales (límites de tolerancia) y a recursos existentes (Austin, 2007; Barve et al., 2011; Ashcroft et al., 2012; Stanton-Geddes et al., 2012).
Los modelos de distribución de especies utilizan la asociación entre los factores ambientales y la presencia conocida de las especies en el área de interés, para la cual se definen las condiciones óptimas en que las especies pueden tener poblaciones viables. Estos métodos se basan en encontrar regiones en el espacio con condiciones ambientales que, en el sentido matemático, reúnan características similares a los sitios donde se observan las especies. De esta manera, es posible producir modelos predictivos con cierto grado de incertidumbre sobre los patrones de distribución de las especies (Peterson, 2001; Peterson, Ortega-Huerta, et al., 2002; Zaniewski et al., 2002; Phillips et al., 2006; Elith et al., 2011; Araújo & Peterson, 2012; Saupe et al., 2012).
El clima influye en casi cada aspecto del ecosistema, desde las respuestas fisiológicas de los organismos hasta la productividad y la circulación de los nutrientes. Particularmente en las especies vegetales, el clima regula el crecimiento y determina la presencia o ausencia de la especie, así como también los límites de distribución por la combinación de variables climáticas (Smith et al., 2007; Araújo & Peterson, 2012). Esta estrecha relación entre la vegetación y el clima está bien documentada, por lo que es posible obtener su distribución en función de variables climáticas (Austin, 2007; Stankowski & Parker, 2011; Saupe et al., 2012; Stanton-Geddes et al., 2012).
Existe una gran variedad de métodos para obtener la distribución de las especies (Merow et al., 2014). Cada método es diferente por diversas razones: por las técnicas que se utilizan para generar cada modelo, por los tipos de datos biológicos de colecta necesarios para el modelado (datos de presencia de las especies, datos de abundancia) o por el formato de las variables ambientales que se requieren. Un ejemplo de esto son los Modelos Lineales Generalizados o el programa MaxEnt, que son métodos de modelado que trabajan con variables tanto continuas como categóricas. Esto, en contraste con otros métodos que solo pueden utilizar variables continuas (Phillips et al., 2006; Elith et al., 2011).
La calidad, la cantidad y el tipo de datos utilizados para generar los modelos de distribución son fundamentales para obtener modelos con un buen desempeño (buenos modelos). En cuanto a la calidad y tipos de datos, actualmente existe una gran variedad de fuentes de información, por lo que es importante seleccionar cuidadosamente las variables ambientales y el tipo de modelado a utilizar, pues de eso dependerán los resultados que se obtengan (Feng et al., 2019; Hao et al., 2020; Simmonds et al., 2020; Zurell et al., 2020; Lee-Yaw et al., 2022). Otro factor que influye en el modelado es el número de registros de colecta. Se ha reportado que muestras pequeñas pueden afectar los análisis estadísticos, lo cual puede resultar en malos modelos. Es por esto que el tamaño de la muestra es una limitante, especialmente cuando se utilizan especies que cuentan con pocos datos (menos de 30 registros) (Hernández et al., 2006; Wisz et al., 2008).
Asumiendo que la base de los modelos de distribución son los datos biológicos de colecta y las variables ambientales que se utilizan para generarlos, el objetivo central de este estudio fue aplicar y comparar diferentes métodos que permitan generar modelos de distribución de especies a partir de diferentes tipos datos biológicos de colecta (datos de presencia, de abundancia y de ausencia), así como con diferentes capas climáticas (tipos de clima y variables bioclimáticas).
MATERIALES Y MÉTODOS
Área de estudio
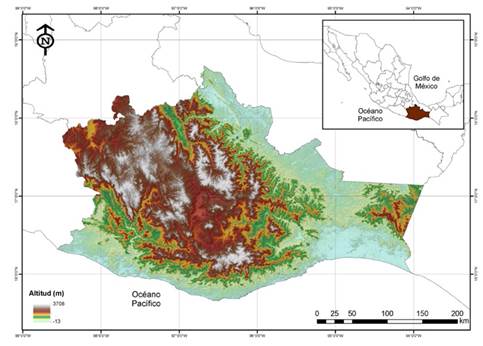
La zona de trabajo fue el estado de Oaxaca (Figura 1), que se encuentra ubicado al suroeste de México y tiene una extensión de 93 757.6 km2. Las coordenadas extremas del estado son 18° 40´ al norte y 15°39´ al sur de latitud norte; y 93° 52´ al este y 98° 33´ al oeste de longitud oeste. El estado de Oaxaca, además de su amplia extensión territorial, se caracteriza por su enorme diversidad cultural, geológica, climática y biológica. Esto está determinado por varios factores, entre los que se encuentran su posición geográfica y su relieve (Trejo, 2004). En cuanto a la diversidad biológica de plantas, para el estado se han reportado 9362 especies, lo cual representa más del 40 % de la flora vascular de México. De todas las especies reportadas, 17 pertenecen al género Pinus y 50 al género Quercus, lo que convierte a Oaxaca en uno de los estados con mayor diversidad de pinos y encinos, que prosperan prácticamente en todas las regiones del estado (García-Mendoza & Meave, 2012).
Figura 1: Ubicación del estado de Oaxaca, México. Modelo de elevación tomado de INEGI.
Selección de especies y datos biológicos de colecta
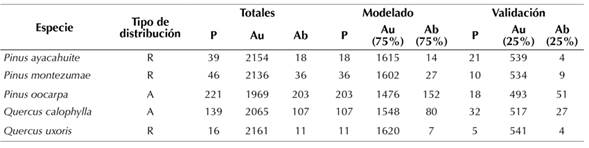
La selección de especies arbóreas pertenecientes a los géneros Pinus y Quercus se realizó de acuerdo con criterios de abundancia, de distribución y de la cantidad de registros de colecta en las diferentes fuentes de información disponibles. El tipo de distribución (amplia y restringida) se basó principalmente en la descripción de la especie en la literatura. El siguiente criterio fue la cantidad de registros de colecta en las diferentes bases de datos, de tal manera que se trabajó con especies que presentaran pocos registros (especies de distribución restringida) y especies con un mayor número de registros (especies de distribución amplia). Las especies de distribución restringida (pocos registros de presencia) utilizadas fueron Pinus ayacahuite Ehrenb. ex Schltdl. (39 registros de presencia), Pinus montezumae Lamb. (46 registros de presencia) y Quercus uxoris McVaugh (16 registros de presencia); mientras que las especies de amplia distribución (mayor número de registros) fueron Pinus oocarpa Scheide (221 registros de presencia) y Quercus calophylla Schltdl. & Cham (139 registros de presencia) (Tabla 1).
Tabla 1: Especies arbóreas seleccionadas. Se muestra el número de registros totales con datos de presencia, ausencia y abundancia en el Estado de Oaxaca, México, así como el número de registros utilizados en el proceso de modelado y validación (R, distribución restringida; A, distribución amplia; P, datos presencia; Au, datos de ausencia; Ab, datos de abundancia).
La información de los registros de presencia de las especies se obtuvo a partir de diferentes bases de datos (CONABIO, 2022; GBIF, 2022), del portal de datos abiertos de la Universidad Nacional Autónoma de México (Dirección General de Repositorios Universitarios, 2022) y de la información proveniente del Inventario Nacional Forestal y de Suelos 2004-2009 (INFyS, 2022) realizado por la Comisión Nacional Forestal (CONAFOR), que cuenta con 2172 sitios de muestreo para el estado de Oaxaca. Con esta información se obtuvieron datos de la presencia, ausencia y abundancia, así como la ubicación geográfica de cada registro.
Los datos obtenidos de CONABIO, GBIF, y la UNAM fueron utilizados como registros de presencia, mientras que la información proveniente del INFyS se utilizó como datos de presencia, abundancia y ausencia (Tabla 1). El presente trabajo consideró como datos de presencia a los sitios de muestreo donde la especie se encuentra registrada, los datos de abundancia corresponden al número de individuos de la misma especie presentes en cada sitio de muestreo, y los datos de ausencia son todos los sitios de muestreo donde la especie no tiene registro.
Insumos cartográficos
Para incorporar las variables ambientales en los modelos de distribución, se hizo una búsqueda de información cartográfica que representara la distribución espacial de los datos y que estuviera disponible. Adicionalmente se realizó cartografía (tipos de clima).
Cartografía recopilada
Variables bioclimáticas. Este conjunto de mapas toma en cuenta datos promedio que van de 1902 a 2011, con una resolución espacial de 926 metros, y provienen del Atlas Climático Digital de México (versión 2), elaborados por el Instituto de Ciencias de la Atmósfera y Cambio Climático de la UNAM (Fernández-Eguiarte et al., 2012). Dichas variables son: temperatura media anual (°C); rango de temperatura media diurna (media mensual de temperatura máxima-temperatura mínima); isotermalidad, índice de variabilidad de la temperatura (P2 / P7) × 100 (razón del rango diurno promedio con respecto al rango anual); estacionalidad de la temperatura (desviación estándar × 100); temperatura máxima del mes más cálido (°C); temperatura mínima del mes más frío (°C); rango de temperatura anual (°C) (temperatura máxima del mes más cálido-temperatura mínima del mes más frío); temperatura promedio del trimestre más lluvioso (°C); temperatura promedio del trimestre más seco (°C); temperatura promedio del trimestre más cálido (°C); temperatura promedio del trimestre más frío (°C); precipitación anual (mm); precipitación del mes más lluvioso (mm); precipitación del mes más seco (mm); estacionalidad de la precipitación (coeficiente de variación); precipitación del trimestre más lluvioso (mm); precipitación del trimestre más seco (mm); precipitación del trimestre más cálido (mm); y precipitación del trimestre más frío (mm).
Modelo digital de elevación. El mapa de altitud proviene del modelo digital de elevación del WorldClim (2022) y tiene una resolución espacial de 926 metros.
Tipos de suelo. Se utilizó el mapa de tipos de suelo de la serie II, elaborado por el Instituto Nacional de Estadística y Geografía (INEGI, 2013), a una escala de 1:250 000, el cual se transformó a formato raster por medio de un sistema de información geográfica a una resolución espacial de 926 metros.
Cartografía elaborada
Se elaboró el mapa de tipos de climas para el estado de Oaxaca, el cual se obtuvo a partir de los datos mensuales de temperatura media y de precipitación (Fernández-Eguiarte et al., 2012), y se realizó la clasificación climática de Köppen (García, 2004). La combinación de elementos climáticos como la temperatura, la cantidad de lluvia que se deposita en un área y sus patrones a lo largo del año permite caracterizar los tipos de clima (Trejo, 2004). Los datos se calcularon para cada píxel (926 m) y, para facilitar el análisis, se utilizó una reclasificación de los tipos climáticos que considera el tipo de clima, el régimen de lluvias y la humedad. De esa manera, se trabajó con 21 tipos de clima posibles para el estado de Oaxaca.
Modelado de la distribución
Para el modelado de la distribución de las especies, se utilizaron los datos de presencia, abundancia y ausencia de los sitios de muestro generados por el INFyS. Se utilizaron los registros de presencia provenientes de CONABIO, GBIF y el portal de datos abiertos de la UNAM para validar los modelos de distribución (datos independientes) (Tabla 1). Se realizó una depuración de los datos de CONABIO, GBIF y el portal de datos abiertos UNAM para eliminar los registros duplicados y los que estuvieran mal georreferenciados (Mitchell et al., 2017). Además, se elaboró una rejilla de 926 metros de resolución (tamaño de píxel de la cartografía utilizada), para que existiera un punto por pixel, evitando así la autocorrelación espacial, que puede afectar los modelos (Smith & Santos, 2020).
Se realizaron dos análisis que se diferencian por el tipo de variables utilizadas para el modelado. En los dos análisis se utilizó la misma capa de tipos de suelo y altitud; la diferencia radicó en las capas climáticas, pues se usó la capa de tipos de clima para el análisis 1 (A1) y las variables bioclimáticas para el análisis 2 (A2). Esto, para identificar qué tipo de variables climáticas se acoplan mejor en el modelado de la distribución de cada especie.
Para cada tipo de análisis, se realizaron tres procesos de modelado, que se diferencian por los tipos de registros de colecta (datos de presencia y ausencia, datos de abundancia, datos de solo presencia). A continuación, se describe cada uno de los procesos de modelado.
Datos de presencia y ausencia. Se elaboró un modelo lineal generalizado del tipo regresión logística binaria (ausencia, presencia) con función de enlace “logit” [y´ = In (y / (1−y))], cuyo inverso [p = (e y´ ) / (1 + e y ´)] da como resultado la probabilidad (p) de presencia de la especie. El valor e se refiere a la constante de Napier y es la base de los logaritmos naturales. Este valor es aproximadamente 2.718. En este tipo de modelado se elaboraron cien modelos lineales, para lo cual se utilizó el 100 % de los datos de presencia y un 75 % de los datos de ausencia, los cuales se seleccionaron aleatoriamente en cada ocasión. Al final de este proceso, se seleccionó el modelo con los valores más altos de devianza y cuyos coeficientes fueran significativos (p≤0.05). La devianza se refiere a la proporción de varianza que es explicada por cada modelo y puede obtener valores que van de 0 a 1, siendo un buen modelo aquel que presenta valores cercanos a 1. La devianza se obtiene con la siguiente fórmula: devianza = (devianza modelonulo - devianza residual) / devianza modelo nulo. Aquí, el modelo nulo se refiere a un modelo sin predictores. El modelo lineal seleccionado se aplicó en un sistema de información geográfica para obtener el mapa de probabilidades de presencia de cada especie. El mapa de presencia se generó a partir del corte de probabilidades, de tal manera que se consideraran áreas donde se obtuviera sólo el 10 % de omisión de puntos de modelado (Pearson et al., 2007; Anderson & González, 2011; Boria et al., 2014). El corte de probabilidades se realizó por medio un sistema de información geográfica.
Datos de abundancia. Se elaboró un modelo lineal generalizado de tipo Poisson con función de enlace “log” [y´ = log (y)], cuyo inverso [I = exp y' ] da como resultado el número de individuos (I) de la especie. En este caso, también se elaboraron 100 modelos lineales, donde se utilizó el 75 % de los datos de abundancia, seleccionados de manera aleatorios en cada ocasión. Se seleccionó la fórmula del modelo lineal con los valores más altos de devianza cuyos coeficientes fueran significativos. Posteriormente, se colocó la fórmula seleccionada en un sistema de información geográfica para obtener el mapa del número de individuos por píxel. Para fines comparativos entre los diferentes procesos de modelado, a partir del mapa de individuos obtenido se realizó un mapa de solo presencia con un sistema de información geográfica, considerando como áreas de presencia todos los sitios cuyos valores de abundancia fueran ≥1 y las áreas restantes como áreas de ausencia.
Datos de presencia. Se utilizaron el programa MaxEnt, versión 3.3.3 (Phillips et al., 2006), y el 100 % de los datos de presencia del INFyS. El mapa de presencia se generó a partir del corte de probabilidades, de tal manera que se consideraran áreas donde se obtuviera solo el 10 % de omisión de puntos de modelado. El corte de probabilidades se realizó por medio de un sistema de información geográfica, y la validación de los modelos a partir de datos de presencia se realizó con los datos de presencia provenientes de CONABIO, GBIF y la UNAM, con un 25 % de ausencias de los datos del INFyS.
Validación de los modelos
La evaluación del desempeño de los modelos se estimó por medio del cálculo de varios índices obtenidos a partir de una matriz de confusión (Tabla 2), donde (a) es el número de puntos de presencia de la especie que caen en el área que predice presencia en el marco del modelo obtenido; (b) es el número de puntos de ausencia que caen en el área que predice presencia (errores de comisión); (c) es el número de puntos de presencia que caen en el área que predice ausencia (errores de omisión); (d) es el número de puntos de ausencia que caen en el área que predice ausencia. Los índices calculados se describen a continuación:
Tabla 2: Matriz de confusión

Índice TSS, True Skill Statistic (Allouche et al., 2006; Mouton et al., 2010): con este índice se obtienen valores que van de -1 a 1, siendo los mejores modelos aquellos con puntuaciones más cercanas a 1. La fórmula para calcular este índice es: TSS = (ad) − (bc) / (a + c) (b + d).
Sensibilidad, Sn (Forbes, 1995; Liu et al., 2005; Mouton et al., 2010), se refiere a la proporción de puntos de presencia de la especie que caen en el área que predice presencia en el modelo obtenido. Los valores que se pueden llegar a obtener van de 0 a 1. Los mejores modelos son aquellos con valores cercanos a 1. La fórmula para calcularla se muestra a continuación: Sn = a / (a + c).
Especificidad, Sp (Forbes, 1995; Liu et al., 2005; Mouton et al., 2010), se refiere a la proporción de puntos de ausencia que caen en el área que predice ausencia en el modelo. Los valores van de 0 a 1, y los mejores modelos acercan su valor a 1. Cuya fórmula es: Sp = d / b + d.
Índice CCI, Correctly Classified Instances (Buckland & Elston, 1993; Fielding & Bell, 1997; Mouton et al., 2010): se refiere a la proporción de puntos de presencia y ausencia que caen en las áreas esperadas de presencia y ausencia que predice el modelo. Los valores también van de 0 a 1, con el mejor cercano a 1. La fórmula para calcular dicho índice se muestra a continuación: CCI = (a + d) / n.
Adicionalmente, se calculó el coeficiente r para evaluar el desempeño de los modelos elaborados a partir de datos de abundancia. Este coeficiente se obtiene al comparar los valores de abundancia obtenidos por los modelos y los valores de abundancia de los puntos que se utilizan para validar. El coeficiente de correlación (r) es una medida de asociación entre dos variables, y los valores que se obtienen van de -1 a 1, donde los mejores modelos son aquellos con valores cercanos a 1.
Todos los índices utilizados tienen la característica de que los modelos con mejor desempeño son aquellos con valores cercanos a 1. Por esta razón, en aras de comparar y seleccionar el mejor modelo por especie, se calculó el promedio de todos los índices calculados y se seleccionó el valor promedio más alto.
RESULTADOS
Pinus ayacahuite
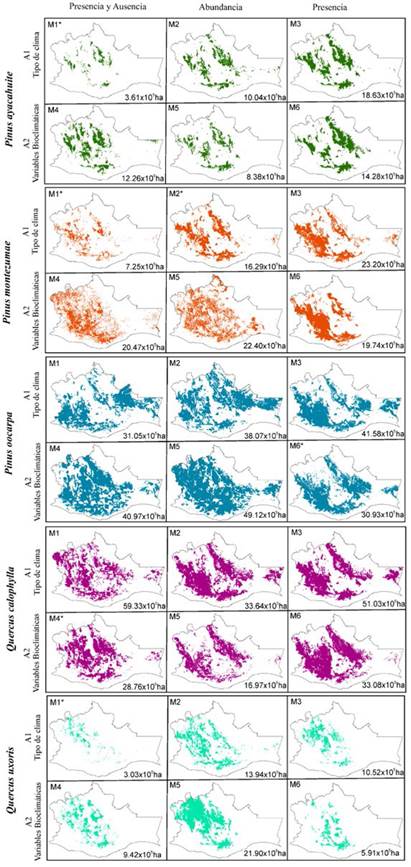
De acuerdo con los valores de los índices y coeficientes obtenidos (Tabla 3), todos los modelos para esta especie tienen un buen desempeño (valores cercanos a 1). El modelo elaborado a partir de datos de presencia y ausencia bajo el A1 (modelo 1, M1) resultó ser el mejor por sus valores más altos de los índices TSS (0.80), CCI (0.94), sensibilidad (0.85) y especificidad (0.95), registrando un valor promedio de 0.89. Para los modelos realizados con datos de abundancia, el valor más alto de coeficiente de correlación (r = 0.81) se obtuvo con el A1 (tipo de clima).
Tabla 3: Valores de los coeficientes e índices calculados según cada modelo de distribución potencial. Se indica con un asterisco (*) el mejor modelo (mejor desempeño) por especie (P/A, datos de presencia y ausencia; A, datos de abundancia; P, datos de presencia).

Como se observa en los mapas de la Figura 2, todos los modelos obtuvieron superficies potenciales de distribución muy diferentes desde la perspectiva espacial y cuantitativa. Para esta especie, los modelos elaborados a partir de datos de presencia son los que registraron una superficie mayor: modelo 3 (M3) 18.63 × 105 ha; modelo 6 (M6), 14.28 × 105 ha). Esto, en comparación con las superficies obtenidas por los demás modelos, donde el modelo elaborado a partir de datos de presencia-ausencia bajo el A1 (tipo de clima, M1) fue el que presentó la menor superficie potencial en el estado (3.61 × 105 ha).
Figura 2: Áreas de distribución potencial de Pinus ayacahuite (verde), Pinus montezumae (naranja), Pinus oocarpa (azul), Quercus calophylla (rosa) y Quercus uxoris (turquesa). Se muestra la superficie potencial en hectáreas (ha) y el modelo con mejor desempeño por especie (*).
Pinus montezumae
Por los valores de los índices TSS (< 0) y sensibilidad (< 0.42) obtenidos para esta especie, todos los modelos mostraron un mal desempeño, pues registraron valores promedio menores a 0.47 (Tabla 3). Caso contrario ocurre con los valores del índice de especificidad, donde todos los modelos obtuvieron valores altos (> 0.68), lo que indica que hay poca sobrepredicción de las áreas de distribución (error de comisión), pero sí hay un sobreajuste de las mismas (error de omisión), dado que se obtuvieron valores de sensibilidad bajos. Para esta especie, dos modelos resultaron tener buen desempeño, el M1 (datos de presencia-ausencia) y el M2 (datos de abundancia), registrando un valor promedio de desempeño de 0.47. De los modelos elaborados a partir de datos de abundancia, el valor más alto de coeficiente de correlación (r = 0.79) se obtuvo con el A1.
Como se observa en la Figura 2, todos los modelos obtuvieron superficies potenciales de distribución contrastantes. Para esta especie, los modelos elaborados a partir de datos de presencia (A1, M3) y datos de abundancia (A2, M5) son los que presentaron una superficie potencial mayor, con 23.20 × 105 ha y 22.40 × 105 ha respectivamente. El modelo elaborado a partir de datos de presencia-ausencia bajo el A1 (M1) fue el que mostró la menor superficie potencial para el estado, con 7.25 × 105 ha. El otro modelo con buen desempeño M2 mostró más del doble de superficie (16.29 × 105 ha), a pesar de registrar el mismo valor promedio de desempeño.
Pinus oocarpa
De acuerdo con los valores de los índices y coeficientes obtenidos (Tabla 3), el modelo elaborado a partir de datos de presencia bajo el A2 (variables bioclimáticas, M6) resultó ser el mejor modelo para esta especie, pues fue el que obtuvo los valores más altos para todos los índices (TSS = 0.32, CCI = 0.60, Sn = 0.94, Sp = 0.60), registrando un valor de desempeño promedio de 0.61. Según los mapas de la Figura 2, el modelo elaborado a partir de datos de abundancia bajo el A2 (M5) fue el que presentó una superficie mayor en comparación con las superficies obtenidas por los demás modelos, con 49.12 × 105 ha, mientras que el modelo elaborado a partir de datos de presencia bajo el A2 (M6) fue el que mostró la menor superficie potencial para el estado con 30.93 × 105 ha.
Quercus calophylla
El modelo elaborado a partir de datos de presencia y ausencia bajo el A2 (M4) presentó un buen desempeño, al registrar los valores de los índices más altos (TSS = 0.39, CCI = 0.67, Sn = 0.71, Sp = 0.67), así como del valor promedio (0.62) (Tabla 3). De acuerdo con los mapas de la Figura 2, todos los modelos obtuvieron superficies potenciales de distribución muy contrastantes, siendo el modelo elaborado a partir de datos de abundancia bajo el A2 (M5) el que registró una superficie menor en comparación con las superficies obtenidas por los demás modelos, con 16.97 × 105 hectáreas. Por otro lado, el modelo elaborado a partir de datos de presencia y ausencia bajo el A1 (M1) fue el que obtuvo la mayor superficie potencial para el estado, con 59.33 × 105 hectáreas.
Quercus uxoris
El modelo generado a partir de datos de presencia y ausencia bajo el A1 (tipo de clima, M1) presentó un buen desempeño, al registrar los valores más altos de los índices (TSS = 0.72, CCI = 0.97, Sn = 0.75, Sp = 0.97), así como del valor promedio 0.85 (Tabla 3). Como se observa en los mapas de la Figura 2, todos los modelos obtuvieron superficies potenciales de distribución muy disímiles desde una perspectiva espacial. Para esta especie, el modelo elaborado a partir de datos de abundancia bajo el A2 (M5) fue el que registró una superficie mayor (21.9 × 105 ha), mientras que el modelo elaborado a partir de datos de presencia y ausencia bajo el A1 (M1) fue el que mostró la menor superficie potencial para el estado (3.03 × 105 hectáreas).
Comparación entre especies
Las especies de distribución restringida (menor número de registros) como P. ayacahuite (39 registros) y Q. uxoris (16 registros) mostraron valores altos de todos los índices calculados (> 0.72) y superficies potenciales menores que 4 × 105 ha. Entretanto, las especies de amplia distribución (mayor número de registros) como P. oocarpa (221 registros) y Q. calophylla (139 registros) obtuvieron valores bajos de desempeño (menores a 0.62) en todos los índices y superficies potenciales mayores que 28 × 105 ha. P. montezumae, a pesar de ser una especie con pocos registros de colecta (46 registros), presentó valores bajos de desempeño (0.47) y superficies entre 7 × 105 ha y 16 × 105 ha.
DISCUSIÓN
En este estudio se utilizaron variables climáticas de dos formas: las primeras son conocidas como variables bioclimáticas (Fernández-Eguiarte et al., 2012) y las segundas están condensadas en una clasificación climática, en este caso la de Köppen (García, 2004). Esto permite analizar dos formas de interpretar la interacción entre las variables que conforman las condiciones climáticas de un sitio. Las diferencias entre la capa de tipos de climas y las variables bioclimáticas toman su importancia en el modelado de la distribución de las especies, la cual radica en la forma de abordar el proceso. Por ejemplo, al utilizar una clasificación de tipos de clima, se trabaja bajo una perspectiva de interacción de los elementos climáticos en un lugar, pues en una sola variable (tipo climático) se consideran principalmente la temperatura, la marcha de la temperatura, la cantidad de lluvia que se deposita y su distribución a lo largo del año. En cambio, en las variables bioclimáticas se consideran los elementos climáticos por separado. La forma en que se integran las variables ambientales se vuelve relevante cuando estas se modelan con métodos como los Modelos Lineales Generalizados o el programa MaxEnt, pues estos no consideran la interacción de las variables. Este último, puede llegar a tomar en cuenta el aporte de cada variable en el modelo, pero no la interacción entre ellas (Stankowski & Parker, 2011).
De la información climática disponible para México, la del Atlas Climático Digital de México (versión 2) (Fernández-Eguiarte et al., 2012) es una buena alternativa, pues los datos se generaron a partir de información de estaciones meteorológicas de México entre 1902 y 2011. Esta información se encuentra a una resolución de aproximadamente 1 km y es la mejor representación espacial disponible. Es necesario reconocer que el mayor problema proviene de la falta de estaciones meteorológicas en puntos críticos en México, lo cual limita la generación de cartografía más detallada.
Generar modelos de distribución brinda una gran gama de opciones para resolver la falta de información biológica, pues existen diversas aplicaciones para los modelos de distribución de especies. El ejemplo más obvio es el de determinar la distribución potencial. No obstante, estos modelos también se pueden aplicar en otros ámbitos, como lo son la protección y la conservación de las especies, la reintroducción de especies amenazadas, el cálculo de riesgo debido a especies invasoras o la distribución de enfermedades infecciosas (Peterson, Sánchez-Cordero et al., 2002; Peterson, 2003; Araújo et al., 2005; Martinez-Meyer et al., 2006; Nogués-Bravo, 2009).
Aun cuando aparentemente existe una extensa gama de fuentes de información relacionadas con la distribución de especies, es importante mencionar que se necesita una minuciosa labor de revisión de los datos para evitar errores. Una primera revisión de los datos incluye la nomenclatura, la redundancia de datos y la georreferenciación. En este último punto cabe resaltar la precisión en la ubicación del individuo colectado y el sistema de coordenadas utilizado para su ubicación son particularmente relevantes (e.g., Datum). La carencia de esta información y los errores incluidos en las bases de datos constituyen una fuente de error indirecta inmersa en los modelos. Si bien estos no se miden directamente, están inmersos en las incertidumbres de cada modelo.
Otro problema es la información disponible en las bases de datos sobre la ubicación de las especies y del tipo de información que existe (generalmente se cuenta con datos de presencia, no de abundancia). Realizar estudios como este con pocos datos cuantitativos de especies limita el análisis y, por ende, las conclusiones que arrojen dichas observaciones. Como se registró en este estudio, no todos los modelos generados a partir de los datos de abundancia resultaron tener un buen desempeño. Una de las razones a las que se puede atribuir esto es la falta de información cuantitativa disponible de las especies, e.g., especies como P. ayacahuite o Q. uxoris, que solo tuvieron 18 y 11 datos de abundancia respectivamente.
Además de las condiciones físico-ambientales, existen otros factores que limitan la distribución. Ejemplo de esto son los factores biológicos como las interacciones bióticas, la capacidad de dispersión, la longevidad de las especies y otras características de su ciclo de vida (Stankowski & Parker, 2011; Ashcroft et al., 2012; Meineri et al., 2012; Stanton-Geddes et al., 2012). Pocas veces se tiene información detallada de las especies, sobre todo de sus requerimientos ambientales en los diferentes procesos ecológicos, pues cada una tiene preferencias ambientales únicas y estrategias ecológicas particulares (Bewley & Krochko, 1982; Bonte et al., 2012),
En este trabajo es notable que, de acuerdo con los tipos de datos empleados, para cada especie resultó mejor aplicar un tipo de modelado distinto. Esto concuerda con estudios previos, donde se ha reportado que no hay un único método de estimación de la distribución que sea el mejor para todas las especies (Shabani et al., 2016), pues cada especie tiende a presentar mejores modelos con ciertas técnicas de modelado (Padalia et al., 2014). De ser posible, y si se cuenta con diferentes tipos de datos, es conveniente aplicar diversas formas de modelado, sobre todo porque se pueden obtener diferentes resultados con cada método (Hernández et al., 2006; Elith et al., 2011).
Como se observó en el presente trabajo, cada especie obtuvo modelos con mejor desempeño con diversos métodos de modelado, considerando los distintos tipos de datos biológicos de colecta, así como las diferentes capas climáticas. Los estudios de distribución de las especies deberían contemplar diferentes fuentes de información para seleccionar los mejores modelos. Para ello, se deberían generar mayores insumos cartográficos y garantizar su disponibilidad, pues dicha información es fundamental para generar los modelos de distribución de las especies.
Se necesita un mayor esfuerzo de muestreo en campo para conocer mejor los recursos con los que se cuenta y conformar bases de datos sólidas que tengan datos suficientes y de calidad. Contar con una localización con mayor precisión de las especies disminuiría la incertidumbre en este tipo de estudios (Mitchell et al., 2017). Lo anterior es muy importante, pues el número de registros para algunas especies es reducido, como es el caso de Q. uxoris (16 registros).
CONCLUSIONES
Como se observó, existen diversos factores que afectan el modelado de la distribución de las especies, tales como el tipo de datos de colecta de las especies y el tipo de capas ambientales con que se modele. Además, no para todas las especies se modela mejor con el mismo tipo de datos (presencia y ausencia, abundancia o presencia).
En cuanto al tipo de variables ambientales, en las especies de distribución restringida estudiadas (P. ayacahuite, P. montezumae y Q. uxoris), los modelos con mejor desempeño fueron aquellos generados con la capa de tipos de clima (análisis 1, A1), mientras que las especies de amplia distribución (P. oocarpa y Q. calophylla) se modelaron mejor con las variables bioclimáticas (análisis 2, A2).
En cuanto a los tipos de datos biológicos de colecta, para especies como P. ayacahuite, P. montezumae, Q. calophylla y Q. uxoris, los mejores modelos fueron elaborados con datos de presencia y ausencia (P/A). Solo una especie obtuvo el mejor modelo a partir de datos de solo presencia, (P. oocarpa).
Lo relevante de este trabajo es hacer evidente que, ya sea por las características inherentes a las especies, por su tipo de distribución o por las propiedades de los datos que se tienen disponibles, no todos los modelos resultan ser los más adecuados para obtener un mejor resultado, por lo que el uso de un solo modelo para diversas especies puede ofrecer subestimación o sobrestimación en las áreas potenciales de distribución.
Acknowledgements
AGRADECIMIENTOS
Erick Gutiérrez (EG) agradece al Posgrado en Ciencias Biológicas de la Universidad Nacional Autónoma de México. EG agradece al Consejo Nacional de Ciencia y Tecnología (Conacyt) por la beca escolar para sus estudios de maestría.
REFERENCIAS
Licencia
Derechos de autor 2023 Colombia forestal

Esta obra está bajo una licencia internacional Creative Commons Atribución-CompartirIgual 4.0.
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).