Metodología para la planeación logística de vías forestales para la cosecha de plantaciones de Eucalyptus globulus Labill. utilizando herramientas de optimización

Leal, R.O., & López, C.A. (2011). Metodología para la planificación logistica de vias forestales para la cosecha de plantaciones de Eucalyptus globulus Labill. utilizando herramientas de optimizaci�n. Colombia Forestal, 14(1), 51-67.

METODOLOGÍA PARA LA PLANEACIÓN LOGÍSTICA DE VÍAS FORESTALES PARA LA COSECHA DE PLANTACIONES DE Eucalyptus globulus Labill. UTILIZANDO HERRAMIENTAS DE OPTIMIZACIÓN

Methodology for logistic planning of forest roads for harvesting Eucalyptus globulus Labill. using optimization tools

Metodologia para o planejamento logístico das vias florestais para a colheita de plantações de Eucalyptus globulus Labill. utilizando ferramentas de optimização

Robert Orlando Leal¹ & César Amílcar López²

¹Ingeniería Forestal de la Universidad Distrital Francisco José de Caldas. rolealp@udistrital.edu.co. Autor para correspondencia.
²Maestría en Ingeniería Industrial de la Universidad Distrital Francisco José de Caldas. clopezb@udistrital.edu.co.

Recepción: Mayo 12 de 2010/Aprobación: Junio 30 de 2010

RESUMEN

Mediante un modelo de red no capacitada y no dirigida, se plantea la metodología para el diseño preliminar de vías forestales de segundo orden en la extracción de productos obtenidos de plantaciones de Eucalyptus globulus por el sistema de cables aéreos, de forma que se minimicen los costos de construcción de la red vial. La metodología planteada tiene en cuenta las condiciones topográficas y los costos de construcción de vía correlacionados con la pendiente del terreno. Para la solución del problema, se utilizó el algoritmo de Dijstrak, que define la ruta más económica que comunica entre sí los patios de apilado preestablecidos y el algoritmo de Kruskal para la obtención del árbol de mínima expansión. Finalmente, se realizó la conexión de la red establecida con una carretera pública para la evacuación de la madera a los centros de consumo. Para el desarrollo de los algoritmos planteados, se diseñó una aplicación en el programa Matlab, que facilitó el manejo cartográfico con los algoritmos propuestos.

Palabras clave: aprovechamiento forestal, modelo de optimización, vías forestales.

ABSTRACT

Using an uncapacitated and nondirected network model, we propose a methodology for the preliminary design of second order forests roads to extract products from Eucalyptus globulus plantations using an aerial cable system to minimize road network construction costs. The model takes into account topographical conditions and road construction costs related to the terrain slope. In order to solve the problem the Dijstrak algorithm was used, in which the minimum cost of the shortest paths that connect all the stockyards are defined. In addition, the Kruskal algorithm was used to obtain the minimum spanning tree. Finally, the network was connected to an open road for the timber to be taken to consumption centers. In order to develop the algorithms mentioned above, an application on Matlab was designed, which gave an easier handling of the cartography data obtained from these algorithms.

Key words: forest harvesting, optimization model, forest roads

RESUMO

Mediante um modelo de rede não capacitada e não dirigida, se estabeleceu a metodología para o desenho preliminar de vías florestais de segunda ordem na extração de produtos obtidos de plantações de Eucalyptus globulus pelo sistema de cabos aéreos, de forma que se minimizem os custos de construção da rede vial. A metodología planteada teve em conta as condições topográficas e os custos de construção da via correlacionada com a declividade do terreno. Para a solução do problema, se utilizou o algarítimo de Dijstrak, que define o caminho mais económico que se comunica com so patios de apilado preestabelecidos e o algarítmo de Kruskal para a obtenção da árvore de mínima expansão. Finalmente, se realizou a conexão da rede estabelecida com uma estrada pública para o transporte da madeira aos centros de consumo. Para o desenvolvimento dos algarítmos propostos, se desenhou uma aplicação do programa Matlab, que facilitou a manipulação cartográfica com os algorítmos propostos.

Palavras chave: Aproveitamento florestal, modelo de optimização, vias florestais.

INTRODUCCIÓN

El aprovechamiento forestal o cosecha forestal es un conjunto de técnicas orientadas a suministrar materia prima a diferentes industrias como: la industria de aserrado, la industria de tableros, la industria de papel y la industria de postes, de forma que este suministro cumpla con la calidad exigida, con los mínimos costos, en los momentos establecidos que respete las condiciones ambientales (Vignote & Jiménez, 1996).

Actualmente, el aprovechamiento de plantaciones de Eucalyptus globulus Labill. en el departamento de Cundinamarca se ha venido incrementando, debido a la demanda de madera para pulpa que la empresa Smurfit Kappa Cartón de Colombia requiere para alimentar la planta productora de papel ubicada en Yumbo (Valle del Cauca). Esta especie es importante por la fibra corta de su madera, ideal para la elaboración de papel blanco y fino.

Puesto que la mayoría de las plantaciones que se negocian actualmente en Cundinamarca fueron sembradas sin un objetivo específico, se presenta una gran heterogeneidad en los aspectos silvícolas –por ejemplo, procedencia genética, densidad de siembra, superficies plantadas, manejos silviculturales– y en factores abióticos –por ejemplo, pendientes, calidad de suelos, infl uencia antrópica, cercanía a infraestructuras viales, entre otras–. Esta variedad de condiciones incide en la calidad de la masa arbórea y se expresa en la amplitud de tamaños de diámetros, alturas y volúmenes de madera por superficie en plantaciones coetáneas; esto dificulta el cálculo del costo de cosecha y, por tanto, el valor de esta (Pinzón & Rubio 2006).

Por otra parte, las experiencias de las empresas de aprovechamiento forestal en Cundinamarca no están documentadas, por no ser este un proceso que se establezca como indispensable por ellas; por tanto, no se puede realizar un análisis confiable de la eficiencia y la eficacia de las operaciones que se llevan a cabo. De acuerdo con diagnósticos que se han realizado y como conclusiones de trabajos relacionados con las cadenas de comercialización de la madera llevados a cabo en Cundinamarca y Boyacá, se resaltan algunos problemas como la falta de planificación y el control de las operaciones de cosecha (diseño y construcción de vías, corta, desembosque y transporte), sumándose a la independencia entre las fases de aprovechamiento, sin una conexión que garantice la optimización de los recursos y la calidad de los productos (Quiroz 2002).

Además de las condiciones expuestas anteriormente, el hecho de que el mercado internacional presiona a las empresas de diferente índole a ser más competitivas incrementando su productividad y disminuyendo los costos de producción, se observa la necesidad de recurrir a herramientas que permitan abordar las complejas relaciones de producción del ámbito forestal, a fin de obtener alternativas que mejoren la productividad.

La adopción de técnicas de optimización para el manejo y ordenación de los bosques se inició a partir de la década de los años setenta, cuando se utilizaron en forma sistemática técnicas de programación matemática para auxiliar el análisis de los temas fundamentales del manejo forestal (Briceño 1993). Estas aplicaciones se han desarrollado, principalmente, en algunos países de zonas templadas (Norteamérica, Escandinavia), donde se han utilizado como herramientas típicas de cualquier problema de toma de decisiones y donde el manejo de los bosques es concebido como la aplicación de técnicas analíticas para elegir aquellas alternativas de manejo que mejor reflejen los objetivos organizativos (Leuschner 1990).

La utilización de herramientas de optimización no garantiza que se puedan resolver todas las preguntas que surgen en cuanto al manejo de los bosques, debido a la complejidad de las relaciones entre los factores de orden económico, ecológico y social que intervienen. Sin embargo, estos modelos presentan como resultados una serie de opciones que le facilitan al administrador del bosque la toma de decisiones para orientar el manejo de este (Stirn 1990).

El avance de nuevas técnicas y algoritmos en la investigación operativa ha sido aprovechado por algunos investigadores forestales en la aplicación y la propuesta de herramientas para el manejo y producción del bosque. Es así como con base en distintos enfoques se han formulado modelos matemáticos que permiten la solución satisfactoria de diferentes problemas que atañen al manejo de los recursos naturales. En el caso específico de cosecha forestal y caminos forestales, Diaz & Prieto (1999) establecen modelos lineales para la planificación forestal. En Wang (1994) y en Wang et al. (1998), se proponen modelos de simulación interactiva para evaluar tres métodos de cosecha y dos equipos de extracción de madera. La programación entera es utilizada por Karlson et al. (2004), en la planeación anual de cosecha; Dahlin & Fredriksoon (1995) establecen por algoritmos la mejor red vial para caminos de extracción; Twaddle & Murphy (1992) estudian los patrones de corta por medio de simulación en Pinus radiata para minimizar costos de transporte, según el producto que se va a cosechar. Más aún, procedimientos heurísticos fueron utilizados por Tan (1999), para la localización espacial de vías; Epstein et al. (2006) realizan una aproximación heurística combinatoria para resolver problemas de diseño de una red incapacitada, del tamaño real de ubicación de maquinaria y diseño de carreteras.

La investigación desarrollada en el presente trabajo está orientada a proponer una solución práctica a uno de los factores que inciden en mayor proporción en los costos de extracción de madera de plantaciones forestales como es el costo de las vías forestales. El tipo de vía, la ubicación y la longitud de esta son para el planificador de un aprovechamiento forestal un tema que defi ne en gran medida los costos que, finalmente, se cargarán a la unidad extraída de madera.

La propuesta desarrollada se orienta a plantaciones forestales de pequeñas superficies con no más de 100 ha y sin vías internas y de acceso; tiene como fi nalidad definir la red vial óptima para la recolección de madera dispuesta por sistemas de extracción ubicados en diferentes sitios. El modelo se basa en el estudio realizado por Epstein et al. (2006). Así, esta metodología permitirá evaluar mediante el algoritmo de Dijkstra todas las combinaciones posibles para el trazado de una red vial que comunique los diferentes patios de acopio de la forma más económica, cumpliendo con especificaciones técnicas de pendiente, para posteriormente determinar el árbol de mínima expansión de esta red por medio del algoritmo de Kruskal, definiendo así la red vial óptima para la extracción de la madera.

MATERIALES Y MÉTODOS

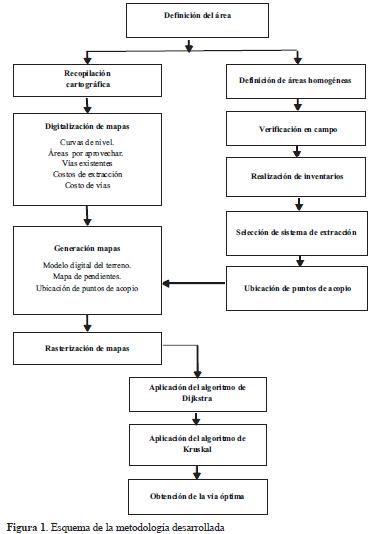
En el desarrollo de la metodología se defi nió una secuencia de actividades, las cuales permitieron establecer claramente los aspectos físicos y bióticos necesarios para el cálculo y trazado de vía óptima para la extracción de madera para pulpa en cualquier área que se requiera; la figura 1 muestra el esquema general de la metodología desarrollada.

DEFINICIÓN DEL ÁREA

Para la aplicación de la metodología propuesta, se realizó una prueba piloto en un área de plantaciones forestales de E. globulus, ubicada en el municipio de Facatativá en la Sabana de Bogotá, la cual se aprovechó para la obtención de pulpa. Se definió una zona de influencia directa, delimitada por el área de acción de las actividades que se relacionan con las operaciones de transformación primaria y transporte de la madera.

RECOLECCIÓN DE INFORMACIÓN BÁSICA

Recopilación cartográca

Se recopiló la cartografía disponible del área a escala 1:10.000, la cual sirvió de base para tomar información referente a curvas de nivel, vías existentes, drenajes y ubicación de infraestructuras. Esta información se analizó y se seleccionó para su procesamiento en las fases siguientes. También se recopilaron fotografías aéreas del área a escala 1:40.000 tomadas en el año 1999.

Denición de áreas homogéneas

Se realizó una interpretación visual de las fotografías aéreas para definir zonas que presentaban características fisionómicas homogéneas dentro de la plantación. Estas diferencias pueden ser consecuencia de distintos manejos silviculturales o bien a diferencia en la calidad de sitio.

Estas diferencias se expresan en la cantidad de madera que oferta cada superficie y que, finalmente, incide en el costo de extracción, dado que a mayor volumen de madera por superficie más económico será el costo de extracción de la unidad cosechada. La información generada se transfirió al mapa base.

Vericación de campo

En esta fase, se realizó la verifi cación cartográfica de las unidades boscosas definidas y diseño de un inventario forestal para la cuantificación maderable en cada una de las unidades homogéneas establecidas. Además, se definieron los corredores de extracción, basados en los requerimientos técnicos del sistema de cables aéreos (Tracto Koller), tales como pendiente mínima y máxima, disponibilidad de árboles mástiles y ubicación de puntos críticos, aspectos fundamentales para el cálculo de tensiones y carga máxima permisible de transporte para este sistema.

Realización de inventarios

Se realizó un muestreo simple mediante cuatro parcelas de 0.05 ha, ubicadas al azar en cada área en las que se dividió la plantación. Esto, con el objeto de estimar el volumen por superficie que oferta cada zona y el volumen total de la plantación. Las variables que se midieron para cada árbol dentro de la parcela fueron: diámetro a la altura del pecho (DAP), altura comercial, altura total y calidad del fuste.

Digitalización de mapas

La información cartográfica básica se digitó generándose el mapa base escala 1:10000, el de volumen de madera ofertada por superficie, el mapa de costos de extracción por superficie y el mapa de infraestructura vial existente. Esta cartografía se digitalizó con ayuda del programa ArcGIS 9.3 en forma manual.

Generación de mapas

Con el mapa topográfico, en el cual la estructura vectorial de la información viene dada por curvas de nivel (polilíneas de altitud constante), lineal (vías existentes o drenajes) o polígonos (superficies boscosas), se generó una estructura TIN (Triangle Irregular Network), basada en triángulos irregulares unidos, quedando el terreno representado por el conjunto de superficies planas. De esta manera, se generó el modelo digital del terreno, que es una representación de la elevación de este en forma numérica.

RASTERIZACIÓN

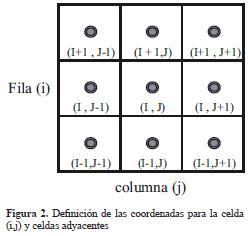
Para facilitar el análisis y posterior procesamiento de la información, el modelo digital se discretizó o rasterizó, dividiéndolo en celdas cuadradas de 10 m x 10 m. A cada celda se asociaron las coordenadas espaciales (x,y,z). Se tomó el centro de cada celda, por lo cual las coordenadas (x,y) se refieren al centro de la celda, mientras que la coordenada (z) indica su altura. Las condiciones físicas y económicas fueron definidas como atributos de las celdas.

La figura 2 muestra las coordenadas de la celda (i,j), en relación con las coordenadas de las celdas vecinas en los ejes X y Y.

A partir del mapa base se generaron los siguientes mapas:

Mapa de elevación: indica el valor de la altura en el centro de la celda. Este mapa facilitó el cálculo posterior de la pendiente de un arco a celdas vecinas y el valor promedio de la pendiente de la celda. Como resultado de este mapa, se generó una matriz de n x m, en la que se indicó el valor de la elevación del centro de la celda. Esta matriz se utilizó para calcular la pendiente hacia las celdas vecinas. El mapa generado de elevación se denominó “Melevación”.

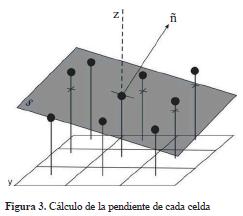
Mapa de pendiente de cada celda: para calcular la pendiente promedio de cada celda, usamos su altura, así como la de las ocho celdas vecinas a esta. Aplicando mínimos cuadrados se calculó el plano S, el cual es el mejor de esos nueve puntos. El método determina el plano que minimiza la suma de las diferencias al cuadrado entre la altura de nueve celdas y la altura que el plano predicho para cada celda. La pendiente de la celda es determinada por ň, que es el vector normal al plano S, como se muestra en la figura 3. El mapa generado se denominó “Pendiente Celda”.

Mapa de pendiente del arco a las celdas vecinas: este mapa nos permitió encontrar los valores aceptables de pendientes para el diseño de una vía cuya pendiente máxima sea el 12 %, partiendo de una celda origen a cualquier celda vecina.

Para calcular la pendiente que existía entre la celda origen y en un vecindario de 3 x 3, es decir, cada una de las ocho celdas vecinas, se calculó, en primer lugar, la distancia que había entre ellas mediante la siguiente ecuación (1):

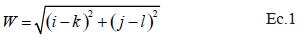
Dónde:
W: distancia unitaria entre celdas.
i: fila celda de origen.
j: columna celda origen,
k: fila celda de llegada.
l: columna celda de llegada.

Posteriormente, se calculó la pendiente a cada celda vecina teniendo en cuenta si esta pertenecía o no a la misma fila o columna de la celda origen.

Cuando la celda destino tenía la misma fila o columna, la pendiente se calculó como:

Dónde:
m: es la pendiente en porcentaje de la celda origen a una celda vecina que se ubica en la misma fila o columna de esta.
Z₁ : es la altura de la celda origen.
Z₂ : es la altura de la celda destino.

Cuando la celda destino no está ubicada en la misma fila ni columna de la celda origen, la pendiente se calculó:

Si al evaluar la pendiente a cualquiera de las ocho celdas vecinas y ninguna cumplía que m ≤ 0.12 entonces se amplío el vecindario a uno de 5 x 5 como se muestra en la figura 4.

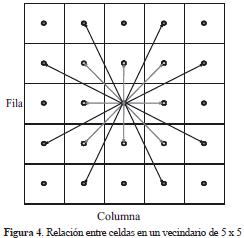
Para el cálculo de la pendiente a cualquiera de las ocho celdas de la capa ampliada se utilizó la siguiente ecuación:

Mapa de celdas infactibles: este mapa se generó para encontrar celdas o puntos en el terreno sin acceso con la pendiente establecida. Se desarrolló una función de peso en la cual las celdas que tienen acceso al menos con una celda vecina, se marcaron con cero en un mapa llamado Pmap y las celdas que no tenían acceso desde ninguna otra se les asignó un 1, generándose así una matriz binaria del tamaño del mapa.

Posteriormente, se tomó el mapa Melevación y las celdas que aparecían en el mapa Pmap, con valor de 1; se reemplazó el valor de elevación por un valor infinito, conformándose la matriz Elevación. Así, las celdas que no tengan acceso, ya que la pendiente supera la máxima permitida, se marca como inaccesible.

Ubicación de los puntos de acopio: estos puntos que previamente, en la fase de campo se habían definido, se ubicaron en el mapa y se pasaron al sistema de coordenadas establecidas, lo que generó una matriz binaria en la cual, si la celda no es un centro de recolección de madera, se identifi có con cero y, por el contrario, si esta celda es un punto de acopio se identificó con 1. Estas celdas donde se acumula la madera extraída, funcionan como nodos en un sistema de flujo de redes.

Mapa de costos de vía: ka vía forestal para el acceso a los puntos de recolección de madera es de tipo secundario (un solo carril, 5 m de ancho, con afirmado y pendientes menores de 12%). El costo de esta se calculó sumando los costos de diseño, trazado y construcción por metro lineal. Como este costo es directamente proporcional a la pendiente del terreno, se estableció, el costo promedio por celda para tres rangos de pendiente, como se muestra en la tabla 1. En consecuencia, el costo asociado en cada celda se establece directamente.

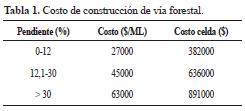
El mapa de pendiente de cada celda sirvió de base para el cálculo de construcción de un tramo de vía sobre esta celda. El costo total de construcción de una vía que comunique dos puntos cualquiera se puede calcular si se suman todos los costos de las secciones de celdas que los comunican.

PROBLEMA DE LA RUTA MÁS CORTA

En general, en la formulación para el camino más corto entre dos nodos j y t, se asume como una red dirigida, el costo C_{i j} es un parámetro asociado a cada arco. Este costo puede ser C_{i j} = 0, mientras los arcos que no son posibles el valor C_{i j} = ∞. El problema por resolver se interpreta como el transporte de una unidad de flujo al mínimo costo a través de la red, desde un nodo origen (s) a un nodo destino (t). Matemáticamente, este problema puede ser formulado como un modelo de programación lineal expresado por las siguientes ecuaciones:

Minimizar

Donde:

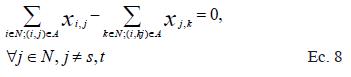
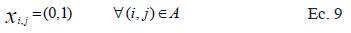
S: nodo origen.
t: nodo destino.
N: conjunto de nodos en la red.
A: conjunto de arcos en la red.
C_i,j: costo de construcción o distancia del arco que conecta el nodo i con el nodo j.

La función objetivo (5) minimiza la suma de todos los costos de los arcos que están en la ruta. Las restricciones (6) y (7) aseguran que el nodo origen y el nodo destino estén presentes en el problema de la ruta más corta. Las restricciones (8) son un balance de flujo en el cual todo flujo que entre a un nodo debe ser igual al flujo que sale de un nodo, exceptuando los nodos origen y destino. Las restricciones (9) declaran que las variables x_i,j son binarias (Phillips & García-Díaz 1990).

Algoritmo de Dijkstra: una alternativa para resolver modelos de la ruta más corta es la utilización de un método conocido como algoritmo de Dijkstra, diseñado para aprovechar la estructura particular del modelo. Se asume que el costo o distancia entre cualquier par de nodos es un número no negativo representado por C_i,j. El algoritmo asigna a todos los nodos una etiqueta la cual puede ser temporal o permanente. Al iniciar el algoritmo, todos los nodos excepto el nodo origen, reciben una etiqueta temporal que representa la distancia directa entre el nodo origen y cada nodo. Al nodo origen se le asigna una etiqueta permanente igual a cero. Cualquier nodo que no tenga relación directa con el nodo origen se le asigna una etiqueta temporal igual a ∞, mientras todos los otros reciben una etiqueta temporal de C_ij, j≠s. Cuando se determine que un nodo debe pertenecer a la ruta mínima este nodo cambia su etiqueta a permanente.

El algoritmo opera con la simple lógica de que si la ruta más corta desde el nodo s al nodo j es conocida, y el nodo k pertenece a esta ruta, entonces, el camino mínimo desde s a k es una porción de la ruta original que termina en el nodo k. El algoritmo inicia con j = s y sucesivamente restablece j hasta que j = t. terminando el proceso de esta forma.

Dado un nodo j, el símbolo ∂_j es usado para representar una estimación de la longitud del camino más corto desde el nodo origen s al nodo destino j. Cuando este valor no puede ser mejorado se marca con etiqueta permanente y se representa por el símbolo ∂j . En cualquier otro caso, se referencia con etiqueta temporal.

Inicialmente, el nodo origen es etiquetado permanentemente. Cualquier otro nodo que tenga conexión directa con el nodo origen es marcado con etiqueta temporal. Para identificar al nodo más cercano al nodo origen, seleccionamos el mínimo de los marcados con etiquetas temporales y se declara permanente. A partir de este punto, el algoritmo se realiza en forma iterativa en dos fases hasta llegar al nodo destino.

En la primera fase del algoritmo, se inspeccionan las etiquetas de los nodos marcados como temporales, se compara cada etiqueta temporal ya asignada con la suma de la última etiqueta permanente y la distancia directa desde el nodo con etiqueta permanente al nodo bajo consideración. La mínima de estas dos distancias es definida como la nueva etiqueta temporal para este nodo. Si la vieja etiqueta temporal sigue siendo mínima, se mantendrá sin cambios.

La segunda fase selecciona la mínima etiqueta temporal y se declara permanente. Si el nodo t está marcado con etiqueta permanente el algoritmo finaliza. De otra forma, se inicia con la primera fase del algoritmo.

Árbol de mínima expansión: un árbol T es un árbol expandido de G, si T es un subgráfo acíclico de G, este árbol expandido contiene todos los n nodos de la red, definiéndose un árbol con n nodos y m arcos donde m = n-1 (Ayuso 1997).

Si asociamos a cada arco de la red un número tal que represente la distancia, costo, tiempo o cualquier otro parámetro para indicar la limitación o capacidad de cada arco, se pueden defi nir las nociones de mínimo o máximo árbol de expansión. El peso del árbol se calculó como la suma de los parámetros de cada arco que conformaban el árbol. Un árbol de mínima expansión es definido como el árbol de mínimo peso.

Árboles expandidos son definidos para redes dirigidas y no dirigidas; sin embargo, para redes que contienen arcos dirigidos es necesario definir la arborescencia, ésta es un árbol que contiene únicamente arcos dirigidos. Una arborescencia posee siempre una raíz, que se define como un nodo en el que se originan arcos dirigidos. Una arborescencia no puede tener más de una raíz (Ahuja et al. 1993).

Variables de decisión:

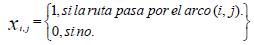
Función objetivo:
Minimizar Z:
Restricciones:

Donde:
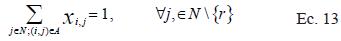
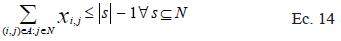
N: conjunto de nodos de la red.
conjunto de arcos de la red.
S: conjunto de nodos de la red subconjunto de N.
r: nodo raíz del árbol de mínima expansión. C_ij: costos de los arcos i, j.

Las restricciones (12) aseguran que exista al menos un arco que salga del nodo raíz (r) hacia todos los demás nodos del árbol. Por otra parte, el conjunto de restricciones (13) señala que a todos los nodos de la red les debe llegar un arco, exceptuando el nodo raíz. Las restricciones (14) eliminan los ciclos que puedan aparecer en el árbol de mínima expansión (Gross & Yellen 2006).

Algoritmo de Kruskal: este algoritmo de tipo “glotón” consiste en ordenar las aristas de una red en forma ascendente de peso; se examinan en este orden y se toman en cuenta en el árbol que se forme, siempre y cuando no constituyan un ciclo con las anteriormente consideradas para establecer una grafica acíclica. El algoritmo termina cuando el número de aristas (m) sea igual al número de vértices (n) menos uno: m= n-1, así se garantiza un árbol expandido de G. En cada iteración la gráfica formada no necesariamente es conexa, excepto en la última iteración.

Sea G = [N,A] una gráfica no dirigida donde N representa el número de vértices y A el conjunto de arcos (x_i , x_j) y sea C la función que asocia a cada elemento de A el parámetro (costo, distancia, tiempo, flujo).

Entonces, la solución de este problema es una gráfica parcial de G, que debe cumplir con una T es convexa, es decir, que exista un camino que una todo par de vértices; T debe ser acíclica; y el costo de T debe ser mínimo.

CÁLCULO DEL CAMINO CORTO ENTRE PATIOS

Conceptualizamos el problema como una red en la cual los nodos representan los centros de celdas y los arcos que las unen son los segmentos de camino que comunican estas y por donde es posible trazar una vía con las condiciones preestablecidas. Desde esta perspectiva, el problema buscó optimizar el diseño de una red vial que comunicara patios al menor costo.

En primer lugar, se estableció, para cada uno de los puntos de acopio el camino más corto a cualquier otro patio. Es decir, se defi nieron todas las combinaciones posibles de rutas donde desde un patio fuera posible la conexión a cualquier otro. Para establecer la conexión (arco) entre dos nodos, se formuló un procedimiento denominado “bestway”, cuyo objetivo era encontrar el camino más económico entre dos puntos (patios de acopio), cruzar por los vértices que cumplen con la condición de rango pendiente establecida, para, así garantizar el menor costo de construcción de vía.

El procedimiento requiere el uso de la matriz Elevación´, descrita anteriormente. De esta forma, se calcularon los vectores de posición de dos puntos: x y y. Para el vector x que es un vector columna de 1 x 2 se definieron las coordenadas horizontales de los puntos de inicio y final de los nodos a unir. Para el vector y, que también es un vector columna de 1 x 2, se determinaron las coordenadas verticales de los puntos de inicio y final. Es así como quedaron localizados los dos puntos de interés en relación con el total de la superficie (Figura 5).

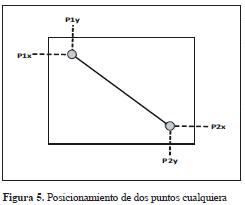
Donde los vectores x y y se definen:

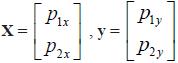
A partir de la matriz Elevación se defi nieron ocho matrices N_p, de tamaño 86 x 83 que establecieron las posiciones de cada celda con sus vecinos como índices lineales, n donde la posición a_ijindicó quién es el vecino en la celda ubicada en la posición relativa p. Es decir, para la matriz N₁, el valor de cada celda de la matriz mostró el vecino ubicado en la posición relativa 1 como lo indica la Figura 6.

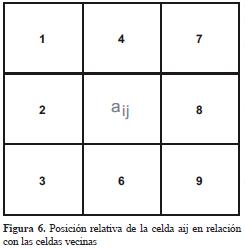
Así, cada una de las posiciones quedaron definidas de la siguiente manera: posición: P₁:a_{(i+1, j-1)}, P₂:a_{(i, j-1)}, P₃:a_{(i-1, j-1)}, P₄:a_{(i+1, j)}, P₅:a_{(i, j)}, P₆:a_{(i-1, j)}, P₇:a_{(i+1, j+1)}, P₈:a_{(i, j+1)}, P₉:a_{(i, j+1)}.

Para las celdas localizadas en los bordes de la matriz y donde no existen celdas vecinas en la posición relativa p, el valor que toma esta celda en la matriz Np es cero. De esta manera, se establecieron las ocho matrices N_p, las cuales eran necesarias para establecer los índices lineales.

Una vez encontradas las matrices: N₁, N₂, N₃, N₄, N₅, N₆, N₇, N₈, N₉, se calcularon ocho matrices de tamaño m x 2 denominadas ARC _p, donde p indica el mismo índice de posición de la matriz Np, es decir, la posición de la celda destino en relación con la celda origen. Estas matrices tienen la función de definir los posibles arcos desde cualquier celda a la adyacente que tiene la posición p, como también el peso del arco que une estas celdas.

Posteriormente, para cada arco generado en las ocho matrices se le calculó la pendiente, los valores de la altura de cada celda, se tomaron de la matriz Elevación. Cuando el valor de p del vector ARC_p es par, se aplicó la fórmula (2), dado que la celda destino se encontraba en la misma fila o columna de la celda origen. Cuando el valor de p era impar, significó que la celda destino era diagonal a la celda origen, por tanto, para el cálculo de pendiente del arco se aplicó la fórmula (3).

Una vez establecida la pendiente de cada arco, se obtuvo el peso del arco, definido este como el costo de construcción del segmento de vía que une los centros de las celdas. Como el costo de vía es directamente proporcional a la pendiente, el costo asociado a cada rango de esta se obtuvo de la tabla 1, donde se había calculado el valor promedio de segmento de vía por celda, el cual incluyó los costos de diseño, trazado y construcción. Así, quedaron constituidas las matrices ARCp de tipo sparce, las cuales contenían todos los arcos y vértices necesarios para encontrar el camino más económico entre dos patios de apilado.

La metodología empleada para encontrar la ruta óptima para unir dos patios se basó en el algoritmo de Dijkstra, en el cual la red G [N, A] tiene costos no negativos en los arcos, donde V es el conjunto de vértices (centros de celdas) y A es el conjunto de arcos que unen todos o algunos de los vértices. La figura 7 muestra la combinación de caminos entre patios (V_i) y los respectivos costos de construcción de vía (W_ij).

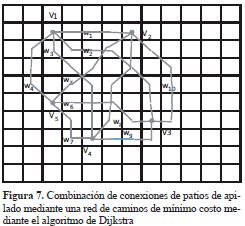
Las celdas que en el mapa Pmap se definieron como infactibles se trasladaron a esta red con costo infinito, de forma que no pudieran ser evaluadas como segmentos posibles entre dos patios.

Una vez encontrado el camino más económico entre dos patios, se tomó la sumatoria de todos los segmentos que lo conformaron como un arco con costo total de construcción igual a la sumatoria de costos de los respectivos segmentos (W_ij).

La información del costo, para todo par de puntos se almacenó en una matriz cuadrada de pesos mínimos de tamaño n x n, donde n representa el número de patios por conectar y w_ij es el costo de construir el arco que une los patios de apilado i y j (Figura 8).

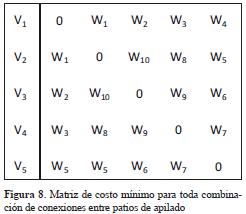
Una vez establecida la red de caminos de costo mínimo que comunicaban los diferentes patios, se procedió a calcular el árbol de mínima expansión mediante el algoritmo de Kruskal, en la red G [N,A], conexa con n vértices y m aristas. De esta forma, quedó establecida la red con mínimo costo que comunicó todos los patios mediante una vía de evacuación (Figura 9).

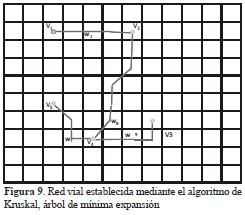
Finalmente, la conexión de la red diseñada desde un punto seleccionado por el experto a una vía pública o preexistente se calculó mediante el algoritmo de Dijkstra; de igual forma, que se hizo al comunicar dos patios de apilado.

RESULTADOS

MODELO DIGITAL DEL TERRENO

Con el mapa topográfico del área seleccionada se estableció el modelo digital del terreno (Figura 10), el cual se generó con el módulo TIN del programa ArcGIS. En primer lugar, este permitió la visualización de la topografía del terreno y, en segundo lugar, se preparó la información para la rasterización de los mapas temáticos.

RASTERIZACIÓN Mapa de elevación

El mapa de elevación en formato raster (Melevacion), quedó representado por una matriz de 86 x 83 pixeles de tamaño 10 m x 10 m en el terreno, es decir, el número de celdas que cubren el área es de 7138, las cuales, en total, suman una superficie de 71.3 ha. Los centros de cada celda están georeferenciados con las coordenadas (x,y,z), lo cual permitió localizar cada celda en el terreno y establecer sus atributos.

Mapa de pendiente de celda

Siguiendo la metodología propuesta, la pendiente de cada celda se calculó en relación con sus vecinas, según lo explicado anteriormente. De esta manera, se conformó una matriz que indicó la pendiente de cada celda en un mapa denominado Pendientecelda.

Mapa de costo de vía

Para el procesamiento de la información requerida en el trazado de la vía, se rasterizaron los mapas de costo de segmento de vía por celda, con el cual se generó la matriz costo de vía, en la cual el valor de cada celda correspondió al costo de construcción de la vía en esta y está asociado a la pendiente de la celda correspondiente.

DESARROLLO DE LA APLICACIÓN

Para facilitar el procesamiento de los algoritmos requeridos para la ejecución de la metodología, se elaboró un programa que permitió visualizar, seleccionar y modelar bajo diferentes valores de parámetros las condiciones que el experto considere más reales.

La aplicación se basó en el lenguaje Matlab 7.6 para la elaboración de un código eficiente y estructurado, que permite, por un lado, desarrollar los algoritmos propuestos de Dijkstra y Kruskal. Por otro, permite una interfaz visual, la cual facilitó la ubicación geográfica de las diferentes características del terreno, del bosque de las vías y de los patios de apilado que se hayan planificado con un sistema de extracción dado. El programa desarrollado se denominó SIG _camino y se ejecutó como una extensión de Matlab, por ello diferentes mapas se visualizaron en el módulo gráfico de Matlab.

CÁLCULO DE LAS CELDAS INFACTIBLES

Las celdas que no pueden ser accesadas desde ningún punto vecino, es decir, cuando no existe un arco con la pendiente requerida desde cualquier celda vecina, quedan aisladas y no es posible establecer un punto de acopio allí, ni trazar una vía de extracción. A estas celdas se les da un valor de infinito en la matriz Elevación; en el mapa los puntos infactibles se representan por un color claro.

UBICACIÓN DE LOS PUNTOS DE ACOPIO

Una vez establecido el sistema de extracción con Tracto-Koller, se procedió a la ubicación de los corredores que son posibles de trazar en terreno, de forma que permitieran la evacuación de la mayor cantidad de madera. Para el trazado de la línea principal de cada corredor, con este sistema, se deben tener en cuenta los siguientes aspectos: Pendiente del terreno: la pendiente mínima del terreno debe ser del 30%; forma del terreno: se deben establecer los puntos críticos en terreno, esto es, los lugares donde el paso del carreto con carga suspendida sea imposible; en este caso, es necesario la instalación de pasacables; presencia de árboles que cumplan la función de mástiles tanto en el fondo de la línea como en el inicio de esta: definición de la dirección de saca: es la dirección con respecto a la pendiente y a la vía de saca, esta puede ser subiendo la madera o bajándola; ancho efectivo del corredor; ubicación de la madera en el terreno; es la forma como se distribuye la madera en el bosque, la cual puede estar uniformemente distribuida o en forma de parches.

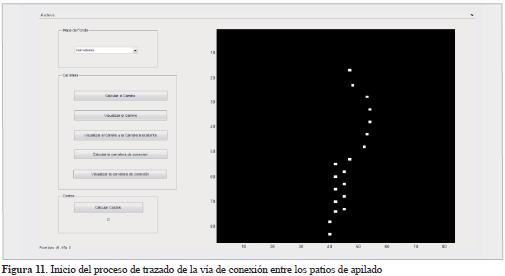
Los corredores se ubicaron en forma paralela. De los diecinueve que se proyectaron, en catorce de estos, la madera se moviliza pendiente abajo hacia la vía de extracción, y en cinco, la madera se sube a la vía que se va a proyectar. De esta forma, los patios de apilado quedaron localizados muy cerca a los mástiles de vía, pudiéndose calcular el volumen del flujo total de madera que pasa por cada uno de los patios. Al determinar las coordenadas de los patios de apilado al plano general, se ubicaron las celdas que correspondían a dichos patios. Estas pasaron a conformar el conjunto de nodos de una red no dirigida que se describe como el conjunto de los diecinueve nodos que pertenecen a N, se pueden observar en la fi gura 11; en ella, los nodos o patios de apilados se deben interconectar entre sí conformando una red que se puede representar como una matriz de incidencia de 19 x 19.

El arco que une dos patios se definió por medio del algoritmo de Dijkstra, en el cual el peso del arco que unía dos nodos W_ij, se calculó como el costo mínimo de construcción de la vía que los unía. De esta forma, se establecieron todas las posibles rutas entre los patios y se configuró la matriz de costo mínimo para toda combinación de conexiones entre estos.

Este proceso es el que requiere mayor capacidad de almacenamiento y procesamiento de información, ya que se realiza una búsqueda exhaustiva de las posibles rutas, hasta encontrar la vía más económica de todas las posibles combinaciones entre celdas.

A continuación, se establece el árbol de mínima expansión para la red G [N,A], conexa con n vértices y m aristas y con costos no negativos, utilizando el algoritmo de Kruskal. Esto con la idea de definir la vía que permita evacuar la madera agrupada en cada patio de apilado. De esta forma, la vía económica que une los patrios queda finalmente establecida como lo muestra la secuencia de las figuras 11 y 12, en forma de árbol conexo, acíclico y del menor costo.

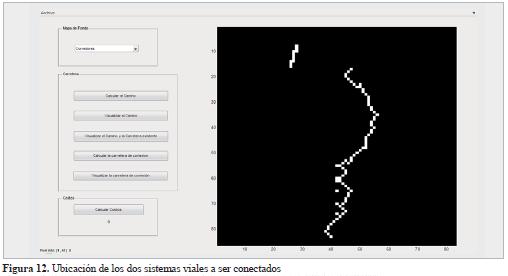
Por último, queda por definir una vía de acceso que conecte la red vial establecida con una vía pública existente para lograr una continuidad en la movilización de la materia prima hasta la industria. Esta conexión inicia con el reconocimiento de campo realizado por el experto, donde se ubican los puntos más convenientes para unir los dos sistemas viales. Como se muestra en la fi gura 12, existen dos tramos independientes que se requiere unir: la red vial que une los patios de apilado y la vía pública preexistente.

La aplicación presenta un módulo que permite elegir los dos puntos de las vías que se quieren enlazar, esto se realiza con el cursor, tocando, en primer lugar, el punto de la vía pública que se haya elegido para la intersección; posteriormente, el segundo punto corresponde al sitio elegido sobre la red vial diseñada. De esta forma, se seleccionan dos puntos que definen dos vectores x y y, los cuales establecen las coordenadas horizontales y verticales de los puntos que se van a unir.

Una vez obtenidas las coordenadas, se procede a calcular el camino más económico mediante el algoritmo de Dijkstra de la misma forma que se hizo para unir dos patios de apilado. Este módulo permite reconsiderar los puntos escogidos para la unión de las vías y recalcular con los nuevos puntos la vía de acceso. Finalmente, si la vía de acceso propuesta satisface las expectativas del experto, se calcula el costo de construcción total de la red vial entre patios y de la vía de acceso (Figura 13).

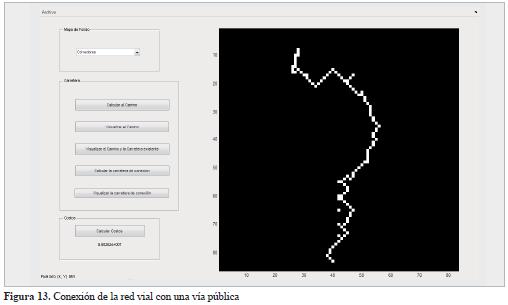
Teniendo en cuenta los valores establecidos de construcción de vía por celda, el costo total de construcción de vías, tanto la que une los patios de apilado como la que permite el acceso al bosque, es de $56000000, el cual, dividido entre el volumen total extraído de 4867 m^3, comprende un valor de $11504 para cada metro cúbico extraído por construcción de vías.

Existen aéreas inaccesibles, donde la construcción de vía con la pendiente establecida es imposible; tal es el caso del patio de apilado 7, que no pudo ser anexado a la red, ya que se ubicó en un área inaccesible, por lo que se requiere su reubicación en un punto cercano que tenga las condiciones de pendiente adecuada.

CONCLUSIONES

Existe una necesidad evidente de las empresas dedicadas a la extracción de productos madereros de reducir costos de operación, de forma que se les facilite ser más competitivas en el ámbito tanto nacional como internacional. Un factor que debe ser tenido en cuenta para la reducción de estos, es la optimización del trazado de vías, de manera que se puedan minimizar los costos de construcción para garantizar la funcionalidad y factibilidad del trazado y construcción de estas.

Actualmente, el trazado y construcción de las vías se realiza con escasa información y de manera empírica, tomando las decisiones de ubicación y trazado en el momento de estar ejecutando la construcción de ellas. Como consecuencia de lo anterior, las vías establecidas no se plantean con criterios de optimización.

Una buena red vial permite reducir las distancias promedio de extracción con cualquier sistema utilizado y garantiza que las diferentes actividades asociadas a la cosecha forestal se benefi cien en función de los costos, así como rendimientos y la calidad de los productos.

La metodología propuesta para el trazado de la red vial permite solucionar el problema de construcción de vías forestales que conecten puntos seleccionados para la recolección de madera para pulpa en plantaciones de la Sabana de Bogotá, de la forma más económica posible. El programa desarrollado SIG_Camino facilita el procesamiento tanto de la información cartográfica como la ejecución de los algoritmos apropiados para encontrar la red vial óptima en un área determinada.

La metodología que se presenta desarrolla una solución óptima al problema del diseño de la red vial para labores de extracción forestal, mediante la combinación de los algoritmos de Dijkstra y Kruskal. El primero define la combinación de posibles conexiones entre todos los nodos (puntos de acopio) con arcos no dirigidos, cuyo valor es el costo de construcción del segmento de vía que une estos dos puntos; una vez definida esta red, se aplica el algoritmo de Kruskal, el cual establece el árbol de mínima expansión que garantiza la conexión de todos los patios al mínimo costo. Finalmente, la vía establecida se anexa a una red vial pública mediante el mismo proceso que se realizó con el algoritmo de Kruskal.

El modelo más completo orientado al proceso de cosecha forestal ha sido el desarrollado por Epstein et al. (2006), el cual obtiene una buena ubicación de maquinaria y vías forestales, dada la superficie para la que fue diseñado (1000 ha). El programa SIG _ camino encuentra la red de caminos óptima para superficies de menos de 100 ha, superficies que son muy frecuentes en la Sabana de Bogotá, tamaños para las cuales no se requieren esfuerzos computacionales tan elaborados.

La planificación de las vías de extracción debe ser realizada con base en cartografía semi-detallada o detallada del área de interés, se deberá realizar con suficiente tiempo de antelación y deberá contar con recursos computacionales y profesionales suficientes, de modo que un buen diseño de caminos de extracción ahorrará dinero y tiempo de ejecución de la construcción y minimizará los impactos que se generen.

La vía planteada por el programa SIG_camino podrá tener alguna variación en el trazado real sobre el terreno, debido a la geometría de las curvas, pero en su forma general mantendrá la poligonal abierta propuesta.

REFERENCIAS BIBLIOGRÁFICAS

Ahuja, R., T. Magnanti & J. Orlin. 1993. Network flows: Theory, algoritms, and applications. Prentice Hall. New Jersey. 846 p.

Ayuso, M. 1997. Introducción a la teoría de redes. Sociedad matemática Mexicana. México. 259 p.

Briceño, M. 1993. Conceptos básicos de manejo forestal. Uteha-Noriega. México. 161 p.

Dahlin, B. & T. Fredriksson. 1995. Computer-assisted forest road planning. A proposed interactive model with especial emphasis on private forest land. International Journal of Forest Engineering 6: 35-39.

Díaz, L. & A. Prieto. 1999. Modelos de planificación forestal basados en la programación lineal investigación agraria: sistemas y recursos forestales: aplicación al monte "Pinar de Nafria". Investigación agraria. Sistemas y Recursos Forestales 8.

Epstein, R., A. Weintraub, P. Sapunar, E. Nieto J. Sessions & F. Bustamante. 2006. A Combinatorial heuristic approach for solving real-size machinery location and road design problems in forestry planning. Operations Research 54: 1017-1027.

Gross, J. & J. Yellen. 2005. Graph theory and its applications, Second Edition (Discrete Mathematics and Its Applications). Chapman & hall/CRC. Boca Raton. 800 p.

Karlson, J., M. Ronnqvist & J. Bergstrom. 2004. An optimization model for annual harvest planning. Canadian Journal of Forest Research 34: 1747-1754.

Leuschner, W. 1990. Forest regulation: Harvest, scheduling and planning techniques. John Wiley & Son. New York. 281 p.

Phillips, D. & A. García-Díaz. 1990. Fundamentals of network analysis. Waveland Press, Inc. Illinois. 474 p.

Pinzón, D. Y. Rubio. 2006. Estudio de rendimientos y estimación de costos de las labores de cosecha de Eucalyptus globulus en la sabana de Bogotá. Tesis de pregrado Ingeniería Forestal. Universidad Distrital. Bogotá. 229 p.

Quiroz, M. 2002. Diagnóstico y cálculo de tiempos de mano de obra en actividades de aprovechamiento para plantaciones de Eucalyptus globulus en la fi nca Tibináma en Tocancipá (Cundinamarca). Tesis de pregrado Ingeniería Forestal. Universidad Distrital Francisco José de Caldas. Bogotá. 160 p.

Stirn, Z. 1990. Adaptative dinamic model for optimal forest management. Forest Ecology and Management 31: 167-188.

Tan, J. 1999. Location forest road by a spatial and heuristic procedure using microcomputers. International Journal of Forest Engineering 10: 91-100.

Twaddle, A. & G. Murphy. 1992. A simulation of the impact pre-emptive cutting for transportation on value recovery. International Journal of Forest Engineering 4: 15-21.

Vignote, S. & F. Jimenez. 1996. Tecnología de la madera. Mundi-Prensa. Madrid. 602 p.

Wang, J., D. Greene & B, Stokes. 1998. Stand, harvest, and equipment interactions in simulated harvesting prescriptions. Forest Products Society 48: 81-86.

Wang, L. 1994. Optimal operation planning for integrated forest harvesting and transport operations From the forest to the mill. Journal of Forest Engineering 16: 15-22.