DOI:
https://doi.org/10.14483/udistrital.jour.colomb.for.2012.2.a07Publicado:
01-07-2012Número:
Vol. 15 Núm. 2 (2012): Julio-DiciembreSección:
Artículos de investigación científica y tecnológicaGENERACIÓN DE PATRONES DE CORTE A PARTIR DE LA PROGRAMACIÓN MATEMÁTICA PARA LA PLANIFICACIÓN TÁCTICA-OPERATIVA DE ASERRÍOS MADEREROS
Generating wood cutting patterns using mathematical programming for tactical-operative planification of sawmills
Palabras clave:
algoritmo, desperdicios, patrones de corte, Pinus caribaea, programación lineal. (es).Palabras clave:
algorithm, waste, cutting patterns, Pinus caribaea, linear programming. (en).Descargas
Referencias
Acosta, I. (2004). Informe nacional Colombia: Estado de tendencias y perspectivas el sector forestal en América latina. Roma: Organización de las Naciones Unidas para la Alimentación y la Agricultura. 113 p.
Aguilar, C., & Sanhueza, R. (2003). Caracterización y estandarización de productos, procesos y equipos en la industria del aserrío. (Trabajo de pregrado, Ingeniería de Maderas). Concepción: Universidad del Bio - Bio. 270 p.
Arce, J., MacDonagh, P., & Friedl, R. (2007). Generacao de padroes otimos de corte a traves de algoritmos de tracamento aplicados a fustes individuales. Revista Arvore, 28(2), 207-217.
Barrera, J.M., & Cuervo, S. (2010). Manual de buenas prácticas en aserraderos de comunidades forestales. México: Consejo Civil Mexicano para la Silvicultura Sostenible, Rainforest Alliance, Reforestamos México. 110 p.
Caballero, R., Gómez, T., Molina, J., Fosado, O., León, M. A., & Garofal, M. (2009). Sawing planning using a multicriteria approach. Journal of Industrial and Management Optimization, 5(2), 308-317.
Cancino, J. (1993). Modelo optimizador de trozado de árboles basado en funciones de ahusamiento y programación dinámica. Turrialba: CATIE. 225 p.
Carnieri, C., & Mendoza, G.A. (2000). A fractional algorithm for optimal cutting of lumber into dimension parts. Annals of Operations Research, 95(1), 83-92.
Faaland, B., & Briggs, D. (1984). Log bucking and lumber manufacturing using Dynamic programing. Management Sciencie, 30(2), 245-257.
FAO [Organización de las Naciones Unidas para la Alimentación y la Agricultura]. (2002). Información para el desarrollo sostenible; Estado de la información en Colombia. Santiago de Chile: Organización de las Naciones Unidas para la Alimentación y la Agricultura.155 p.
Fosado, O. (1999). Tratamiento económico - operativo del proceso de aserrado en la madera (Tesis Doctoral). Pinar del rio: Universidad Pinar del rio. 158 p.
GAMS [General Algebraic Modeling System]. (1988). General algebraic modeling system (version 23.7). Washington: GAMS Development Corporation ISBN: 0-201-54664-7, recuperado de http://www.gams.com/.
Gaudreault, J., Frayret, J.-M., Rousseau, A., & D’Amours, S. (2010). Combined planning and scheduling in a divergent production system with co-production: A case study in the lumber industry. Computers & Operations Research, 38(9), 1238-1250.
Gracia, C. (2008). Métodos y algoritmos para resolver problemas de corte unidimensional en entornos realistas. Aplicación a una empresa del sector siderúrgico. (Tesis Doctoral). Valencia: Universidad politécnica de Valencia. 221 p.
Hifi, M. (2004). Exact algorithms for unconstrained three-dimensional cutting problems: a comparative study. Computers & Operations Research, 31(5), 657-674.
Hillier, F., & Lieberman, G. (1997). Introducción a la investigación de operaciones. Atlampa: Mc Graw Hill. 500 p.
Kivinen, V.-P., Uusitalo, J., & Nummi, T. (2005). Comparison of four measures designed for assesing the fit between the demand and output distributions of logs. Canadian Journal of Forest, 35(3), 693-702.
Lagos, R. (2006). Comparación de dos software de simulación para la industria del aserrío de Pinus radiata D. Don. (Trabajo de pregrado, Ingeniería de Maderas). Valdivia: Universidad Austral de Chille. 136 p.
Maturana, S., Pizani, E., & Vera, J. (2010). Scheduling production for a sawmill: A comparison of a mathematical model versus a heuristic. Computers & Industrial Engineering, 59(4), 667-674.
Mcphalen, J. (1978). A method of evaluating bucking and sawing strategies for sawlogs (Master thesis). Vancouver: University of British Columbia. 160 p.
Mendoza, G., Sprouse, W., Luppold, W., Araman, P., & Meimban, R. (1991). An integrated management support and production control system for hardwood forest products. Computers in Industry, 16(1), 343-350.
Molinos, V. (2005). Mercados selectos para madera aserrada, dimensionada y seca de pino y sus manufacturas, producidas en Colombia. Bogotá: USAID. 19 p.
Murara, M.I., Rocha, M.P.d., & Junior, R. (2005). Rendimento em madeira serrada de pinus taeda para duas metodologias de desdobro. Floresta, 35(3), 473-483.
Novak, R.d.S. (2007). Um sistema de otimizaçao aplicada ao desdobro de madeira. (Tesis de Maestría). Curitiba: Federal do Paraná. 141 p.
Occeña, L. (1991). Computer integrated manufacturing issues related to the hardwood log sawmill. Forest Engineering, 3(1), 39-45.
Pileggi, G., Morabito, R., & Arenales, M.N. (2007). Heurísticas para os problemas de generacao e sequenciamiento de padroes de corte bidimensionais. Pesquisa operacional, 27(3), 549-568.
Pradenas, L., Peñailillo, F., & Ferland, J. (2004). Agregate production planning problem. A new algorithm, Electronic Notes in Discrete Mathematics, 18(1), 193-199.
Quintero, M., & Rosso, F. (2001). Propuesta de un simulador de aserraderos para la industria forestal Venezolana. Revista Forestal de Venezuela, 45(1), 95-101.
Rebolledo, M., & Baesler, F. (2001). Uso de inteligencia artificial para la optimización de un modelo de simulación aplicado a un proceso de remanufactura de pino radiata. Maderas de ciencia y tecnología, 3(2), 52- 62.
Romero, R., Poblete, M., & Baesler, F. (2004). Modelo de programación de la producción para la industria del aserrío. Revista Ingenieria Industrial, 3(1), 19-23.
Todoroki, C.L., & Rönnqvist, E. (1999). Combined primary and secondary log breakdown optimization. Operational Research Society, 50(3), 219-229.
Zavala, D.Z., & Cortés, R. H. (2000). Análisis del rendimiento y utilidad del proceso de aserrío y troceria de pino. Madera y Bosques, 6(2), 88-94.
Zanjani, K., Ait-Kadi, D.M., & Nourelfath. M. (2010). Robust production planning in a manufacturing environment with random yield: A case in sawmill production planning. European Journal of Operational Research, 201(3), 882-891.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
GENERACIÓN DE PATRONES DE CORTE A PARTIR DE LA PROGRAMACIÓN MATEMÁTICA PARA LA PLANIFICACIÓN TÁCTICA-OPERATIVA DE ASERRÍOS MADEREROS
Generating wood cutting patterns using mathematical programming for tactical-operative planification of sawmills
Jonnier Fabián Herrera-Medina1 & Robert Orlando Leal-Pulido2
1Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. jfabian88@gmail.com. Autor para correspondencia.
2Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. rolealp@udistrital.edu.co
Recepción. 1 de octubre de 2012 / Aprobación. 29 de diciembre de 2012
RESUMEN
Este trabajo propone una metodología para la generación de patrones de corte óptimos en operaciones de aserrío, para minimizar los niveles de desperdicios en la obtención de productos aserrados. Se utilizó primero un modelo de programación lineal, el cual genera patrones de cortes factibles y óptimos para las diferentes clases diamétricas que caracterizan la oferta maderera, a partir de las características de transformación que posee la empresa tomada como centro de estudio. Luego, se planteó la utilización de un modelo fraccional, el cual asigna de manera eficiente los patrones de corte obtenidos de acuerdo a la demanda y oferta maderera existente en patio. Se obtuvieron en total 42 patrones de corte factibles con un nivel de aprovechamiento del 79 %; además, en la asignación eficiente de patrones de corte a demanda se obtuvieron desperdicios de alrededor del 25 % bajo ciertos supuestos de características de la materia prima.
Palabras clave: algoritmo, desperdicios, patrones de corte, Pinus caribaea, programación lineal.
ABSTRACT
This paper proposes a methodology for generating optimal cutting patterns in sawmills operations that minimize waste production. Firstly, a linear programming model was used to generate patterns of feasible and optimal cuts for different diameter classes. Secondly, a model which assigns efficient cutting patterns based on the supply and demand of the timber yard was employed. A total of 42 cutting patterns were assessed with a utilization level of 79 %. Levels of loss were around 25 % depending on the characteristics of the raw material.
Key words: algorithm, waste, cutting patterns, Pinus caribaea, linear programming.
INTRODUCCIÓN
Históricamente, los cambios en la estructura de distribución de diámetros, longitudes y especies a transformar han influido en el aumento de costos de la industria de la transformación forestal (la materia prima ocupa alrededor del 50-60 % del costo total de producción). Debido al incremento en el precio de adquisición del insumo maderero, los planificadores forestales se han visto forzados a generar alternativas de producción que cada vez más aumenten el uso del recurso maderero (Murara et al., 2005). Los cambios en las tecnologías de transformación de la industria maderera se deben a la necesidad de ser cada día más competitivos. Para esto la política de producción del aserrío debe estar encaminada a aumentar los volúmenes de producto generado, disminuyendo los costos de operación por proceso de transformación maderera.
En Colombia, el avance tecnológico en la industria del aserrío ha sido lento, actualmente la oferta de recursos naturales del país y la extracción de estos sin ningún criterio de sostenibilidad estimulan a mantener los precios deprimidos del insumo maderero. La mayor parte del recurso (76 %) se extrae del bosque natural (Acosta, 2004), el restante se obtiene de plantaciones forestales.
El escenario descrito generó una estructura de industria atomizada y desarticulada, con equipos de transformación que datan de 1950, situación que persistirá, pues de 50 millones de ha de oferta maderera, solo 0.1 % proviene de plantaciones forestales. Sin embargo, el consumo de especies plantadas (ciprés, pino, eucalipto, entre otras) presenta tasas de crecimiento anuales del 63 % (Molinos, 2005). De esta manera, el desarrollo tecnológico que permitirá apalancar ventajas competitivas no se desarrollará mientras no se generen opciones tecnológicas de transformación viables.
En el país, el sistema de aserrado de trozas no cuenta con una clasificación y no posee una definición exacta de tipo de corte por clase diamétrica, esto ha generado mayor número de productos no demandados y desperdicios. Por otra parte, las decisiones de corte y obtención de productos recaen sobre el operario encargado, quien define la mejor manera de seccionar en función de su experiencia, esto hace que este método sea un sistema de transformación empírico. Estudios relacionados demuestran una pérdida del valor comercial del fuste entre un 10 % y 35 %, comparando el rendimiento del trozado normal o empírico contra la generación de una solución óptima (Cancino, 1993).
Sumado a esto, la ineficiencia tecnológica de la industria forestal ha contribuido en la multipli-cación de pequeños productores con tecnologías primarias, responsables en gran parte del desperdicio de la materia prima y la generación de costos de oportunidad altos a consecuencia de no captar la renta de madera que hubiese podido ser generada por el comercio (FAO, 2002). Estas características hacen que en Colombia el volumen de materia prima elaborada, que entra realmente al proceso de manufactura, sea alrededor del 40 % (Acosta, 2004).
En concordancia con lo expuesto anteriormente, la industria de transformación colombiana tiene como principal objetivo comercial adaptar sus procesos y líneas de producción gradualmente ante el cambio inminente de la oferta maderera del país, debido a la incorporación de nuevas especies y productos de transformación a obtener, y a la generación de nuevos procesos industriales. Estas adaptaciones aseguran el éxito y la permanencia de los aserríos en el país. Por otro lado, las industrias deben trabajar para usar la madera más eficientemente mediante la tecnificación de las líneas industriales primarias (transformación de madera aserrada y procesos de cosecha forestal).
El estudio de la planificación operativa en la indus-tria de transformación maderera consiste en una gran opción que abrirá las puertas al mejoramiento de los procesos industriales, a la adaptación del sector y a una alta capacidad de reacción a cambios en la demanda de productos y materia prima, generando un mayor valor agregado (Aguilar & Sanhueza, 2003); de esta manera se contribuirá a alcanzar los objetivos del sector.
Una de las principales dificultades en la organización del proceso de aserrado es la generación de planes de producción y asignación de esquemas de corte a trozas, los cuales satisfagan una determinada demanda de productos, provean rendimientos adecuados en el aprovechamiento de la madera teniendo en cuenta el tiempo de producción y el stock de materia prima de la empresa.
Según Quintero & Rosso (2001), la planificación operativa del aserrado de la madera reduce los gastos de materia prima, posibles incumplimientos de los planes de producción, incremento de los niveles de inventario de madera aserrada por la elaboración de surtidos no demandados, entre otros posibles malos resultados en los cuales se incurre por una determinación de esquemas de corte de manera empírica. Para lograr esto es necesario estar en la capacidad de asegurar un mejoramiento continuo en los procesos industriales en el aserrío, con la intención de procurar siempre la obtención de productos de madera de buena calidad y bajos costos de producción, así como evaluar los rendimientos volumétricos obtenidos de madera aserrada por trozas que ingresaron al proceso con el fin de competir en el mercado. Esto consiste en el problema de asignar, de la mejor manera posible, los recursos limitados entre actividades competitivas, es decir, de manera óptima.
Alternativas como la generación de modelos de optimización y simulación en el marco de la investigación operativa son herramientas que facilitan la modelación y resolución de problemas industriales (Quintero & Rosso, 2001; Rebolledo & Baesler, 2001; Aguilar & Sanhueza, 2003; Caballero et al., 2009). En este sentido, hacia la década de los años ochenta se generalizó su aplicación en el sector forestal, ante la necesidad de remplazar los métodos clásicos de ordenación y planificación forestal.
En el caso de los aserríos se han generado abstra-cciones matemáticas que permiten interpretar las relaciones entre elementos físico-morfológicos de la troza y los elementos de producción. Esto se planteó con el objetivo de generar esquemas de corte que garanticen la calidad de las piezas por obtener, niveles altos de aprovechamiento en materia prima, y métodos que se encuentren en la capacidad de generar predicciones de la oferta y la demanda, con el objetivo de tomar estos factores en el tiempo y basado en esto proponer mejoras que puedan ser verificables.
Como ejemplo de modelos y técnicas propuesto para resolver problemas con respecto a la industria del aserrío, se encuentra la asignación óptima de productos a trozas de pino. Esto se hace mediante la combinación de programación lineal-dinámica y usando la descomposición Dantzig-Wolfe y el algoritmo de generación de columnas. Esto permite desagregar el problema, donde la formulación lineal determina la estrategia de corta óptima apoyada por la programación dinámica en la generación de planes factibles de corte (Mcphalen, 1978).
Faaland & Briggs (1984) evaluaron la secuencia de producción de apeo y transformación en aserrío, para lo cual formularon un modelo dinámico en donde los criterios de decisión de corta produjeron una secuencia de etapas o subproblemas a resolver. Asimismo, Todoroki & R�nnqvist (1999) plantearon según los principios de la programación dinámica dos modelos de recurrencia que maximizan el valor de la producción, con base en el escaneo de las trozas y la maximización del valor de esta, en función de la asignación eficiente de productos con la precaución de evitar posibles defectos presentes en la troza en cuanto al ancho y al largo.
Por otra parte, Fosado (1999) ha dirigido sus estu-dios a la planificación del aserrado por medio de la maximización del valor de la producción, con base en modelos lineales enteros, solucionados mediante un algoritmo de ramificación y acotación. Para la planificación de la producción y siguiendo la misma formulación basada en modelos lineales de los autores anteriores, Romero et al. (2004) desarrollaron un modelo de apoyo a la toma de decisiones para la programación de la producción de aserraderos, el cual permite evaluar los efectos económicos y operacionales de los pedidos a ela-borar, mediante la maximización de la utilidad por producto, obtenido en una clase diamétrica determinada de troza.
Novak (2007), tal como Mcphalen (1978), apoya su formulación bajo dos módulos complementarios. El primero se encarga de generar los posibles patrones de corte por clase diamétrica mediante una formulación recurrente. Los resultados conforman el conjunto inicial de solución en un algoritmo de generación de columnas que constituye la herramienta del segundo modulo de solución del modelo propuesto. Murara et al. (2005), calcularon la tasa de rendimiento de la implementación de un sistema de corte optimizado frente al convencional o empírico que se realiza en las operaciones de transformación y encontraron un aumento del 20 % en la utilización de materia prima con patrones de corte óptimos. Lagos (2006) evaluó dos software de simulación en la generación de patrones de corte óptimos en diferentes clases diamétricas y encontró patrones con factor de aprovechamiento de materia prima en promedio de 60 %.
Carnieri & Mendoza (2000) plantearon una formu-lación fraccional con base en los postulados de Gilmore y Gomory (knapsack problem) y gene-raron diferentes escenarios de validación, como flexibilidad de la demanda y la variación en el tiempo. Por otro lado, Caballero et al. (2009) establecieron un modelo multiagentes, en donde cada agente u objetivo representa un proceso productivo y estos agentes están relacionados entre sí. Con el fin de maximizar el beneficio económico y reducir el tiempo de producción en la asignación eficiente de productos a trozas, los autores evalua-ron objetivos de producción de: utilización de materia prima, factor de aprovechamiento por patrones de corte utilizados e inventario no demandado generado.
El problema de corta ha sido solucionado por otros autores utilizando técnicas heurísticas y metaheurísticas. Rebolledo & Baesler (2001), por ejemplo, emplearon una metodología de optimización y simulación al proceso de rema-nufactura de pino radiata (Pinus radiata), con base en un modelo de simulación integrado con una metaheurística de algoritmos genéticos. Este mismo algoritmo de inteligencia artificial fue utilizado por Kivinen et al. (2005) y Occeña (1991), para predecir la demanda de productos aserrados, chapas y pulpa por parte de la industria del sector forestal. Así mismo, Pradenas & Peñailillo (2004) propusieron, para maximizar las utilidades, un algoritmo de búsqueda de tabú para la solución de un modelo lineal que caracteriza el problema de planificación en la producción de madera aserrada.
Maturana et al. (2010), evaluaron la programación de la producción maderera obtenida de un modelo exacto, frente a la alcanzada por la implementación de técnicas heurísticas. Además, examinaron los requerimientos computacionales en la generación de la solución y la desviación entre el óptimo y los factibles generados en la heurística. Con el objetivo de generar planes de surtido Zanjani et al. (2010), agregaron al problema de corte parámetros de planeación como periodos de producción e indicadores de cumplimiento como nivel de servicio, de esta manera tenían en cuenta la incertidumbre en la demanda y la obtención de materia prima. Para cumplir el objetivo en la minimización de stock generado por incumplimiento de producción y desperdicios, los autores plantearon dos modelos basados en optimización robusta bajo diferentes escenarios de producción.
La integración de técnicas de optimización y simulación ha generado buenos resultados; en ese sentido, mediante la generación de matrices de valor por árbol individual, Gaudreault et al. (2010) desarrollaron un sistema de optimización de trozado en función del valor del producto, lo cual permite satisfacer la demanda de los aserríos. El estudio se fundamentó en la simulación del suministro y la producción. Mendoza et al. (1991) proponen un modelo de inventario que sirve como base para una herramienta de simulación, que permita la planificación de la producción integrada, además genera sistemas de control de producción de los aserríos; este sistema permite la actualización constante de las existencias y la demanda. Quintero & Rosso (2001) generaron un simulador de diagramas de corte basados en las características de la troza (forma, defectos, especie). También plantearon un modelo de inventario de trozas y tipo de maquinaria utilizada en el proceso de transformación.
Así, el objetivo de esta investigación es modelar matemáticamente la asignación eficiente de productos aserrados a partir de trozas provenientes de plantaciones forestales, mediante la inclusión del concepto de patrones de corte óptimos, con el fin de satisfacer la demanda de producción, minimizar desperdicios generados en la transformación y mejorar la gestión de inventarios. Se espera un aumento en los volúmenes de aprovechamiento de madera y un mejor uso del recurso, por medio de la planificación de la producción con base en la demanda de productos y oferta de materia prima.
MATERIALES Y MÉTODOS
DATOS DE ENTRADA UTILIZADOS PARA LA OPTIMIZACIÓN DE CORTE
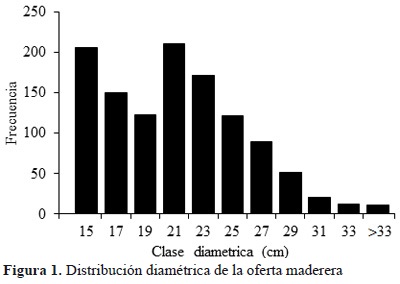
El sistema de análisis y optimización fue probado con datos reales de oferta y demanda obtenidos por la empresa centro de estudio. La información de oferta corresponde a 87.3 m3 de materia prima proveniente de plantaciones de P. caribaea, volumen que fue clasificado en 11 clases diamétricas, con un total de 1170 trozas destinadas a suplir la demanda (Figura 1).
Los datos de productos demandados corresponden a información generada aleatoriamente, debido a que por políticas de confidencialidad de la empresa, no fue posible basar la demanda en datos reales; sin embargo, se cuenta con una prioridad de producción.
Oferta
Se trabajó con datos de volumen para cada clase diamétrica i, los cuales se obtuvieron aplicando la teoría de la cubicación de cuerpos teóricos en rotación. A partir de las áreas transversales de cada troza y el largo de la misma se implementó la ecuación volumétrica formulada por Smalian (Ecuaciones 1 y 2).
donde, Vi es el volumen (m3), gb y g corresponden al área transversal inicial y final de la troza i, db y ds son el diámetro inicial y final de la troza (cm) y l es la longitud de troza.
Demanda
Los datos de productos demandados están compuestos por la unión entre espesor, ancho y largo, con lo cual se determina ochenta tipos de productos l diferentes a obtener. El volumen de los productos se obtendrá de (Ecuación 3).
donde, Vp en el volumen del producto (m3), E el espesor del producto (m), A el ancho del producto (m) y L el largo producto (m).
Rendimiento real
El coeficiente de aprovechamiento de las trozas procesadas se determinó por la relación volumen madera aserrada vp y volumen de trozas vt, en unidades métricas y expresadas en porcentaje. Esto se realizó considerando el volumen en dimensiones nominales de productos obtenidos por tipos de trozas (Ecuación 4).
FORMULACIÓN MATEMÁTICA DEL PROBLEMA
El sistema de optimización implementado en el presente trabajo está compuesto por un conjunto de módulos principales que se interrelacionan. En las secciones posteriores se describe en detalle cada uno y el tipo de modelación matemática utilizada. La resolución de los modelos planteados en la investigación se llevó a cabo en la plataforma de programación matemática General Algebraic Modeling Systemversión 23.7 (GAMS, 1988). Para el presente trabajo de investigación se delimitó el sistema de aserrado desde el momento en que ingresa la troza al patio de acopio del aserrío, hasta cuando es transformada en múltiples productos que posteriormente son apilados.
Generación de patrones corte óptimos
El conjunto de posibles combinaciones entre productos aserrados, obtenidos de diferentes diá-metros de trozas en patio de apilado, se conoce como patrones de corte. Una combinación eficiente entre productos demandados es aquella que optimiza algún criterio de producción (i.e. minimizar la pérdida de material cortado, maximizar el retorno económico de producción). La materia prima es transformada de acuerdo con el plano de corte; igualmente, la factibilidad para implementar un patrón de corte está en función del proceso tecnológico del aserrío. Por ejemplo, las características de las sierras limitan el tipo de corte y números de corte por troza.
En este trabajo la optimización del corte está fundamentada en la minimización volumétrica del desperdicio por troza, en las diferentes operaciones de aserrado. Por tanto, se consideraron las siguientes opciones: a) Patrones de corte factibles en las diferentes clases diamétricas, con tolerancia de desperdicio impuesta por el decisor y b) Patrones de corte óptimos por clase diamétrica.
Este primer modelo se enmarca en la programación lineal-entera mixta (Hillier & Lieberman, 1997), debido a que la variable de decision del modelo es de tipo entera y se rige bajo los siguientes supuestos: a) el largo de los productos a obtener por troza es igual a longitud de la misma, b) se maximiza sobre el menor diámetro de la troza y c) se asume un cilindro perfecto que tiene como diámetro el menor diámetro de la troza. Los problemas de este tipo se caracterizan por la siguiente notación.
Sujeto a,
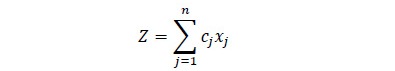
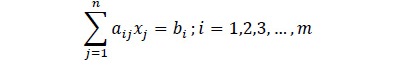
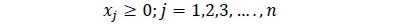
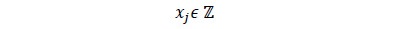
donde, cj es un vector fila de costo asociado al conjunto de datos j, mientras que xj, bi son vectores columna que están relacionados a la variable objetivo y un parámetro restrictivo del modelo (Hillier & Lieberman, 1997).
Equilibrio entre patrones de corte óptimos y demanda de producción
La asignación eficiente de diferentes patrones de corte a las clases diamétricas disponibles, de manera que se cumpla con una demanda de producto tipo (Pl), es el objetivo de este modelo. La formulación está basada en los principios de programación fraccional y es resultado de la relación inversa entre desperdicio y utilización de materia prima, de esta manera se busca la disminución del desperdicio volumétrico en el proceso de aserrado por la asignación de patrones de corte a clases diamétricas, mientras se maximiza la utilización de materia prima.
En este caso, la demanda de producción estará caracterizada sólo por las dimensiones de ancho y espesor del tipo de producto generado en el aserrío (longitud continua). De tenerse en cuenta la longitud deberá agregarse un supuesto más de intersección de conjuntos de datos de trozas y productos, donde sólo es posible obtener productos de trozas con igual longitud, caso que operativamente no es cierto, ya que también se pueden obtener productos de diferente longitud por troza siempre y cuando la longitud de esta sea mayor.
Para ilustrar los problemas de tipo fraccional, suponga que la función Z es de la forma fraccional (Hillier & Lieberman, 1997)
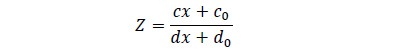
De manera que la función Z estará sujeta a restricciones de oferta, producción y demanda, donde c y d son vectores fila, la variable de decisión x es un vector columna y c0 y d0 son escalares. Este tipo de formulación se puede solucionar con la programación lineal con el despeje de la función, pero en este caso particular para la solución del modelo se tomó como modelo de programación no lineal, dada la facilidad de aplicación en el software utilizado.
Una vez planteados los módulos de optimización, la secuencia de solución es determinada por la relación existente entre estos; por esta razón, primero se muestran los resultados obtenidos en la generación de patrones de corte y luego se termina con la relación entre esquemas de corte y parámetros de producción.
RESULTADOS
GENERACIÓN DEL ÓPTIMO Y FACTIBILIDAD EN PATRONES DE CORTE
Secuencia de niveles de corte inscritos por tipo de troza (l)
La razón entre el diámetro de la troza respecto de la suma entre el espesor de producto y el Kerf o canal de corte de la sierra (dimensión objetivo de aserrado) determina el número de tablas con orillo a espesor objetivo que serán aserradas posteriormente en ancho. Cada una de estas tablas representa una etapa o nivel productivo en donde se determinará la mejor combinación en anchos de producto (Ecuación 5), la sumatoria de productos obtenidos por nivel conforma un patrón de corte factible.
donde, Li/j son los posibles niveles de producción, di el diámetro de la troza tipo i, ej es el espesor de producción tipo j y θ es la tolerancia de medidas adicionales por factores de corte y contracción de la especie (7.8 % en el eje tangencial)
Distancia por nivel de corte (2σl)
Con el fin de establecer el ancho o la longitud disponible por nivel de corte, donde se van a obtener los posibles anchos de producción, se estableció una relación trigonométrica entre el radio de la cara menor en la troza y los diferentes niveles de producción (Figura 2). La longitud (σl) es calculada mediante el despeje del teorema de Pitágoras (Ecuación 6), asumiendo la simetría de la circunferencia con diámetro igual al diámetro menor de la troza, la longitud real equivale a 2 veces σl.
donde, σl es el ancho disponible, ri el radio de la sección circular y ej espesor de corte
Generación de combinaciones factibles en ancho de producción
Se adaptó un algoritmo heurístico propuesto por Arce et al. (2007) en su trabajo de optimización del trozado. El algoritmo describe la secuencia de sentencias que determinan el conjunto de combinaciones de corte que son posibles de obtener a partir de los cuatro anchos de producción.
Paso 1. Calcule la longitud mínima de una secuencia de anchos de producción (k = 1, 2, 3,�, J); defina (kmin + 2,�, K).
Paso 2. Calcule el valor de posibles combinaciones entre (k = 1, 2, 3�. K), elimine aquellos valores de puntos equivalentes generados en la combinación de (Lj = 1, 2, 3�. J).
Paso 3. Genere un vector (Ul) a partir de los valores calculados en los pasos 1 y 2, en orden de menor a mayor longitud (k).
Paso 4. A partir del diámetro de la mayor clase diamétrica (di max) ubique el vector (Ul) hasta que Ul ≈ di max. De no cumplirse la condición vuelva al paso 3, de lo contrario termine.
El conjunto de combinaciones factibles de corte está conformado por 13 posibles longitudes para ser aserradas en ancho.
Rendimiento volumétrico por niveles de corte (φl, k)
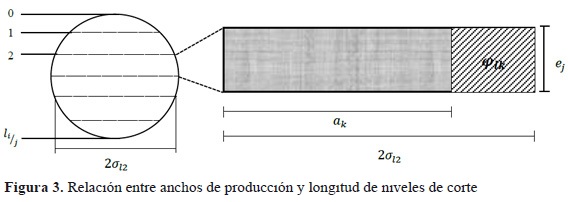
Se establece para cada nivel de producción las posibilidades de corte en ancho y respectivamente el nivel de aprovechamiento asociado a esta relación (Figura 3). La ecuación 7 determina el factor de aprovechamiento por tipo de troza i, de manera que la sumatoria del factor de aprovechamiento en los diferentes niveles de corte establece la producción neta por troza.
donde, φl, k es el factor de aprovechamiento de asignar el ancho de producción k en la longitud del nivel de corte l, ak es la longitud de ancho de producción.
La información generada es consignada en una matriz de l niveles de corte por k productos, la cual consiste en la entrada de datos principales para generar los patrones de corte óptimos, dado que implícitamente se encuentran todas las posibles combinaciones entre productos a obtener.
Modelo matemático
El modelo a plantear busca maximizar el factor de aprovechamiento volumétrico de las diferentes trozas, mediante la asignación de patrones de corte óptimos dentro de las múltiples combinaciones que pueden ser generadas en el sistema de corte.
Para la función teórica, la variable de decisión representa el número de veces que está el ancho de producción k en la longitud de cada nivel de corte evaluado por troza xlk. La notación matemática de los parámetros restrictivos del modelo son: vi volumen de troza tipo i en m3 (tal que i = 1, 2,3,�, I), ej y ak el espesor y ancho de producción en m (tal que j = 1, 2, 3, �, J y k = 1, 2, 3,�, K), li/j es la secuencia de niveles de corte en troza tipo i con el espesor objetivo de corte tipo j (tal que l=1, 2, 3,�, L), 2σl es la distancia por nivel de corte en el nivel de corte tipo l, en el espesor de corte objetivo tipo j (en m) y φl, k es el rendimiento volumétrico por nivel de corte l y ancho de producción tipo k.
Los subíndices denotados anteriormente representan los siguientes conjuntos: tipos de trozas agrupadas por clases diamétricas i, los posibles espesores y anchos de producción que dan dimensión al producto final j, k. Una vez definidos los conjuntos del modelo, los parámetros restrictivos y la variable de decisión del modelo se plantea el modelo de optimización (Ecuación 8).
La función objetivo planteada en la ecuación 8 pretende hacer máximo el uso de la materia prima tratando de asignar el mayor número de anchos de producción por nivel de corte evaluado, teniendo en cuenta todos los tipos de troza y los espesores de producción. El conjunto de solución es limitado por las funciones propuestas en las ecuaciones 9, 10 y 11.
La función que representa la ecuación 9 establece la restricción de longitud, el ancho de los diferentes productos finales generados no puede superar la longitud de cada nivel de corte en las diferentes trozas evaluadas, conocida como la restricción de la mochila (Hifi, 2004; Pileggi et al., 2007; Gracia, 2008). De esta manera la sumatoria por niveles de corte de aquellas combinaciones en ancho que cumplan la desigualdad son considerados como patrones de corte factibles.
Es necesario imponer al modelo de optimización una cota mínima de aprovechamiento en los diferentes niveles de corta, para esto, en la función presentada en la ecuación 10, el autor propone que solo deben ser tenidas en cuenta aquellas combinaciones en anchos de producción que aprovechen más del 60 % de la madera disponible en cada nivel de corte.
Por último, al ser la variable de decisión de tipo discreta, es necesario aclarar que la solución debe pertenecer a la familia de los enteros positivos.
ASIGNACIÓN EFICIENTE DE PATRONES DE CORTE A PARTIR DE OFERTA DE MATERIA PRIMA Y DEMANDA DE PRODUCCIÓN
Con una demanda de producción Pl y una oferta volumétrica agrupada por clases diamétricas Ci, donde cada clase diamétrica posee una serie de patrones de corte z y rendimientos volumétricos asociados a la implementación de cada combinación de producción (φi, z), se pretende equilibrar la relación entre oferta y demanda.
El conjunto de datos de entrada al modelo corresponde a los resultados generados en la formulación anterior, i corresponde a clases diamétricas y z patrones de corte factibles por clase diamétrica, al tener en cuenta la demanda se genera el conjunto l, que representa el tipo de producto final que se fabrica. A continuación se describen los parámetros que se tuvieron en cuenta en la formulación del modelo teórico.
nizl es el número de productos tipo l (generados en el patrón de corte z en la troza con clase diamétrica tipo i), vl es el volumen en m3 de productos tipo l (tal que l =1, 2, 3,�, L), vi es el volumen en m3 de troza tipo i (tal que i = 1, 2, 3,�, I), vz es el volumen en m3 del patrón de corte tipo z (tal que z = 1, 2, 3,�, Z), ciz es el volumen m3 de troza tipo i consumido implementando el patrón de corte tipo z, Ci es el volumen total de troza tipo i disponible en patio y φi, z es el valor de desperdicio del patrón de corte tipo z en la troza tipo i.
Las variables de decisión xiz y hl están orientadas a: la primera designa el número de trozas tipo i, las cuales se cortarán de acuerdo con el patrón de corte tipo z de manera que se satisface la demanda requerida y se minimiza el desperdicio generado, la segunda representa la generación de productos no demandados, variable representada en la ecuación 13. Esta última se considera como variable de desviación del sistema.
Modelo matemático
La diferencia volumétrica entre producción de-mandada y oferta disponible es desagregada en las funciones presentadas en las ecuaciones 12 y 13. La primera representa el desperdicio generado en las operaciones de transformación por la implementación de patrones de corte y la segunda simboliza la generación de productos no demandados o coproductos.
El modelo teórico es planteado de manera relativa y no lineal para entender el desperdicio como el cociente entre la producción y el volumen total, teniendo en cuenta los planteamientos de Caballero et al. (2009). Al proponer la diferencia absoluta entre estos dos parámetros, no es posible comparar qué tan grande es la magnitud de desperdicio con respecto al volumen.
Suponga una formulación lineal de tipo X-Yδ
donde, X es igual a 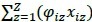 Y es
Y es 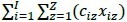 y δ equivale al desperdicio total en producción, la diferencia absoluta indica simplemente el volumen total desperdiciado en la operación. Este resultado no permite inferir el tamaño del desperdicio, dado que no es contrastable con ningún parámetro. Ejemplo: suponga que (δ = 50 %) se evaluaron dos opciones de corte con los siguientes valores:
y δ equivale al desperdicio total en producción, la diferencia absoluta indica simplemente el volumen total desperdiciado en la operación. Este resultado no permite inferir el tamaño del desperdicio, dado que no es contrastable con ningún parámetro. Ejemplo: suponga que (δ = 50 %) se evaluaron dos opciones de corte con los siguientes valores:
X1 = 100 m3; Y1 = 165 m3
X2 = 200 m3; Y2 = 400 m3
Para el primer caso se tendría: (X1 �Y1δ) = 17.3 m3, mientras que (X2 �Y2δ) = 20 m3. A partir del objetivo de minimizar el desperdicio, la primera opción sería tomada en el modelo. Sin embargo, comparando el resultado con la diferencia relativa (X/Y) = δ, tenemos: (X1/Y1) = 0.61, lo cual indica que el 61 % del volumen de trozas con esa opción de corte fue desperdiciado. Con la segunda posibilidad de corte obtenemos: (X2/Y2)= 0.55 (55 % desperdiciado). Mientras que en la formulación ideal, la primera opción minimiza el objetivo; con la segunda, la relación fraccional disminuye el desperdicio. De esta manera, el modelo que minimiza el desperdicio, teniendo en cuenta oferta y demanda, se expresa como (Ecuación 14)
Donde la ecuación 14 representa la función obje-tivo. La minimización del desperdicio se entiende como la suma entre la pérdida de materia prima por factores de proceso (patrones de corte) y los residuos generados por productos no demandados (coproductos). Al no tener en cuenta en esta primera formulación horizontes o periodos de órdenes de compra de productos, se asume la generación de coproductos como desperdicio. Las restricciones de demanda, producción y oferta son representadas en las funciones que se presentan en las ecuaciones 15, 16 y 17, respectivamente.
La minimización del exceso de producción me-diante la diferencia entre oferta y demanda se representa en la ecuación 15. En la función, el sustraendo (coproductos) representa un parámetro de holgura. El equilibrio entre oferta y demanda será posible mientras que la holgura se acerque a 0. De esta forma se generan únicamente los productos demandados, disminuyendo el costo y volumen asociado al inventario de productos de la empresa.
Es necesario limitar el volumen de productos generados. Por esta razón, el valor no puede ser mayor que el volumen de la troza de la cual se obtuvo esa combinación de productos (Ecuación 16).
Un indicador relevante en la evaluación de la eficiencia en el proceso de aserrado es la cantidad de materia prima utilizada en el cumplimiento de las órdenes de producción. En este caso, el planteamiento en la ecuación 17 está orientado a satisfacer la demanda a partir del volumen existente en patio. De esta manera, el volumen utilizado en la implementación de diferentes esquemas de corte que surten la demanda de producción no puede sobrepasar el volumen total existente en el patio.
Por último, el número de trozas a las cuales se le implementó determinado patrón de corte z debe ser un número entero positivo, debido a que la variable de decisión es de tipo discreto (Ecuación 18).
De esta manera, con la integración de los dos modelos formulados se espera suplir las órdenes de producción y mejorar el nivel de aprovechamiento de gestión de inventarios en el aserrío tomado como centro de estudio.
SOLUCIÓN COMPUTACIONAL
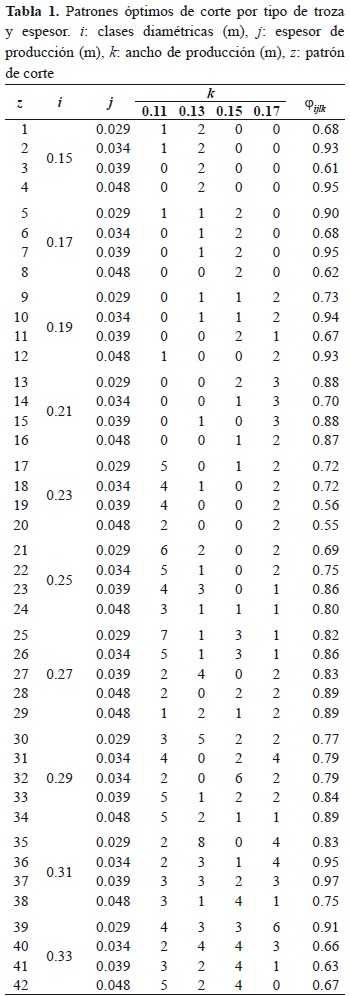
La resolución del modelo generó 42 patrones de corte óptimos (Tabla 1), con aprovechamiento por troza y espesor del 79 % en promedio. El modelo está compuesto por 8161 ecuaciones y 73 441 variables, esto maximiza el producto entre factor de aprovechamiento y número de anchos de producción, Z = 34.34.
De esta manera, un patrón de corte tipo z, asociado a una clase diamétrica i y espesor j, es representado por un vector de m dimensiones, el cual contiene la información contabilizada del número de productos obtenidos, donde h representa el número de productos de ancho k, en el espesor j, en la troza tipo i
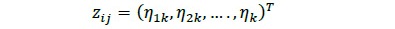
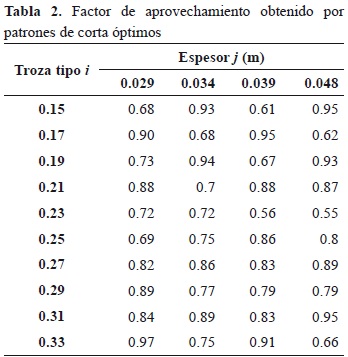
Teniendo en cuenta los factores de uso de la materia prima (Tabla 2), las trozas de las cuales se hace un mejor uso, sin importar el espesor de corte, corresponden a las clases diamétricas con marca de clase: 0.27 y 0.31 m. Las que presentaron menor nivel de aprovechamiento fueron los espesores 0.039 - 0.048 en la marca de clase 0.23. Además, en la mayoría de clases diamétricas, el factor de aprovechamiento está en función del espesor de producción al cual sean cortadas (i = 0.15, 0.17, 0.19, 0.23, 0.33).
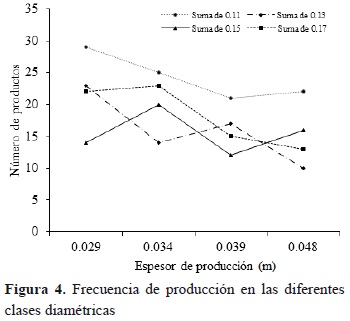
Al evaluar la tendencia de producción de los patrones de corte óptimos, como estos han sido generados con el objetivo de maximizar el uso de las trozas, se empuja la producción hacia la obtención del mayor número de productos (aserrado no cualitativo). Por esta razón, la dimensión que más genera los patrones de corte son los productos con el menor ancho bajo los diferentes espesores de producción (Figura 4).
De aplicar una estrategia de corte en escenarios reales de producción, los patrones óptimos presentan baja frecuencia de producción de los siguientes productos l = e k (en m); entonces, l1 (0.029*0.15 m), l2 (0.034*0.13 m), l3 (0.039*0.15 m), l4 (0.048*0.13 m). De presentarse un escenario en el cual estos productos constituyan la demanda principal de producción, la estrategia de corte requerirá mayor volumen bruto para satisfacer la demanda.
Resultados en la asignación eficiente de patrones de corte a trozas
El modelo está compuesto por 27 ecuaciones y 447 variables, de esta manera se minimiza el desperdicio total asociado a la aplicación de diferentes patrones de corte y generación de excedente de producción en Z = 0.22. Este resultado se traduce en desperdicios del orden del 22 % por cada metro cúbico aserrado. Por ejemplo, del volumen total aserrado de 110.25 m3 se desperdició 24.26 m3, que representa un nivel de aprovechamiento de cerca del 75 %.
Para esto, inicialmente se planteó un escenario de producción con una demanda Pl (Tabla 3), la cual debe ser abastecida con el número de trozas existentes, asignadas a los diferentes 42 patrones de corte generados en la primera formulación.
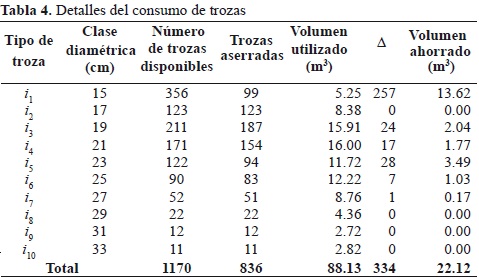
El modelo de minimización generó un plan de aserrado que consume 836 trozas para cumplir con la demanda impuesta en la tabla anterior, con un volumen utilizado de 88.13 m3 (Tabla 4). La tercera parte de la distribución de trozas no fue utilizada, a partir del stock existente; la primera clase diamé-trica (i1= 15 cm) fue la que menos trozas asignó de acuerdo con el número existente en patio, tan solo se empleó el 27 % disponible, mientras que las trozas i3 e i5 fueron las que presentaron mayor frecuencia de uso. En general no hubo necesidad de pedir madera de la plantación siendo entonces si = 0.
Una vez asignadas las trozas a los diferentes patrones de corte utilizados se evalúa la variable hi la generación de productos no demandados es mínima con 231 unidades generadas y volumen de 3.43 m3. Los productos que presentan exceso de producción (i2, i3, i4) son aquellos que registran baja frecuencia de generación en los diferentes patrones de corte. Esta relación puede atribuirse a la presión del modelo a asignar la mayor cantidad de trozas a aquellos patrones de corte donde se encuentren estos productos dentro de su combinación, con el requerimiento de una mayor cantidad de volumen bruto para suplir la demanda de estos.
La tabla 5 muestra de manera detallada los patrones de corte utilizados y el número de trozas asignadas a cada uno de ellos. Los patrones más utilizados son: z2, z8, z10 y z14 con el 45 % de participación de la producción total. En términos de volumen estos suplen 27.4 m3 de la demanda global. Por otra parte, los patrones z5, z17, z31, z36 y z41 fueron asignados en tan solo el 3 % de la frecuencia de asignación.
Este nivel de detalle en el resultado permite organizar la producción para cada uno de los productos a elaborar, establecer las trozas de las diferentes clases diamétricas disponibles necesarias para aserrar y cuantificar el excedente restante en patio. Asimismo, permite asignar los días necesarios para cumplir con el pedido y organizar el número de días de corta de los diferentes espesores objetivo. De esta manera se constituye en una herramienta fundamental en la planificación operativa del sistema de aserrado.
DISCUSIÓN
ESTRUCTURA DEL ESCENARIO CONVENCIONAL DE ASERRADO
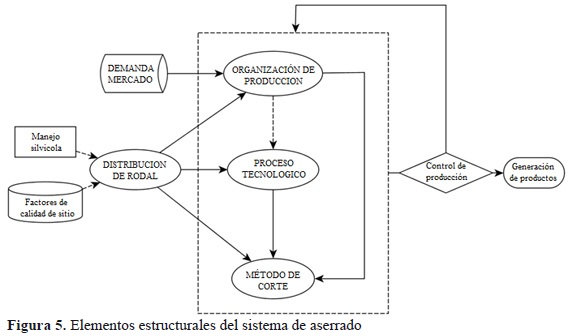
Es preciso empezar el análisis del estudio identificando los elementos relevantes del sistema de aserrado que han influenciado el método de corta convencional. Estos pueden ser de carácter externo condicionando el sistema o ser elementos propios del proceso; la determinación de los elementos conduce a reconocer las tendencias invariantes del sistema (Figura 5).
Inexorablemente, la distribución del rodal y la organización de la producción constituyen, en gran parte, la tendencia del escenario de aserrado actual, puesto que influyen en la mayoría de elementos del sistema y dependen poco de otros elementos del sistema de aserrado. El manejo adecuado de estos generará repercusiones positivas en todo el proceso de transformación (Maturana et al., 2010).
OFERTA POTENCIAL
La aleatoriedad en la transformación de madera día a día, debido al desconocimiento de la frecuencia de la distribución diamétrica, dificulta la planeación del proceso de aserrado y favorece la existencia de bajos índices de producción. Esto se debe al reproceso en el manejo de la materia prima por parte del operario encargado (Barrera & Cuervo, 2010), lo cual genera un aumento en el nivel de desperdicio en el intento de alinear el abastecimiento de las trozas a aserrar con la demanda de producción.
Los datos de la tabla 6 concuerdan con lo expuesto por Zavala & Cortés (2000), el porcentaje de volumen utilizable por troza aumenta a medida que se incrementa el diámetro. Por otra parte, se evidencia la heterogeneidad de diámetros exis-tentes y, por consiguiente, de combinaciones de producción, donde cada uno de estos patrones asocia diferentes índices de utilización. Esto dificulta la toma de decisiones en la obtención de los variados productos demandados por parte de los operarios encargados del proceso.
De esta forma, la oferta potencial es en promedio solamente del 40 % del volumen existente en patio, nivel de desperdicio que concuerda con los valores obtenidos por Caballero et al. (2009), en aserríos de P. caribaea en aserríos cubanos (45 %). Murara et al. (2005) reportan índices de utilización del 52 % en operaciones de aserrado en P. taeda, de esta manera es posible inferir que la tendencia de utilización de la materia prima, aplicando patrones de corte empíricos, no supera el 50 % de aprovechamiento m3-1.
Estructura de costos de adquisición
La materia prima equivale al 50 % de los costos operacionales del sistema de transformación maderero (Molinos, 2005). De este porcentaje, el 60 % del monto es invertido en aserrín, costaneras y astillas. Dado que este porcentaje representa el desperdicio en la operación de aserrado, influye drásticamente en el aumento del costo unitario por producto generado. Frente a esta situacion, para que la actividad sea rentable, se requiere procesar mayor cantidad de volumen (altos puntos de equilibrio). El aserrío tomado como centro de estudio está en condición de asumir los altos costos debido a la oferta volumétrica disponible en pie.
Murara et al. (2005) calcularon el costo de adquisición de trozas equivalente al 74 % del total de los costos de proceso para un método de corta convencional en aserríos de Pinus taeda. Esto demuestra la importancia de generar estrategias capaces de innovar en el manejo de los elementos estructurales del sistema, con la creación de cambios como: aumento de la producción, incrementos en el nivel de utilización de la materia prima, entre otros frentes de mejoramiento.
CONSTRUCCIÓN DE ESCENARIO DESEADO (DEFINICIÓN DE MECANISMOS GENERADORES DE CAMBIO)
El escenario deseado es aquel donde la transformación de madera en rollo en madera aserrada se haga de manera eficiente, optimizando el cociente de aprovechamiento y el nivel de servicio, y disminuyendo el costo unitario de producción.
En este contexto se hace necesaria la incorporación gradual de buenas prácticas que ayuden a mejorar el proceso de transformación. Se propone, entonces, con base en la formulación matemática planteada y los resultados obtenidos en la optimización del rendimiento volumétrico, estrategias orientadas a mitigar el desperdicio y cambio en la organización productiva del aserrío.
Manejo y control de trozas en patio (organización de la oferta volumétrica)
Además de disponer de una materia prima clasificada y organizada, esta estrategia permite generar un flujo constante de alimentación al proceso de aserrío de trozas homogéneas en diámetro, de esta manera contribuye al consumo de toda la oferta disponible y asigna de manera oportuna patrones de corte en función de la demanda productiva. Por otra parte, disminuye los tiempos muertos en operación de aserrado por manipulación de las trozas en el volteo y escuadrado, al reducir la desviación de la distribución diametral aserrada por jornada de trabajo.
Asignación eficiente de trozas a patrones de producción (planeación y programación de la producción)
Este es el planteamiento central del sistema de optimización. Aunque no es viable modificar las características intrínsecas de la troza, es posible hacer una mejor utilización del volumen total de estas. Esto se puede hacer asignando simplemente las trozas a los posibles conjuntos de producción existentes de manera eficiente. Generalmente esta asignación es llevada a cabo por el operario encargado del proceso. Sin embargo, y sin importar el nivel de experticia que tenga, es imposible que calcule la mejor combinación del total de opciones disponibles en el momento de aserrar la troza. Esta es la justificación de por qué este mecanismo puede influir positivamente en la organización de la producción, por esta razón se planteó, en primera instancia, la generación de patrones óptimos de corte por troza. Bajo los supuestos de modelación se encontraron patrones de corte con niveles de aprovechamiento muy altos, escenario poco alcanzable debido a las características de calidad y forma de la troza. Por tanto, es importante considerar, además de la combinación óptima de producción por diámetro y troza, el conjunto de patrones de corte que cumplen con niveles de aprovechamiento superiores al 60 %. Para esto es necesario evaluar las permutaciones generadas por troza y espesor evaluado, este conjunto conforma el espacio de búsqueda inicial en la asignación eficiente de la estrategia de corte en función de una demanda productiva.
De acuerdo con los datos encontrados, a partir del sistema de optimización se logró tener desperdicios de 22 %, este valor es generado bajo una serie de supuestos ideales de la calidad y forma de la troza. Con base en el estudio de generación de desperdicios realizado por (Murara et al., 2005), se asume un desperdicio adicional del 18 % adjudicado a costaneras, productos con arista faltante y demás defectos en los productos debido a la calidad de las trozas. Esta característica no se tuvo en cuenta por ausencia de datos y complejidad de incluir la probabilidad de que una troza tenga cierta calidad en la formulación. Así, el desperdicio, luego de aplicar el sistema de optimización, se ubica en el 40 %, el cual, en comparación con el sistema convencional, redujo el desperdicio en 20 %.
De esta manera, el resultado no difiere de los reportes de optimización hechos por Mcphalen (1978), con una reducción en el uso volumétrico del recurso maderero del 26 %. Murara et al. (2005) reportan factores de minimización de desperdicios de 45 %, mientras que Caballero et al. (2009) lograron reducir el desperdicio en un 50 %. Estos valores están sujetos al tipo de formulación empleada en la optimización y a las características de los elementos del sistema de transformación de cada aserrío.
Por otra parte, los resultados generados en la optimización permiten determinar el conjunto de trozas y patrones principales (Pareto), con el cual se cumple el 80 % de la demanda (Figura 6); esas trozas pertenecen a las clases diamétricas (i3- i6).
Este resultado no solamente genera los lineamientos de producción, sino que también permite identificar el diámetro ideal de las trozas; así como, analizar en reversa las medidas dasométricas y silvícolas necesarias para que el turno de corta de las masas forestales, que abastecen el aserrío, esté orientado a obtener trozas de diámetro medio y desviación diametral en relación con las más utilizadas en el sistema de aserrado.
Manejo de madera aserrada en patio
Frente a esto, el modelo propuesto evalúa el exceso de producción de madera aserrada. Este indicador en conjunto con información de datos de demanda, tiempos de entrega, descuentos por defectos, estructura de costos permite maximizar el nivel de servicio con base en la disponibilidad de madera aserrada, ya que una de las salidas del sistema optimizador cuantifica el nivel de inventario generado y establece montos de stock de seguridad para los diferentes productos, con el objetivo de que no existan faltantes de cualquier tipo de referencia de madera aserrada.
CONCLUSIONES
Una planeación competente se puede lograr mediante una buena administración de los recursos existentes, en este caso, la generación y asignación eficiente de productos por troza aumenta el factor de aprovechamiento por troza del 45 al 55 %, que fue el porcentaje mínimo presentado en la generación de los patrones de corte óptimos. El 10 %, que corresponde a la diferencia, se refleja en la minimización del volumen bruto procesado, mejor uso de materia prima en proceso y disminución en la estructura de costos.
El sistema de optimización propuesto es un método novedoso en el proceso de transformación maderero, ya que permite la integración de la investigación de operaciones para generar cambios en el proceso de aserrado. Aunque es un tema ampliamente tratado a nivel mundial, en nuestro país este es uno de los primeros trabajos realizados en este ámbito. Por esta razón genera un aporte valioso a la innovación tecnológica forestal en beneficio de mejorar las características competitivas del sector forestal.
La aplicación de la investigación operacional permite al decisor formular los parámetros importantes del sistema de transformación e interrelacionarlos en función de optimización de un atributo de interés. De esta manera, esta herramienta se constituye una base fundamental del análisis de procesos industriales en el sector forestal colombiano.
AGRADECIMIENTOS
Agradecemos al ingeniero Javier Medina por permitir el ingreso a la planta de transformación maderera y sus aportes técnicos acerca del proceso de aserrado; al profesor Cesar López por la colaboración en el ajuste del modelo matemático. A la Universidad Distrital Francisco José de Caldas y al proyecto curricular de Ingeniería forestal por permitir los espacios académicos para el desarrollo del estudio y en general a todos aquellas personas que aportaron ideas en pro del desarrollo de esta investigación.
REFERENCIAS BIBLIOGRÁFICAS
Acosta, I. (2004). Informe nacional Colombia: Estado de tendencias y perspectivas el sector forestal en América latina. Roma: Organización de las Naciones Unidas para la Alimentación y la Agricultura. 113 p.
Aguilar, C., & Sanhueza, R. (2003). Caracterización y estandarización de productos, procesos y equipos en la industria del aserrío. (Trabajo de pregrado, Ingeniería de Maderas). Concepción: Universidad del Bio - Bio. 270 p.
Arce, J., MacDonagh, P., & Friedl, R. (2007). Generacao de padroes otimos de corte a traves de algoritmos de tracamento aplicados a fustes individuales. Revista Arvore, 28(2), 207-217.
Barrera, J.M., & Cuervo, S. (2010). Manual de buenas prácticas en aserraderos de comunidades forestales. México: Consejo Civil Mexicano para la Silvicultura Sostenible, Rainforest Alliance, Reforestamos México. 110 p.
Caballero, R., Gómez, T., Molina, J., Fosado, O., León, M. A., & Garofal, M. (2009). Sawing planning using a multicriteria approach. Journal of Industrial and Management Optimization, 5(2), 308-317.
Cancino, J. (1993). Modelo optimizador de trozado de árboles basado en funciones de ahusamiento y programación dinámica. Turrialba: CATIE. 225 p.
Carnieri, C., & Mendoza, G.A. (2000). A fractional algorithm for optimal cutting of lumber into dimension parts. Annals of Operations Research, 95(1), 83-92.
Faaland, B., & Briggs, D. (1984). Log bucking and lumber manufacturing using Dynamic programing. Management Sciencie, 30(2), 245-257.
FAO [Organización de las Naciones Unidas para la Alimentación y la Agricultura]. (2002). Información para el desarrollo sostenible; Estado de la información en Colombia. Santiago de Chile: Organización de las Naciones Unidas para la Alimentación y la Agricultura.155 p.
Fosado, O. (1999). Tratamiento económico - operativo del proceso de aserrado en la madera (Tesis Doctoral). Pinar del rio: Universidad Pinar del rio. 158 p.
GAMS [General Algebraic Modeling System]. (1988). General algebraic modeling system (version 23.7). Washington: GAMS Development Corporation ISBN: 0-201-54664-7, recuperado de http://www.gams.com/.
Gaudreault, J., Frayret, J.-M., Rousseau, A., & D�Amours, S. (2010). Combined planning and scheduling in a divergent production system with co-production: A case study in the lumber industry. Computers & Operations Research, 38(9), 1238-1250.
Gracia, C. (2008). Métodos y algoritmos para resolver problemas de corte unidimensional en entornos realistas. Aplicación a una empresa del sector siderúrgico. (Tesis Doctoral). Valencia: Universidad politécnica de Valencia. 221 p.
Hifi, M. (2004). Exact algorithms for unconstrained three-dimensional cutting problems: a comparative study. Computers & Operations Research, 31(5), 657-674.
Hillier, F., & Lieberman, G. (1997). Introducción a la investigación de operaciones. Atlampa: Mc Graw Hill. 500 p.
Kivinen, V.-P., Uusitalo, J., & Nummi, T. (2005). Comparison of four measures designed for assesing the fit between the demand and output distributions of logs. Canadian Journal of Forest, 35(3), 693-702.
Lagos, R. (2006). Comparación de dos software de simulación para la industria del aserrío de Pinus radiata D. Don. (Trabajo de pregrado, Ingeniería de Maderas). Valdivia: Universidad Austral de Chille. 136 p.
Maturana, S., Pizani, E., & Vera, J. (2010). Scheduling production for a sawmill: A comparison of a mathematical model versus a heuristic. Computers & Industrial Engineering, 59(4), 667-674.
Mcphalen, J. (1978). A method of evaluating bucking and sawing strategies for sawlogs (Master thesis). Vancouver: University of British Columbia. 160 p.
Mendoza, G., Sprouse, W., Luppold, W., Araman, P., & Meimban, R. (1991). An integrated management support and production control system for hardwood forest products. Computers in Industry, 16(1), 343-350.
Molinos, V. (2005). Mercados selectos para madera aserrada, dimensionada y seca de pino y sus manufacturas, producidas en Colombia. Bogotá: USAID. 19 p.
Murara, M.I., Rocha, M.P.d., & Junior, R. (2005). Rendimento em madeira serrada de pinus taeda para duas metodologias de desdobro. Floresta, 35(3), 473-483.
Novak, R.d.S. (2007). Um sistema de otimiza�ao aplicada ao desdobro de madeira. (Tesis de Maestría). Curitiba: Federal do Paraná. 141 p.
Occeña, L. (1991). Computer integrated manufacturing issues related to the hardwood log sawmill. Forest Engineering, 3(1), 39-45.
Pileggi, G., Morabito, R., & Arenales, M.N. (2007). Heurísticas para os problemas de generacao e sequenciamiento de padroes de corte bidimensionais. Pesquisa operacional, 27(3), 549-568.
Pradenas, L., Peñailillo, F., & Ferland, J. (2004). Agregate production planning problem. A new algorithm, Electronic Notes in Discrete Mathematics, 18(1), 193-199.
Quintero, M., & Rosso, F. (2001). Propuesta de un simulador de aserraderos para la industria forestal Venezolana. Revista Forestal de Venezuela, 45(1), 95-101.
Rebolledo, M., & Baesler, F. (2001). Uso de inteligencia artificial para la optimización de un modelo de simulación aplicado a un proceso de remanufactura de pino radiata. Maderas de ciencia y tecnología, 3(2), 52- 62.
Romero, R., Poblete, M., & Baesler, F. (2004). Modelo de programación de la producción para la industria del aserrío. Revista Ingenieria Industrial, 3(1), 19-23.
Todoroki, C.L., & R�nnqvist, E. (1999). Combined primary and secondary log breakdown optimization. Operational Research Society, 50(3), 219-229.
Zavala, D.Z., & Cortés, R. H. (2000). Análisis del rendimiento y utilidad del proceso de aserrío y troceria de pino. Madera y Bosques, 6(2), 88-94.
Zanjani, K., Ait-Kadi, D.M., & Nourelfath. M. (2010). Robust production planning in a manufacturing environment with random yield: A case in sawmill production planning. European Journal of Operational Research, 201(3), 882-891.
Licencia
Colombia Forestal conserva los derechos patrimoniales (copyright) de las obras publicadas, y favorece y permite la reutilización de las mismas bajo la licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional por lo cual se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que:
Se reconozcan los créditos de la obra de la manera especificada por el autor o el licenciante (pero no de una manera que sugiera que tiene su apoyo o que apoyan el uso que hace de su obra).



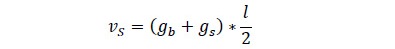 Ec. 1
Ec. 1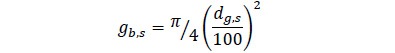 Ec. 2
Ec. 2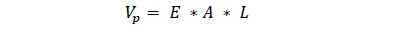 Ec. 3
Ec. 3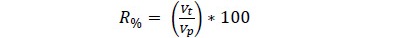 Ec. 4
Ec. 4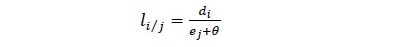 Ec. 5
Ec. 5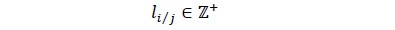
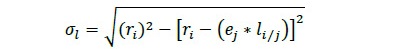 Ec. 6
Ec. 6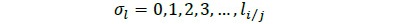

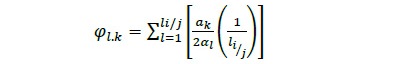 Ec. 7
Ec. 7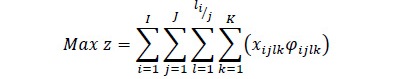 Ec. 8
Ec. 8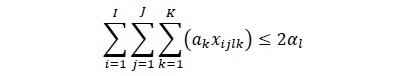 Ec. 9
Ec. 9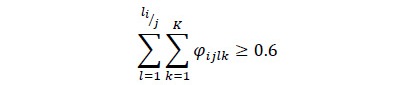 Ec. 10
Ec. 10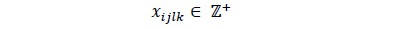 Ec. 11
Ec. 11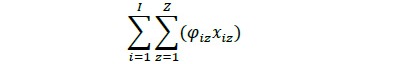 Ec. 12
Ec. 12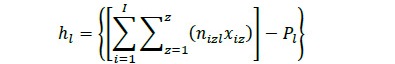 Ec. 13
Ec. 13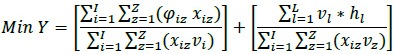 Ec. 14
Ec. 14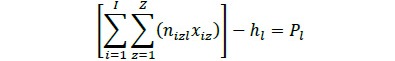 Ec. 15
Ec. 15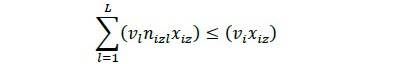 Ec. 16
Ec. 16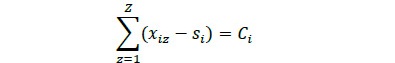 Ec. 17
Ec. 17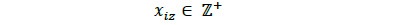 Ec. 18
Ec. 18