DOI:
https://doi.org/10.14483/23448393.16144Published:
2020-07-27Issue:
Vol. 25 No. 2 (2020): May - AugustSection:
Electrical and Electronic EngineeringEstudio Comparativo de Tres Estrategias de Control para la Regulaci´on de Frecuencia de una Micro Red en Operaci´on Aislada
Comparative Study of Three Control Strategies for the Frequency Regulation of an Isolated Microgrid
Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 12 de abril de 2020; Revisión recibida: 1 de junio de 2020; Aceptado: 19 de junio de 2020
Resumen
Contexto:
La reducción de combustibles fósiles, la necesidad de disminuir las emisiones de dióxido de carbono (CO2) en el planeta y el interés por garantizar una seguridad energética ha incrementado la investigación en la producción de energía eléctrica utilizando fuentes de energías renovables incorporadas a microrredes o MG (por sus siglas en inglés de microgrids). Este panorama presenta desafíos técnicos que deben ser cubiertos para garantizar niveles de confiabilidad adecuados.
Método:
Este estudio compara tres estrategias de control basadas en el control predictivo del modelo o MPC (por sus siglas en inglés de model predictive control), el control óptimo LQ-Servo (por sus siglas en inglés de linear quadratic servo) y el control proporcional integral o PI, con el objetivo de regular la frecuencia frente a incertidumbres en la carga y perturbaciones ambientales, considerando un modelo lineal aislado de microrred que incluye generadores convencionales y renovables, dispositivos de almacenamiento de energía y cargas.
Resultados:
Las simulaciones de la MG en operación aislada, en presencia de perturbaciones de viento, carga y potencia solar, muestran un mejor desempeño bajo diferentes escenarios de los controladores MPC y LQ-Servo con respecto a las características dinámicas que presenta la desviación de frecuencia y la señal de control.
Conclusiones:
La estrategia de control óptimo LQ-Servo, poco investigada en MG, se presenta como una opción viable a considerar en el diseño de controladores secundarios de MG en operación aislada, debido a las características de desempeño mostradas en la regulación de frecuencia. Consideración de modelos que incluyan restricciones en las variables de control y en los estados de la MG, así como la implementación de los mismos, quedan como trabajo futuro.
Palabras clave:
Función costo, generación renovable, optimización, perturbación, sintonización.Abstract
Context:
The reduction of fossil fuels, the need to reduce emissions of carbon dioxide (CO2) on the planet and the interest in guaranteeing energy security have increased research in production of electrical energy using renewable energy sources incorporated into microgrids (MGs). This scenario presents technical challenges that must be covered to guarantee adequate levels of reliability.
Method:
This study compares three control strategies based on the predictive control of the model or MPC (Model Predictive Control), the optimal control LQ-Servo (Linear Quadratic Servo) and the control integral proportional or PI, with the aim of regulating the frequency against uncertainties in the load and environmental disturbances, considering an isolated linear microgrid model, which includes conventional and renewable generators, energy and load storage devices.
Results:
The simulations of the microgrid in isolated operation, in the presence of wind, load and solar power disturbances, show a better performance under different scenarios of the MPC and LQ-Servo controllers with respect to the dynamic characteristics presenting the frequency deviation and the control signal.
Conclusions:
The LQ-Servo optimal control strategy, little researched in microgrids, is presented as a viable option to consider in the design of secondary microgrid controllers in isolated operation, due to the characteristics of performance shown in the frequency regulation. Consideration of models that include restrictions in the control variables and in the states of the microgrid, as well as their implementation, remain for future work.
Keywords:
Cost function, disturbance, optimization, renewable generation, tuning.Introducción
Debido a la reducción de combustibles fósiles y la necesidad de disminuir las emisiones de dióxido de carbono (CO2) en el planeta [14], además del interés por tener un sistema eléctrico confiable que supla el aumento de la demanda de energía y garantice seguridad energética, se ha incrementado la investigación en la producción de energía eléctrica utilizando fuentes de energías renovables o RES (por sus siglas en inglés de renewable energy source), tales como paneles solares o PV (por sus siglas en inglés de photovoltaic panel), turbinas eólicas o WTG (por sus siglas en inglés de wind turbine generator), biomasa y geotermia [25]. Según [17], la composición de la canasta energética mundial irá cambiando hacia una mayor participación de energéticos limpios, se estima que su participación superará el 10% en 2035, sin incluir la hidroenergía.
Este creciente interés en integrar fuentes de energía renovables intermitentes (solar, eólica) en un sistema de generación distribuida o DER (por sus siglas en inglés de distributed energy resource) presenta desafíos técnicos que deben ser cubiertos para garantizar los niveles de confiabilidad [23]. Una alternativa atractiva para enfrentar dichos desafíos es el concepto de microred o MG (por sus siglas en inglés de microgrid), cuyo propósito es ser un sistema de distribución de bajo voltaje compuesto de fuentes DER (microturbinas, generadores diesel, celdas de carga, paneles solares, etc.), dispositivos de almacenamiento de energía (baterías, banco de capacitores, flywheels, etc.) y cargas [15]. La MG puede operar de una manera no autónoma si está conectada a la red principal o de una manera autónoma si está desconectada de la misma (operación aislada). La operación aislada puede darse por razones económicas, por fallas en la red principal o por suministro de energía a zonas no interconectadas [2]. Esta condición requiere una coordinación propia y eficiente del sistema, ya que los picos de demanda de potencia no coinciden necesariamente con los picos de generación, dada la producción no determinística e intermitente de algunas fuentes de generación. Similar a los sistemas de potencia convencionales, las MG operan usando lazos de control, los cuales pueden ser clasificados en: primario (local), secundario, terciario (emergencia) y global. El control primario generalmente corresponde a un controlador proporcional descentralizado (droop control) de acción rápida, el cual reduce las desviaciones de frecuencia y voltaje de la MG. El control secundario asegura que las desviaciones de frecuencia y voltaje de la MG sean reguladas a cero después de cambios en las dinámicas del sistema, actuando sobre las referencias de los controladores primarios. El control terciario cubre todos los esquemas de emergencia con el fin de mantener el sistema estable y disponible en caso de contingencia. Por último, el control global permite la operación de la MG dentro de un óptimo económico y organiza la relación entre la MG y la red de distribución, así como también la relación con otras MG [3].
Diferentes estudios de investigación sobre MG en operación aislada se han desarrollado.Varias aproximaciones para el modelo y control son presentadas en [21] y [10]. Las dinámicas de un sistema autónomo que está conformado por un generador diesel y una turbina eólica usando modelos simplificados son investigadas en [24]. Un análisis de estabilidad de pequeña señal para un sistema híbrido autónomo de generación de energía que incluye generación renovable es investigado en [20]. Una combinación de lógica difusa y la técnica PSO (por sus siglas en inglés de particle swarm optimization) para la sintonización óptima de un controlador proporcional integral o PI (por sus siglas en inglés de proportional integral) en una MG en operación aislada es presentada en [6]. Un esquema de control secundario distribuido utilizando un controlador PI para eliminar las desviaciones de frecuencia y voltaje es aplicado en [26].
En [8], [13] y [7] estrategias de control secundario distribuido usando técnicas de consensus o sistemas multiagente son aplicadas. En [4] y [1] técnicas de control robusto son aplicadas a microrredes en operación aislada para la regulación de frecuencia y voltaje, además, arquitecturas de control predictivo para MG son investigadas en [19], [27] y [30]. Una combinación estructurada de controladores difusos en cascada con controladores PI-PD para el control secundario de frecuencia es utilizada en [12], mientras que una evaluación comparativa de técnicas de administración de potencia para MG DC (por sus siglas en inglés de corriente continua) es investigada en [11].
Debido a la importancia descrita acerca del análisis e investigación de MG, técnicas de control secundario para la regulación de frecuencia de una MG en operación aislada utilizando un modelo lineal son presentadas en este artículo. Considerando un modelo de respuesta en frecuencia de una MG encontrado en [4] y [5], se implementan tres estrategias de control: MPC (por sus siglas en inglés de model predictive control), LQ-Servo (por sus siglas en inglés de linear quadratic servo) y PI, con el fin de eliminar las desviaciones de frecuencia generadas por perturbaciones en la carga y por los generadores PV y WTG. El objetivo es mostrar las bondades que presentan el controlador LQ-Servo (poco utilizado en este contexto) y el controlador MPC con respecto a las características dinámicas en la regulación de frecuencia y la señal de control para diferentes escenarios, comparándolos con el desempeño del controlador robusto aplicado en [4] y el controlador PI.
Metodología
Modelo dinámico de respuesta en frecuencia de MG aislada
La MG híbrida propuesta, encontrada en [4] y [5], está compuesta de generadores tipo WTG, PV, DEG (por sus siglas en inglés de diesel engine generator), MT (por sus siglas en inglés de micro turbine) y FC (por sus siglas en inglés de fuel cell), dispositivos de almacenamiento de energía tipo FES (por sus siglas en inglés de flywheel energy storage) y BES (por sus siglas en inglés de battery energy storage), y cargas. La Figura 1 ilustra la configuración de la MG simplificada. Los generadores distribuidos son conectados al bus AC por medio de dispositivos electrónicos de potencia usados para la sincronización de las fuentes AC, es decir, DEG, MT y WTG, y para la inversión de las fuentes DC, tales como FC y PV. Conversores AC/DC son considerados para BES y FES en modo carga y DC/AC en modo descarga.
Figura 1: Esquema simplificado de MG aislada
La Figura 2 muestra el modelo dinámico de respuesta en frecuencia de la MG linealizado en torno al punto de operación (60Hz), en el cual los DG (por sus siglas en inglés de distributed generator) y ESS (por sus siglas en inglés de energy storage system) se modelan como sistemas de primer orden y las variables de la MG son desviaciones en torno al punto de operación. En este modelo las fluctuaciones de carga ΔPLoad y los cambios en la potencia de las RES: ΔPWTG y ΔPPV son consideradas como perturbaciones del sistema, mientras que ΔPMT , ΔPDEG y ΔPFC son considerados como generadores despachables, ya que no dependen de las condiciones ambientales para suministrar potencia. Las constantes de tiempo T, la inercia del sistema M y la constante de amortiguamiento D de la MG considerada se presentan en la Tabla I.
![Modelo dinámico de respuesta en frecuencia de MG aislada [5]](https://revistas.udistrital.edu.co/index.php/reving/article/download/16144/version/12073/16612/97650/0121-750X-inge-25-02-179-gf2.png)
Figura 2: Modelo dinámico de respuesta en frecuencia de MG aislada [5]
Tabla I: Parámetros del modelo de respuesta en frecuencia [4]
El modelo en espacio de estados de laMGde la Figura 2 utilizado en el diseño de los controladores se presenta en las ecuaciones (1) y (2), donde x corresponde al vector de variables de estado, w al vector de perturbaciones, u la señal de control y y la salida.
Las matrices A, B1, B y C están dadas por:
Esquemas de control propuestos
Para el modelo dinámico de respuesta en frecuencia (Figura 2) se utilizan tres esquemas de control secundario (MPC, LQ-Servo y PI), los cuales buscan eliminar la desviación de frecuencia Δf ocasionada por cambios en la generación de potencia de los PV (ΔP PV ) y WTG (ΔP WTG ), además de cambios en la carga ΔPLoad. Los controladores buscan disminuir el tiempo de asentamiento, el error acumulativo, el esfuerzo de control y la energía de seguimiento, entre otras características. A continuación, se presentan el procedimiento de diseño de dichos controladores.
Control predictivo por modelo (MPC)
El objetivo básico del MPC es encontrar la secuencia de control óptima ΔU dentro de un horizonte de predicción Np, tal que minimice una función de error entre la referencia y la salida, utilizando el modelo en espacio de estados (1) de la MG. Si se quiere, la función costo puede incluir un término de penalización para la señal de control. Aunque la secuencia de control óptima es calculada para Nc (horizonte de control) muestras futuras, la implementación del control predictivo usa solamente la primera muestra Δu(ki) mientras ignora el resto [29].
El problema de optimización que refleja el objetivo del control es planteado en (3).
Donde Rs es el vector de referencia de longitud Np, Q una matriz diagonal rqINpxNp ,
una matriz diagonal rwINcxNc y Y la salida del sistema predicha utilizando el modelo (1). rq y rw son usados como parámetros de sintonización para reflejar la importancia relativa del error y penalizar la señal de control respectivamente; estos fueron sintonizados de manera heurística. A continuación, se describe el procedimiento realizado para el diseño del MPC de acuerdo con [29].
1. Discretización: para cumplir con el teorema de Nyquist, se utilizó un tiempo de muestreo Ts de 0,01 s, para la discretización del sistema (1), teniendo en cuenta las constantes de tiempo en la Tabla I. Ad, B1d, Bd y Cd son las matrices discretas obtenidas en MATLAB.
2. Modelo aumentado: utilizando los incrementos de las variables en (4), se deduce el modelo en espacio de estados aumentado mostrado en (5).
Donde 0T = [0 0 … 0]1xn y n es la dimensión de Ad. La forma compacta del modelo expandido esta dada en (6) y (7).
3. Predicción de salida: todas las variables predichas son calculadas en términos del valor actual de los estados x(ki) y del control futuro Δu(ki + j), donde j = 0; 1; …;Nc - 1. Definiendo los vectores (8), la predicción de la salida del sistema para un horizonte de predicción Np y un horizonte de control Nc, puede ser calculada por medio de (9).
Donde
Cabe resaltar que la predicción de salida del sistema se realizó sin tener en cuenta las perturbaciones, ya que se supone que tienen un comportamiento no determinístico.
4. Optimización: para encontrar el óptimo ΔU que minimice J, es necesario reemplazar la ecuación (9) en la función costo (3), de la siguiente manera:
La condición necesaria para encontrar el mínimo de la función de costo J es que
, por lo que se sigue (10).
Despejando ΔU se obtiene la señal de control óptima, esto es (11) y (12).
Solo el primer elemento de ΔU es implementado, es decir, por cada muestra de las variables de estado se optimiza en un horizonte de tiempo finito, pero se implementa únicamente la ranura de tiempo actual.
Control óptimo LQ-Servo
Una aproximación alternativa para el control de la MG, que asegura error en estado estable cero, es usar la estructura de control óptimo conocida como LQ-Servo [16]. Esta aproximación adiciona un nuevo estado al sistema (1) sin tener en cuenta las perturbaciones, la cual integra el error de seguimiento
. De esta manera, se obtiene el sistema (13).
Teniendo el sistema (13) se diseña un regulador cuadrático lineal (LQR), ignorando r en el diseño de u. El criterio de desempeño a ser minimizado en un LQR, de acuerdo con [18], es presentado en (14).
Donde el tiempo final t f es fijo, H y Q son matrices reales simétricas semidefinidas positivas y R es una matriz real simétrica definida positiva. Se asume que no existen limitaciones sobre los estados y controles y que x(tf) es libre. Lo que se busca es mantener x cercano a cero sin demasiado esfuerzo de control, sintonizando los parámetros en las matrices Q y R. Esta sintonización se hizo de manera heurística. De acuerdo con la teoría de control óptimo aplicando el hamiltoniano y las condiciones necesarias de optimalidad, se obtiene (15).
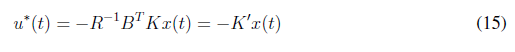
Kalman muestra que si la planta es completamente controlable, A, B, R y Q son matrices constantes y H = 0, K es una matriz constante cuando tf ?? [18]. Bajo estas condiciones, para determinar la matriz K y en consecuencia la solución del LQR, basta con solucionar la ecuación de Riccati dada por (16).
La matriz de controlabilidad [B AB A2B … A7B] de la MG (1) no es de rango completo; sin embargo, es un sistema estabilizable, ya que los estados no controlables son estables. Por lo tanto, es posible aplicar la ecuación (16).
Control proporcional integral (PI)
Los controladores PID son los más conocidos y utilizados en la industria, de ahí que los nuevos estudios en técnicas de control son generalmente comparados con ellos. La sintonización de las constantes del PID puede no ser difícil; sin embargo, encontrar las constantes que aseguren un desempeño óptimo del sistema de control es una tarea compleja. Para ello, una de las herramientas disponibles es el PID Tuner de MATLAB, el cual se basa en un algoritmo que provee una interfaz simple para la sintonización de los parámetros automáticamente [22]. El algoritmo busca una solución óptima de los parámetros para encontrar estabilidad en lazo cerrado, desempeño y robustez, de acuerdo con requerimientos de diseño. Además, existenmétodos de sintonización de PID robustos como el IMC, los cuales buscan un desempeño deseable a pesar de incertidumbres en el modelo [28]. Para la MG (1) se diseñó un controlador PI utilizando la herramienta PID Tuner, lo anterior en busca de un equilibrio en las características dinámicas de la desviación de frecuencia y la señal de control. Aplicando el método IMC se obtuvieron resultados similares.
Resultados
En esta sección, simulaciones en el dominio del tiempo de la MG(1), en presencia de perturbaciones de viento, carga y potencia solar son presentadas. Las simulaciones son realizadas en el software MATLAB. El objetivo es eliminar las desviaciones de frecuencia en torno al punto de operación (mantener Δf = 0) generadas por cambios en las dinámicas del sistema. Para ello tres estrategias de control (MPC, LQ-Servo y PI) son comparadas para diferentes escenarios, entre ellos algunos propuestos en [4].
Escenario 1 (fluctuación potencia de viento ΔPWind): fluctuaciones en la potencia del viento son consideradas para los tres controladores con el fin de determinar los efectos sobre la desviación de frecuencia y la señal de control. En primer lugar, cambios tipo escalón de potencia eólica son analizados. La Figura 3a muestra la perturbación eólica y los comparativos de la desviación de frecuencia y la señal de control. En segundo lugar, las fluctuaciones en la generación de potencia eólica son modeladas a través de una función de distribución de Weibull, la cual es utilizada en sistemas eólicos de acuerdo con [9]. La función densidad de probabilidad de Weibull puede ser expresada como se muestra en (17).
Figura 3: Escenario 1. Perturbación potencia de viento, desviación de frecuencia y señal de control
Donde f(V; k; c) es la probabilidad de potencia del viento (V), c es el parámetro de escala, k el parámetro de forma y V ³ 0,k > 1,c > 0. La Figura 3b muestra la perturbación de la potencia del viento utilizando (17), la desviación de frecuencia y la señal de control. Las señales de respuesta visualizadas en las dos situaciones (Figura 3) muestran que los controladores MPC y LQ-Servo llevan a cero de manera rápida la desviación de frecuencia en comparación con el controlador PI. Al comparar solamente el MPC y el LQ-Servo, apoyándose en el acercamiento mostrado en la gráfica y en la respuesta obtenida con la perturbación de Weibull, se puede observar que para este escenario el controlador LQ-Servo tiene un desempeño superior, ya que regula la desviación de frecuencia de manera rápida utilizando menos energía en la señal de control.
Escenario 2 (fluctuación de carga ΔP Load ): desviaciones tipo escalón, con cambios a los 0, 20 y 40 segundos, son considerados para la potencia que demanda la carga. La Figura 4 muestra la desviación de potencia de carga, la respuesta de la desviación de frecuencia y las señales de control para los tres controladores. Al igual que en el escenario anterior, los controladores MPC y LQ-Servo presentan mejor desempeño que el controlador PI con respecto a las características transitorias de la desviación de frecuencia y la señal de control; sin embargo, son menos notorias que en el prime escenario. Para este escenario el tiempo de asentamiento y el sobre pico del MPC es menor que el del LQ-Servo a costa de mayores oscilaciones en la desviación de frecuencia.
Figura 4: Escenario 2. Perturbación de potencia de carga, desviación de frecuencia y señal de control
Escenario 3 (fluctuación de potencia solar ΔPϕ): cambios tipo escalón y tipo rampa en la desviación de potencia solar son considerados bajo este escenario. En primer lugar, cambios escalón múltiples en intervalos de 10 segundos son examinados para la potencia de la irradiación solar (Figura 5a). En segundo lugar, perturbaciones en la potencia solar tipo rampa mezcladas con un cambio tipo escalón a los 55 segundos son analizadas (Figura 5b).
Figura 5: Escenario 3. Perturbación potencia solar, desviación de frecuencia y señal de control
En la Figura 5 se observa la perturbación solar, la respuesta en la desviación de frecuencia y las señales de control para los tres controladores sometidos a los dos tipos de perturbación. Se realiza un acercamiento a la desviación de frecuencia para comparar con detalle el comportamiento del MPC y del LQ-Servo. Nuevamente es evidente para este escenario que el desempeño de los controladores LQ-Servo y MPC es superior al PI, con respecto a la desviación de frecuencia, sin importar el tipo de perturbación considerada; además, es importante resaltar que el desempeño del controlador LQ-Servo es superior al MPC bajo este escenario, ya que controla la desviación de frecuencia de una manera suave utilizando una señal de control con un gasto de energía menor.
Escenario 4 (cambio simultáneos en ΔP W ind , ΔPϕ y ΔP Load ): en este escenario, perturbaciones simultáneas en las desviaciones de potencia eólica, solar y carga a los 0, 20 y 40 segundos son consideradas. La Figura 6 muestra el comportamiento de la desviación de frecuencia ante el patrón de perturbaciones descrito, donde se evidencia el desempeño superior de los controladores MPC y LQ-Servo con respecto al PI en las características transitorias de la desviación de frecuencia.
Figura 6: Escenario 4. Perturbaciones simultaneas de potencia eólica, solar y carga, desviación de frecuencia
Conclusiones
En este artículo, un modelo de MG en operación aislada encontrado en [4] y [5] se ha usado para el diseño de estrategias de control secundario de frecuencia. Controladores MPC, LQ-Servo y PI son diseñados para regular la desviación de frecuencia (mantener Δf = 0) con base en un modelo de espacio de estados linealizado, sometido a perturbaciones de carga, potencia solar y potencia eólica. De acuerdo con los resultados obtenidos en cuatro de los escenarios propuestos en [4], es evidente que el desempeño de los controladores MPC y LQ-Servo es superior al controlador PI, con respecto a las características dinámicas que presenta la desviación de frecuencia y la señal de control en presencia de perturbaciones e incertidumbres.
Además, es importante resaltar que al comparar dichas respuestas con las obtenidas utilizando el control robusto propuesto en [4] se observan mejores características dinámicas en la desviación de frecuencia bajo todos los escenarios de los controladores en mención. Esto hace de los controladores LQ-Servo (estrategia poco investigada enMG) yMPC alternativas viables a considerar en el diseño de controladores secundarios de MG en operación aislada, teniendo en cuenta que presentan un desempeño similar y sus diferencias están marcadas por la sintonización de sus parámetros, los cuales para este estudio se obtuvieron de manera heurística.
La consideración de modelos que incluyan restricciones en las variables de control y en los estados de laMGquedan como trabajo futuro, además de modelos de optimización para la sintonización de los parámetros Np, Nc, rq y rw del MPC y de las matrices Q y R del LQ-Servo.
Referencias
License
Copyright (c) 2021 Edwin Alexis Pineda Muñoz, Alain Gauthier Selleir
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.
2.jpg)
