DOI:
https://doi.org/10.14483/23448393.2714Publicado:
2004-11-30Número:
Vol. 10 Núm. 2 (2005): Julio - DiciembreSección:
Ciencia, investigación, academia y desarrolloIntroducción a las Desigualdades Lineales Matriciales y su Aplicación en Control Automático
Palabras clave:
control no lineal, control automático, desigualdades lineales matriciales, estabilidad cuadrática, métodos numéricos, optimización (es).Descargas
Referencias
A. Ben-Tal y A. Nemirovsky, «Lectures on Modern Convex Optimization: Analysis, Algorithms and Engineering Applications», Society for Industrial and Applied Mathematics: Mathematical Programming Society, 2001.
J. G. VanAntwerp y R. D. Braatz, «A tutorial on linear and bilinear matrix inequalities», Journal of Process Control, vol. 10, pp. 363-385, 2000.
S. Boyd, L. El Ghaoui, E. Feron y V. Balakrishnan, «Linear Matrix Inequalities in Systems and Control Theory», Studies in Applied Mathematics, Society for Industrial and Applied Mathematics, vol. 15, 1994.
S. Boyd y L. El Ghaoui, «Method of Centers for Minimizing Generalized Eigenvalues», Linear Algebra and Applications, Special. issue on Numerical Lin. Algebra methods in Control, Signals and Syst., vol. 188, pp. 63-111, 1993.
M. Grötschel, L. Lovász y A. Schrijver, «Geometric Algorithms and Combinatorial Optimization», Springer-Verlag, 2da. ed., 1993.
Yu. Nesterov y A. Nemirovsky, «Interior-point Polynomial Methods in Convex Programming», Studies in Applied Mathematics, Society for Industrial an Applied Mathematics, vol. 13, 1994.
L. Vandenberghe y S. Boyd, «Semidefinite Programming», Society for Industrial and Applied Mathematics Review, vol. 38, pp 49 95, 1996.
C.W. Richter Jr., G.B. Sheblé, «Modern Control Engineering», Prentice Hall, 3ra. ed., 1997.
D. Muench y A. Titli, «Introduction to the Design of Fuzzy Controlers Using Linear Matrix Inequalities», Final Internship Report, Laboratorio LAAS, Toulouse, Francia, 1999.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Ingeniería, 2005-00-00 vol:10 nro:2 pág:30-37
Introducción a las desigualdades lineales matriciales y su aplicación en control automático
Mauricio Junca Peláez
Profesor Asistente Departamento de Matemáticas,
Universidad de los Andes.
Víctor Hugo Grisales Palacio
Profesor investigador Laboratorio de Automática, Microelectrónica e Inteligencia Computacional (LAMIC), Universidad Distrital FJDC.
Alain Gauthier Sellier
Profesor Titular Facultad de Ingeniería e Investigador del Grupo de Investigación en Automatización y Producción (GIAP),
Universidad de los Andes.
Resumen
Este artículo presenta una breve introducción y aplicaciones de las desigualdades lineales matriciales en control automático. Esta nueva técnica matemática consiste en llevar los problemas de control a problemas de optimización convexa y resolverlos por medio de eficientes algoritmos computacionales disponibles hoy en día. Usando métodos numéricos se pueden resolver en un tiempo razonable un buen número de problemas de control automático que no se les conoce solución analítica o no la tienen. En este trabajo se consideran como aplicaciones el análisis de estabilidad cuadrática así como las especificaciones de desempeño en términos de restricciones. Estos conceptos se emplean para el diseño de un sistema de control para un péndulo invertido. Los resultados de simulación ilustran la aplicación de la técnica y muestran el cumplimiento de las especificaciones de diseño planteadas.
Palabras clave:
control no lineal, control automático, desigualdades lineales matriciales, estabilidad cuadrática, métodos numéricos, optimización.
Abstract
This article presents a brief introduction and applications of the linear matrix inequalities in automatic control. This new mathematical technique consists of transforming the control problems to convex optimization problems and to solve them by means of efficient computational algorithms available nowadays. A good number of automatic control problems, for which there are not analytic solution or they dont have it, can be solved by using numeric methods in a reasonable time. In this work they are considered as applications the analysis of quadratic stability as well as the performance specifications in terms of restrictions. These concepts are used to design a control system for an inverted pendulum. The simulation results illustrate the application of the technique and show the fulfillment of the design specifications established.
Key words:
nonlinear control, automatic control, linear matrix inequalities (LMIs), quadratic stability, numeric methods, optimization.
1. INTRODUCCIÓN
Numerosos avances a lo largo de las últimas dos décadas han dado como resultado soluciones numéricas a problemas procedentes del control automático [1] [2]. En primer lugar, el continuo crecimiento en el poder computacional, en segundo lugar, los adelantos en la teoría de optimización generando algoritmos, especialmente en optimización convexa, y en tercer lugar, los recientes avances en álgebra lineal numérica.
Los problemas de optimización que involucran Desigualdades Lineales Matriciales (LMI por sus siglas en inglés) constituyen una especial y amplia clase de problemas de optimización convexa que atrae considerable atención de teóricos de la optimización e investigadores en control [3]-[5]. Dos razones que explican este interés son la gran variedad de especificaciones y restricciones de diseño que se pueden expresar mediante LMIs; y que una vez formulado en términos de LMIs, un problema se puede resolver mediante algoritmos muy eficientes de optimización convexa, especialmente los basados en métodos de punto interior [6] [7]. Como consecuencia, usando métodos numéricos, se pueden resolver actualmente una gran variedad de problemas de control automático cuya solución analítica es desconcida o no la tienen. El campo de aplicaciones se extiende a diversas técnicas, como control robusto, control óptimo y control difuso, entre otros.
En este artículo se presentarán algunas propiedades y especificaciones de diseño para sistemas describibles mediante ciertas inclusiones diferenciales lineales, que se pueden plantear en términos de LMIs. El artículo está organizado de la siguiente forma: la sección dos introduce algunos problemas definibles con desigualdades lineales matriciales. En la sección tres se presentan las inclusiones diferenciales lineales de interés. Luego, en la sección cuatro, se aborda el análisis de estabilidad cuadrática en el sentido de Lyapunov y en la sección cinco, el diseño con restricciones en la salida de control. Estos conceptos se emplean para el diseño de un sistema de control de equilibrio de un péndulo invertido [8] [9], el cual es ilustrado en la sección seis. Finalmente se presentan las conclusiones y perspectivas de trabajo futuro.
2. ALGUNOS PROBLEMAS DEFINIBLES CON LMIs
Una desigualdad lineal matricial (LMI) es una restricción convexa [2], expresada usualmente de la forma
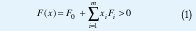
donde x∈m, Fi ∈ ℜnxn. Las matrices simétricas Fi ,i=0,1,...,m son fijas y x es la variable. Por tanto F(x) es una función afín de los elementos de x. La LMI (1) significa que F(x) es una matriz definida positiva. También se puede dar en la forma F (x)0. Es fácil ver que una LMI define un conjunto convexo; es decir, el conjunto X={xF(x)>0} es convexo; además, no necesariamente tiene una frontera suave. Se define la función
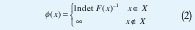
Esta función tiene la propiedad de ser finita únicamente en X y de tender a infinito cuando se acerca a su frontera. Las curvas de nivel de la función ø dan una aproximación suave de la forma del conjunto factible X. Esta aproximación por líneas de contorno es ilustrada en la Figura 1.
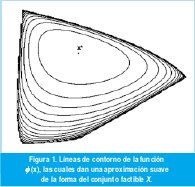
Varias LMIs F1(x),...,Fj(x) se pueden expresar como la LMI diag(F1(x),...,Fj(x))>0. Una LMI también permite expresar finitas desigualdades lineales. Si se quiere expresar Ax b (es claro que esta desigualdad es componente por componente) de la forma (1), se toma F0=diag(b1,...,bm) y Fi=diag(-a1i,...,-ami ), donde aij son las entradas de la matriz A y bi las del vector b. Una restricción cuadrática convexa (Ax+b)T(Ax+b)-cTx-d 0, con x ∈ ℜ, se puede escribir, usando los complementos de Schur [2] [3], de la forma
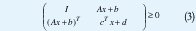
la cual se puede escribir de la forma (1) con
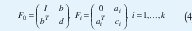
donde A=(a1,...,ak). Así mismo, la restricción |Z(x)|| <1, donde Z(x) es una matriz, no necesariamente cuadrada, que depende de x, se puede expresar como:
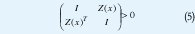
pues |Z(x)|| <1, es equivalente a I-Z(x)TZ(x)>0 También se puede plantear el problema de mi nimizar ||Z(x) de la forma
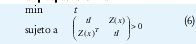
con variables x y t. Al tipo de programa matemático que minimiza una función lineal con restricciones expresadas como LMIs se le denomina programa semidefinido. Desigualdades en las que las variables son matrices son comunes en problemas que vienen de la teoría de control, tal es el caso de la desigualdad de Lyapunov
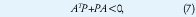
donde A es una matriz de n x n y P =PT es la variable. La desigualdad (7) se puede expresar de la forma (1) así: Sean P1,P2,...,Pm una base para las matrices simétricas de n x n (m = n(n+1)/2), entonces se toma F0=0 y Fi=-ATPi-Pi A . Así que no se hará distinción entre las formas (1) ó (7) de expresar una LMI. Los problemas siguientes son llamados problemas estándar, necesarios para plantear las aplicaciones en control que se tratarán adelante.
2.1. Problema LMI
Dada una LMI, F(x)>0, el correspondiente problema LMI (LMIP) es encontrar un x* tal que F(x*)>0 ó determinar que tal x* no existe; es decir, que la LMI no es factible.
2.2. Problema de valores propios
El problema de valores propios (EVP) es minimizar el valor propio máximo de una matriz que dependa de alguna variable, sujeto a una LMI, por ejemplo
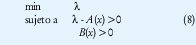
Un EVP también puede aparecer como un programa semidefinido; es decir, de la forma
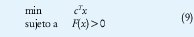
2.3. Problema de valores propios generalizado
El problema anterior se puede extender a minimizar el máximo valor propio generalizado de un par de matrices que dependen de alguna variable sujeto a una LMI (GEVP). Su forma general es
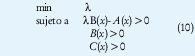
3. INCLUSIONES DIFERENCIALES LINEALES
Una Inclusión Diferencial (DI) se describe por:
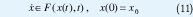
donde F es una función de ℜn x ℜ+ en una familia de subconjuntos de ℜn. Cualquier x:ℜ+n → ℜn que satisface la DI se le llama trayectoria. Es claro que hay muchas trayectorias para una DI dada. Un caso particular de DI es la lineal. Una Inclusión Diferencial Lineal (LDI) está dada por:
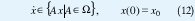
donde Ω es un conjunto de matrices de n x n. La anterior definición se puede generalizar a sistemas con múltiples entradas y salidas de la siguiente forma:
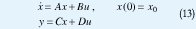
donde x:ℜ+ → ℜn es el vector de estado, u:ℜ+ → ℜm es el vector de entradas, y:ℜ+s → ℜs es la salida y las matrices satisfacen que
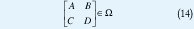
para todo t 0 y es un conjunto de matrices de (n+s)×(n+m). En adelante solo interesarán las siguientes clases de LDIs.
3.1. Sistemas lineales invariantes en el tiempo (LTI)
Son sistemas en los cuales Ω es unitario:
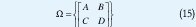
3.2. LDIs Politópicos (PLDI)
En esta clase se encuentran los sistemas donde es un politopo descrito por sus vértices, esto es, tiene la forma
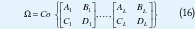
donde Co es la envolvente convexa del conjunto de matrices. Esto permite evaluar todos los estados intermedios incluidos en el politopo.
4. ESTABILIDAD CUADRÁTICA
Se consideran LDIs donde Ω tiene alguna de las formas descritas anteriormente. Una condición suficiente para que cualquier trayectoria de una LDI converja al origen cuando t →∞ es la estabilidad cuadrática; es decir, que exista una función cuadrática V(ξ)=ξTP ξ con P > 0 decreciente a lo largo de cualquier trayectoria no trivial de la LDI. A esta función V se le llama función cuadrática de Lyapunov. Si V(ξ)=ξTP es una función cuadrática de Lyapunov, entonces
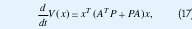
luego V es decreciente si y solo si AT+PA<0 T para toda A ∈ Ω.
4.1. Sistemas en tiempo continuo
Así, que una LDI sea cuadráticamente estable, es equivalente a que exista una matriz P tal que
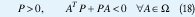
Por tanto, para sistemas LTI la condición (18) es entonces
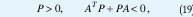
que es el criterio clásico de estabilidad de Lyapunov para sistemas LTI. Ahora, para una PLDI, la condición (18) toma la forma
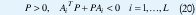
La tasa de decaimiento, también llamada el mayor exponente de Lyapunov, de una LDI, se define como el mayor tal que
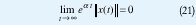
para todas las trayectorias de la LDI. La función cuadrática de Lyapunov V(ξ)=ξTPξ sirve para establecer una cota inferior para la tasa de decaimiento. Si
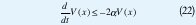
para toda trayectoria x, entonces V(x(t))≤e-2tV(x(0)) Así que,
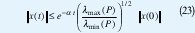
para todas las trayectorias, luego la tasa de decaimiento es al menos . Ahora, la condición (22) es equivalente a
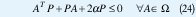
Así que, para los tipos de sistemas enunciados, la máxima cota inferior para la tasa de decaimiento que se puede encontrar usando funciones cuadráticas de Lyapunov, se halla resolviendo los siguientes GEVP [3] con variables P y α
4.1.1. LTI
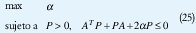
4.1.2. PLDI
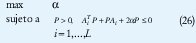
Los problemas anteriores se pueden plantear también como EVPs de la siguiente forma: Dividiendo P por el valor propio mínimo de P y por el doble de tal valor en la ecuación (24), se obtienen > 0 y P≥ I tales que
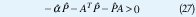
Como P≥I , entonces
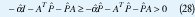
Entonces el problema se plantea como
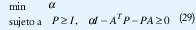
ajustándolo a cada uno de los sistemas enunciados. A un sistema se le llama establilizable cuadráticamente si existe una ganancia de retroalimentación de estado K tal que el sistema en lazo cerrado sea cuadráticamente estable. Si se fija una matriz K, un sistema es cuadráticamente estable si y solo si existe una matriz P>0 tal que

ó con la expresión equivalente, si existe Q>0 tal que
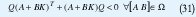
Ninguna de las dos expresiones anteriores es una desigualdad convexa en las matrices K y P o Q, pero con el cambio de variable Y =KQ en la segunda desigualdad, se obtiene la expresión equivalente
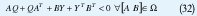
Este LMIP, con variables Q y Y , resulta factible si y solo si el sistema es estabilizable cuadráticamente, con ganancia de retroalimentación de estado K =YQ-1.
4.2. Sistemas en tiempo discreto
A los sistemas en tiempo discreto (DT) también se les puede hacer un análisis de estabilidad y estabilización cuadrática por medio de LMIs. Estos sistemas se pueden describir de la siguiente forma

donde A ∈ Ω y es un conjunto como los descritos. Un DT es cuadráticamente estable si existe una función cuadrática definida positiva tal que
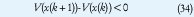
para toda x que satisfaga (33) con x0#0. Dada una función cuadrática de Lyapunov V(ξ)=ξTP ξ, con P>0, se tiene
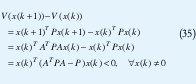
así que, una condición necesaria y suficiente para la estabilidad cuadrática de un DT es la existencia de una matriz P>0 tal que
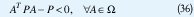
Una forma alternativa de presentar esta condición, usando los complementos de Schur, es la factibilidad de la LMI
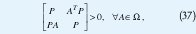
con P simétrica. Condiciones para la estabilidad cuadrática de sistemas no autónomos en tiempo discreto también se pueden expresar por medio de LMIs. Todas las definiciones concernientes se pueden extender a DT. Así, una condición equivalente a la estabilización cuadrática del sistema es la existencia de las matrices K y P>0 tales que
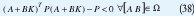
Ahora, si se multiplica la desigualdad por P-1a izquierda y derecha y se hace Q=
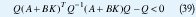
y con el cambio de variable Y=KQ y usando el complemento de Schur se llega a la LMI
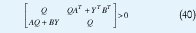
5. RESTRICCIONES EN LA SALIDA DEL CONTROL
Una elipsoide centrada en el origen es invariante para una LDI si para toda trayectoria x, x(t0) ∈ ξ implica que x(t) para todo t ∈ ξ para todo t≥to. Esto permite dar una nueva interpretación de la estabilidad cuadrática, pues, la elipsoide ξ, definida por la matriz Q>0, es invariante para una LDI si la función V(t)=x(t) TQ-1x(t) es no creciente, lo que equivale a que
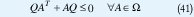
Cuando la condición inicial es conocida, se puede encontrar una cota máxima en la norma de la salida del control u=Kx. En efecto, sean Q>0 y Y matrices que estabilizan cuadráticamente un sistema dado y además se supone que x(0)TQ-1x(0)1. La última condición implica x(t) ∈ ξ para t≥0 ( ξ es una elipsoide invariante), así que

Luego, la restricción ||u(t)|| c µ para todo t≥0 se garantiza con λmax(YQ-1 Y T)≤µ2, que es equivalente, usando complementos de Schur, a
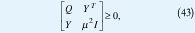
a su vez, la condición x(0)TQ -1 x(0)≤1 es equivalente, por el mismo teorema, a
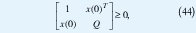
6. EJEMPLO
Se considera el problema de poner en equilibrio un péndulo invertido con un grado de libertad, el cual se encuentra sobre un carro [8] [9]. Los resultados del ejemplo se obtuvieron usando la LMI Toolbox de MatLab. Las ecuaciones de movimiento son:
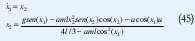
donde x1 es el ángulo del péndulo medido en radianes con respecto al eje vertical, x2 es la velocidad angular del péndulo y u es la fuerza aplicada al carro en Newtons. Los otros parámetros se muestran en la Tabla I:

Este es un sistema no lineal con dos variable de estado. Una representación aproximada de este sistema es una PLDI con dos vértices, correspondientes a la linealización alrededor de dos puntos extremos, e.g., x1=0 y x1=4/9. A partir de esta representación es posible evaluar todos los estados intermedios incluidos en el politopo. De esta forma, se tiene:
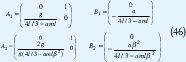
con β=cos(4 π/9). Lo primero que se obtuvo fue la no estabilidad cuadrática del sistema, esto es, el LMIP:
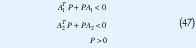
no es factible. Ahora se busca una ley de control que estabilice el sistema. Se resolvió el LMIP:
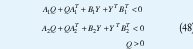
con el cual se obtiene que
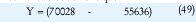

satisfacen las desigualdades, luego
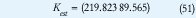
estabiliza cuadráticamente el sistema. Los resultados de simulación con esta matriz de retroalimentación se muestran en la Figura 2. La condición inicial es bastante exigente, pues se parte con el péndulo en un ángulo de 1.2 radianes. Ahora, se resolvió el EVP

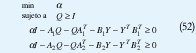
con el cual se obtiene una matriz de retroalimentación que hace menor el tiempo de respuesta. Esta matriz es

La respuesta del sistema en este caso se ilustra en la Figura 3.
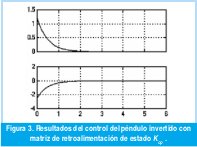
Con la matriz Kest y empezando con el péndulo en 0.5 radianes se necesita una fuerza superior a 100N para estabilizarlo, obteniendo resultados muy cercanos a los mostrados en la Figura 2. Se desarrolló el correspondiente LMIP imponiendo una restricción en la acción de control para que la fuerza máxima fuera de 60N y se obtuvo la matriz

La Figura 4 muestra como la respuesta del sistema se afecta ante esta restricción en la entrada. Como era de esperarse, el tiempo de estabilización se hace mucho más grande, alrededor de 10 segundos contra 4 sin la restricción.
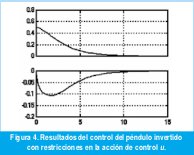
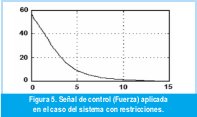
La Figura 5 muestra el comportamiento de la señal de control (fuerza) usada en el caso del sistema con restricciones. Se aprecia claramente que la señal de control respeta la restricción de diseño, permaneciendo por debajo del límite superior impuesto de 60 N.
Con C1=C2=(1 0) este es un sistema con una entrada y una salida (el ángulo del péndulo). Se buscó un control que siguiera una señal de referencia tipo paso. Puesto que se agrega una variable de estado, correspondiente a la adición de un integrador, el LMIP de estabilidad cuadrática, con las matrices aumentadas
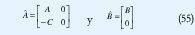
arroja la matriz de retroalimentación Kser y la ganancia K asociada al integrador. Los resultados que se obtuvieron fueron los siguientes

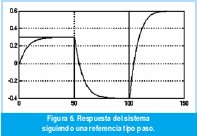
La Figura 6 muestra el seguimiento a la señal de referencia. Se aprecia que se llega a error nulo ante la entrada escalón, por la acción del integrador, y que el tiempo de respuesta es más grande que para el caso precedente de estabilización.
7. CONCLUSIONES Y TRABAJO FUTURO
Con este artículo se buscó un acercamiento a nuevas técnicas matemáticas de análisis y diseño de sistemas de control automático. Inicialmente se introdujeron las desigualdades lineales matriciales (LMIs), dando algunas de sus generalidades y mostrando su potencial en la resolución de problemas usando técnicas de optimización convexa. En segunda instancia se mostraron aplicaciones de las LMIs a problemas de análisis de estabilidad de sistemas no lineales y síntesis de leyes de control.
A nivel de la aplicación se presentó el control de un péndulo invertido de un grado de libertad. Se consideraron los casos de estabilización cuadrática, restricción en la señal de control y seguimiento ante una entrada tipo paso, obteniendo resultados satisfactorios, cumpliendo con las especificaciones fijadas. Sin embargo, los resultados fueron un poco conservadores, como sucede en el caso de exigencias de desempeño importantes o bien de una inclusión diferencial lineal politópica (PLDI) con muchos vértices. La puesta en práctica de estas técnicas es, con la ayuda de paquetes de software especializados en LMIs, simple.
Las aplicaciones acá presentadas fueron solo una pequeña muestra del poder de las LMIs para la resolución de problemas de control automático. Trabajos futuros pueden ir encaminados en su aplicación en sistemas multivariables, así como en otras técnicas de control susceptibles de utilizar modelos mediante inclusiones diferenciales lineales politópicas, como puede ser el caso del control óptimo, el control robusto y el control difuso, entre otros.
8. RECONOCIMIENTOS
Víctor Hugo Grisales desea expresar su reconocimiento por el apoyo económico de la Universidad Distrital FJDC y el Instituto Colombiano para el Desarrollo de la Ciencia y la Tecnología, COLCIENCIAS, a través de su Programa de Apoyo a Doctorados Nacionales, para la dedicación parcial en el presente trabajo de investigación en el marco de los estudios de Doctorado en Ingeniería.
9. REFERENCIAS BIBLIOGRÁFICAS
[1] A. Ben-Tal y A. Nemirovsky, «Lectures on Modern Convex Optimization: Analysis, Algorithms and Engineering Applications», Society for Industrial and Applied Mathematics: Mathematical Programming Society, 2001.
[2] J. G. VanAntwerp y R. D. Braatz, «A tutorial on linear and bilinear matrix inequalities», Journal of Process Control, vol. 10, pp. 363-385, 2000.
[3] S. Boyd, L. El Ghaoui, E. Feron y V. Balakrishnan, «Linear Matrix Inequalities in Systems and Control Theory», Studies in Applied Mathematics, Society for Industrial and Applied Mathematics, vol. 15, 1994.
[4] S. Boyd y L. El Ghaoui, «Method of Centers for Minimizing Generalized Eigenvalues», Linear Algebra and Applications, Special. issue on Numerical Lin. Algebra methods in Control, Signals and Syst., vol. 188, pp. 63-111, 1993.
[5] M. Grötschel, L. Lovász y A. Schrijver, «Geometric Algorithms and Combinatorial Optimization», Springer-Verlag, 2da. ed., 1993.
[6] Yu. Nesterov y A. Nemirovsky, «Interior-point Polynomial Methods in Convex Programming», Studies in Applied Mathematics, Society for Industrial an Applied Mathematics, vol. 13, 1994.
[7] L. Vandenberghe y S. Boyd, «Semidefinite Programming», Society for Industrial and Applied Mathematics Review, vol. 38, pp 49 95, 1996.
[8] C.W. Richter Jr., G.B. Sheblé, «Modern Control Engineering», Prentice Hall, 3ra. ed., 1997.
[9] D. Muench y A. Titli, «Introduction to the Design of Fuzzy Controlers Using Linear Matrix Inequalities», Final Internship Report, Laboratorio LAAS, Toulouse, Francia, 1999.
Mauricio Junca Peláez
Nació en Bogotá, Colombia. Es Ingeniero Eléctrico y Matemático de la Universidad de los Andes, Bogotá, Colombia. Actualmente adelanta la Maestría en Matemáticas en la misma universidad. Se ha desempeñado como Profesor Asistente del Departamento de Matemáticas de la Universidad de los Andes y actualmente adelanta trabajos de investigación en el área de optimización y precondicionares numéricos. e-mail: m-junca@uniandes.edu.co
Víctor Hugo
Grisales Palacio Nació en Bogotá, Colombia. Es Ingeniero Electrónico de la Universidad Distrital, Bogotá. Obtuvo su titulo de Maestría en Ingeniería Eléctrica en 2002 en la Universidad de los Andes, de Bogotá. Es candidato a PhD en Ingeniería (Automática) en la Universidad de los Andes de Bogotá y en la Universidad Paul Sabatier, de Toulouse, Francia.Se desempeñó durante varios años como ingeniero en el área de automatización y control en diversos sectores industriales de Colombia. Desde 1999 está vinculado como Profesor de la Facultad de Ingeniería de la Universidad Distrital FJDC. Actualmente se desempeña como profesor en el área de Automática en el Programa de Ingeniería Electrónica de la Universidad Distrital, de Bogotá y es investigador del Laboratorio de Automática, Microelec-trónica e Inteligencia Computacional (LAMIC), donde realiza estudios aplicados en sistemas inteligentes y control automático de procesos. e-mail: vhgrisales@ieee.org
Alain Gauthier Sellier
Es Ingeniero Eléctrico del Institute Universitaire de Technologie, de Grenoble, Francia. Obtuvo sus títulos de Maestría y Doctorado en Automática en 1974 y 1977, respectivamente, en el Laboratoire d'Automatique de Grenoble. INPG, Francia.Se desempeñó como investigador con la industria privada francesa, en donde desarrolló varios proyectos relacionados con centrales nucleares. Desde 1982 está vinculado con la Universidad de los Andes, en donde se desempeña como profesor titular en el área de automática. Es investigador titular del Grupo de Investigación en Automatización y Producción (GIAP), Universidad de los Andes. Sus áreas de interés son el control no lineal, la robótica y los sistemas inteligentes. email: agauthie@uniandes.edu.co
Creation date:
Licencia
A partir de la edición del V23N3 del año 2018 hacia adelante, se cambia la Licencia Creative Commons “Atribución—No Comercial – Sin Obra Derivada” a la siguiente:
Atribución - No Comercial – Compartir igual: esta licencia permite a otros distribuir, remezclar, retocar, y crear a partir de tu obra de modo no comercial, siempre y cuando te den crédito y licencien sus nuevas creaciones bajo las mismas condiciones.





2.jpg)