DOI:
https://doi.org/10.14483/23448393.2193Published:
1999-11-30Issue:
Vol. 5 No. 2 (2000): July - DecemberSection:
Science, research, academia and developmentDeterminación de la capacidad de almacenamiento en un puerto marítimo considerando el flujo en unidades de carga
Keywords:
almacén puerto, modelo estadístico, factor pico (es).Downloads
References
Concepción, M. "Modellierung der landseitigen Transportbeziehungen von Seehaefen". Tesis Doctoral. Universidad de Rostock, Alemania 1987, p.p. 96.
Schulz e, G. "Modellierung hafenbetrieblicher Prozesse " transpres VEB Verlagfuer Verkehrswesen, Berlin, 1977.
Potthoff, G. "Verkehrsstroemungslehre Band 5". transpress Berlin, 1975.
"Tables of the Individual and Cumulative Terms of Poisson Distribution". Van Nostrand, Princeton, N.J., 1962.
Richter, K-J.; Fischer, P Schneider, H. " Statistische Methoden fuer Verkehrsuntersuchungen" transpres VEB Verlag fuer Verkehrswesen, Berlin, 1974.
[ 6 ] Krampe, H. ; Kubat , J.; Runge, W. "Bedienunsmodelle. Leitfaden fuer die praktische Anwendung" Verlag Die Wirschaft, Berlin, 1974.
Concepcion, M.; Schulz e, G.; Schoenrock, G. "Simulation hafenbetrieblicher Prozessablaeufe am Konsultationsstuetzpunkt Seehafendurchlassfaehigkeit" Wissenschaftliche Zeitschrift der Wilhelm-Pieck-Universitaet Rostock- 34. Jahrgang 1985 Gesellschaftswissenschaftliche Reihe, Heft 10.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2000-00-00 vol:5 nro:2 pág:53-55
Determinación de la capacidad de almacenamiento en un puerto marítimo considerando el flujo en unidades de carga
Manuel Concepción Fanego
Resumen
El comercio exterior constituye en cualquier país un elemento económico fundamental. Este se ejecuta en gran medida por medio de los puertos. El almacén de un puerto efectúa una acción de resorte entre el flujo de arribo de cargas y la salida de las mismas. En el trabajo se determina la capacidad de almacenamiento techado necesaria en un puerto marítimo considerando el flujo en unidades de carga. Se plantea un modelo matemático-estadístico para resolver el problema con datos ficticios de un puerto convencional pequeño.
Palabras clave:
almacén puerto, modelo estadístico, factor pico.
Abstract
The external trade constitutes in any country a fundamental economic element. It is executed in great measure by means of the ports. The warehouse of a port makes a spring action between the flow of arrival of loads and the exit of the same ones. In this article is determined the necessary capacity of roofed storage in a marine port considering the flow in load units. A mathematical-statistical model thinks about to solve the problem with fictitious data of a small conventional port.
Key words:
warehouse port, statistical model, peak factor.
INTRODUCCIÓN
El transporte de cargas constituye una actividad económica fundamental en cualquier país, en particular para aquellos que, como islas, sólo pueden realizar su comercio con el exterior por vía marítima o aérea. Con la globalización económica el transporte de cargas cobra aún mayor importancia. El transporte marítimo ha sido desde la antigüedad el medio más utilizado para ese fin, aunque el transporte aéreo ha ganado en importancia en los últimos años, todavía el mayor volumen de cargas es transportado por medios marítimos.
El desarrollo tecnológico, para carga general, tanto en nuevos tipos de buques como en los medios de carga ha conllevado a la especialización por ejemplo, RO-RO (Roll on- Roll off ) y Container. Limitaremos nuestro análisis al transporte de carga general en un puerto operando con los medios de carga del puerto o del buque.
Por otra parte, el flujo de cargas que arriba, por lo general es mayor que la capacidad de salida del puerto, por lo que el almacén se constituye en el resorte que hace que el flujo se suavice. Por tanto, la determinación de la capacidad de almacenamiento techada necesaria constituye uno de los parámetros esenciales de un puerto.
DESARROLLO
Consideremos una zona portuaria de carga general y la cantidad de carga diaria q formada en clases. La probabilidad de ocurrencia de un arribo de q unidades puede ser expresada mediante una función matemática, por ejemplo,
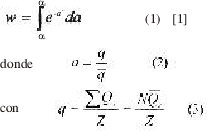
q‐ es la cantidad promedio de carga que arriba por día y QS es la cantidad de carga por barco, Z =365 días.
La Tabla 1 muestra la distribución de frecuencia de la cantidad de carga que arriba por día para ∑ QS = 478174 toneladas, bajo el supuesto de que (1) es aplicable.
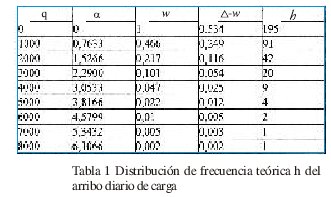
Si consideramos w = 1/Z = 1/365 obtenemos l probabilidad de que en un día del año arribe l carga qmax y por (1) con
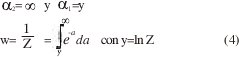
Luego, de (2), la cantidad máxima de carga diaria probable viene dada por q max=yq‐(5)
Una curva frontera de la entrada de cargas puede ser calculada por
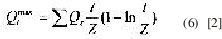
la que bajo la consideración de que en el primer día del intervalo de tiempo en estudio se tiene el mayor arribo diario y a partir de ésta se puede construir el arribo de los restantes días.
La cantidad promedio de carga que arriba por día q puede ser sobrepasada cuando la pendiente de la curva frontera es mayor que la de una recta qt mientras que con una pendiente
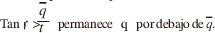
La curva de probabilidad acumulada del arribo de carga puede ser determinada si consideramos el arribo de carga por día como variable aleatoria [3]. La probabilidad wt del arribo de q cargas en t días sucesivos se calcula de (1) con una modificación,
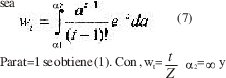
t=1(1)Z se determina, con el uso de una tabla de Poisson [4], el límite inferior de integración yt=at y con la aplicación de
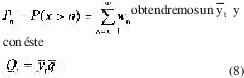
El coeficiente es el factor pico del flujo de salida del puerto [6].
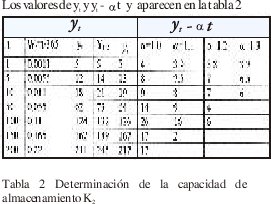
Tomando como base la tabla 2 se obtienen los siguientes resultados:
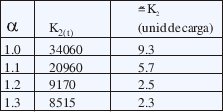
Como se observa la capacidad de almacenamiento necesaria se obtiene en función del factor pico del flujo de salida [7].
CONCLUSIONES
Los resultados obtenidos permiten obtener la capacidad de almacenamiento techado necesaria en función del factor pico del flujo de salida del puerto.
Otras consideraciones para determinar la capacidad de almacenamiento serían, por ejemplo, midiendo en la unidad "carga de buque" o el modelo de Retención.
REFERENCIAS
[1] Concepción, M. "Modellierung der landseitigen Transportbeziehungen von Seehaefen". Tesis Doctoral. Universidad de Rostock, Alemania 1987, p.p. 96.
[2] Schulz e, G. "Modellierung hafenbetrieblicher Prozesse" transpres VEB Verlagfuer Verkehrswesen, Berlin, 1977.
[3] Potthoff, G. "Verkehrsstroemungslehre Band 5". transpress Berlin, 1975.
[4] "Tables of the Individual and Cumulative Terms of Poisson Distribution". Van Nostrand, Princeton, N.J., 1962.
[5] Richter, K-J.; Fischer, P Schneider, H. "Statistische Methoden fuer Verkehrsuntersuchungen" transpres VEB Verlag fuer Verkehrswesen, Berlin, 1974.
[ 6 ] Krampe , H . ; Kubat , J . ; R u n g e , W. "Bedienunsmodelle. Leitfaden fuer die praktische Anwendung" Verlag Die Wirschaft, Berlin, 1974.
[7] Concepcion, M.; Schulz e, G.; Schoenrock, G. "Simulation hafenbetrieblicher Prozessablaeufe am Konsultationsstuetzpunkt Seehafendurchlassfaehigkeit" Wissenschaftliche Zeitschrift der Wilhelm-Pieck-Universitaet Rostock- 34. Jahrgang 1985 Gesellschaftswissenschaftliche Reihe, Heft 10.
Manuel C. Concepción Fanego
Especialista en Matemática, Universidad Central de Las Villas, Cuba. Profesor, Universidad Central de Las Villas. Doctor en Economía, Universidad de Rostock, Alemania. Profesor Facultad de Ingeniería, Universidad Distrital.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.





2.jpg)










