DOI:
https://doi.org/10.14483/23448393.8381Published:
2015-08-10Issue:
Vol. 20 No. 2 (2015): July - DecemberSection:
ArticleAlgoritmo de Dimensionamiento de Almacenes para Obras de Edificación del Sector de la Construcción
Warehouse sizing algorithm for edification works of construc-tion sector
Keywords:
Algoritmo, Almacén, Dimensionamiento, Unidad de carga (es).Keywords:
Algorithm, warehouse, sizing, load unit (en).Downloads
References
DANE. Comunicado de prensa. 19 de Junio de 2014, Disponible en:
http://www.dane.gov.co/files/investigaciones/boletines/pib/bol_PIB_Itrime14.pdf
Santiago, Manrique. (2010) Identificación de los principales problemas en la logística de abastecimiento de las empresas constructoras Bogotanas y propuestas de mejoras, Consultado 15 de Mayo de 2014, disponible en:
http://javeriana.edu.co/biblos/tesis/economia/tesis189.pdf
Andrés Hualpa, Carolina Suarez (2013) Ubicación y dimensionamiento como parámetros en el diseño de almacenes: revisión del estado del arte, Revista de Ingeniería, Volumen 18-1, (ISSN 0121-750X) 65-83
Jinxiang Gu, Marc Goetschalckx, Leon F. McGinnis, (2007) Research on warehouse operation: A comprehensive review, European Journal of Operational Research, Volume 177, Issue 1, (ISSN 0377-2217) 1-21
M.S. Hung, John C. Fisk, (1984) Economic sizing of warehouses: A linear programming approach, Computers & Operations Research, Volume 11, Issue 1, (ISSN 0305-0548) 13-18.
Charles J. Malmborg, Swaminathan Balachandran, Daniel M. Kyle, (1986) A model based evaluation of a commonly used rule of thumb for warehouse layout, Applied Mathematical Modelling, Volume 10, Issue 2, (ISSN 0307-904X) 133-139
Kumar Bhaskaran, Charles J. Malmborg, (1990) Economic tradeoffs in sizing warehouse reserve storage area, Applied Mathematical Modelling, Volume 14, Issue 7, (ISSN 0307-904X) 381-385
Charles J. Malmborg, Krishnakumar Bhaskaran, (1990) A revised proof of optimality for the cube-per-order index rule for stored item location, Applied Mathematical Modelling, Volume 14, Issue 2, (ISSN 0307-904X) 87-95.
O. Hounkonnou, (1990) Modelling and simulation of an automated warehouse in activity, Mathematical and Computer Modelling, Volume 14, (ISSN 0895-7177) 1100-1102.
Gilles Cormier, Eldon A. Gunn, (1992) A review of warehouse models, European Journal of Operational Research, Volume 58, Issue 1, (ISSN 0377-2217) 3-13
Charles J. Malmborg, (1996) An integrated storage system evaluation model, Applied Mathematical Modelling, Volume 20, Issue 5, (ISSN 0307-904X) 359-370.
A.K. Rao, M.R. Rao, (1998) Solution procedures for sizing of warehouses, European Journal of Operational Research, Volume 108, Issue 1, (ISSN 0377-2217) , 16-25
René de Koster, Tho Le-Duc, Kees Jan Roodbergen, (2007) Design and control of warehouse order picking: A literature review, European Journal of Operational Research, Volume 182, Issue 2, (ISSN 0377-2217) 481-501.
Semih Önüt, Umut R. Tuzkaya, Bilgehan Doğaç, (2008) A particle swarm optimization algorithm for the multiple-level warehouse layout design problem, Computers & Industrial Engineering, Volume 54, Issue 4, (ISSN 0360-8352) 783-799.
Venkata Reddy Muppani (Muppant), Gajendra Kumar Adil, (2008) A branch and bound algorithm for class based storage location assignment, European Journal of Operational Research, Volume 189, Issue 2, (ISSN 0377-2217) 492-507.
Lu Chen, André Langevin, Diane Riopel, (2011) A tabu search algorithm for the relocation problem in a warehousing system, International Journal of Production Economics, Volume 129, Issue 1, (ISSN 0925-5273) 147-156.
F. Guerriero, R. Musmanno, O. Pisacane, F. Rende, (2012) A mathematical model for the Multi-Levels Product Allocation Problem in a warehouse with compatibility constraints, Applied Mathematical Modelling, (ISSN 0307-904X)
Felix T.S. Chan, H.K. Chan, (2011) Improving the productivity of order picking of a manual-pick and multi-level rack distribution warehouse through the implementation of class-based storage, Expert Systems with Applications, Volume 38, Issue 3, (ISSN 0957-4174) 2686-2700
Klaus Moeller, (2011) Increasing warehouse order picking performance by sequence optimization, Procedia - Social and Behavioral Sciences, Volume 20, (ISSN 1877-0428) 177-185.
Luis, Joyanes, Concepción Fernandez y Ignacio, Zahonero. (2005) Programación en C: Metodología, algoritmos y estructura de datos. Mc Graw Hill. Ed 2.
Instituto de Desarrollo Urbano, (2008) Procedimiento para el almacenamiento de materiales en campamentos, centros de acopio y frentes de obra, Disponible en: http://webidu.idu.gov.co:9090/jspui/bitstream/123456789/32643/23/60014765-12.pdf
Gianpaolo Ghiani, Gilbert, Laporte y Roberto, Musmanno. (2004) Introduction to logistics systems: Planning and control. Editorial John Wiley & Sons. 193-199
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Algoritmo de dimensionamiento de almacenes para empresas de edificación en el sector de la construcción
Stores sizing algorithm for edification companies in the construction sector
Andrés Mauricio Hualpa Zúñiga, Universidad Cooperativa De Colombia Andres.hualpa@campusucc.edu.co
Cesar Amílcar López Bello, Universidad Distrital Francisco José de Caldas clopezb@udistrital.edu.co
Recibido: 07-04-2015 Modificado: 30-05-2015 Aceptado: 30-06-2015
Resumen
Este artículo contiene el desarrollo de un algoritmo aplicado a la solución de problemas de dimensionamiento de espacios en el almacenamiento en empresas del sector de la construcción. Este problema se justifica bajo el grado de informalidad que se presenta al momento de asignar áreas de almacenamiento, sin considerar parámetros relacionados con las etapas de construcción, las características del producto y las disposiciones de área en la obra. En un estudio previo se identifica que el grado de informalidad al momento de asignar áreas de almacenamiento genera índices de utilización de la capacidad y la entrega de pedidos de manera incompleta.
El diseño del algoritmo está soportado por un modelo integral de dimensionamiento sujeto a un sistema de ecuaciones con variables de cantidad, volumen y dimensiones de material, para establecer finalmente el área necesaria del almacén. El algoritmo es adaptado a lenguaje de programación con el objeto de presentar los resultados en lenguaje gráfico en donde sea visible el dimensionamiento de espacios de almacenamiento. Estos resultados son validados mediante la evaluación de la utilización de la capacidad de almacenamiento y pedidos completamente entregados para diferentes unidades de carga, demostrando mejoras en estos indicadores.
Palabras claves: Algoritmo, almacén, dimensionamiento, unidad de carga.
Abstract
This article contains the development of an algorithm applied to the solution of problems of sizing of storage spaces in companies in the construction sector. This problem is justified under the degree of informality that occurs at the time of assigning storage areas, without considering parameters related to stages of construction, the characteristics of the product and the provisions of the work area. In a previous study itis identified that the degree of informality at the moment of assigning storage areas, generates poor rates of capacity utilization and delivery of incomplete orders.
The design of the algorithm is supported by a comprehensive model of sizing subjected to a system of equations with variables of quantity, volume and material dimensions, to finally establish the necessary storage area. The algorithm is adapted to programming language in order to present the results in graphic language where the sizing of storage spaces is visible. These results are validated through the evaluation of storage capacity utilization and completely delivered orders for different cargo units,where improvements in these indicators are shown.
Keywords: Algorithm, warehouse, sizing, load unit.
1. Introducción
La industria de la construcción es uno de los sectores más importantes y estratégicos para el desarrollo de Colombia. Según estadísticas presentadas por el Departamento Administrativo Nacional de Estadística, el PIB en el año 2014 creció en 5,4% con relación al año anterior. Al analizar las variaciones por ramas de actividad, se registra mayor crecimiento en este sector con un 17.2% [1]. De acuerdo con lo anterior este incremento proporciona la necesidad de ejercer mayores acciones de abastecimiento y almacenamiento de materiales en obras civiles y de edificación. Particularmente, el almacenamiento de materiales es una tarea especializada y compleja, porque está sujeta a las condiciones de manipulación, espacio necesario y disponible, desplazamientos periódicos de material, temporalidad de almacenamiento, entre otros. Estos aspectos son considerados características diferenciales con otros sistemas de abastecimiento, debido a que son temporales, al ser desmontados al finalizar la obra. Estos aspectos hacen que el proceso de flujo de material este condicionado a un componente de planeación en el cual es prioritario realizar "trazado" en el que se asigna y dimensiona las áreas de almacenamiento para la obra de construcción.
A pesar del crecimiento significativo de este sector, el desarrollo que ha tenido en Colombia presenta diversos problemas generados por el aumento de costos, incumplimiento en los plazos de entrega, desperdicios y almacenaje inoficioso en las obras [2]. Particularmente las funciones de trazado de áreas de almacenamiento se realizan de manera subjetiva, limitando la utilización de espacios y en algunos casos genera interferencias en la sincronización del flujo de material. Para poder formalizar el proceso de diseño de almacenes en obras de construcción, es necesario estandarizarlo mediante una serie de pasos en los que se evalúen las condiciones de abastecimiento y se agilice la función de trazado temporal. De acuerdo con investigaciones desarrolladas desde los años setentaa la actualidad, en el diseño de almacenes se integran factores de ubicación y dimensionamiento así como la distribución de materiales dentro del mismo, derivándose de estos elementos condicionantes como el tamaño de las unidades de carga, las tendencias de demanda, las tasas de rotación, entre otros [3]. Por otra parte la estructura y diseño interno del almacén, la selección de equipos de manipulación de material y la selección de estrategias operacionales también son considerados factores para el diseño del almacén [4].
El diseño de almacenes ha sido objeto de estudio en diversas investigaciones en las que se han desarrollado modelos específicos de dimensionamiento. Los métodos más utilizados son la programación lineal [5], el diseño basado en costos de inventario [6], la programación estocástica en la que se integran variables de costo de reposición, así como el índice cúbico de pedido [7] [8]. Es de resaltar que desde la década de los noventa, se evidencia mayor utilización de la simulación en el dimensionamiento de almacenes. Es así que mediante la combinación de modelos matemáticos y computacionales se desarrollan estudios para evaluar niveles de automatización y la capacidad de almacenaje [9] [10]. La aleatoriedad de la demanda ha sido otra característica de estudio. Mediante la formulación de esta variable se puede obtener el tamaño óptimo de un almacén [11] [12]. De la misma manera la disposición interna de materiales y los métodos de enrutamiento para el procesamiento de pedidos han sido considerados factores de dimensionamiento [13].
El diseño de almacenes también ha tenido desarrollo mediante la aplicación de algoritmos que buscan solución a problemas de distribución, orientación de estanterías de almacenamiento, asignación de espacios entre otros, generando soluciones con múltiples objetivos [14]. Por ejemplo el algoritmo Branch and Bound ha sido aplicado en el dimensionamiento de almacenes, fundamentado en los costos de manejo de materiales. [15]. Los resultados del algoritmo demuestran ser más eficientes que las soluciones mediante programación dinámica o lineal. De la misma manera se ha desarrollado modelos de dimensionamiento aplicando el algoritmo de búsqueda tabú, en el que mediante una formulación de programación entera se genera una solución inicial y posteriormente se refina con el algoritmo [16]. Otro parámetro integrado en el desarrollo de algoritmos es la asignación de materiales en instalaciones disponibles, en el que se comparan soluciones obtenidas entre un modelo matemático lineal y un algoritmo de búsqueda local iterativa [17]. El objetivo es reducir tiempos de entrega, niveles de inventario, costos de almacenamiento e incrementar el nivel de servicio, demostrando así que el uso de algoritmos genera soluciones en menor tiempo y esfuerzo computacional de cálculo.
Existe un amplio desarrollo de técnicas aplicadas en el diseño de almacenes, en el que se asocian variables dimensionales de las unidades de carga y tasas de rotación de material [18]. También la configuración del almacén y la secuencia de programación de alistamiento de pedidos [19]. Sin embargo este desarrollo ha tenido impacto en sectores diferentes al sector de la construcción, estableciendo la necesidad de formalizar protocolos y/o pasos ordenados para sistemas de abastecimiento y almacenamiento dinámico.
El objeto de este artículo es presentar un algoritmo de dimensionamiento de almacenes compatible con las características de abastecimiento de una obra de construcción, para facilitar la estandarización del proceso de diseño de este tipo de almacenes temporales.
2. Materiales y métodos
Los resultados presentados en este artículo fueron desarrollados mediante una investigación proyectiva en la que se propone un algoritmo como solución a un problema o necesidad de tipo práctico en el sector de la construcción. Los lineamientos metodológicos desarrollados parten de la identificación de características, factores y procedimientos que permiten definir variables de diseño de instalaciones de almacenamiento. A partir de esto se propone unadescripciónsistemática diseñada en tres fases: análisis del problema, diseño del algoritmo y resolución del problema con computadora. Esta metodología es acogida de acuerdo a los estudios recientes en las ciencias de la computación, en la que expertos tienen la noción de convertir la solución de un problema en un conjunto de instrucciones o pasos ordenados que convergen a una solución eficiente. Sin embargo este estudio puede ser complejo según las características del problema, generando la necesidad de tener varias opciones de tratamiento y/o solución [20]. El desarrollo metodológico del diseño del algoritmo se presenta en este artículo.
2.1. Materiales y métodos
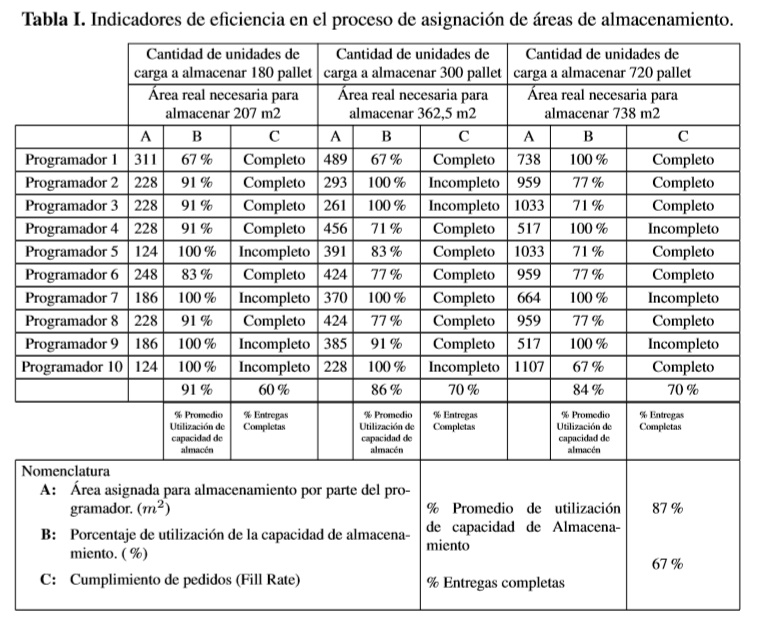
La asignación de espacios de almacenamiento en obras de construcción es un proceso que con frecuencia se desarrolla por la experiencia e intuición de las personas encargadas de planificar el trazado de áreas. Para esta práctica son desconocidos los indicadores de cumplimiento de pedidos y utilización de espacios disponibles que se generan en la medida que avanza la obra, lo cual hace considerar que no sean constantes debido a las características de almacenamiento temporal y dinámico de materiales. En este orden de ideas inicialmente se realizó un experimento con un grupo de diez personas encargadas de planificar y programar el almacenamiento de materiales en tres obras de construcción en la ciudad de Bogotá (programadores en la TablaI), quienes generaron registros en un instrumento de recolección de datos, estableciendo las siguientes condiciones:
a. Asignación estándar del almacén para pallets como unidad de carga experimental con dimensiones de 1 por 1,2 metros, con disponibilidad de estanterías convencionales para almacenamiento de pallet con tres niveles de altura.
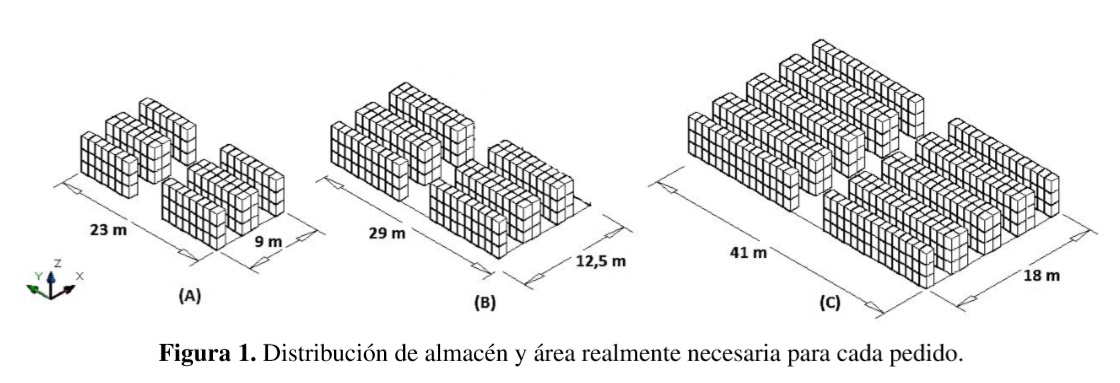
b. Tres cantidades de pedido: 180 pallet, 300 pallet y 720 pallet integrados por diferentes materiales para construcción que totalizan a estos niveles. Según previo cálculo de área y volumen se identifica que para cada nivel de pedido se debe asignar 207m2, 362,5m2 y 738m2 de área real de almacenamiento respectivamente. Los cálculos de área se realizan inicialmente de manera manual a partir de la ocupación de pallet en estanterías de tres niveles. La distribución de almacén y dimensiones en el eje X e Y para cada pedido se presenta en la figura 1.
Estos resultados se justifican de la siguiente manera: Para el pedido de 180 pallet se determina una distribución en el almacén de 4 slot sobre el eje X, 15 slot sobre el eje Y y 3 slot sobre el eje Z. La longitud en el eje X e Y para este almacén es de 9 y 23 metros, obteniendo un área total de 207m2. En los pasillos laterales y central se tiene un ancho de 2,5 metros y 5 metros respectivamente.Para el pedido de 300 y 720 pallet se determina una distribución de 5 y 8 slot sobre el eje X y 20 y 30 slot sobre el eje Y respectivamente.
c. Calculo de porcentaje de utilización de capacidad según el cociente entre el área asignada y el área real de almacenamiento.
d. Se Identifica "pedido completo" cuando en la obra se recibe la totalidad del material solicitado por que se encontraba disponible en el almacén. Por lo contrario existe la posibilidad de no tener disponible todo el material solicitado debido a que no se tenía suficiente capacidad de almacenamiento, generando "pedido incompleto".
Según estas condiciones se obtienen los datos de asignación de área por cada uno de los programadores y los indicadores de utilización de capacidad de almacenamiento con cumplimiento de pedidos (Fill Rate). Estos resultados son presentados en la Tabla I.
Según los resultados obtenidos, se establece que de acuerdo al grado de informalidad y/o subjetividad de las personas encargadas del trazado para asignación de áreas de almacenamiento, en promedio se está generando un 87% de utilización de capacidad de almacenamiento y tan sólo un 67% de entrega de pedidos de manera completa. En otros términos existe una variabilidad de dimensionamiento al asignar áreas del almacén que reflejan desabastecimiento interno por diversos factores. Como se define inicialmente, el objeto de este artículo es presentar un algoritmo de dimensionamiento de almacenes compatible con las características de abastecimiento de una obra de construcción, para facilitar la estandarización del proceso de diseño temporal de este tipo de almacenes. Para el caso específico del diseño del algoritmo de dimensionamiento de almacenes, es necesario determinar las características de planeación en el proceso de trazado (dimensionamiento de áreas), así como las variables, parámetros y criterios relacionados con el abastecimiento de materiales en el sector de la construcción. A continuación se presentan estas características.
2.2. Variables y parámetros de abastecimiento
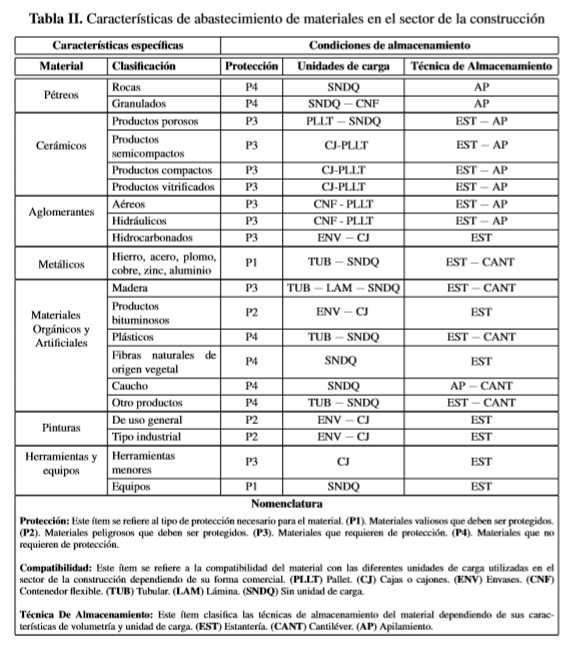
Como fue mencionado previamente, en el análisis del problema para el diseño del algoritmo de dimensionamiento es necesario identificar variables y parámetros de abastecimiento del sector de la construcción. Para esto se diseñó un estudio diagnóstico en el que participaron empresas constructoras a las que se consultó las características de abastecimiento de materiales. Los resultados iniciales de este estudio permitieron identificar que existen diversos factores, entre ellos las etapas de construcción que pueden clasificarse en tres: estructural, mecánica y estética y/o refinamiento. De la misma manera el tipo de material clasificado en siete categorías generales y 22 subcategorías, las consideraciones de protección diferenciadas en cuatro niveles y siete unidades de carga principalmente sujetas a tres técnicas de almacenamiento. La relación de estos factores se presenta en la Tabla II.
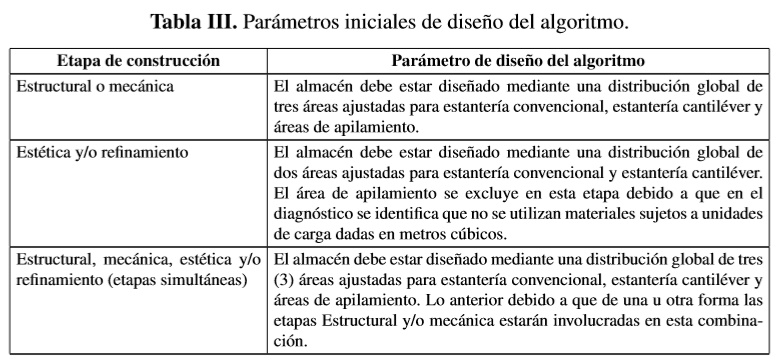
De acuerdo con las características de abastecimiento en el sector de la construcción, el tipo y cantidad de material está condicionado a la manera en que evoluciona cada una de sus etapas, porque los materiales utilizados en una etapa no son necesariamente los mismos que se utilizan en otras. Otro resultado importante del estudio es que todas las unidades de carga son utilizadas en cada una de las etapas de construcción, a excepción de la etapa estética y refinamiento debido a que en su generalidad no aplica metros cúbicos como unidad de carga. A partir de esto se definen en la Tabla III los parámetros iniciales para el diseño del algoritmo:
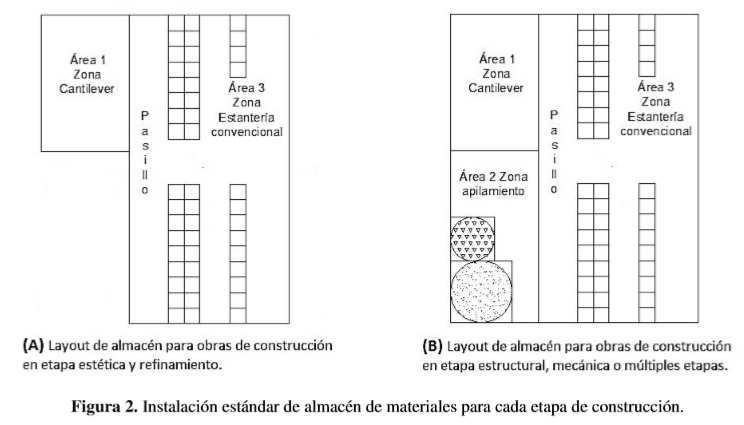
A partir de lo anterior, los parámetros para diseño del algoritmo establecen instalaciones estándar de almacenamiento en una obra de construcción. En la Figura 2 se presentan dos tipos de instalaciones necesarias para cada una de las etapas de construcción en la que se puede visualizar dos o tres áreas genéricas de acuerdo a la técnica de almacenamiento.
Las dimensiones en términos de área para cada una de las zonas presentadas en la Figura 2, dependerán de la cantidad de material necesario en cada etapa de construcción, es decir, la zona de apilamiento tendrá un área en m2 dependiendo de la cantidad de m3 a almacenar. Esta área se caracteriza por concentrar en un mismo lugar los materiales apilables, cuando generalmente son ubicados en diferentes lugares de la obra generando reproceso por desplazamientos de material. Por otra parte la zona de estantería convencional tendrá un área en m2 dependiendo de la cantidad de unidades de carga compatibles con pallet. La zona cantiléver tendrá un área sujeta a las dimensiones de este tipo de estanterías. Finalmente el área del almacén se obtiene mediante la sumatoria de áreas de estas tres zonas.
3. Modelos de dimensionamiento
De acuerdo con las variables y parámetros definidos,es necesario identificar modelos de dimensionamiento relacionados con estos, para integrarlas a un algoritmo. Para ello es necesario tener en cuenta la zona cantiléver, apilamiento y estantería convencional. A continuación se presentan las características de cada uno de estos modelos de dimensionamiento.
3.1. Modelo dimensionamiento zona cantiléver
La técnica de almacenamiento por estantería cantiléver se caracteriza por ser un sistema de almacenaje de unidades de carga largas y/o pesadas,perfiles, tuberías, tableros, láminas, listones, molduras, etc, y a que ningún elemento de la estructura dificulta el manejo de la carga por muy larga que esta sea. De acuerdo con la estructura de este tipo de estantería, su instalación requiere un área disponible de 6m2 aproximadamente. Sin embargo para casos en los que la capacidad no supere el almacenamiento de más de 4 tipos de materiales con unidades de carga larga, se recomienda la utilización de una sola cara de la estantería eliminando así espacio.En este segundo caso el área necesaria se reduciría a 3m2.
3.2. Modelo dimensionamiento zona de apilamiento
La técnica de apilamiento se caracteriza por ser un sistema de almacenaje para materiales que no tienen unidad de carga definida. Este es el caso de materiales pétreos, granulares, cerámicos, entre otros. De acuerdo a las condiciones definidas en la guía de almacenamiento de materiales GA-14, los materiales sin unidad de carga deben almacenarse en cajones de madera que ocupan un área de 2m2 y están condicionados a almacenar cantidades que no superen 2.4 m3 de material aproximadamente. Para los casos en que la cantidad sea mucho mayor a esta capacidad de almacenamiento se recomienda confinar el material sobre suelo, el cual debe estar cubierto de polietileno o cualquier otro material impermeable para evitar la erosión del mismo. Debido a que este sistema mantiene una forma irregular al acumular granel solido sobre un plano, se propone ajustar su proporción a la forma de un cono truncado como se presenta en la Figura 3.
Para establecer un nuevo parámetro de diseño del algoritmo es necesario asignar un área para materiales sin unidad de carga. En este caso el área dependerá del diámetro de la base del cono, es decir dos veces el radio mayor (R). Para despejar el valor de radio mayor de la ecuación 1, es necesario convertir la ecuación de volumen en una polinómica. A partir de lo anterior se obtiene la ecuación 2 de la forma aX2 +bX +C = 0 donde a = 1, X = R, b = r y c es la parte fraccional. En este caso para calcular el área necesaria, se requiere identificar que valores están disponibles. En principio el volumen (V ) se conoce ya que es un valor que depende de la cantidad de material que se almacenará temporalmente. La altura (h) puede establecerse a través del ángulo de reposo formado entre la generatriz del cono y su base. Para las aplicaciones en materiales de construcción como arena seca, grava, piedra, yeso, entre otros, se mantiene un ángulo de reposo entre 25° a 40° aproximadamente según la humedad del material. En este caso la altura es determinada como el producto entre la tangente de a y el radio mayor, donde a es el ángulo de reposo. Sin embargo esta ecuación no es aplicable en el modelo debido a que el radio mayor es una variable desconocida.Por esta razón se realiza una simplificación del cálculo de la altura, atendiendo las condiciones definidas en la guía de almacenamiento de materiales GA-14, en la que se establece que los agregados pétreos y/o granulares serán apilados a una altura no mayor a 2 metros. Por tanto h = 2 como valor constante. El radio menor (r) es un valor que puede estimarse bajo la condición que sea menor que el radio mayor (r < R). Como parámetro para el diseño del algoritmo, se identifica que para calcular el área necesaria de almacenamiento de materiales sin unidad de carga se puede utilizar finalmente la ecuación 3.
3.3. Modelo dimensionamiento zona estantería convencional
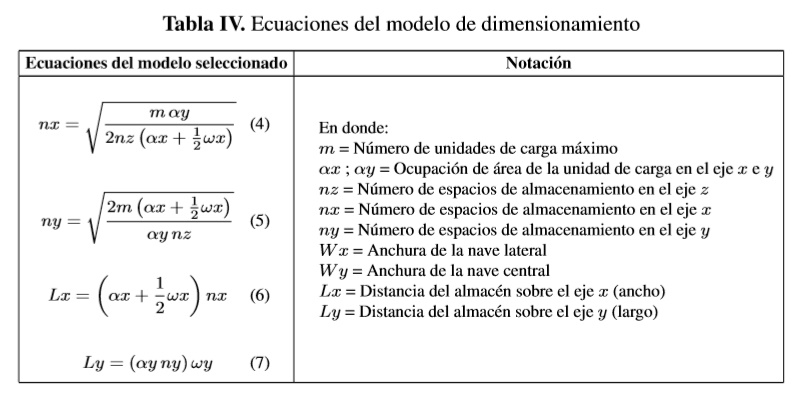
De acuerdo con los modelos de dimensionamiento desarrollados en diversas investigaciones se puede destacar la propuesta presentada por Ghiani, Laporte y Musmano en el año 2004, en los que se determina mediante un sistema ecuaciones, la variable distancia del almacén sobre el eje X e Y [22]. Estas ecuaciones son compatibles con las condiciones geométricas definidas en la Figura2, debido a que proporcionan el área necesaria de almacenamiento. En la Tabla IV se presenta el conjunto de ecuaciones útiles para el cálculo de las dimensiones de un almacén.
Específicamente las ecuaciones 4 y 5 integran variables y parámetros fijos de entrada que calculan el número de slots o espacios de almacenamiento necesarios en el eje X e Y. La variable de entrada "m" está sujeta a la cantidad de material que se proyecta almacenar en un periodo de planeación y que determina la capacidad necesaria de almacenamiento. Los parámetros fijos de entrada están sujetos a las dimensiones de la unidad de carga a almacenar, los niveles de altura sujetos a las características de los racks o estanterías y el ancho de los pasillos de circulación, cuya longitud depende de los equipos de alistamiento de pedidos. Finalmente las ecuaciónes 6 y 7 establecen la longitud necesaria para acondicionar una instalación de almacenamiento teniendo en cuenta los parámetros definidos anteriormente. Las variables dimensionales del almacén dependerán del eje X - Y definidos inicialmente para el layout del almacén, ya que la posición de las unidades de carga, los pasillos centrales, laterales y sus respectivas dimensiones pueden variar. Las dimensiones de la unidad de carga dependen de las características de manipulación y almacenamiento de los materiales. Estos pueden almacenarse en contenedor, pallet, cajas, bultos, etc. Las dimensiones de los pasillos dependerán de las dimensiones y grado de maniobrabilidad del equipo de apoyo para la manipulación del material. Finalmente las distancias en el eje X-Y del almacén determinaran el área en m2 necesaria para su construcción.
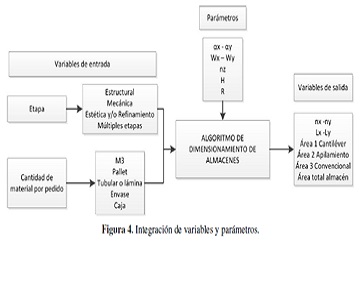
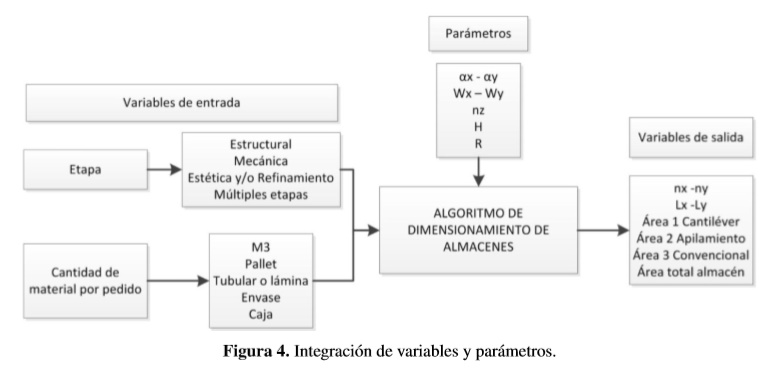
3.4. Integración de variables y parámetros para el diseño del algoritmo de dimensionamiento de almacenes
Para el diseño del algoritmo es necesario integrar variables y parámetros de entrada y salida.Para ello en la caracterización del abastecimiento en el sector de la construcción se identificó que está sujeto a tres etapas de construcción, cinco unidades de carga compatibles con tres técnicas de almacenamiento, de las cuales son aplicables tres modelos de dimensionamiento. De estos modelos se generan parámetros como la longitud de la unidad de carga, la longitud de los pasillos del almacén, el número de slots en el eje Z que dependen de la altura de la estantería a utilizar y la altura y radio permitido para el material apilado. Finalmente se obtienen variables de salida como la longitud y área necesaria para cada técnica de almacenamiento generando así el área total de un almacén en función de un pedido específico.Por lo anterior el algoritmo de dimensionamiento puede aplicarse tantas veces como pedidos se realicen. La integración de variables y parámetros se presentan en la Figura 4.
4. Resultados
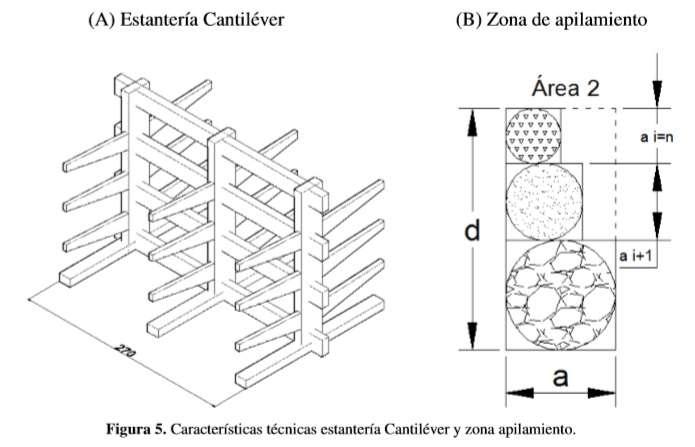
En el desarrollo del algoritmo es necesario establecer un modelo general de dimensionamiento debido a que el proceso de almacenamiento está supeditado a diversas combinaciones de variables y parámetros para obtener el área total del almacén. Esto quiere decir que la solución debe ser integrada mediante el dimensionamiento de tres áreas dedicadas para unidades de carga compatibles con instalaciones cantiléver, apilamiento y estantería convencional. Específicamente el área 1 está dedicada para ubicación de materiales con unidades de carga tubular y/o laminar que son compatibles con estantería cantiléver en la que su capacidad es de 6 slots y área aproximada de 6m2, debido a que las dimensiones de este tipo de estantería es de 2,7m y 2m como se presenta en la figura 5 (A).Por otra parte el área 2 está dedicada para ubicación de materiales sin unidad de carga definida como lo son los pétreos y/o granulares y que son almacenados mediante técnica de apilamiento. El dimensionamiento de ésta área se obtiene mediante la relación del volumen de pedido para cada material, generando así un área específica de apilamiento para cada uno de ellos.En la figura 5(B) se presenta esta relación en la que se obtiene el área total para la zona de apilamiento.
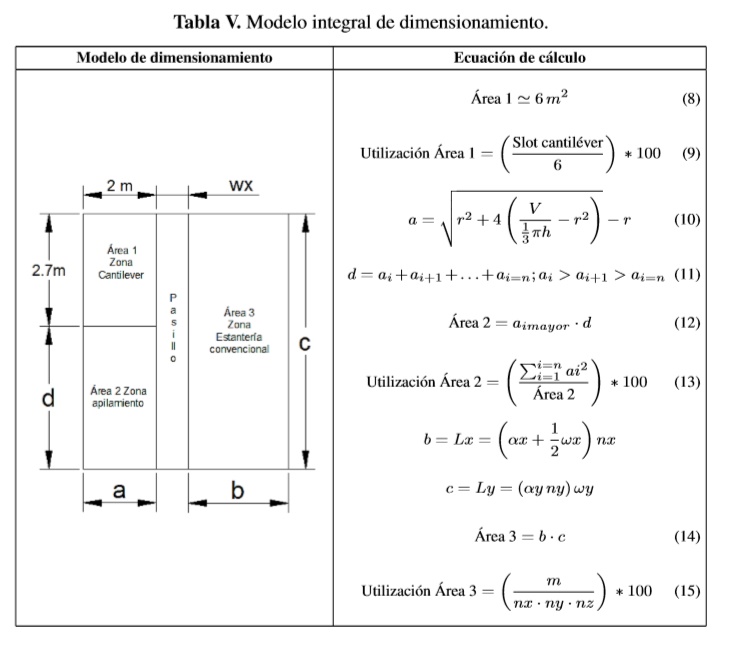
De acuerdo con la figura 5(B), el lado "a" de la zona de apilamiento dependerá del pedido que tenga mayor volumen y el lado "d" de la sumatoria de las áreas necesarias para cada material de este tipo. Finalmente el área 3 está dedicada para materiales con unidades de carga como lo son, cajas, envases y/o pallet, unificando todas a esta última para lograr compatibilidad con estantería de tipo convencional. En la Tabla V se presenta el modelo integral de dimensionamiento con sus respectivas ecuaciones de cálculo.
De acuerdo con la Tabla V la ecuación 10 se obtiene a partir de la ecuación 3, calculando
únicamente un lado del área necesaria para almacenar materiales sin unidad de carga (apilamiento).El lado "b" y "c"de la zona de estantería convencional, están asociadas a la ecuación 6 y 7 de la tabla 4. Finalmente el área total del almacén se obtiene mediante la sumatoria de todas las áreas que la integran, agregando en esta sumatoria el área necesaria para pasillo central que estará intermedio al área 1, 2 y 3. Finalmente las ecuaciones 16 y 17 calculan el área total necesaria y utilización promedio para el almacenamiento de materiales respectivamente.
4.1. Algoritmo de dimensionamiento
De acuerdo con la definición de parámetros, variables de entrada y salida del modelo integral de dimensionamiento de almacenes en el sector de la construcción,se presenta a continuación los pasos propuestos para el algoritmo.
1. Inicio.
2. ¿Obra de construcción etapas simultáneas?
3. Sí.
4. Determinar la combinación de etapas de construcción que intervienen en el diseño del almacén.
5. Establecer cantidad y/o volumen de pedido por tipo de material m3, pallet (m) y/o cantiléver.
6. Definir parámetros h y r
7. Calcular 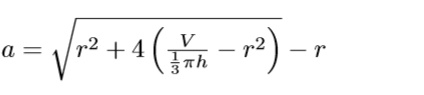
8. Calcular d = ai + ai+1 + ... + ai=n
9. Calcular área 2 = aimayor . d
10. Calcular Utilización área 2 = 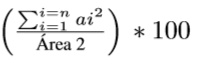
11. Definir parámetros αx, αy, Wx, Wy, nz,
12. Definir área 1 = 6m2
13. Calcular Utilización área 1 = 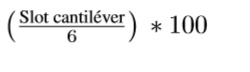
14. Calcular nx = 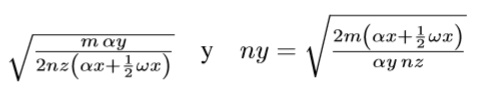
15. Calcular ![]()
16. Calcular área 3 = b*c
17. Calcular Utilización área 3 = ![]()
18. Calcular área total = área 1 + área 2 + área 3 + (wx . c)
19. Calcular Utilización promedio almacén = 
20. Si no.
21. ¿Etapa de construcción Estructural o Mecánica?
22. Sí.
23. Repetir paso 5 al 19
24. Si no Etapa Estética y Refinamiento
25. Repetir paso 11 al 19
26. Generar Layout con dimensiones calculadas
27. Fin.
4.2. Diagrama de flujo del algoritmo de dimensionamiento
El diagrama de flujo anterior representa la secuencia de pasos del algoritmo para dimensionar almacenes en obras de construcción. Inicialmente se genera un elemento condicional para clasificar la(s) etapa(s) en que se encuentra la obra. Para este caso puede aplicar la combinación de etapas simultáneas o sólo alguna de ellas. A partir de esto se determinan los valores de entrada, entre ellos los metros cúbicos de material de apilamiento, la cantidad de unidades compatibles con estantería cantiléver y convencional, entre otros. De la misma manera se definen los parámetros de unidad de carga y ancho de pasillos de acuerdo a las restricciones de espacio y condiciones de maniobrabilidad de los equipos de manipulación. Finalmente el algoritmo genera el cálculo de área necesaria para cada una de las unidades de carga, así como el área general del almacén con su respectiva utilización promedio proyectada. Con esto se obtienen los parámetros de diseño del layout para realizar el trazado de áreas de almacenamiento en la obra de construcción. Cabe resaltar que para el caso de etapas únicas se tiene los mismos pasos,con la diferencia que en la etapa estética y refinamiento aplica únicamente área cantiléver y convencional, de acuerdo a la configuración obtenida en la definición de variables y parámetros de abastecimiento. La secuencia presentada en este algoritmo genera el diseño procedimental para el desarrollo de una aplicación en lenguaje de programación visual basic, con la que se realiza el proceso de aplicación y validación del mismo. Figura 6
4.3. Validación del algoritmo
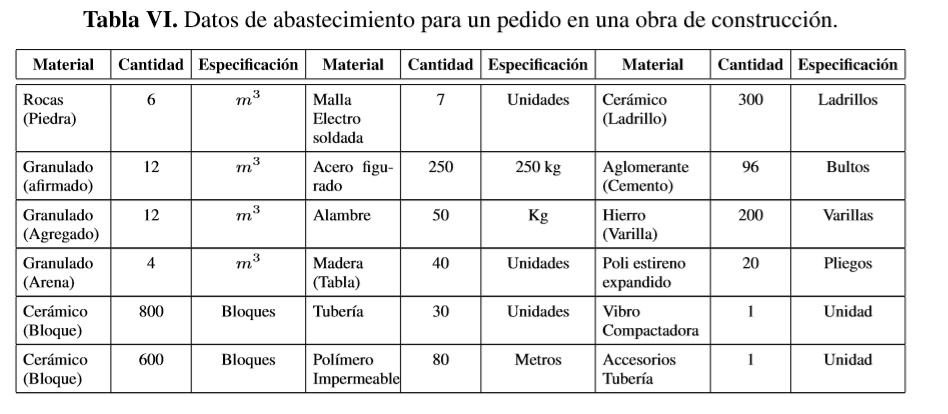
Una vez diseñado el algoritmo se procede a validar su aplicabilidad en el proceso de dimensionamiento dinámico de almacenes. Para esto se obtienen datos de abastecimiento de una obra de construcción residencial. Las características de pedido de la obra se presentan en la Tabla VI.
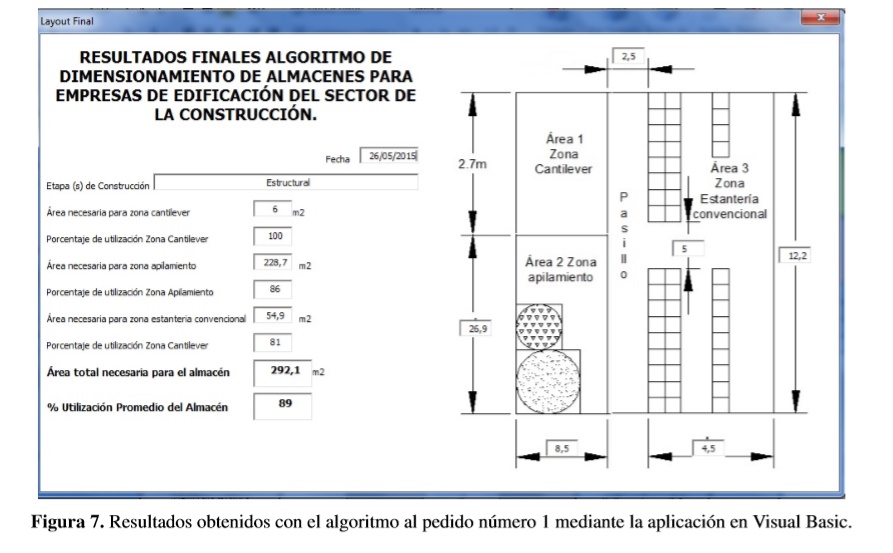
La obra está proyectada para construir un edificio multifamiliar de tres niveles. Para la aplicación del algoritmo se tomará como muestra un total de cuatro pedidos de material realizados en diferentes etapas de construcción. Cabe resaltar que el primer pedido se caracteriza por ser etapa única "Estructural", los dos siguientes pedidos son etapas simultáneas "Estructural y Mecánica" y el último estética y refinamiento. Los datos de los pedidos y los resultados obtenidos con la aplicación computacional del algoritmo son los siguientes:
- Los resultados obtenidos para el primer pedido aplican para tres áreas de almacenamiento con un total de 292m2. La proyección de utilización del almacén es del 89%. De acuerdo con el layout obtenido, la zona cantiléver debe tener una asignación mínima de 6m2 obtenida a partir de 2 y 2,7 metros en lo sejes X-Y respectivamente.Por otra parte la zona de apilamiento debe tener una asignación de 228,7m2 obtenida a partir de 8,5 y 26,9 metros en los ejes X -Y respectivamente, proyectando una utilización del 86%. Finalmente la zona de estantería convencional debe tener una asignación de 54,9m2 obtenida a partir de 4,5 y 12,2 metros en los ejes X - Y respectivamente, proyectando una utilización del 81%.
- Los resultados obtenidos para el segundo pedido aplican para tres áreas de almacenamiento con un total de 183,8m2.La proyección de utilización del almacénes del 93%.
- Los resultados obtenidos para el tercer pedido aplican para tres áreas de almacenamiento con un total de 198,4m2. La proyección de utilización del almacén es del 92%.
- Los resultados obtenidos para el cuarto pedido aplican para tres áreas de almacenamiento con un total de 52m2. La proyección de utilización del almacén es del 94%.
5. Discusión de los resultados
El presente estudio identifica el avance investigativo en el proceso de abastecimiento y almacenamiento de materiales, en el que técnicas matemáticas, heurísticas y de algoritmos comprenden el principal desarrollo de métodos y/o modelos aplicados a la gestión de almacenes. Entre ellos se enmarca un modelo geométrico de dimensionamiento de almacenes que de acuerdo a sus características, es compatible con las condiciones del sector de la construcción, siendo necesario hacer ajustes para poderlo adaptar a procesos de construcción de vivienda. Por otra parte, en la caracterización del sector de la construcción se identifican siete categorías y veintidós subcategorías de material, cuatro categorías de protección, tres técnicas de almacenamiento, siete unidades de carga y tres etapas de construcción, estableciendo así variables y parámetros para el diseño del algoritmo.
De acuerdo con la necesidad de ejercer mayores acciones de almacenamiento debido al creciente abastecimiento de materiales en obras de construcción, se desarrolla un algoritmo de dimensionamiento que combina tres zonas de almacenamiento que varían de acuerdo a la unidad de carga a utilizar. Según los resultados, estas zonas son compatibles con las siete unidades de carga previamente identificadas, definiendo como estándar la integración de zonas cantiléver, apilamiento y estantería convencional (paletizada).
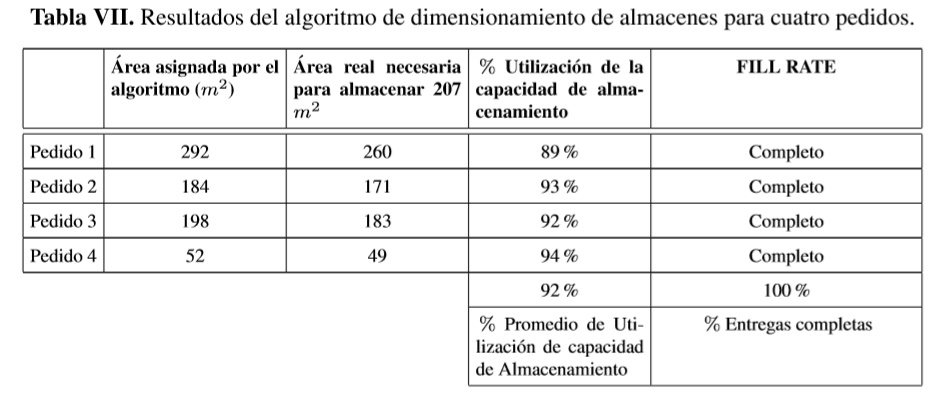
Adiferencia de la aplicación de otros algoritmos que buscan generar soluciones a problemas de distribución para reducir tiempos de entrega, niveles de inventario, entre otros, el algoritmo de dimensionamiento propuesto busca mejorar el nivel de servicio garantizando la entrega de pedidos completos al tener suficiente material disponible en diferentes unidades de carga en el almacén. Según los resultados obtenidos en la aplicación del algoritmo para cuatro pedidos en una obra de construcción, se identifica que el trazado para asignación de áreas de almacenamiento tendrá proyectado una utilización promedio del 92%. La entrega de pedidos completos tendrá un rendimiento del 100% debido a que las áreas asignadas disponen de capacidad suficiente para almacenar los materiales solicitados. Los resultados específicos de estos indicadores para cada pedido se presentan en la Tabla VII.
En la Tabla VII se registra pedido entregado "completo" cuando la capacidad necesaria es inferior a la capacidad asignada o en otras palabras se recibe la totalidad del material solicitado porque se encontraba disponible en el almacén, generando un porcentaje de utilización inferior al 100%. De acuerdo con los resultados, se presenta incremento promedio del 5% en la utilización de la capacidad de almacenamiento, lo cual relativamente es bajo. En el análisis del problema se identifica que por medio de la experiencia de personas encargadas de planificar áreas de almacenamiento, la utilización de capacidad promedio es del 87% lo cual es un indicador inicial muy bueno. Esto hace deducir que el algoritmo de dimensionamiento mantiene en sus resultados una asignación sin mayor variabilidad comparada con la obtenida por la experiencia de los programadores. Contrario a esto, los resultados obtenidos con el algoritmo para el segundo indicador presentan un incremento del 23%, generando una variabilidad positiva en la entrega de pedidos.
El aporte del algoritmo de dimensionamiento propuesto establece bondades de aplicación en procesos de gestión de abastecimiento de obras de construcción, ya que no sólo se puede destinar a reducir el grado de informalidad y subjetividad en el momento de realizar asignación de espacios de almacenamiento, sino garantizar la entrega de pedidos completos apoyando el proceso de planeación de obras y facilitando la estandarización de almacenes en un sistema dinámico y temporal.
6. Conclusiones
El diseño del algoritmo de dimensionamiento integra variables de entrada, parámetros y variables de salida que se adaptan a la opción de una o múltiples etapas de construcción, constituyendo así un total de 27 pasos. En estos pasos se involucra adicionalmente el cálculo de utilización de capacidad como indicador primario para validar la viabilidad del algoritmo.
Con la aplicación del algoritmo de dimensionamiento se obtiene una mejora en el nivel de servicio incrementando de un 67% a un 100% en la entrega de pedidos. Este incremento se logró ya que el algoritmo garantiza la asignación de capacidad superior a la necesaria. Sin embargo los resultados de utilización de esta capacidad no presentan incremento representativo ya que mantiene la misma utilización generada en el experimento. Lo anterior hace que el algoritmo con múltiples criterios de evaluación aplicado en la solución de problemas de dimensionamiento de espacios de almacenamiento en empresas de edificación sea viable únicamente para garantizar la entrega completa de pedidos.
Se recomienda para futuras investigaciones la integración de parámetros de ubicación del almacén en obra al algoritmo, es decir definir una secuencia de pasos que permitan realizar ubicación dinámica de almacenamiento en la medida que avanza la obra. También la distribución interna materiales acondicionando métodos en los que se garantice disminución de tiempos de alistamiento de pedidos, con el objeto de generar una solución completa a los problemas comunes que se presentan en el abastecimiento de materiales en el sector de la construcción. También es necesario adaptar los resultados del algoritmo a un lenguaje gráfico (autocad, soliedge, entre otros), para generar informes más detallados y comprensibles por parte de programadores de obra. Para el caso de querer aplicar el algoritmo en otro tipo de obras de construcción, es necesario repetir el proceso de validación sin necesidad de modificar variables y parámetros de entrada y a que estos son genéricos para el sector de la construcción.
Referencias
1. DANE. Comunicado de prensa. 19 de Junio de 2014, Disponible en: http://www.dane.gov.co/files/investigaciones/boletines/pib/bol PIB Itrime14.pdf
2. Santiago, Manrique. (2010) Identificación de los principales problemas en la logística de abastecimiento de las empresas constructoras Bogotanas y propuestas de mejoras, Consultado 15 de Mayo de 2014, disponible en: http://javeriana.edu.co/biblos/tesis/economia/tesis189.pdf
3. Andrés Hualpa, Carolina Suarez (2013) Ubicación y dimensionamiento como parámetros en el diseño de almacenes: revisión del estado del arte, Revista de Ingeniería, Volumen 18-1, (ISSN 0121-750X) 65-83
4. Jinxiang Gu, Marc Goetschalckx, Leon F. McGinnis, (2007) Research on warehouse operation: A comprehensive review, European Journal of Operational Research, Volume 177, Issue 1, (ISSN 0377-2217) 1-21
5. M.S. Hung, John C. Fisk, (1984) Economic sizing of warehouses: A linear programming approach, Computers & Operations Research, Volume 11, Issue 1, (ISSN 0305-0548) 13-18.
6. CharlesJ. Malmborg, S waminathan Balachandran, Daniel M.Kyle, (1986) A model based evaluation of a commonly used rule of thumb for warehouse layout, Applied Mathematical Modelling, Volume 10, Issue 2, (ISSN 0307-904X) 133-139
7. Kumar Bhaskaran, Charles J. Malmborg, (1990) Economic tradeoffs in sizing warehouse reserve storage area, Applied Mathematical Modelling, Volume 14, Issue 7, (ISSN 0307-904X) 381-385
8. Charles J. Malmborg, Krishnakumar Bhaskaran, (1990) A revised proof of optimality for the cube-per-order index rule for stored item location, Applied Mathematical Modelling, Volume 14, Issue 2, (ISSN 0307-904X) 87-95.
9. O. Hounkonnou, (1990) Modelling and simulation of an automated warehouse in activity, Mathematical and Computer Modelling, Volume 14, (ISSN 0895-7177) 1100-1102.
10. Gilles Cormier, Eldon A. Gunn, (1992) A review of warehouse models, European Journal of Operational Research, Volume 58, Issue 1, (ISSN 0377-2217) 3-13
11. Charles J.Malmborg,(1996) An integrated storage system evaluation model, Applied Mathematical Modelling, Volume 20, Issue 5, (ISSN 0307-904X) 359-370.
12. A.K. Rao, M.R. Rao, (1998) Solution procedures for sizing of warehouses, European Journal of Operational Research, Volume 108, Issue 1, (ISSN 0377-2217) , 16-25
13. René de Koster, Tho Le-Duc, Kees Jan Roodbergen, (2007) Design and control of warehouse order picking: A literature review, European Journal of Operational Research, Volume 182, Issue 2, (ISSN 0377-2217) 481-501.
14. Semih Önüt, Umut R. Tuzkaya, Bilgehan Dogac, (2008) A particle swarm optimization algorithm for the multiple-level warehouse layout design problem, Computers & Industrial Engineering, Volume 54, Issue 4, (ISSN 0360-8352) 783-799.
15. Venkata Reddy Muppani (Muppant), Gajendra Kumar Adil, (2008) A branch and bound algorithm for class based storage location assignment, European Journal of Operational Research, Volume 189, Issue 2, (ISSN 0377-2217) 492-507.
16. Lu Chen, André Langevin, Diane Riopel, (2011) A tabu search algorithm for the relocation problem in a warehousing system, International Journal of Production Economics, Volume 129, Issue 1, (ISSN 0925-5273) 147-156.
17. F.Guerriero,R.Musmanno,O.Pisacane,F.Rende,(2012)A mathematical model for the Multi - Levels Product Allocation Problem in a warehouse with compatibility constraints, Applied Mathematical Modelling, (ISSN 0307-904X)
18. Felix T.S. Chan, H.K. Chan, (2011) Improving the productivity of order picking of a manual-pick and multilevel rack distribution warehouse through the implementation of class-based storage, Expert Systems with Applications, Volume 38, Issue 3, (ISSN 0957-4174) 2686-2700
19. Klaus Moeller, (2011) Increasing warehouse order picking performance by sequence optimization, Procedia Social and Behavioral Sciences, Volume 20, (ISSN 1877-0428) 177-185.
20. Luis, Joyanes, Concepción Fernandez y Ignacio, Zahonero. (2005) Programación en C:Metodología,algoritmos y estructura de datos. Mc Graw Hill. Ed 2.
21. Instituto de Desarrollo Urbano, (2008) Procedimiento para el almacenamiento de materiales en campamentos, centros de acopio y frentes de obra, Disponible en: http://webidu.idu.gov.co:9090/jspui/bitstream/123456789/32643/23/60014765-12.pdf
22. Gianpaolo Ghiani, Gilbert, Laporte y Roberto, Musmanno. (2004) Introduction to logistics systems: Planning and control. Editorial John Wiley & Sons. 193-199
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.


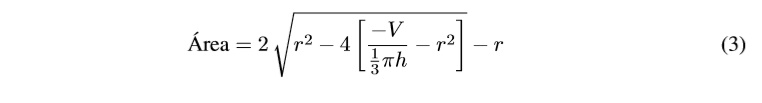




2.jpg)










