DOI:
https://doi.org/10.14483/22484728.5515Publicado:
2013-12-09Número:
Vol. 7 Núm. 2 (2013)Sección:
Visión de CasoModelo de la marcha bipeda humana usando modelica
Model of gait bipedal human using modelica
Palabras clave:
Bipedal gait, control, model, mathematical model, simulation, systems (en).Palabras clave:
Marcha bípeda, control, modelo, modelo matemático, simulación, sistemas (es).Descargas
Referencias
S. Collado, “Análisis de la marcha humana con plataformas dinamométricas. Influencia del transporte de carga”, Memoria presentada para optar al grado de doctor [en línea], disponible: http://eprints.ucm.es/4401/1/med3.pdf, consultado: 21 de abril de 2011.
C. Marco S, Cinesiología de la marcha humana normal.[en línea], disponible: http://wzar.unizar.es/acad/cinesio/Documentos/Marcha%20humana.pdf
J. Larriva, E. Guillermo, J. Trelles y O. Vele, Diseño y construcción de un robot bípedo experimental [en línea], disponible: http://mail.ups.edu.ec/universitas/publicaciones/universitas/contenidospdf//disenorobotbipedoUniversitas8.pdf
D. Martin, “Cinemática inversa [en línea], disponible: http://www.x-robotics.com/cinematica.htm, consultado: 15 de marzo de 2011.
Modelica [en línea], disponible: http://en.wikipedia.org/wiki/Modelica, consultado: 12 de febrero de 2011
“Addlink software científico”, S.L. MathModelica Professional [en línea], disponible: http://www.addlink.es/productos.asp?pid=37, consultado: 8 de enero de 2011.
Linköping University, Programming Environments Laboratory, “Modelica” [en línea], disponible: http://www.ida.liu.se/~pelab/realsim/library/ModelicaAdditions/docu/ModelicaAdditions.htm, consultado: 10 de febrero de 2011.
E. Kofman, “Introducción a Modelica”, Laboratorio de Sistemas Dinámicos, Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario, Argentina.
J. Diego-Más, “Biomecánica (esfuerzos estáticos coplanares)” [en línea], disponible: http://www.ergonautas.upv.es/metodos/biomecanica/biomecanica-ayuda.php, consultado: 23 de mayo
de 2011.
Serway, Física, tomo II, 3ª ed., México: McGraw-Hill, 1993.
O. Vele, Planificación de caminata para un robot bípedo [en línea], 2005, disponible: http://loslocosrh.blogspot.com/
O. Vele, Simulación mecánica de un robot humanoide en Matlab [en línea], 2005, disponible: http://loslocosrh.blogspot.com/
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
MODELO DE LA MARCHA BÍPEDA HUMANA USANDO MODELICA
MODEL OF GAIT BIPEDAL HUMAN USING MODELICA
Fecha de envío: noviembre de 2012
Fecha de recepción: noviembre de 2012
Fecha de aceptación: octubre de 2013
Lely A. Luengas
Ingeniera electrónica, Fundación Universidad Autónoma de Colombia (Colombia). Especialista en Pedagogía y Docencia Universitaria, Universidad de San Buenaventura (Colombia). Magíster en Ingeniería Eléctrica, Universidad de Los Andes (Colombia). Estudiante de Doctorado en Ingeniería, Pontificia Universidad Javeriana (Colombia). Docente del programa de Tecnología Electrónica, Universidad Distrital Francisco José de Caldas (Colombia). Investigadora del grupo de investigación Metis. Correo electrónico: laluengasc@udistrital.edu.co
Carlos A. Marín
Tecnólogo electrónico, Universidad Distrital Francisco José de Caldas (Colombia). Estudiante de Ingeniería de Telecomunicaciones, Universidad Distrital Francisco José de Caldas (Colombia). Correo electrónico: Carlosart_ Men88@hotmail.com
Jonathan F. González
Tecnólogo electrónico, Universidad Distrital Francisco José de Caldas (Colombia). Estudiante de Ingeniería de Telecomunicaciones, Universidad Distrital Francisco José de Caldas (Colombia). Correo electrónico: Jonathan_d.r.b@hotmail.com
Resumen:
Este artículo describe la investigación para generar un aplicativo donde se visualiza la marcha bípeda humana, haciendo uso del software Modelica 2.1.2 ® y sus herramientas para la visualización en tres dimensiones. Para ello se desarrolló un modelo físico-matemático con el cual se configuraron los sistemas y subsistemas propios del software. Para la simulación se tuvo en cuenta el funcionamiento básico de la caminata que efectúa un robot bípedo y su respectiva teoría de cinemática inversa y directa, al igual que las acciones de controles proporcionalderivativa (PD), proporcional-integral (PI) y proporcional-integral-derivativa (PID) en lazo cerrado, y especificaciones de sintonización para la regulación de ángulo de las articulaciones de las piernas y mantener un nivel del piso sobre el cual se realice el desplazamiento del objeto. Esta investigación permitió obtener la visualización de la caminata bípeda en un plano, observando que el control tomando como referencia la posición angular, es uno de los métodos más efectivos en el momento de generar los pasos del robot, pues básicamente se calculan y se controlan las fuerzas que se interponen en este proceso.
Palabras Clave:
Marcha bípeda, control, modelo, modelo matemático, simulación, sistemas
Abstract:
This paper describes research to generate an application where human bipedal gait displayed, using the Modelica 2.1.2 ® software and tools for visualization in 3 dimensions. This provides a physical- mathematical model which is configured own systems and software subsystems. For the simulation, we took into account the basic operation of the walk that makes a biped robot theory and their respective direct and inverse kinematics as well as the actions of proportional-derivative control (PD), proportional-integral (PI) and proportional-integral-derivative (PID) closed loop tuning and specifications for adjusting the angle of the leg joints and maintain a level ground on which to perform the displacement of the object, the product is expected to serve as based educational program developed based on, for the design and implementation of advanced devices : whether robots that emulate the human gait, for entertainment and even virtual reality for human use, or to create a prosthesis control that allows a disabled person have the ability to walk.
Keywords:
Bipedal gait, control, model, mathematical model, simulation, systems
1. Introducción
El análisis de la marcha bípeda ha sido de interés desde hace ya algún tiempo. Ha sido estudiando con diferentes técnicas: por ejemplo, a través de plataformas de fuerza, en estudio realizado por Collado [1], quien obtuvo parámetros similares a los mencionados en la literatura [2]. También se ha estudiado para fabricar robots que asemejen su marcha a la humana [3].
Las investigaciones realizadas permiten valorar los distintos parámetros de la marcha de forma objetiva y eficaz, apreciar los factores que pueden modificarla, diagnosticar alteraciones del patrón de marcha en diversas patologías y lesiones traumáticas y realizar un control y seguimiento de pacientes para observar su evolución [1]. Asimismo, generar modelos matemáticos que llevados a un modelo físico aplicado a un entorno electromecánico pueden reproducir la marcha. La investigación realizada obtuvo un modelo mediante el cual se modela, simula y analiza la marcha humana, haciendo uso del software Modelica 2.1.2 ®. El modelo está basado en la cinemática inversa.
El artículo se estructura de la siguiente forma: primero se muestra un marco teórico donde se aborda el concepto y las singularidades de la marcha humana, además de la teoría básica de la cinemática inversa y se presenta el software utilizado. En segundo lugar, se presenta el modelo desarrollado y los parámetros que se tuvieron en cuenta. En tercer lugar está la simulación realizada y los resultados arrojados. Por último y en cuarto lugar, las conclusiones de la investigación.
2. Marco teórico
2.1. Marcha bípeda
La marcha humana es un modo de locomoción bípeda con actividad alternada de los miembros inferiores, que se caracteriza por una sucesión de doble apoyo y de apoyo unipolar; es decir, que durante la marcha el apoyo no deja nunca el suelo, mientras que en la carrera, como en el salto, existen fases aéreas en las cuales el cuerpo queda suspendido durante un instante.
El ciclo de marcha es la secuencia de acontecimientos que tienen lugar desde el contacto de un talón con el suelo, hasta el siguiente contacto del mismo talón con el suelo. Durante un ciclo de marcha completo, cada miembro inferior considerado pasa por dos fases:
- Fase de apoyo: en la cual el pie de referencia está en contacto con el suelo.
- Fase de oscilación: en la que el pie de referencia está suspendido en el aire.
La fase de apoyo constituye alrededor del 60 % del ciclo y la fase de oscilación representa el 40 % restante. Las fases del ciclo de marcha, para facilitar su estudio suelen dividirse, todavía, en componentes más pequeños o subfases, según la siguiente secuencia: el ciclo se inicia con el impacto del talón en el suelo; al 15 % el antepié también contacta con el suelo, por lo que esta subfase se denomina “pie plano sobre el suelo” o media; al 40 % del ciclo, el talón comienza a elevarse del suelo (subfase de despegue de talón o final); al 50 % despega el antepié, que culmina al 60 % del ciclo con el despegue de los dedos, lo que indica también el comienzo de la fase de oscilación.
La atribución de percentiles en esta fase es algo imprecisa, pero en la primera parte se realiza el avance del miembro oscilante hasta alcanzar el miembro contralateral. La extensión de rodilla completa el avance del miembro inferior. Al 100 % del ciclo, se produce de nuevo el impacto de talón, con el mismo pie [2].
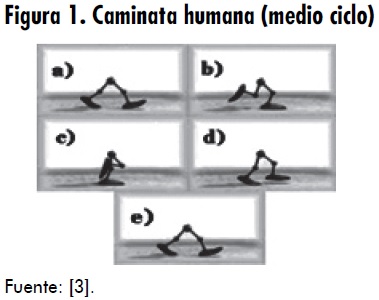
En la figura 1 se observa medio ciclo, ya que la otra mitad del ciclo de la caminata es la misma, con la diferencia de que la pierna que realiza el movimiento ahora es la pierna de apoyo, y la de apoyo es la que ahora realiza el movimiento [2].
2.1.1. Cinética de la marcha
En la marcha el cuerpo humano utiliza al máximo la fuerza de gravedad, la de reacción y la inercia. Junto con la fricción o rozamiento, estas son las principales fuerzas que influyen en la marcha.
La fuerza de gravedad: la marcha se caracteriza por la traslación del centro de gravedad del cuerpo hacia adelante, llegando momentáneamente más allá del borde anterior de la base de sustentación, lo que origina una pérdida transitoria del equilibrio. La acción de la gravedad tiende a hacer caer el cuerpo hacia adelante y abajo, incrementando la velocidad y transformando la energía potencial en cinética. En este punto el pie que oscilaba se sitúa en el suelo, recuperando el equilibrio, al ofrecer una base de sustentación mucho más amplia y evitando la caída del cuerpo.
La fuerza de reacción es la que ejerce el suelo sobre el individuo, a través de los pies y que es de igual magnitud que el impulso hacia abajo del pie durante la marcha, pero en sentido contrario. La marcha requiere además una fricción adecuada entre el pie y el suelo para no resbalar. La fuerza de fricción o de rozamiento dependerá del tipo de materiales en contacto y de las fuerzas que ejercen presiones entre ellos. La inercia, entendida como la incapacidad del cuerpo para cambiar su estado de reposo o de movimiento sin la intervención de alguna fuerza, debe ser vencida en cada paso y cuanto mayor sea el peso del cuerpo mayor será la inercia que se ha de vencer [2].
2.1.2. Planificación de la marcha
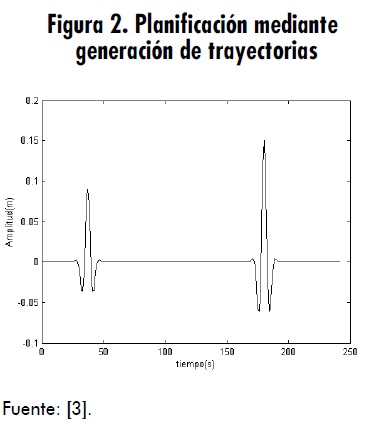
En la planificación de marcha se hace uso de varios métodos, uno de ellos es el de generación de trayectorias, donde se incide indirectamente sobre las articulaciones, ya que se trabaja con la posición y orientación de los efectores finales; por ello se requiere la cinemática inversa. En la figura 2 se muestra el efecto de usar este método de planificación.
Analizando las ventajas de este método, se encuentra que es un proceso sistemático que permite la fácil interpretación y planificación de la caminata. Además, se podrían analizar velocidades, aceleraciones, etc., de los efectores finales [3].
2.2. Cinemática inversa
El objetivo de la cinemática inversa consiste en encontrar el gesto que deben adoptar las diferentes articulaciones para que el final del sistema articulado llegue a una posición concreta.
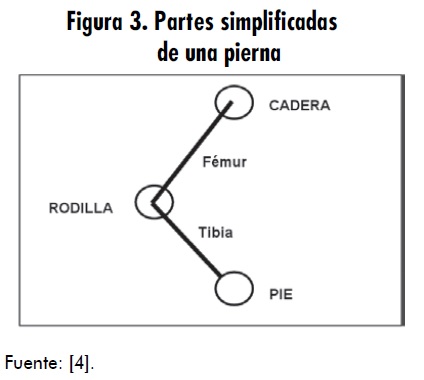
Por ejemplo, se puede imaginar un robot con piernas. Estas surgen de la cadera y a continuación estaría el fémur, la rodilla, la tibia y el pie. En la figura 3 se observa el sistema que pretende imitar una pierna. Como es lógico, la posición de la cadera es fija o se puede calcular en relación con el cuerpo del robot o anclaje, pero ahora el problema que surge es posicionar el pie.
Tomando como base un sistema de coordenadas cartesianas, se puede definir la posición que se quiere que tome el pie, pero surgen las preguntas: ¿qué ángulo debe adoptar el fémur respecto a la cadera?, ¿qué ángulo debe adoptar la tibia respecto a la rodilla?, y ¿dónde posicionar la rodilla para que el pie tome la posición que se quiere adoptar? La cinemática inversa pretende solucionar el problema mediante cálculos trigonométricos que permitan determinar las respuestas a las inquietudes planteadas [4].
2.3. Modélica ®
Modélica® es un programa orientado a objetos, declarativo. Es un lenguaje de modelado multidominio de componentes orientados a la modelización de sistemas complejos; por ejemplo: sistemas de mecánica, eléctrica, electrónica, hidráulica, térmica, control, energía eléctrica o subcomponentes orientados al proceso. Este software cuenta con herramientas específicas que permiten describir las relaciones constitutivas de los distintos componentes de cada modelo y las relaciones estructurales que definen la interacción entre dichos componentes. De esta manera, el lenguaje permite asociar cada componente de un sistema a una instancia de una clase de Modélica®. Asimismo, puede expresar relaciones estructurales de un modelo que permiten construir su estructura de una manera totalmente gráfica [5].
La ventaja de utilizar este software de simulación es que se optimiza el análisis matemático y en muchos de los casos se obtienen importantes deducciones en forma eficaz y rápida. Otra ventaja de los programas de simulación es que su complejidad en el diseño y análisis no aumenta a medida que se adiciona un mayor número de grados de libertad. Se ha mencionado que la simulación sustituye de cierta forma al análisis físico-matemático, pero cabe destacar que para realizar una simulación que represente de buena forma a la realidad se deben tener muy claros los conceptos y principios fundamentales de la física [2].
2.3.1. MathModelica®
La herramienta utilizada para la simulación de la marcha bípeda es MathModelica Profesional 2.1.2.®, de la compañía sueca AB MathCore Ingeniería. Esta es una potente plataforma de simulación de sistemas dinámicos y diseño basado en modelos para ingeniería. Proporciona un entorno gráfico interactivo y un conjunto de librerías de componentes totalmente personalizable [6]. Consta de dos partes integrantes: System Designer®, que permite el diseño de modelos mediante funciones de “arrastrar y soltar”, y su entorno de trabajo está basado en la librería 1.3.1 de Modélica®; y Simulation Center®, que posibilita el análisis de los resultados en gráficos, visualiza e interactúa con sistemas dinámicos en un entorno 3D [7].
3. Simulación completa de la marcha bípeda
La simulación determina los requerimientos básicos implicados en el proceso de la marcha, como lo es el posicionamiento necesario de cada articulación para efectuar una posición angular final. La planificación de la caminata se implementó con el método de generación de trayectorias. Con este método de proyección se incide indirectamente sobre las articulaciones, ya que se trabaja con la posición y orientación de los efectores finales. De ahí que se requiera la resolución de la cinemática inversa. En cuanto al controlador, se ha escogido trabajar el control PD que está en la rama de los sistemas de retroalimentación y según la literatura estudiada presenta óptimos resultados.
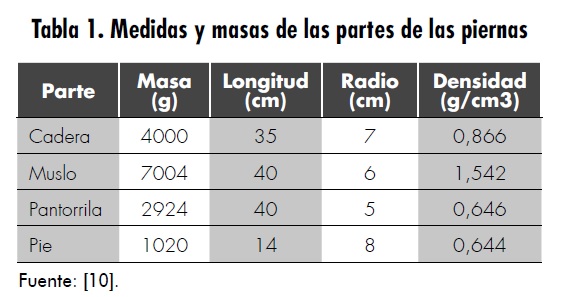
Como principio fundamental, se debe tener en cuenta la función e importancia de la implementación de control. En primer lugar, se establece la longitud y la masa de los segmentos respecto a la edad [8] y la masa total del individuo. Se ha elegido realizar la simulación con un individuo de veinte años, 165 cm de estatura y con masa corporal de 70 kg. Se ha elegido esta edad porque los músculos y huesos ya se encuentran desarrollados y se tiene el patrón de marcha definido [2]. Con los valores dados de altura y masa y haciendo uso de las herramientas de estimación de peso y longitud de los segmentos corporales de la Universidad Politécnica de Valencia [9], se obtuvieron los valores requeridos para la simulación de la marcha. Se ha considerado cada segmento como un cilindro sólido. Por ello, se obtuvo el radio de cada segmento. En la tabla 1 se observan las medidas y la masa corporal de cada una de las partes.
3.1. Cinemática inversa
Se ha tomado la posición de la cadera como punto de origen de los vectores muslo y pantorrilla. Estos vectores tienen un radio y largo invariables. Como ejemplo se toman 0,4 m de cada uno, con lo que el radio máximo que la pierna puede alcanzar será de 0,8 cm. Para simplificar los cálculos es importante que la longitud de muslo y pantorrilla sea la misma, como se observa más adelante [4,11].
El posicionamiento del tobillo se realizó en el sistema cartesiano. Para ello, se estableció un punto con coordenadas (x,y) con relación a la cadera. Luego se formó un triángulo rectángulo entre los puntos de cadera y tobillo, lo cual presenta dos catetos equivalentes a las posiciones x e y en el sistema de representación cartesiano. Así pues, con la ecuación (1) se calcula la hipotenusa de este triángulo.
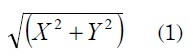
Por ejemplo: si se quiere posicionar el tobillo en y = -0,721842925 y x = -0,115168287, aplicando la ecuación (1) se obtiene el valor de hipotenusa de 0,73 (ver ecuación 2).
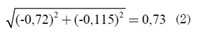
El valor de la hipotenusa determina la distancia entre los puntos de origen y destino (cadera a tobillo). Para calcular el ángulo que forma la hipotenusa con respecto al eje x se usa la ecuación (3).
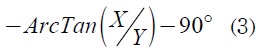
Trabajando con los valores dados de posición y = -0,721842925 y x = -0,115168287, el ángulo obtenido es -99,065 grados, como se muestra en la ecuación (4).
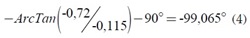
Definido en coordenadas polares el punto donde se quiere poner el tobillo, se calcula el ángulo formado entre el muslo y la cadera para que el pie apunte justo a esa posición. Como el muslo y la pantorrilla tienen una longitud exactamente igual, el punto donde convergen caerá siempre en la vertical de la mitad de la distancia entre cadera y pie, y la rodilla siempre estará en esa línea.
Se observa que entre los puntos de cadera, rodilla y el punto medio entre cadera a tobillo se forma un triángulo rectángulo como en el caso anterior, solo que ahora la hipotenusa es el propio muslo, y se conoce su longitud, con lo que solo se tiene que calcular el ángulo descrito del muslo con respecto al eje x.
Para calcular el ángulo del fémur con respecto a la vertical de 0,3654863 m (recordar que es la mitad de la longitud entre cadera y tobillo), la hipotenusa (muslo) mide exactamente 0,4 m, con lo cual se calcula el seno de este triángulo rectángulo como en la ecuación (5).
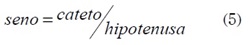
Reemplazando los valores dados anteriormente, se tiene la ecuación (6).
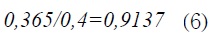
Se obtiene el arco seno. Para saber el ángulo buscado se aplica la ecuación (7).
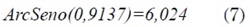
El valor calculado corresponde al ángulo agudo del triángulo rectángulo, así que hay que restarle a 90º este valor para obtener el ángulo incógnita, y esto sumado al ángulo formado por la línea entre cadera y tobillo da el ángulo total referenciado al sistema de coordenadas cartesiano, o lo que es lo mismo, referenciado al anclaje de la pierna o cuerpo [4]. La ecuación (8) muestra el cálculo del ángulo del muslo.
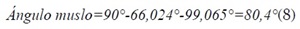
Así, ya se tiene el muslo en su sitio y solo falta calcular el ángulo de la pantorrilla, pero este cálculo es mucho más simple pues tal ángulo es el doble del ángulo agudo calculado anteriormente, y restándole 180 para que este referenciado al eje x del muslo, la ecuación (9) permite el cálculo del ángulo.
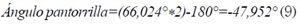
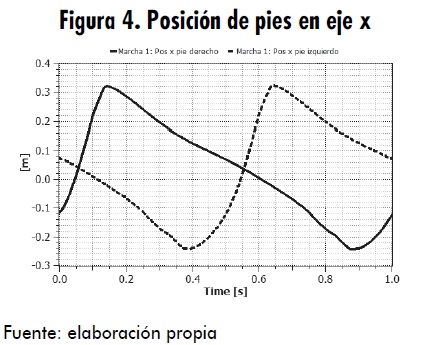
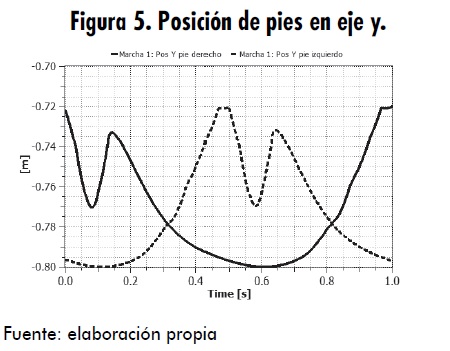
Llegado este punto, ya se ha conseguido el objetivo de saber el ángulo que deben adoptar las extremidades de una supuesta pierna para alcanzar un punto concreto [4]. A partir de esto se toman los datos obtenidos en la tabla 1 (longitud de las partes) y en las figuras 4 y 5 (posición de los pies en los ejes x e y), para poder encontrar los ángulos necesarios.
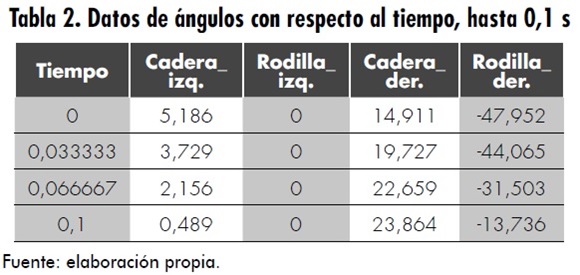
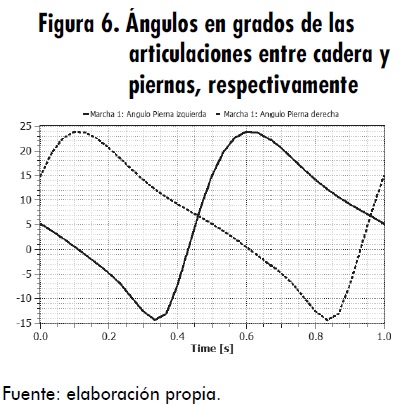
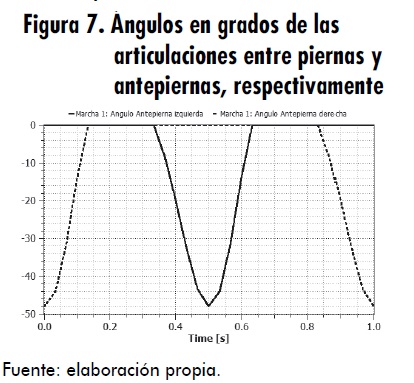
En la tabla 2 se muestran algunos de estos datos ya calculados, es decir, los ángulos de los tobillos en diversos instantes de tiempo. Posteriormente, se realiza la correspondiente interpolación para generar la señal de posición angular sin interrupciones; estas se muestran en las figuras 6 y 7.
Estas “señales” se pueden introducir en la plataforma de MathModelica como señal de referencia por medio del bloque TimeTable, para generar una señal de salida por interpolación lineal en una tabla. Los puntos de tiempo y valores de la función se almacenan en una tabla matriz [i, j], donde la primera columna contiene los puntos de tiempo y la segunda los datos que se van a interpolar.
3.2. Estructuración de la simulación
Para realizar el diagrama de bloques completo en MathModelica System Designer®, se ha tomado a la cadera como elemento de referencia para las demás partes del cuerpo, es decir, a partir de la cadera se construye toda la simulación. El proceso se muestra en la figura 8.
3.2.1. Modelado de una pierna
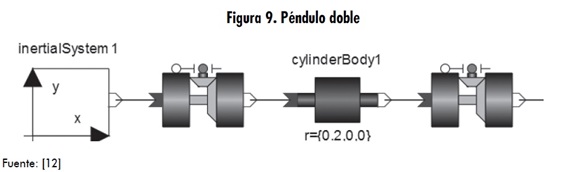
Se ha considerado el comportamiento de la pierna como un péndulo doble, que puede ser representado como se observa en la figura 9 [12].
De este modelo se ha formado el péndulo doble con dos grados de libertad de rotación, pero este no se mueve en forma controlada, por lo que es necesario utilizar el modelo de servomotor.
3.2.2. Modelado del control de una articulación
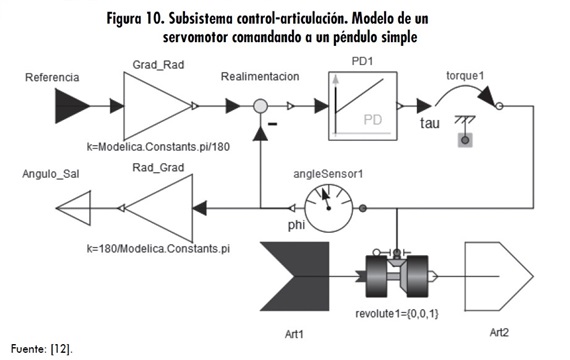
Los servomotores son motores que se caracterizan por tener un control de posición, es decir, se ubican inmediatamente en una determinada posición angular dentro de un rango de trabajo. El modelo para el control de la articulación consiste en un péndulo simple comandado por un servomotor [12] ( figura 10).
El diagrama de bloques se basa en el control de posición angular. Para esto se realiza un sistema de control en lazo cerrado, haciendo uso de un controlador PD (proporcional-derivativo), donde “Referencia” indica la señal de entrada angular, “torque1” es el actuador de fuerza en la rotación y “angleSensor1” determina el ángulo en el que se encuentra ubicado. Los bloques “Art1” y “Art2” permiten la interfaz entre el subsistema y el sistema general. Los bloques “Referencia” y “Angulo_ Sal” corresponden a la entrada y salida de datos, respectivamente [12].
3.2.3. Modelado del piso
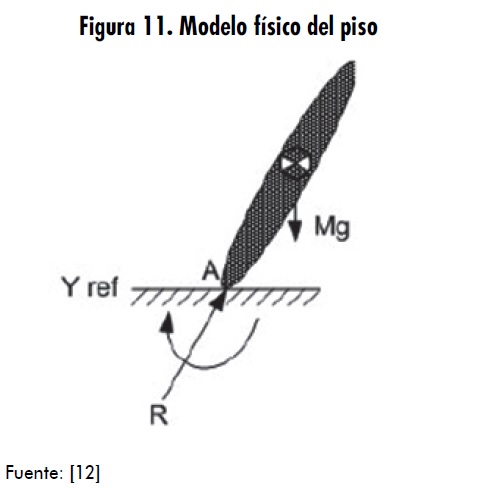
Partiendo de la tercera ley de Newton, de acuerdo con la cual “para toda acción existe una reacción igual y opuesta” [10], se procederá a simular el piso como un punto en el cual se ejerce una fuerza y un momento equivalentes que permiten al robot desplazarse sobre una superficie. En la figura 11 se muestra el esquema físico correspondiente [12].
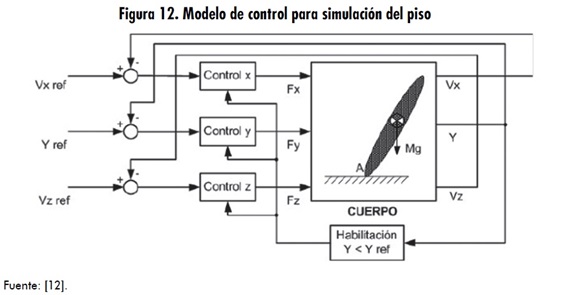
En el esquema en mención, el punto A es el punto de contacto del cuerpo con el piso, en el cual actúan la fuerza (F) y el momento (M) de reacción del piso. Para cumplir con este objetivo (simular el piso), se han realizado sistemas de control para los tres ejes (x,y,z) de acción de la fuerza neta que ejerce el piso sobre el cuerpo, tal como se esquematiza en la figura 12 [12].
Siendo Vx ref y Vz ref las velocidades deseadas del cuerpo (en el punto A) en los ejes x,z; Y ref la posición del punto A en el eje y; Vx, Vz, Y, son las velocidades y posiciones sensadas en el cuerpo y Fx, Fy ,Fz las componentes de la fuerza (F) que actúa en el punto A. Se puede observar también que existen tres controladores en este sistema, uno para cada eje, los cuales están habilitados si se cumple con la condición de que Y < Y ref; es decir, cuando el punto A esté “por debajo” del nivel del piso virtual (Y ref). Para el eje Y se utiliza un control de posición, pues el nivel del piso está regido por un valor absoluto constante (Y ref), en cambio para los ejes x,z, se utiliza un control de velocidad, pues cuando el cuerpo se esté moviendo no existirá una referencia global constante de posición en estos ejes. Para que no exista deslizamiento, los valores de referencia son Y ref= -0,9,Vx ref = 0 y Vz = 0.
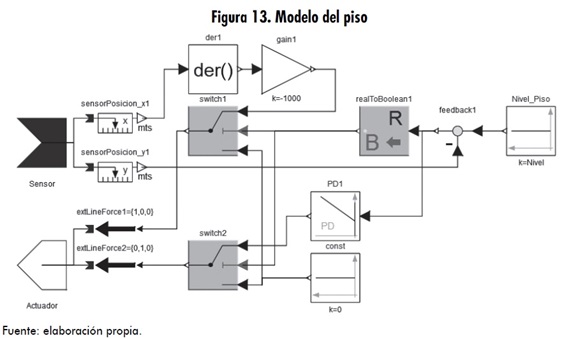
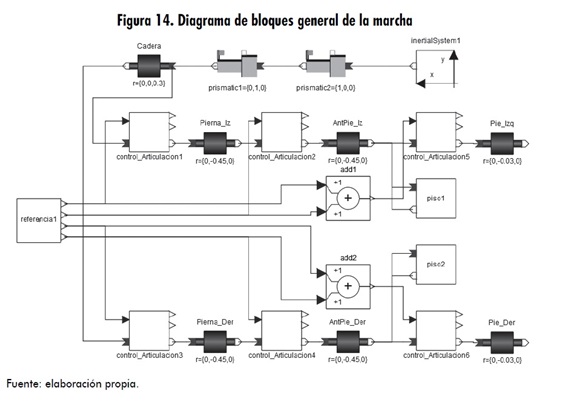
Dicho de otra forma, el control en el eje Y simula la reacción vertical neta del piso, la cual se equilibra con la fuerza hacia abajo creada por el cuerpo, haciendo que este (punto A) permanezca en el valor Y ref; en cambio, los controles en los ejes x, z simulan las fuerzas de rozamiento, impidiendo que el punto A se deslice. Se ha logrado experimentar que este sistema de control mediante fuerzas de reacción es una muy buena aproximación del fenómeno de contacto con el piso. El modelo del piso que se realiza en Modélica se muestra en la figura 13. En la figura 14 se puede ver el modelo de cinco eslabones (cadera y dos piernas), además de los dos puntos de contacto del piso en cada pierna.
El bloque “referencia1” contiene los vectores con los valores angulares para cada articulación, para así lograr la caminata bípeda. En los bloques “Piso1” y “Piso2”, se tiene el diagrama de la figura 13, que no es más que el modelo en MathModelica® del esquema de control de la figura 12.
3.2.4. Ajuste controladores PD y PID
Al finalizar el modelado del sistema completo, se debe realizar el ajuste de los controladores utilizados en los bloques “control_Articulacion” y “piso” (específicamente para el eje y). En la simulación se realizó un ajuste por tanteo, ya que teniendo la herramienta de simulación, se puede realizar cualquier cambio en el proceso y realizar el análisis de los cambios.
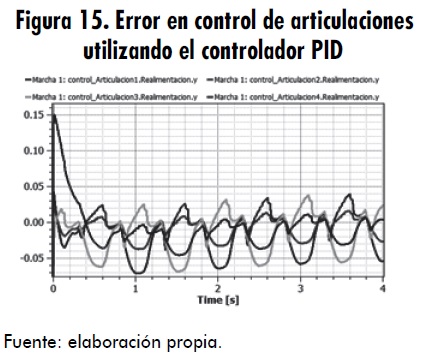
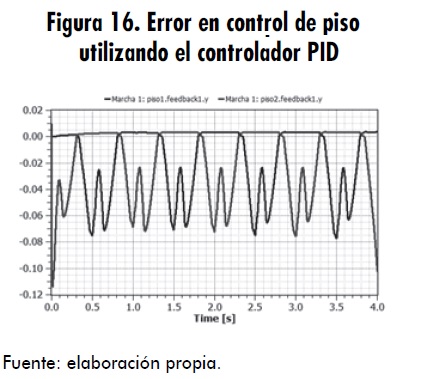
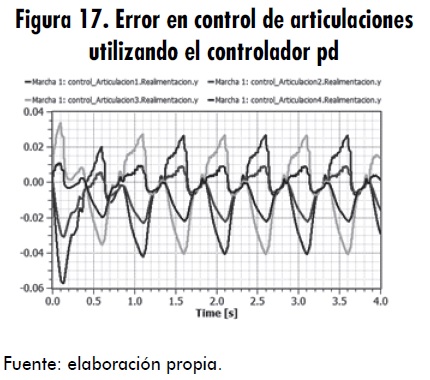
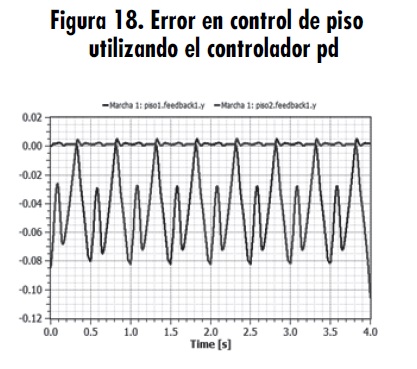
Los controles PD y PID fueron los controladores seleccionados a partir de la simulación de un péndulo simple. Se pusieron a prueba estos dos controladores en el modelo final, analizando diversas respuestas en estabilidad, desviación del error y consumo de recursos computacionales. En las figuras 15, 16, 17, y 18, se ilustra la respuesta de los controladores PID y PD con ajuste diferente. Se debe tener en cuenta que la ganancia proporcional es Kp, el tiempo de integración Ti=1/Ki y el tiempo de derivación Td=Kd.
Tiempo de construcción de experimento: 255 s. Tiempo de simulación (stop time = 4 s.): 376 s. Tamaño de archivo de simulación: 3105 MB. Número de funciones evaluadas: 434382.
Tiempo de construcción de experimento: 240 s. Tiempo de simulación (stop time = 4 s): 99 s. Tamaño de archivo simulación: 931 MB. Número de funciones evaluadas: 128.642.
Con esta representación se puede observar claramente que el control que mejor se adapta a lo requerido es el controlador PD, debido a que le da una mayor estabilidad, se aproxima más a la señal de referencia; es decir, presenta menos error y consume menos recursos computacionales. En las figuras 15 y 16 se comprueba que la parte integral del controlador genera que poco a poco el error vaya en crecimiento, hasta generar un desbordamiento o descontrol total.
Para el ajuste por tanteo del controlador PD se realizaron los siguientes pasos:
- Se inició con Kp pequeña y Td cero.
- Se aumentó gradualmente la Kp por pasos, cada uno el doble del valor anterior, dejando estabilizar a la medición entre paso y paso, y continuando hasta que se hizo ciclos. Cuando esto ocurrió, la Kp se disminuyó regresando al último paso en que no hubo ciclos en la medición. A partir de allí, de nuevo se incrementó la Kp, pero con pasos menores hasta obtener nuevamente ciclos en la medición.
- Para la obtención del valor de Td se aumentó su valor en pequeños pasos hasta que la medición se estabilizó en el punto de referencia, con la rapidez y la amortiguación más adecuada para el proceso. Este no es un análisis sistemático, pero funciona bastante bien. Además, con las herramientas de simulación se puede hacer cualquier cantidad de pruebas, sin averiar el proceso o sistema de control.
4. Resultados
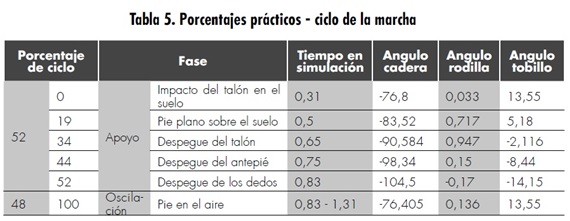
Una vez diseñado todo el sistema de control de la caminata bípeda, se procedió a realizar la simulación en el software Modélica, con lo cual se obtuvieron gráficas de comportamiento de las diferentes articulaciones involucradas, a partir de las cuales se establecieron tablas de ángulos de los movimientos realizados por estas articulaciones.
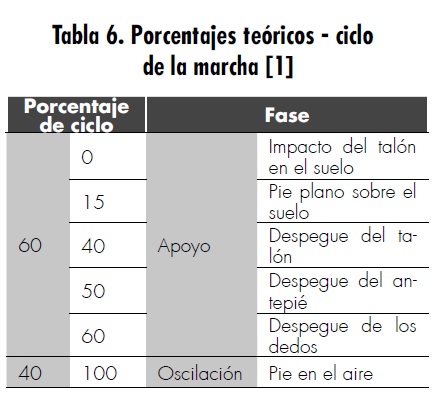
Una de las tablas obtenidas fue la tabla 5 de fases de la marcha, donde se muestra el porcentaje del ciclo presente en cada fase y subfase, así como el tiempo en simulación, el ángulo cadera y el ángulo del tobillo. Estos valores se comparan con los dados en la literatura, mostrados en la tabla 6, y se observa que son bastante cercanos.
Otra simulación realizada fue el movimiento de descripción del ciclo de marcha, donde se observa similitud con lo observado en una marcha bípeda.
5. Conclusiones
Para realizar la simulación con este software primero se tuvo que realizar un estudio exhaustivo de su manejo y formas de uso, al igual que las diferentes plataformas que incluyen las herramientas Modélica®. Así, se logró un aprendizaje amplio con respecto a la utilización de Modélica® y más específicamente los programas MathModelica®, Open- Modelica® y Simulation X®.
Con base en la marcha bípeda, desde el punto de vista de la robótica, se obtuvieron resultados óptimos para la caminata en un plano. Se pudo observar que el control tomando como referencia la posición angular, es uno de los métodos más efectivos en el momento de generar los pasos del robot, básicamente encontrando y controlando las fuerzas que se interponen en este proceso.
Al trabajar con librerías unidimensionales combinadas con librerías que contengan grados de libertad, en este caso rotacional y traslacional, se pueden generar sistemas complejos en tres dimensiones que le permitirán al usuario realizar múltiples tareas de análisis, prueba de errores, comparaciones entre sistemas, etc., en un ambiente totalmente virtual, y se verá reflejado significativamente el ahorro en los costos de inversión en el desarrollo de un proyecto.
De acuerdo con los resultados obtenidos en la simulación, se observa que existen pequeñas diferencias porcentuales respecto a los porcentajes teóricos del ciclo de la marcha. De esta manera, queda demostrado que se pueden obtener resultados muy próximos a los reales a partir de los análisis, desarrollos y simulaciones que implica el modelado realizado a un bajo costo.
Referencias
[1] S. Collado, “Análisis de la marcha humana con plataformas dinamométricas. Influencia del transporte de carga”, Memoria presentada para optar al grado de doctor [en línea], disponible: http://eprints.ucm.es/4401/1/med3.pdf, consultado: 21 de abril de 2011.
[2] C. Marco S, Cinesiología de la marcha humana normal.[en línea], disponible: http://wzar.unizar.es/acad/cinesio/Documentos/ Marcha%20humana.pdf
[3] J. Larriva, E. Guillermo, J. Trelles y O. Vele, Diseño y construcción de un robot bípedo experimental [en línea], disponible: http://mail.ups.edu.ec/universitas/publicaciones/universitas/ contenidospdf//disenorobotbipedoUniversitas8.pdf
[4] D. Martin, “Cinemática inversa [en línea], disponible: http:// www.x-robotics.com/cinematica.htm, consultado: 15 de marzo de 2011.
[5] Modelica [en línea], disponible:http://en.wikipedia.org/wiki/Modelica, consultado: 12 de febrero de 2011
[6] “Addlink software científico”, S.L. MathModelica Professional [en línea], disponible: http://www.addlink.es/productos.asp? pid=37, consultado: 8 de enero de 2011.
[7] Linköping University, Programming Environments Laboratory, “Modelica” [en línea], disponible: http://www.ida.liu.se/~pelab/ realsim/library/ModelicaAdditions/docu/ModelicaAdditions.htm, consultado: 10 de febrero de 2011
[8] E. Kofman, “Introducción a Modelica”, Laboratorio de Sistemas Dinámicos, Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario, Argentina.
[9] J. Diego-Más, “Biomecánica (esfuerzos estáticos coplanares)” [en línea], disponible: http://www.ergonautas.upv.es/metodos/ biomecanica/biomecanica-ayuda.php, consultado: 23 de mayo de 2011.
[10] Serway, Física, tomo II, 3ª ed., México: McGraw-Hill, 1993.
[11] O. Vele, Planificación de caminata para un robot bípedo [en línea], 2005, disponible: http://loslocosrh.blogspot.com/
[12] O. Vele, Simulación mecánica de un robot humanoide en Matlab [en línea], 2005, disponible: http://loslocosrh.blogspot.com/



.png)




.jpg)





