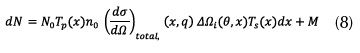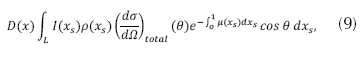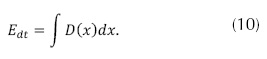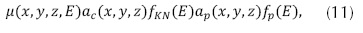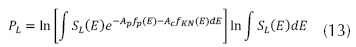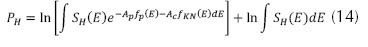DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2016.1.a10Publicado:
01-01-2016Número:
Vol. 20 Núm. 47 (2016): Enero - MarzoSección:
RevisiónTomografía computarizada: proceso de adquisición, tecnología y estado actual
Computed tomography: acquisition process, technology and current state
Palabras clave:
Imágenes médicas, métodos de adquisición, rayos-X, tomografía computarizada. (es).Palabras clave:
acquisition methods, computed tomography, medical imaging X-ray (en).Descargas
Referencias
Alpuche, J.E.; Pistorius, S.; Gordon, R. & Elbakri, I.A. (2011). A Novel Hybrid Reconstruction Algorithm for First Generation Incoherent Scatter CT (ISCT) of Large Objects with Potential Medical Imaging Applications. Journal of X-Ray Science and Technology 19(1), 35-56.
Astra Tomography Toolbox (s.f.). A High-Performance GPU MATLAB Toolbox for 2D and 3D Tomography. Recuperado de: http://sourceforge.net/p/astra-toolbox/wiki/Introduction/
Barroso, R.C.; Lopes, R.T.; De Jesus, E.F.O. & Oliveira, L.F. (2001). X-Ray diffraction Microtomography Using Synchrotron Radiation. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 471(2), 75-79.
Barroso, R.C.; Lopes, R.T.; Jesus, E.F.O.; De Oliveira, L.F. & Description, A.B. (2000). Synchrotron Biomedical Applications Using X-Ray Diffraction Tomography. En: IEEE Conference Record, Nuclear Science Symposium 2, 855-859. Seattle, WA.
Beath, S.R. & Cunningham, I.A. (s.f.) (2009). Pseudo-Monoenergetic X-Ray Diffraction Measurements Using Balanced Filters for Coherent-Scatter Computed Tomography. Medical Physics 36(5), 1839–1847.
Bernardi, R.T. & Martz, H. E. (1995). Nuclear Waste Drum Characterization with 2 MeV X-Ray and Gamma-Ray Tomography. Proc. SPIE 2519, X-Ray and Ultraviolet Sensors and Applications, 140. DOI:10.1117/12.211897.
Bharkhada, H. & Yu, H.L. (2009). Line-source based X-ray tomography. International Journal of Biomedical Imaging. DOI:10.1155/2009/534516.
Bronnikov, A.V. (2006). Phase-Contrast CT: Fundamental Theorem and Fast Image Reconstruction Algorithms. SPIE, Developments in X-Ray Tomography, 63180Q, DOI:10.1117/12.679389.
Buzug, T.M. (2007). Computed Tomography: From Photon Statistics to Modern Cone-Beam CT. Berlín-Heidelberg: Springer Verlag.
Candes, E.J. & Tao, T. (2006). Near-Optimal Signal Recovery From Random Projections : Universal Encoding Strategies? IEEE Transactions on Information Theory 52(12), 5406-5425.
Candès, E.J.; Romberg, J. & Tao, T. (2006). Robust Uncertainty Principles: Exact Signal Reconstruction From Highly Incomplete Frequency Information. IEEE Transactions on Information Theory 52(2), 489-509.
Changizi, V., Oghabian, M. A., Speller, R., Sarkar, S., & Kheradmand, A. A. (2005). Application of Small Angle X-ray Scattering (SAXS) for Differentiation between Normal and Cancerous Breast Tissue. Int J Med Sci 2(3), 118–121.
Chen, J.; Member, S.; Cong, J.; Vese, L.A. & Villasenor, J. (2012). A Hybrid Architecture for Compressive Sensing 3-D CT Reconstruction. IEEE Journal on Emerging and Selected Topics in Circuits and Systems 2(3), 616-625.
Cho, M.K.; Youn, H.; Jang, S.Y.; Lee, S.; Han, M.C. & Kim, H.K. (2012). Digital Tomosynthesis in Cone-Beam Geometry for Industrial Applications: Feasibility and Preliminary Study. International Journal of Precision Engineering and Manufacturing 13(9), 1533-1538.
Choi, K. & Brady, D.J. (2009). Coded Aperture Computed Tomography. En: Proc. SPIE 7468, Adaptive Coded Aperture Imaging, Non-Imaging, and Unconventional Imaging Sensor Systems, 74680B. DOI:10.1117/12.825277.
Chong, J. & Essue, J. (2008). Innovations in Cardiac Computed Tomography: Cone Beam CT/Volume CT and Dual Source CT. UWOMJ 77(2), 6-11.
Cong, W. & Wang, G. (2011). X-Ray Scattering Tomography for Biological Applications. J. Xray. Sci. Technol. 19(2), 219-227.
Darshini P., and Karandharaj, P. (2014). Medical image processing schemes for cancer detection: A survey. In International Conference on Green Computing Communication and Electrical Engineering (pp. 1–6).
Dobbins, J.T. (2009). Tomosynthesis Imaging: At a Translational Crossroads. Medical Physics 36(6), 1956-–1967. DOI:10.1118/1.3120285.
Donoho, D.L. (2006). Compressed Sensing. IEEE Transactions on Information Theory 52(4), 1289-1306.
Galvis, D.F.; Mejía, Y.H. & Argüello, H. (2014). Efficient Reconstruction of Raman Spectroscopy Imaging Based on Compressive Sensing. DYNA 81(118), 116-124.
Gang, T. & Ji, F.D. (2009). The Research & Application of the Detection Capability of Dangerous Goods in Dual-Energy X-Ray Security Equipment. In IEEE International Conference on Intelligent Computation Technology and Automation 2, 352–355. DOI: 10.1109/ICICTA.2009.321.
Gehrke S. & Wirth, K.E. (2005). Application of Conventional- and Dual-Energy X-Ray Tomography in Process Engineering. IEEE Sens. J. 5(2), 183-187.
Geng, J. & Member, S. (2008). Volumetric 3D Display for Radiation Therapy Planning. Journal of Display Technology 4(4), 437-450.
Ghonge, N.P. (2013). Computed Tomography in the 21st Century : Current Status & Future Prospects. JIMSA 26(1), 35-42.
Goldman, L.W. (2007). Principles of CT and CT Technology. J. Nucl. Med. Technol. 35(3), 115-28.
Hu, C.; Youtcheff, J.; Wang, D.; Zhang, X.; Kutay, E. & Thyagarajan, S. (2012). Characterization of Asphalt Mixture Homogeneity Based on X-ray Computed Tomography. Journal of Testing and Evaluation 40(7), 1103-1111.
Jerjen, I.; Revol, V.; Kottler, C. & Kaufmann, R. (2011). The Benefits and Challenges of Differential Phase Contrast Imaging for Material Science. International Symposium on Digital Industrial Radiology and Computed Tomography ((pp. 1-8). Berlín.
Jian F., (2012). Phase Contrast Computed Tomography, Computed Tomography - Clinical Applications. En: L. Saba (ed.). InTech.
Jian, F.; Bin, L.; Hao, Z.; Xingyu, Z.; Zhenggan Z. & Dongbo, W. (2009). X-Ray Phase-Contrast Imaging Methods for Biological Structures. En: BMEI ’09. 2nd International Conference on Biomedical Engineering and Informatics (pp. 1-3). DOI: 10.1109/BMEI.2009.5305651.
Johnson, T. (2012). Dual-Energy CT: General Principles. AJR. Am. J. Roentgenol 119(5), S3-8.
Johnson, T. R. C., Krauss, B., Sedlmair, M., Grasruck, M., Bruder, H., Morhard, D. … Becker, C. R. (2007). Material differentiation by dual energy CT: initial experience. European Radiology 17(6), 1510-1517.
Kapadia, A.J.; Sharma, A.C.; Tourassi, G.D.; Bender, J.E.; Howell, C.R.; Crowell, A.S. & Floyd, C.E. (2008). Neutron Stimulated Emission Computed Tomography for Diagnosis of Breast Cancer. IEEE Transactions on Nuclear Science 55(1), 501-509.
Kaza, R.; Platt, J.; Cohan, R.; Caoili, E.; Al-Hawary, M. & Wasnik, A. (2012). Dual-Energy CT with Single- and Dual-Source Scanners : Current Appli- cations in Evaluating the Genitourinary Tract. Radiographics 32(2), 353-69.
Ketcham, R.A. & Carlson, W.D. (2001). Acquisition, Optimization and Interpretation of X-Ray Computed Tomographic Imagery: Applications to the Geosciences. Computers & Geosciences 27(4), 381-400.
Knackstedt, M., Carnerup, A., Golab, A., Sok, R., Young, B., & Riepe, L. (2013). Petrophysical Characterization of Unconventional Reservoir Core At Multiple Scales. Petrophysics 54(3), 216-223.
Levakhina, Y. (2013). Three-Dimensional Digital Tomosynthesis. Iterative Reconstruction, Artifact Reduction and Alternative Acquisition Geometry. Wiesbaden: Springer Fachmedien Wiesbaden.
Lewitt, R.M.; Member, S.; Matej, S. & Member, S. (2003). Overview of Methods for Image Reconstruction From Projections in Emission Computed Tomography. Proceedings of the IEEE 91(10), 1588-1611.
Li, J.; Zhu, P. & Sun, Y. (2012). An Approximate Reconstruction Method for Helical Cone-Beam Differential Phase-Contrast Computed Tomography Images. Physics in Medicine and Biology 57(8), 2347-2356.
Li, T.T.; Li, H. & Diao, L.H. (2008). Cone-Beam Tomography of Propagation-Based Imaging. Applied Physics Letters, 93, 221114-221114–3.
Lima, I.; Assis, J.T.; Apoloni, C.R.; Mendonca de Souza, S.M.; Duarte, M. E. & Lopes, R.T. (2009). Non-Destructive Imaging Materials Investigation by Microfocus 3D X-Ray Computed Tomography. IEEE Transactions on Nuclear Science 56(3), 1448-1453.
Liu, Y.; Member, S.; Fernando, G.P. & Sinusas, A.J. (2006). A New Method for Hot-Spot Quantification of Hybrid SPECT / CT Cardiac Images : Methodology and Preliminary Phantom Validation. IEEE Transactions on Nuclear Science 53(5), 2814-2821.
Lu, Y., Longman, E., Davis, K. G., Ortega, Á. J., Grossmann, G., Michaelsen, T. E., … Harding, S. E. (2006). Crystallohydrodynamics of Protein Assemblies : Combining Sedimentation , Viscometry , and X-Ray Scattering. Biophys J., 91(5), 1688–1697.
MacCabe, K.P.; Holmgren, A.D.; Tornai, M.P. & Brady, D.J. (s.f.) (2013). Snapshot 2D Tomography Via Coded Aperture X-Ray Scatter Imaging. Appl. Opt. 52(19), 4582-4589.
Maire, E. & Withers, P.J. (2014). Quantitative X-ray tomography. Int. Mater. Rev. 59(1), 1-43.
Malcolm, A.A.; Liu, T.; Ng, I.K. & Teng, W.Y. (2013). A Large Scale Multiple Source X-ray CT System for Aerospace Applications. International Symposium on NDT in Aerospace. Singapore.
Mayo, S.C.,; Miller, P.R.; Wilkins, S.W.; Davis, T.J.; Gao, D.; Gureyev, T.E.; Paganin, D.; Parry, D.J.; Pogany, A.; Robb, T. & Stevenson, A.W. (2002). Phase-Contrast X-Ray Projection Microscopy for Materials Characterisation. Mater. Forum, 26, 15-19.
Niemi, E.; Lassas M. & Siltanen, S. (2013). Dynamic X-ray tomography with multiple sources. 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA) (pp.618-621). DOI: 10.1109/ISPA.2013.6703813.
Ning, R.; Chen, B.; Yu, R.; Conover, D.; Tang, X. & Ning, Y. (2000). Flat Panel Detector-Based Cone-Beam Volume CT Angiography Imaging: System Evaluation. IEEE Transactions on Medical Imaging 19(9), 949-63.
Pani, S., Cook, E. J., Horrocks, J. a, Jones, J. L., & Speller, R. D. (2010). Characterization of breast tissue using energy-dispersive X-ray diffraction computed tomography. Applied Radiation and Isotopes : Including Data, Instrumentation and Methods for Use in Agriculture, Industry and Medicine, 68(10), 1980–7.
Prince, J.L. & Links, J. (2005). Medical Imaging Signals and Systems. 2a. ed. Prentice-Hall, Springer.
Revol, V.; Kottler, C.; Kaufmann, R.; Straumann, U. & Urban, C. (2010). Noise Analysis of Grating-Based X Ray Differential Phase Contrast Imaging. The Review of Scientific Instruments 81(7), 073709-073709–7.
Riepe, L. & Suhaimi, M. (2011). Application of High Resolution Micro-CT-Imaging and Pore Network Modeling (PNM) for the Petrophysical Characterization of Tight Gas Reservoirs-A Case History. En: In SPE Middle East Unconventional Gas Conference and Exhibition (pp. 1-13). Muscat, Oman. DOI: http://dx.doi.org/10.2118/142472-MS.
Russo, P.; Lauria, A.; Mettivier, G. & Montesi, M.C. (2008). X ray cone-beam breast computed tomography: Phantom studies. En: 2008 IEEE Nucl. Sci. Symp. Conf. Rec., 4803–4810. DOI: 10.1109/NSSMIC.2008.4774317.
Schlomka, J., Harding, A., Harding, G., Stevendaal, U. Van, & Grass, M. (2003). Coherent Scatter X-ray Computed Tomography In Medical Applications. IEEE Nuclear Science, 2, 900-901.
Seeram, E. (2008). Computed tomography: Physical Principles, Clinical Applications, and Quality Control. 3a. ed. Elsevier Health Sciences.
Sevak, M.M.; Thakkar, F.N.; Kher, R.K. & Modi, C.K. (2012). CT Image Compression Using Compressive Sensing and Wavelet Transform. In International Conference on Communication Systems and Network Technologies, 138-142, DOI: 10.1109/CSNT.2012.39.
Shannon, C.E. (1998). Communication in the Presence of Noise. Proceedings of the IEEE 86(2), 447-457.
Shefer, E.; Altman, A.; Behling, R.; Goshen, R.; Gregorian, L.; Roterman, Y. & Zarchin, O. (2013). State of the Art of CT Detectors and Sources: A Literature Review. Current Radiology Reports 1(1), 76-91.
Su, P.; Yang, J.; Lu, K.; Yu, N.; Wong, S.T.; Xue, Z. & Member, S. (2013). A Fast CT and CT-Fluoroscopy Registration Algorithm With Respiratory Motion Compensation for Image-Guided Lung Intervention. IEEE Transactions on Biomedical Engineering 60(7), 2034-2041.
Taina, I.A.; Heck, R.J.; Deen, W. & Ma, E.Y.T. (2013). Quantification of Freeze–Thaw Related Structure in Cultivated Topsoils Using X-Ray Computer Tomography. Canadian Journal of Soil Science 93(4), 533-553.
UGCT (2015). Centre for X-ray Tomography of the Ghent University (UGCT). Recupperado de: http://www.ugct.ugent.be
Uriondo, O.; Garc, L.; Deustotech-life, Z. & Avda, D. (2011). Computed Tomography CAD System for Monitoring and Modeling the Evolution of Lung Cancer Nodule. IEEE International Symposium on Signal Processing and Information Technology, 484-489. DOI: 10.1109/ISSPIT.2011.6151610.
Vine, D.J.; Paganin, D.M.; Pavlov, K.M.; Kräußlich, J.; Wehrhan, O.; Uschmann, I. & Förster, E. (2007). Analyzer-Based Phase Contrast Imaging and Phase Retrieval Using a Rotating Anode X-Ray Source. Applied Physics Letters 91(25), 254110-254113.
Vontobel, P.; Lehmann, E. & Carlson, W.D. (2005). Comparison of X-Ray and Neutron Tomography Investigations of Geological Materials. IEEE Transactions on Nuclear Science 52(1), 338-341.
Wakin, M.B. (2008). An Introduction to Compressive Sampling. IEEE Signal Processing Magazine 25(2), 21-30.
Wang G., Yu H. & De Man, B. (2008). An Outlook on X-Ray CT Research and Development. Med. Phys. 35(3), 1051-1063.
Webb, S. (1987). A Review of Physical Aspects of X-Ray transmission Computed Tomography. IEEE Proc. A Phys. Sci. Meas. Instrumentation, Manag. Educ. Rev. 134(2), 126-135.
Westmore M.S. & F’enster, A., C.I.A. (1995). Investigation of Coherent-Scatter Computed Tomography. Physics of Medical Imaging, 2432, 24-32.
Westmore, M.S.; Fenster, A. & Cunningham, I.A. (1997). Tomographic Imaging of the Angular-Dependent Coherent-Scatter Cross Section. Medical Physics, 24, 3-10.
Ying, Z.; Naidu, R. & Crawford, C.R. (2006). Dual Energy Computed Tomography for Explosive Detection. Journal of X-Ray Science and Technology, 14, 235-256.
Yoneyama, A.; Yamada, S. & Takeda, T. (2011). Fine Biomedical Imaging Using X-Ray Phase-Sensitive Technique. Advanced Biomedical Engineering. En: G. Gargiulo (ed.). InTech. DOI: 10.5772/20456.
Yu, H. & Wang, G. (2009). Compressed sensing based interior tomography. Physics in Medicine and Biology 54(9), 2791-2805.
Yuasa, T.; Akiba, M.; Takeda, T.; Kazama, M.; Hoshino, A. & Watanabe, Y. (2002). Incoherent-Scatter Computed Tomography with Monochromatic Synchrotron X Ray : Feasibility of Multi-CT Imaging System for Simultaneous Measurement of Fluorescent and Incoherent Scatter X Rays. IEEE Transactions on Nuclear Science 44(5), 1760-1769.
Zhang, R.; Member, S.; Thibault, J.; Bouman, C.A.; Sauer, K.D.; Hsieh, J. & Member, S. (2013). Model-Based Iterative Reconstruction for Dual-Energy X-Ray CT Using a Joint Quadratic Likelihood Model. IEEE Transactions on Medical Imaging 33(1), 117-134.
Zhu, Z.; Wahid, K.A. & Babyn, P. (2012). CT Image Reconstruction from Partial Angular Measurements Via Compressed Sensing. En: IEEE Canadian Conference on Electrical & Computer Engineering (pp. 3-6). DOI: 10.1109/CCECE.2012.6334926.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.1.a10
Tomografía computarizada: proceso de adquisición, tecnología y estado actual
Computed tomography: acquisition process, technology and current state
Óscar Javier Espitia Mendoza1, Yuri Hercilia Mejía Melgarejo2, Henry Arguello3
1 Ingeniero de Sistemas, estudiante de Maestría en Ingeniería de Sistemas e Informática de la Universidad Industrial de Santaner. Bucaramanga, Colombia. Contacto: oscar.espitia@saber.uis.edu.co
2 Ingeniera Electrónica, magíster en Ingeniería Electrónica, estudiante de doctorado en Ingeniería Electrónica de la Universidad Industrial de Santander. Bucaramanga, Colombia. Contacto: yuri.yejia@saber.uis.edu.co
3 Ingeniero Electricista, magíster en Potencia Eléctrica, doctor Electrical and Computer Engineering. Profesor titular de la Universidad Industrial de Santander. Bucaramanga, Colombia. Contacto: henarfu@uis.edu.co
Fecha de recepción: 10 de marzo de 2015 Fecha de aceptación: 18 de septiembre de 2015
Cómo citar: Espitia Mendoza, Ó. J., Mejía Melgarejo, Y. H., & Arguello Fuentes, H. (2016). Tomografía computarizada: proceso de adquisición, tecnología y estado actual. Revista Tecnura, 20(47), 119-135. doi: 10.14483/udistrital.jour.tecnura.2016.1.a10
Resumen
La tomografía computarizada (CT) es una técnica de escaneo no invasivo ampliamente aplicada en sectores como la medicina, la industria y la geología. Esta técnica permite la reconstrucción tridimensional de la estructura interna de un objeto que es iluminado con una fuente de rayos-X. La reconstrucción se forma con imágenes bidimensionales de cortes transversales del objeto. Cada corte se obtiene a partir de las medidas de fenómenos físicos como la atenuación, la dispersión y la difracción de los rayos-X, como resultado de la interacción con el objeto. En general, la adquisición de las medidas se realiza con métodos basados en alguno de estos fenómenos y empleando diversas arquitecturas clasificadas en generaciones. Por otro lado, en respuesta a la necesidad de simular sistemas de adquisición para CT se ha desarrollado software dedicado a esta tarea. El objetivo de este artículo es determinar el estado actual de las técnicas de CT, para esto, se presenta una revisión de los métodos, las distintas arquitecturas usadas para la adquisición y algunas de sus aplicaciones. Adicionalmente, se presentan los resultados de simulaciones realizadas. Las principales contribuciones de este trabajo son la descripción detallada de los métodos de adquisición y la presentación de las posibles tendencias de la técnica en general.
Palabras clave: imágenes médicas, métodos de adquisición, rayos-X, tomografía computarizada.
Abstract
Computed tomography is a noninvasive scan technique widely applied in areas such as medicine, industry, and geology. This technique allows the three-dimensional reconstruction of the internal structure of an object which is lighted with an X-rays source. The reconstruction is formed with two-dimensional cross-sectional images of the object. Each cross-sectional is obtained from measurements of physical phenomena, such as attenuation, dispersion, and diffraction of X-rays, as result of their interaction with the object. In general, measurements acquisition is performed with methods based on any of these phenomena and according to various architectures classified in generations. Furthermore, in response to the need to simulate acquisition systems for CT, software dedicated to this task has been developed. The objective of this research is to determine the current state of CT techniques, for this, a review of methods, different architectures used for the acquisition and some of its applications is presented. Additionally, results of simulations are presented. The main contributions of this work are the detailed description of acquisition methods and the presentation of the possible trends of the technique.
Keywords: computed tomography, X-ray, X-ray acquisition methods, medical imaging.
Introducción
La tomografía computarizada (CT, por su sigla en inglés) es una tecnología establecida para obtener imágenes, de forma no invasiva, de la estructura interna de los objetos en tres dimensiones (3D) (Russo, Lauria, Mettivier y Montesi, 2008). Las tomografías se obtienen a partir de proyecciones bidimensionales usando rayos-X. CT es considerada de gran importancia debido a que brinda mejores posibilidades de diagnóstico que otros métodos como la radiología convencional (Lewitt, Member, Matej y Member, 2003); además sus aplicaciones abordan diversas áreas de investigación en la actualidad (Maire y Withers, 2014; Mayo et al., 2002; Jian et al., 2009; Vontobel, Lehmann y Carlson, 2005; Barroso, Lopes, De Jesus y Oliveira, 2001).
El diagnóstico por medio de rayos-X ha sido utilizado durante más de 50 años; los primeros acercamientos a CT pueden ligarse al procedimiento de tomosíntesis analógica, que existe desde 1920 (Gehrke y Wirth, 2005; Levakhina, 2013). Sus raíces se encuentran en el descubrimiento de los rayos-X en 1895, por Wilhelm Conrad Röntgen, quien logró obtener la primera visión de la composición interna de un objeto. En 1917, Radon describió de forma matemática la reconstrucción de un objeto desde sus proyecciones. A partir de dichos eventos, la exploración mediante CT se ha convertido en uno de los métodos de diagnóstico por imágenes más utilizado (Lewitt, Member, Matej y Member, 2003; Buzug, 2007).
Debido a que con CT convencional no siempre se logran imágenes del contraste deseado, se desarrollan métodos de adquisición que basan sus principios en las diferentes características de los rayos-X. El método tradicional de CT, conocido como CT de transmisión (transmission CT), se basa en la obtención de la atenuación de los rayos al traspasar un objeto (Webb, 1987). CT de contraste de fase (phase contrast CT) se fundamenta en la adquisición de la medida de los cambios de fase de un haz de rayos-X al pasar a través de un objeto (Bronnikov, 2006). CT de dispersión (scattering CT) consiste en la reconstrucción de la distribución de la densidad de electrones en un objeto a partir de la medida de la dispersión dentro de un rango angular (Cong y Wang, 2011). CT de difracción (Diffraction CT) tiene en cuenta propiedades de difracción de los rayos-X (Westmore y F'enster, 1995). CT de doble energía (Dual energy CT) considera la medición de los diferentes valores de atenuación dados por la proyección de rayos-X con distinta energía (Johnson, 2012). Recientemente se ha desarrollado la técnica de muestreo compresivo, la cual se ha aplicado a CT convencional y compone un método conocido como CT compresiva (compressive CT) (Zhu, Wahid y Babyn, 2012).
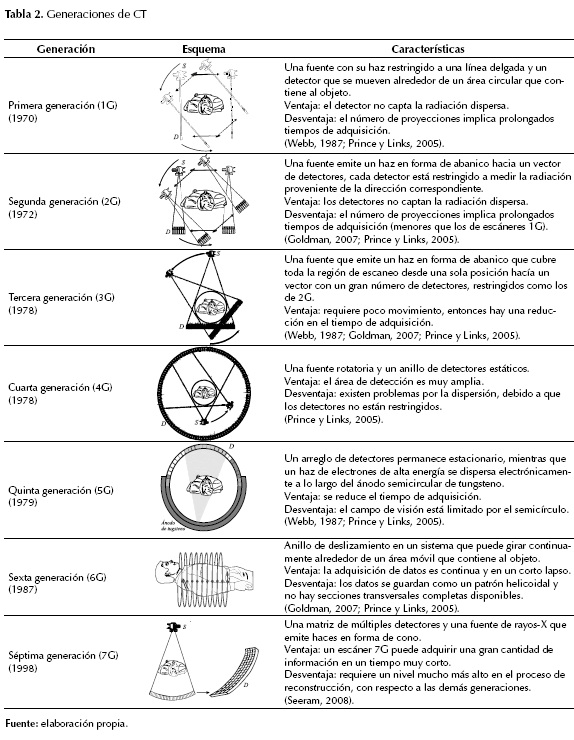
Con el fin de explotar la técnica y reducir tiempos de adquisición, se han desarrollado siete generaciones de escáneres. Esta clasificación se da a partir de la disposición de los componentes y el movimiento mecánico necesario para recopilar datos. Las generaciones denotan el orden en que se han introducido los diseños; sin embargo, el número de la generación no implica que un sistema sea superior a otro (Goldman, 2007; Ghonge, 2013).
En medicina, CT se ha utilizado con éxito por más de cuatro décadas. Además, durante varios años ha ayudado a los ingenieros en ensayos no destructivos de componentes fabricados o en el estudio de diferentes materiales. Recientemente se han desarrollado trabajos de investigación que se enfocan en incluir la técnica de CT en ciencia de los materiales, geología e industria (Mayo et al., 2002; Cong y Wang, 2011; Cho et al., 2012; Lima et al., 2009).
El objetivo de esta investigación es determinar las tendencias y el estado actual de las técnicas de CT, para lo cual se presenta una revisión de los métodos de adquisición, se describe la tecnología usada en las generaciones, las diversas aplicaciones y se muestran los resultados de simulaciones correspondientes a los dos generaciones de CT. Para especificar los resultados del trabajo se plantea la siguiente estructura en el documento: la sección "Métodos de adquisición" detalla la arquitectura y el modelo para adquisición de proyecciones en cada método de adquisición CT; la sección "Generaciones CT" describe los aspectos físicos de las generaciones de CT; la sección "Reconstrucción" menciona generalidades sobre reconstrucción; la sección "Aplicaciones CT" presenta algunas aplicaciones actuales de CT; la sección "Casos de prueba" muestra las simulaciones para el método tradicional de CT, y por último, se plantean las conclusiones.
Métodos de adquisición
En los últimos años se han desarrollado formas de medir los cambios de intensidad usando rayos con diferente energía e instrumentos ópticos que modulan los haces, en busca de mejor calidad y reducción de la dosis. Además, algunas propiedades físicas de los rayos-X, como la dispersión y difracción, se han tenido en cuenta en las medidas. En las siguientes subsecciones se presentan los principales métodos de adquisición de imágenes tomográficas basados en estos conceptos.
CT de transmisión
La figura 1 muestra la discretización de un objeto Q iluminado con luz de rayos-X desde la fuente S. Esta representación está compuesta por voxeles que forman Q1 secciones transversales, cada una con dimensiones superficiales Q2 x Q3. A cada vóxel (de dimensiones dx x dy dz) se le asigna una atenuación µ.
Considerando un rayo de intensidad I0, que atraviesa el objeto con una distribución no homogénea de atenuaciones µ(x), la intensidad del rayo I(x) medida por el detector D depende tanto de la distancia atravesada x, como de la atenuación µ(x) de cada punto en su trayectoria. Esto puede modelarse con la ecuación (1).
Este fenómeno obedece a la ley de Lambert Beer, y puede reescribirse a partir de la ecuación (2).
La ecuación (2) se describe como la fracción de luz transmitida a través del objeto y puede asignarse a una proyección unidimensional, captada con respecto a un ángulo de incidencia. La reconstrucción consiste en estimar la distribución de los coeficientes de atenuación µ(x) (Buzug, 2007).
Cuando la luz atraviesa un objeto, no solo cambia su intensidad, sino también su fase. Los rayos-X pueden ser tratados como ondas electromagnéticas. Entonces, un objeto se describe por medio de su índice de refracción n=1-δ + iβ. El término δ corresponde al decremento de la parte real del índice de refracción y la parte imaginaria β describe el índice de absorción. Mediante el uso de estos componentes, el cambio de intensidad se puede expresar a partir de la ecuación (3),
Donde λ es la longitud de onda de la radiación. El cambio de fase dθ está dado por la ecuación (4).
Donde Q1 es el espesor de la muestra. Cuando los rayos-X pasan a través de objetos con regiones de diferente densidad y composición, su atenuación se escribe a partir de la ecuación (5).
Donde la integración se hace a lo largo de la trayectoria de los rayos-X. Por otro lado, el desplazamiento de fase dθ, causado por la muestra, se escribe como la ecuación (6).
Esta expresión representa la proyección de la parte real del índice de refracción. La diferencia entre las dos ecuaciones anteriores está en δ y β. Por tanto, la reconstrucción en CT de contraste de fase puede realizarse de la misma manera que en CT convencional, mediante la información de cambio de fase (Yoneyama, Yamada y Takeda, 2011).
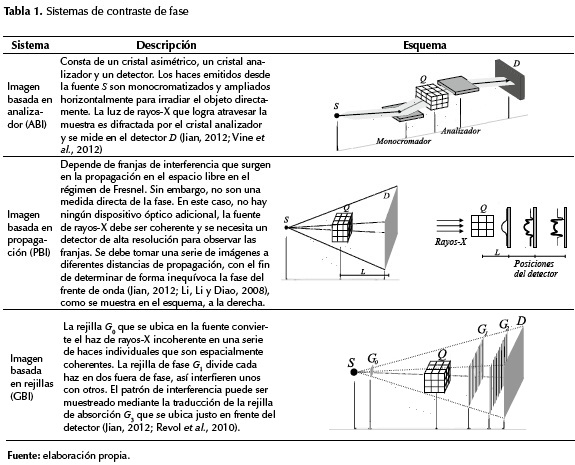
Este método es el resultado de los esfuerzos para combinar las imágenes de contraste de fase con CT (Li, Zhu y Sun, 2012), las reconstrucciones obtenidas proporcionan la distribución de la densidad de electrones del objeto (Bronnikov, 2006). En la actualidad, existen principalmente tres clases de CT de contraste de fase (Jian, 2012). La tabla 1 muestra las clases de sistemas de CT de contraste de fase.
CT de difracción
CT de difracción se basa en las propiedades de difracción de los rayos-X, es decir, en la medida de la desviación de los rayos cuando interactúan con un objeto. Con esta técnica se puede hacer una discriminación selectiva de los elementos que componen una muestra escaneada, mediante la fijación del ángulo de Bragg que produzca un pico de interferencia (Barroso et al., 2000). El diferencial de dispersión de una sección transversal está dado por la ecuación (7).
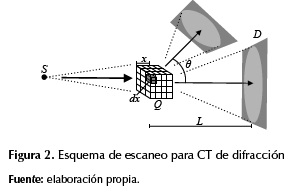
Donde rc es el radio del electrón 2,82x10-15[m], θ es el ángulo de difracción, F (q,Z) es el factor de forma atómico, q =sin (θ/2)/λ es la transferencia de energía cinética. El ángulo θ entre el haz primario y el haz difractado es el denominado ángulo de Bragg. La figura 2 muestra un esquema del escaneo en CT de difracción.
La radiación difractada, desde el elemento dx del objeto Q en la posición x, que se capta por el i-ésimo elemento del detector puede expresarse mediante la ecuación (8).
Donde N0 es el número de fotones que inciden sobre el objeto, Tp(x) es la transmisión de haz primario a dx, n0 es el número de centros de difracción por unidad de volumen en x, (dσ/dΩ)total es la dispersión coherente e incoherente de la sección transversal por unidad de volumen y por centro de difracción, q representa la transferencia de momento para el elemento de objeto en x, ΔΩi(θ,x) es el ángulo sólido del detector i, Ts(x) la transmisión del haz difractado desde 𝑥 hasta el detector y M el componente de difracción múltiple. Es posible reconstruir las imágenes tomográficas, basadas en patrones de difracción, con una serie de supuestos simplificadores (Westmore y F'enster, 1995; Westmore, Fenster y Cunningham, 1997; Beath y Cunningham, s.f.).
CT de dispersión
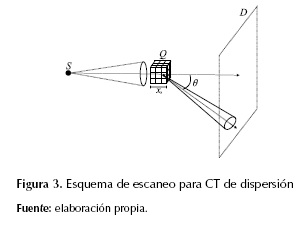
Después de que un haz de rayos-X interactúa con los elementos internos de los tejidos, algunos fotones serán desviados de la dirección de desplazamiento original (figura 3), fenómeno denominado dispersión de fotones. La dirección y la intensidad de los fotones dispersados están directamente relacionados con la distribución de densidad de electrones dentro del tejido. CT de dispersión consiste en la reconstrucción de la distribución de la densidad de electrones en un objeto, por medio de la dispersión medida dentro de un rango angular específico (Cong y Wang, 2011; Yuasa et al., 2002; Alpuche, Pistorius, Gordon y Elbakri, 2011).
La intensidad de dispersión de rayos-X en la posición x del detector se describe a partir del diferencial de dispersión de fotones en una sección transversal (ecuación (9)).
Donde L es la distancia de la fuente hasta el objeto, θ es el ángulo de dispersión que está dado por 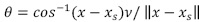 , v es la dirección del rayo y ρ(xs) es la densidad del electrón en la posición xs. Por tanto, la energía de dispersión total, Edt, adquirida por un detector puede ser formulada a partir de la ecuación (10).
, v es la dirección del rayo y ρ(xs) es la densidad del electrón en la posición xs. Por tanto, la energía de dispersión total, Edt, adquirida por un detector puede ser formulada a partir de la ecuación (10).
CT de doble energía (DECT)
Las interacciones entre los rayos-X, con energía fotónica entre 30 keV y 200 keV, y la materia están dominadas por la dispersión Compton y el efecto fotoeléctrico. Estos últimos son dependientes tanto de los materiales como de la energía y cada uno de ellos se modela a partir de la ecuación (11).
Donde (x,y,z) son las coordenadas de la muestra, µ(x,y,z,E) es la atenuación total, E es la energía incidente, ac(x,y,z) es el coeficiente de Compton, αp(x,y,z) es el coeficiente fotoeléctrico, ƒKN(E) es el diferencial de dispersión de Compton o dispersión incoherente y ƒp(E) se aproxima a la dependencia de energía de la interacción fotoeléctrica (ecuación (12)).
Los coeficientes son funciones de las propiedades físicas de los materiales, como la masa, la densidad y el número atómico. Un escáner de CT de doble energía obtiene dos conjuntos de proyecciones logarítmicas descritas en las ecuaciones (13) y (14).
Donde 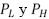 corresponden a las proyecciones con baja y alta energía, respectivamente,
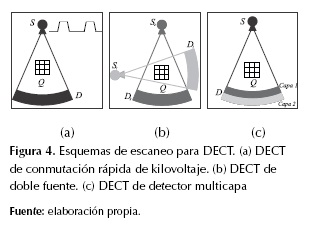
corresponden a las proyecciones con baja y alta energía, respectivamente, 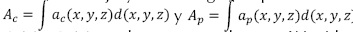 son los espectros de rayos-X incidentes de baja y alta energía, respectivamente (Ying, Z.; Naidu, R. & Crawford, 2006; Zhang et al., 2013). En general, las proyecciones se adquieren mediante tres mecanismos: DECT de conmutación rápida de kilovoltaje, donde la fuente varía la energía de radiación dentro de un rango definido; DECT de doble fuente, en el cual se usan dos fuentes independientes para cubrir el campo de visión desde dos puntos distintos; y DECT de detector multicapa, que posee dos capas de detectores con diferente sensibilidad (Johnson, 2012; Kaza et al., 2012). En la figura 4 se muestra un esquema de los sistemas mencionados.
son los espectros de rayos-X incidentes de baja y alta energía, respectivamente (Ying, Z.; Naidu, R. & Crawford, 2006; Zhang et al., 2013). En general, las proyecciones se adquieren mediante tres mecanismos: DECT de conmutación rápida de kilovoltaje, donde la fuente varía la energía de radiación dentro de un rango definido; DECT de doble fuente, en el cual se usan dos fuentes independientes para cubrir el campo de visión desde dos puntos distintos; y DECT de detector multicapa, que posee dos capas de detectores con diferente sensibilidad (Johnson, 2012; Kaza et al., 2012). En la figura 4 se muestra un esquema de los sistemas mencionados.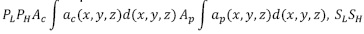
CT compresiva
El muestreo compresivo (CS de su sigla en inglés) es una nueva teoría para adquirir y reconstruir señales (Donoho, 2006). A diferencia del proceso de adquisición de señales tradicional, la teoría de CS permite que las señales compresibles sean muestreadas a una frecuencia cercana a su tasa de información intrínseca, que está muy por debajo de la tasa de Nyquist (Shannon, 1998). CS se fundamenta en dos condiciones: a) que las señales digitales sean dispersas y b) la incoherencia de la matriz de medición (Wakin, 2008).
Se dice que una imagen es dispersa si la mayoría de sus elementos están cerca o son iguales a cero. Asumiendo un proceso de medición lineal que calcula M « N productos internos entre ƒ y una colección de vectores 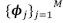 como
como 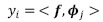 (ecuación (15)).
(ecuación (15)).
Donde el conjunto de proyecciones yi forman el vector y de M elementos, Φ es la matriz de medición con dimensiones M X N, con filas 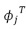 y ƒ es la señal de rayos-X original. Teniendo en cuenta la reconstrucción de ƒ a partir de y, se sabe que existen infinitas soluciones para la ecuación (15), porque la dimensionalidad de y es mucho menor que la de ƒ.
y ƒ es la señal de rayos-X original. Teniendo en cuenta la reconstrucción de ƒ a partir de y, se sabe que existen infinitas soluciones para la ecuación (15), porque la dimensionalidad de y es mucho menor que la de ƒ.
Un requisito clave para la aplicación de la teoría de CS es que la imagen sea dispersa. Muchas de las señales de la naturaleza se pueden volver dispersas adoptando una transformación adecuada con un número pequeño de coeficientes (Candès, Romberg y Tao, 2006; Sevak, Thakkar, Kher y Modi, 2012).
Matemáticamente, una señal discreta 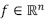 puede ser expresada a partir de la ecuación (16).
puede ser expresada a partir de la ecuación (16).
Donde x es la secuencia de coeficientes de f y la base ψ es una matriz con columnas φ1,...φG Claramente, f y x son representaciones equivalentes de la misma señal, f es una combinación lineal de apenas F vectores base, con F « G (Shannon, 1998), (Wakin, 2008). De acuerdo con las ecuaciones (15) y (16) se obtiene la ecuación (17).
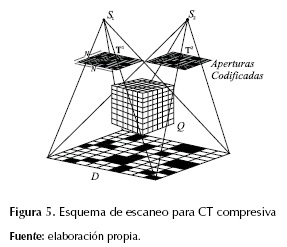
CS se ha usado como base para la reconstrucción en CT de transmisión y de dispersión (Bronnikov, 2006; Choi y Brady, 2009; Yu y Wang, 2009; Chen et al., 2012). Una forma de implementar la teoría de CS en una configuración de CT de transmisión es incluir elementos en el sistema que permitan codificar las medidas para tomar muestras comprimidas. Estos elementos pueden ser aperturas codificadas, debido a los efectos que tienen sobre la luz (Galvis, Mejía y Argüello, 2014; Candès y Tao, 2006). Las aperturas codificadas corresponden a arreglos bidimensionales con patrones de materiales opacos a la luz, las secciones que no contienen material opaco definen su transmitancia, es decir, la fracción de luz que puede atravesarlas (MacCabe, Holmgren, Tornai y Brady, s.f.; Choi y Brady, 2009). En la figura 5 se muestra un esquema de un sistema de muestreo para CT con la inclusión de las aperturas codificadas T1 y T2, que modulan los haces proyectados desde las fuentes S1 y S2 y hacia un plano de múltiples detectores que miden la atenuación generada por un objeto 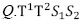
Este método se ha introducido con ventajas en cuanto a los tiempos de adquisición y dosis de radiación. Con un sistema de CS para CT, se reducen las medidas y el tiempo para tomarlas, lo que significa que un objeto bajo estudio se expone a una cantidad menor de radiación (Choi y Brady, 2009).
Generaciones de CT
Un sistema de CT posee dos piezas claves: una fuente de rayos-X y un detector o arreglo de detectores. En las fuentes se producen fotones con alta energía por medio de aceleración y desaceleración de electrones. Por otro lado, los detectores miden la cantidad de luz que pasa a través del objeto bajo estudio. Las fuentes, por lo general, son tubos de rayos-X. Sin embargo, existen trabajos y aplicaciones en las que se usa el sincrotrón. Actualmente, los detectores son de estado sólido, analógicos o digitales, usan celdas electrónicas y fotodiodos para hacer conteo de fotones. El desarrollo tecnológico referente a CT se ha enfocado en estas dos piezas específicamente, así que sus características definen cada generación (Shefer et al., 2013).
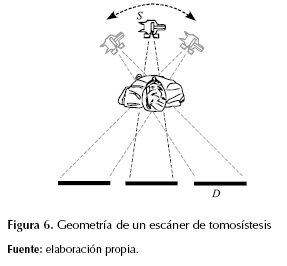
Previo a la introducción de la tecnología de los escáneres CT se estableció la tomosíntesis, una técnica tomográfica que produce un conjunto de imágenes de cortes transversales apilados, a partir de un número limitado de proyecciones, con bajas dosis de radiación, adquiridas dentro de un campo angular limitado (Dobbins, 2009). En la figura 6 se muestra la geometría de un escáner de tomosíntesis.
Años después, en la década de 1970 se impulsó el desarrollo de tecnologías que mejoraran el alcance de esta técnica, punto de partida para las denominadas generaciones CT. En tabla 2 se presentan los principales aspectos de cada generación y la descripción de la geometría correspondiente.
En los últimos años se han desarrollado formas de medir los cambios de intensidad usando múltiples fuentes e instrumentos ópticos que modulan los haces, en busca de mejor calidad y reducción de la dosis.
Recientemente se han propuesto sistemas basados en la influencia del número de fuentes de rayos-X sobre las reconstrucciones de CT. Por ejemplo, los sistemas Pioneering Dynamic Spatial Reconstructor of Mayo Clinic (Wang, Yu De Mann, 2008), Line Sources CT (Bharkhada y Yu, 2009), Inverse-Geometry CT y Ultimately a Rebirth of Stationary CT (Niemi, Lassas y Siltanen, 2013) poseen múltiples fuentes de rayos-X distribuidas de diversas maneras. El uso de más de una fuente permite disminuir el tiempo de adquisición de los datos, y por tanto, reducir la dosis de radiación. Aunque los desarrollos en tecnologías de adquisición se han centrado en los sistemas de detección, se espera que los próximos avances se enfoquen en el uso de múltiples fuentes de rayos-X.
Reconstruccón
El problema de la reconstrucción consiste en calcular la estructura del objeto bajo estudio a partir de las medidas de intensidad, determinadas por el efecto fotoeléctrico, la dispersión y la difracción. La adquisición de los datos deja como resultado una matriz conocida como sinograma, de la cual se obtiene una imagen bidimensional correspondiente a un corte transversal. Existen métodos analíticos o iterativos esta tarea. Los métodos analíticos comprenden herramientas matemáticas propias del análisis de Fourier como el teorema de proyecciones y la convolución; entre estos se encuentran la retroproyección y la retroproyección filtrada (FBP). Los métodos iterativos incluyen el método algebraico y los métodos estadísticos (Buzug, 2007).
Aplicaciones de CT
CT es considerada una tecnología avanzada que tiene una amplia aplicación en la medicina. Ha permitido ensayos no destructivos en otras áreas como la geología, la ingeniería y la industria. A continuación, se resaltan las generalidades sobre las aplicaciones en estas áreas. Su selección se debe al impacto que tienen y al interés que han despertado en diversos sectores de Colombia.
Medicina
En medicina, CT es un procedimiento aceptado para diagnóstico, guía en procedimientos o monitoreo de la efectividad de los tratamientos para enfermedades como el cáncer (Uriondo, Garc, Deustotech-life y Avda, 2011; Kapadia et al., 2008). Mediante escáneres CT se obtienen imágenes de alto contraste en las que es posible identificar traumas óseos o tumores y estudiar órganos en tiempo real. En la actualidad, CT se usa en procedimientos como fluoroscopia, imágenes y visualización 3D, angiografía e imágenes cardiacas.
La fluoroscopia es un procedimiento de diagnóstico en el que se estudian las estructuras del cuerpo en movimiento en tiempo real, esto se logra con una tasa de procesamiento muy alta (Goldman, 2007; Su et al., 2013). La visualización 3D es una técnica de CT usada en planeación de tratamientos, imágenes craneofaciales, planeación de cirugías y ortopedia (Geng y Member, 2008). La angiografía es la CT de los vasos sanguíneos, opacados por medios de contraste, en este procedimiento se escanea el área de interés durante la inyección de contraste y las imágenes se registran cuando los vasos están completamente opacados para mostrar la condición arterial o venosa (Ning et al., 2000). Con el desarrollo de escáneres que reducen los efectos del movimiento continuo del corazón se logran imágenes cardíacas, dando amplias posibilidades de diagnóstico de enfermedades (Liu, Member, Fernando y Sinusas, 2006).
Recientemente, CT se usa para obtener imágenes de las personas sanas, como un medio para la detección temprana de enfermedades. Este concepto se conoce como CTscreening y es investigado como una herramienta potencial para obtener imágenes de individuos asintomáticos (Seeram, 2008).
Geología
Aunque CT fue introducido como un procedimiento médico, se ha reconocido su uso en otras áreas como geología e ingeniería. Las primeras aplicaciones incluyen estudios en los campos de la ciencia del suelo, meteoritos, paleontología, geotecnia y la geología del petróleo. En la actualidad, se usa CT de alta resolución (micro y nano CT) (Ketcham y Carlson, 2001) en la inspección de muestras geológicas para la exploración de recursos.
Los sistemas CT de alta resolución proporcionan imágenes tridimensionales a nivel microscópico de las muestras. En la ciencia del suelo, las muestras son escaneadas para visualizar estructura, componentes o raíces, por ejemplo, para optimización de cultivos o productividad (Taina, Heck, Deen y Ma, 2013). CT se aplica a muestras de meteoritos con el fin de determinar características como la edad y su composición química (Ketcham y Carlson, 2001). También, se considera una técnica que brinda amplias posibilidades para estudiar fósiles (Vontobel, Lehmann y Carlson, 2005). Por otro lado, se usa para el análisis cualitativo y cuantitativo de las características internas de los materiales asfálticos y cementos en el área de la geotecnia (Hu et al., 2012). En la geología del petróleo es un importante avance en este momento en países como Colombia. Este procedimiento ayuda a revelar los detalles de la estructura interna de los poros de una roca petrolífera y a comprender las condiciones que afectan la producción del hidrocarburo (Riepe y Suhaimi, 2011; Knackstedt et al., 2013).
Industria
En la industria, CT se ha usado por varios años en ensayos no destructivos de los elementos fabricados. Uno de los usos más estudiados en la actualidad se relaciona con los sistemas de detección de explosivos. También se ha investigado en el estudio de materiales fabricados y manejo de residuos peligrosos.
En los aeropuertos se usan escáneres de CT para explorar el equipaje y detectar explosivos a partir de la densidad, masa y otras propiedades de los objetos en el interior de los contenedores (Ying, Naidu y Crawford, 2006; Gang y Yi, 2009). Por otra parte en las grandes fábricas se usa el escaneo en control de calidad, ya que con CT es posible hacer estudios no destructivos de los productos fabricados (Gehrke y Wirth, 2005; Malcolm, Liu, Ng y Teng, 2013). Por último, ha sido aplicado en el manejo de residuos peligrosos, como herramienta para determinar condiciones del contenido de los recipientes en que se depositan desechos que emiten radiación (Bernardi y Martz, 1995).
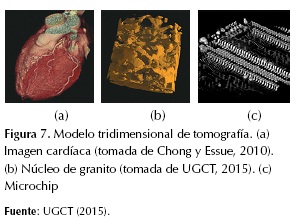
La figura 7 muestra tres ejemplos de tomografías: a) una imagen cardíaca (Chong y Essue, 2010), b) la reconstrucción de los poros de un núcleo de granito (UGCT, 2015) y c) el modelo tridimensional obtenido del escaneo de un microchip (UGCT, 2015). Estas imágenes corresponden a resultados de investigaciones en medicina, geología e industria, respectivamente.
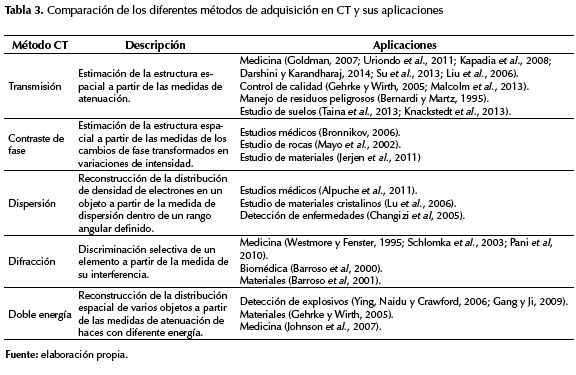
En la tabla 3 se presenta un resumen de los métodos de adquisición y sus respectivas aplicaciones.
CT es aplicada ampliamente y se posiciona como uno de los procedimientos radiológicos más usados e investigados en la actualidad para ensayos no destructivos. Por otro lado, el método de transmisión es el más explotado, esto quizá se deba a que corresponde al método tradicional. Además, el área de la que más datos de investigaciones se tienen es la medicina.
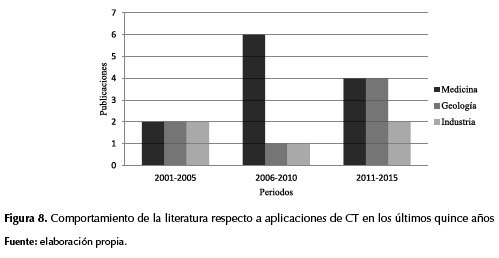
En la figura 8 se muestra el comportamiento de la literatura referente a aplicaciones de CT en las áreas mencionadas anteriormente en los últimos 15 años, el máximo de publicaciones por año es seis y el mínimo es uno. Se evidencia un mayor número de publicaciones en aplicaciones médicas y es posible inferir un creciente auge de la aplicación de la técnica en geología.
Casos de prueba
Dentro del software para simulaciones de CT se destacan las herramientas de Astra, un paquete del software Matlab de código abierto desarrollado para tomografía (Astra Tomography Toolbox, s.f.). Este permite simular el procedimiento con distintas geometrías, correspondientes a las generaciones. Está basado en el método de transmisión, debido a que se reconstruye la estructura espacial mediante la estimación de coeficientes de atenuación a partir de medidas de intensidad. Por último, Astra contiene los algoritmos de reconstrucción mencionados en la sección "Reconstrucción".
El trabajo de la herramienta comienza con la generación de datos sintéticos que corresponden al objeto a escanear y la definición de la geometría de proyección. Con esta información se calculan las proyecciones y se genera el sinograma. Adicionalmente, se definen las dimensiones, distancias, los ángulos de proyección y el tipo de algoritmo de reconstrucción. La figura 9 muestra un ejemplo de una simulación realizada con dos geometrías, la geometría en paralelo y la geometría en abanico. Las imágenes de muestra tienen dimensiones de 128 por 128 píxeles, 256 detectores, 500 ángulos y un rango de 360 grados para el desplazamiento de la fuente. La (a) presenta una imagen fantasma (phantom), usada tradicionalmente para representar el objeto escaneado en CT; la (b) y (c) ilustran los sinogramas correspondientes a los experimentos simulados con geometrías en paralelo y en abanico, respectivamente; las (d) y (e) muestran los resultados de la reconstrucción, realizada con el algoritmo FBP para cada experimento.
Una herramienta para expresar resultados de forma cuantitativa es el cálculo del PSNR (Peak Signal-to-Noise Ratio). La diferencia entre las reconstrucciones de las figuras 9(d) y 9(e) se calcula con el PSNR, que es de 27,81 y 32,47 [dB], respectivamente. Esto se debe a la cantidad de medidas por ángulo. Mientras se mide una proyección lineal con una arquitectura en paralelo, se toman varias proyecciones del mismo tipo con una configuración en abanico. Por tanto, se espera que la reconstrucción con la configuración en abanico sea mejor, lo que se verifica con los valores de PSNR obtenidos.
Conclusiones
CT es una herramienta importante en varias áreas de investigación. Como se mostró en esta revisión, desde los años 1970, el uso de rayos-X en ensayos no destructivos está envuelto en una continua evolución, que comprende aspectos físicos, algorítmicos y tecnológicos.
Este avance se da como respuesta a las necesidades generadas por el uso de la técnica, como por ejemplo disminuir los tiempos de adquisición y aumentar el nivel de detalle en las reconstrucciones. Una de las preocupaciones latentes es la dosis de radiación. Para responder a esta preocupación se ha investigado un nuevo método de adquisición usando la teoría de muestreo compresivo. Además de establecer el estado actual del CT, en esta revisión se presentan los primeros trabajos enfocados en la técnica de muestreo compresivo aplicada al método tradicional.
CT se ha destacado como un procedimiento médico, sin embargo, como se detalló en este trabajo, se evidencia su impacto en la industria y en la geología. Se espera que parte de las próximas investigaciones en CT estén dedicadas a estas áreas. Por otro lado, Aunque los desarrollos en tecnologías de adquisición se han centrado en los sistemas de detección, se espera que los próximos avances se enfoquen en el uso de múltiples fuentes de rayos-X.
Agradecimientos
Los autores agradecen a la Vicerrectoría de Investigación y Extensión de la Universidad Industrial de Santander por apoyar este trabajo registrado bajo el proyecto "Diseño y simulación de una arquitectura de tomografía computarizada para el censado compresivo de imágenes de rayos-X" (código VIE 1803).
Referencias
Alpuche, J.E.; Pistorius, S.; Gordon, R. & Elbakri, I.A. (2011). A Novel Hybrid Reconstruction Algorithm for First Generation Incoherent Scatter CT (ISCT) of Large Objects with Potential Medical Imaging Applications. Journal of X-Ray Science and Technology. 19(1), 35-56.
Astra Tomography Toolbox (s.f.). A High-Performance GPU MATLAB Toolbox for 2D and 3D Tomography. Recuperado de: http://sourceforge.net/p/astra-toolbox/wiki/Introduction/.
Barroso, R.C.; Lopes, R.T.; De Jesus, E.F.O. & Oliveira, L.F. (2001). X-Ray diffraction Microtomography Using Synchrotron Radiation. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 471(2), 75-79.
Barroso, R.C.; Lopes, R.T.; Jesus, E.F.O.; De Oliveira, L.F. & Description, A.B. (2000). Synchrotron Biomedical Applications Using X-Ray Diffraction Tomography. En: IEEE Conference Record, Nuclear Science Symposium. 2, 855-859. Seattle, WA.
Beath, S.R. & Cunningham, I.A. (s.f.) (2009). Pseudo-Monoenergetic X-Ray Diffraction Measurements Using Balanced Filters for Coherent-Scatter Computed Tomography. Medical Physics. 36(5), 1839-1847.
Bernardi, R.T. & Martz, H. E. (1995). Nuclear Waste Drum Characterization with 2 MeV X-Ray and Gamma-Ray Tomography. Proc. SPIE 2519, X-Ray and Ultraviolet Sensors and Applications, 140. DOI:10.1117/12.211897.
Bharkhada, H. & Yu, H.L. (2009). Line-source based X-ray tomography. International Journal of Biomedical Imaging. DOI:10.1155/2009/534516.
Bronnikov, A.V. (2006). Phase-Contrast CT: Fundamental Theorem and Fast Image Reconstruction Algorithms. SPIE, Developments in X-Ray Tomography, 63180Q, DOI:10.1117/12.679389.
Buzug, T.M. (2007). Computed Tomography: From Photon Statistics to Modern Cone-Beam CT. Berlín-Heidelberg: Springer Verlag.
Candes, E.J. & Tao, T. (2006). Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? IEEE Transactions on Information Theory. 52(12), 5406-5425.
Candès, E.J.; Romberg, J. & Tao, T. (2006). Robust Uncertainty Principles: Exact Signal Reconstruction From Highly Incomplete Frequency Information. IEEE Transactions on Information Theory. 52(2), 489-509.
Changizi, V., Oghabian, M. A., Speller, R., Sarkar, S., & Kheradmand, A. A. (2005). Application of Small Angle X-ray Scattering (SAXS) for Differentiation between Normal and Cancerous Breast Tissue. Int J Med Sci. 2(3), 118-121.
Chen, J.; Member, S.; Cong, J.; Vese, L.A. & Villasenor, J. (2012). A Hybrid Architecture for Compressive Sensing 3-D CT Reconstruction. IEEE Journal on Emerging and Selected Topics in Circuits and Systems. 2(3), 616-625.
Cho, M.K.; Youn, H.; Jang, S.Y.; Lee, S.; Han, M.C. & Kim, H.K. (2012). Digital Tomosynthesis in Cone-Beam Geometry for Industrial Applications: Feasibility and Preliminary Study. International Journal of Precision Engineering and Manufacturing. 13(9), 1533-1538.
Choi, K. & Brady, D.J. (2009). Coded Aperture Computed Tomography. En: Proc. SPIE 7468, Adaptive Coded Aperture Imaging, Non-Imaging, and Unconventional Imaging Sensor Systems, 74680B. DOI:10.1117/12.825277.
Chong, J. & Essue, J. (2008). Innovations in Cardiac Computed Tomography: Cone Beam CT/Volume CT and Dual Source CT. UWOMJ 77(2), 6-11.
Cong, W. & Wang, G. (2011). X-Ray Scattering Tomography for Biological Applications. J. Xray. Sci. Technol. 19(2), 219-227.
Darshini P., and Karandharaj, P. (2014). Medical image processing schemes for cancer detection: A survey. In International Conference on Green Computing Communication and Electrical Engineering (pp. 1-6).
Dobbins, J.T. (2009). Tomosynthesis Imaging: At a Translational Crossroads. Medical Physics. 36(6), 1956--1967. DOI:10.1118/1.3120285.
Donoho, D.L. (2006). Compressed Sensing. IEEE Transactions on Information Theory. 52(4), 1289-1306.
Galvis, D.F.; Mejía, Y.H. & Argüello, H. (2014). Efficient Reconstruction of Raman Spectroscopy Imaging Based on Compressive Sensing. DYNA. 81(118), 116-124.
Gang, T. & Ji, F.D. (2009). The Research & Application of the Detection Capability of Dangerous Goods in Dual-Energy X-Ray Security Equipment. In IEEE International Conference on Intelligent Computation Technology and Automation. 2, 352-355. DOI: 10.1109/ICICTA.2009.321.
Gehrke S. & Wirth, K.E. (2005). Application of Conventional- and Dual-Energy X-Ray Tomography in Process Engineering. IEEE Sens. J. 5(2), 183-187.
Geng, J. & Member, S. (2008). Volumetric 3D Display for Radiation Therapy Planning. Journal of Display Technology. 4(4), 437-450.
Ghonge, N.P. (2013). Computed Tomography in the 21st Century: Current Status & Future Prospects. JIMSA 26(1), 35-42.
Goldman, L.W. (2007). Principles of CT and CT Technology. J. Nucl. Med. Technol. 35(3), 115-28.
Hu, C.; Youtcheff, J.; Wang, D.; Zhang, X.; Kutay, E. & Thyagarajan, S. (2012). Characterization of Asphalt Mixture Homogeneity Based on X-ray Computed Tomography. Journal of Testing and Evaluation 40(7), 1103-1111.
Jerjen, I.; Revol, V.; Kottler, C. & Kaufmann, R. (2011). The Benefits and Challenges of Differential Phase Contrast Imaging for Material Science. International Symposium on Digital Industrial Radiology and Computed Tomography ((pp. 1-8). Berlín.
Jian F., (2012). Phase Contrast Computed Tomography, Computed Tomography-Clinical Applications. En: L. Saba (ed.). InTech.
Jian, F.; Bin, L.; Hao, Z.; Xingyu, Z.; Zhenggan Z. & Dongbo, W. (2009). X-Ray Phase-Contrast Imaging Methods for Biological Structures. En: BMEI '09. 2nd International Conference on Biomedical Engineering and Informatics (pp. 1-3). DOI: 10.1109/BMEI.2009.5305651.
Johnson, T. (2012). Dual-Energy CT: General Principles. AJR. Am. J. Roentgenol 119(5), S3-8.
Johnson, T. R. C., Krauss, B., Sedlmair, M., Grasruck, M., Bruder, H., Morhard, D. ... Becker, C. R. (2007). Material differentiation by dual energy CT: initial experience. European Radiology 17(6), 1510-1517.
Kapadia, A.J.; Sharma, A.C.; Tourassi, G.D.; Bender, J.E.; Howell, C.R.; Crowell, A.S. & Floyd, C.E. (2008). Neutron Stimulated Emission Computed Tomography for Diagnosis of Breast Cancer. IEEE Transactions on Nuclear Science 55(1), 501-509.
Kaza, R.; Platt, J.; Cohan, R.; Caoili, E.; Al-Hawary, M. & Wasnik, A. (2012). Dual-Energy CT with Single- and Dual-Source Scanners: Current Appli- cations in Evaluating the Genitourinary Tract. Radiographics 32(2), 353-69.
Ketcham, R.A. & Carlson, W.D. (2001). Acquisition, Optimization and Interpretation of X-Ray Computed Tomographic Imagery: Applications to the Geosciences. Computers & Geosciences 27(4), 381-400.
Knackstedt, M., Carnerup, A., Golab, A., Sok, R., Young, B., & Riepe, L. (2013). Petrophysical Characterization of Unconventional Reservoir Core At Multiple Scales. Petrophysics 54(3), 216-223.
Levakhina, Y. (2013). Three-Dimensional Digital Tomosynthesis. Iterative Reconstruction, Artifact Reduction and Alternative Acquisition Geometry. Wiesbaden: Springer Fachmedien Wiesbaden.
Lewitt, R.M.; Member, S.; Matej, S. & Member, S. (2003). Overview of Methods for Image Reconstruction From Projections in Emission Computed Tomography. Proceedings of the IEEE 91(10), 1588-1611.
Li, J.; Zhu, P. & Sun, Y. (2012). An Approximate Reconstruction Method for Helical Cone-Beam Differential Phase-Contrast Computed Tomography Images. Physics in Medicine and Biology 57(8), 2347-2356.
Li, T.T.; Li, H. & Diao, L.H. (2008). Cone-Beam Tomography of Propagation-Based Imaging. Applied Physics Letters, 93, 221114-221114-3.
Lima, I.; Assis, J.T.; Apoloni, C.R.; Mendonca de Souza, S.M.; Duarte, M. E. & Lopes, R.T. (2009). Non-Destructive Imaging Materials Investigation by Microfocus 3D X-Ray Computed Tomography. IEEE Transactions on Nuclear Science 56(3), 1448-1453.
Liu, Y.; Member, S.; Fernando, G.P. & Sinusas, A.J. (2006). A New Method for Hot-Spot Quantification of Hybrid SPECT / CT Cardiac Images: Methodology and Preliminary Phantom Validation. IEEE Transactions on Nuclear Science 53(5), 2814-2821.
Lu, Y., Longman, E., Davis, K. G., Ortega, Á. J., Grossmann, G., Michaelsen, T. E., ... Harding, S. E. (2006). Crystallohydrodynamics of Protein Assemblies: Combining Sedimentation , Viscometry , and X-Ray Scattering. Biophys J., 91(5), 1688-1697.
MacCabe, K.P.; Holmgren, A.D.; Tornai, M.P. & Brady, D.J. (s.f.) (2013). Snapshot 2D Tomography Via Coded Aperture X-Ray Scatter Imaging. Appl. Opt. 52(19), 4582-4589.
Maire, E. & Withers, P.J. (2014). Quantitative X-ray tomography. Int. Mater. Rev.59(1), 1-43.
Malcolm, A.A.; Liu, T.; Ng, I.K. & Teng, W.Y. (2013). A Large Scale Multiple Source X-ray CT System for Aerospace Applications. International Symposium on NDT in Aerospace. Singapore.
Mayo, S.C.,; Miller, P.R.; Wilkins, S.W.; Davis, T.J.; Gao, D.; Gureyev, T.E.; Paganin, D.; Parry, D.J.; Pogany, A.; Robb, T. & Stevenson, A.W. (2002). Phase-Contrast X-Ray Projection Microscopy for Materials Characterisation. Mater. Forum, 26, 15-19.
Niemi, E.; Lassas M. & Siltanen, S. (2013). Dynamic X-ray tomography with multiple sources. 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA) (pp.618-621). DOI: 10.1109/ISPA.2013.6703813.
Ning, R.; Chen, B.; Yu, R.; Conover, D.; Tang, X. & Ning, Y. (2000). Flat Panel Detector-Based Cone-Beam Volume CT Angiography Imaging: System Evaluation. IEEE Transactions on Medical Imaging 19(9), 949-63.
Pani, S., Cook, E. J., Horrocks, J. A, Jones, J. L., & Speller, R. D. (2010). Characterization of breast tissue using energy-dispersive X-ray diffraction computed tomography. Applied Radiation and Isotopes: Including Data, Instrumentation and Methods for Use in Agriculture, Industry and Medicine, 68(10), 1980-7.
Prince, J.L. & Links, J. (2005). Medical Imaging Signals and Systems. 2a. ed. Prentice-Hall, Springer.
Revol, V.; Kottler, C.; Kaufmann, R.; Straumann, U. & Urban, C. (2010). Noise Analysis of Grating-Based X Ray Differential Phase Contrast Imaging. The Review of Scientific Instruments 81(7), 073709-073709-7.
Riepe, L. & Suhaimi, M. (2011). Application of High Resolution Micro-CT-Imaging and Pore Network Modeling (PNM) for the Petrophysical Characterization of Tight Gas Reservoirs-A Case History. En: In SPE Middle East Unconventional Gas Conference and Exhibition (pp. 1-13). Muscat, Oman. DOI: http://dx.doi.org/10.2118/142472-MS.
Russo, P.; Lauria, A.; Mettivier, G. & Montesi, M.C. (2008). X ray cone-beam breast computed tomography: Phantom studies. En: 2008 IEEE Nucl. Sci. Symp. Conf. Rec., 4803-4810. DOI: 10.1109/NSSMIC.2008.4774317.
Schlomka, J., Harding, A., Harding, G., Stevendaal, U. Van, & Grass, M. (2003). Coherent Scatter X-ray Computed Tomography In Medical Applications. IEEE Nuclear Science, 2, 900-901.
Seeram, E. (2008). Computed tomography: Physical Principles, Clinical Applications, and Quality Control. 3a. ed. Elsevier Health Sciences.
Sevak, M.M.; Thakkar, F.N.; Kher, R.K. & Modi, C.K. (2012). CT Image Compression Using Compressive Sensing and Wavelet Transform. In International Conference on Communication Systems and Network Technologies, 138-142, DOI: 10.1109/CSNT.2012.39.
Shannon, C.E. (1998). Communication in the Presence of Noise. Proceedings of the IEEE 86(2), 447-457.
Shefer, E.; Altman, A.; Behling, R.; Goshen, R.; Gregorian, L.; Roterman, Y. & Zarchin, O. (2013). State of the Art of CT Detectors and Sources: A Literature Review. Current Radiology Reports 1(1), 76-91.
Su, P.; Yang, J.; Lu, K.; Yu, N.; Wong, S.T.; Xue, Z. & Member, S. (2013). A Fast CT and CT-Fluoroscopy Registration Algorithm With Respiratory Motion Compensation for Image-Guided Lung Intervention. IEEE Transactions on Biomedical Engineering 60(7), 2034-2041.
Taina, I.A.; Heck, R.J.; Deen, W. & Ma, E.Y.T. (2013). Quantification of Freeze-Thaw Related Structure in Cultivated Topsoils Using X-Ray Computer Tomography. Canadian Journal of Soil Science 93(4), 533-553.
UGCT (2015). Centre for X-ray Tomography of the Ghent University (UGCT). Recuperado de: http://www.ugct.ugent.be.
Uriondo, O.; Garc, L.; Deustotech-life, Z. & Avda, D. (2011). Computed Tomography CAD System for Monitoring and Modeling the Evolution of Lung Cancer Nodule. IEEE International Symposium on Signal Processing and Information Technology, 484-489. DOI: 10.1109/ISSPIT.2011.6151610.
Vine, D.J.; Paganin, D.M.; Pavlov, K.M.; Kräußlich, J.; Wehrhan, O.; Uschmann, I. & Förster, E. (2007). Analyzer-Based Phase Contrast Imaging and Phase Retrieval Using a Rotating Anode X-Ray Source. Applied Physics Letters 91(25), 254110-254113.
Vontobel, P.; Lehmann, E. & Carlson, W.D. (2005). Comparison of X-Ray and Neutron Tomography Investigations of Geological Materials. IEEE Transactions on Nuclear Science 52(1), 338-341.
Wakin, M.B. (2008). An Introduction to Compressive Sampling. IEEE Signal Processing Magazine 25(2), 21-30.
Wang G., Yu H. & De Man, B. (2008). An Outlook on X-Ray CT Research and Development. Med. Phys. 35(3), 1051-1063.
Webb, S. (1987). A Review of Physical Aspects of X-Ray transmission Computed Tomography. IEEE Proc. A Phys. Sci. Meas. Instrumentation, Manag. Educ. Rev. 134(2), 126-135.
Westmore M.S. & F'enster, A., C.I.A. (1995). Investigation of Coherent-Scatter Computed Tomography. Physics of Medical Imaging, 2432, 24-32.
Westmore, M.S.; Fenster, A. & Cunningham, I.A. (1997). Tomographic Imaging of the Angular-Dependent Coherent-Scatter Cross Section. Medical Physics, 24, 3-10.
Ying, Z.; Naidu, R. & Crawford, C.R. (2006). Dual Energy Computed Tomography for Explosive Detection. Journal of X-Ray Science and Technology, 14, 235-256.
Yoneyama, A.; Yamada, S. & Takeda, T. (2011). Fine Biomedical Imaging Using X-Ray Phase-Sensitive Technique. Advanced Biomedical Engineering. En: G. Gargiulo (ed.). InTech. DOI: 10.5772/20456.
Yu, H. & Wang, G. (2009). Compressed sensing based interior tomography. Physics in Medicine and Biology 54(9), 2791-2805.
Yuasa, T.; Akiba, M.; Takeda, T.; Kazama, M.; Hoshino, A. & Watanabe, Y. (2002). Incoherent-Scatter Computed Tomography with Monochromatic Synchrotron X Ray: Feasibility of Multi-CT Imaging System for Simultaneous Measurement of Fluorescent and Incoherent Scatter X Rays. IEEE Transactions on Nuclear Science 44(5), 1760-1769.
Zhang, R.; Member, S.; Thibault, J.; Bouman, C.A.; Sauer, K.D.; Hsieh, J. & Member, S. (2013). Model-Based Iterative Reconstruction for Dual-Energy X-Ray CT Using a Joint Quadratic Likelihood Model. IEEE Transactions on Medical Imaging 33(1), 117-134.
Zhu, Z.; Wahid, K.A. & Babyn, P. (2012). CT Image Reconstruction from Partial Angular Measurements Via Compressed Sensing. En: IEEE Canadian Conference on Electrical & Computer Engineering (pp. 3-6). DOI: 10.1109/CCECE.2012.6334926.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.