DOI:
https://doi.org/10.14483/22487638.12807Publicado:
2018-04-01Número:
Vol. 22 Núm. 56 (2018): Abril - JunioSección:
InvestigaciónAprovechamiento de los tipos de pensamiento matemático en el aprendizaje de la programación funcional
Types of mathematical thinking implemented in the learn process of functional programming
Palabras clave:
learning, discovery, mathematics, functional programming, logic, meaning (en).Palabras clave:
aprendizaje, descubrimiento, matemáticas, programación funcional, significado, lógica. (es).Descargas
Referencias
Ausubel, D. (2012). The acquisition and retention of knowledge. Washington, EE. UU.: Springer.
Ballester, A. (2011). Meaningful Learning in practice. Islas Canarias: Universitat de les Illes Ballears.
Bruner, J. (2006). Hacia una teoría de la instrucción. México: Editorial Limusa.
Bruner, J. (2009). Actos de significado. Madrid, España: Alianza Editorial.
Díaz, F. y Hernández, G. (2002). Estrategias docentes para un aprendizaje significativo. México: McGraw-Hill.
Felleisen, M. et al. (2005). How to design programs. Boston: MIT Press.
Havenge, M. et al. (2013). Metacognitive and problem solving skills to promote self directed learning in computer programming. SA-eDUC Journal, 10(2), 11-25.
Kline, M. (2012). El pensamiento matemático. De la antigüedad a nuestros días. Madrid: Alianza Editorial.
Ministerio de Educación Nacional (MEN) (2005). Estándares básicos de competencias matemáticas. Bogotá.
Pham, P. et al. (junio de 2014). Learning computer programming in CDIOs teams. 10th Annual International CDIO Conference, 7(2), 40-52.
Trejos, O. (2000). La esencia de la lógica de programación. Pereira, Colombia: Centro Editorial Universidad de Caldas.
Trejos, O. (2004). Fundamentos de programación. Pereira, Colombia: Editorial Papiro.
Trejos, O. (2012). Significado y competencias. Pereira, Colombia: Editorial Papiro.
Trejos, O. (2017). Programación imperativa con lenguaje C. Bogotá: Ecoe Ediciones.
Van Roy, P. y Haridi, S. (2004). Concepts, Techniques, and Models of computer programming. Boston, EE. UU.: MIT Press.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 3 de diciembre de 2017; Aceptado: 23 de febrero de 2018
Resumen
Contexto:
En el presente artículo se exponen y analizan los resultados de una investigación realizada en el aula, en el contexto del aprendizaje de la programación funcional a nivel universitario en Ingeniería de Sistemas y Computación, a partir de la aplicación de los tipos de pensamiento matemático y de su uso en el lenguaje de programación DrRacket. El propósito fue establecer nexos entre los tipos de pensamiento matemático y la programación de computadores (para los estudiantes de primer semestre).
Metodología:
Para el desarrollo de esta investigación se trabajó con un grupo de estudiantes de primer, aplicando la metodología propuesta. Las evaluaciones, basadas en los tipos de pensamiento matemático, se hicieron en otro grupo que estaba recibiendo la asignatura por los métodos convencionales. En este solamente se adelantaron las pruebas evaluativas; no se hizo ningún monitoreo al respecto de su aprendizaje.
Resultados:
Los resultados muestran grandes ventajas cuando se articulan matemáticas y programación dentro del contexto de una asignatura que les confiere sentido a ambas áreas.
Conclusiones:
Se concluye que la programación funcional se aprende de una manera más fácil cuando se relaciona con los tipos de pensamiento matemático y viceversa.
Palabras clave:
aprendizaje, descubrimiento, matemáticas, programación funcional, significado, lógica.Abstract
Context:
This article presents and analyzes the results of a research carried out in a classroom, in the context of the learning of functional programming at university level in Systems Engineering and Computing program, from the application of the types of mathematical thinking and their use in the DrRacket programming language. The purpose was to establish links between the types of mathematical thinking and computer programming (for first-semester students).
Methodology:
For the development of the research, we worked with a group of first-year students, applying the proposed methodology of mathematical thinking. The evaluations, based on the types of mathematical thinking, were made in another group that was receiving the subject by conventional methods. In this group only the evaluative tests were carried out; no monitoring of their learning was done.
Results:
The results show great advantages when articulating mathematics and computer programming within the context of a subject that gives meaning to both areas.
Conclusions:
It is concluded that functional programming is learned in an easier way when it is related to the types of mathematical thinking and vice versa.
Keywords:
learning, discovery, mathematics, functional programming, logic, meaning.Introducción
Para el desarrollo de esta investigación, se ha planteado como base el problema de saber que a los estudiantes de básica secundaria, de acuerdo con los estándares en formación de competencia matemática, se les imbuye en el concepto de los cinco tipos de pensamiento matemático, pero pocas veces se les permite que este, tan útil en todas las dimensiones del conocimiento humano, sea funcional para otras áreas y, específicamente, otras asignaturas.
Todo el currículo de la básica secundaria está orientado a fortalecer (muchas veces sin lograrlo) la apropiación, asimilación, aplicación y retroalimentación de los cinco tipos de pensamiento matemático. También, existen casos exitosos en los cuales se logra este propósito. Sin embargo, sea que se logre o no, el problema sobreviene en que las matemáticas se conciben como una ínsula académica aparte, y pareciera que no tuviera relación con otras áreas de conocimiento según el desarrollo de los contenidos temáticos de las demás asignaturas.
La programación de computadores es la expresión tecnológica de los modelos matemáticos (Pham et al., 2014) y es, al tiempo, el camino a través del cual el estudiante puede hacer realidad lo que, en el tablero, se le ha explicado. Las simulaciones, los juegos, los escenarios y las vidas virtuales son tan solo algunos ejemplos en donde la programación ha interpretado la realidad, desde su implementación en el computador gracias a las bondades de un lenguaje de programación.
Si bien, es claro que matemáticas y programación de computadores tienen espacios comunes en más de una escena del mundo académico; también, son pocos los docentes (en ambas áreas) que lo concretan según se deriva de las entrevistas que sustentan este proyecto de investigación. Este artículo es un producto del proyecto de investigación “Análisis de la relación, implicaciones e incidencia del aprendizaje de las ciencias básicas y del conocimiento básico en el proceso de formación de ingenieros de sistemas” tramitado ante el Consejo de Facultad de Ingenierías de la Universidad Tecnológica de Pereira, e inscrito en la Vicerrectoría de Investigaciones, Innovación y Extensión.
El tema de investigación se justifica desde tres aspectos: a) se le posibilita, al estudiante, una visión clara y aplicativa de los conceptos vistos en matemáticas; b) se le brinda un sentido al estudio y fortalecimiento de los cinco tipos de pensamiento matemático, y c) se cristaliza, por la vía de la implementación, el entendimiento de los nexos tan cercanos entre las matemáticas y la programación, en la que aquella es fundamento de esta, y gracias a lo que es posible comprender el código de un lenguaje de programación como la manera de hacer efectivo con la tecnología todo aquello que proveen las matemáticas.
Si bien, en muchos escritos emanados por las instituciones educativas tanto de básica secundaria como de nivel universitario, se habla de la gran importancia de las matemáticas como fundamento para el desarrollo del pensamiento lógico; en realidad, tan solo en el aula, la distancia entre esta y las demás áreas es notoria, por ello se pierde el sentido de las matemáticas dificultando la apropiación de su significado. La programación de computadores se ha tomado en esta investigación como un camino posible para que no se pierda ese significado relevante de las matemáticas; de manera que programación y matemáticas refuercen mutuamente su significado y su sentido dentro del contexto de formación de ingenieros de sistemas.
Para el desarrollo de esta investigación se acudió a teorías del aprendizaje, principalmente, significativo y por descubrimiento. También se recurrió a la consulta de documentos de las instituciones educativas y se confrontaron con la realidad vivida tanto por parte de estudiantes como de profesores y de egresados. El espacio disponible para este artículo impide hacer una relatoría detallada de todos los elementos de juicio que se involucraron y que emergieron del avance de este proyecto, por esta razón se ha optado por centrar el corpus de su contenido en la experiencia en el aula.
¿Es posible establecer nexos entre las matemáticas y otras áreas, de manera que recíprocamente se fortalezcan y que se aproveche la formación intensiva en los cinco tipos de pensamiento matemáticos que se promueven oficialmente con la formación por competencias? La respuesta, en parte, está contenida en este artículo y esta hipótesis abre el camino para pensar que no solo la programación de computadores, en ingeniería de sistemas, sea una solución posible interrogante planteado, sino que otras áreas bien podrían servirse de dichos tipos de pensamiento para hacer efectiva la apropiación y asimilación de su propio corpus de conocimiento por parte de los estudiantes. Esta hipótesis marca el objetivo de esta investigación y, con ello, define el sentido del presente artículo en lo que corresponde a la experiencia en el aula.
La investigación se realizó en el primer semestre de Ingeniería de Sistemas y Computación de la Universidad Tecnológica de Pereira en la asignatura “Programación I”, durante los dos periodos académicos de 2015, 2016 y 2017.
Fundamentos teóricos
Posiblemente no exista un área más formativa tanto en la básica secundaria como en la universidad que las matemáticas. Es el área que nunca pasa desapercibida pues genera tantos quereres y malquereres que, en muchos casos, termina siendo el puente para que unos estudiantes escojan su camino de formación profesional por la senda de las llamadas ciencias duras o también que para que otros se orienten por las ciencias blandas, en donde esperan no encontrarlas. Sin querer decir que esta sea la única base sobre la cual los estudiantes de secundaria grado 11 toman sus decisiones de cara a su formación profesional, las matemáticas ocupan un lugar importante en dichas decisiones.
Las ingenierías, en general, encuentran en las matemáticas el fundamento para que los estudiantes logren, por lo menos, cinco objetivos: a) sirven como base para que se puedan plantear y resolver problemas de orden lógico que, en muchos casos, tiene un nexo claro con la vida real; b) permite modelar situaciones del mundo real y, con ello, posibilita la aproximación y predicción a sus posibles comportamientos y alteraciones producto de su interacción con su entorno; c) posibilita bases para una comunicación activa entre estudiantes, ya sea por el camino de los elementos formales que proveen las matemáticas, o por el de las razones que estas brindan para que se acuda a las informalidades propias del lenguaje; d) abre las puertas para que los estudiantes conozcan apropien y apliquen razonamientos apoyados en elementos de juicio que sean lógicos desde la perspectiva tanto de las mismas matemáticas como las de la interacción social, cultural y vivencial, y d) facilitar el planteamiento, uso y ejercitación de determinados procedimientos que, de una u otra forma, le presentan al estudiante formas organizadas y sistemáticas de resolverlos a partir de algoritmos preestablecidos (MEN, 2005).
Si bien, en la teoría, estos propósitos son más que necesarios para que el ser humano aproveche su gran capacidad de razonamiento, la sistematice, la ajuste a unas reglas y construya sobre eso procedimientos que faciliten y universalicen la manera de abordar, interpretar y modelar problemas, debe tenerse en cuenta que no siempre se logran en la proporción en que debían lograrse (Trejos, 2012). En la realidad, los resultados obtenidos en esta investigación, y que se salen del corpus del contenido de este artículo, parecieran evidenciar que, si bien los estudiantes superan y aprueban las asignaturas del área de matemáticas, tanto en los últimos años de formación básica secundaria como en los primeros de formación profesional, no siempre le encuentran el sentido apropiado de aplicación que debieran encontrarle.
Los estándares de competencias en matemáticas, y el análisis científico de esta área, indican que, a partir de las matemáticas, en su apropiación, su asimilación y aplicación, se debe fortalecer el pensamiento lógico que pretende tener un conjunto de reglas y relaciones que permitan modelar situaciones, analizarlas y plantear diferentes caminos para su resolución (Ballester, 2011). Ser matemáticamente competente se concreta de manera específica en el pensamiento lógico y el pensamiento matemático, el cual se subdivide en cinco tipos que inspiran tanto este artículo como la investigación asociada: a) pensamiento numérico y los sistemas numéricos, b) pensamiento espacial y los sistemas geométricos, c) pensamiento métrico y los sistemas métricos o de medidas, d) pensamiento aleatorio y los sistemas de datos y e) pensamiento variacional y los sistemas algebraicos y analíticos (MEN, 2005).
Vale la pena recordar que el estudiante se mueve permanentemente en medio de tres contextos que son los que fundamentan muchas de las reflexiones con las cuales mira el mundo (Díaz y Hernández, 2002): a) el aula, que involucra todo lo que sucede allí dentro, b) el institucional, que concierne a lo que sucede en la institución, pero fuera del aula de clases y c) el extraescolar o extrainstitucional, que incluye lo que sucede por fuera de los linderos de la escuela, colegio o universidad.
Vale la pena resaltar que diferentes estudios han demostrado que, si bien se desea que el contexto que más influya en el alumno sea el del aula, que es (teóricamente) en donde se adquieren los conocimientos, en realidad el contexto que más influye en la formación de reglas lógicas y su relación con la sociedad y su entorno personal es el extrainstitucional (Bruner, 2009). De allí por qué es tan importante fortalecer el sentido de las matemáticas confiriéndoles significado dentro de estos tres contextos, pero haciendo hincapié en el de mayor influencia tanto para los jóvenes que terminan su formación básica secundaria, como para los que están comenzando su carrera universitaria.
La enseñanza de la programación de computadores se ha convertido, poco a poco, en un área desde la cual el estudiante (sea cual fuere el nivel formativo en el cual se encuentre) puede conocer y apropiar unas reglas, aplicarlas en la modelación y planteamiento de unas soluciones, y verificar si dicha solución resuelve el problema (Trejos, 2000). La programación de computadores se basa en unos paradigmas para plantear soluciones, y estos no son más que formas de concebir el problema para visualizar la solución por un camino simple, alcanzable, implementable y viable.
Durante mucho tiempo, enseñar programación de computadores se ha convertido en un reto para los docentes -quienes a nivel de colegio corresponden al área de matemáticas y a nivel universitario, a ingenieros-, puesto que se requiere que el alumno conozca, apropie y aplique un sistema similar al que se usa en las matemáticas, solo que esta vez, a partir de una lógica computacional (Trejos, 2017) y que dista notoriamente de la lógica deliberativa humana.
Esto implica que la resolución de problemas y su implementación dentro de las posibilidades que ofrece un lenguaje de programación, pasa por el filtro de la lógica computacional que, en palabra sencillas, es la expresión reducida de la lógica matemática llevada a los términos que la tecnología provee (Trejos, 2004) que posibilita la implementación de soluciones a problemas que se clasifican entre los llamados computables, es decir, aquellos que pueden ser resueltos con la intervención del computador.
Aunque en la actualidad existen diferentes paradigmas, o formas de ver la solución de un problema computable y, asimismo, de implementarla (Van Roy y Haridi, 2004), el curso en donde se ha realizado la investigación es el inicial de un programa de ingeniería de sistemas y computación y en él, su contenido se ha orientado hacia el conocimiento, apropiación y aplicación del paradigma funcional que concibe las soluciones desde la perspectiva que ofrece el concepto de función y la estrategia divide y vencerás.
Una función es la célula de trabajo de un programa funcional que se puede describir como un fragmento de código con independencia e interdependencia (Felleisen et al., 2005), que cumple un objetivo específico y que puede retornar valores. La estrategia divide y vencerás consiste en la concepción de una solución a partir del diseño, implementación e interacción de diferentes funciones que, cumpliendo cada una un pequeño objetivo específico, en conjunto e hiladas apropiadamente logran el propósito general que el problema requiere. La programación funcional está basada en la aplicación del cálculo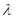 
propuesto y refinado por Alonzo Church y Stephen Kleene en 1930, para ser usado como mecanismo matemático que permita definir claramente el concepto de función computable (Kline, 2012), cuya característica principal es la supresión de tipos de datos y cuya herramienta más fuerte es el concepto de recursión.
La teoría del aprendizaje significativo se fundamenta en que todo aprendizaje se hace más efectivo si el conocimiento aprendido tiene significado para quien lo aprende (Ausubel, 2012) y para ello prioriza tres elementos: a) el conocimiento previo, que corresponde al conjunto de teorías, conceptos y modelos que el estudiante tiene en su mente y que pueden haber sido adquiridos en cualquier de los tres contextos de aprendizaje, pero que rigen su manera de ver el mundo; b) el nuevo conocimiento, que corresponde a teorías, conceptos y modelos que modifican, alteran, cuestionan o reemplazan el conocimiento previo y que pueden ser adquiridos en cualquiera de los tres contextos aunque deseablemente debieran ser adquiridos en el aula a partir de un proceso formal de aprendizaje, y c) la actitud del estudiante que involucra, entre otros factores, la capacidad de establecer nexos entre los saberes previos y los nuevos conocimientos; y la motivación del estudiante.
Es de anotar que la capacidad de relacionar el conocimiento previo con el nuevo es un reto que podría ser, en gran medida, producto del mismo proceso de aprendizaje y de la manera como el docente lo conduzca (Havenge et al., 2013) y la motivación se puede definir como la voluntad indeclinable de aprender en la cual tiene gran incidencia el docente puesto que, en tiempos modernos, este se convierte en acompañante, tutor, coequipero y motivador de los procesos de aprendizaje para que en medio de estrategias con acompañamiento y estrategias autónomas, el alumno puede acceder, apropiar, asimilar, aplicar y retroalimentar el conocimiento que se espera que adquiera.
El aprendizaje por descubrimiento se basa en que todo lo que el ser humano descubre lo aprende a largo plazo y, por consiguiente, puede aplicarlo suficientemente bien en el momento en que se requiera (Bruner, 2006). La experimentación, la exploración, el ensayo y el error constituyen los fundamentos de esta teoría de aprendizaje que marca la diferencia con el aprendizaje significativo, en la manera como el estudiante interactúa, en las primeras de cambio, con el conocimiento que se espera que adquiera.
De la misma manera, la fascinación por lo nuevo y lo insólito es una base para que el estudiante se motive a aprender aquello que aún no sabe y que, conducido apropiadamente por el docente, puede formar parte de sus elementos de juicio que le permitan interpretar, modelar, intervenir, optimizar y mejorar el mundo que le rodea.
Metodología
En esta investigación se abordaron tres grupos de personas que tenían relación con el objetivo: docentes, egresados y estudiantes de primer semestre. Con los primeros se hizo un trabajo de exploración en cuanto a la opinión que estos tenían sobre la importancia de las matemáticas, la claridad sobre los cinco tipos de pensamiento matemático, sus significados y sus usos, y la puesta en práctica de la lógica matemática y sus vertientes frente a otras áreas de conocimiento.
Con los egresados se indagó acerca de cómo ellos concibieron el área de las matemáticas en su programa de ingeniería de sistemas, y la claridad que observaron en las metodologías de enseñanza para que los docentes les indicaran el camino de aplicación de las matemáticas en relación con otras áreas. Asimismo, se preguntó hasta dónde habían percibido la estrecha relación entre la programación de computadores y los cinco tipos de pensamiento matemático. En este artículo se omiten resultados, análisis y discusión en relación con lo que se obtuvo por parte de los docentes y los egresados, puesto que este es tema de otro artículo. La parte central de la investigación, que inspira este escrito, la constituyen los estudiantes de primer semestre con quienes se procedió de la siguiente manera: en principio, se les explicó el propósito y los alcances de la investigación, es decir, la orientación que iba a tener la asignatura de “Programación I” cuyo contenido se fundamenta en el paradigma de programación funcional y su implementación en DrRacket.
Igualmente, se explicó el sustento teórico, de una forma simple y sencilla, que corresponde a las teorías del aprendizaje significativo y del aprendizaje por descubrimiento, preámbulo sobre el cual se indicaron las actividades a realizar. Durante la asignatura se iba a hacer hincapié en ejercicios, enunciados y problemas que se fundamentaran en cada tipo de pensamiento matemático, y se señaló que los parciales se harían de manera individual. Se planearon cinco pruebas parciales a lo largo del semestre, sin incluir el examen final que sería sobre todo lo visto en el curso. Dado que el semestre académico cuenta con 16 semanas, las pruebas parciales se realizarían cada 3 semanas con un peso porcentual igual en todas. Cada prueba parcial equivaldría a 15 %; el examen final, a un 30 % y se les concedería una nota apreciativa, a manera de motivación, que constituye el 10 % restante.
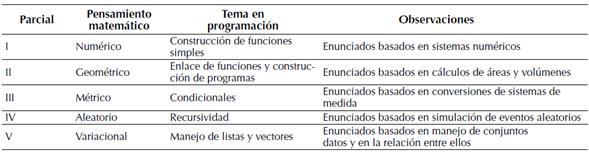
Simultáneamente a la explicación de los conceptos propios de la programación funcional, se iban planteando ejercicios que abordaran un tipo de pensamiento específico. La tabla 1 presenta la distribución de los temas en lo que corresponde a programación y su relación con los tipos de pensamiento matemático. Cabe anotar que durante el desarrollo de la asignatura, y sin que formara parte de su contenido -pero considerando que fuera necesario-, se explicaron elementos de cada tipo de pensamiento matemático, relacionados en cuanto a su utilidad, aplicación y uso en diferentes situaciones de la vida real.
Fuente: elaboración propia.
Tabla 1: Distribución de temas
De la misma manera, durante las sesiones magistrales se invitó a que los estudiantes propusieran ejercicios y enunciados relacionados con cada tipo de pensamiento matemático. Esto les permitió articularse tanto con lo puramente matemático como con lo que correspondía a la programación como tal. Debe anotarse, como detalle curioso, que muchos manifestaban no saber nada acerca de los tipos de pensamiento matemático y, aunque ese detalle no se tuvo en cuenta para las diferentes evaluaciones parciales de conocimiento, vale la pena mencionarlo con beneficio de inventario y posterior análisis.
Como se puede observar en la tabla 1, se buscó que cada tipo de pensamiento matemático se articulara con un tema específico de la programación funcional de manera que, mutuamente, cada uno le concediera un significado al otro. Desde las matemáticas a través de situaciones, ejemplos y enunciados que se enmarcaban en cada tipo de pensamiento y desde la programación de computadores con la implementación de soluciones que resolvieran los problemas planteados. Cada uno de los enunciados, ejercicios y problemas planteados en los exámenes parciales requerían de una respuesta basada en lo puramente matemático y de un programa, apoyado en programación funcional por razones del contenido de la asignatura “Programación I”, que permitiera que el computador mostrara la respuesta en pantalla. Todos los parciales se hicieron planteando cada punto en el formato de una pregunta y cuatro distractores. Debe anotarse que, cuando se avanzaba nivel en lo que respecta a la programación, también se iba avanzando en el tipo de pensamiento matemático que, en un sentido que provee la perspectiva histórica, evolucionó desde el pensamiento numérico (como primer pensamiento natural del ser humano) hasta el pensamiento variacional (expresión de las matemáticas que prioriza la abstracción como suprema forma de representación de la realidad). Al finalizar el curso correspondiente, siempre se solicitó una opinión escrita y anónima de cada estudiante al respecto de tres temas: a) la metodología utilizada, b) los cinco tipos de pensamiento matemático y c) la programación de computadores paradigma funcional como mecanismo para implementar las soluciones que, teóricamente, proveen las matemáticas.
Resultados
La tabla 2 presenta la cantidad de estudiantes que se involucraron en el proyecto bien desde la aplicación directa de la metodología (grupo que se ha identificado con la letra A) o bien desde la perspectiva de la resolución de los exámenes parciales (grupos que se han identificado con las letras B y C) para tener un comparativo con la metodología tradicional.
Fuente: elaboración propia.
Tabla 2: Estudiantes que participaron
Año
Sem.
Grupo A
Grupo B
Grupo C
2015
I
19
22
21
II
22
25
25
2016
I
21
23
23
II
20
24
23
2017
I
23
22
21
II
22
21
19
Total
127
137
132
Los resultados obtenidos a partir de las entrevistas con docentes y egresados, se han excluido en este artículo para centrar los análisis en lo que se obtuvo con los estudiantes. Dichos resultados serán objeto de otro artículo. Como las pruebas que se realizaron en cada grupo de investigación también se realizaron en otros dos grupos que estaban recibiendo la asignatura “Programación I” con otros docentes y por métodos tradicionales, en la tabla 3 se detalla el promedio de los resultados cuantitativos en cada grupo. En el grupo A se aplicó la metodología que se ha explicado y que inspira este artículo. En los B y C solamente se realizaron las pruebas escritas al margen de cualquier metodología, estrategia o desarrollo que sucediera en su correspondiente grupo de “Programación I”. Por considerarse una medida de tendencia central suficiente para los análisis respectivos, se ha acudido al promedio de las notas por grupo.
Fuente: elaboración propia.
Tabla 3: Promedio de evaluaciones parciales
Año
Sem.
Grupo A
Grupo B
Grupo C
Parte mat.
Parte prog.
Parte mat.
Parte prog.
Parte mat.
Parte prog.
2015
I
4,5
4,3
3,2
3,9
3,2
3,6
II
4,3
4,3
3,4
3,8
3,4
3,3
2016
I
4,2
4,3
3,1
3,7
3,2
3,4
II
4,2
4,6
3,6
3,8
3,3
3,5
2017
I
4,2
4,2
3,2
3,6
3,3
3,4
II
4,3
4,3
3,3
3,6
3,2
3,4
Promedio
4,3
4,3
3,3
3,7
3,3
3,4
Al recolectar las opiniones de los estudiantes, estas se clasificaron en tres grupos: a) opiniones favorables (OF), aquellas que destacaban bondades de la metodología, que expresaban gran identificación de los estudiantes con lo realizado o en donde manifestaban ventajas en la parte matemática o en la de programación; b) opiniones desfavorables (OD), las que no hacían mención a ninguna bondad de la metodología, en las cuales los estudiantes no destacaban nada que les pareciera favorable o en donde el estudiante no destacaba algo diferente a las metodologías tradicionales; c) opiniones neutras (ON), aquellas que no pudieron clasificarse ni como favorables o desfavorables (tabla 4).
Fuente: elaboración propia.
Tabla 4: Clasificación de opiniones
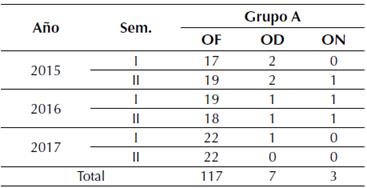
Las opiniones favorables por parte de los estudiantes destacan elementos como la relación entre las matemáticas y la programación, la utilidad de las matemáticas, el significado que adquieren estas cuando se articulan con otras áreas y la facilidad que proveen para expresar de manera universal la posible solución a un determinado problema. Por su parte, entre las OD se destaca la necesidad de profundizar un poco más en la relación entre matemáticas y otras áreas, no solo programación; la necesidad de incrementar el tiempo para estudiar un poco más el vínculo entre matemáticas y programación, y la utilidad que podría tener conformar grupos de trabajo para resolver los problemas, enunciados y ejercicios que se presentaron en las diferentes pruebas parciales.
En cuanto a las ON, se recogieron conceptos como que la universidad era un excelente espacio para la formación profesional, que era muy bueno poder tener contacto con docentes investigadores y que cuando había pasión por las matemáticas o por la programación todo se hacía muy interesante. Como se puede observar, opiniones de este tipo no se pueden clasificar claramente como favorables o desfavorables, por ello se han ubicado en el grupo de las ON.
Discusión
Si bien es cierto que podrían encontrarse diferentes caminos para formar la lógica concibiéndola como el conjunto de reglas y relaciones entre ellas que permiten tomar las decisiones apropiadas dentro de un contexto determinado, posiblemente sean las matemáticas las que mejor ejemplifican esto, por lo cual el objetivo de su estudio intensivo, tanto en la básica secundaria como en los primeros semestres de los programas universitarios, radica en que proporcione las bases para que, a la luz de un lenguaje universal, los estudiantes puedan interpretar, modelar, intervenir, optimizar, mejorar y evaluar el entorno que les rodea, así como simular situaciones que, de otra forma, sería imposible hacerlo. El fortalecimiento de las matemáticas posibilita el desarrollo de un pensamiento científico fundamentado en unos principios y en una forma de escribirlos que son aceptados universalmente.
En un sentido más amplio, las ciencias básicas posibilitan tener más herramientas para aproximarse a la realidad a través del estudio y profundización de áreas de conocimiento como biología, química, física y matemáticas en lo que corresponde a las ciencias duras, y también a través de humanidades, ciencias sociales, estadística y el estudio del arte en lo que corresponde a las ciencias blandas. Todas ellas conforman un corpus académico que le permite al estudiante entender el mundo que lo rodea, intentar modelarlo, intervenirlo y mejorarlo sobre unas bases que posibiliten avizorar situaciones y escenarios futuros sin que se afecte el sistema actual. La inclusión del estudio de las ciencias básicas, y particularmente de las matemáticas, permite que estudiantes de ingeniería entren en contacto con el gran fundamento del conocimiento disciplinar. La pregunta que surge es: ¿Qué tanto sentido tiene para los estudiantes de ingeniería un estudio tan intensivo de las matemáticas si, normalmente, se sumergen más en los procedimientos que en la aplicación y uso de las teorías, modelos y conceptos? Allí la realidad es contundente y efectivamente tanto a nivel de los últimos años de la básica secundaria como los primeros semestres de los programas de ingeniería se encuentra que los estudiantes son conducidos por los caminos de la profundización de procedimientos y muy pocas veces son llevados por la adquisición de sentido a través de la aplicación que esos conocimientos pudieran tener en la vida práctica y en cualquiera de los tres contextos en donde se desenvuelve.
La relación entre los conceptos, teorías y modelos que se adquieren en un aula en el área de las matemáticas y su aplicación en el mundo real es una tarea que, en tiempos modernos, permite que el estudiante puede llegar a ser competente al saber no solo cuáles son los saberes que requiere sino también al manejarlos con experticia y aplicarlos en diferentes situaciones, incluso en aquellas en las cuales no se ha entrenado. El concepto de competencia abre el camino para que los docentes de hoy busquen estrategias que aproximen a los estudiantes, de una parte, al conocimiento específico y, de otra, a su aplicación y sentido que se traduce en su significado. Entre tanto, la programación de computadores se ha ido convirtiendo en una necesidad en todos los programas de ingenierías, pues esta área es un excelente ejemplo de aplicación de lo que puede heredarse de las matemáticas. En su más simple definición, la programación de computadores consiste en el uso de unas reglas lógicas y una sintaxis específica para implementar una solución a un problema determina que puede ser resuelto con la utilización del computador.
La dupla matemáticas/programación, puesta en escena en el desarrollo de una misma asignatura, permite fortalecer cada una de las áreas involucradas y, al tiempo, que ambas se complementen a través de las matemáticas, brindando situaciones y enunciados problémicos que deben ser resueltos bajo la óptica de los cinco tipos de pensamiento matemático, y a través de la programación, implementando todo aquello que se puede resolver con un computador y que, en muchos casos, los incluye. En este sentido, debe anotarse que una experiencia investigativa similar vale la pena tenerla en las asignaturas cuyo contenido temático incluye otros paradigmas, como el paradigma imperativo y el orientado a objetos. De la misma manera, podría pensarse en que se establezcan criterios comparativos en relación con los logros alcanzados en cada asignatura para poder dejar que los datos hablen y llegar a inferencias que orienten el buen uso de los cinco tipos de pensamiento matemáticos en un rango más amplio de análisis.
Particularmente, la experiencia de la programación a la luz del paradigma funcional y su relación con los tipos de pensamiento matemático ha resultado ser de alto beneficio para los estudiantes pues a través de esta estrategia no solo han encontrado mucho sentido a cada situación que se presentan y que pueden ser resueltas con las matemáticas, sino que, escalando de nivel, pueden advertir la presencia de un problema computable y la posibilidad de implementar su solución en un lenguaje funcional como DrScheme.
Otra situación interesante a evaluar desde la perspectiva de la investigación educativa podría ser la relación posible entre los cinco tipos de pensamiento matemáticos y otras áreas de conocimiento, como las ciencias sociales o la biología, por citar apenas dos de ellas, dado que son áreas en donde las matemáticas han aportado mucho y todavía tienen mucho que decir. Para los estudiantes, estas son áreas muy distantes de las matemáticas y valdría la pena investigar si su comprensión puede fortalecerse, como ha sucedido con la programación de computadores, a partir de los nexos que se pueden establecer con las matemáticas.
En cuanto a los resultados obtenidos en las pruebas parciales, al entrar a analizar los promedios presentados en la tabla 3, la valoración cuantitativa es mucho más alta en el grupo con el cual se aplicó la metodología que con los otros dos, a los cuales solo se les solicitó la presentación de las pruebas parciales. Internamente, en el grupo A (sobre el cual se realizó la investigación) siempre se mantuvieron notas muy similares tanto en la parte de las matemáticas como en la parte de la programación teniendo en cuenta que en las pruebas parciales era requerido que se resolvieran ambas partes por diferentes métodos, la parte matemática por métodos puramente matemáticos y la parte de programación a través de la solución implementada en código DrScheme.
De otra parte, puede observarse que los promedios en ambas áreas, con el grupo investigado, son muy similares mientras que en los otros pareciera ser más alcanzable lo que correspondió a la parte de programación de computadores que a la de matemáticas. Aunque no necesariamente esto obedece a que los tipos de pensamiento matemático no estén claros, puede inferirse que es un factor que influye en estos resultados y que, por tanto, debe tenerse en cuenta, pues con ello se confirma el mutuo beneficio entre las dos áreas y el beneficio tanto para el estudiante que es quien está en el proceso de aprendizaje como para el docente que es quien está conduciendo dicho proceso.
Conclusiones
Los resultados tanto cuantitativos y como cualitativos de esta investigación permiten concluir que el buen aprovechamiento de los cinco tipos de pensamiento matemático posibilita el fortalecimiento tanto de otras áreas como de la misma matemática. La programación de computadores, en los primeros cursos, tiene un sentido muy práctico si se relaciona con las matemáticas y se fundamenta en el paradigma de programación funcional que, en últimas, es simplemente una expresión tecnológica del cálculo lambda.
Involucrar a los estudiantes en este tipo de estudios se hace mucho más efectivo y productivo, toda vez que se les dé a conocer todo el proceso, de los logros que se quieren alcanzar y de la manera como ellos mismos pueden verse beneficiados si se alcanzan dichos logros. La comparación con otros grupos y otras metodologías siempre será un mecanismo de validar, corregir y mejorar las estrategias que se estén utilizando dentro de un curso determinado sea que se esté desarrollando una investigación o no.
En este tipo de estudios, abrir espacios de opinión anónimos permite conocer lo que piensan los estudiantes desde una óptica abierta y franca. Si bien los resultados cualitativos no se han presentado en este artículo, por razones de espacio, la cuantificación que se ha hecho de ellos valida lo positivo que fue para los estudiantes la participación en este tipo de investigaciones, los réditos académicos que le quedan y la perspectiva que puede abrirse en otras áreas, si se aprovechan los cinco tipos de pensamiento matemático.
Referencias
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.
