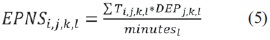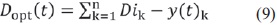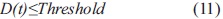DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2013.1.a01Publicado:
01-01-2013Número:
Vol. 17 Núm. 35 (2013): Enero - MarzoSección:
InvestigaciónOptimization of maintenance management of trees in powerdistribution systems
Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Optimization of maintenance management of trees in power distribution systems
Optimización de la gestión de mantenimiento de árboles en sistemas de distribución de potencia
José Alexander Martínez1, Fredy Hernán Martínez S.2
1 Ingeniero Eléctrico. Ingeniero de Codensa S.A. Esp. Bogotá, Colombia. Contacto: jmartinezv@endesacolombia.com.co
2 Ingeniero Eléctrico, candidato a doctor en Ingeniería de Sistemas y Computación de la Universidad Nacional de Colombia. Docente e investigador de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: fhmartinezs@udistrital.edu.co
Fecha de recepción: 12 de abril de 2012 Fecha de aceptación: 27 de noviembre de 2012
Abstract
We propose a data-analysis-based methodology for maintaining trees that affect power distribution networks. From the information captured in the field, we use fuzzy-logic-based techniques and models together with genetic algorithms so as to focus maintenance activities on the optimal time and place. The strategy is aimed at two key aspects: first, the history of failure events caused by trees on medium-voltage power supply systems; this information is used to calculate quality indicators such as energy-not-supplied (ENS) and number-of-users (NU) affected due to falling trees only. In this case we use a fuzzy-logic-based system to weight and find the critical circuits on which forest maintenance should be performed. Second, we construct an objective function based on tree-to-network distances and growth patterns of trees (classifed per species) in order to simulate forest maintenance; this is achieved using a genetic algorithm to determine optimum pruning cycles for a given power supply system. We use real historical data of medium voltage circuits for system setting as well as for performance evaluation.
Key words: fuzzy systems, genetic algorithms, maintenance, power distribution networks, trees.
Resumen
Se propone una metodología basada en análisis de datos para el mantenimiento de árboles que afectan las redes de distribución de energía. A partir de información capturada en campo, se utilizan técnicas y modelos basados en lógica difusa y algoritmos genéticos que permiten focalizar el mantenimiento en el lugar y tiempo óptimos. La estrategia está centrada en dos aspectos clave: primero, el histórico de fallas causadas por árboles en alimentadores de media tensión; esta información es usada para calcular indicadores de calidad (energía no suministrada ENS y número de usuarios afectados NU) debidos únicamente a fallas causadas por árboles. Luego, se utiliza un sistema basado en lógica difusa para ponderar y encontrar los circuitos críticos sobre los cuales debe realizarse el mantenimiento forestal. En segundo lugar, se construye una función objetivo basada en distancias árbol-red, y curvas de crecimiento de árboles por especie con el fin de simular el mantenimiento forestal, usando un algoritmo genético para determinar el ciclo de poda óptimo de un determinado alimentador. Se utilizan datos históricos reales de circuitos de media tensión tanto en el ajuste del sistema como en la evaluación final de desempeño.
Palabras clave: sistemas difusos, algoritmos genéticos, mantenimiento, redes de distribución de energía, árboles.
1. Introduction
The electricity distribution aerial networks may be affected by temporary or permanent contact with trees, at the expense of service quality. This is the reason why distribution companies of electricity in Colombia include forest care in maintenance programs, which entails a large investment.
On behalf of the Colombian government, the Energy Regulatory and Gas Commission (CREG) with resolution 097 of 2008 [1] established the methodology and quality indices ITAD (Grouped Quarterly Index of Discontinuity), IAAD (Grouped Annual Index of Discontinuity), and IRAD (Grouped Benchmark Index of Discontinuity) to which it applies the new scheme of incentives and compensation to users, allowing network operator (OP) increase or decrease their usage charges of connected assets to Local Distribution System (SDL). The aim of this new regulation is to standardize the quality of service around the average quality, i.e. reduce the dispersion of quality improving the indices for the worst users served. The issue of trees takes center stage because the new regulatory philosophy requires improving quality indices in rural areas.
To manage the ITAD part involving the maintenance of networks, i.e., the NTG (Quarterly Level of Discontinuity by Quality Group) component (the part not manageable in maintenance is corresponding to Energy Sales VT, this component is inversely proportional to the ITAD and its management is of commercial nature), we pro-pose an analysis involving only the interruptions caused by trees. In this way, we think that we can identify the circuits with higher energy not supplied and most users affected, parameters that directly affect the ITAD.
Our ideas for the projection of tree maintenance are strongly infuenced by research on maintenance services priority in electrical feeders [2]-[7]. According to these researches, there is a strong relationship between system parameters such as reliability and power quality and environmental parameters such as the vegetation presence, seasonal loading and even vandalism.
To prioritize the circuits, we are first inspired by the power of abstraction used in fuzzy systems [4], [8]-[10]. As is common in many approaches, we use the experience of experts to establish the growth of trees as high impact variable in the failure of circuits in the city of Bogota D.C. (Colombia). Subsequently, we perform a graphical analysis of the hierarchy obtained in order to perform a technical analysis to validate the results.
Our research also wants to find answers to questions that arise once we have found the critical circuits: What trees should I intervene? When should I intervene and how much maintenance costs? These problems have been addressed from different perspectives. One option uses the philosophy of Reliability Centered Maintenance (RCM), based on four principles: best pruning techniques, documentation of the work, training and competence requirements, quality control and auditing [11].
Another approach documented, which is also related to our work, uses a mathematical model based on Artificial Neural Network (ANN) [12], which relates the failure rates of the feeders with variables that affect the nature of vegetation as the ambient temperature, the rain and the time elapsed since the last pruning. A variation of the latter model uses a genetic algorithm (GA) [13], involving variables such as the feeder length, height and growth rates of trees by species, and time of year, giving costs associated with maintenance and estimated ENS. Our research also estimates the optimum time for pruning through a genetic algorithm, which uses models of growth of native trees.
The paper is organized as follows. Section 2 presents preliminary concepts and problem formulation Sections 3 illustrates the methodology of work, details of the prioritization of the circuits and the optimal pruning cycle. Section 4 presents the behavior of the methodology developed and Section 5 concludes the paper.
2. Problem formulation
Let W⊂R be the closure of a contractible open set in the line that has a connected open interior. Let P⊂W be the priority values assigned to the prioritization of the circuits, which is the open subset of W. Let E⊂R be the closure of a contractible open set in the line that has a connected open interior. Let EPNS⊂E be the average energy not supplied for a given breakdown, transformer and circuit, which is the open subset of E. Let N⊂R be the closure of a contractible open set in the line that has a connected open interior. Let NU⊂N be the number of users affected for a given breakdown, transformer and circuit, which is the open subset of N. The prioritization model depicted in Figure 1 is obtained by a prioritization mapping of the form:
In which:
We define 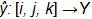 be the priority assignment that is obtained from
be the priority assignment that is obtained from  by applying fuzzy inference for a given interruption i, transformer j, and circuit k.
by applying fuzzy inference for a given interruption i, transformer j, and circuit k.
Let Z⊂R be the closure of a contractible open set in the line that has a connected open interior. Let C⊂W be the maintenance cost values assigned by a process of uninformed search of the optimal cost, which is the open subset of Z. Let M⊂RxR be the closure of a contractible open set in the space that has a connected open interior. Let Mn⊂M be the information matrix for n trees in a given circuit encoding: the tree ID, the cost code, the species code and the Di, which is the open subset of M. Let K⊂R be the closure of a contractible open set in the line that has a connected open interior. Let NC⊂K be the circuits to be considered for forest maintenance, which is the open subset of K. The optimization model depicted in Figure 2 is obtained by an optimization mapping of the form:
In which:
We define 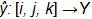 to be the valuation of cost of maintenance that is obtained from by applying genetic search for a given circuit k.
to be the valuation of cost of maintenance that is obtained from by applying genetic search for a given circuit k.
3. Methodology
The first part of the analysis establishes a maintenance priority for each network circuit of medium voltage, from a "measure"; of criticality due to forestry events. The second part of the analysis is that once are identifed the most critical circuits, we analyze the characteristic of them in order to define a period of pruning, a quantity of pruning, and a stable budget for each feeder.
3.1 Prioritization of Circuits
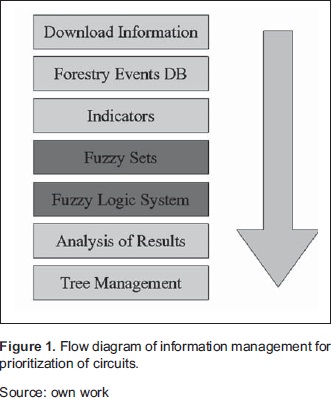
The prioritization of the circuit begins with downloading and debugging information from the unifed system information registry from the network operator (OR). We only retrieve information related to forestry events, taking into account the events for transitory faults, permanent faults, circuits associated with events, duration of interruptions, customers affected by transformer and transformer energy demand (Figure 1).
With the downloaded information, we implement a forestry database to calculate the indicators EPNS (not included in the Equation 5 the load factor) and the NU. These are the input data that feed the fuzzy logic systems, system which is responsible for prioritizing the circuits. This calculation should be performed by transformer, circuit and period.
EPNS variable is defined as the average energy not supplied due to the interruption i, for the transformer j, circuit k, in the period l. This variable is calculated as:
Where:
Ti,j,k,l is the duration in minutes of interruption and DEPj,k,l is the average energy demand.
Similarly we calculate the sum of users affected NU, as the number of users affected by interruption i, transformer j, circuit k, in period l.
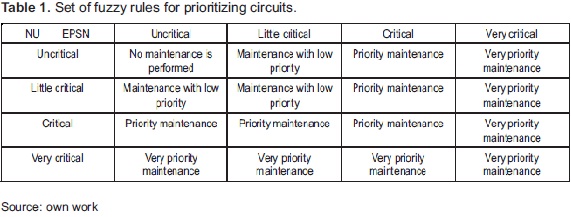
Both the system output variable, priority P, as input variables EPNS and NU, are associated with linguistic variables defines fuzzy sets. An overview of rules that govern the inference engine is illustrated in Table 1.
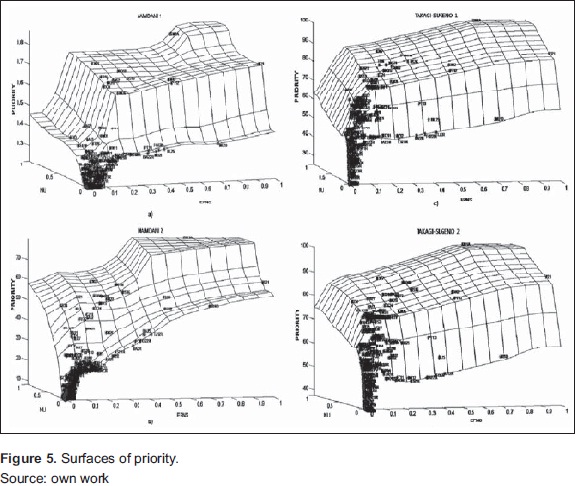
The prioritization performed by the fuzzy logic system can be visualized as a 3D surface where X and Y axes correspond to the inputs and the Z axis to the output. We evaluate the prioritization using both Mamdani as Takagi-Sugeno inference, using different sets of rules. In Figure 5 we show the result of four of these exercises.
The fuzzy logic system provides the possibility of periodic monitoring of indicators of critical circuits on which it is applied preventive and corrective measures. Graphically speaking, we expect that all circuits tend to come together at the lower part of the surface with the majority of the population.
3.2 Optimal Pruning Cycle
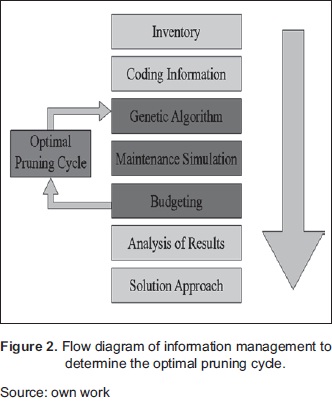
At this stage we process the information collected in the field, which corresponds to forest inventories conducted for each feeder. The inventory information is entered into a genetic algorithm (GA), and so we get a curve that describes the optimal pruning cycle (CPO) and the budget.
Among the most important data that contains an inventory are: location of tree, species, physical condition, health, geographical coordinates, height, diameter at breast height (DAP), plate identifcation, intervention performed (pruning or felling) and a photographic record for each individual. From this database, in our research, we use for the optimization process the following data: identifcation plate, height, species, and tree-network distance (distance between the medium voltage network and the nearest point of the tree).
The time between pruning done at the same tree is called pruning cycle (CP). The optimal pruning cycle is then the optimal time that should elapse between forest maintenance performed on a circuit, in order to minimize the possibility of contact between the trees and the medium voltage network and thus minimize service interruptions.
The analysis methodology is summarized in Figure 2. The inventory information is encoded in a matrix. This matrix is composed of n rows representing the number of trees, and four columns that correspond to the parameters: Tree ID, Cost code, Species code, and Di.
The ID identifes a unique tree The Cost code is the cost of pruning the tree according to his height. We assign to this parameter three possible values: 0, 1 and 2. Thus, 0 corresponds to a height of less than 7 m, 1 is to a height between 7 m and 15 m, and 2 correspond to greater heights. The species are coded with values from 0 to 18. Finally, Di is the initial tree-network distance in cm.
We handle a total of 19 native species to the savannah of Bogota. The growth curves for these species were determined by previous research [14]. That research describes the cumulative growth of trees after having been subjected to pruning. With this information, we can simulate the implementation of forest maintenance, and in this way, we can make the performance evaluation of the genetic algorithm.
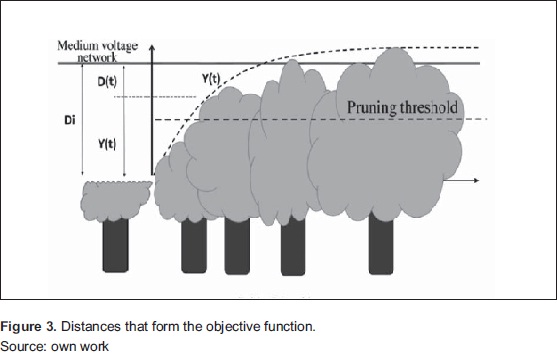
We build the objective function to minimize from two elements: the tree-network distance coming from the inventory, and growth models by species (Figure 3) We define three distances:
- D(t)= Distance to optimize [cm].
- Di= Initial distance [cm]. It's the same treenetwork distance.
- y(t)= Cumulative growth [cm] of the tree in time t [days] This depends on the growth function of each species.
- Pruning threshold. Is the distance that serves as a criterion to discriminate between trees should be pruned and which should not be pruned.
The optimum distance for an individual tree is defined as the distance difference between initial and cumulative growth. Thus, Equation 6 attempts to find the maximum time t to wait for pruning, i.e., the time at which the distance D is equal to or approaching zero.
Negative values of D in Equation 6 (when y(t)>Di) are produced by the growth of a tree which is already higher than the desired value, that is, greater than the tree-network distance found in the inventory. Accordingly, the optimal distance should not have negative values, therefore:
Equation 8 is the constraint equation to optimize D without getting negative values.
Since along an air electricity network there are a certain number of trees of different species and heights, it is necessary find, not the cycle of pruning each tree but the best pruning cycle which can perform general maintenance. For a number n of trees, the objective function (FO) is defined as the sum of distances D for all trees in the inventory, namely:
Likewise, for a number n of trees, we define n constraint equations as follows:
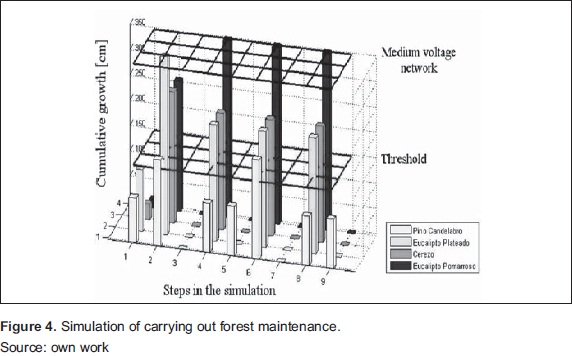
The simulation of maintenance is shown in Figure 4 From this figure it can analyze the behavior by individual or species according to the cumulative growth. The process happens at each step corresponds to:
1. We recorded the distance Di in the inventory as found in the field
2. In the first Pe the growth y(t) is calculated and subtracted to Di (Equation 9). Then it is estimated that trees are within the threshold of pruning, i.e.:
3. Then we assume that necessary pruning are performed by assigning a new value of Di (for this example of 350 cm) for those trees whose cumulative growth is within the threshold, according to the value previously set. The new value of Di for trees that are not within threshold, D(t) is the same as calculated above, i.e.:
4. Then we repeat the three previous steps as the number of cycles to simulate, according to a previously defined value.
Finally, we obtain curves that describe the CP characteristic of the circuit and the amount of pruning performed in each cycle. On these graphs, we analyze the execution time of maintenance and the number of individuals to intervene. The cost of maintenance in each CP value is calculated according with the pruning of costs according to the Cost Codeassociated with each tree. Note that this budget is the minimum required in each CP to minimize the possibility that some trees generated outages. The methodology concludes with an analysis of the data obtained from the simulation and proposals for solution in accordance with the analysis.
4. Results and performance
We prioritize the circuits first introducing to the fuzzy logic system the historic events for the year 2009 for all unplanned events caused by trees, in the medium-voltage circuits, in the area of infuence of Bogota and the neighboring municipalities of the savannah. In the upper surface of Figure 5 are the most critical circuits, and is a clear priority among them. By contrast, in the bottom of the figure is the majority of the population.
It is obvious that the modifcation of rules and fuzzy sets directly affects the way the system prioritizes the circuits, but this becomes visible when comparing the four graphs. We work the two Mamdani systems with three fuzzy sets in the output. The design difference between them is that it has changed the core and the boundary of the input fuzzy sets, and the scale priority. With these changes the output is a bit more uniform and hierarchy between priority circuits is more visible.
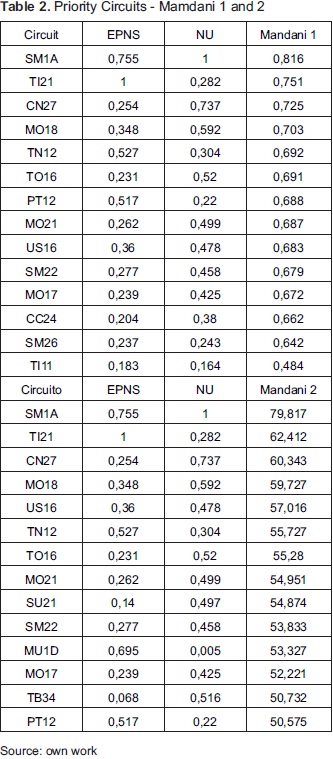
The first system ranks the 44% of the population, while the remaining 56% were grouped in the bottom of the graph with the same priority value. With the second Mamdani system we ranked 95% of the population and only 5% share the same value. We also changed some rules to give more priority to circuits with a very high rate relative to the other; the effect of this is seen in Table 2.
Mamdani's 2 ranking is achieved include circuits that were not previously but which deserved more priority characteristics, this is the case of circuits SU21, MU1D and TB34 By analyzing their indicators, we can observe that they have industrial customer profile, i.e., high consumption and low users, or otherwise, many users and low consumption. Both cases are of concern, both for the profile and by eolombian regulatory framework Importantly, if sales of energy are low in proportion to the number of users, the ITAD increases.
In the figure, these customers tend toward the ends, which is very useful because it displayed sectors in that are grouped circuits with special characteristics. Another example of this is in the bottom-right edge of the surface, where they have been located some 34,5 kV circuits (suffx R) These circuits are also very important because although they have few users, the service of substations or industrial customers depends on them, hence the EPNS is high. While some of them are not included in the ranking, view them may be useful as a warning flag.
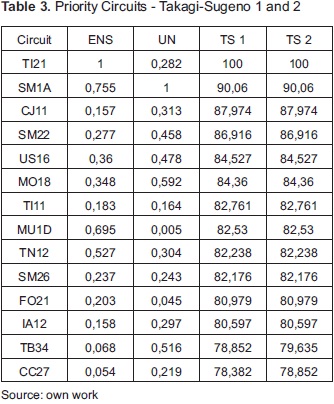
Figure 5(c) and 5(d) correspond to two Takagi-Sugeno systems with four fuzzy sets in the output. The most obvious difference compared to Mamdani systems is that the surface is uniform, i.e., the prioritization is more uniform. The organization along the z axis is more vertical; consequently, there is a better distribution of the data range In the first case, an 83% of the data were ranked completely, while in the second an 85%. As in the previous comparison, the second case has a change in the rules to give some importance to circuits with extreme indicators; however, this is not visible in the ranking of the most important because in the high hierarchy not there were differences.
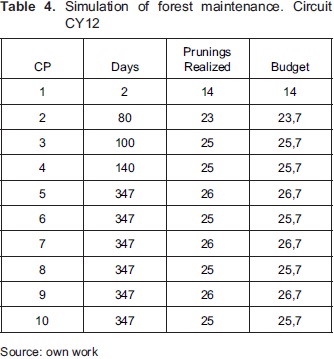
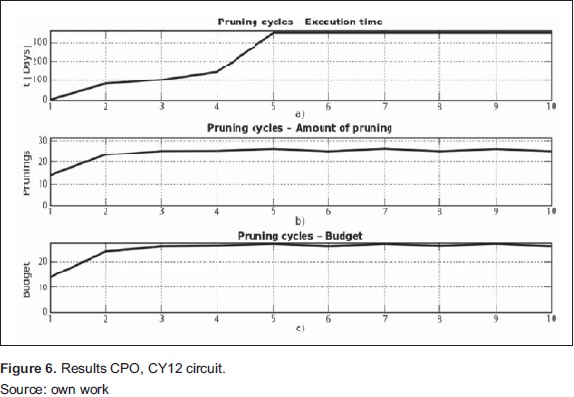
To evaluate the optimal pruning cycle, we use a forest inventory of 2009, of the circuit CY12 code, which contains 27 trees distributed in six species: Acacia Melanoxylum, FicusAndicola, PrunusSerotina, CupressusLusitanica, Eucalyptus Globulus and Salix Humboldtiana. According to information processing detailed in Figure 2 we coded the information with the following parameters: threshold = 200 cm, Di = 400 cm, CP = 10. The results are shown in Table 4.
According to the simulation, the first maintenance is performed in the very short term, but this time gradually increased until a point of stability. In the same way it happened with the amount of pruning, stabilizing between 25 and 26 pruning per CP.
To simulate the maintenance cost, we assume values to the type of pruning: Code 0 costs 0.9, Code 1 costs 1, and Code 2 costs 1.4. By optimizing the amount of pruning is also optimized the budget Figure 6.
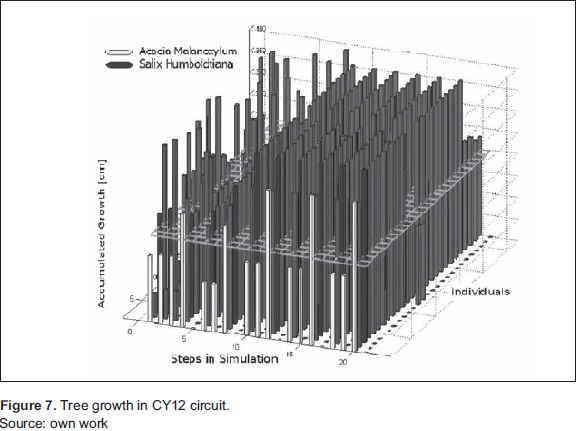
Figure 7 shows the behavior of the trees along the simulation In this figure highlights two individuals whose growth contrasts, the growth curve of the Salix Humboldtiana, is faster than the curve of Acacia Melanoxylum. The red stripe passes the threshold in all cycles of pruning, so the tree should be pruned in all cycles of pruning. On the other hand, the yellow stripe passes the threshold in only five times This last individual never reaches the maximum point. The pruning cycle period depends on the individual faster.
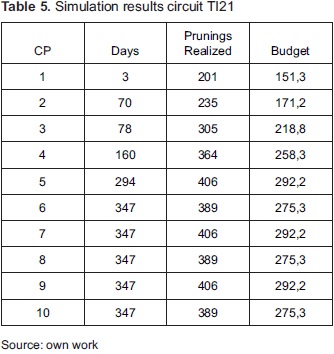
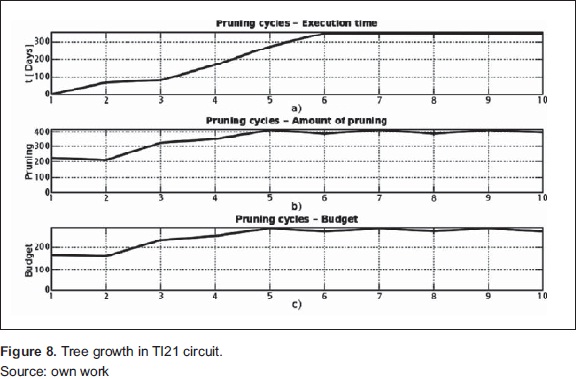
To verify the performance of the algorithm with more data is entered TI21 circuit inventory, which is among the most critical, according to initial weighting The exercise is performed with 463 individuals, which are divided into eleven species. The results are shown in Table 5 and Figure 8. In this case, the number of trees was not inconvenient to find a point of stability.
The last methodological block is the approach to solutions. For this it is necessary to propose alternatives that emerge as the analysis of the simulated results, as a technical analysis of the design conditions of the medium voltage network, geography, and individual trees. Some possible solutions found are:
- Identify the optimum time of pruning, when the best solution is to simply perform pruning along the circuit.
- By combining the analysis of CP with the location of individual trees along the network, we can identify sectors in which take technical measures to mitigate the indicators and/or extend the CP.
- It is possible to identify individuals whose management tree is not expensive or complicated, in exchange for extending the CP, such as cuttings, transportation network, replacement of species, and the other coming from each particular case.
5. Conclusions and future work
In this paper we apply fuzzy logic techniques to design a tool that would guide the management of trees in medium voltage networks globally. This tool also allows grouping, view and track circuits according to the linguistic qualifers that denote key technical criteria in the management of maintenance, additionally considering the quality indicators established by the regulator. From a specifc point of view, we find that there is a stable pruning time for all trees that affect a circuit, despite the diversity of species and the uneven growth of these.
The methodologies proposed, but from real data, are purely theoretical and the nature of the problem require monitoring for at least the medium term. The prioritization of circuits must be a periodic process that evidences the effectiveness of the maintenance performed, and the projection of the indicators of the circuits. Similarly, analysis of the optimal CP requires monitoring and fee dback both growth curves used and the pruning to be done. For the application of the integrated methodology we propose:
- Pilot tests should be performed for implementing and monitoring of maintenance, allowing for adjustment of the growth curves either by mistake or in the model including environmental factors such as humidity, temperature, soil conditions, time of year and in general any other factor affecting the growth of trees. Here we take into account the follow any technical measure applied and its impact to the CP.
- Should be continued the work in [14], developing the cumulative growth curves for species that have not yet.
- Should be design and implement a fuzzy logic system as proposed in this research, but allows prioritizing circuits using all possible causes of failure.
Referencias
[1] Comisión de Regulación de Energía y Gas (CREG), Resolución 097 de 2008", 2008. [Online]. Available: http://www.creg.gov.co
[2] P. Hilber and L. Bertling, "Multiobjective maintenance policy for a distribution system an application study", Proc. 10th Int. Conf. Probabilistic Methods Applied to Power Systems PMAPS 2008, pp. 1�6, 2008.
[3] I. G. Torne and S. L. Choy, "Considerations about the maintenance in electrical networks", Proc. IEEE Russia Power Tech, pp. 1�3, 2005.
[4] L. Canha, A. Abaide, F. Farret, E. Daza and G. Cassel, "Automatic priority of the maintenance activities in distribution systems using multicriterial analysis and fuzzy techniques", Proc. Int. Conf. Power Engineering, Energy and Electrical Drives POWERENG 2007, pp. 237-242, 2007.
[5] J. J. Tian, "Research on the maintenance strategy of electrical supply equipment based on rcm", Proc. Int Information Management, Innovation Management and Industrial Engineering (ICIII) Conf, Vol. 1, pp. 105-108, 2010.
[6] G. Parise and L. Martirano, "System management strategy to monitor insulated power cables", Proc. 39th IAS Annual Meeting Industry Applications Conf. Conf. Record of the 2004 IEEE, Vol. 3, pp. 1755-1759, 2004.
[7] J. A. Wischkaemper, C. L. Benner, and B. D. Russell, "Electrical characterization of vegetation contacts with distribution conductors-investigation of progressive fault behavior", Proc. T&D Transmission and Distribution Conf. and Exposition IEEE/PES, pp 1-8, 2008.
[8] M. A. Awadallah and M. M. Morcos, "Application of ai tools in fault diagnosis of electrical machines and drives-an overview", Vol. 18, No. 2, pp. 245-251, 2003.
[9] B. Nemeth, S. Laboncz, and I. Kiss, "Condition monitoring of power transformers using dga and fuzzy logic", Proc. IEEE Electrical Insulation Conf. EIC 2009, pp. 373-376, 2009.
[10] K. V. Kumar, S. S. Kumar, B. Praveena, J. P. John, and J. E. Paul, "Soft computing based fault diagnosis", Proc. Int Computing Communication and Networking Technologies (ICCCNT) Conf, pp. 1-7, 2010.
[11] M. F. Ariffin, "Advances and challenges in mitigating tree-related faults in TNB distribution network", Proc. th Int Advances in Power System Control, Operation and Management (APSCOM 2009) Conf, pp. 1-6, 2009.
[12] D. T. Radmer, P. A. Kuntz, R. D. Christie, S. S. Venkata, and R. H. Fletcher, "Predicting vegetation-related failure rates for overhead distribution feeders", Vol. 17, No. 4, pp. 1170-1175, 2002.
[13] A. V. Liliani, and J. R. Sanches, "Modelo de programacao matematica para controle do crescimento da vegetacao sob redes de distribuicao de energía eléctrica", Sba Controle & Automacao Sociedade Brasileira de Automatica, Vol. 22, pp. 284-295, 2011.
[14] T. Contreras and D. K. Rojas, Modelacion del crecimiento de quince especies arbóreas que interfieren con redes electricas de media tensión en Bogota luego de ser sometidas a podas, [Master's thesis], Distrital University, 2010.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.