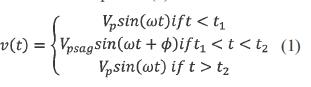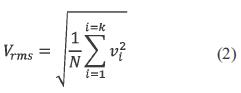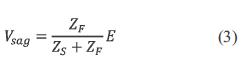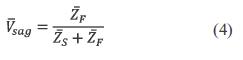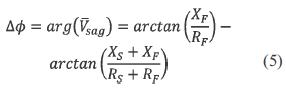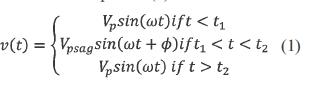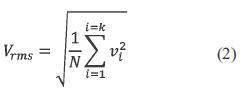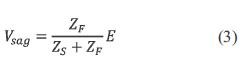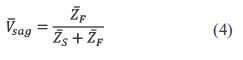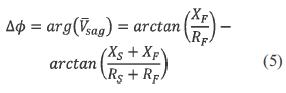DOI:
https://doi.org/10.14483/22487638.7234Published:
2013-09-18Issue:
Vol. 17 (2013): Special EditionSection:
ResearchSimulation of Voltage Sag Characteristics in Power Systems
Simulación de las características de los huecos de tensión en sistemas de potencia
Keywords:
Matlab/Simulink, Protection system, Power system fault, Voltage sag (es).How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Simulation of voltage sag characteristics in power systems
Simulación de las características de los huecos de tensión en sistemas de potencia
Joaquín Eduardo Caicedo Navarro1, Luis Felipe Navarro Julio2, Edwin Rivas Trujillo3, Francisco Santamaría Piedrahita4
1Student of electrical engineering of Distrital University Francisco José de Caldas,
Electromagnetic Compatibility and Interference Group GCEM. Bogotá, Colombia. Contact: jecaicedon@correo.udistrital.edu.co
2Student of electrical engineering of Distrital University Francisco José de Caldas,
Electromagnetic Compatibility and Interference Group GCEM. Bogotá, Colombia.
Contact: lfinavarroj@correo.udistrital.edu.co
3Electrical engineer, Ph.D. in Engineering. Profesor at the Distrital University
Francisco José de Caldas, Electromagnetic Compatibility and Interference Group
GCEM. Bogotá, Colombia. Contact: erivas@udistrital.edu.co
4Electrical engineer, Ph.D. candidate in Engineering. Profesor at the Distrital University
Francisco José de Caldas, Electromagnetic Compatibility and Interference Group GCEM. Bogotá, Colombia. Contact: fsantamariap@udistrital.edu.co
Fecha de recepción: 7 de abril de 2012 Fecha de aceptación: 16 de octubre de 2012
Abstract
This paper describes a methodology for voltage sag characterization using Matlab/Simulink. It includes single-phase and three-phase fault simulations in different power systems for voltage sag magnitude calculation using Simulink, based on the SimPowerSystems toolbox, and also considering electrical protection-systems modeling for sag duration calculation. Other sag characteristics, such as phase-angle jump and shape, are described and simulated.
Key words: Matlab/Simulink, protection system, power system fault, voltage sag.
Resumen
Este artículo describe una metodología para caracterizar un hueco de tensión usando Matlab/ Simulink. Se incluyen simulaciones de fallas trifásicas y monofásicas en diferentes sistemas de potencia usando Simulink, con base en el paquete de software SimPowerSystems, considerando el modelado de los sistemas de protección eléctrica para calcular la duración de un hueco de tensión. Otras características, como el salto de ángulo de fase y la forma del perfil de tensión, son descritas y simuladas.
Palabras clave: falla en el sistema de potencia, hueco de tensión, Matlab/Simulink, sistema de protección.
1. Introduction
Voltage sags are considered one of the most harmful power quality problems, because they affect the proper operation of several types of end-user equipment. This phenomenon is a short-duration reduction in rms voltage caused by events such as power system faults, load variations and the start of large induction motors [1].
The most common cause of voltage sags is the fow of fault current through the power system impedance to the fault location. Hence, power system faults in transmission or distribution can affect respectively a large or small number oficustomers. A fault in a transmission line affects sensitive equipment up to hundreds of kilometers away from the fault [2]. In both, transmission and distribution, voltage sags due to faults in parallel feeders, produce incorrect operation of industrial customer equipment [3]. Thus, in this paper a system fault in a parallel feeder is simulated for voltage sag characterization.
Large induction motors, which are widely used in industries, can also cause voltage sags [4]. In this case, voltage sags are characterized by the non-rectangular shape caused by the increase of the motor starting current. In this paper, the start of an induction motor is also simulated to study the shape of voltage sags.
Magnitude, duration, phase-angle jump and shape define voltage sags. To obtain these characteristics it is necessary to consider the power system performance during the event occurrence (system fault, the start of a large induction motor, load variation, etc.). Generally, real data of power system performance are not available for educational or research purposes, hence, simulation tools are required.
In this paper, voltage sags are characterized using the Sim Power Systems toolbox of Matlab/ Simulink. The simulated scenarios are: system faults, protection systems, phase-angle jump and the start of induction motors.
2. Definitions
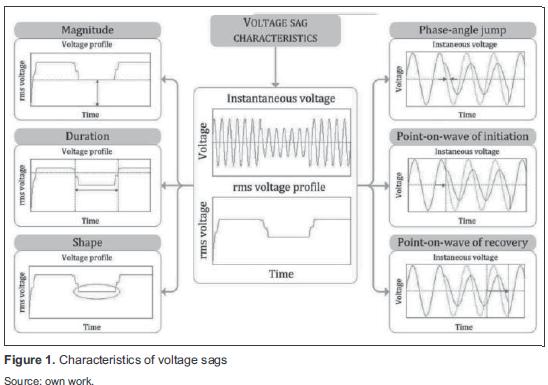
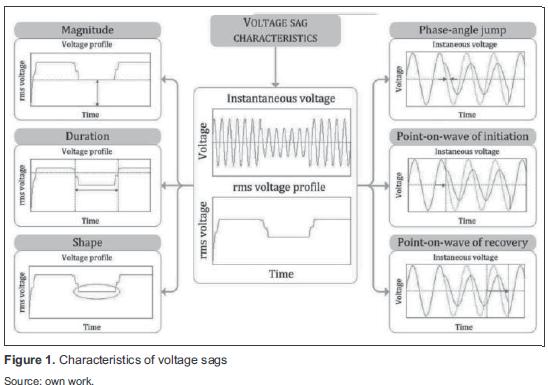
In this section, the definition of voltage sag and its main characteristics are presented (figure 1):
- Voltage sag: A decrease to between 0,1 and 0,9 pu in rms voltage or current at the power frequency for durations of 0,5 cycle to 1 min [5].
- Magnitude: The lowest rms value of the voltage during a voltage sag [1].
- Duration: The time during which the rms value of voltage is under the threshold (0,9pu) [1].
- Phase-angle jump: The difference between the phase-angle of the voltage during an event and the phase-angle of the voltage before the event [1].
- Shape: It defines the behavior of the rms voltage profile during voltage sags. According to their shape, voltage sags are classified as rectangular (rms voltage value is constant) and non-rectangular (rms voltage value varies) [6].
- Point-on-wave of sag initiation: The phaseangle of the fundamental voltage wave at the instant of sag initiation [1].
- Point-on-wave of voltage recovery: The phase-angle of the fundamental voltage wave at the instant of voltage recovery [1].
- Pre-fault voltage: Voltage value during an interval ending with the inception of a fault [1].
3. Methodology
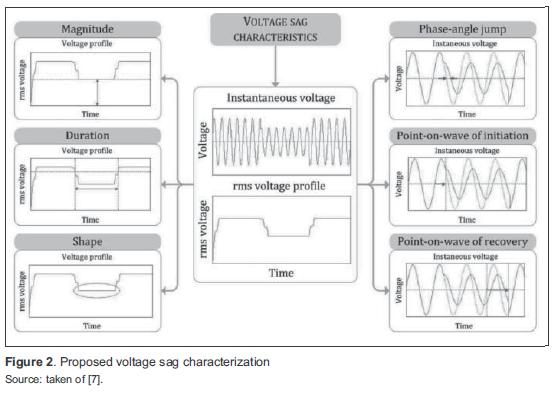
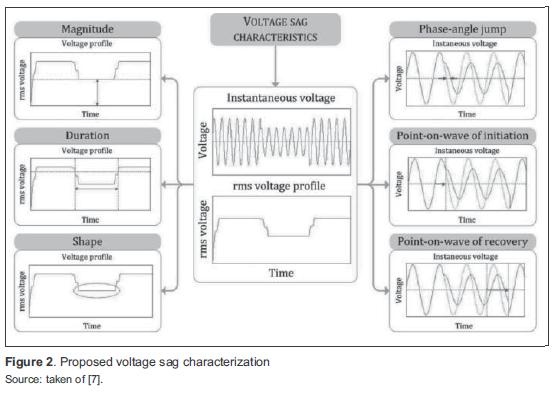
Voltage sag characterization consists in defining and quantifying the most relevant parameters of this disturbance, such as: magnitude, duration, phase-angle jump and shape. Specific scenarios, in a given power system, are studied by using simulation tools to determine and quantify the parameters of interest, according to the following criteria [7]:
- Sag duration depends on fault clearing time provided by the electrical protection in a power system. It can be determined by simulating electrical protection behavior when dealing with system faults.
- Magnitude and phase-angle jump depend on fault location and line impedance. They can be determined at different nodes of a power system by simulating system faults.
- Voltage profile shape is another characteristic taken into consideration. Non-rectangular sags can be studied by modeling and simulating the start of large induction motors in power systems.
Different scenarios for voltage sag characterization are simulated using Matlab/Simulink. figure 2 summarizes the proposed procedure for characterizing voltage sags.
3.1 Sine and rms functions
A voltage sag can be represented using a function defined by parts, based on its most important characteristics as equation (1).
where:
Vp: Peak pre-fault voltage
ω: Angular frequency
Vpsag: Peak voltage during the sag
Φ: Phase-angle jump
t1: Time of sag initiation
t2: Time of voltage recovery
Δt= t1-t2: Duration (8,33 ms<Δt< min
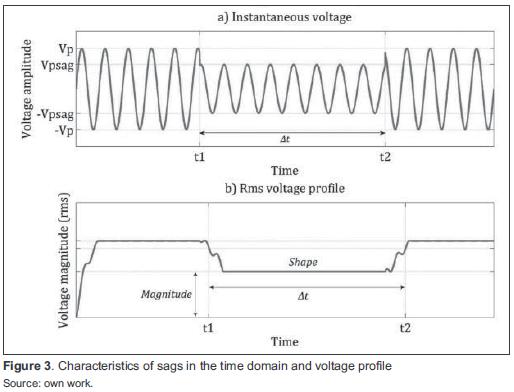
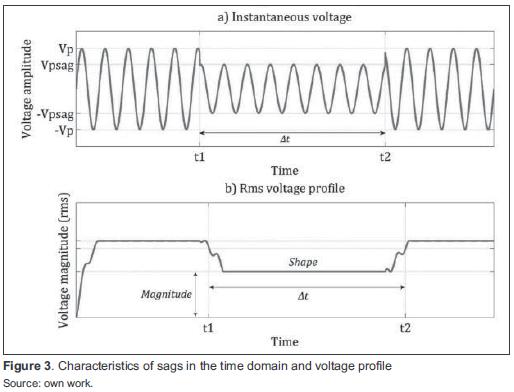
Voltage sag can be represented by sinusoidal function and rms voltage profile (figure 3).
RMS value is calculated from the sine wave voltage with equation(2) [1].
where:
N: Number of samples per cycle
vi: Sampled voltages in time domain
For the simulations the sample frequency used is 15,36 kHz, or N = 256 samples per 60 Hz cycle.
3.2 Theoretical calculation of magnitude
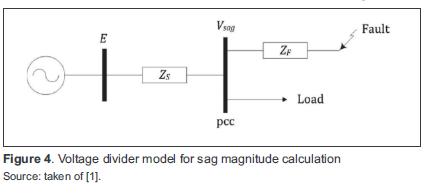
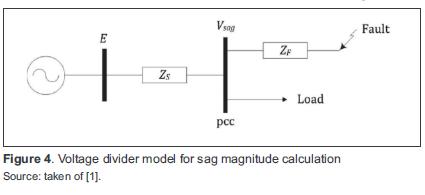
Figure 4 shows a basic model for calculating the magnitude of voltage sag during a three-phase fault on a radial system.
The current through the load before and during the fault is negligible, thus the voltage at the pcc is calculated with equation(3).
where:
ZF: Feeder impedance (between pcc and the fault point)
ZS: Source impedance (between the source and pcc)
E: Source voltage
3.3 Duration and power system protection
Sag duration corresponds to the period of time during which the protective equipment allows fault current to fow. There are several types of protective equipment in the power system and each one has a minimum fault clearing time. Additionally, a delay for protection coordination must be included. In the case of temporary faults, some of the protective devices have a reclose function to restore service within a short time [8].
Transmission system faults are cleared faster than distribution systems faults [1]. In transmission lines, distance relays and differential relays are fast-acting, while in distribution networks, overcurrent protection typically requires higher delays for protection coordination. An exception in distribution systems is the use oficurrent-limiting fuses which act faster (half a cycle) [8].
3.4 Phase-angle jump theoretical calculation
The voltage divider model in figure 4 can also be used for theoretical analysis of phase-angle jump, considering ZS and ZF as complex quantities, denoted asand. Using per-unit calculation, namely the voltage source E = 1, Equation (3) is rewritten as equation (4).
whereand ZS = RS + jXS and ZF + jXF. The argument of Vsag, equivalent to the phase-angle jump, is given by equation (5).
If (XS / RS) = (XF / RF), ΔΦ would be zero and there would be no phase-angle jump. Hence, phaseangle jump only occurs if the X/R ratios of source and feeder are different.
4. Results
4.1 Magnitude simulation and results
The voltage sags due to power system faults simulated are compared with the ones presented in [8] and [9]. In those papers, the voltage sags caused by faults in parallel feeders are studied, including the effect of power system protections.
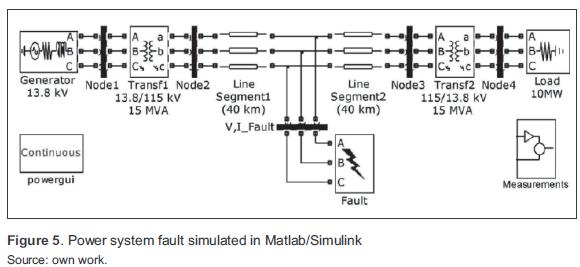
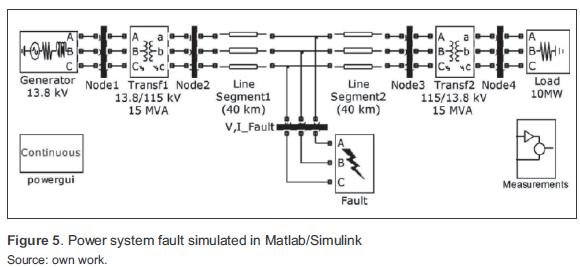
Models of the main components of power systems: generators, transformers, motors, transmission lines, loads, switches and measuring systems are included in the Matlab/Simulink software package. figure 5 shows a power system underground fault conditions simulated in Matlab/(4) Simulink used in this paper.
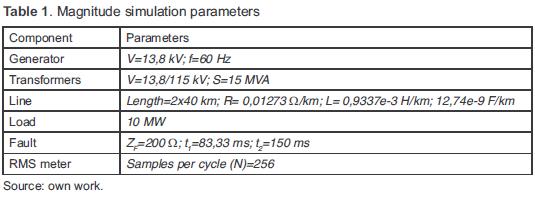
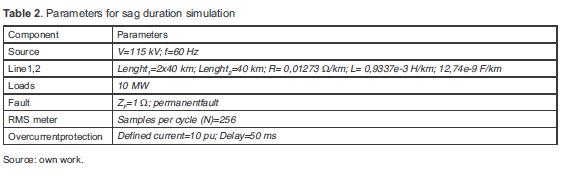
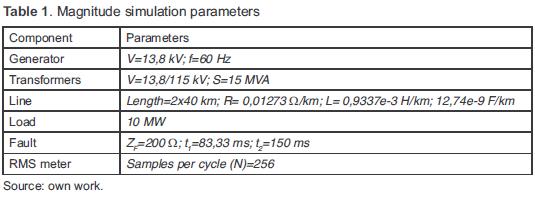
The system includes a 13,8 kV power generation center, a 15 MVA transformer to increase the voltage up to 115 kV and an 80 km transmission line. Then, a 15 MVA transformer reduces the voltage to 13,8 kV to feed a 10 MW load in the distribution system. Measuring systems display voltage and current signals at the system nodes. Two scenarios were simulated: a three-phase fault and a single-phase fault occurred in the middle of the transmission line (40 km from the transformation center). Table 1 summarizes the parameters for sag magnitude simulation.
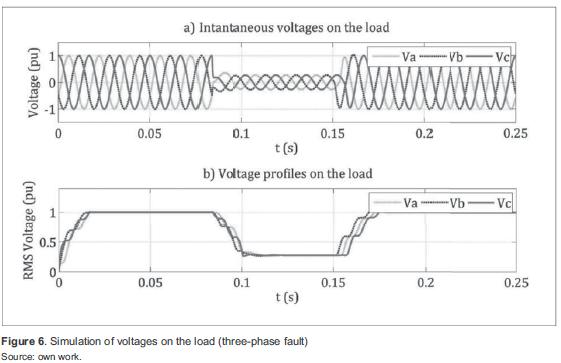
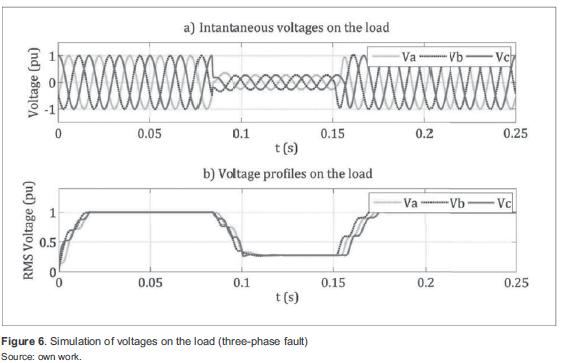
Figure 6 shows the three-phase fault simulation results, a) three-phase sine wave with its magnitude in per-unit, b) rms voltage profiles. A 0,25pu three-phase voltage sag occurred as a result of the fault. The sag duration was 4 cycles at 60 Hz.
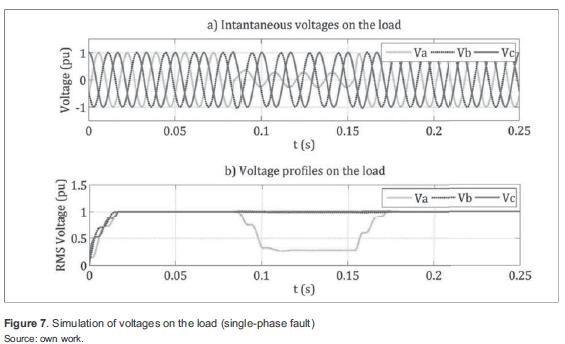
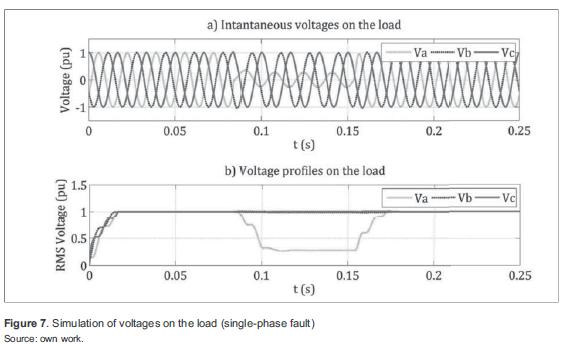
Results of the single-phase fault simulation are shown in figure 7. In this case, a 0,25pu voltage sag as a result of a fault is observed. In both cases, signals were recorded in the Node4 (see figure 5), to show the effect of faults on the load.
4.2 Simulation of voltage sag duration and results
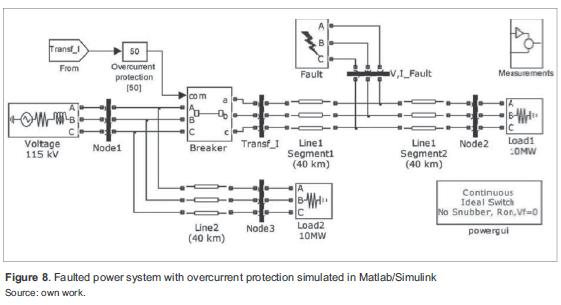
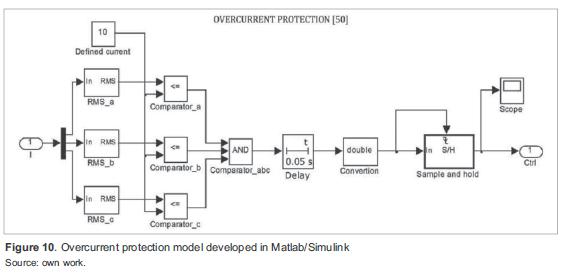
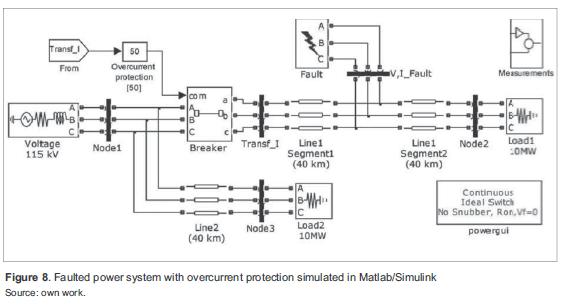
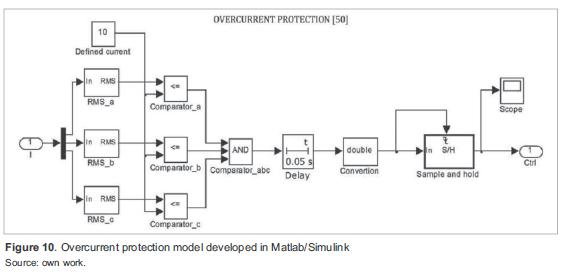
Building models of electrical protection devices on Matlab/Simulink is necessary for simulations, because this tool does not include those models. A power system was simulated with overcurrent protection (figure 8), because this is the most widely used relay (function 50, according to ANSI) [10].
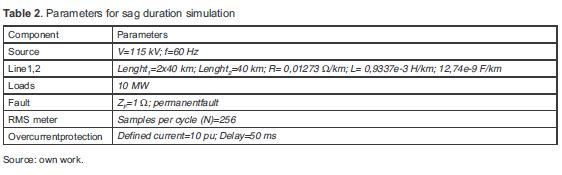
The simulated system consists of two 115 kV parallel transmission lines, with a length of 80 km (line 1) and 40 km (line 2). Each line feeds a 10 MW load (loads 1 and 2 respectively). This simulation presented a solid and permanent three-phase fault to ground in the middle of line 1, which produce an interruption on load 1 and a decrease in voltage on load 2. Two scenarios were simulated for the described case: without overcurrent protection and with overcurrent protection. Table 2 summarizes the parameters for duration simulation.
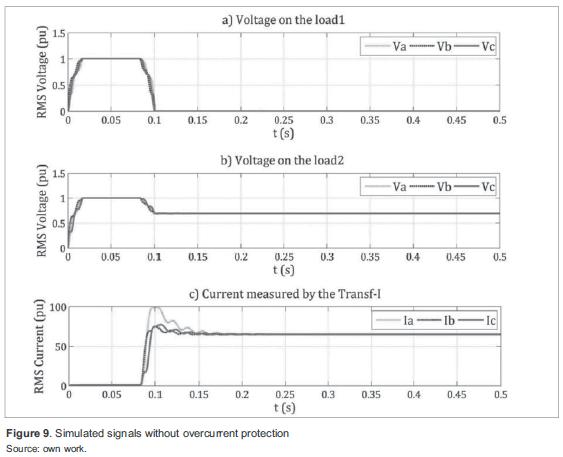
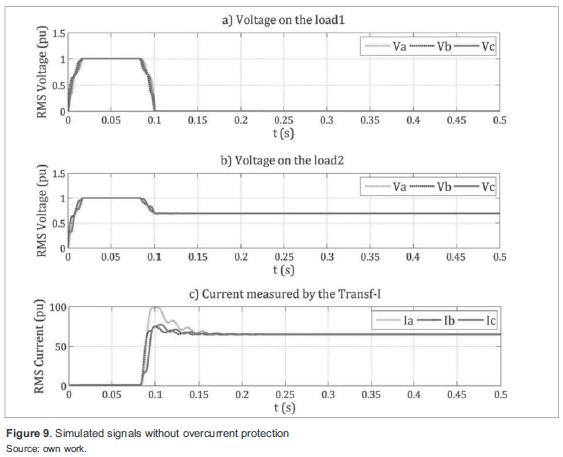
Figure 9 shows the simulation results of the first scenario. In a) an interruption occurs on load 1 as a result of the fault; in b) voltage on load 2 drops to 0,7 pu; and in c) the peak current measured at the faulted line is 100 pu and stabilizes at 65 pu, it is evident a permanent fault.
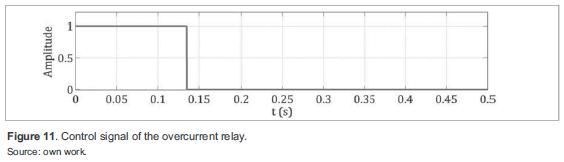
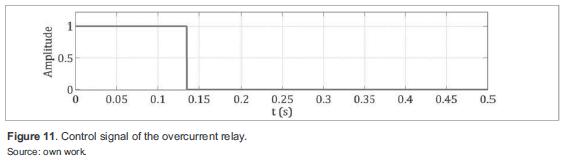
For the second scenario, an overcurrent protection model was implemented in Matlab/Simulink (figure 10). In the model, rms phase currents are compared with a defined current in pu, which represents the protection activation threshold (if any of the phase currents exceeds the threshold, the protection is activated). The model includes a delay for protection coordination as well as for reducing the probability of incorrect operation. figure 11 shows the control signal of the overcurrent relay. When the signal is true, the associated breaker is closed (protection off), hence, the protected line remains energized. When the control signal is false, the breaker is open (protection on) and de-energizes the line to isolate the fault point. Initially, the overcurrent protection detects when the current is ten times greater than nominal (85 ms) and changes the state after the specif ed delay (50 ms in figure 10), thus opening the breaker to isolate the fault point.
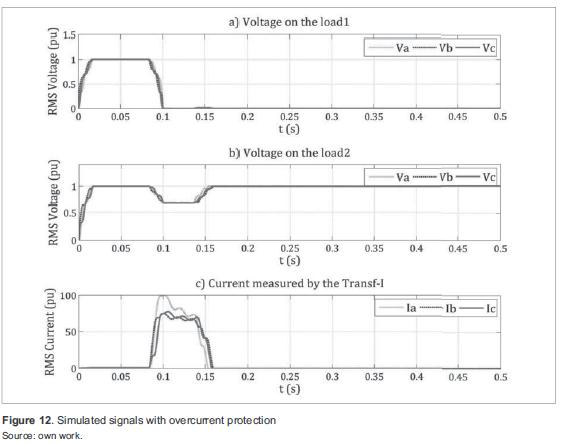
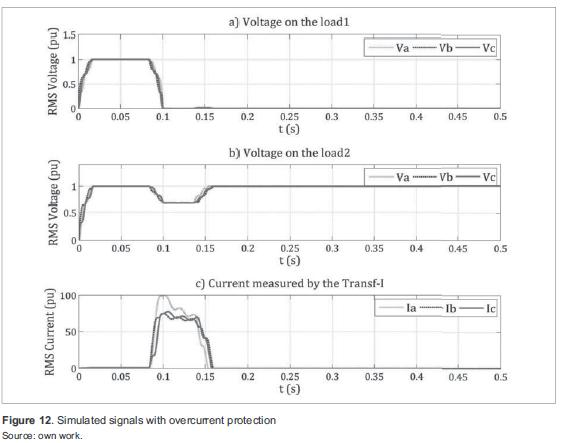
Figure 12 shows the simulation results with overcurrent protection. In a) voltage on load 1 drops to zero when the fault occurs. When the protection operates, remains at zero, because the line has been de-energized; in b) load 2 is affected by a 0,7 pu voltage sag, whose duration is given by the fault clearing time of the overcurrent protection (approximately 50 ms); and in c) current in line 1 increases as a result of the fault. When the protection operates, the current is reduced to zero, indicating that the line has been de-energized.
4.3 Phase-angle jump simulation and results
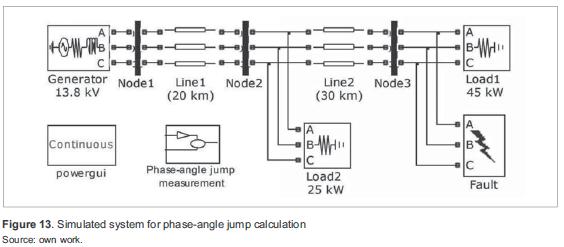
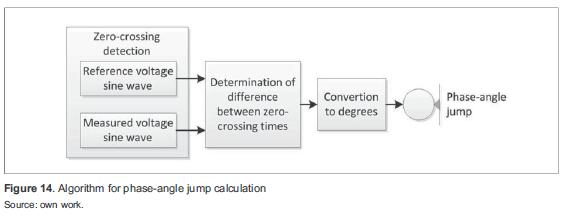
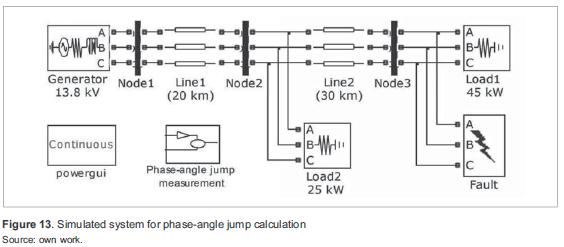
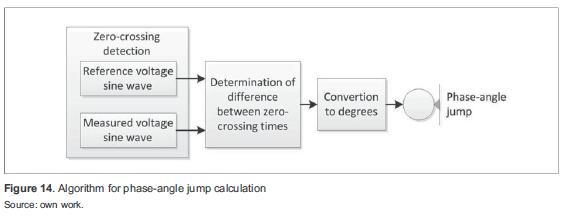
Figure 13 shows the simulated system for phaseangle jump simulation. Table 3 summarizes the parameters. An algorithm for phase-angle jump was developed as shown in figure 14.
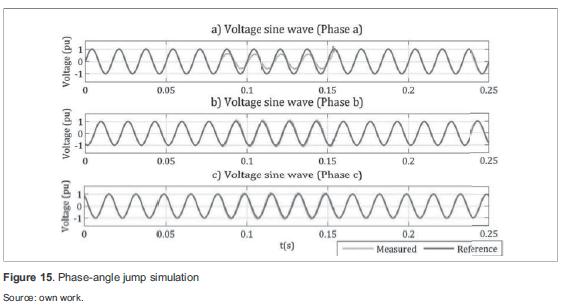
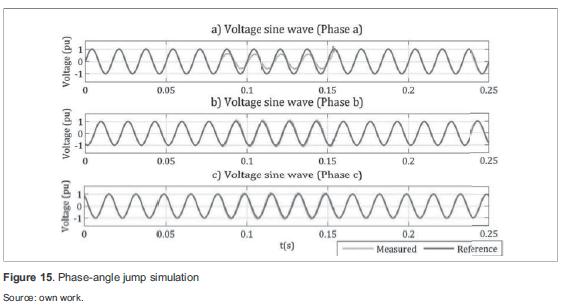
Simulation results in the three phases are shown in figure 15. The results of the developed algorithm for the simulated case are: phase-angle jump in phase "a" 14,47 degrees; in phase "b" 6,54 degrees; and in phase "c" 7,56 degrees.
4.4 Shape - Induction motor starting simulation and results
Another cause of voltage sags is the start of large induction motors. During start up, an induction motor requires a higher current supply than the nominal (typically five to six times as much).
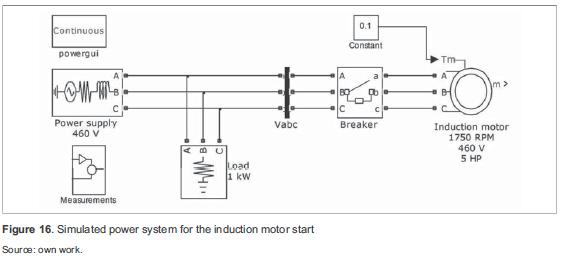
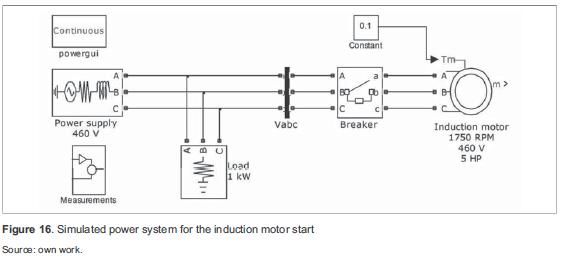
This current remains high until the motor gradually reaches its rated speed [1]. As a result, non-rectangular voltage sag occurs. The impact of induction motor in voltage was simulated using Matlab/Simulink as shown in figure 16.
A 460 V source feeding a 1 kW load and a 5 HP (3,73 kW) induction motor was simulated, including a breaker, which closes after 100 ms to observe the effect of motor start.
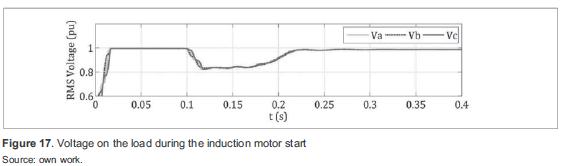
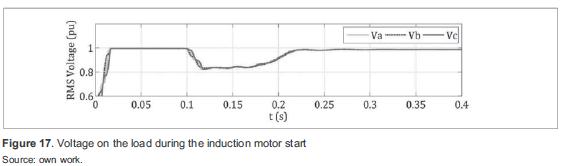
Figure 17 shows the voltage on the load, which presents a non-rectangular voltage sag of 0,8pu and 80 ms (time that the motor takes to reach its rated speed).
The results of the induction motor starting simulation are compared and validated with a typical voltage profile shown in [6] and a real recorded voltage profile during the start of an induction motor shown in [8].
5. Conclusion
Voltage sag characterization can be carried out through computer simulation using existent software tools such as Matlab/Simulink. Nevertheless, further developments should be made in Matlab/Simulink to achieve a more accurate voltage sag characterization.
In this paper, models of electrical protective devices for sag duration simulation, and other specific tools for power quality analysis were developed and implemented in Matlab/Simulink as a part of the power system tool.
Further research into voltage sag characterization through computer simulation should address the development ofinew software tools for the specific phenomena, or complementary toolboxes for powerful existent software applications, in this case Matlab/Simulink.
Referencias
[1] M. Bollen, Understanding Power Quality Problems: Voltage Sags and Interruptions. IEEE Press on Power Engineering, 2000, pp. 139-251.
[2] IEEE Recommended Practice for Evaluating Electric Power System Compatibility With Electronic Process Equipment, IEEE Std 1346, 1998.
[3] R. Dugan, Electrical Power Systems Quality, 2nd ed. McGraw-Hill, 2004, pp. 43-110.
[4] X. Yang, Q. Gui, Y. Tian, and A. Pan, "Research on Calculation Model of Voltage Sags Due to High Voltage and Great Power Motor Starting", Electricity Distribution (CICED), pp. 1-9, September, 2010.
[5] IEEE Recommended Practice for monitoring electric power quality, IEEE Std 1159, 1995.
[6] CIGRE/CIRED/UIE Joint Working Group C4.110, Voltage Dip Immunity of Equipment and Installations, 2010.
[7] J. Caicedo, F. Navarro, E. Rivas and F. Santamaría, "The state of the art and new developments in voltage sag immunity", Ingeniería e investigación, vol. 31, pp. 8187, October, 2011.
[8] IEEE Recommended Practice for the Design of Reliable Industrial and Commercial Power Systems, IEEE Std 493, 1997.
[9] L. Conrad, K. Little and C. Grigg, "Predicting and Preventing Problems Associated with Remote Fault-Clearing Voltage Dips", IEEE Transactions on industry applications, vol. 27, no. 1, January/February, 1991.
[10] J. Blackburn and T. Domin, Protective Relaying. Principles and Applications, 3rd ed. CRC Press, 2006.
Simulation of voltage sag characteristics in power systems
Simulación de las características de los huecos de tensión en sistemas de potencia
Joaquín Eduardo Caicedo Navarro1, Luis Felipe Navarro Julio2, Edwin Rivas Trujillo3, Francisco Santamaría Piedrahita4
1Student of electrical engineering of Distrital University Francisco José de Caldas,
Electromagnetic Compatibility and Interference Group GCEM. Bogotá, Colombia. Contact: jecaicedon@correo.udistrital.edu.co
2Student of electrical engineering of Distrital University Francisco José de Caldas,
Electromagnetic Compatibility and Interference Group GCEM. Bogotá, Colombia.
Contact: lfinavarroj@correo.udistrital.edu.co
3Electrical engineer, Ph.D. in Engineering. Profesor at the Distrital University
Francisco José de Caldas, Electromagnetic Compatibility and Interference Group
GCEM. Bogotá, Colombia. Contact: erivas@udistrital.edu.co
4Electrical engineer, Ph.D. candidate in Engineering. Profesor at the Distrital University
Francisco José de Caldas, Electromagnetic Compatibility and Interference Group GCEM. Bogotá, Colombia. Contact: fsantamariap@udistrital.edu.co
Fecha de recepción: 7 de abril de 2012 Fecha de aceptación: 16 de octubre de 2012
Abstract
This paper describes a methodology for voltage sag characterization using Matlab/Simulink. It includes single-phase and three-phase fault simulations in different power systems for voltage sag magnitude calculation using Simulink, based on the SimPowerSystems toolbox, and also considering electrical protection-systems modeling for sag duration calculation. Other sag characteristics, such as phase-angle jump and shape, are described and simulated.
Key words: Matlab/Simulink, protection system, power system fault, voltage sag.
Resumen
Este artículo describe una metodología para caracterizar un hueco de tensión usando Matlab/ Simulink. Se incluyen simulaciones de fallas trifásicas y monofásicas en diferentes sistemas de potencia usando Simulink, con base en el paquete de software SimPowerSystems, considerando el modelado de los sistemas de protección eléctrica para calcular la duración de un hueco de tensión. Otras características, como el salto de ángulo de fase y la forma del perfil de tensión, son descritas y simuladas.
Palabras clave: falla en el sistema de potencia, hueco de tensión, Matlab/Simulink, sistema de protección.
1. Introduction
Voltage sags are considered one of the most harmful power quality problems, because they affect the proper operation of several types of end-user equipment. This phenomenon is a short-duration reduction in rms voltage caused by events such as power system faults, load variations and the start of large induction motors [1].
The most common cause of voltage sags is the fow of fault current through the power system impedance to the fault location. Hence, power system faults in transmission or distribution can affect respectively a large or small number oficustomers. A fault in a transmission line affects sensitive equipment up to hundreds of kilometers away from the fault [2]. In both, transmission and distribution, voltage sags due to faults in parallel feeders, produce incorrect operation of industrial customer equipment [3]. Thus, in this paper a system fault in a parallel feeder is simulated for voltage sag characterization.
Large induction motors, which are widely used in industries, can also cause voltage sags [4]. In this case, voltage sags are characterized by the non-rectangular shape caused by the increase of the motor starting current. In this paper, the start of an induction motor is also simulated to study the shape of voltage sags.
Magnitude, duration, phase-angle jump and shape define voltage sags. To obtain these characteristics it is necessary to consider the power system performance during the event occurrence (system fault, the start of a large induction motor, load variation, etc.). Generally, real data of power system performance are not available for educational or research purposes, hence, simulation tools are required.
In this paper, voltage sags are characterized using the Sim Power Systems toolbox of Matlab/ Simulink. The simulated scenarios are: system faults, protection systems, phase-angle jump and the start of induction motors.
2. Definitions
In this section, the definition of voltage sag and its main characteristics are presented (figure 1):
- Voltage sag: A decrease to between 0,1 and 0,9 pu in rms voltage or current at the power frequency for durations of 0,5 cycle to 1 min [5].
- Magnitude: The lowest rms value of the voltage during a voltage sag [1].
- Duration: The time during which the rms value of voltage is under the threshold (0,9pu) [1].
- Phase-angle jump: The difference between the phase-angle of the voltage during an event and the phase-angle of the voltage before the event [1].
- Shape: It defines the behavior of the rms voltage profile during voltage sags. According to their shape, voltage sags are classified as rectangular (rms voltage value is constant) and non-rectangular (rms voltage value varies) [6].
- Point-on-wave of sag initiation: The phaseangle of the fundamental voltage wave at the instant of sag initiation [1].
- Point-on-wave of voltage recovery: The phase-angle of the fundamental voltage wave at the instant of voltage recovery [1].
- Pre-fault voltage: Voltage value during an interval ending with the inception of a fault [1].
3. Methodology
Voltage sag characterization consists in defining and quantifying the most relevant parameters of this disturbance, such as: magnitude, duration, phase-angle jump and shape. Specific scenarios, in a given power system, are studied by using simulation tools to determine and quantify the parameters of interest, according to the following criteria [7]:
- Sag duration depends on fault clearing time provided by the electrical protection in a power system. It can be determined by simulating electrical protection behavior when dealing with system faults.
- Magnitude and phase-angle jump depend on fault location and line impedance. They can be determined at different nodes of a power system by simulating system faults.
- Voltage profile shape is another characteristic taken into consideration. Non-rectangular sags can be studied by modeling and simulating the start of large induction motors in power systems.
Different scenarios for voltage sag characterization are simulated using Matlab/Simulink. figure 2 summarizes the proposed procedure for characterizing voltage sags.
3.1 Sine and rms functions
A voltage sag can be represented using a function defined by parts, based on its most important characteristics as equation (1).
where:
Vp: Peak pre-fault voltage
ω: Angular frequency
Vpsag: Peak voltage during the sag
Φ: Phase-angle jump
t1: Time of sag initiation
t2: Time of voltage recovery
Δt= t1-t2: Duration (8,33 ms<Δt< min
Voltage sag can be represented by sinusoidal function and rms voltage profile (figure 3).
RMS value is calculated from the sine wave voltage with equation(2) [1].
where:
N: Number of samples per cycle
vi: Sampled voltages in time domain
For the simulations the sample frequency used is 15,36 kHz, or N = 256 samples per 60 Hz cycle.
3.2 Theoretical calculation of magnitude
Figure 4 shows a basic model for calculating the magnitude of voltage sag during a three-phase fault on a radial system.
The current through the load before and during the fault is negligible, thus the voltage at the pcc is calculated with equation(3).
where:
ZF: Feeder impedance (between pcc and the fault point)
ZS: Source impedance (between the source and pcc)
E: Source voltage
3.3 Duration and power system protection
Sag duration corresponds to the period of time during which the protective equipment allows fault current to fow. There are several types of protective equipment in the power system and each one has a minimum fault clearing time. Additionally, a delay for protection coordination must be included. In the case of temporary faults, some of the protective devices have a reclose function to restore service within a short time [8].
Transmission system faults are cleared faster than distribution systems faults [1]. In transmission lines, distance relays and differential relays are fast-acting, while in distribution networks, overcurrent protection typically requires higher delays for protection coordination. An exception in distribution systems is the use oficurrent-limiting fuses which act faster (half a cycle) [8].
3.4 Phase-angle jump theoretical calculation
The voltage divider model in figure 4 can also be used for theoretical analysis of phase-angle jump, considering ZS and ZF as complex quantities, denoted asand. Using per-unit calculation, namely the voltage source E = 1, Equation (3) is rewritten as equation (4).
whereand ZS = RS + jXS and ZF + jXF. The argument of Vsag, equivalent to the phase-angle jump, is given by equation (5).
If (XS / RS) = (XF / RF), ΔΦ would be zero and there would be no phase-angle jump. Hence, phaseangle jump only occurs if the X/R ratios of source and feeder are different.
4. Results
4.1 Magnitude simulation and results
The voltage sags due to power system faults simulated are compared with the ones presented in [8] and [9]. In those papers, the voltage sags caused by faults in parallel feeders are studied, including the effect of power system protections.
Models of the main components of power systems: generators, transformers, motors, transmission lines, loads, switches and measuring systems are included in the Matlab/Simulink software package. figure 5 shows a power system underground fault conditions simulated in Matlab/(4) Simulink used in this paper.
The system includes a 13,8 kV power generation center, a 15 MVA transformer to increase the voltage up to 115 kV and an 80 km transmission line. Then, a 15 MVA transformer reduces the voltage to 13,8 kV to feed a 10 MW load in the distribution system. Measuring systems display voltage and current signals at the system nodes. Two scenarios were simulated: a three-phase fault and a single-phase fault occurred in the middle of the transmission line (40 km from the transformation center). Table 1 summarizes the parameters for sag magnitude simulation.
Figure 6 shows the three-phase fault simulation results, a) three-phase sine wave with its magnitude in per-unit, b) rms voltage profiles. A 0,25pu three-phase voltage sag occurred as a result of the fault. The sag duration was 4 cycles at 60 Hz.
Results of the single-phase fault simulation are shown in figure 7. In this case, a 0,25pu voltage sag as a result of a fault is observed. In both cases, signals were recorded in the Node4 (see figure 5), to show the effect of faults on the load.
4.2 Simulation of voltage sag duration and results
Building models of electrical protection devices on Matlab/Simulink is necessary for simulations, because this tool does not include those models. A power system was simulated with overcurrent protection (figure 8), because this is the most widely used relay (function 50, according to ANSI) [10].
The simulated system consists of two 115 kV parallel transmission lines, with a length of 80 km (line 1) and 40 km (line 2). Each line feeds a 10 MW load (loads 1 and 2 respectively). This simulation presented a solid and permanent three-phase fault to ground in the middle of line 1, which produce an interruption on load 1 and a decrease in voltage on load 2. Two scenarios were simulated for the described case: without overcurrent protection and with overcurrent protection. Table 2 summarizes the parameters for duration simulation.
Figure 9 shows the simulation results of the first scenario. In a) an interruption occurs on load 1 as a result of the fault; in b) voltage on load 2 drops to 0,7 pu; and in c) the peak current measured at the faulted line is 100 pu and stabilizes at 65 pu, it is evident a permanent fault.
For the second scenario, an overcurrent protection model was implemented in Matlab/Simulink (figure 10). In the model, rms phase currents are compared with a defined current in pu, which represents the protection activation threshold (if any of the phase currents exceeds the threshold, the protection is activated). The model includes a delay for protection coordination as well as for reducing the probability of incorrect operation. figure 11 shows the control signal of the overcurrent relay. When the signal is true, the associated breaker is closed (protection off), hence, the protected line remains energized. When the control signal is false, the breaker is open (protection on) and de-energizes the line to isolate the fault point. Initially, the overcurrent protection detects when the current is ten times greater than nominal (85 ms) and changes the state after the specif ed delay (50 ms in figure 10), thus opening the breaker to isolate the fault point.
Figure 12 shows the simulation results with overcurrent protection. In a) voltage on load 1 drops to zero when the fault occurs. When the protection operates, remains at zero, because the line has been de-energized; in b) load 2 is affected by a 0,7 pu voltage sag, whose duration is given by the fault clearing time of the overcurrent protection (approximately 50 ms); and in c) current in line 1 increases as a result of the fault. When the protection operates, the current is reduced to zero, indicating that the line has been de-energized.
4.3 Phase-angle jump simulation and results
Figure 13 shows the simulated system for phaseangle jump simulation. Table 3 summarizes the parameters. An algorithm for phase-angle jump was developed as shown in figure 14.
Simulation results in the three phases are shown in figure 15. The results of the developed algorithm for the simulated case are: phase-angle jump in phase "a" 14,47 degrees; in phase "b" 6,54 degrees; and in phase "c" 7,56 degrees.
4.4 Shape - Induction motor starting simulation and results
Another cause of voltage sags is the start of large induction motors. During start up, an induction motor requires a higher current supply than the nominal (typically five to six times as much).
This current remains high until the motor gradually reaches its rated speed [1]. As a result, non-rectangular voltage sag occurs. The impact of induction motor in voltage was simulated using Matlab/Simulink as shown in figure 16.
A 460 V source feeding a 1 kW load and a 5 HP (3,73 kW) induction motor was simulated, including a breaker, which closes after 100 ms to observe the effect of motor start.
Figure 17 shows the voltage on the load, which presents a non-rectangular voltage sag of 0,8pu and 80 ms (time that the motor takes to reach its rated speed).
The results of the induction motor starting simulation are compared and validated with a typical voltage profile shown in [6] and a real recorded voltage profile during the start of an induction motor shown in [8].
5. Conclusion
Voltage sag characterization can be carried out through computer simulation using existent software tools such as Matlab/Simulink. Nevertheless, further developments should be made in Matlab/Simulink to achieve a more accurate voltage sag characterization.
In this paper, models of electrical protective devices for sag duration simulation, and other specific tools for power quality analysis were developed and implemented in Matlab/Simulink as a part of the power system tool.
Further research into voltage sag characterization through computer simulation should address the development ofinew software tools for the specific phenomena, or complementary toolboxes for powerful existent software applications, in this case Matlab/Simulink.
Referencias
[1] M. Bollen, Understanding Power Quality Problems: Voltage Sags and Interruptions. IEEE Press on Power Engineering, 2000, pp. 139-251.
[2] IEEE Recommended Practice for Evaluating Electric Power System Compatibility With Electronic Process Equipment, IEEE Std 1346, 1998.
[3] R. Dugan, Electrical Power Systems Quality, 2nd ed. McGraw-Hill, 2004, pp. 43-110.
[4] X. Yang, Q. Gui, Y. Tian, and A. Pan, "Research on Calculation Model of Voltage Sags Due to High Voltage and Great Power Motor Starting", Electricity Distribution (CICED), pp. 1-9, September, 2010.
[5] IEEE Recommended Practice for monitoring electric power quality, IEEE Std 1159, 1995.
[6] CIGRE/CIRED/UIE Joint Working Group C4.110, Voltage Dip Immunity of Equipment and Installations, 2010.
[7] J. Caicedo, F. Navarro, E. Rivas and F. Santamaría, "The state of the art and new developments in voltage sag immunity", Ingeniería e investigación, vol. 31, pp. 8187, October, 2011.
[8] IEEE Recommended Practice for the Design of Reliable Industrial and Commercial Power Systems, IEEE Std 493, 1997.
[9] L. Conrad, K. Little and C. Grigg, "Predicting and Preventing Problems Associated with Remote Fault-Clearing Voltage Dips", IEEE Transactions on industry applications, vol. 27, no. 1, January/February, 1991.
[10] J. Blackburn and T. Domin, Protective Relaying. Principles and Applications, 3rd ed. CRC Press, 2006.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.