Estimación de volumen de Abies religiosa (Kunth) Schltdl. & Cham. en diferentes entidades federativas de México

Área de estudio

Los sitios de estudio se llevaron a cabo en ocho entidades federativas, con sus respectivas unidades de manejo forestal (Umafor): Guerrero (1203), Puebla (2101, 2105 y 2108), Tlaxcala (2901 y 2902), Veracruz (3004 y 3012), Michoacán (1604, 1605, 1607 y 1608), Jalisco (1404, 1406 y 1410), Hidalgo (1303) y Estado de México (1503, 1507, 1508, 1509 y 1510) (Instituto Nacional de Estadística y Geografía, 2016). Los datos de todas las Umafores en cada entidad se agruparon con la finalidad de llevar a cabo los ajustes.

Tamaño de muestra

La información de campo se obtuvo de 21 Umafor, con un total de 2747 árboles; mismos que provienen de zonas de aprovechamiento, así como y de áreas no autorizadas para el derribo. Para el primer caso se utilizó el muestreo destructivo consistió en derribar, seccionar y medir los árboles; mientras que para las áreas no autorizadas las mediciones se hicieron en árboles en pie de manera escalonada y con forcípula láser Haglof Digitech Professional para medir el diámetro a distintas alturas; considerando diferentes categorías diamétricas (tabla 1). En cada sitio el diámetro normal (Dn) fue medido en pie con una cinta diamétrica alemana Forestry Suppliers, Inc. P.O. BOX 8397 y forcípula Haglof Mantax Blue, medido a 1.30 sobre el nivel del suelo; y la altura total (Ht) con el Hipsómetro Haga^®; en este caso, los individuos derribados fueron medidos con el flexómetro Uline Accuc-Lock H-1766.

Tabla 1: Resumen de las variables dasométricas

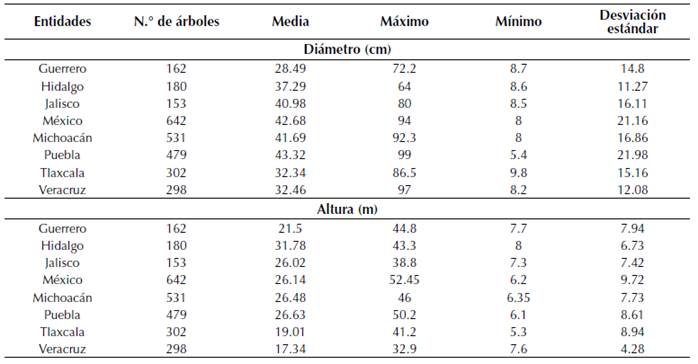
Para cada árbol se registraron las siguientes variables: diámetro normal medido a 1.3 m sobre el nivel del suelo (Dn, cm), altura total (Ht, en metros) y diámetros con corteza a distintas alturas (d_i, en cm) a lo largo del fuste con respecto al suelo (h_i, en m). Las primeras mediciones se realizaron en dos secciones de 0.30 m por encima del tocón; posterior a eso, la siguiente sección fue en el diámetro normal (1.30 m); y después las secciones fueron cortadas de manera constante a 2.54 m de longitud hasta llegar a la punta del árbol. De igual forma, se midieron todas las ramas mayores o iguales a 5 cm, mismas que fueron seccionadas a distintas longitudes (d_ri en cm). Tanto los árboles derribados, como los que se midieron en pie, fueron cubicados por secciones, en donde el volumen de cada sección de fuste y de rama se estimó mediante la fórmula de Smalian; las puntas se cubicaron mediante la ecuación del cono. El volumen total del árbol se estimó sumando el volumen del fuste y de las ramas (Vargas-Larreta et al., 2017).

Ecuaciones ajustadas

Se ajustaron seis ecuaciones para calcular la relación entre el volumen rollo total árbol y una ecuación para estimar el volumen de ramas (vrta, vramas); teniendo como variables independientes el diámetro y la altura total. Posteriormente, se realizó un ajuste simultáneo para estimar el volumen total de los árboles (vta) de cada una de las entidades federativas; que consiste en la suma de las ecuaciones anteriores (tabla 2). Sin embargo; en las regiones de Tlaxcala y Veracruz la ecuación de ramas (7) se excluyó, ya que no hubo información suficiente.

En la tabla 2 se muestran las ecuaciones utilizadas:

Tabla 2: Ajustes de ecuaciones de volumen (vrta, vramas y vta). V= volumen (m3), D= diámetro normal (cm), d= diámetro de ramas (cm), H= altura total (m), ai = parámetros a ser estimados (i = 0, 1, 2)

Método de ajuste y selección de modelos

Los modelos ajustados fueron de tipo no lineal, ya que desde un punto biológico estas ecuaciones tienen un comportamiento más consistente en la curva (Huang et al., 1992). La estimación de los parámetros se usó el método de mínimos cuadros ordinarios (OLNS), ya que esta técnica permite minimizar los errores de los parámetros. Para evitar la convergencia de los parámetros a un óptimo local se usaron los valores obtenidos por Vargas-Larreta et al. (2017) . Las ecuaciones fueron ajustadas con el software SAS/ETS^â (SAS Institute Inc. 2008). El análisis de la capacidad de ajuste de los modelos se basó en comparaciones numéricas y gráficas.

La expresión de los estadísticos de bondad de ajustes es la siguiente:

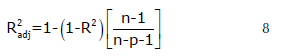
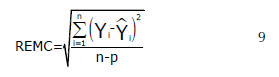
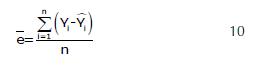
Donde: R²adj= coeficiente de determinación ajustada, REMC= raíz del error medio cuadrático, (ē) = Sesgo. p= es el número de parámetros a estimar, n= es el tamaño de muestra, Y_i= son los valores observados, Ŷ_i =son los valores predichos.

Además, se hizo un análisis gráfico de los residuos frente a los valores predichos de altura total, ya que este procedimiento se considera una de las maneras más eficientes de evaluar la capacidad de ajuste de un modelo (Diéguez-Aranda et al., 2005; Guzmán-Santiago et al., 2019) al permitir detectar posibles tendencias sistemáticas de los datos, así como para seleccionar factores de ponderación si fuesen necesarios debido a la presencia de heterocedasticidad (Neter et al., 1996).

Corrección de heterocedasticidad

Para garantizar las estimaciones de los parámetros se corrigió el efecto de heterocedasticidad (varianza no constante), para lo cual se realizó una ponderación aplicando los mismos pesos a la inversa de la varianza de cada observación. La varianza desconocida se estimó con la función potencial . Los valores de γ y del exponente k se optimizaron empleando los errores del modelo ajustado sin pesos como variable dependiente en el modelo potencial de varianza del error (Harvey, 1976). Finalmente, el peso considerado fue 1/D² para la ecuación de volumen de las ramas con corteza y 1/D² * H para la ecuación de volumen rollo total árbol.

Ecuaciones ajustadas

Estadísticamente el modelo de Spurr Potencial (Ec. 1) fue ligeramente superior que el resto de las ecuaciones. Sin embargo, en el análisis gráfico causó algunos problemas de precisión. Por lo anterior, en las entidades de Jalisco, México y Puebla se seleccionó la ecuación de Schumacher y Hall (1933) (Ec. 3); mientras que en Guerrero, Hidalgo, Michoacán, Tlaxcala y Veracruz se optó por la ecuación 1, ya que mostró excelentes resultados. En este sentido, la ecuación 3 en el volumen de rollo total árbol (vrta) presentó un sesgo que va de 0.028 a 0.034 m³, con una raíz de error medio cuadrático (REMC) menor a 0.44 m³, así como un coeficiente de determinación ajustada (R² _adj) de 96 %, respectivamente (tabla 3).

Tabla 3: Parámetros y estadísticos de bondad de ajuste del volumen rollo total árbol (Vrta)

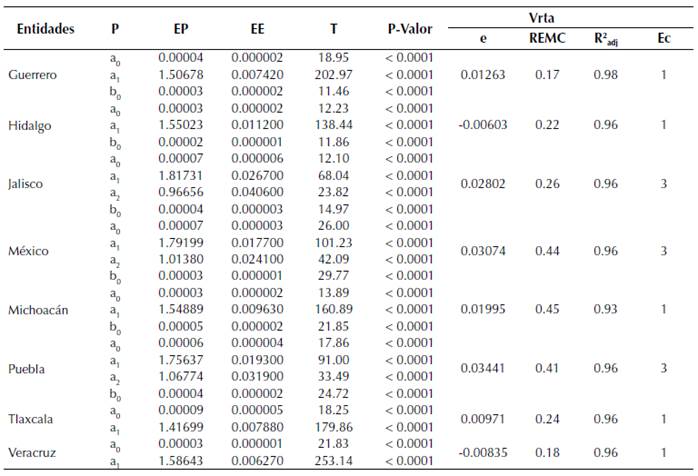
Para el volumen de ramas (vramas), el sesgo es menor a 0.001 m³; mientras que la REMC promedio corresponde a 0.08 m³; además, presentó una R² _adj superior a 0.44 (tabla 4). Como consecuencia en el volumen total árbol (vta) se obtuvo un sesgo promedio de 0.033 m³, donde la bondad de ajuste es aceptable estadísticamente (REMC < a 0.45 m³; R² _adj =96 %). Para el caso del modelo 1, el sesgo se encuentra entre -0.008 y 0.01 m³, mismo que muestra una REMC menor a 0.45 m³, y un 93 % de la varianza total de la variable explicada en el vrta. Además, se observa en el volumen de ramas (vramas), que el sesgo está por debajo de -0.002, con errores que oscila entre 0.04 y 0.12 m³ (R² _adj > a 0.25), y que por consecuencia se refleja en el Vta la capacidad del modelo de explicar a la variable (tabla 5).

Tabla 4: Parámetros y estadísticos de bondad de ajuste del volumen de ramas (Vramas)

Tabla 5: Parámetros y estadísticos de bondad de ajuste del volumen total árbol (Vta)

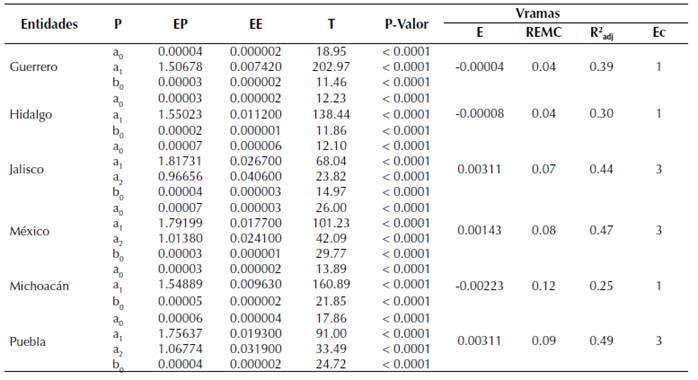
P= parámetros, EP= estimador de parámetros, EE= error estándar, P>t = valor de la probabilidad de la distribución de la t de Stu dent, e= sesgo, REMC= raíz del error medio cuadrático, R²adj= coeficiente de determinación ajustada.

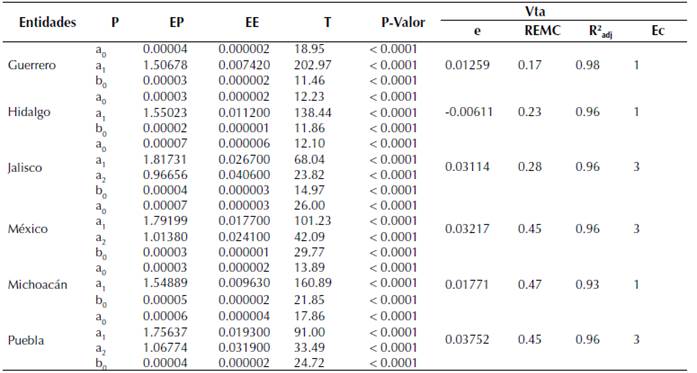
Comparación entre entidad federativa

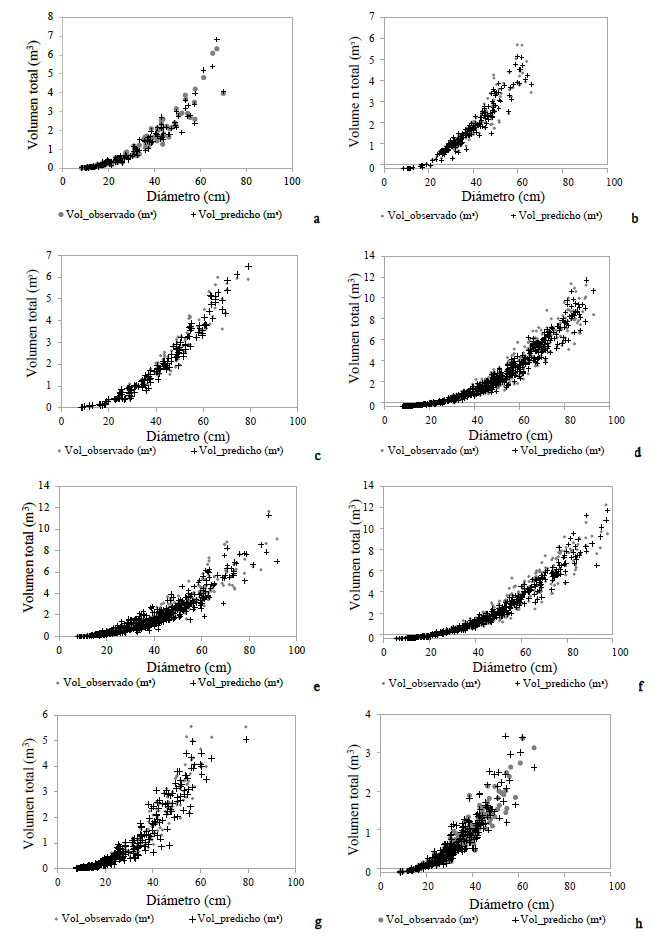
En la figura 1 se aprecia las curvas de ajuste de la ecuación 1 sobre los datos de campo de cada una de las entidades, en la que en los sitios de Guerrero (a) e Hidalgo (b) se obtuvieron categorías diamétricas hasta de 70 cm; así como un volumen total máximo de 7 y 6 metros cúbicos (m³), aproximadamente. Para la entidad de Michoacán (e) se obtuvo información de volumen de 13 m³ con categorías máximas de 95 cm. Por otra parte, en Tlaxcala (g) el volumen rollo total árbol (vrta) fue de 5.7 m³, ligeramente superior en que Veracruz (h), en la cual generó un volumen 3.6 m³.

Figura 1: Volúmenes observados vs. predichos: a= Guerrero, b= Hidalgo, c= Jalisco, d= México, e= Michoacán, f= Puebla, g= Tlaxcala, h= Veracruz.

La ecuación 3 estima una buena proyección sobre los datos provenientes de la Ciudad de México (d) y Puebla (f), en donde ambos obtuvieron volumen de 12.3 m³ con categorías de hasta 95 cm; mientras que en Jalisco (c) hubo una menor cantidad volumétrica (6.7 m³) con diámetros menores a 80 cm. En las ciudades de México, Puebla y Michoacán se aprecia la mayor concentración en volumen maderable; además, en Hidalgo y Tlaxcala se observa que no existe una marcada diferencia a pesar de que el segundo sitio (g) no contiene información de ramas; esto quizás se deba por la cantidad de muestras obtenidas.

Evolución del sesgo

En la figura 2 se observa que el sesgo generado por la ecuación 1 para las entidades de Guerrero (a) y Michoacán (e) se encuentra cercano a cero en diámetros que van de 5 a 45 cm; mientras que en datos de 50 a 63 cm el modelo subestima con un grado de error más notable; a partir de diámetros superiores a 64 se observa un marcado grado de sobreestimación. En el caso de Hidalgo (b) el grado de error se observa con más claridad en categorías mayores de 40 cm, mientras que en Tlaxcala (g) tiene una distribución normal (cercano a cero) en diámetros de 5 a 59 cm, y en categorías mayores a 60 cm el modelo tiende a subestimar la información volumétrica (vrta), sobre todo en diámetro 64 ya que alcanza un error de 0.62 m³.

Figura 2: Sesgos de categorías diamétricas: a= Guerrero, b= Hidalgo, c= Jalisco, d= México, e= Michoacán, f= Puebla, g= Tlaxcala, h= Veracruz.

Para el caso de Veracruz (h) el sesgo es prácticamente nulo en árboles con categorías menores a 49 cm. Sin embargo, en diámetros de 50 a 59 cm se observa una ligera sobreestimación. Los errores con subestimación notable se presentan en los datos mayores a 60 cm.

De igual forma se comporta la ecuación 3 para la entidad de Jalisco (c), pues sobreestima ligeramente los datos en diámetros menores a 37 cm, mientras que categorías de 38 a 69 se observa la subestimación; en diámetros mayores a 70 sucede todo lo contrario, tomando valores de -0.20. En la Ciudad de México (d), el margen de error notable se presenta en diámetros superiores a 40 cm, ya que subestiman el volumen con un error de 0.30 m³. Por otra parte, en Puebla (f) se observa que el modelo estima adecuadamente en categorías menores a 50 cm; mientras que en categorías de 55 a 78 cm tiende a subestimar el volumen hasta de 0.50 m³, de igual forma para diámetros mayores a 79 cm se observa una distribución con margen de error de -0.58 a 0.39 m³.

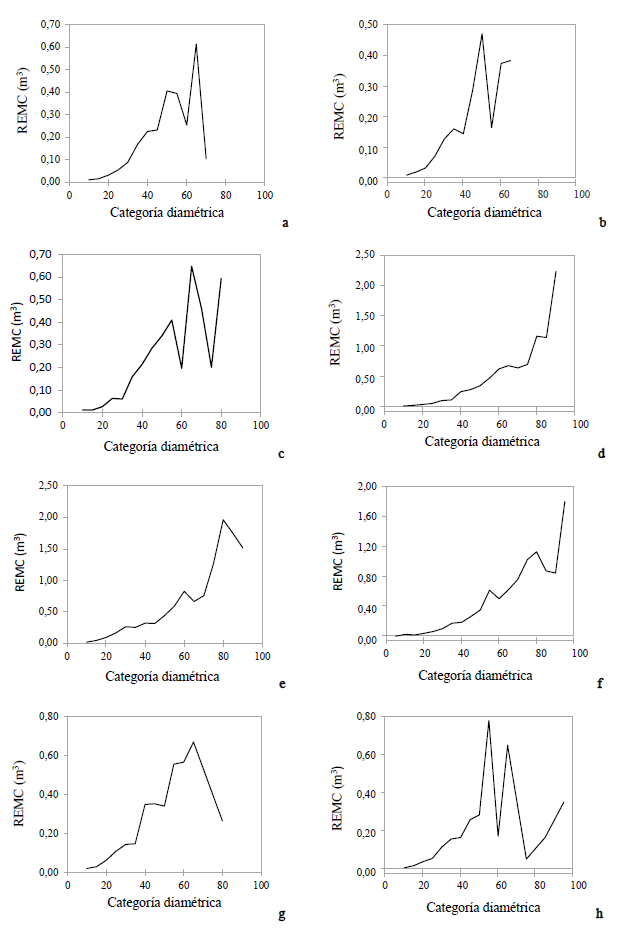
Evolución de la raíz del error medio cuadrático (REMC)

La ecuación de Spurr Potencial (Ec. 1) tiene en general un buen comportamiento sobre las clases diamétricas. Se observa que, para las entidades de Guerrero (a) e Hidalgo (b) en diámetros menores a 19 cm presentan errores mínimos; sin embargo, de 20 a 59 cm tiende a subir de forma constante; mientras que para categorías de 65 en el sitio a, presenta el error más alto 0.62 m³ y luego la curva disminuye con aproximación a cero. En el caso del sitio b, el punto más alto de error está en diámetro de 50 cm; y no tiene un comportamiento constante para el resto de las categorías; al igual que en Michoacán (e), donde el modelo prácticamente tiende a incrementar ligeramente hasta las categorías de 80 cm.

Para el caso de Tlaxcala (g) y Veracruz (h) se observa que en ambos sitios el error tiende a incrementar a medida que aumentan las categorías diamétricas, alcanzando su máximo error (0.65 m³) en diámetros de 65 cm (G) y 55 cm (0.77 m³) para el sitio h y, posteriormente, tienden a decrecer.

En cuanto a la ecuación de Schumacher y Hall (Ec. 3) para la zona de Jalisco (c) se observa que el error mayor se presenta en las categorías de 65 cm, ya que alcanza un error de 0.65 m³. Esto también se puede apreciar en los sitios de la Ciudad de México (d) y Puebla (f), donde los errores crecen ligeramente conforme aumentan las categorías diamétricas; aunque no se ve afectada en gran medida la estimación, ya que la mayoría de los árboles son de categorías menores a 70 cm, tal como se muestra en el estudio realizado por Pineda-López et al. (2013), en el que la mayoría de los árboles se encuentran diámetros de 10 a 35 cm.