Modelo de Solución - difusión - imperfección en el proceso de acondicionamiento de aguas mediante tecnologías limpias.

Colombia Forestal, Diciembre del 2004 vol:8 nro:17 pág:94-102

Modelo solución-difusión-imperfección en el proceso de acondicionamiento de aguas mediante tecnologías limpias

Carlos F. García Olmos

Proyecto de Investigación realizado en el Departamento de Ingeniería Química y Tecnología del Medio Ambiente de la Universidad de Oviedo, con participación de la Universidad Distrital.

José R. Álvarez Sáiz

Carlos F García-Olmos, Ingeniero Civil, MSc, PhD, Profesor Titular del Proyecto Curricular de Ingeniería Forestal, Facultad del Medio Ambiente y Recursos Naturales, Universidad Distrital Francisco José de Caldas, Bogotá, D.C., Colombia. cfgarciao@udistrital.edu.co

Susana Luque Rodríguez

José Coca Prados

José R Álvarez Sáiz, Susana Luque Rodríguez y José Coca Prados. Ingenieros Químicos, PhD, Departamento de Ingeniería Química y Tecnología del Medio Ambiente, Universidad de Oviedo, España,. Tel. +34-985103028, Fax: +34-985103434, jras@correo.uniovi.es

Resumen

Esta investigación se desarrolló con el propósito de modelizar un proceso que reemplace al de intercambio iónico en el acondicionamiento de aguas para uso industrial, como es el caso de las calderas, en razón de las ventajas de tipo técnico, ambiental y económico que tienen las tecnologías limpias como las que utilizan membranas.

En las membranas de ósmosis inversa, como las estudiadas por Sourirajan, hay acoplamiento entre el flujo de solvente y solutos a través de ellas, pero en un grado mucho menor que en las membranas de flujo viscoso. Para ellas se han propuesto varios modelos, corno el de solución-difusión-imperfección, del cual se presenta su aplicación.

Se utilizaron tres membranas poliméricas en espiral (ESPA1, CPA2 y PAC). En las ecuaciones de su modelización los coeficientes fueron determinados en forma experimental. El modelo fue optimizado con el algoritmo de los mínimos cuadrados y ajustado con una función objetivo.

La aplicación del modelo se hizo utilizando sus predicciones de flujo total y retención de solutos en el diseño de un sistema de acondicionamiento de aguas para uso industrial, en este caso para una caldera.

Palabras Clave: modelización, tecnologías con membranas, acondicionamiento de aguas.

Abstract

This research deals with an intermediate membrane category, in which the joining ofthe flows exists, but in a much smaller degree that in the viscous flow. In this work different models have been proposed, such that represent these intermediate characteristics, as those reported by Sourirajan 5 for cellulose acetate low- porous membranes.

Three spiral polymeric reverse osmosis membranes (ESPA1, CPA2 and PAC) were used. Coefficients used in the proposed model were obtained from flow and conductivity experimental data using these membranes.

The model was optimised by means ofthe least squares algorithm and adjusted with a function objective, to obtain definitive coefficients for each membrane. Finally, model predictions were used for a boiler water conditioning system design.

Key Words: modelling, membrane technology , water conditioning.

INTRODUCCIÓN

El pretratamiento requerido del agua de alimentación que permite el acondicionamiento para uso industrial, como es el del ciclo líquido--vapor de una caldera, se suele realizar mediante un proceso de intercambio jónico, el cual tiene problemas como el de que las resinas se ensucien y requieran limpiarse y regenerarse en cierto lapso de tiempo, causando un mayor coste en la operación del sistema, y arrojando como residual un efluente de agua altamente contaminante, con efectos ambientales si no se trata adecuadamente.

El caso del que se ocupa este trabajo es el de modelizar el pretratamiento del agua para uso industrial, como el de las calderas, utilizando membranas de nanofiltración y de ósmosis inversa, que se presentan como respuesta a los problemas planteados. Las técnicas con membranas reducen los inconvenientes comentados y se espera que se puedan emplear como alternativa de solución para sustituir total o parcialmente las resinas de intercambio iónico.

Sourirajan (1964), estableció inicialmente que las membranas de acetato de celulosa poco porosas podían ser progresivamente modificadas por tratamiento al calor para llegar a ser más y más selectivas, hasta que sus propiedades se aproximaran a las membranas de solución-difusión, y son las denominadas como de poros finos.

En las membranas de poros finos el acoplamiento de los flujos de solutos y solvente existe a través de ellas, pero en un grado mucho menor que en las membranas de flujo viscoso.

La investigación que se presenta consiste en la modelización de estas membranas según el principio de Solución-Difusión-Imperfección, enfocando el modelo hacia su posterior aplicación en el diseño de un sistema de acondicionamiento de aguas para uso industrial, como el de las calderas.

Esta investigación se realizó en el Departamento de Ingeniería Química y Tecnología del Medio Ambiente de la Universidad de Oviedo (España), con participación de la Facultad del Medio Ambiente y Recursos Naturales de la Universidad Distrital Francisco José de Caldas de Bogotá D.C. (Colombia) y el apoyo de la Fundación para el Fomento en Asturias de la Investigación Científica Aplicada y la Tecnología (FICYT), en el periodo de enero de 2000 a diciembre de 2002.

OBJETIVOS

OBJETIVO PRINCIPAL

- Determinar la aplicabilidad del modelo solución- difusión-imperfección en el proceso de acondicionamiento de aguas para uso industrial mediante membranas de ósmosis inversa y nanofiltración.

OBJETIVOS ESPECÍFICOS

· Establecer una metodología para hallar los coeficientes de las ecuaciones del modelo, con base en la experimentación con las membranas.

· Comparar los resultados de la modelización con los datos experimentales, de acuerdo con el criterio de una función objetivo.

· Optimizar los resultados hallados mediante el método de los mínimos cuadrados.

MARCO TEÓRICO

PROCESOS CON MEMBRANAS

La membrana es un medio que separa dos fases y permite, mediante el uso de una fuerza impulsora, el paso a su través de disolvente y algunos solutos, rechazando otros de un modo selectivo (Osada y Nakagawal988).

Constituyen un amplio campo, y se clasifican según la fuerza de impulsión que utilizan y que depende también del tipo de fluido que se requiere tratar. Esta fuerza de impulsión puede ser una presión hidráulica, una diferencia de concentración entre las soluciones en contacto con la membrana, una diferencia de potencial eléctrico o una diferencia de presión parcial (Luque y Álvarez, 2000).

A escala industrial, las principales aplicaciones de las membranas se llevan a cabo en la producción de agua potable a partir del agua de mar, tratamiento de aguas residuales urbanas, descontaminación de efluentes industriales y recuperación de productos de elevado valor añadido (Perry, 1989, Mulder, 1991, Luque, 1999).

Las técnicas con membranas se aplican con éxito hoy en día, principalmente en España, Francia, Alemania, Gran Bretaña, Escandinavia, Estados Unidos y Arabia, especialmente en los procesos señalados anteriormente.

Las membranas se clasifican según el tamaño de las partículas del soluto que va a atravesar la membrana, valiéndose para ello del denominado umbral de corte, que es un parámetro referido al peso molecular medido en Dalton, del producto más pequeño que es retenido por la membrana en un 90 o 95%, aunque en la retención influyen otros factores como la forma y carga de las moléculas, otros solutos, etc. (Mulder, 1991).

Estas técnicas con membranas, cuya fuerza impulsora es la presión, son: Microfiltración (MF), Ultrafiltración (UF), Nanofiltración (NF) y Ósmosis inversa (RO), como puede verse en la Figura 1.

La Microfiltración retiene partículas en suspensión con un diámetro medio de upa micra, con tamaños que van de 0,05 a 10 micrómetros. Utiliza membranas porosas y el mecanismo de exclusión. Las presiones que se aplican van de 0,5 a 3 bar y se dispone de membranas con un amplio rango de materiales.

La Ultrafiltración retiene macromoléculas, pero utiliza el peso molecular como índice de rechazo, ya que por tamaño de las moléculas no se puede determinar el umbral de corte. El intervalo está entre 1000 y 50000 Dalton, o de 2 a 100 nanómetros. Utiliza como principio el mecanismo de exclusión mediante membranas porosas, de material polimérico o inorgánico. Presentan el problema del ensuciamiento.

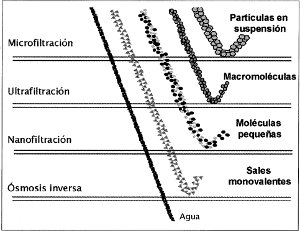
La Nanofiltración ocupa un lugar intermedio entre la Ultrafiltración (UF) y la Ósmosis Inversa (RO). Es un proceso relativamente reciente, y utiliza membranas compuestas, con tamaño de poro menor de 2 nanómetros. Separa las moléculas de bajo peso molecular, de 200 a 1000 Dalton, y se aplican gradientes de presión de 3 a 25 bar, que son menores a los utilizados por la RO. El espesor de las membranas es del orden de los 150 µm, y son en gran parte poliméricas.

La nanofiltración es capaz de retener especies iónicas bivalentes (aniones y cationes), lo cual es una ventaja frente a la UF. Interesa la retención de los iones bivalentes que dan la dureza al agua, y que trae como consecuencia la formación de incrustaciones en instalaciones de uso industrial, como por ejemplo las calderas. Estas membranas pueden alcanzar una retención de los iones de calcio y magnesio en un intervalo del 85 al 95%, que es un buen índice para considerar los costes del proceso en comparación con los que implican otros procesos para el mismo fin, como son el intercambio iónico (I0) y la ósmosis inversa (RO).

En la ósmosis inversa la separación del soluto no se debe a su tamaño, y es un mecanismo de disolución-difusión a través de la membrana. Éstas sólo permiten el paso del agua (Mulder, 1991). La técnica de ósmosis inversa es la que tiene el mayor poder de retención, que alcanza hasta el no permitir el paso de las sales monovalentes disueltas, del orden de hasta los 10 A. En el caso del NaCl llega hasta el 99,9% de retención, y en la retención de compuestos de bajo peso molecular dependerá de la naturaleza y estructura de la membrana.

En general, del 95 al 99% de los materiales disueltos en el agua pueden ser eliminados, dependiendo del abastecimiento del agua de entrada. El agua limpia producida puede estar entre 25000 y 500000 ohm/ cm de conductividad. El agua residual o concentrada es entonces enviada al drenaje. Las membranas no se ensucian, y sólo necesitan ser limpiadas sobre una base anual, dependiendo de las condiciones del agua de entrada.

PRINCIPIO DE SOLUCIÓN-DIFUSIÓN- IMPERFECCIÓN

Es una extensión del principio de solución-difusión para incluir el flujo de poros, así como también la difusión del soluto y el solvente a través de la membrana. En este modelo se reconoce que las imperfecciones (poros) existen sobre la superficie de la membrana, y que por ellos puede fluir el soluto y el solvente. La velocidad de permeación del agua con el soluto a través de la membrana (J_v) es:

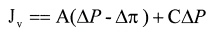
donde:

A = coeficiente de permeabilidad del agua pura

ΔP=₁diferencia de presión transmembranar

Δ π= diferencia transmembranar de presiones osmóticas

C = coeficiente de acoplamiento.

C contribución de los poros al flujo del agua.

La velocidad de permeación del soluto J_s está dada por:

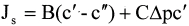
donde:

B=P_s/l

CΔc` es el flujo del soluto a través de los poros de la membrana

Para el modelo Solución-Difusión-Imperfección la retención (R') se estima como:

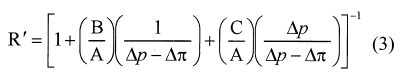
donde:
A, B y C son los mismos del modelo de solución- difusión

Cuando se hacen estimaciones de diseño con este modelo de tres coeficientes, hay serias limitaciones debido a su dependencia de la concentración y la presión (Soltanieh y Gill, 1981).

ASPECTOS METODOLÓGICOS

EXPERIMENTACIÓN

La instalación experimental se observa en la Figura 2. Consta de un tanque de alimentación con capacidad de 120 litros que recibe el agua del sistema de abastecimiento; luego ésta es impulsada por la bomba hacia la membrana en ensayo. El permeado va a un calderín que simula el proceso de producción de vapor en una caldera y el rechazo se recircula al tanque de alimentación.

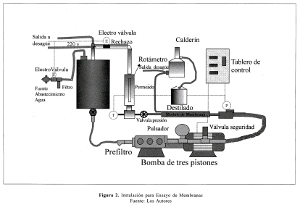
De acuerdo con los objetivos de la investigación de hacer acondicionamiento de aguas para calderas empleando membranas de poros finos que permitan reemplazar el proceso típico del intercambio iónico, se seleccionaron membranas altamente selectivas que eliminan hasta el 99.6 % de iones bivalentes como los de calcio, que producen depósitos importantes en las calderas.

Las membranas escogidas son poliméricas (poliamida/polisulfona), en módulo de espiral por su ventajosa relación entre área de membrana y volumen de permeado 4. Sus dimensiones son de 53 mm de diámetro y 1016 rnm- de longitud. Se identifican como: ESPA1-2540 (nanofiltración), CPA2-2540 y PAC-2540 AP (ósmosis inversa), y se consiguen comercialmente todas. Éstas se ensayaron en forma individual en la instalación experimental.

MODELIZACION SEGÚN EL PRINCIPIO DE SOLUCIÓN-DIFUSIÓN- IMPERFECCIÓN

Ecuaciones:

Velocidad de permeado total (J_v)

El coeficiente A de la ecuación (1) se determinó como la pendiente de la recta de (J_w) del agua destilada frente a la diferencia de presión aplicada ΔP.

Velocidad de permeado del soluto (J_s)

Primer Método:

a. Se hizo el siguiente desarrollo de la ecuación (1) para llegar a una ecuación lineal, que permite determinar el coeficiente "C₁":

b. Se obtiene un coeficiente "B" a partir de la retención " R"', ecuación (3), con lo qué se llega a la siguiente expresión:

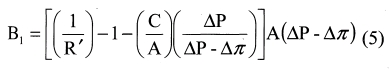
c. Una vez determinados "B 1 " y "C1", se calcula con ellos los J_s , ecuación (2), y se hace la correlación lineal:

De donde se obtiene la ecuación de una recta, cuya representación gráfica permite la determinación de "B" y "C".

Al ser determinados "B" y "C", se calculan J_v,J_s, y R, los cuales se comparan con los observados.

Retención de soluto (R)

Con A, B y C obtenidos se calcularon las retenciones "R", para comparar con las observadas.

Segundo Método:

a. Se hallan los L a utilizar en el siguiente paso como el producto de los J_vo * C_so, ambos observados.

b. Se hace el siguiente desarrollo para llegar a una representación lineal, que permite determinar los coeficientes "B" y "C".

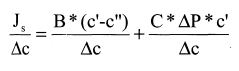
Por consiguiente, queda:

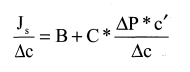
De donde se obtiene la ecuación de una recta, cuya representación gráfica permite la determinación de "B" y "G".

b. Una vez determinados "B" y "C", se calculan J_v, J_s y R, los cuales se comparan con los observados.

EVALUACIÓN DEL MODELO

Para establecer la aproximación del modelo a los datos experimentales, se utilizó una función objetivo, la cual se especificó como FOT (función objetivo total) si se refería a tener en cuenta la información experimental para todas las concentraciones de cloruro de sodio.

La función objetivo unitaria (FOU) equivale a dividir la FOT por el número de datos tenidos en cuenta, en razón de que en cada experimento y tipo de membrana resultó diferente este número, debido al comportamiento de cada membrana. Se halló la FOT de ΔJ_v(%) y ΔR(%) para cada tipo de membrana.

Con la función objetivo y con base en ΔJ_v (%) y ΔR(%) de acuerdo con las ecuaciones se hace su aplicación con cada uno de los datos obtenidos (Figuras 3 y 4).

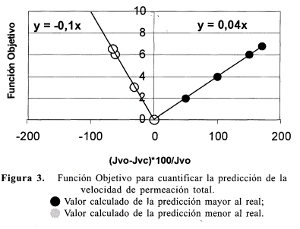
La función objetivo unitaria es menor mientras más cercano sea el modelo al comportamiento real de las membranas. Esta FOU es una forma de valorar la aproximación del modelo a los datos experimentales.

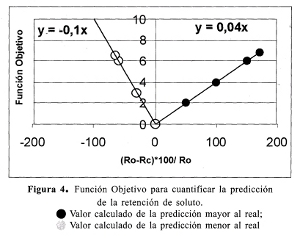
Los resultados de la modelización de las membranas se compararon con base en la función objetivo unitaria, de tal manera que la mejor modelización corresponde a la membrana que tenga la función objetivo unitaria mínima, siendo éstas las mejores predicciones, y en consecuencia es el mejor modelo para esa membrana.

RESULTADOS

Se hizo optimización y ajuste de las modelizaciones con base en las 2 ecuaciones básicas, (1) y (2). Lo anterior significa que se pueden mejorar los valores calculados afinando los de los coeficientes de cada ecuación, pero observando que el ajuste en una no induzca un desajuste en la otra.

Posteriormente los coeficientes fueron optimizados por mínimos cuadrados. Las ecuaciones de "R" y "J_v" se evaluaron y ajustaron luego de acuerdo con una función objetivo

En la Figura 5 se representa el comportamiento de la retención de solutos (%), que en este caso llega hasta el 99.6 % con la membrana ESPA1, y en la Figura 6 se presenta las comparaciones respectivas a las velocidades de permeación total (J_v), que muestra la aproximación del modelo al comportamiento experimental.

Entre los coeficientes relacionados "B/A" y "CIA", obtenidos en la modelización por correlaciones, y los hallados finalmente por optimización de la FOU mínima, en lo posible para concentraciones de 0.1%, no cambiaron significativamente, a excepcióri -de la membrana CPA2. Estos coeficientes sí tuvieron un cambio significativo cuando a partir de los coeficientes de la modelización se hizo su optimización general (con toda la información) por mínimos cuadrados/Sin embargo, esta optimización general no es la más indicada para esta aplicación, puesto que las predicciones que hace son en gran parte de estimación con exceso a la retención real, lo cual no es lo más conveniente, puesto que esperar retenciones superiores a las reales es estimar un mejor comportamiento de las membranas en comparación con el que realmente tienen.

De acuerdo a la Tabla 1, después de optimizaciones, se puede decir que la membrana PAC es la rrie -nos porosa, lo cual no implica que sea la de mayor retención, ya que en ella no sólo influye este factor, y según el model6 en cuestión, para unas mismas condiciones de presión efectiva aplicada y de solución de alimentación, va a depender también de "A" y "C".

En general, las predicciones de la retención que se alcanzaron con este modelo fueron más cercanas a los valores reales, en comparación con el modelo solución-difusión.

La variación media en la predicción de la retención, estimado entre todos los datos experimentales y calculados de las membranas, fue del 0.17%, y de acuerdo a la FOU, el error apenas sí se llega a aproximar al 0.1%, donde la membrana que alcanzó las mejores predicciones fue la CPA2, cuyo error de predicción se puede estimar en 0.06%, según se observa en la Tabla 1.

CONCLUSIONES

· El modelo basado en el principio de solución- difusión-imperfección representa en forma correcta el comportamiento de las membranas de ósmosis inversa y nanofiltración, por cuanto tiene en cuenta no sólo el transporte a través de la membrana por el proceso de solución-difusión, sino el flujo viscoso que ocurre por la presencia de una fuerza externa que actúa en los poros de la membrana, alcanzando así este modelo una mayor aproximación en la predicción del comportamiento de la ósmosis inversa.

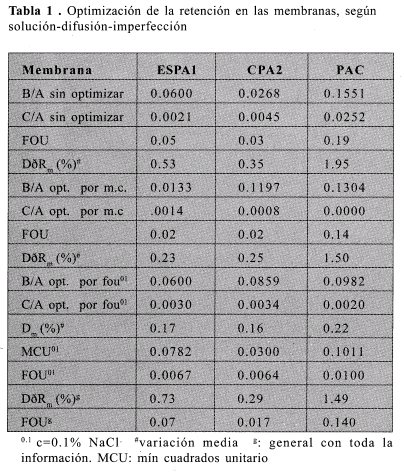
· La retención de solutos de acuerdo con el modelo de solución-difusión-imperfección, depende no sólo de la presión efectiva transmembranar, sino de los coeficientes "A", "B" y "C", de tal forma que mientras sean menores las relaciones "B/A" y "C/A", la retención será mayor.

· Los coeficientes "C" que se escogieron fueron los calculados por el segundo método de ajuste de "J_s", por ser los más consecuentes con el comportamiento de las membranas.

· Los resultados indican que gran parte del permeado va a pasar por la membrana debido a que cada componente de la solución de alimentación se disuelve, y luego se difunde en ella, por diferencias de concentración y de presión que se crean a ambos lados de la membrana, y que el flujo viscoso es el menor valor, variando para cada membrana como lo ilustran los resultados.

· Para todas las membranas, las predicciones de "J_s" siguen la tendencia de los datos experimentales, siendo más notable esta condición a concentraciones del 0.1 %, para las cuales se buscó el mayor ajuste del modelo.

· La optimización general (con toda la información) por mínimos cuadrados no es la más indicada para estos modelos, donde las predicciones que se obtienen no consultan la diferencia entre las estimaciones con exceso y las hechas con defecto a la retención real, lo cual no es igual desde el punto de vista práctico.

· La retención tuvo una variación media del 0.17 % en las predicciones, y de acuerdo a la FOU (función objetivo unitaria) el error apenas si llega a aproximarse al 0,1 %. La membrana que alcanzó las mejores predicciones fue la CPA2, con un error del 0.06 %.

· Las predicciones de la retención obtenidas con este .modelo son más próximas a los valores experimentales, en comparación con las del modelo solución-difusión, en virtud del reconocimiento de las imperfecciones de las membranas.

· Las correlaciones que se basan en la retención y la velocidad de permeación del soluto obtenida experimentalmente para modelizar "J_s", son herramientas útiles para acceder a unos coeficientes "B" y "C" en la búsqueda de un buen ajuste. Los indicadores MCU (mínimos cuadrados unitario), FOU y ΔJ_s, así lo demuestran.

· La modelización bajo el principio de solución-difusión-imperfección se verifica en esta investigación como una precisión más del principio fundamental de la solución-difusión.

· La velocidad de permeación total es resultante de la optimización de "J_s", y se puede ver cómo este modelo da un mayor acercamiento de los valores calculados a los experimentales, en comparación con el modelo solución-difusión.

RECONOCIMIENTOS

Por su apoyo institucional y financiero a la Fundación para el Fomento en Asturias de la Investigación Científica Aplicada y la Tecnología (FICYT), a la Facultad del Medio Ambiente y Recursos Naturales de la Universidad Distrital Francisco José de Caldas de Bogotá D.C. (Colombia) y al Departamento de Ingeniería Química y Tecnología del Medio Ambiente de la Universidad de Oviedo (España).

REFERENCIAS BIBLIOGRAFICAS

LUQUE, S. y ÁLVAREZ, J.R. 2000. "Notas del Curso sobre Tecnologías Límpias", Departamento de Ingeniería Química y Tecnología del Medio Ambiente, Universidad de Oviedo, España.

MULDER, M. 1991. "Basic Principles of Membrane Technology", Kluwer Academic Publishers, Dordrecht, Netherlands.

OSADA, Y., NAKAGAWA, T. 1988. "Membrane Science and Technology", Marcel Dekker, New York.

PERRY, M., LINDER, C. 1999. "Alternative Separation Processes", en Chemical Engineering Processes, pp. 22-48 a 22-52.

SOLTANIETH, M., GILL, W. 1981. Review of osmosis membranes and transport models. Chemical Engineering Communications, 12, 279-363.

SOURIRAJAN, S. 1964. Ind. Eng. Chem. Fundamentals Quarterly 3, 206.