Aplicación del modelo de poros finos en el acondicionamiento de aguas para calderas

Artículos de investigación científica y tecnológica

Colombia Forestal, 2005-11-00 vol:9 nro:18 pág:149-156

Aplicación del modelo de poros finos en el acondicionamiento de aguas para calderas

Carlos F. García Olmos

Universidad Distrital Francisco José de Caldas
cfgarciao@udistrital.edu.co

José R. Álvarez Sáiz

Susana Luque Rodríguez

José Coca Prados

Universidad de Oviedo
jep@uniovi.es

Resumen

Esta investigación se desarrolló con el propósito de reemplazar el proceso de intercambio iónico en el acondicionamiento de aguas para calderas, debido a las ventajas de tipo técnico, ambiental y económico que tienen las tecnologías limpias que utilizan membranas, como es el caso de la ósmosis inversa.

En las membranas de poros finos hay acoplamiento entre el flujo de solvente y solutos, pero en un grado mucho menor que en las membranas de flujo viscoso. Éstas fueron reportadas por Sourirajan (1964). Para ellas se han propuesto varios modelos, tal como el presentad() por. Merten (1966), del que se deriva esta aplicación.

En este trabajo se utilizaron tres membranas poliméricas en espiral (ESPA1, CPA2 y PAC). Los coeficientes utilizados en las ecuaciones para su modelización se determinaron de forma experimental a partir de los datos de flujos y conductividades. El modelo de poros finos fue optimizado con el algoritmo de los mínimos cuadrados y ajustado con una función objetivo. La aplicación del modelo se hizo utilizando sus predicciones de flujo total y retención de solutos en el diseño de un sistema de acondicionamiento de aguas para caldera.

Palabras claves:
Modelización, poros finos, acondicionamiento de aguas, membranas, ósmosis inversa.

Abstract

This investigation deals with the use of an intermediate membrane category for boiler water conditioning, in which the joining of the flows exists, but in a much smaller degree that In the viscous flow. In this work, different models have been proposed for this membrane application, such that represent these intermediate characteristics, as those reported by Sourirajan (1964) for cellulose acetate low-porous membranes.

Three spiral polymeric reverse osmosis membranes (ESPA1, CPA2 and PAC) were used. Coefficients used in the model equations were obtained from flow and conductivity experimental data using these membranes.

The model was optimized by means of the least squares algorithm and adjusted with a function objective, to obtain definitive coefficients for each membrane. Finally, model predictions were used for a boiler water conditioning system design.

Key words:
Modelling, fine pores, water conditioning.membranes, reverse osmosis.

INTRODUCCIÓN

En las plantas térmicas para generación de energía eléctrica se utilizan las calderas. Ellas cumplen un ciclo termodinámico del agua, con su calentamiento, evaporación, expansión en la turbina y condensación (ciclo líquido-vapor). En la expansión ocurre el paso de energía térmica a energía eléctrica.

El agua para uso industrial en calderas requiere alta calidad, entendida especialmente a que en ella haya una baja concentración de iones bivalentes, en particular de calcio, magnesio y otros contaminantes (concentraciones menores al 0,06 gramos/litro), debido a que por las altas temperaturas a que es sometida, se disminuye la solubilidad de sales como el carbonato de calcio, produciendo precipitados denominados depósitos, en las paredes y conducciones de la caldera.

Los depósitos en las calderas pueden causar recalentamiento, como también restricciones en la circulación del agua. La calidad de agua requerida se logra al aplicarle un pretratamiento de acondicionamiento.

Para obtener la calidad del agua para la alimentación de la caldera se suele utilizar un proceso de intercambio iónico, que tiene como problema añadido el de que las resinas se ensucien y requieran limpiarse y regenerarse en determinado tiempo, con mayor coste en la operación del sistema, y resultando como residual un efluente de agua altamente contaminante, con efectos ambientales si no se le maneja en forma adecuada.

Como solución al problema planteado se propone el uso de las técnicas con membranas, específicamente de nanofiltración y ósmosis inversa, como pueden ser las que se comportan según el modelo de poros finos, que reducen los inconvenientes comentados y se espera que se puedan emplear como alternativa de solución para sustituir total o parcialmente las resinas de intercambio iónico.

Desde hace mucho tiempo se conoce la capacidad de las membranas para separar, pero sólo hasta 1960 tienen alguna importancia con Loeb y Sorirajan, cuando consiguieron la primera membrana sintética simétrica, utilizada en la obtención de agua potable a partir de agua de mar, y desde entonces esta técnica ha evolucionado mucho, y se han obtenido membranas de muy variadas condiciones, resistentes a diversos agentes químicos.

Los procesos con membranas han tenido un aumento en aplicaciones en el tratamiento del agua para la industria, debido a diversas ventajas, cuando son comparados con procesos alternativos:

· Bajos requerimientos de energía, puesto que no involucran un cambio de fase en función de la temperatura.

· Proceso en continuo, lo cual permite un control automático y una operación estable.

· Bajos costos de mantenimiento, puesto que el sistema tiene un mínimo de partes móviles y es fácil de operar y mantener. Son más rápidos y económicos que las técnicas que tradicionalmente se habían venido aplicando (Coca, J., Luque, S., 1999).

· Es fácil realizar el cambio de escala, y no es necesario agregar nuevos componentes para llevar a cabo la separación, hechos que la hacen una tecnología atractiva, que tiene un crecimiento grande en su empleo.

En la década de los años setenta los procesos con membranas emergieron como una tecnología limitada y costosa que podría usarse con aguas salobres. Estos sistemas de alto costo limitaban los procesos de ósmosis inversa, hasta que aparecieron las configuraciones de módulos en espiral que permitieron una conipetitividad, al reducirse los costos.

Sourirajan (1964) estableció inicialmente que las membranas de acetato de celulosa poco porosas podían ser progresivamente modificadas por tratamiento al calor para llegar a ser cada vez más selectivas, hasta que sus propiedades se aproximaran a las membranas de solucióndifusión, y son las denominadas como de poros finos.

En las membranas de poros finos el acoplamiento de los flujos de solutos y solvente existe a través de ellas, pero en un grado mucho menor que en las membranas de flujo viscoso. En esta investigación se hizo la modelización de estas membranas, identificadas en su comportamiento por Sourirajan (1964), con aplicación al acondicionamiento de aguas para calderas.

PRINCIPIO DE LOS POROS FINOS

Una membrana con gran cantidad de poros se caracteriza por su flujo viscoso, en el cual el acoplamiento es su característica principal. La velocidad de permeación total a través de una membrana altamente porosa puede expresarse por la ley de Poiseuille:

Donde,

En el modelo de poros finos se tienen en cuenta fuerzas de fricción que no solo afectan a la permeabilidad de 'la membrana al soluto, sino que también lo hacen con su permeabilidad hidrodinámica.

La fuerza de fricción por unidad de volumen en los poros del fluido debe añadirse al gradiente de presión para hallar la fuerza total que actúa por unidad de volumen en los poros del fluido.

Añadiendo a la ecuación (1) la fuerza externa, se puede expresar para soluciones diluidas:

Donde,

Sobre cada molécula de soluto, como resultad() de su interacción con el material de la membrana. Esta es una fuerza externa debida a la interacción del soluto y la membrana, y es la fuerza por mol multiplicada por la concentración molar del fluido en los poros, X_AM/εM_S, siendo "M_S" el peso molecular del soluto y "ε" la fracción de poros de la membrana, y donde:

El flujo volumétrico puede calcularse como una función de la presión a través de los poros de la membrana, con base en la ecuación (2) y teniendo en cuenta que J_s=J_v, c_s:

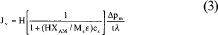
Donde,

c_s= concentración del permeado (mol/litro)

t = factor de tortuosidad, que indica que la longitud de poros es mayor que el espesor de la membrana

Mediante una serie de simplificaciones matemáticas, se llegó a la siguiente expresión:

Donde,

A= HC/λ= R²_w C / (8µ (tλ/ε)); unidades: (litros/m2 .h.bar) es el coeficiente de permeabilidad del agua pura, que se obtiene como la pendiente de la recta de "j_w", que es la velocidad de permeación del agua destilada contra la diferencia de presión aplicada ΔP.

B= X_AM (HC/tλ) (tλ/ε) (litros/mol) determina el flujo de solutos a través de los poros de la membrana. En "B" se condensan características muy importantes de la membrana, como su permeabilidad hidrodinámica y su densidad de poros, y características de interacción de la membrana con el fluido y su composición, como es el coeficiente de fricción entre el soluto y la membrana, y la densidad molar del fluido. El coeficiente "B" determina una mayor o menor facilidad de los solutos a pasar a través la membrana.

ΔP= diferencia de presión transmembranár (bar)

ΔΠ= diferencia de presión osmótica a través de la membrana (bar)

Spiegler et al. (1958) han presentado tratamientos extensivos de modelos sobre fricción en membranas.

De acuerdo con el modelo de poros finos, la retención se calculó como:

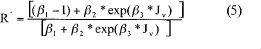
β_i, β₂, y β₃" son coeficientes que dependen de las características del soluto, solvente y membrana (Álvarez S., 2000) y "J_v," es la velocidad de permeación total.

EXPERIMENTACIÓN

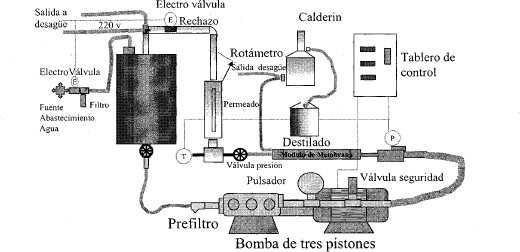
La instalación experimental se observa en la Figura 1. Consta de un tanque de alimenta ción con capacidad de 120 litros que recibe el agua del sistema de abastecimiento; luego ésta es impulsada por la bomba hacia la membrana en ensayo. El permeado va a un calderín que simula el proceso de producción de vapor en una caldera, y el rechazo recircula al tanque de alimentación.

De acuerdo con los objetivos de la investigación de lograr acondicionamiento de aguas para calderas, empleando membranas de poros finos que permitan reemplazar el proceso típico del intercambio fónico, se seleccionaron membranas altamente selectivas que eliminan hasta el 99.6% de iones bivalentes como los de calcio, que producen depósitos considerables en las calderas. Las membranas escogidas son poliméricas (poliamida/polisulfona), en módulo de espiral por su ventajosa relación entre área de membrana y volumen de permeado (Mulder, 1996). Sus dimensiones son de 53 mm de diámetro y 1016 mm de longitud. Se identifican como: ESPA1-2540 (nanofiltración), CPA2-2540 y PAC-2540 AP (ósmosis inversa), y se consiguen comercialmente todas. Éstas se ensayaron en forma individual en la instalación experimental.

RESULTADOS

Se hizo optimización y ajuste de las modelizaciones con base en las dos ecuaciones básicas (4 y 5), que son optimizables y de forma independiente. Ello significa que se pueden optimizar en forma separada los coeficientes de cada ecuación, sin que el ajuste en una ecuación induzca un desajuste en la otra. La determinación de los coeficientes " β₁ β₂ y β₃" en la ecuación de la retención se hizo con una regresión no lineal de los datos experimentales. Luego estos coeficientes fueron optimizados por mínimos cuadrados.

Para la velocidad de permeación total "J"_v" se determinó "B" directamente por mínimos cuadrados. Las ecuaciones de "R" y "J_v se evaluaron y ajustaron luego de acuerdo con una función objetivo.

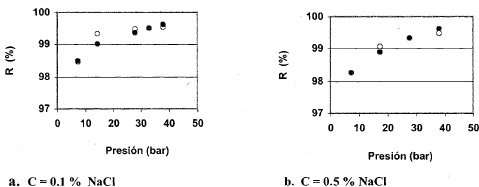
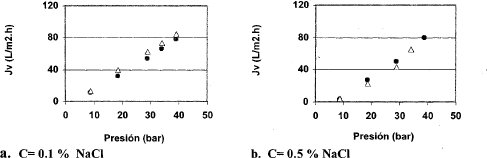
En la Figura 2 se representa el comportamiento de la retención de solutos (%), que en este caso llega hasta el 99.7 % con la membrana ESPA1, y en la Figura 3 se presentan las comparaciones respectivas a las velocidades de permeación total (J_v).

La ecuación (4) sirve para estimar el flujo que se produce por solución-difusión, y también el que se produce por las imperfecciones de los poros, y además la reducción de la velocidad de permeación si hay resistencia a perméar por parte de la membrana, bloqueo de poros, adsorción, formación de capa de gel, polarización de la concentración, o ensuciamiento (García O., 2002). Así es que:

Si B < O, ocurre permeación por solución-difusión, más permeación por poros finos.

Si B > O, ocurre permeación por solución-difusión, reducida por las resistencias.

Si B = O, ocurre sólo permeación por solución-difusión.

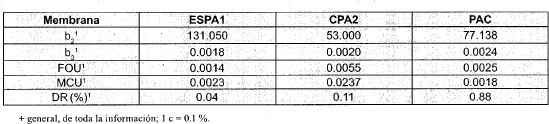
Con base en los resultados de la modelización, Tabla 1, las membranas ESPA1 y PAC permiten el flujo viscoso por sus imperfecciones de pequeños poros, en una magnitud proporcional al diámetro medio de ellos.

Igualmente se considera que la membrana CPA2 experimenta una resistencia a permear, que hace que tenga velocidades de permeación menores a las de la solución-difusión. Sin embargo, este resultado tendrá que contrastarse con análisis que se hagan en modelizaciones por disolución-difusión-imperfección y termodinámica irreversible.

Los resultados de la modelización de "J_v" ya habían quedado optimizados por mínimos cuadrados, por haber sido el método de determinación de "B"; así es que luego se optó por aplicar un proceso de minimización de la Función Objetivo Unitaria "FOU" a "J_v,". La función objetivo es una función lineal que para "J_v" califica las predicciones obteniendo un valor menor de la función cuando las predicciones son menores a los datos experimentales y viceversa. El mejor ajuste de acuerdo con las predicciones deseadas es el de la membrana PAC (véase Tabla 1).

La función objetivo unitaria es la función objetivo dividida entre el número de datos, y la MCU es la suma de los mínimos cuadrados de las diferencias entre valores observados y calculados dividida entre el número de datos.

Para la retención "R", por correlación exponencial entre 1/(1-R) y J_v, se determinaron unos coeficientes "β" que resultaron ajustados a los datos experimentales, como lo demuestran los indicadores MCU, FOU y ΔR de los resultados en la Tabla 2, tanto a nivel general como para concentraciones del 0.1%, destacando la ESPA1 como la más cercana al tipo de predicciones que se busca.

Los indicadores de correlación "R 2", obtenidos de relacionar "1/(1-R)" con "J_v " en forma exponencial, no fueron altos, pero eso sí, fue, posible obtener un buen ajuste de los valores experimentales a los predichos posteriormente, sobre todo si se tiene en cuenta que desde un principio ya se hallaron con la ecuación de la retención valores bajos de la FOU (de 0.02 a 0.035), que permiten su aceptación, aun sin procesos posteriores de optimización.

La optimización de la expresión obtenida de "R" con la mínima FOU, con especial interés en concentraciones del 0.1 %, obtuvo como resultado reducciones de por lo menos 3 veces de la FOU, respecto a las determinaciones antes de este proceso.

En general, la membrana con que se obtuvieron mejores ajustes de la retención fue la ESPA1, con un nivel medio de error del 0.014%.

CONCLUSIONES

· Con la aplicación del modelo de poros finos se logró simular adecuadamente el comportamiento de las membranas poliméricas (poliamida/polisulfona) en el proceso de permeación que permite acondicionar el agua para calderas, y reemplazar el de intercambio fónico.

· Mediante esta investigación se obtuvieron unas ecuaciones de carácter aplicativo práctico del modelo de poros finos presentado por Merten (1964), donde los coeficientes se determinan con los datos experimentales del proceso de permeación de las membranas, evitando tener que determinar sus características físicas propias como su espesor y relación de poros, no siempre disponibles.

· La ecuación simplificada de la velocidad de permeación permite estimar todos los comportamientos que se pueden presentar en las membranas, como el de disolución difusión, flujo acoplado como el viscoso, y el de flujo intermedio entre los anteriores, o sea el de poros finos.

· El comportamiento de las membranas ensayadas se pudo representar mediante el modelo de poros finos cuya aplicación se obtuvo, pero con mayor fidelidad para el comportamiento de la membrana ESPA1,que para la retención obtuvo un nivel medio de error del 0.014%.

RECONOCIMIENTOS

Por su apoyo institucional y financiero a la Fundación para el Fomento en Asturias de la Investigación Científica Aplicada y la Tecnología (FICYT), a la Facultad del Medio Ambiente y Recursos Naturales de la Universidad Distrital Francisco José de Caldas de Bogotá (Colombia) y al Departamento de Ingeniería Química y Tecnología del Medio Ambiente de la Universidad de Oviedo (España).

REFERENCIAS BIBLIOGRÁFICAS

• ÁLVAREZ, J. R., 2000. "Notas sobre el modelo de poros finos." Departamento de Ingeniería Química y Tecnología del Medio Ambiente, Universidad de Oviedo, España.
• GARCÍA O., C. F., 2002. "Aplicación de la ósmosis inversa y la nanofiltración en el acondicionamiento de aguas para calderas". Departamento de Ingeniería Química y Tecnologíá del Medio Ambiente, Universidad de Oviedó,Tesis Doctoral.
• MERTEN, U., 1966. Desalination by reverse osmosis. Massachusetts Institute of Technology.
• MULDER, M., 1996. Basic Principles of Membrane Technology. Kluwer Academic Publishers, Dordrecht, Netherlands.
• SOURIRAJAN, S., 1964. Ind, Eng. Chem.Fundamentals Quarterly 3, 206.
• SPIEGLER, K. S., 1958. Trans. Faraday Soc.54, 1408.