DOI:
https://doi.org/10.14483/25009311.12935Publicado:
2018-01-09Número:
Vol. 4 Núm. 4 (2018): enero-junioSección:
Sección CentralSimbiosis: Composición para bandola andina colombiana y entidades sónicas
Simbiosis: Composition for Colombian Andean Bandola and sonic entities
Palabras clave:
Aprendizaje automático, composición algorítmica, computación evolutiva, electrónica evolutiva, entidades sónicas, relaciones simbióticas (es).Palabras clave:
Automatic learning, algorithmic composition, evolutionary computation, evolutionary electronics, sonic entities, symbiotic relationships (en).Descargas
Referencias
Alfonseca, M., Cebrián, M., y Ortega, A. (2007). A Simple Genetic Algorithm for Music Generation by Means of Algorithmic Information Theory. En 2007 IEEE Congress on Evolutionary Computation. pp. 3035–3042. https://doi.org/10.1109/CEC.2007.4424858
Amiot, E. (2007). David Lewin and Maximally Even Sets. Journal of Mathematics and Music, 1 (3), 157–172. https://doi.org/10.1080/17459730701654990
Asimov, I. (1984). Asimov’s New Guide to Science. New York: Basic Books. Basharin, G. P., Langville, A. N., y Naumov, V. A. (s.f.). The Life and Work of a. a. Markov. PMid:6237023
Buchler, M. (2000). Broken and Unbroken Interval Cycles and Their Use in Determining Pitch-class Set Resemblance. Perspectives of New Music, 52–87. https://doi.org/10.2307/833659
Callender, C. (2007). Continuous Harmonic Spaces. Journal of Music Theory, 51 (2), 277–332. https://doi.org/10.1215/00222909-2009-004
Casta-eda, A. A. E. (2016). Máquinas sonoras: Aplicaciones de las ciencias de la complejidad a la creación musical y sonora (Tesis Doctoral no publicada). Universidad Autónoma de México, Facultad de Música.
Collins, T., Laney, R., Willis, A., & Garthwaite, P. H. (Diciembre de 2011). Chopin, Mazurkas and Markov. Significance, 8(4), 154-159.
Cope, D. (2001). Virtual Music. Cambridge: The MIT Press.
Childs, E. (2002). Achorripsis: A sonification of Probability Distributions.
Ching, W. K., y Ng, M. K. (2006). Markov Chains. Springer.
Dodge, C., y Jerse, T. A. (1997). Computer Music: Synthesis, Composition and Performance. Macmillan Library Reference.
Donnelly, P., y Sheppard, J. (2011). Evolving Four-part Harmony Using Genetic Algorithms. En European Conference on the Applications of Evolutionary Computation (pp. 273–282). https://doi.org/10.1007/978-3-642-20520-0_28
Dunn, F., Hartmann, W., Campbell, D., Fletcher, N., y Rossing, T. (2015). Springer Handbook of Acoustics.
Fernández, J. D., y Vico, F. (2013). AI Methods in Algorithmic Composition: A Comprehensive Survey. Journal of Artificial Intelligence Research, 48, 513–582.
Forte, A. (1973). The Structure of Atonal Music (Vol. 304). Yale: Yale University Press.
Haeckel, E. H. P. A., Miquel, S. S., y Senti-ón, G. (1887). Morfología general de los organismos. Blas Carrera.
Hanson, H. (1960). Harmonic Materials of Modern Music: Resources of the Tempered Scale. Irvington Pub. https://doi.org/10.2307/3389365
Holland, J. H. (1992). Genetic Algorithms. Scientific American, 267 (1), 66–72. https://doi.org/10.1038/scientificamerican0792-66
Horner, A., y Goldberg, D. E. (1991). Genetic Algorithms and Computer-assisted Music Composition. Urbana, 51 (61801), 437–441.
Husbands, P., Copley, P., Eldridge, A., & Mandelis, J. (2007). An Introduction to Evolutionary Computing for Musicians. En E. R.
Miranda, & J. A. Biles, Evolutionary Computer Music (págs. 1-27). Londres: Springer-Verlag. https://doi.org/10.1007/978-1-84628-600-1_1
Isaacson, E. J. (1990). Similarity of Interval-class Content Between Pitch-class Sets: The Icvsim Relation. Journal of Music Theory, 1–28. https://doi.org/10.2307/843860
Jensen, J. H. (2011). Evolutionary Music Composition: A Quantitative Approach.
Johnson, C., Ciesielski, V., Correia, J., y Machado, P. (2015). Evolutionary and Biologically Inspired Music, Sound, Art and Design. Springer. https://doi.org/10.1007/978-3-319-12541-1
Katok, A., y Hasselblatt, B. (1997). Introduction to the Modern Theory of Dynamical Systems. (Vol. 54). Cambridge: Cambridge University Press.
Kolman, B., y Hill, D. R. (2006). Álgebra lineal. Pearson Educación.
Kurzweil, R. (2000). The Age of Spiritual Machines: When Computers Exceed Human Intelligence. Penguin Publishing Group. Descargado de «https://books.google.com.co/ books?id=lbl4MN3iUHsC»
Kurzweil, R., y Schneider, M. L. (1990). The Age of Intelligent Machines (Vol. 579). Cambridge: MIT Press Cambridge.
Lewin, D. (1959). Re: Intervallic Relations Between Two Collections of Notes. Journal of Music Theory, 3(2), pp. 298–301. https://doi.org/10.2307/842856
López-Montes, J. (2013). Genomus. Prospección de técnicas de creatividad asistida por computadora mediante la metaprogramación de genotipos musicales (Tesis de Master no publicada). Universidad Rey Juan Carlos. Facultad de Ciencias del Turismo, Departamento de Ciencias de la Educación, el Lenguaje, la Cultura y las Artes.
Miranda, E. R., y Al Biles, J. (2007). Evolutionary Computer Music. Springer. https://doi.org/10.1007/978-1-84628-600-1
Mitsaigs, S. H. I. C. (s.f.). Set Theory in Xenakis’ Eonta.
Nierhaus, G. (2009). Algorithmic Composition: Paradigms of Automated Music Generation. Springer Science & Business Media. https://doi.org/10.1007/978-3-211-75540-2
Oxford Living Dictionaries. (2016, November). «https:// en.oxforddictionaries.com/definition/stochastic»
Pope, S. T. (1993). Music Composition and Editing by Computer. Oxford: Oxford University Press.
Purcel, E. J., & Valberg, D. (1992). Cálculo con geometría analítica. Naucalpan: Prentice Hall Hispanoamérica, S.A.
Quinn, I. (2006). General Equal-tempered Harmony (introduction and part I). Perspectives of New Music, 114–158.
Roeder, J. (1987). A Geometric Representation of Pitch-class Series. Perspectives of New Music, 362–409.
Ross, K & Wright, C. (1990). Matemáticas Discretas. México D.F.: Prentice Hall.
Sánchez, G. L. F. (2017a). Del suspiro en el alba hasta el abrazo en el ocaso: una composición evolutiva. Bogotá: Universidad Distrital Francisco José de Caldas.
Sánchez, G. L. F. (2017b). Estrategias de organización. Bogotá: Universidad Distrital Francisco José de Caldas.
Schillinger, J. (1948). The Mathematical Basis of the Arts.
Scott, D., y Isaacson, E. J. (1998). The Interval Angle: A Similarity Measure for Pitchclass Sets. Perspectives of New Music, pp. 107–142. https://doi.org/10.2307/833526
Sethares, W. A. (2005). Tuning, Timbre, Spectrum, Scale. Springer Science & Business Media.
Shafranovich, Y. (2008). Common Format and Mime Type for Comma-separated Values (csv) Files. [sl], 2005. Disponible en: «http://www.ietf.org/rfc/rfc4180.txt.»
Sher, C. (1988). The New Real Book: Jazz Classics, Choice Ctandards, Pop-fusion Classics: Created by Musicians, for Musicians (Vol. 1). Sher Music Co. PMid:22359165
Smalley, D. (1986). Spectro-morphology and Structuring Processes. En The language of Electroacoustic Music, pp. 61–93. Springer. https://doi.org/10.1007/978-1-349-18492-7_5
Smalley, D. (1997). Spectromorphology: Explaining Sound-Shapes. Organised Sound, 2 (02), pp. 107–126. https://doi.org/10.1017/S1355771897009059
Solomos, M. (2011). Xenakis First Compositon in Musique Concrete: Diamorphoses. En Xenakis International Symposium.
Teitelbaum, R. (1965). Intervallic Relations in Atonal Music. Journal of Music Theory, 9 (1), pp. 72–127. https://doi.org/10.2307/843150
Turing, A. (1950). Computing Machinery and Intelligence. Mind, 49, pp. 433-460. https://doi.org/10.1093/mind/LIX.236.433
Udvardy, M. F. (1959). Notes on the Ecological Concepts of Habitat, Biotope and Niche. Ecology, 40 (4), pp. 725–728. https://doi.org/10.2307/1929830
Von Zur Gathen, J., y Gerhard, J. (2013). Modern Computer Algebra. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139856065
Vriend, J. (1981). “Nomos alpha” for Violoncello Solo (Xenakis 1966), Analysis and Comments.
Vuza, D. T. (1991). Supplementary Sets and Regular Complementary Unending Canons (part one). Perspectives of New Music, pp. 22–49. https://doi.org/10.2307/833429
Williams, G. (2012). Linear Algebra with Applications. Jones & Bartlett Publishers.
Xenakis, I. (1992). Formalized Music: Thought and Mathematics in Composition (n°.6). Pendragon Press.
Zattra, L. (2005). Analysis and Analyses of Electroacoustic Music. Sound and Music Computing (SMC05), Salerno, Italia, 36. PMid:15917707
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita

Simbiosis: Composición para bandola andina colombiana y entidades sónicas
Simbiosis: Composition for Colombian Andean Bandola and sonic entities
Simbiosis : Composition pour bandola andine colombienne et des entités soniques
Simbiose: Composição para bandola andina colombiana e entidades sônicas
Estudios Artísticos
Universidad Distrital Francisco José de Caldas, Colombia
ISSN: 2500-6975
ISSN-e: 2500-9311
Periodicidad: Semestral
vol. 4, núm. 4, 2018
Recepción: 20 Septiembre 2017
Aprobación: 28 Octubre 2017
Resumen: La relación entre el ser humano y la máquina, desde una perspectiva simbiótica, posibilita un nuevo paradigma para comprender, concebir y percibir el sonido, lo cual nos permite experimentar situaciones creativas sustancialmente innovadoras, siendo fundamental el caos, el indeterminismo y la aleatoriedad. Simbiosis, es una composición en donde se pretende aplicar algunos conceptos y técnicas de la inteligencia artificial, la computación evolutiva y estrategias bio-inspiradas; es decir, mecanismos de programación basados o inspirados en procesos de evolución y selección biológica. Em este artículo, resultado de un proyecto de investigación-creación, se pretende extrapolar el concepto simbiosis en una composición musical, pretende explorar las relaciones que pueden surgir entre un intérprete humano y la máquina, en este caso una población de entidades sónicas autónomas, esta relación simbiótica es determinada, controlada y/o direccionada por un director/interprete (mentor) en tiempo real.
Palabras clave: Aprendizaje automático, composición algorítmica, computación evolutiva, electrónica evolutiva, entidades sónicas, relaciones simbióticas.
Abstract: The relationship between the human being and the machine, from a symbiotic perspective, enables a new paradigm to understand, conceive and perceive sound, which allows us to experience substantially innovative creative situations with chaos, indeterminism and randomness as fundamental components. Simbiosis is a composition that intends to apply some concepts and techniques of artificial intelligence, evolutionary computation and bio-inspired strategies; that is, of programming mechanisms based on or inspired by processes of evolution and biological selection. This article, the result of a research-creation project, aims to extrapolate the concept of symbiosis in a musical composition, in order to explore the relationships that may arise between a human interpreter and the machine, in this case a population of autonomous sonic entities. This symbiotic relationship is determined, controlled and / or directed by a director / interpreter (mentor) in real time.
Keywords: Automatic learning, algorithmic composition, evolutionary computation, evolutionary electronics, sonic entities, symbiotic relationships .
Résumé: La relation entre l’être humain et la machine, d’un point de vue symbiotique, permet un nouveau paradigme pour comprendre, concevoir et percevoir le son, ce qui nous permet de vivre des situations créatives essentiellement innovantes et ayant comme des éléments fondamentaux le chaos, l’indéterminisme et le hasard. Simbiosis est une composition où nous essayons d’appliquer quelques concepts et techniques d’intelligence artificielle, de calcul évolutif et de stratégies bio-inspirées : c’est-à-dire des mécanismes de programmation basés ou inspirés par des processus d’évolution et de sélection biologique. Cet article, fruit d’un projet de recherche-création, vise à extrapoler le concept de symbiose dans une composition musicale, afin d’explorer les relations qui peuvent naître entre un interprète humain et la machine, dans ce cas une population d’entités sonores autonomes. Cette relation symbiotique est déterminée, contrôlée et / ou dirigé par un directeur / interprète (mentor) en temps réel. Mots clés Apprentissage automatique, composition algorithmique, calcul évolutif, électronique évolutive, entités sonores, relations symbiotiques. Simbiose: Composição para bandola andina colombiana e entidades sônicas
Resumo: A relação entre o ser humano e a máquina, desde uma perspectiva simbiótica, possibilita um novo paradigma para compreender, conceber e perceber o som, o que nos permite experimentar situações criativas substancialmente inovadoras, sendo fundamental o caos, o indeterminismo e a aleatoriedade. Simbiosis é uma composição na qual se pretende aplicar alguns conceitos e técnicas da inteligência artificial, da computação evolutiva e estratégias bio-inspiradas; isto é, mecanismos de programação baseados ou inspirados em processos de evolução e seleção biológica. Este artigo, resultado de um projeto de pesquisa-criação, pretende extrapolar o conceito simbiosis em uma composição musical, com o fim de explorar as relações que podem surgir entre um intérprete humano e a máquina, neste caso uma população de entidades sônicas autônomas, esta relação simbiótica é determinada, controlada e/ou direcionada por um diretor/intérprete (mentor) em tempo real.
Palavras-chave: Aprendizagem automática, composição algorítmica, computação evolutiva, eletrônica evolutiva, entidades sônicas, relações simbióticas.
With intelligences of different species and genera, there is the possibility at least of a symbiotic relationship, in which all will cooperate to learn how best to understand the laws of nature and how most benignly we might cooperate with them. Certainly, the cooperation will do better than any intelligence variety on its own.
Isaac Asimov, Asimov’s New Guide to science
En mucha de la literatura de ciencia ficción ha habido sistemas informáticos de inteligencia artificial capaces de enfrentar procesos creativos o actividades que muchas veces se atribuyen como aptitudes netamente humanas, un ejemplo de ello es el holograma médico de emergencia de la serie Star Trek: Voyager, el cual, debido a su programación adaptativa llego a desarrollar gustos y habilidades para la dramaturgia, la fotografía, la opera e incluso llego a sostener relaciones románticas. Actualmente las investigaciones en el campo de la ciencia, la ingeniería y la computación se orientan hacia el estudio de las interacciones entre el ser humano y la máquina, aspirando a programar maquinas con un sentido del mundo, capaces de aprender y entender, esto con el fin de diseñar sistemas simbióticos que aumenten el rendimiento humano. Es por esto que el presente proyecto de investigación nace de la fascinación por la interacción entre el ser humano y la máquina, la composición musical algorítmica como estrategia para encontrar nuevas formas de creación y percepción del sonido; además del gusto por la programación, la Inteligencia Artificial (I.A.) y la ciencia.
Métodos y Técnicas de Inteligencia Artificial
Componer música implica una serie de actividades y procesos, los cuales pueden ser automatizados mediante el uso de computadoras, a esto se le denomina composición algorítmica. En consecuencia, se han desarrollado varias técnicas computacionales vinculadas con la IA (Pope, 1993). Tres puntos de partida para la investigación del estado del arte de la música asistida por ordenador son Computer Music Journal1, International Computer Music Conference, organizada anualmente por la International Computer Music Association,2 y en especial la que más compete al presente trabajo de investigación-creación por su enfoque en la computación evolutiva: EvoMusart (Evolutionary and Biologically Inspired Music, Sound, Art and Design), organizada anualmente por Evostar3 (Johnson y cols., 2015). Algunos autores han realizado varias sistematizaciones y/o taxonomías de los métodos de IA usados en la composición algorítmica, entre ellos están Nierhaus (2009) y Fernández y Vico (2013), quienes destacan cuatro grandes categorías: la inteligencia simbiótica (basada en reglas o en conocimiento), la optimización, el aprendizaje automático (Machine learning) y los sistemas complejos.
Estructura del Sistema Simbiosis
Simbiosis es un sistema dinámico4en el cual participan 3 agentes: las entidades sónicas, el instrumentista y el mentor.
Describe el comportamiento del sistema en una interpretación, su flujo de información y la relación entre los agentes.
La siguiente notación indica distintos tipos de vínculos existentes en el sistema:
• La línea punteada con flecha indica que el agente tiene control sobre la información u otro agente.
• La línea constante con flecha indica que ese agente tiene una relación con otro agente o algún dispositivo, pero no ejerce control directo sobre su información. • La línea con rombo indica simplemente flujo de información.
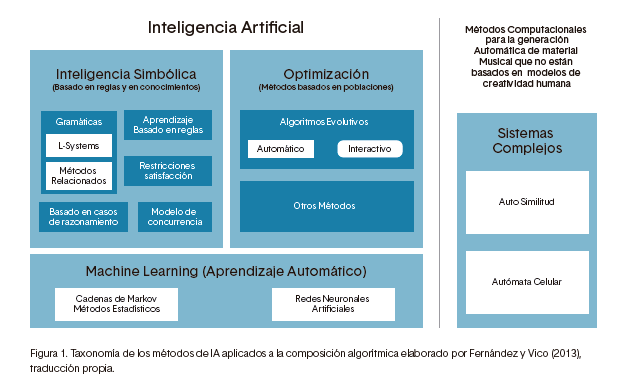
Figura 1. Taxonomía de los métodos de IA aplicados a la composición algorítmica elaborado por Fernández y Vico (2013), traducción propia.
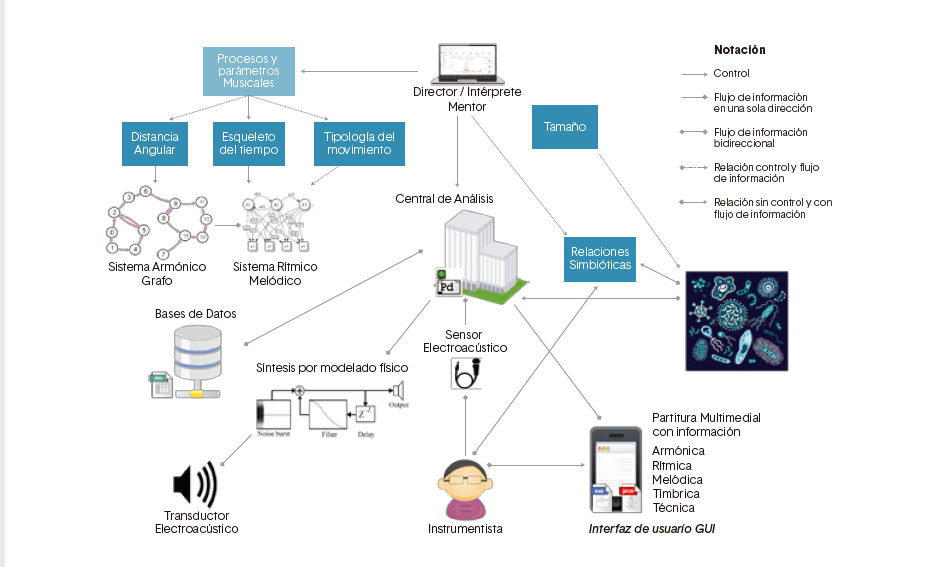
Figura 2. Estructura del sistema Simbiosis
A continuación, se describen cada uno de los componentes del sistema:
• Bases de datos: aquí están contenidos en archivos .cvs5 y .txt, toda la información referente al sistema armónico y al sistema rítmico, los cuales son tablas de datos que son leídas por la central de análisis, constituyendo una representación de conocimiento musical en lo que respecta a alturas y duraciones. En ese sentido, toda la información de alturas constituye un universo armónico definido por conjuntos de elementos y distancias entre los mismos, como se explica más adelante. • Central de Análisis: desde acá se transmite y modifica la información que fluye en todo el sistema. También se convierten los datos numéricos en sonido y están contenidos los parámetros que constituyen las entidades sónicas.
• Mentor/Director: este agente es quien gobierna y controla gran parte de la información del sistema; tiene control del sistema armónico, melódico y rítmico ya sea escogiendo el campo armónico o restringiendo los parámetros rítmico-melódicos en tiempo real. También, tiene control del tamaño de la población de las entidades sónicas y de sus parámetros de inicialización. Todo lo anterior por medio de un dispositivo que se comunica con la central de análisis.
• Instrumentista: es otro agente humano que interviene a través de un instrumento musical. Al ser Simbiosis una composición que no necesariamente se restringe a un único instrumento, existe la posibilidad de que sea ejecutada con diferentes instrumentos, para lo cual debe cargarse en la base de datos la información referente al instrumento que se va usar (posibilidades técnicas, tímbricas, afinación, entre otras), en ese sentido, puede pensarse como una obra modular en cuanto a instrumentación.
• Entidades Sónicas: este agente, al poseer cierto grado de autonomía, tiene control de la central de información en lo que respecta a sí mismo, es por esto que el flujo de información con la central de análisis es representado con una línea bidireccional. Además, la relación que tiene con el instrumentista, es una relación en la cual fluye información, pero no existe control directo del uno sobre el otro; en otras palabras, el instrumentista y la población de entidades sónicas intercambian información sonora y se retroalimentan, pero la población de entidades sónicas no puede alterar o modificar lo que debe interpretar el instrumentista y viceversa. De otra parte, los datos o información de las entidades sónicas son trasformados en sonido por medio de síntesis por modelado físico.
• Sistema Cuadrafónico: es el espacio acústico y biotopo6 en donde conviven y se desplazan las entidades sónicas junto con el material sonoro producido por el instrumentista. En este espacio acústico el mentor distribuye a gusto, efectos de sonido que alteran y modifican a las entidades sónicas cuando estas pasan o recorren el lugar donde están dispuestos estos efectos.
Entidades Sónicas
An intelligent entity could be made of protein, mechanical relays, transistors, or anything else, so long as it can process symbols.
Artificial Intelligence: A New Synthesis, -Nils J. Nilsson-.
Varios autores han acogido y usado el concepto de entidad/maquina sónica/sonora autónoma, las cuales son modelos computacionales de seres virtuales capaces de interrelacionarse y modificarse entre sí mismos para alterar el entorno acústico. Castañeda (2016), realizó una tipología de las maquinas sonoras: las entidades sonoras se ubican dentro de los sistemas híbridos, puesto que tienen la característica de las maquinas teleológicas en cuanto a que tienen una estructura lingüística (bases de datos de universos armónicos), son autónomas ya que actúan por periodos extensos sin la intervención humana, se mueven por si mismas por el entorno sin la intervención humana. De otro lado, los métodos/algoritmos evolutivos/ genéticos permiten generar música no-determinista o que ocurre de forma diferente cada vez que es interpretada.
Las entidades sónicas en Simbiosis, fueron diseñadas para atender cinco parámetros de la construcción musical: las alturas, el ritmo, la intensidad, el timbre y el espacio. Cabe aclarar que la definición de las entidades sónicas moldea la inmediatez en la obra, mientras que los procesos de mediano y largo plazo son controlados en tiempo real por el mentor, quien acota los comportamientos, temporalidades y condiciones de restricción para la elección de materiales de las entidades sonoras.
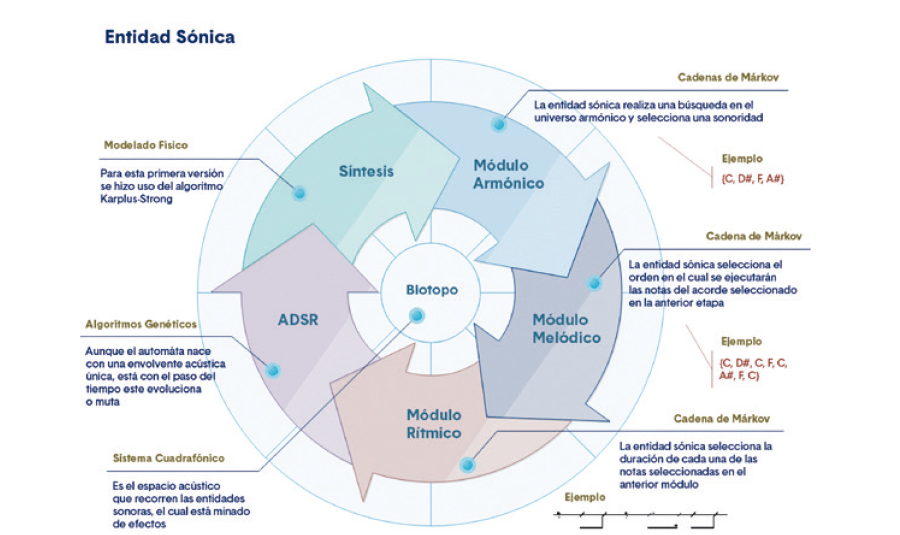
Figura 3. Funcionamiento de una entidad sónica en Simbiosis. Elaboración propia
Las entidades sónicas en Simbiosis, fueron diseñadas para atender cinco parámetros de la construcción musical: las alturas, el ritmo, la intensidad, el timbre y el espacio. Cabe aclarar que la definición de las entidades sónicas moldea la inmediatez en la obra, mientras que los procesos de mediano y largo plazo son controlados en tiempo real por el mentor, quien acota los comportamientos, temporalidades y condiciones de restricción para la elección de materiales de las entidades sonoras.
Se muestra la definición de los parámetros mencionados a través de módulos, siendo pertinente mencionar para los primeros casos (módulos armónico, melódico y rítmico) el uso de cadenas de Márkov, que es una forma de permitir un alto grado de autonomía a la máquina, permitiendo un modelamiento de comportamientos semideterminísticos, pero con amplio margen de variación en el tiempo, como el tránsito entre diferentes sonoridades presentes en la base de datos, el orden de las alturas para ser presentadas con un ritmo particular.
La ventaja que supone para este tipo de obras el uso de estos esquemas, es la posibilidad de analizar grandes volúmenes de información en tiempos muy cortos, sin que esto se convierta en una elección al azar, sino una organización que modela la esencia de sistematizaciones musicales como la armonía como un conjunto de probabilidades, relaciones y restricciones. Este concepto se explica con mayor profundidad en el apartado V de este artículo.
De otra parte, el módulo de intensidad es un ejemplo de variación en el tiempo a través de esquemas bio-inspirados. En el apartado VI de este artículo se explica con mayor detalle el funcionamiento de los algoritmos genéticos usados en la definición de las entidades sonoras y su consecuencia en la creación de la obra.
Universos Armónicos
Simbiosis hace uso de la teoría de conjuntos y la teoría de grafos; la primera aporta conceptos con los cuales se categorizan y relacionan objetos musicales, mientras que la segunda se encarga del estudio de las relaciones entre diferentes presentaciones de la información. Los precursores en la teoría de conjuntos en la música fueron Howard Hanson 1960) y Allan Forte (1973)7 a través de sus publicaciones, pero vale la pena mencionar que su uso también puede atribuirse a Milton Babbitt.
En el ámbito de la cuantificación de las relaciones entre los conjuntos de clases tónicas, se encuentra que diversos autores han propuesto operaciones para medir la diferencia entre sonoridades. Algunos de ellos son: el índice de similitud (Teitelbaum, 1965), la similitud sobre el vector de clases interválicas IcVSIM (E. J. Isaacson, 1990), el ángulo entre vectores interválicos ANGLE (Scott e Isaacson, 1998), la distancia euclidiana y ángulo en el espacio de Fourier hexadimensional (Callender, 2007).8 A continuación se describen algunos conceptos y operaciones que fueron fundamentales para el desarrollo del sistema armónico del proyecto.
De otra parte, el módulo de intensidad es un ejemplo de variación en el tiempo a través de esquemas bio-inspirados. En el apartado VI de este artículo se explica con mayor detalle el funcionamiento de los algoritmos genéticos usados en la definición de las entidades sonoras y su consecuencia en la creación de la obra.
SPECTRA
Clifton Callender (2007), desarrolló una caracterización armónica para conjuntos de clases tónicas, que permite la comparación de diferentes temperamentos iguales e incluso, temperamentos basados en proporciones diversas, a través del uso de la transformada de Fourier, para que de esta manera se represente numéricamente el contenido armónico de cualquier acorde (Amiot, 2007), (Quinn, 2006), (Vuza, 1991), lo que resulta apropiado para generar representaciones computarizadas, así como para la cuantificación de una relación en un espacio armónico dado.
El procedimiento se puede describir como el cálculo de los componentes bidimensionales en un espacio de ciclos interválicos, permitiendo llegar a ideas de equilibrio para las sonoridades, de una manera similar a la propuesta por Quinn (2006) y que había sido propuesta inicialmente planteada como equilibrios de Fourier por Lewin (1959). Al obtener un único dato numérico que representa la magnitud resultante de la interacción de los componentes tónicos de una sonoridad en varios ciclos interválicos diferentes, es posible crear un conjunto de valores sobre los cuales crear el espacio euclidiano en el que se calculan la distancia y ángulo, esto es, pensar en un espacio con seis cualidades que describen la posición de las sonoridades para realizar las mediciones mencionadas. La siguiente ecuación resume el procedimiento para cada ciclo interválico:
Magnitud de la transformada de Fourier del conjunto Q con ciclo interválico l. Extraída de Callender (2007).
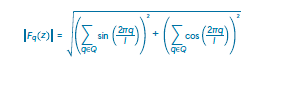
Donde q es cada componente de la sonoridad Q y l el tamaño de los ciclos interválicos a ser considerados. A continuación, se realiza la aplicación práctica de la ecuación con el conjunto [0, 2, 6] y los ciclos interválicos propuestos por Callender (2007) para la comparación de sonoridades en temperamento igual de doce divisiones. Se evalúa el primer componente del acorde (0) con cada uno de los componentes de la serie armónica, en este caso evaluaremos 6 parciales en el sistema temperado de 12 notas, por lo tanto, los componentes serán [12, 6, 4, 3, 2.4, 2].
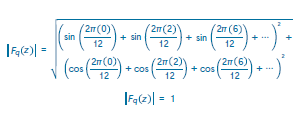
Para el segundo componente,
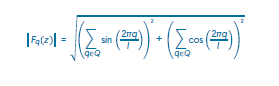
Y así, sucesivamente con los componentes restantes, lo cual nos arroja el siguiente vector:
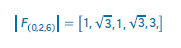
Este vector representa el SPECTRA del acorde [C, D, F#], esto es, las coordenadas en el espacio hexadimensional de Fourier sobre el cual calcular métricas que permiten la cuantificación de la relación entre dos sonoridades a la vez, lo que a su vez, puede permitir la consolidación de las relaciones armónicas en un espacio dado. Esto fue lo que posibilitó el manejo de alturas en la obra Simbiosis, a través de la construcción de un sistema para buscar rangos de valores y permitir la conexión de sonoridades desde lo indicado por el mentor.
Distancia Angular
En álgebra lineal, la distancia angular está dada para valores entre 0 ≤ Ø ≤ π (Williams, 2012). Pero para su uso en música, la diferencia angular (ANGLE) mide la independencia, no la oposición del sonido. Es perfectamente apropiado que su
valor máximo sea 90 (es decir π/2 ), representando perpendicularidad, en lugar de 180, representando una dirección negativa. (Scott e Isaacson, 1998). La distancia angular está definida por la siguiente ecuación:
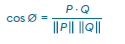
Simbiosis contiene una lista de tablas con algunas de las escalas más conocidas, a las que se les extrajeron sus respectivos subconjuntos, se les calculó su respectivo SPECTRA y posteriormente la distancia angular entre ellos, realizando también una depuración con respecto a su vector interválico para suprimir las transposiciones de las escalas. Para calcular las posibles combinaciones de un conjunto de cardinalidad n se hace uso de la fórmula de combinaciones sin repetición, o combinación de n objetos tomando r a la vez (Kolman y cols., 1997).
Combinación sin repetición
Extendiendo el cálculo para las diferentes sonoridades incluidas en una escala, conjunto con cardinalidad alta o universo de alturas, se puede totalizar la cantidad de subconjuntos a través de la siguiente ecuación (Sánchez, 2017b), donde n es la cardinalidad del conjunto base y r es la cardinalidad del subconjunto, siempre r es menor que n e i es la menor cardinalidad a ser considerada.
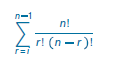
Si se toma como ejemplo la escala presentada en la figura 4, y un mínimo de elementos para los subconjuntos de tres clases tónicas hasta ocho clases tónicas, hay 219 subconjuntos en total: 1 octacordio, 8 heptacordios, 28 hexacordios, 56 pentacordios, 70 tetracordios y 56 tricordios. Puesto que el volumen de datos es considerablemente grande, calcular el SPECTRA y la distancia angular entre todos estos conjuntos sería una tarea bastante laboriosa si no se automatiza, nada más la cantidad de relaciones entre los subconjuntos (su distancia angular) llega a las 47962 posibilidades. Es por esto que se hace necesario el uso de herramientas computacionales que realicen estos cálculos, lo cual fue solucionado a través del desarrollo de programas con este propósito haciendo uso del lenguaje de programación Pyhton.9
Para la anterior escala, al considerar las relaciones de cada conjunto hacia los demás presentes en la misma, se particulariza la distancia y, a través de la teoría de grafos se construye una red de relaciones que se representa a continuación en la figura 5, ilustrando como círculos de colores los diferentes subconjuntos y, a través de líneas, la relación hacia otros conjuntos con un valor asociado.
Como se puede observar la densidad de las relaciones es tal que no puede diferenciarse en una representación gráfica. Así como se mencionó que es posible cargar diferentes módulos que respondan al instrumento elegido, en la obra Simbiosis es posible considerar como escala base o universo de alturas cualquier conjunto, constituyendo una base de datos de conjuntos y relaciones que representan un entramado que puede ser moldeado y recorrido por las entidades sonoras, desde las restricciones que defina el mentor.
A continuación, ejemplifican algunas restricciones que pueden ser usadas por el mentor/director durante la interpretación de la obra, lo cual permite ver sólo algunas de las relaciones, pues actúa a manera de filtro, restringiendo el tránsito entre las diferentes sonoridades y a la vez, permitiendo modelar el nivel de diferenciación que se puede entender como tensión armónica. De otro lado, la figura 9, muestra en detalle el acercamiento a un nodo particular del grafo, y la posibilidad de paso a otros conjuntos, todos representados numéricamente.
Teoría de la probabilidad
Puesto que este proyecto hace uso de procesos estocásticos1011y aleatorios, es importante definir el concepto “Cadena de Márkov”, propio de la teoría de la probabilidad, el cual es fundamental para la programación de autómatas y vida artificial. El modelo de Márkov fue introducido por el ruso Andrey Andreyevich Márkov (1856- 1992) (Basharin y cols., s.f.) y describe un proceso estocástico discreto; una secuencia de variables o eventos aleatorios correspondientes a un sistema en cual la probabilidad de que ocurra un evento depende del evento anterior (Ching y Ng, 2006)
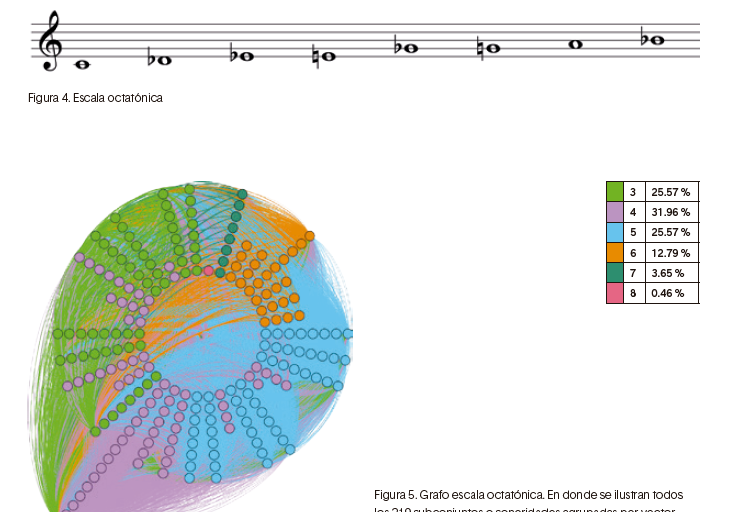
Figura 5. Grafo escala octatónica. En donde se ilustran todos los 219 subconjuntos o sonoridades agrupadas por vector interválico.
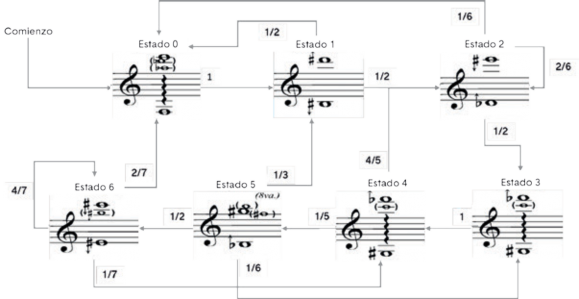
La figura 10, ilustra un ejemplo de cadena de Márkov a partir de multifónicos en el clarinete como estados y la tabla 2.5, detalla su respectiva matriz de transición.12.
Computación Evolutiva
La computación evolutiva (CE), ha sido un campo de desarrollo que tiene sus raíces en algunas ideas generadas a mediados del siglo XX, Alan Turing, hacia 1950 postulaba ya ideas acerca de máquinas con capacidad de aprendizaje y un esquema de cambios o mutaciones, así como una asistencia externa vista como la selección natural (Turing, 1950). Desde la década de 1960 gracias al impulso provisto por el avance tecnológico, fue posible comenzar a construir diversos esquemas centrados en el aprendizaje de las máquinas para resolver problemas de optimización, aunque el gran desarrollo de este campo tuvo una formalización y definición en las últimas dos décadas del siglo XX (Husbands, Copley, Eldridge, & Mandelis, 2007).
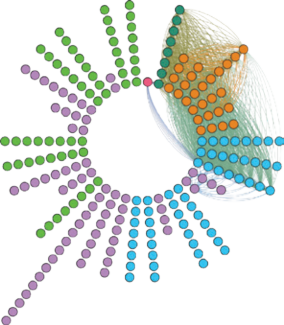
Figura 6. Grafo escala octatónica con una restricción de 0° a 11°.

Figura 7. Grafo escala octatónica con una restricción de 43° a 44°
![Figura 8. Algunas posibilidades de conexiones en el grafo escala octatónica con una restricción de 8° a 14°, El conjunto de partida es [0, 1, 4, 6,7], se ocultan los conjuntos a los cuales no puede direccionarse y se resaltan los conjuntos a los cuales si puede dirigirse.](https://revistas.udistrital.edu.co/index.php/estart/article/download/12935/version/9497/17153/104196/4922187003_gf15.png)
Figura 8. Algunas posibilidades de conexiones en el grafo escala octatónica con una restricción de 8° a 14°, El conjunto de partida es [0, 1, 4, 6,7], se ocultan los conjuntos a los cuales no puede direccionarse y se resaltan los conjuntos a los cuales si puede dirigirse.
En el campo musical también se han aplicado esquemas computacionales diversos para la composición y modelamiento del estilo musical, por ejemplo a través un estudio estadístico es posible generar cadenas de Márkov que pueden producir composiciones al estilo de Chopin, dando cuenta de los patrones identificables en parámetros como el ritmo o la altura (Collins, Laney, Willis, & Garthwaite, 2011). En este sentido, la identificación de sistemas de reglas y la representación del conocimiento musical, principalmente de la altura y el ritmo, juegan un rol esencial a diversos niveles de estructura, desde lo motívico hacia escalas temporales de mayor duración como secciones o la forma misma (Cope, 2001).
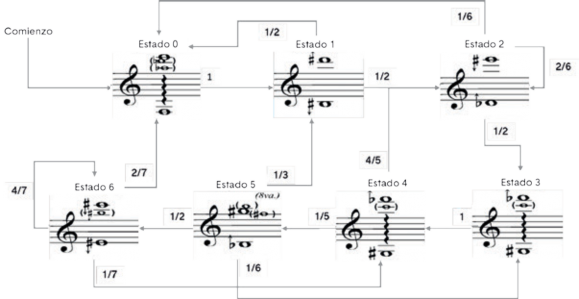
Figura 9. Cadena de Márkov de Multifónicos en el Clarinete. Elaboración Propia.
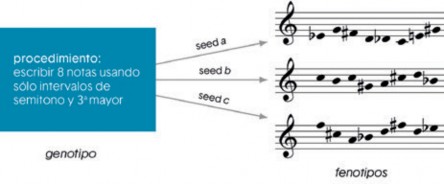
Genotipo y fenotipo
En biología, un genotipo es el conjunto de los genes que existen en el núcleo celular de un organismo. El fenotipo es la realización visible del genotipo, es decir, el propio ser portador de los genes, cuyos caracteres son el resultado de la interacción entre el genotipo y el medio. Un genotipo musical
es una expresión que codifica procedimientos musicales. Un fenotipo musical es el fragmento musical generado por un genotipo. Al igual que en biología, un genotipo musical puede dar lugar a muchos fenotipos diferentes, en función del medio (López-Montes, 2013).
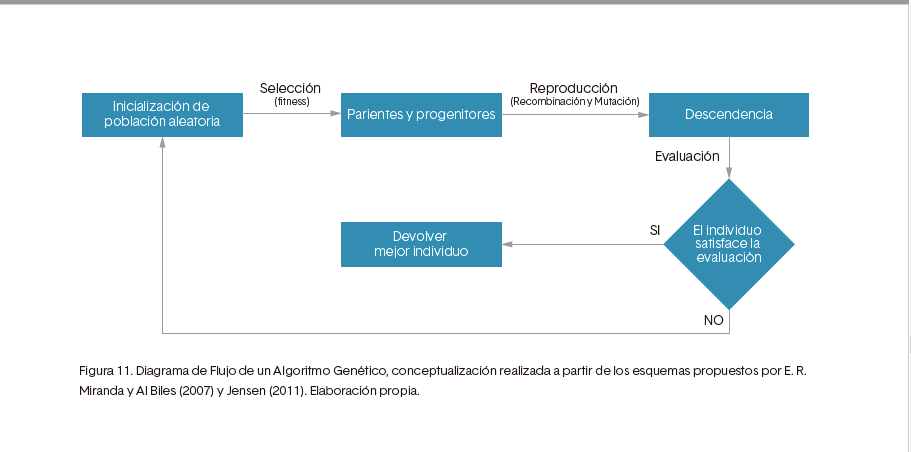
Algoritmo genético
El algoritmo genético fue desarrollado por John Holland en 1960, quien se propuso estudiar el fenómeno biológico de adaptación en la naturaleza y trasladarlo a sistemas computacionales. Un algoritmo genético contiene los siguientes pasos:
1. Iniciar una población aleatoriamente.
2. Seleccionar progenitores.
3. Reproducción (cruce y mutación).
4. Descendencia.
5. Evaluación (fitness).
Lo anterior será ilustrado con la canción All of Me de John Legend.
Codificación (Encoding):
como primer paso, codificamos el primer fragmento en un vector compuesto de duplas en donde el primer número representa la altura en MIDI y el segundo la duración en milisegundos.
Generando variación:
Existen diversas formas de variación genética, las más usadas son expuestas a continuación:
Mutación: Consiste en reemplazar un elemento aleatorio del genotipo por otro elemento aleatorio en el mismo intervalo. En este caso nos referimos a: Modificar la duración de una nota, modificar el tono de una nota, agregar o eliminar una nota a la melodía, intercambiar dos notas, clonar, interpolar, entre muchos otros más (Alfonseca y cols., 2007), (Donnelly y Sheppard, 2011).
Cruce o recombinación: En este algoritmo los genotipos de ambos progenitores se combinan utilizando diferentes procedimientos para generar los genotipos progenie (Alfonseca y cols., 2007), (Donnelly y Sheppard, 2011).
Cruce mono punto (Single point crossover): Se intercambia información genética a partir de un determinado punto.
Cruce de doble punto (two-point crossover): Se intercambia el material genético comprendido entre dos puntos.
Al realizar una recombinación de tres puntos el hijo contiene información de la madre y del padre tal como lo ilustra la imagen.
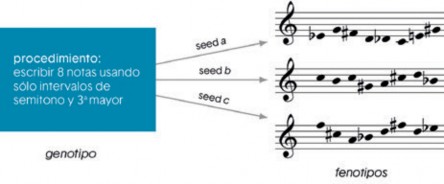
Figura 10. Ejemplo de un genotipo musical el cual tiene 3 semillas1 producen 3 fenotipos. Imagen tomada de López-Montes (2013).
Elaboración propia
Otras operaciones: A continuación se describe otras operaciones que son usuales en la aplicación de algoritmos genéticos en música (Horner y Goldberg, 1991).
• Añadir: se agrega un elemento al genoma. • Eliminar: se elimina un elemento del genoma. • Rotación: se gira o invierte el genoma. • Rotación incorrecta: se giran elementos en posiciones “incorrectas” del genoma. • Intercambio incorrecto: se intercambian elementos en posiciones “incorrectas” del genoma.
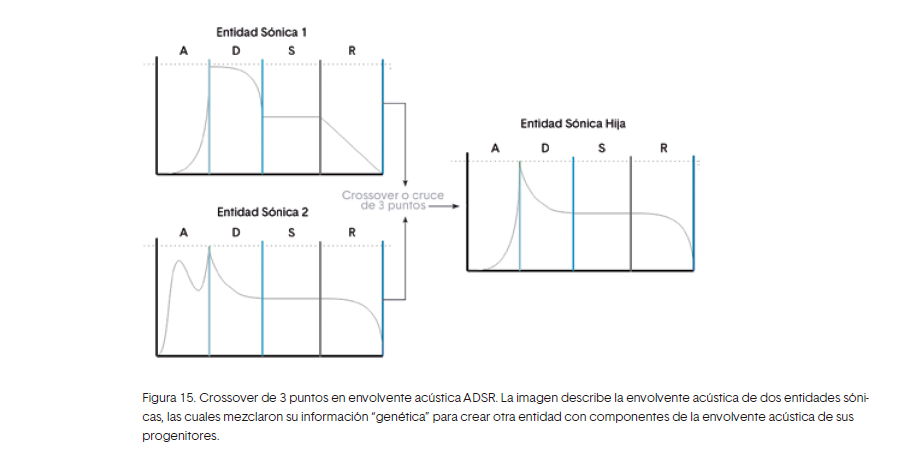
Envolvente acústica evolutiva Algo que caracteriza a cada instrumento es su envolvente acústica, el cual es la variación de la amplitud y el contenido espectral de un sonido con respecto al tiempo (Dodge y Jerse, 1997) (Sethares, 2005) (Dunn y cols., 2015). En síntesis de sonido es común hacer uso de un generador de envolvente, el cual controla los distintos parámetros de un sonido, siendo los más comunes:
• Ataque: tiempo de entrada, lo que demora el sonido en escucharse desde que es ejecutado hasta que alcanza su máxima amplitud. • Decaimiento: es el tiempo en que tarda en disminuir la amplitud hasta que se suelta la tecla o el punto de inducción vibratoria en el instrumento.
• Sostenimiento: tiempo en el cual la amplitud se mantiene constante. • Relajación: tiempo en el cual el sonido disminuye toda su amplitud.
Para Simbiosis, la envolvente acústica representa un atributo de cada entidad sonora, es lo que las distingue y diferencia entre ellas. Este atributo con el tiempo muta, se transforma o se recombina a partir de la interacción que exista entre ellas por medio de algoritmos genéticos o de una función de aptitud que establezca el director.
Se puede observar que la entidad sónica hija tiene el ataque de la entidad sónica 1, además tiene el decaimiento y relajación de la entidad sónica 2. Por último, el sostenimiento es un parámetro, el cual es el mismo en las dos entidades sónicas progenitoras
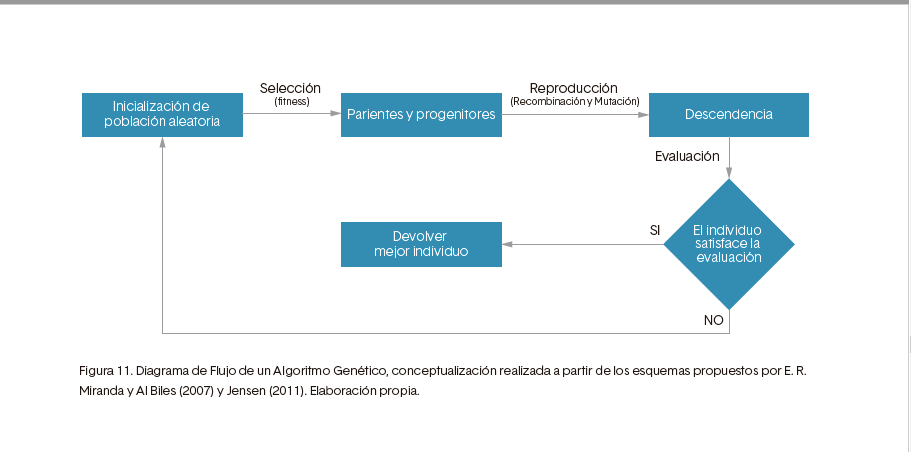
Figura 11. Diagrama de Flujo de un Algoritmo Genético, conceptualización realizada a partir de los esquemas propuestos por E. R. Miranda y Al Biles (2007) y Jensen (2011). Elaboración propia.
Fuentes aparentes de ambientes virtuales
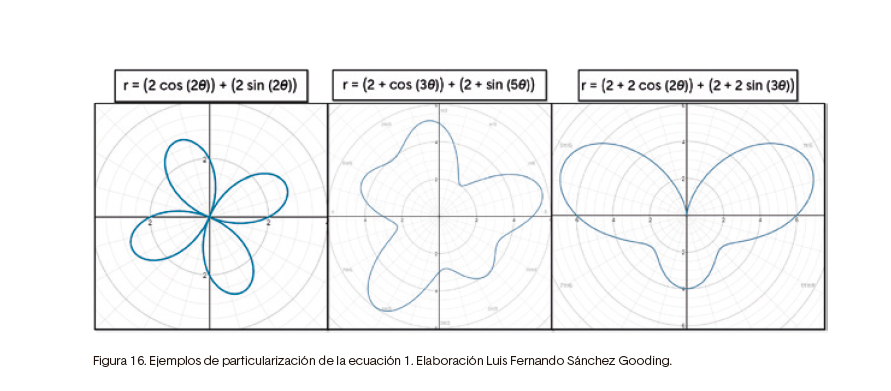
Uno de los comportamientos o mejor, un híbrido entre comportamiento y fenotipo, fue definido para el recorrido en un espacio virtual, esto es, la simulación de espacio para la fuente sonora. Al estar basado en ecuaciones polares, los contornos de recorrido pueden ser variados y generar curvaturas que resultan propicias para la percepción del cambio de direccionalidad en un modelo que tiene en cuenta el efecto doppler y un filtrado dependiente de la ubicación. En la ecuación 5 se muestra la generalización usada que contiene la definición de cardioides, caracoloides, rosas y lemniscatas (Purcel & Valberg, 1992). Esto fue desarrollado e implementado por el maestro Luis Fernando Sánchez Gooding, en su obra “del suspiro en el alba hasta el abrazo en el ocaso” (2014), otro ejemplo de música evolutiva.
En dicha obra, al nacer los seres virtuales, las variables a, b y c se generan aleatoriamente teniendo como posibilidad ser cero, uno o un número mayor que uno, permitiendo que se genere una mezcla de las figuras o una sola de ellas. De igual manera, la dirección de la figura se define desde las funciones seno y coseno que, dependiendo de los valores generados aleatoriamente, creará una inclinación particular como se muestra en los ejemplos

Figura 12. Genoma del motivo de All of Me, sección de la partitura extraída de Sher (1988). Elaboración Propia.

Figura 13. Mutaciones en el Genoma del Motivo de All of Me. Secciones de la partitura extraídas de Sher (1988). El color rojo indica mutación en la altura y el azul en el ritmo o duración. Se observa como la altura muta de un C a un B, en nota MIDI pasa de un 72 a 71. Por otro lado, el ritmo muta al sumar los valores de los 3 tresillos de negra más las dos blancas ligadas a la corchea, es decir 4500ms + 666.66ms + 666.66ms + 666.66ms = 6500ms. Elaboración propia.
Tipología del movimiento
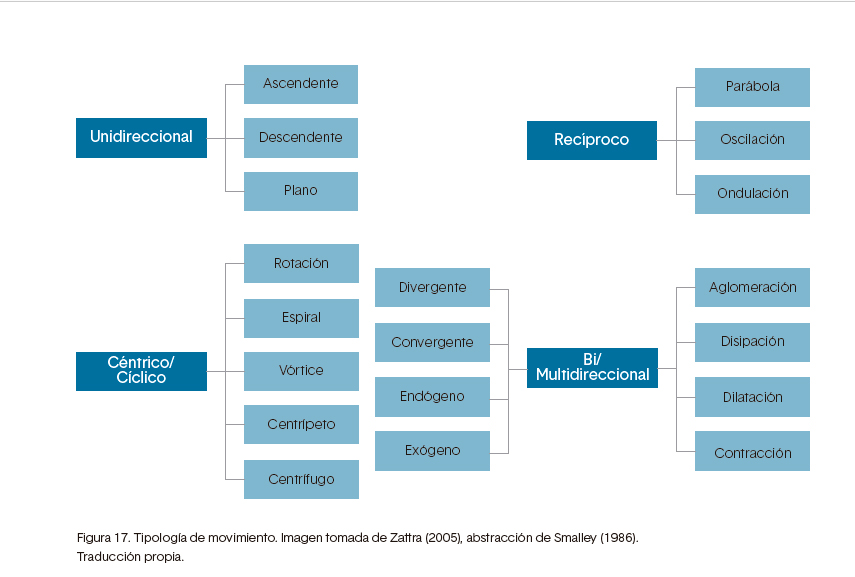
Smalley (1986), realizo una clasificación de los diferentes tipos de movimiento, los cuales pueden ser una amalgama compleja de varios tipos y tendencias, ambigüedades y contracciones, existiendo 5 categorías representativas: uni-direccional, bi- direccional, reciproco, céntrico/cíclico y excéntrico/multi-direccional.
Como parte de los mecanismos programados para las entidades sónicas en Simbiosis, el control a través de las definiciones de movimiento mencionadas, permite la selección de comportamientos asignados a la generación de melodías. Supongamos que el mentor propone que las entidades usen comportamientos ascendentes unidireccionales, para lo cual las entidades cuentan con un listado como el que se encuentra en la figura 18, a través de una escogencia aleatoria un resultado posible

Figura 14. Recombinación (Cruce de tres puntos) entre dos genomas; la línea verde representa el genoma del padre, la línea negra el genoma de la madre.
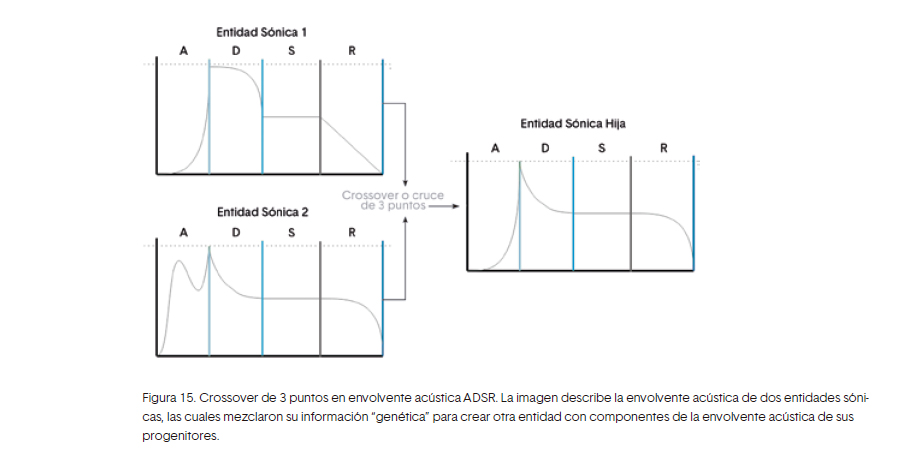
Figura 15. Crossover de 3 puntos en envolvente acústica ADSR. La imagen describe la envolvente acústica de dos entidades sóni-cas, las cuales mezclaron su información “genética” para crear otra entidad con componentes de la envolvente acústica de sus progenitores.
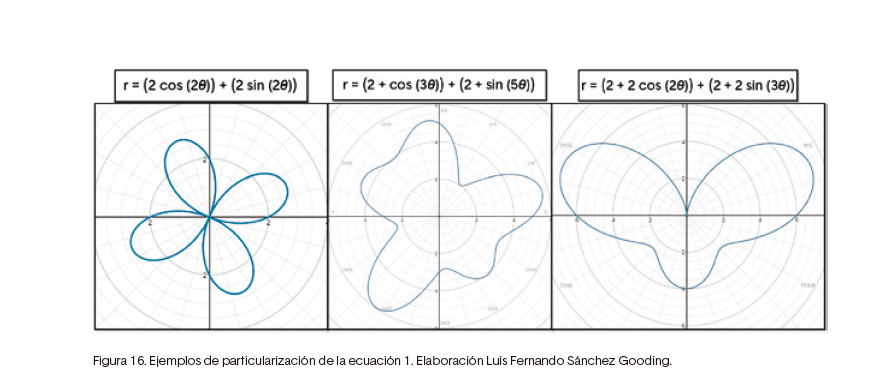
Figura 16. Ejemplos de particularización de la ecuación 1. Elaboración Luis Fernando Sánchez Gooding
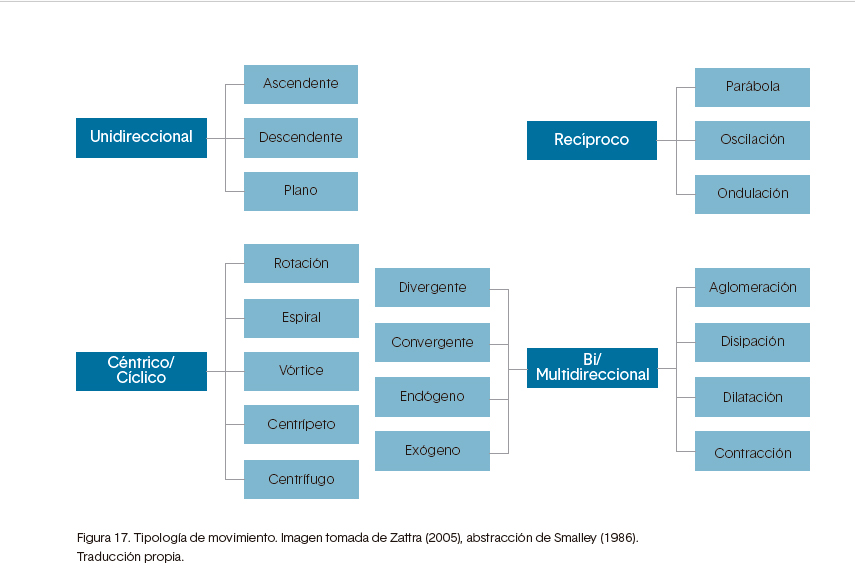
Figura 17. Tipología de movimiento. Imagen tomada de Zattra (2005), abstracción de Smalley (1986). Traducción propia.

Figura 18. Permutaciones de una melodía ascendente. Elaboración propia
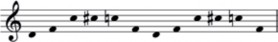
Figura 19. Ejemplo de una melodía ascendente. Elaboración propia.

Figura 20. Ejemplo melodía parabólica. Elaboración propia.
Otros tipos de movimiento que se utilizaron en el proyecto de investigación-creación fueron:
Centrifugo: inicia desde la nota central del acorde o sonoridad hacia afuera. El proceso inverso (de las notas exteriores a las del centro) se denomina centrípeto.

Figura 21. Ejemplo melodía con movimiento centrífugo. Elaboración propia.
Convolución: en matemáticas una convolución, es un operador matemático que transforma dos funciones f y g en una tercera función. A veces es útil ver la convolución como un producto matricial, como una matriz de Toeplitz, la cual es una matriz cuadrada en la que los elementos de sus diagonales (de izquierda a derecha) son constantes (Von Zur Gathen y Gerhard, 2013). Una matriz de Toeplitz presenta la siguiente estructura:

Figura 22. Ejemplo ondulación melódica. Elaboración propia.
Conclusiones
Implicaciones de la creatividad artificial Este tipo de investigaciones suelen suscitar preguntas tales como: ¿La máquina puede ser realmente creativa? ¿Es posible superar la prueba de Turing con este tipo de sistemas informáticos en música? ¿Cuál es la relación entre creatividad y computación? Adicionalmente, las que se plantea Raymond Kurzweil13: ¿Quién es el artista: el compositor siendo emulado, el software, o el compositor frente a sí mismo? Si bien ya existen sistemas computacionales capaces de imitar el estilo de diversos compositores, considero que el potencial de las maquinas, la IA y los sistemas computacionales no radica en qué tanto puede imitar el estilo de determinado compositor, qué tanto se parece a un ser humano, si pueden pensar, sentir, tener conciencia de sí mismo, entre otras posibilidades.
Precisamente, el potencial de las máquinas y de la inteligencia artificial radica en sus cualidades únicas que la diferencian del ser humano, una de las cuales es que son capaces de procesar grandes volúmenes de datos en un tiempo corto, algo que para el ser humano es una tarea complicada. Sin embargo, hasta ahora la inteligencia artificial no tiene la capacidad de un juicio u orientación estética.
Es por esto que una relación apropiada en este tipo de creación, puede ser configurada entre el ser humano y la máquina desde una perspectiva simbiótica, en donde el ser humano actúa como un sistema experto con juicio estético y la IA como una entidad capaz de procesar grandes volúmenes de datos. Dicha relación simbiótica hace posible que nuevos paradigmas surjan para comprender, concebir y percibir el sonido, lo cual nos lleva a situaciones creativas sustancialmente innovadoras, siendo fundamental el caos, el indeterminismo y la aleatoriedad.
Aplicaciones de las matemáticas en la música
El uso de las matemáticas y la aplicación de sistemas no lineales en la creación musical, por medio de sistemas estocásticos, técnicas de control y optimización no lineal, no solo permiten entender y analizar las propiedades del sonido y de la música, sino que también posibilita el desarrollo de nuevos paradigmas estéticos en la creación artístico-musical, en donde la IA juega un papel importante proponiendo ideas de carácter creativo novedosas e imprevistas.
Programar es meta-componer Como bien lo afirma José López-Montes (2012) en su trabajo GenoMus: prospección de técnicas de creatividad asistida por computadora mediante la metaprogramación de genotipos musicales, el diseñar algoritmos para generar música contiene decisiones de carácter compositivo, y si bien al programar no se compone música, los algoritmos son como el lienzo o la herramienta que constituye parámetros que harán posible la creación musical. Y aunque es verdad que no todo compositor debe saber programar, es preciso citar a Ortega y Gasset, quien siendo consciente de que la temporalidad del hombre es consustancial a su persona afirmó “somos hijos de nuestro tiempo”. Por lo tanto, si bien en el pasado la partitura fue la herramienta compositiva por excelencia, hoy es preciso integrar la programación como herramienta meta-compositiva.
Referencias
Alfonseca, M., Cebrián, M., y Ortega, A. (2007). A Simple Genetic Algorithm for Music Generation by Means of Algorithmic Information Theory. En 2007 IEEE Congress on Evolutionary Computation. pp. 3035–3042. https://doi.org/10.1109/CEC.2007.4424858
Amiot, E. (2007). David Lewin and Maximally Even Sets. Journal of Mathematics and Music, 1 (3), 157–172. https://doi.org/10.1080/17459730701654990
Asimov, I. (1984). Asimov’s New Guide to Science. New York: Basic Books. Basharin, G. P., Langville, A. N., y Naumov, V. A. (s.f.). The Life and Work of a. a. Markov. PMid:6237023
Buchler, M. (2000). Broken and Unbroken Interval Cycles and Their Use in Determining Pitch-class Set Resemblance. Perspectives of New Music, 52–87. https://doi.org/10.2307/833659
Callender, C. (2007). Continuous Harmonic Spaces. Journal of Music Theory, 51 (2), 277–332. https://doi.org/10.1215/00222909-2009-004
Castañeda, A. A. E. (2016). Máquinas sonoras: Aplicaciones de las ciencias de la complejidad a la creación musical y sonora (Tesis Doctoral no publicada). Universidad Autónoma de México, Facultad de Música.
Collins, T., Laney, R., Willis, A., & Garthwaite, P. H. (Diciembre de 2011). Chopin, Mazurkas and Markov. Significance, 8(4), 154-159.
Cope, D. (2001). Virtual Music. Cambridge: The MIT Press.
Childs, E. (2002). Achorripsis: A sonification of Probability Distributions.
Ching, W. K., y Ng, M. K. (2006). Markov Chains. Springer.
Dodge, C., y Jerse, T. A. (1997). Computer Music: Synthesis, Composition and Performance. Macmillan Library Reference.
Donnelly, P., y Sheppard, J. (2011). Evolving Four-part Harmony Using Genetic Algorithms. En European Conference on the Applications of Evolutionary Computation (pp. 273–282). https://doi.org/10.1007/978-3-642-20520-0_28
Dunn, F., Hartmann, W., Campbell, D., Fletcher, N., y Rossing, T. (2015). Springer Handbook of Acoustics.
Fernández, J. D., y Vico, F. (2013). AI Methods in Algorithmic Composition: A Comprehensive Survey. Journal of Artificial Intelligence Research, 48, 513–582.
Forte, A. (1973). The Structure of Atonal Music (Vol. 304). Yale: Yale University Press.
Haeckel, E. H. P. A., Miquel, S. S., y Senti-ón, G. (1887). Morfología general de los organismos. Blas Carrera.
Hanson, H. (1960). Harmonic Materials of Modern Music: Resources of the Tempered Scale. Irvington Pub. https://doi.org/10.2307/3389365
Holland, J. H. (1992). Genetic Algorithms. Scientific American, 267 (1), 66–72. https://doi.org/10.1038/scientificamerican0792-66
Horner, A., y Goldberg, D. E. (1991). Genetic Algorithms and Computer-assisted Music Composition. Urbana, 51 (61801), 437–441.
Husbands, P., Copley, P., Eldridge, A., & Mandelis, J. (2007). An Introduction to Evolutionary Computing for Musicians. En E. R.
Miranda, & J. A. Biles, Evolutionary Computer Music (págs. 1-27). Londres: Springer-Verlag. https://doi.org/10.1007/978-1-84628-600-1_1
Isaacson, E. J. (1990). Similarity of Interval-class Content Between Pitch-class Sets: The Icvsim Relation. Journal of Music Theory, 1–28. https://doi.org/10.2307/843860
Jensen, J. H. (2011). Evolutionary Music Composition: A Quantitative Approach.
Johnson, C., Ciesielski, V., Correia, J., y Machado, P. (2015). Evolutionary and Biologically Inspired Music, Sound, Art and Design. Springer. https://doi.org/10.1007/978-3-319-12541-1
Katok, A., y Hasselblatt, B. (1997). Introduction to the Modern Theory of Dynamical Systems. (Vol. 54). Cambridge: Cambridge University Press.
Kolman, B., y Hill, D. R. (2006). Álgebra lineal. Pearson Educación.
Kurzweil, R. (2000). The Age of Spiritual Machines: When Computers Exceed Human Intelligence. Penguin Publishing Group. Descargado de «https://books.google.com.co/ books?id=lbl4MN3iUHsC»
Kurzweil, R., y Schneider, M. L. (1990). The Age of Intelligent Machines (Vol. 579). Cambridge: MIT Press Cambridge.
Lewin, D. (1959). Re: Intervallic Relations Between Two Collections of Notes. Journal of Music Theory, 3(2), pp. 298–301. https://doi.org/10.2307/842856
López-Montes, J. (2013). Genomus. Prospección de técnicas de creatividad asistida por computadora mediante la metaprogramación de genotipos musicales (Tesis de Master no publicada). Universidad Rey Juan Carlos. Facultad de Ciencias del Turismo, Departamento de Ciencias de la Educación, el Lenguaje, la Cultura y las Artes.
Miranda, E. R., y Al Biles, J. (2007). Evolutionary Computer Music. Springer. https://doi.org/10.1007/978-1-84628-600-1
Mitsaigs, S. H. I. C. (s.f.). Set Theory in Xenakis’ Eonta.
Nierhaus, G. (2009). Algorithmic Composition: Paradigms of Automated Music Generation. Springer Science & Business Media. https://doi.org/10.1007/978-3-211-75540-2
Oxford Living Dictionaries. (2016, November). «https:// en.oxforddictionaries.com/definition/stochastic»
Pope, S. T. (1993). Music Composition and Editing by Computer. Oxford: Oxford University Press.
Purcel, E. J., & Valberg, D. (1992). Cálculo con geometría analítica. Naucalpan: Prentice Hall Hispanoamérica, S.A.
Quinn, I. (2006). General Equal-tempered Harmony (introduction and part I). Perspectives of New Music, 114–158.
Roeder, J. (1987). A Geometric Representation of Pitch-class Series. Perspectives of New Music, 362–409.
Ross, K & Wright, C. (1990). Matemáticas Discretas. México D.F.: Prentice Hall.
Sánchez, G. L. F. (2017a). Del suspiro en el alba hasta el abrazo en el ocaso: una composición evolutiva. Bogotá: Universidad Distrital Francisco José de Caldas.
Sánchez, G. L. F. (2017b). Estrategias de organización. Bogotá: Universidad Distrital Francisco José de Caldas.
Schillinger, J. (1948). The Mathematical Basis of the Arts.
Scott, D., y Isaacson, E. J. (1998). The Interval Angle: A Similarity Measure for Pitchclass Sets. Perspectives of New Music, pp. 107–142. https://doi.org/10.2307/833526
Sethares, W. A. (2005). Tuning, Timbre, Spectrum, Scale. Springer Science & Business Media.
Shafranovich, Y. (2008). Common Format and Mime Type for Comma-separated Values (csv) Files. [sl], 2005. Disponible en: «http://www.ietf.org/rfc/rfc4180.txt.»
Sher, C. (1988). The New Real Book: Jazz Classics, Choice Ctandards, Pop-fusion Classics: Created by Musicians, for Musicians (Vol. 1). Sher Music Co. PMid:22359165
Smalley, D. (1986). Spectro-morphology and Structuring Processes. En The language of Electroacoustic Music, pp. 61–93. Springer. https://doi.org/10.1007/978-1-349-18492-7_5
Smalley, D. (1997). Spectromorphology: Explaining Sound-Shapes. Organised Sound, 2 (02), pp. 107–126. https://doi.org/10.1017/S1355771897009059
Solomos, M. (2011). Xenakis First Compositon in Musique Concrete: Diamorphoses. En Xenakis International Symposium.
Teitelbaum, R. (1965). Intervallic Relations in Atonal Music. Journal of Music Theory, 9 (1), pp. 72–127. https://doi.org/10.2307/843150
Turing, A. (1950). Computing Machinery and Intelligence. Mind, 49, pp. 433-460. https://doi.org/10.1093/mind/LIX.236.433
Udvardy, M. F. (1959). Notes on the Ecological Concepts of Habitat, Biotope and Niche. Ecology, 40 (4), pp. 725–728. https://doi.org/10.2307/1929830
Von Zur Gathen, J., y Gerhard, J. (2013). Modern Computer Algebra. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139856065
Vriend, J. (1981). “Nomos alpha” for Violoncello Solo (Xenakis 1966), Analysis and Comments.
Vuza, D. T. (1991). Supplementary Sets and Regular Complementary Unending Canons (part one). Perspectives of New Music, pp. 22–49. https://doi.org/10.2307/833429
Williams, G. (2012). Linear Algebra with Applications. Jones & Bartlett Publishers.
Xenakis, I. (1992). Formalized Music: Thought and Mathematics in Composition (n°.6). Pendragon Press.
Zattra, L. (2005). Analysis and Analyses of Electroacoustic Music. Sound and Music Computing (SMC05), Salerno, Italia, 36. PMid:15917707
Notas
Recibido: 20 de septiembre de 2017; Aceptado: 28 de octubre de 2017
Resumen
La relación entre el ser humano y la máquina, desde una perspectiva simbiótica, posibilita un nuevo paradigma para comprender, concebir y percibir el sonido, lo cual nos permite experimentar situaciones creativas sustancialmente innovadoras, siendo fundamental el caos, el indeterminismo y la aleatoriedad. Simbiosis, es una composición en donde se pretende aplicar algunos conceptos y técnicas de la inteligencia artificial, la computación evolutiva y estrategias bio-inspiradas; es decir, mecanismos de programación basados o inspirados en procesos de evolución y selección biológica. Em este artículo, resultado de un proyecto de investigación-creación, se pretende extrapolar el concepto simbiosis en una composición musical, pretende explorar las relaciones que pueden surgir entre un intérprete humano y la máquina, en este caso una población de entidades sónicas autónomas, esta relación simbiótica es determinada, controlada y/o direccionada por un director/interprete (mentor) en tiempo real.
Palabras clave
Aprendizaje automático, composición algorítmica, computación evolutiva, electrónica evolutiva, entidades sónicas, relaciones simbióticas.Abstract
The relationship between the human being and the machine, from a symbiotic perspective, enables a new paradigm to understand, conceive and perceive sound, which allows us to experience substantially innovative creative situations with chaos, indeterminism and randomness as fundamental components. Simbiosis is a composition that intends to apply some concepts and techniques of artificial intelligence, evolutionary computation and bio-inspired strategies; that is, of programming mechanisms based on or inspired by processes of evolution and biological selection. This article, the result of a research-creation project, aims to extrapolate the concept of symbiosis in a musical composition, in order to explore the relationships that may arise between a human interpreter and the machine, in this case a population of autonomous sonic entities. This symbiotic relationship is determined, controlled and / or directed by a director / interpreter (mentor) in real time.
Keywords
Automatic learning, algorithmic composition, evolutionary computation, evolutionary electronics, sonic entities, symbiotic relationships .Résumé
La relation entre l’être humain et la machine, d’un point de vue symbiotique, permet un nouveau paradigme pour comprendre, concevoir et percevoir le son, ce qui nous permet de vivre des situations créatives essentiellement innovantes et ayant comme des éléments fondamentaux le chaos, l’indéterminisme et le hasard. Simbiosis est une composition où nous essayons d’appliquer quelques concepts et techniques d’intelligence artificielle, de calcul évolutif et de stratégies bio-inspirées : c’est-à-dire des mécanismes de programmation basés ou inspirés par des processus d’évolution et de sélection biologique. Cet article, fruit d’un projet de recherche-création, vise à extrapoler le concept de symbiose dans une composition musicale, afin d’explorer les relations qui peuvent naître entre un interprète humain et la machine, dans ce cas une population d’entités sonores autonomes. Cette relation symbiotique est déterminée, contrôlée et / ou dirigé par un directeur / interprète (mentor) en temps réel. Mots clés Apprentissage automatique, composition algorithmique, calcul évolutif, électronique évolutive, entités sonores, relations symbiotiques. Simbiose: Composição para bandola andina colombiana e entidades sônicas
Resumo
A relação entre o ser humano e a máquina, desde uma perspectiva simbiótica, possibilita um novo paradigma para compreender, conceber e perceber o som, o que nos permite experimentar situações criativas substancialmente inovadoras, sendo fundamental o caos, o indeterminismo e a aleatoriedade. Simbiosis é uma composição na qual se pretende aplicar alguns conceitos e técnicas da inteligência artificial, da computação evolutiva e estratégias bio-inspiradas; isto é, mecanismos de programação baseados ou inspirados em processos de evolução e seleção biológica. Este artigo, resultado de um projeto de pesquisa-criação, pretende extrapolar o conceito simbiosis em uma composição musical, com o fim de explorar as relações que podem surgir entre um intérprete humano e a máquina, neste caso uma população de entidades sônicas autônomas, esta relação simbiótica é determinada, controlada e/ou direcionada por um diretor/intérprete (mentor) em tempo real.
Palavras-chave
Aprendizagem automática, composição algorítmica, computação evolutiva, eletrônica evolutiva, entidades sônicas, relações simbióticas.
With intelligences of different species and genera, there is the possibility at least of a symbiotic relationship, in which all will cooperate to learn how best to understand the laws of nature and how most benignly we might cooperate with them. Certainly, the cooperation will do better than any intelligence variety on its own.
Isaac Asimov, Asimov’s New Guide to science
En mucha de la literatura de ciencia ficción ha habido sistemas informáticos de inteligencia artificial capaces de enfrentar procesos creativos o actividades que muchas veces se atribuyen como aptitudes netamente humanas, un ejemplo de ello es el holograma médico de emergencia de la serie Star Trek: Voyager, el cual, debido a su programación adaptativa llego a desarrollar gustos y habilidades para la dramaturgia, la fotografía, la opera e incluso llego a sostener relaciones románticas. Actualmente las investigaciones en el campo de la ciencia, la ingeniería y la computación se orientan hacia el estudio de las interacciones entre el ser humano y la máquina, aspirando a programar maquinas con un sentido del mundo, capaces de aprender y entender, esto con el fin de diseñar sistemas simbióticos que aumenten el rendimiento humano. Es por esto que el presente proyecto de investigación nace de la fascinación por la interacción entre el ser humano y la máquina, la composición musical algorítmica como estrategia para encontrar nuevas formas de creación y percepción del sonido; además del gusto por la programación, la Inteligencia Artificial (I.A.) y la ciencia.
Métodos y Técnicas de Inteligencia Artificial
Componer música implica una serie de actividades y procesos, los cuales pueden ser automatizados mediante el uso de computadoras, a esto se le denomina composición algorítmica. En consecuencia, se han desarrollado varias técnicas computacionales vinculadas con la IA (Pope, 1993). Tres puntos de partida para la investigación del estado del arte de la música asistida por ordenador son Computer Music Journal 1 , International Computer Music Conference, organizada anualmente por la International Computer Music Association, 2 y en especial la que más compete al presente trabajo de investigación-creación por su enfoque en la computación evolutiva: EvoMusart (Evolutionary and Biologically Inspired Music, Sound, Art and Design), organizada anualmente por Evostar 3 (Johnson y cols., 2015). Algunos autores han realizado varias sistematizaciones y/o taxonomías de los métodos de IA usados en la composición algorítmica, entre ellos están Nierhaus (2009) y Fernández y Vico (2013), quienes destacan cuatro grandes categorías: la inteligencia simbiótica (basada en reglas o en conocimiento), la optimización, el aprendizaje automático (Machine learning) y los sistemas complejos.
Estructura del Sistema Simbiosis
Simbiosis es un sistema dinámico4en el cual participan 3 agentes: las entidades sónicas, el instrumentista y el mentor.
Describe el comportamiento del sistema en una interpretación, su flujo de información y la relación entre los agentes.
La siguiente notación indica distintos tipos de vínculos existentes en el sistema:
• La línea punteada con flecha indica que el agente tiene control sobre la información u otro agente.
• La línea constante con flecha indica que ese agente tiene una relación con otro agente o algún dispositivo, pero no ejerce control directo sobre su información. • La línea con rombo indica simplemente flujo de información.
Figura 1. Taxonomía de los métodos de IA aplicados a la composición algorítmica elaborado por Fernández y Vico (2013), traducción propia.
A continuación, se describen cada uno de los componentes del sistema:
• Bases de datos: aquí están contenidos en archivos .cvs5 y .txt, toda la información referente al sistema armónico y al sistema rítmico, los cuales son tablas de datos que son leídas por la central de análisis, constituyendo una representación de conocimiento musical en lo que respecta a alturas y duraciones. En ese sentido, toda la información de alturas constituye un universo armónico definido por conjuntos de elementos y distancias entre los mismos, como se explica más adelante. • Central de Análisis: desde acá se transmite y modifica la información que fluye en todo el sistema. También se convierten los datos numéricos en sonido y están contenidos los parámetros que constituyen las entidades sónicas.
• Mentor/Director: este agente es quien gobierna y controla gran parte de la información del sistema; tiene control del sistema armónico, melódico y rítmico ya sea escogiendo el campo armónico o restringiendo los parámetros rítmico-melódicos en tiempo real. También, tiene control del tamaño de la población de las entidades sónicas y de sus parámetros de inicialización. Todo lo anterior por medio de un dispositivo que se comunica con la central de análisis.
• Instrumentista: es otro agente humano que interviene a través de un instrumento musical. Al ser Simbiosis una composición que no necesariamente se restringe a un único instrumento, existe la posibilidad de que sea ejecutada con diferentes instrumentos, para lo cual debe cargarse en la base de datos la información referente al instrumento que se va usar (posibilidades técnicas, tímbricas, afinación, entre otras), en ese sentido, puede pensarse como una obra modular en cuanto a instrumentación.
• Entidades Sónicas: este agente, al poseer cierto grado de autonomía, tiene control de la central de información en lo que respecta a sí mismo, es por esto que el flujo de información con la central de análisis es representado con una línea bidireccional. Además, la relación que tiene con el instrumentista, es una relación en la cual fluye información, pero no existe control directo del uno sobre el otro; en otras palabras, el instrumentista y la población de entidades sónicas intercambian información sonora y se retroalimentan, pero la población de entidades sónicas no puede alterar o modificar lo que debe interpretar el instrumentista y viceversa. De otra parte, los datos o información de las entidades sónicas son trasformados en sonido por medio de síntesis por modelado físico.
• Sistema Cuadrafónico: es el espacio acústico y biotopo6 en donde conviven y se desplazan las entidades sónicas junto con el material sonoro producido por el instrumentista. En este espacio acústico el mentor distribuye a gusto, efectos de sonido que alteran y modifican a las entidades sónicas cuando estas pasan o recorren el lugar donde están dispuestos estos efectos.
Entidades Sónicas
An intelligent entity could be made of protein, mechanical relays, transistors, or anything else, so long as it can process symbols.
Artificial Intelligence: A New Synthesis, -Nils J. Nilsson-.
Varios autores han acogido y usado el concepto de entidad/maquina sónica/sonora autónoma, las cuales son modelos computacionales de seres virtuales capaces de interrelacionarse y modificarse entre sí mismos para alterar el entorno acústico. Castañeda (2016), realizó una tipología de las maquinas sonoras: las entidades sonoras se ubican dentro de los sistemas híbridos, puesto que tienen la característica de las maquinas teleológicas en cuanto a que tienen una estructura lingüística (bases de datos de universos armónicos), son autónomas ya que actúan por periodos extensos sin la intervención humana, se mueven por si mismas por el entorno sin la intervención humana. De otro lado, los métodos/algoritmos evolutivos/ genéticos permiten generar música no-determinista o que ocurre de forma diferente cada vez que es interpretada.
Las entidades sónicas en Simbiosis, fueron diseñadas para atender cinco parámetros de la construcción musical: las alturas, el ritmo, la intensidad, el timbre y el espacio. Cabe aclarar que la definición de las entidades sónicas moldea la inmediatez en la obra, mientras que los procesos de mediano y largo plazo son controlados en tiempo real por el mentor, quien acota los comportamientos, temporalidades y condiciones de restricción para la elección de materiales de las entidades sonoras.
Figura 3. Funcionamiento de una entidad sónica en Simbiosis. Elaboración propia
Las entidades sónicas en Simbiosis, fueron diseñadas para atender cinco parámetros de la construcción musical: las alturas, el ritmo, la intensidad, el timbre y el espacio. Cabe aclarar que la definición de las entidades sónicas moldea la inmediatez en la obra, mientras que los procesos de mediano y largo plazo son controlados en tiempo real por el mentor, quien acota los comportamientos, temporalidades y condiciones de restricción para la elección de materiales de las entidades sonoras.
Se muestra la definición de los parámetros mencionados a través de módulos, siendo pertinente mencionar para los primeros casos (módulos armónico, melódico y rítmico) el uso de cadenas de Márkov, que es una forma de permitir un alto grado de autonomía a la máquina, permitiendo un modelamiento de comportamientos semideterminísticos, pero con amplio margen de variación en el tiempo, como el tránsito entre diferentes sonoridades presentes en la base de datos, el orden de las alturas para ser presentadas con un ritmo particular.
La ventaja que supone para este tipo de obras el uso de estos esquemas, es la posibilidad de analizar grandes volúmenes de información en tiempos muy cortos, sin que esto se convierta en una elección al azar, sino una organización que modela la esencia de sistematizaciones musicales como la armonía como un conjunto de probabilidades, relaciones y restricciones. Este concepto se explica con mayor profundidad en el apartado V de este artículo.
De otra parte, el módulo de intensidad es un ejemplo de variación en el tiempo a través de esquemas bio-inspirados. En el apartado VI de este artículo se explica con mayor detalle el funcionamiento de los algoritmos genéticos usados en la definición de las entidades sonoras y su consecuencia en la creación de la obra.
Universos Armónicos
Simbiosis hace uso de la teoría de conjuntos y la teoría de grafos; la primera aporta conceptos con los cuales se categorizan y relacionan objetos musicales, mientras que la segunda se encarga del estudio de las relaciones entre diferentes presentaciones de la información. Los precursores en la teoría de conjuntos en la música fueron Howard Hanson 1960) y Allan Forte (1973) 7 a través de sus publicaciones, pero vale la pena mencionar que su uso también puede atribuirse a Milton Babbitt.
En el ámbito de la cuantificación de las relaciones entre los conjuntos de clases tónicas, se encuentra que diversos autores han propuesto operaciones para medir la diferencia entre sonoridades. Algunos de ellos son: el índice de similitud (Teitelbaum, 1965), la similitud sobre el vector de clases interválicas IcVSIM (E. J. Isaacson, 1990), el ángulo entre vectores interválicos ANGLE (Scott e Isaacson, 1998), la distancia euclidiana y ángulo en el espacio de Fourier hexadimensional (Callender, 2007).8 A continuación se describen algunos conceptos y operaciones que fueron fundamentales para el desarrollo del sistema armónico del proyecto.
De otra parte, el módulo de intensidad es un ejemplo de variación en el tiempo a través de esquemas bio-inspirados. En el apartado VI de este artículo se explica con mayor detalle el funcionamiento de los algoritmos genéticos usados en la definición de las entidades sonoras y su consecuencia en la creación de la obra.
SPECTRA
Clifton Callender (2007), desarrolló una caracterización armónica para conjuntos de clases tónicas, que permite la comparación de diferentes temperamentos iguales e incluso, temperamentos basados en proporciones diversas, a través del uso de la transformada de Fourier, para que de esta manera se represente numéricamente el contenido armónico de cualquier acorde (Amiot, 2007), (Quinn, 2006), (Vuza, 1991), lo que resulta apropiado para generar representaciones computarizadas, así como para la cuantificación de una relación en un espacio armónico dado.
El procedimiento se puede describir como el cálculo de los componentes bidimensionales en un espacio de ciclos interválicos, permitiendo llegar a ideas de equilibrio para las sonoridades, de una manera similar a la propuesta por Quinn (2006) y que había sido propuesta inicialmente planteada como equilibrios de Fourier por Lewin (1959). Al obtener un único dato numérico que representa la magnitud resultante de la interacción de los componentes tónicos de una sonoridad en varios ciclos interválicos diferentes, es posible crear un conjunto de valores sobre los cuales crear el espacio euclidiano en el que se calculan la distancia y ángulo, esto es, pensar en un espacio con seis cualidades que describen la posición de las sonoridades para realizar las mediciones mencionadas. La siguiente ecuación resume el procedimiento para cada ciclo interválico:
Magnitud de la transformada de Fourier del conjunto Q con ciclo interválico l. Extraída de Callender (2007).
Donde q es cada componente de la sonoridad Q y l el tamaño de los ciclos interválicos a ser considerados. A continuación, se realiza la aplicación práctica de la ecuación con el conjunto [0, 2, 6] y los ciclos interválicos propuestos por Callender (2007) para la comparación de sonoridades en temperamento igual de doce divisiones. Se evalúa el primer componente del acorde (0) con cada uno de los componentes de la serie armónica, en este caso evaluaremos 6 parciales en el sistema temperado de 12 notas, por lo tanto, los componentes serán [12, 6, 4, 3, 2.4, 2].
Para el segundo componente,
Y así, sucesivamente con los componentes restantes, lo cual nos arroja el siguiente vector:
Este vector representa el SPECTRA del acorde [C, D, F#], esto es, las coordenadas en el espacio hexadimensional de Fourier sobre el cual calcular métricas que permiten la cuantificación de la relación entre dos sonoridades a la vez, lo que a su vez, puede permitir la consolidación de las relaciones armónicas en un espacio dado. Esto fue lo que posibilitó el manejo de alturas en la obra Simbiosis, a través de la construcción de un sistema para buscar rangos de valores y permitir la conexión de sonoridades desde lo indicado por el mentor.
Distancia Angular
En álgebra lineal, la distancia angular está dada para valores entre 0 ≤ Ø ≤ π (Williams, 2012). Pero para su uso en música, la diferencia angular (ANGLE) mide la independencia, no la oposición del sonido. Es perfectamente apropiado que su
valor máximo sea 90 (es decir π/2 ), representando perpendicularidad, en lugar de 180, representando una dirección negativa. (Scott e Isaacson, 1998). La distancia angular está definida por la siguiente ecuación:
Simbiosis contiene una lista de tablas con algunas de las escalas más conocidas, a las que se les extrajeron sus respectivos subconjuntos, se les calculó su respectivo SPECTRA y posteriormente la distancia angular entre ellos, realizando también una depuración con respecto a su vector interválico para suprimir las transposiciones de las escalas. Para calcular las posibles combinaciones de un conjunto de cardinalidad n se hace uso de la fórmula de combinaciones sin repetición, o combinación de n objetos tomando r a la vez (Kolman y cols., 1997).
Combinación sin repetición
Extendiendo el cálculo para las diferentes sonoridades incluidas en una escala, conjunto con cardinalidad alta o universo de alturas, se puede totalizar la cantidad de subconjuntos a través de la siguiente ecuación (Sánchez, 2017b), donde n es la cardinalidad del conjunto base y r es la cardinalidad del subconjunto, siempre r es menor que n e i es la menor cardinalidad a ser considerada.
Si se toma como ejemplo la escala presentada en la figura 4, y un mínimo de elementos para los subconjuntos de tres clases tónicas hasta ocho clases tónicas, hay 219 subconjuntos en total: 1 octacordio, 8 heptacordios, 28 hexacordios, 56 pentacordios, 70 tetracordios y 56 tricordios. Puesto que el volumen de datos es considerablemente grande, calcular el SPECTRA y la distancia angular entre todos estos conjuntos sería una tarea bastante laboriosa si no se automatiza, nada más la cantidad de relaciones entre los subconjuntos (su distancia angular) llega a las 47962 posibilidades. Es por esto que se hace necesario el uso de herramientas computacionales que realicen estos cálculos, lo cual fue solucionado a través del desarrollo de programas con este propósito haciendo uso del lenguaje de programación Pyhton. 9
Para la anterior escala, al considerar las relaciones de cada conjunto hacia los demás presentes en la misma, se particulariza la distancia y, a través de la teoría de grafos se construye una red de relaciones que se representa a continuación en la figura 5, ilustrando como círculos de colores los diferentes subconjuntos y, a través de líneas, la relación hacia otros conjuntos con un valor asociado.
Como se puede observar la densidad de las relaciones es tal que no puede diferenciarse en una representación gráfica. Así como se mencionó que es posible cargar diferentes módulos que respondan al instrumento elegido, en la obra Simbiosis es posible considerar como escala base o universo de alturas cualquier conjunto, constituyendo una base de datos de conjuntos y relaciones que representan un entramado que puede ser moldeado y recorrido por las entidades sonoras, desde las restricciones que defina el mentor.
A continuación, ejemplifican algunas restricciones que pueden ser usadas por el mentor/director durante la interpretación de la obra, lo cual permite ver sólo algunas de las relaciones, pues actúa a manera de filtro, restringiendo el tránsito entre las diferentes sonoridades y a la vez, permitiendo modelar el nivel de diferenciación que se puede entender como tensión armónica. De otro lado, la figura 9, muestra en detalle el acercamiento a un nodo particular del grafo, y la posibilidad de paso a otros conjuntos, todos representados numéricamente.
Teoría de la probabilidad
Puesto que este proyecto hace uso de procesos estocásticos 10 11 y aleatorios, es importante definir el concepto “Cadena de Márkov”, propio de la teoría de la probabilidad, el cual es fundamental para la programación de autómatas y vida artificial. El modelo de Márkov fue introducido por el ruso Andrey Andreyevich Márkov (1856- 1992) (Basharin y cols., s.f.) y describe un proceso estocástico discreto; una secuencia de variables o eventos aleatorios correspondientes a un sistema en cual la probabilidad de que ocurra un evento depende del evento anterior (Ching y Ng, 2006)
Figura 5. Grafo escala octatónica. En donde se ilustran todos los 219 subconjuntos o sonoridades agrupadas por vector interválico.
La figura 10, ilustra un ejemplo de cadena de Márkov a partir de multifónicos en el clarinete como estados y la tabla 2.5, detalla su respectiva matriz de transición. 12 .
Computación Evolutiva
La computación evolutiva (CE), ha sido un campo de desarrollo que tiene sus raíces en algunas ideas generadas a mediados del siglo XX, Alan Turing, hacia 1950 postulaba ya ideas acerca de máquinas con capacidad de aprendizaje y un esquema de cambios o mutaciones, así como una asistencia externa vista como la selección natural (Turing, 1950). Desde la década de 1960 gracias al impulso provisto por el avance tecnológico, fue posible comenzar a construir diversos esquemas centrados en el aprendizaje de las máquinas para resolver problemas de optimización, aunque el gran desarrollo de este campo tuvo una formalización y definición en las últimas dos décadas del siglo XX (Husbands, Copley, Eldridge, & Mandelis, 2007).
Figura 6. Grafo escala octatónica con una restricción de 0° a 11°.
Figura 7. Grafo escala octatónica con una restricción de 43° a 44°
Figura 8. Algunas posibilidades de conexiones en el grafo escala octatónica con una restricción de 8° a 14°, El conjunto de partida es [0, 1, 4, 6,7], se ocultan los conjuntos a los cuales no puede direccionarse y se resaltan los conjuntos a los cuales si puede dirigirse.
En el campo musical también se han aplicado esquemas computacionales diversos para la composición y modelamiento del estilo musical, por ejemplo a través un estudio estadístico es posible generar cadenas de Márkov que pueden producir composiciones al estilo de Chopin, dando cuenta de los patrones identificables en parámetros como el ritmo o la altura (Collins, Laney, Willis, & Garthwaite, 2011). En este sentido, la identificación de sistemas de reglas y la representación del conocimiento musical, principalmente de la altura y el ritmo, juegan un rol esencial a diversos niveles de estructura, desde lo motívico hacia escalas temporales de mayor duración como secciones o la forma misma (Cope, 2001).
Figura 9. Cadena de Márkov de Multifónicos en el Clarinete. Elaboración Propia.
Genotipo y fenotipo
En biología, un genotipo es el conjunto de los genes que existen en el núcleo celular de un organismo. El fenotipo es la realización visible del genotipo, es decir, el propio ser portador de los genes, cuyos caracteres son el resultado de la interacción entre el genotipo y el medio. Un genotipo musical
es una expresión que codifica procedimientos musicales. Un fenotipo musical es el fragmento musical generado por un genotipo. Al igual que en biología, un genotipo musical puede dar lugar a muchos fenotipos diferentes, en función del medio (López-Montes, 2013).
Algoritmo genético
El algoritmo genético fue desarrollado por John Holland en 1960, quien se propuso estudiar el fenómeno biológico de adaptación en la naturaleza y trasladarlo a sistemas computacionales. Un algoritmo genético contiene los siguientes pasos:
1. Iniciar una población aleatoriamente.
2. Seleccionar progenitores.
3. Reproducción (cruce y mutación).
4. Descendencia.
5. Evaluación (fitness).
Lo anterior será ilustrado con la canción All of Me de John Legend.
Codificación (Encoding):
como primer paso, codificamos el primer fragmento en un vector compuesto de duplas en donde el primer número representa la altura en MIDI y el segundo la duración en milisegundos.
Generando variación:
Existen diversas formas de variación genética, las más usadas son expuestas a continuación:
Mutación: Consiste en reemplazar un elemento aleatorio del genotipo por otro elemento aleatorio en el mismo intervalo. En este caso nos referimos a: Modificar la duración de una nota, modificar el tono de una nota, agregar o eliminar una nota a la melodía, intercambiar dos notas, clonar, interpolar, entre muchos otros más (Alfonseca y cols., 2007), (Donnelly y Sheppard, 2011).
Cruce o recombinación: En este algoritmo los genotipos de ambos progenitores se combinan utilizando diferentes procedimientos para generar los genotipos progenie (Alfonseca y cols., 2007), (Donnelly y Sheppard, 2011).
Cruce mono punto (Single point crossover): Se intercambia información genética a partir de un determinado punto.
Cruce de doble punto (two-point crossover): Se intercambia el material genético comprendido entre dos puntos.
Al realizar una recombinación de tres puntos el hijo contiene información de la madre y del padre tal como lo ilustra la imagen.
Figura 10. Ejemplo de un genotipo musical el cual tiene 3 semillas1 producen 3 fenotipos. Imagen tomada de López-Montes (2013).
Otras operaciones: A continuación se describe otras operaciones que son usuales en la aplicación de algoritmos genéticos en música (Horner y Goldberg, 1991).
• Añadir: se agrega un elemento al genoma. • Eliminar: se elimina un elemento del genoma. • Rotación: se gira o invierte el genoma. • Rotación incorrecta: se giran elementos en posiciones “incorrectas” del genoma. • Intercambio incorrecto: se intercambian elementos en posiciones “incorrectas” del genoma.
Envolvente acústica evolutiva Algo que caracteriza a cada instrumento es su envolvente acústica, el cual es la variación de la amplitud y el contenido espectral de un sonido con respecto al tiempo (Dodge y Jerse, 1997) (Sethares, 2005) (Dunn y cols., 2015). En síntesis de sonido es común hacer uso de un generador de envolvente, el cual controla los distintos parámetros de un sonido, siendo los más comunes:
• Ataque: tiempo de entrada, lo que demora el sonido en escucharse desde que es ejecutado hasta que alcanza su máxima amplitud. • Decaimiento: es el tiempo en que tarda en disminuir la amplitud hasta que se suelta la tecla o el punto de inducción vibratoria en el instrumento.
• Sostenimiento: tiempo en el cual la amplitud se mantiene constante. • Relajación: tiempo en el cual el sonido disminuye toda su amplitud.
Para Simbiosis, la envolvente acústica representa un atributo de cada entidad sonora, es lo que las distingue y diferencia entre ellas. Este atributo con el tiempo muta, se transforma o se recombina a partir de la interacción que exista entre ellas por medio de algoritmos genéticos o de una función de aptitud que establezca el director.
Se puede observar que la entidad sónica hija tiene el ataque de la entidad sónica 1, además tiene el decaimiento y relajación de la entidad sónica 2. Por último, el sostenimiento es un parámetro, el cual es el mismo en las dos entidades sónicas progenitoras
Figura 11. Diagrama de Flujo de un Algoritmo Genético, conceptualización realizada a partir de los esquemas propuestos por E. R. Miranda y Al Biles (2007) y Jensen (2011). Elaboración propia.
Uno de los comportamientos o mejor, un híbrido entre comportamiento y fenotipo, fue definido para el recorrido en un espacio virtual, esto es, la simulación de espacio para la fuente sonora. Al estar basado en ecuaciones polares, los contornos de recorrido pueden ser variados y generar curvaturas que resultan propicias para la percepción del cambio de direccionalidad en un modelo que tiene en cuenta el efecto doppler y un filtrado dependiente de la ubicación. En la ecuación 5 se muestra la generalización usada que contiene la definición de cardioides, caracoloides, rosas y lemniscatas (Purcel & Valberg, 1992). Esto fue desarrollado e implementado por el maestro Luis Fernando Sánchez Gooding, en su obra “del suspiro en el alba hasta el abrazo en el ocaso” (2014), otro ejemplo de música evolutiva.
En dicha obra, al nacer los seres virtuales, las variables a, b y c se generan aleatoriamente teniendo como posibilidad ser cero, uno o un número mayor que uno, permitiendo que se genere una mezcla de las figuras o una sola de ellas. De igual manera, la dirección de la figura se define desde las funciones seno y coseno que, dependiendo de los valores generados aleatoriamente, creará una inclinación particular como se muestra en los ejemplos
Figura 12. Genoma del motivo de All of Me, sección de la partitura extraída de Sher (1988). Elaboración Propia.
Figura 13. Mutaciones en el Genoma del Motivo de All of Me. Secciones de la partitura extraídas de Sher (1988). El color rojo indica mutación en la altura y el azul en el ritmo o duración. Se observa como la altura muta de un C a un B, en nota MIDI pasa de un 72 a 71. Por otro lado, el ritmo muta al sumar los valores de los 3 tresillos de negra más las dos blancas ligadas a la corchea, es decir 4500ms + 666.66ms + 666.66ms + 666.66ms = 6500ms. Elaboración propia.
Smalley (1986), realizo una clasificación de los diferentes tipos de movimiento, los cuales pueden ser una amalgama compleja de varios tipos y tendencias, ambigüedades y contracciones, existiendo 5 categorías representativas: uni-direccional, bi- direccional, reciproco, céntrico/cíclico y excéntrico/multi-direccional.
Como parte de los mecanismos programados para las entidades sónicas en Simbiosis, el control a través de las definiciones de movimiento mencionadas, permite la selección de comportamientos asignados a la generación de melodías. Supongamos que el mentor propone que las entidades usen comportamientos ascendentes unidireccionales, para lo cual las entidades cuentan con un listado como el que se encuentra en la figura 18, a través de una escogencia aleatoria un resultado posible
Figura 14. Recombinación (Cruce de tres puntos) entre dos genomas; la línea verde representa el genoma del padre, la línea negra el genoma de la madre.
Figura 15. Crossover de 3 puntos en envolvente acústica ADSR. La imagen describe la envolvente acústica de dos entidades sóni-cas, las cuales mezclaron su información “genética” para crear otra entidad con componentes de la envolvente acústica de sus progenitores.
Figura 16. Ejemplos de particularización de la ecuación 1. Elaboración Luis Fernando Sánchez Gooding
Figura 17. Tipología de movimiento. Imagen tomada de Zattra (2005), abstracción de Smalley (1986). Traducción propia.
Figura 18. Permutaciones de una melodía ascendente. Elaboración propia
Figura 19. Ejemplo de una melodía ascendente. Elaboración propia.
Figura 20. Ejemplo melodía parabólica. Elaboración propia.
Otros tipos de movimiento que se utilizaron en el proyecto de investigación-creación fueron:
Centrifugo: inicia desde la nota central del acorde o sonoridad hacia afuera. El proceso inverso (de las notas exteriores a las del centro) se denomina centrípeto.
Figura 21. Ejemplo melodía con movimiento centrífugo. Elaboración propia.
Convolución: en matemáticas una convolución, es un operador matemático que transforma dos funciones f y g en una tercera función. A veces es útil ver la convolución como un producto matricial, como una matriz de Toeplitz, la cual es una matriz cuadrada en la que los elementos de sus diagonales (de izquierda a derecha) son constantes (Von Zur Gathen y Gerhard, 2013). Una matriz de Toeplitz presenta la siguiente estructura:
Figura 22. Ejemplo ondulación melódica. Elaboración propia.
Implicaciones de la creatividad artificial Este tipo de investigaciones suelen suscitar preguntas tales como: ¿La máquina puede ser realmente creativa? ¿Es posible superar la prueba de Turing con este tipo de sistemas informáticos en música? ¿Cuál es la relación entre creatividad y computación? Adicionalmente, las que se plantea Raymond Kurzweil13: ¿Quién es el artista: el compositor siendo emulado, el software, o el compositor frente a sí mismo? Si bien ya existen sistemas computacionales capaces de imitar el estilo de diversos compositores, considero que el potencial de las maquinas, la IA y los sistemas computacionales no radica en qué tanto puede imitar el estilo de determinado compositor, qué tanto se parece a un ser humano, si pueden pensar, sentir, tener conciencia de sí mismo, entre otras posibilidades.
Precisamente, el potencial de las máquinas y de la inteligencia artificial radica en sus cualidades únicas que la diferencian del ser humano, una de las cuales es que son capaces de procesar grandes volúmenes de datos en un tiempo corto, algo que para el ser humano es una tarea complicada. Sin embargo, hasta ahora la inteligencia artificial no tiene la capacidad de un juicio u orientación estética.
Es por esto que una relación apropiada en este tipo de creación, puede ser configurada entre el ser humano y la máquina desde una perspectiva simbiótica, en donde el ser humano actúa como un sistema experto con juicio estético y la IA como una entidad capaz de procesar grandes volúmenes de datos. Dicha relación simbiótica hace posible que nuevos paradigmas surjan para comprender, concebir y percibir el sonido, lo cual nos lleva a situaciones creativas sustancialmente innovadoras, siendo fundamental el caos, el indeterminismo y la aleatoriedad.
El uso de las matemáticas y la aplicación de sistemas no lineales en la creación musical, por medio de sistemas estocásticos, técnicas de control y optimización no lineal, no solo permiten entender y analizar las propiedades del sonido y de la música, sino que también posibilita el desarrollo de nuevos paradigmas estéticos en la creación artístico-musical, en donde la IA juega un papel importante proponiendo ideas de carácter creativo novedosas e imprevistas.
Programar es meta-componer Como bien lo afirma José López-Montes (2012) en su trabajo GenoMus: prospección de técnicas de creatividad asistida por computadora mediante la metaprogramación de genotipos musicales, el diseñar algoritmos para generar música contiene decisiones de carácter compositivo, y si bien al programar no se compone música, los algoritmos son como el lienzo o la herramienta que constituye parámetros que harán posible la creación musical. Y aunque es verdad que no todo compositor debe saber programar, es preciso citar a Ortega y Gasset, quien siendo consciente de que la temporalidad del hombre es consustancial a su persona afirmó “somos hijos de nuestro tiempo”. Por lo tanto, si bien en el pasado la partitura fue la herramienta compositiva por excelencia, hoy es preciso integrar la programación como herramienta meta-compositiva.
Referencias
Notas
Licencia

Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Para los contenidos publicados antes de 2023, la revista utilizó la licencia Creative Commons Atribución (CC BY).A partir del año 2023 en adelante, la revista adoptó la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0).
POLÍTICA DE PLAGIO
La Revista ESTUDIOS ARTÍSTICOS expone las directrices sobre buenas prácticas en la publicación científica, como marco para el desarrollo y la implementación de sus propias políticas y sistema de ética en la publicación. Los Editores de la Revista ESTUDIOS ARTÍSTICOS , seleccionan los revisores bajo unas directrices de imparcialidad y profesionalidad, a fin de que se puedan asegurar evaluaciones justas, los Editores garantizan a los autores que se seleccionan a los revisores apropiados para las revisiones de sus trabajos, y los lectores puedan confiar en el proceso de revisión por pares.
Los Editores de ESTUDIOS ARTÍSTICOS son conscientes del trabajo necesario para la toma de decisiones firmes y la creación de procesos editoriales sólidos, diseñados para gestionar sus intereses y fomentar un sistema de publicación eficiente y sostenible, que beneficiará a las instituciones académicas, a los editores de revistas, a los autores, a quienes financian la investigación y a los lectores. Las buenas prácticas en la publicación científica, no se desarrollan espontáneamente sino que se establecen conscientemente y se promueven activamente.
Responsabilidades de los autores de los trabajos
Todos los autores que se reflejan en el trabajo deben haber contribuido activamente en el mismo.
ESTUDIOS ARTÍSTICOS proporciona a los autores unas instrucciones claras donde se explican los conceptos de autoría académica, especificando que las contribuciones deben quedar claras. Los editores de ESTUDIOS ARTÍSTICOS piden la declaración a los autores de que cumplen con los criterios de la revista en relación a la autoría. En caso de darse un conflicto en la autoría de un trabajo publicado, los Editores de ESTUDIOS ARTÍSTICOS se pondrán en contacto con el autor que reclama su autoría para establecer la veracidad del caso. Si los Editores lo estiman oportuno, se cerrará el acceso temporalmente al artículo en cuestión, hasta que se tome una decisión final.
Los documentos a publicar, no deben haber sido publicados antes
ESTUDIOS ARTÍSTICOS considerará sólo aquellos trabajos que no hayan sido publicados antes en otra Editorial y en cualquier formato. En este sentido, se considera que la literatura científica puede ser sesgada por una publicación redundante, con consecuencias importantes. ESTUDIOS ARTÍSTICOS pide a los autores que una declaración de que la obra presentada, sobre todo en su comunicación esencial, no ha sido publicada antes, y no está siendo considerada para su publicación en otros envíos
Los Editores de ESTUDIOS ARTÍSTICOS tienen derecho a exigir un trabajo original y cuestionar los autores acerca de si los artículos de opinión (por ejemplo, editoriales, cartas, revisiones no sistemáticas) han sido publicados antes.
Promover la integridad de la investigación
La mala conducta de Investigación
Si los Editores de ESTUDIOS ARTÍSTICOS sospechan de una mala conducta en la investigación llevada a cabo en un trabajo (por ejemplo, la generación de datos, falsificación o plagio), consultarán a los autores del trabajo sobre el procedimiento desarrollado para la investigación y estos deberán proporcionar cuanta información se les solicite.
La revisión por pares a veces puede detectar indicios de mala conducta en la investigación, en estos casos, los revisores plantearán sus dudas y de ser confirmadas, se considerarán como una falta grave (por ejemplo, la fabricación de datos, la falsificación, la manipulación de imágenes inapropiadas o plagio). No obstante, en todo caso los autores tienen derecho a responder a esas denuncias y demostrar que las investigaciones se han llevado a cabo con diligencia y con la velocidad adecuada.
La protección de los derechos de los participantes / sujetos de investigación
Los Editores de ESTUDIOS ARTÍSTICOS trabajan para crear políticas de publicación que promuevan prácticas éticas y responsables de investigación. Se buscarán garantías de que los estudios han sido aprobados por los organismos pertinentes. Si en la investigación se ha trabajado con datos de personas, los trabajos resultantes, deben ir acompañados de una declaración de consentimiento por parte de las mismas. Los Editores se reservan el derecho a rechazar el trabajo si hay dudas acerca de si se han seguido los procedimientos adecuados.
El respeto de las culturas y el patrimonio
Los Editores de ESTUDIOS ARTÍSTICOS expresan su sensibilidad a la hora de publicar imágenes de objetos que podrían tener un significado cultural o ser causa de delito.
Informar a los lectores acerca de la investigación y la publicación de la mala conducta
Los Editores advertirán a los lectores si se han producido violaciones éticas. En estos casos, ESTUDIOS ARTÍSTICOS publicará las oportunas correcciones cuando estos errores puedan afectar a la interpretación de los datos y a la información, cualquiera que sea la causa del error. Del mismo modo, ESTUDIOS ARTÍSTICOS publicará un escrito de rectificación si se ha demostrado que el trabajo puede ser fraudulento, o si los Editores tienen sospechas fundadas de que se ha desarrollado la investigación bajo una mala conducta. En este caso, la revista publicará una corrección como fe de erratas o la rectificación que incluirá las palabras "Fe de erratas" o "Corrección", se publicará en una página numerada y aparecerá en el índice de contenidos de la revista. Esta rectificación permitirá al lector identificar y entender la corrección en el contexto de los errores cometidos, o explicará por qué se corrigió del artículo, o recogerá las preocupaciones del Editor sobre el contenido del artículo. Estará vinculado electrónicamente con la publicación electrónica original.

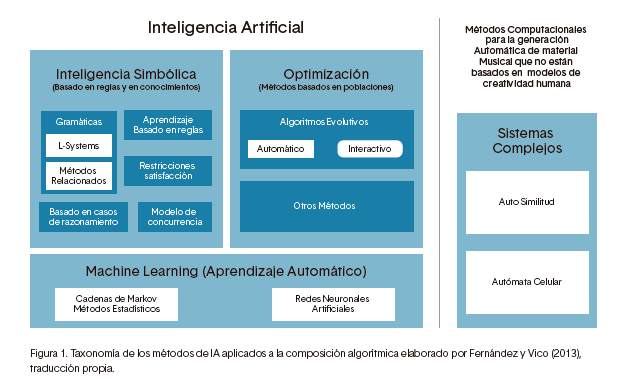
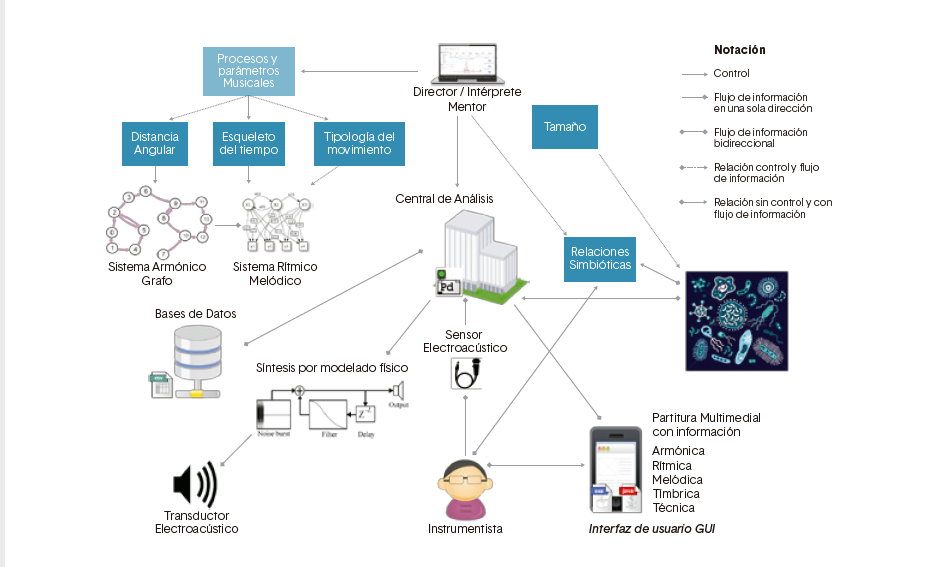
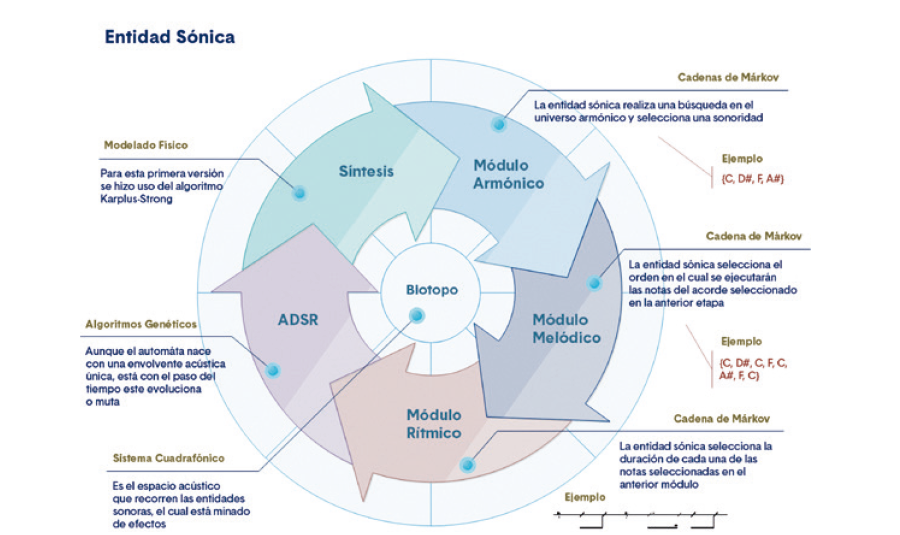

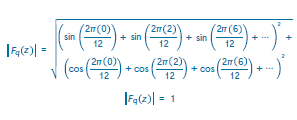
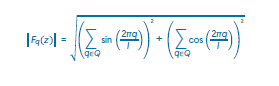
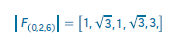
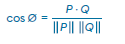
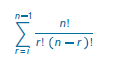
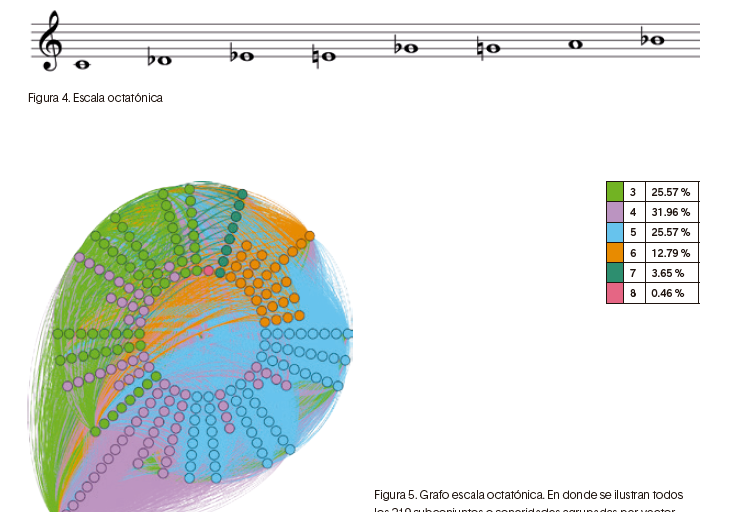
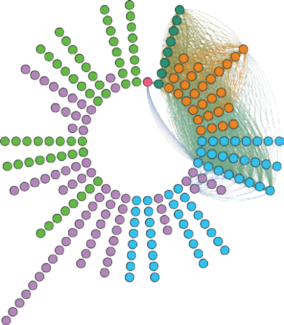

![Figura 8. Algunas posibilidades de conexiones en el grafo escala octatónica con una restricción de 8° a 14°, El conjunto de partida es [0, 1, 4, 6,7], se ocultan los conjuntos a los cuales no puede direccionarse y se resaltan los conjuntos a los cuales si puede dirigirse.](https://revistas.udistrital.edu.co/index.php/estart/article/download/12935/version/9497/17154/104227/4922187003_gf15.png)