Procesos de unitización y de normación en la construcción de un objeto de la transición aritmética-álgebra: la multiplicación como cambio de unidad-Process normación unitization and the construction of an object of arithmetic-field transition of the multiplication unit and shift

Procesos de unitización y de normación en la construcción de un objeto de la transición aritmética-álgebra: la multiplicación como cambio de unidad¹

Process normación unitization and the construction of an object of arithmetic-field transition of the multiplication unit and shift

Processo de individualização normación e a construção de um objecto de transição aritmética-campo da unidade de multiplicação e deslocamento

Jaime Humberto Romero Cruz²

Pedro Javier Rojas Garzón³

Martha Alba Bonilla Estévez⁴

¹Artículo de investigación que presenta una primera sistematización de resultados de investigaciones relacionadas con el pensamiento multiplicativo y el álgebra escolar, realizadas en estos últimos diez años por el grupo de investigación Matemáticas Escolares de la Universidad Distrital – MESCUD.

²PProfesores de la Universidad Distrital Francisco José de Caldas. Contacto: jaimeedumat@udistrital.edu.co

³PProfesores de la Universidad Distrital Francisco José de Caldas. Contacto: pedroedumat@udistrital.edu.co

⁴PProfesores de la Universidad Distrital Francisco José de Caldas. Contacto: marthaedumat@udistrital.edu.co

Fecha de recepción: febrero 2014, Fecha de aceptación: julio de 2014

Resumen

En este artículo se presenta una posibilidad de acogimiento de la diversidad en el aula de matemáticas. Para ello, se tematiza la multiplicación como cambio de unidad en una relación funcional, vista como elemento de la transición aritmética-álgebra. Se utilizan los conceptos unitización y normación como elementos de análisis de algoritmos usados por antiguas culturas —egipcia, mesopotámica, babilónica y griega— y se reporta evidencia sobre la plausibilidad de promover esta mirada de la multiplicación en el aula. Las diversas formas de construcción de unidades utilizadas por dichas culturas, además de originarias, resultan fecundas para comprender y acoger la diversidad de procesos realizados por niños y jóvenes en la actividad matemática, y posibilitan explicitar y socializar construcciones diversas acerca de la multiplicación, que dan cuenta de un pensamiento relacional, como constructo básico del pensamiento multiplicativo.

Palabras clave: Unitización, normación, multiplicación como cambio de unidad, diversidad, pensamiento multiplicativo.

Abstract

In this article a possibility of fostering diversity in the mathematics classroom is presented. For this, the multiplication unit and shift thematized a functional relationship as seen arithmetic element-transition algebra. Unitization and normación concepts as elements of analysis algorithms used by ancient cultures -egipcia, Mesopotamian, Babylonian and Greece-are used and reported evidence on the plausibility of promoting this view of the multiplication in the classroom. The various ways of building units used by those cultures, and originating, are fruitful to understand and embrace the diversity of processes performed by children and youth in mathematical activity, and allow various constructions explicit and socialize about multiplication, which give account of a relational thinking as a basic construct of multiplicative thinking.

keywords:Unitization, normación, multiplication and Unit change, diversity, multiplicative thinking.

Resumo

Neste artigo é apresentada a possibilidade de promover a diversidade na sala de aula de matemática. Para isso, a unidade de multiplicação e deslocamento tematizou uma relação funcional como visto aritmética álgebra elemento de transição. Unitização e conceitos normación como elementos de algoritmos de análise utilizados por culturas antigas -egipcia, Mesopotâmia, Babilônia e Grécia são utilizadas e relatadas evidências sobre a plausibilidade de promover essa visão da multiplicação na sala de aula. As várias formas de unidades de construção utilizados por essas culturas e originários, são frutíferos para entender e abraçar a diversidade de processos realizados por crianças e jovens na actividade matemática, e permitir que várias construções explícita e socializar sobre a multiplicação, que dão conta de um pensamento relacional como uma construção de base de pensamento multiplicativo.

Palavras-chave: Unitização, normación, multiplicação e mudança de unidade, a diversidade, o pensamento multiplicativo.

Introducción

Algunos investigadores, así como algunos estamentos del sistema educativo, han introducido y problematizado el fenómeno de la diversidad en el aula. En el presente es recurrente hablar de diversidad cultural, étnica, social, lingüística y también cognitiva (Alfa III, 2013). En la medida en que distintos Estados pretenden una educación para todos, sus sistemas educativos exigen a los profesores —de manera explícita o implícita— acoger tal diversidad. Desde este punto de vista, para que este acogimiento suceda en el aula de matemáticas se requiere que el profesor pueda comprender y posibilitar la emergencia de distintas formas de práctica matemática, pero además promover su articulación. En el campo del pensamiento multiplicativo, un tratamiento que posibilita acoger la diversidad es abordar procesos de unitización y normación (Lamon, 1994), para reconceptualizar formas de multiplicación como cambio de unidad (Mora y Romero, 2004).

Glasersfeld (1981) describió y tematizó procesos de construcción de unidades, caracterizándolos como primigenios y fecundos. Steefe (1994) describió y analizó producciones de niños (6-8 años) logrando una caracterización de secuencias y tipos de unidades conducentes a la configuración de unidades multiplicativas. Lamon (1994) presentó una teorización acerca de las unidades multiplicativas. El Grupo Mescud (Mora y Romero, 2004; Romero y Rojas, 2007) ha estado en la búsqueda de una caracterización de multiplicación basada en los procesos de unitización y normación. En este artículo se tematiza que una caracterización de la multiplicación, como cambio de unidad en una relación funcional, permite entenderla como elemento de la transición aritmética-álgebra y, además, posibilita el acogimiento de la diversidad en las aulas de matemáticas.

Para Lamon (1994), la unitización es el proceso de construir unidades de referencia —o unidad–todo— a partir de agrupamientos de diferente orden, que permite ver simultáneamente los miembros agregados e individuales de un conjunto, mientras que la normación es el proceso de reconceptualizar un sistema en relación con alguna unidad fijada o estandarizada. Para incluir procesos de construcción de unidades continuas, no necesariamente realizables mediante agrupamientos —por ejemplo, dadas tres rectas hallar una cuarta proporcional; obtener un rectángulo de lado dado, de igual tamaño que otro rectángulo fijo; dados los ceros de una función, en un sistema de referencia fijo, encontrar los ceros de otra función obtenida mediante una traslación de la primera.

El Grupo Mescud plantea la necesidad de extender estas definiciones y entender la unitización como el proceso y el efecto de construir, a partir de unidades dadas, nuevas unidades de referencia permitiendo ver simultáneamente ambos tipos de unidad; y, la normación como el proceso y el efecto de reconceptualizar un sistema en relación con alguna unidad establecida, o con un sistema de relaciones entre unidades de referencia. Si se mira la producción matemática desde estos constructos teóricos, se puede identificar que dichos procesos son tan antiguos como las prácticas mismas de hacer matemáticas,3 y han estado instaurados en diversas culturas.

En este artículo, se intenta mostrar que, en las soluciones dadas a ciertos problemas multiplicativos, por las culturas egipcia, mesopotámica y griega, se pueden ver estrategias y usos diferenciados de unitizar y normar. También se prentende mostrar que estos procesos aparecen recurrentemente en las estrategias que algunos niños y jóvenes, partícipes de aulas que promueven la participación, cuando resuelven problemas multiplicativos escolares. Por ello, se concluye que abordar unitización y normación como procesos iniciales para comprender formas de multiplicación como cambio de unidad, resultan potentes para acoger la diversidad en el aula de matemáticas.

En lo que sigue, se muestra: 1) cómo algunas de las construcciones de multiplicación realizadas por egipcios, mesopotamios, babilonios, griegos, árabes y europeos del renacimiento utilizan nociones como doblar y duplicar, mecanismos para hacer igualdad, construcción de distintas formas y tipos de unidad y un propósito común de elaborar desde las cosas para configurar estructuras matemáticas; 2) que resultados de las investigaciones realizadas con niños y jóvenes, cuando abordan problemas que requieren y promueven procesos de normación y unitización, de construcción de sistema de unidades similares y de unidades múltiples, a través de formas de representación perceptual —inicialmente icónicas—,permiten indicar un camino de construcción de la multiplicación como cambio de unidad.

CONSTRUCCIONES DE MULTIPLICACIÓN EN CULTURAS ANTIGUAS

En esta sección se presentan construcciones de multiplicación realizadas por egipcios, mesopotámicos, babilonios y griegos, centrando la mirada en el uso que hacen de unidades diversas, así como en los procesos asociados.

• • La multiplicación y la división egipcia: aunque su sistema de numeración fue decimal, desarrollaron el sistema binario. Sus algoritmos para multiplicar y dividir están compuestos de procesos para duplicar, mediar, sumar y restar. Los anteriores hechos están documentados en el papiro de Moscú y en el de Rhind. Los problemas que se presentan a continuación son descritos por Maza (2003):

Este autor resalta dos hechos:

(1) Alguno de los repartos anteriores marca la progresión característica de las fracciones Horus, una cantidad para el primero, la mitad para el segundo, la cuarta parte para el tercero, y

(2) [...] la complejidad de [...] los conocimientos matemáticos que mostraban los escribas. En particular, se encuentra una aplicación doble del método de 'falsa posición' en el del papiro Rhind.

Además de esos hechos, se resalta la manera en que los egipcios usaron esta información para resolver el problema: duplicar, mediar, suponer y expresar las cantidades en binario. En la suposición, aparece una relación inicial fijada y tratada como una unidad, expresable de diversas maneras. En el problema 75, suponen un valor probable de la condición pesu 20 como 1(1 heqats, 20 panes), esto es, unitizan; y luego la transforman conservándola mediante duplicaciones, mediaciones y sumas:

La anterior solución fue obtenida por el "método de la falsa posición". Por ello se supuso un valor para el montón y si se hubiera verificado la igualdad, ese valor hubiese sido la solución, pero dado que no ocurrió así, mediante cálculos adecuados a partir del supuesto se obtuvo la solución exacta. Como se puede apreciar, el método lleva a manipular (7 + 1/7 ∙ 7) como una sola unidad. La siguiente proposición de elementos está en relación con el principio aritmético del método.

Proposición V,4. Si una primera (magnitud) guarda la misma razón con una segunda que una tercera con una cuarta, cualesquiera equimúltiplos de la primera y la tercera guardarán la misma razón con cualesquiera equimúltiplos de la segunda y la cuarta respectivamente, tomados en el orden correspondiente.

Comentario 1. En los procedimientos anteriores se puede identificar cuatro unidades: 1, 1heqats, 20 panes y (1 heqats, 20 panes); cada una de las cuales es usada como tal, como una entidad. Estas cuatro unidades tienen diferente referente y son de distinta naturaleza; en particular, (1 heqats, 20 panes) es una relación funcional bidimensional (lineal). Tanto la relación como la construcción de unidades las podemos ubicar con respecto a las siguientes proposiciones de Euclides (Libro V):

Proposición 1. Si hay un número cualquiera de magnitudes respectivamente equimúltiplos de cualesquiera otras iguales en número, cuantas veces una sea múltiplo de otra, tantas veces lo serán todas de todas.

Proposición 2. Si una primera magnitud es el mismo múltiplo de una segunda que una tercera lo es de una cuarta, y una quinta es también el mismo múltiplo de la segunda que una sexta de la cuarta, la suma de la primera y la quinta será el mismo múltiplo de la segunda que la suma de la tercera y la sexta de la cuarta.

Proposición 4. Si una primera magnitud guarda la misma razón con una segunda que una tercera con una cuarta, cualquier equimúltiplo de la primera y la tercera guardaran la misma razón con cualquier equimúltiplo de la segunda y la cuarta respectivamente, tomados en el orden correspondiente.

Comentario 2. En la primera fase de la solución del problema 75 hay división, 155  20, mientras que en la segunda hay una multiplicación 30(7+1/2+¼). Sin embargo, los procedimientos de obtención de cada respuesta son similares: se basan en escogencias y cambios adecuados de unidad.

Comentario 3. Es importante reconocer que si empezamos con (1 heqats, 20 panes) podemos obtener tanto 155 panes, como cualquier número de panes que con respecto a 20 tenga un divisor común diferente de 1, pues lo importante aquí son los coeficientes de los elementos de la base. De hecho, tanto en los procedimientos referidos como en las proposiciones enunciadas, subyacen procesos de unitización y normación.

• • La multiplicación y división mesopotámica: además de su conocida numeración sexagesimal posicional, se destacan manifestaciones de una particular forma de pensar, que hace uso reiterado de la media aritmética para procesos de acotación y cálculo, que genera una técnica de aproximación. La técnica involucra un análisis —al menos implícito— de procesos geométricos, que se manifiesta en la estimación de raíces de números y en la consecución de soluciones de relaciones aditivas entre la «cosa», su cuadrado y una cantidad.

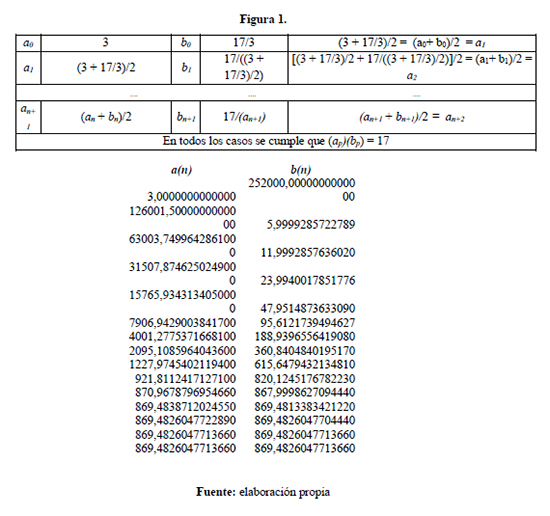
Aaboe (1964) presenta una trascripción de una tablilla escrita en cuneiforme, procedente de la Antigua Babilonia, en la cual aparecen tres números: a=30, c=42,25,35 y b=1,24,51,10. La hipótesis por él sustentada es que estos tres números son respectivamente: “a” longitud del lado de un cuadrado, “c” diagonal del mismo y, finalmente, “b” una “buena” aproximación de √2, como en el presente se deduce que la relación pitagórica debería ser c=30√2, valor que se obtiene en base sesenta aunque aproximada al hacer 30(1,24,51,10). Para Aaboe esta tablilla indicaría que los babilonios sabían la relación pitagórica 1200 años antes que hubiera nacido Pitágoras. En la actualidad se sabe que se trataba de obtener un cuadrado a partir de un rectángulo de superficie 2 unidades.

En esta otra aplicación del procedimiento, pero usando base diez, se trata de cuadrar el rectángulo de área 756000 y lados a=3, b=756000/3. Luego de la décimo segunda iteración, la longitud de los lados del rectángulo coinciden, al menos, en el orden de mil millonésimas (10-9). Por otra parte, se puede notar que cada una de las sucesiones a(n) y b(n) de longitudes de los lados de los rectángulos, convergen a √756000. En algunos otros problemas, el uso de esta técnica pone de manifiesto el conocimiento y uso reiterado de la propiedad de que “entre los rectángulos de igual perímetro el de mayor área es el cuadrado”.

Comentario 4: En el procedimiento descrito se presenta de manera realmente fuerte el uso de al menos cuatro tipos de unidades. En principio tres de ellas: la de longitud, la de superficie, y la que es iterada, esto es, la media de la suma de las longitudes de los lados del rectángulo (unitización). En tanto proceso recursivo, en cada paso k-ésimo, k >1, se toma como base la unidad obtenida en el paso k-1 ésimo. Es decir, aparece un proceso de sustitución de unidades, cada una de las cuales es probable respuesta y debe ser verificada. La cuarta unidad, mucho más compleja, es una secuencia de racionales potencialmente infinita convergiendo a un número irracional.

• • La multiplicación y división griega. El desarrollo del concepto de razón, unido al de proporción y orden (lineal), es una de sus formas de pensar, de ver y de expresar el mundo de las matemáticas, con la que operan, predicen y calculan, y que parece extenderse sobre la conformación de otros aspectos de su organización social. Aquellos conceptos son su expresión matemática y su forma de matematizar. Tal vez, el desarrollo de la teoría general de razones y proporciones, cuya organización algebraica está esquematizada en Elementos (libro V), es el mayor legado que el pensamiento matemático griego ha dejado a la comunidad matemática posterior.

Los modos egipcio y mesopotamio de pensar y hacer matemáticas son tematizados, sintetizados y sistematizados desde una perspectiva griega en el trabajo euclideano. Miremos por ejemplo, algunas ideas conexas a las nociones comunes quinta y sexta propuestas en Elementos (libro I), que tanto desde el tratamiento técnico operativo como en la elaboración argumentativa juegan un rol importante (Euclides, 1991, p.200):

5. Y las mitades de una misma cosa son iguales entre sí

6. Y los dobles de una misma cosa son iguales entre sí Ideas como bisecar rectas y ángulos para producir perpendiculares y por lo tanto ángulos rectos; probar relaciones aritméticas entre cada ángulo externo y sus correspondientes ángulos internos y opuestos (Mescud, 2011). Estas ideas intervienen en la actividad operativa y en la argumentativa para obtener dos relaciones euclidianas supremas: la comúnmente llamada pitagórica y la invarianza de la suma de los ángulos internos de todo triángulo euclideo. Duplicar y mediar cosas le ayuda a Euclides a conformar su mundo matematizado.

Euclides usa nuevamente el proceso de mediar y duplicar en el Libro II como elemento operatorio, en el Libro III obtiene el ángulo central como el doble del inscrito cuando son subtendidos por el mismo arco de circunferencia. En el libro V define y usa la razón duplicada, aunque como manera de expresar la composición de una razón consigo misma; en el libro VI establece una relación entre mediar ángulos y construir colecciones de pares de segmentos que guardan la misma razón:

Proposición VI, 3. Si se divide en dos partes iguales el ángulo de un triángulo, y la recta que corta el ángulo corta también a la base, los segmentos de la base guardarán la misma razón que los lados del triángulo que queden; y, si los segmentos de la base guardan la misma razón que los lados que quedan del triángulo, la recta dibujada desde el vértice hasta la sección dividirá en dos partes iguales al ángulo del triángulo.

En la entrada del libro X la mediación reiterada hace su presencia de forma explícita, a saber:

Proposición X, 1. Dadas dos magnitudes desiguales, si de la mayor se resta una magnitud mayor que su mitad y de lo que queda otra magnitud mayor que su mitad y se repite continuamente este proceso, quedará una magnitud menor que la menor de las magnitudes dadas Esta proposición procura elementos para una teoría de la aproximación controlada de la convergencia. Además de las ideas asociadas a duplicar y mediar, se encuentran otras ideas que vinculan la multiplicación con la proporción y que proveen una colección infinita de bases posicionales para expresar magnitudes homogéneas con una magnitud dada, ideas sobre las cuales se encuentra evidencia en los trabajos de egipcios y mesopotamios. ¿Cuáles son los otros elementos que intervienen?

1. El “algoritmo” de Euclides para magnitudes.
2. El algoritmo de Euclides para números.
3. Cuarta proporcional.
4. Extrema y media razón.
5. Colecciones de magnitudes continuamente proporcionales.
6. Composición de razones.
7. Relación número magnitud.
8. Colecciones de números continuamente proporcionales.

Esta proposición procura elementos para una teoría de la aproximación controlada de la convergencia. Además de las ideas asociadas a duplicar y mediar, se encuentran otras ideas que vinculan la multiplicación con la proporción y que proveen una colección infinita de bases posicionales para expresar magnitudes homogéneas con una magnitud dada, ideas sobre las cuales se encuentra evidencia en los trabajos de egipcios y mesopotamios. ¿Cuáles son los otros elementos que intervienen?

Todos estos elementos son de carácter multiplicativo, al punto que aparece una forma de potenciación de razones como elemento configurador de las colecciones, de números y de magnitudes en proporción continua, infinitamente numerosas —potencialmente—; colecciones que se comportan bien para el producto.

• Proporción continuada y unidad similar. Euclides inicia la instauración de la proporción continua en el libro V, a través de las siguientes definiciones:

• Una proporción entre tres términos es la menor posible [V, Def. 8].

• Cuando tres magnitudes son proporcionales, se dice que la primera guarda con la tercera una razón duplicada de la que (guarda) con la segunda [V, Def. 9].

• Cuando cuatro magnitudes son proporcionales, se dice que la primera guarda con la cuarta una razón triplicada de la que (guarda) con la segunda, y así siempre, sucesivamente, sea cual fuere la proporción (V, Def. 10).

Asimismo establece elementos operativos para comparar colecciones equinumerosas de magnitudes continuamente proporcionales como:

Una razón por igualdad se da cuando, habiendo varias magnitudes y otras iguales a ellas en número que, tomadas de dos en dos, guardan la misma razón, sucede que como la primera es a la última -entre las primeras magnitudes-, así -entre las segundas magnitudes- la primera es a la última; o, dicho de otro modo, consiste en tomar los extremos sin considerar los medios (V, Def. 17).

En lo que sigue se presentarán las proposiciones del libro VI, en algunas se explicitan unitizaciones y normaciones a través de formular un problema en la que en cada caso éstas intervengan. Se empieza enunciando la proposición VI, 2:

Proposición VI.2. Si se dibuja una recta paralela a uno de los lados de un triángulo, cortará proporcionalmente los lados del triángulo. Y si se cortan proporcionalmente los lados de un triángulo, la recta que une los puntos de sección será paralela al lado que queda del triángulo.

Ahora bien, la proposición VI, 12 puede verse como un problema cuya formulación y solución depende de la proposición VI, 2 según aparece a continuación:

En relación con unitización y normación se puede ver que, a partir del sistema de tres unidades, AB, EF y CD las tres rectas dadas, dos de ellas relacionadas —guardan razón, definición V, 4—, se configura un sistema de nuevas unidades: un triángulo (GKJ) uno de cuyos lados es la unidad GK=GH,HK debiéndose hallar la unidad GJ=GI,IJ —unidad conocida más unidad a conocer—. La estrategia euclidiana pasa, además, por el uso de rectas paralelas para establecer la misma relación entre tamaños con las unidades rectilíneas GK y GJ así como entre las partes unitarias que las conforman.

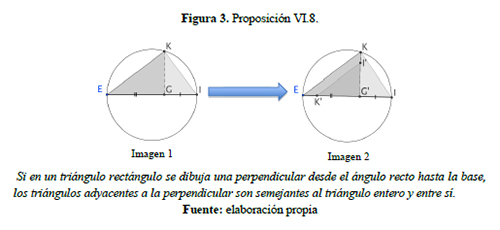
En la proposición VI, 2 aparecen en ciernes ideas y elementos de la teoría de semejanza, que dan pie a la configuración de lo que Harel y Confrey (1994) llaman unidad similar. Estos elementos se usan con fuerza entre otras en la proporción VI.8

Si en un triángulo rectángulo se dibuja una perpendicular desde el ángulo recto hasta la base, los triángulos adyacentes a la perpendicular son semejantes al triángulo entero y entre sí.

Aunque el modo euclidiano de argumentar es otro (ver figura 3, VI.8), se llama la atención acerca de que si se rota el triángulo GIK alrededor de G un ángulo recto y en sentido contrario a las manecillas del reloj, demostrar esta proposición se transforma en la de demostrar que EK e I’K’ son rectas paralelas (ver en la figura 3 las imágenes 1 y 2) por lo que cual aparecen las condiciones de uso de la proposición V.2 obteniéndose que GH:HK :: GI:IJ. Así formulada, la demostración de esta proposición se basa directamente en el uso de la proposición VI.2. De cualquier modo, aparecen unitizaciones y normaciones: se nota que esta proposición pide establecer un sistema de relaciones entre tres unidades dos de las cuales son descomposición de una unidad inicial; dicho de otra manera, aparece un sistema de relaciones entre tres unidades una de las cuales es composición de las otras dos.

Por una parte, la proposición VI.13 puede verse también como el problema de la extrema y media razón cuya formulación y solución depende de la proposición VI.8 según aparece a continuación:

Con lo dicho, se sabe que (1) dadas dos líneas rectas JH y MN que guarden razón, es posible hallar ZT tal que JH:MN :: MN:ZT; pero, resulta además que (2) la proporción V.14 al afirmar que:

Proposición V.14. Si una primera magnitud guarda con una segunda la misma razón que una tercera con una cuarta y la primera es mayor que la tercera, la segunda será también mayor que la cuarta, y si igual igual y si menor, menor.

Permite ordenar las magnitudes involucradas en las proporciones. Dado que si, por ejemplo, se tiene que JH:MN :: MN:ZT, se cumple que la colección JH, MN, ZT de magnitudes queda ordenada según alguna de las siguientes tres maneras:

• si JH>MN entonces MN>ZT y se obtiene JH>MN>ZT o

• si JH=MN entonces MN=ZT y se obtiene JH=MN=ZT o

• si JH < MN entonces MN < ZT y se obtiene JH < MN< ZT.

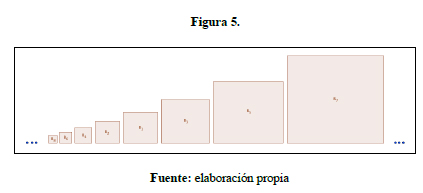
Al iterar sobre la proporción continuada, al menos con líneas rectas, lo expresado en 1) y 2) aparece un algoritmo para generar colecciones potencialmente infinitas, de magnitudes ordenadas que, tomadas consecutivamente, guardan la misma razón. Una colección de este tipo, conformada por Figuras similares (cuadrados) aparece en la figura 5:

En la que se tiene que … B8:B6 :: B6:B4 :: B4:B2 :: B2:B1 :: B1:B3 :: B3:B5 :: B5:B7

Se han presentado estas proposiciones VI, 8 y VI, 13 dado que:

1. Brindan un ejemplo paradigmático de unitización y normación que pone en juego unidades similares: todo triángulo rectángulo es partible en dos unidades menores, ordenadas y semejantes —similares— a este trazando una perpendicular a la hipotenusa desde el vértice opuesto. Y dado un triángulo rectángulo puede hallarse un triángulo rectángulo semejante a él tal que al agregarse adecuadamente producen un nuevo triángulo rectángulo mayor y semejante a los dos anteriores.
2. Permiten cuadrar cualquier figura rectilínea. Puesto que: 1) toda figura plana rectilínea es descomponible en triángulos, 2) todo triángulo es paralelogramizable, 3) la proposición I.43 permite, dado un paralelogramo , hallar otro paralelogramo AB, de lado AC, igual a , y 4) otra manera de enunciar la proposición VI.13 es la siguiente: hallar un cuadrado igual a un rectángulo dado.
3. Demuestran la existencia de un tipo de magnitud, a saber: línea recta, en el que dadas dos magnitudes que guardan razón, existe un algoritmo para generar secuencias ordenadas, potencialmente infinitas de estas magnitudes.
4. Con la posibilidad de expresar mediante los elementos de cualquiera de dichas colecciones, cualquier magnitud homogénea con las magnitudes iniciales, con el grado de precisión deseado que otorga la siguiente proposición:

(Proposición X.1. Dadas dos magnitudes desiguales, si de la mayor se resta una magnitud mayor que su mitad y de lo que queda otra magnitud mayor que su mitad y se repite continuamente este proceso, quedará una magnitud menor que la menor de las magnitudes dadas.

Se forma un nuevo tipo de unidad: el de las bases de magnitudes que tomadas ordenadamente dos a dos guardan una misma razón. Así que, al menos entre dos magnitudes que guarden razón, representable como la razón entre dos líneas rectas, es posible generar bases de magnitud tomando como unidad cualquiera de las dos magnitudes dadas.

Todas estas series de proporciones se basan en la composición de razones cuyo comportamiento, aplicado a las colecciones de magnitudes continuamente proporcionales, genera los intervalos de equimultiplicidad de razones. De similar manera, estos dos hechos se presentan en nuestra base de numeración, la base diez: 1:10::10:100::100:1000, de la que se obtiene (1:10)3 :: 1:103 pudiéndosele generalizar inductivamente sobre el orden de composición (exponente) n, así: para todo n  Ν, (1:10)n :: 1:10n y, a su vez, ésta se puede generalizar inductivamente sobre la base k, así: para todo k  Ν, para todo n  Ν, (1: k)n :: 1: kn

Dichas proporciones y generalizaciones refieren hechos particulares de la relación entre el universo de las magnitudes y el universo de los números propuesta en la proposición X.5.

Proposición X.5. Las magnitudes conmensurables guardan entre sí la misma razón que un número guarda con un número.

Esta proposición hace posible que todas las que refieren propiedades de secuencias de números cuyos elementos consecutivos guardan la misma razón, también describan propiedades de secuencias de magnitudes en proporción continuada. Por ejemplo, la proposición 8 del libro VIII:

Si entre dos números caen números en proporción continua (con ellos), entonces cuantos números caen entre ellos en proporción continua, tantos caerán también en proporción continua entre los que guardan la misma razón (con los números iniciales).

Que parafraseándola en términos de magnitudes dice que si, en una colección de magnitudes continuamente proporcionales, se extraen dos subcolecciones de tal manera que la primera y la última de la primera subcolección guarden la misma razón que la guardada por la primera y la última magnitud de la segunda subcolección, entonces las dos subcolecciones de magnitudes son equinumerosas.

Para Vega (1991, p.87) el libro VIII puede verse como una teoría de las series geométricas de razones. Desde nuestro punto de vista, hace parte de una aritmetización de la teoría de las magnitudes conmensurables. Pero como se ha argumentado, a través de los procesos unitización y normación además, la proposición X.1 permite ampliar dicha aritmetización, modelación, que incluye una manera de expresar las magnitudes —conmensurables o inconmensurables— que guarden razón, fijando una unidad para generar a partir de ella, una base de magnitud manteniendo la razón dada.

Comentario 5.. La proporción continua es el principio formador de las bases posicionales tanto de numeración como de magnitud; las definiciones V.9 y V.10 revelan la estructura de multiplicación repetida que hay en ellas.

UNITIZACIÓN Y NORMACIÓN EN TRABAJOS DE AULA

En esta sección se presentan evidencias sobre la construcción de unidades múltiples de referencia por parte de niños y jóvenes (10-13 años) para resolver situaciones problema. Así como la reinterpretación que estos realizan de las situaciones a partir de dichas unidades, esto es, el uso de procesos de unitización y normación (Lamon, 1994) en la resolución de problemas, sustentados en habilidades básicas requeridas para recuperar la unidad. En este contexto, se les solicita a los estudiantes encontrar procesos de solución, trabajando en grupo y exponiendo sus hallazgos a los demás, en un ambiente regulado por normas sociomatemáticas (Rojas, y otros, 2011, pp. 74-75), con la intención explícita que, como producto de su actividad matemática, generen métodos para resolver los problemas y no que apliquen procedimientos previamente aprendidos.

Problema de los extraterrestres. Considere los siguientes cuadros que relacionan extraterrestres y porciones de comida.

Sobre la línea doble, usted puede ver algunos extraterrestres y la cantidad de raciones de comida que necesitan para vivir por un día. Asuma que todos los extraterrestres comen la misma cantidad. Diga si cada uno de los grupos de extraterrestres bajo la línea doble, tiene más raciones, menos raciones o el número correcto de raciones de comida requeridas para vivir por un día.

Si bien, en principio, éste podría considerarse un problema típico, la manera icónica —en registro figural— en que se presenta la información de la relación dada, en un formato en el que no se pide un valor desconocido, hace que se conserve la relación visualizada desde el inicio (1 a 3) usando la instrumentación dispuesta. Algunos manteniéndose en lo icónico y otros estableciendo correspondencias. Si bien todos reconocen unidades múltiples, las maneras de unitizar son diferenciadas, mientras en el primer caso de la figura 3 el estudiante combina las unidades —ración y extraterrestres— para formar una nueva unidad mezcla, con la cual reinterpreta la situación, en el segundo arma unidades diferenciadas, siempre explicitando la relación 1 a 3.

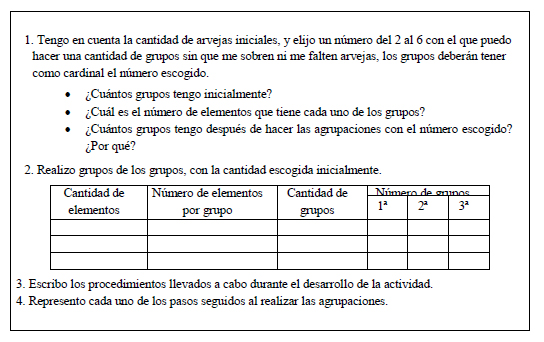
En las respuestas presentadas en las figuras 8 y 9 se evidencia un desprendimiento de lo icónico, pero manteniendo la coordinación entre los dos tipos de unidades: una ración de alimento por cada tres extraterrestres (unidad múltiple), usando esquemas multiplicativos diferenciados, en unos casos haciendo uso de un doble conteo y en otros manteniendo la relación 1 a 3. Problema de los granos y la construcción de unidades de similaridad. A un grupo de estudiantes de 4º grado (10-11 años) se le presentó la tarea denominada Granos. En ella se entregó un número de granos de arveja y se les dispuso una tabla, como la abajo presentada, para organizar la información que se pedía generar.

Esta actividad requería escoger de entre los números 2, 3, 4, 5, 6 uno que al multiplicarse de manera repetida obtuviera el número total de granos o uno que empezando por dividir el número total de granos y continuara dividiendo a los cocientes respectivos, en el proceso obtuviera residuo 0.

Los estudiantes probaron haciendo uso de la división para escoger el número: “Nosotros escogimos el número 3, porque a 81 lo divido en 3 y me salen 27 grupos de 3” Algunos hicieron división repetida:

“Nosotros tenemos 243 que es la cantidad de elementos. Y tenemos 3 que es el número de elementos por grupo, tenemos 81 que es la cantidad de grupos, 27 es cuando se agrupa una vez, 9 es cuando se agrupa dos veces y 3 es cuando se agrupa tres veces”.

Durante este proceso que modela la acción de agrupar manteniendo la cardinalidad de la unidad, generaron en cada paso una nueva unidad logrando predominio de la acción sucesora dividir por sobre la unidad convencional del conteo. Una exigencia implícita que aparece en la configuración de la actividad es la coordinación entre los momentos de la situación y lo que resulta cada vez que se ejecuta la acción sucesora.

En cuanto a las representaciones de las agrupaciones formadas desde la colección inicial de granos, notamos que los agrupamientos conducen a usar la menor unidad para generar de manera progresiva nuevas unidades de orden superior. La naturaleza de los objetos involucrados en la situación amplió la posibilidad de mantener y diferenciar al mismo tiempo en el campo visual tanto el uno anterior como el uno nuevo. De esta manera pudieron mantener control frente a distintos elementos que vinculan una situación de carácter recursivo; ellos avanzaron como aparece en Romero (2002, p. 93):

Mediante “uno más” al tiempo que se vuelve al uno originario reconstruyendo su estructura, el uno es ahora una colección [...]. Con lo cual aparecen dos significados usuales de la palabra «recurrir», “volver una cosa al lugar de donde salió” y “emplear medios no comunes para el logro de un objetivo” (Ezquerra, 1995).

Aunque no toda situación en la que se reconstruya el uno y se actúe con esta reconstrucción recoge procesos infinitos, necesarios para un significado más cercano a la recursión en matemáticas y al dominio numérico de lo continuo (Lakoff y Nuñez, 2000), una representación como la siguiente, realizada por el estudiante Selio (10 años) en clase, sí lo permite.

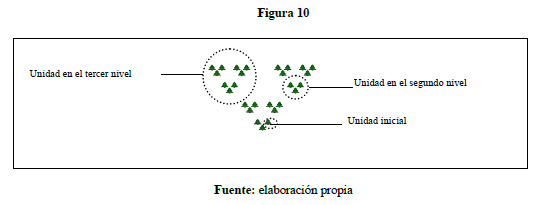
Pues muestra que las unidades obtenidas para la agrupación de los elementos de la situación son diferenciables pero se coordinan en una misma estructura, es decir la unidad inicial —un grano— es diferenciable con la unidad utilizada en el segundo nivel —grupo de tres unos de primer nivel—, la unidad del segundo nivel es diferenciable con la unidad utilizada en el tercer nivel —un grupo de tres unos de segundo nivel—, y el todo como una unidad de cuarto nivel manteniendo la misma estructura de la unidad anterior de manera visible por la disposición espacial de la representación (Narváez y Urrutia, 2005, p.63) y al retornar a la forma anterior genera condiciones para la compresión de una noción general de límite mediante la metáfora básica del infinito Lakoff y Núñez (2000, pp.186-207).

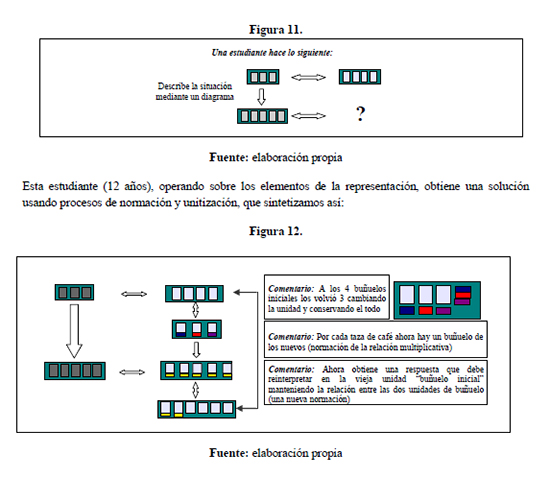
Problema del café y los buñuelos.

Para unas onces hay en la mesa tres tazas de café y cuatro buñuelos. Pero llegan cinco comensales. Si a cada comensal se le debe dar una taza de café, y se quiere mantener la relación inicial entre el número de tazas de café y la cantidad de buñuelos, ¿Cuántos buñuelos debe servirse?

Esta estudiante (12 años), operando sobre los elementos de la representación, obtiene una solución usando procesos de normación y unitización, que sintetizamos así:

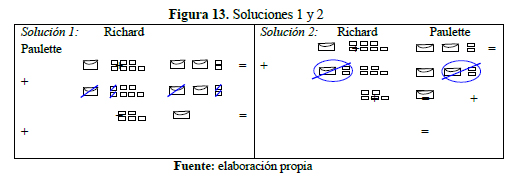
Problema de los sobres. El siguiente problema verbal, propuesto por Radford (2002) como inicio al trabajo con ecuaciones, se usó en una experiencia realizada con estudiantes de un programa de formación para ser profesor de matemáticas (Romero y Rojas, 2011), en la cual se les pidió resolverlo sin usar álgebra.

Una de las soluciones estuvo orientada por un sistema de equivalencias de las cantidades, “quitando” lo mismo a cada lado, marcando o “tachando” los objetos equivalentes en los respectivos “espacios ecuacionales”. Otra de las soluciones consistió en construir en cada espacio ecuacional una unidad común entre sobres y boletas, la máxima posible —unitización y normación—, y quitarla utilizando el procedimiento antes mencionado, así:

En la socialización de estas soluciones, algunos estudiantes no sólo reconocieron que en ellas se usó álgebra, argumentando que “se está trabajando con igualdades y realizando cancelaciones como en álgebra”, sino también la importancia del uso del sobre —representación icónica—, en tanto posibilidad de “representar y manipular lo desconocido”. Es decir, se trata al menos al inicio, de operar con representaciones que refieren cosas, ¿es casualidad que mesopotámicos, babilonios, griegos y árabes usaran precisamente esta palabra –aunque con diversas interpretaciones de entrada– para eregir sus construcciones matemáticas? En una línea de pensamiento cercana con esta reflexión, Radford (2002, p. 35) sugiere lo siguiente:

... entre la amplia variedad de signos, desde un punto de vista didáctico, los íconos pueden ser artefactos transicionales útiles para redesignar cantidades desconocidas antes de que un tratamiento formal pleno sea posible para los estudiantes. Verdad, los íconos tienen obvias limitaciones. Por una cosa, no es posible escribir un compendio de la sintaxis de los íconos. Pero, para nuestros propósitos, esto puede no ser necesario, como no fue necesario para los escribas babilonios que maravillosamente manejaron para resolver, mediante métodos icónicos, ecuaciones de segundo grado [Traducción libre].

CONCLUSIONES

En las secciones anteriores, a partir de soluciones dadas a problemas, se ha explicitado la diversidad de formas de pensar y razonar, así como la construcción de los procedimientos requeridos en la actividad matemática, ligadas a hechos culturales. En antiguas culturas y en contextos escolares actuales, a partir de acciones como doblar, mediar, partir y comparar, se pueden reconocer construcciones y usos de unidades diversas para dar solución a los problemas, en otras palabras, reconocer la unitización y la normación como procesos que posibilitan, en particular, la construcción de un objeto de la transición aritmética-álgebra: la multiplicación como cambio de unidad en una relación funcional.

Autores como Kieran (1992), para quien el álgebra no es una aritmética generalizada, hace explícita la ruptura existente entre estos dos campos conceptuales, llamando la atención sobre la necesidad que los estudiantes cambien sus formas aritméticas de pensar desplazándose a unas formas algebraicas en las que se razona sobre operaciones y relaciones y la generalidad de las mismas. Butto y Rojano (2004, 2010) reconocen una conexión entre la aritmética y el álgebra, proponiendo como rutas de acceso al pensamiento algebraico el razonamiento proporcional y los procesos de generalización. En investigaciones como las referidas anteriormente se reconoce la dificultad que encuentran los estudiantes para comprender, por ejemplo, la diferencia entre la expresión aritmética 2+3 y la expresión algebraica x+y (conflicto proceso-producto). Así como dificultades asociadas con el uso del signo igual y con las interpretaciones de la letra en contextos matemáticos (Küchemann, 1981); evidencias que les permiten concluir que para evitar la persistencia de tales dificultades se requiere crear “puentes” entre la aritmética y el álgebra escolar, creados, por ejemplo, a partir de la introducción en el currículo del álgebra temprana (early algebra) (Schliemann, Carraher y Brizuela, 2007).

Rojas, y otros autores (2011), por su parte, han planteado abordar la problemática de la transición aritmética-álgebra desde otra perspectiva. Para dar una imagen de ello se acudirá a una metáfora de tipo geográfica: no se trata de un “puente” entre dos “terrenos” claramente diferenciados y separados en la matemática escolar: la aritmética y el álgebra. Se trata más de un terreno, en el cual podemos reconocer dos secciones claramente diferenciadas en cuanto a su composición y una sección compartida, con componentes “difusos” de ambos terrenos; otra metáfora podría ser la siguiente: si bien se diferencia la zona continental de la zona del mar, no es posible definir unívocamente su frontera ya que no está claramente definida, y varía permanentemente.

Resulta posible entonces conceptualizar la transición aritmética-álgebra como un campo conceptual, asociado a conceptos como razón, proporción y proporcionalidad, y a procesos como unitización y normación. Sin embargo, la organización curricular incentiva que los esquemas de pensamiento elaborados y la instrumentación usada por los estudiantes para resolver problemas multiplicativos relacionados con dichos conceptos se vean como disconexos (Mora, Romero, Bonilla y Rojas, 2006; D’Amore, 2006; Mescud, 2005; Harel, Behr, Post y Lesh, 1994; Fischbein, Deri, Nello y Marino, 1985) generando así unos aprendizajes de conocimientos desarticulados (ver, por ejemplo, resultados en pruebas como TIMSS y PISA). Estos resultan posibles de conectar desde un tratamiento distinto, proponiendo procesos de formación que pueden originarse en lo aritmético y progresivamente acercarse a procesos algebraicos (Rojas Y otros, 2011).

Reconocer o no una continuidad entre aritmética y álgebra depende de la manera en que se aborde la actividad matemática, constituida por objetos, procesos y procedimientos cuya conformación se origina en la aritmética escolar y que pueden evolucionar hasta llegar a ser un objeto claramente algebraico. Por ejemplo, x+y puede verse como un objeto de la transición aritmética-álgebra; en el siguiente sentido: para realizar la suma de los números 2 y 3, es decir, 2+3 (proceso), se dispone previamente de una unidad común, el uno (3 unos y 2 unos), y obtenemos como resultado (producto) el 5, diferenciando claramente proceso de producto. Ahora, si se requiere sumar dos racionales la unidad no está dada de antemano y se debe establecerla en cada caso (puede variar), para sumar ½ y ¼ se puede tomar ¼ como unidad (2 de ¼ y 1 de ¼; también se podría haber escogido 1/8 ó 1/32), obteniendo como resultado ¾, aunque para sumar ½ y 1/3 no sirve la unidad anterior y es necesario encontrar otra (si se toma 1/6, se obtiene como resultado 5/6). Sin embargo, para sumar dos números reales cualesquiera, como 2 y √3, no disponemos de una unidad común, ni es posible encontrarla, y la expresión 2+√3 representa tanto el proceso como el producto, y se debe aceptar que 2+√3 es una expresión adecuada para sumar 2 y √3.

Así, la propuesta de incluir la multiplicación como cambio de unidad (Mora y Romero, 2004; Mescud, 2006; Rojas y otros, 2011) como un objeto de la transición aritmética-algebra, asumiendo que: 1) al multiplicar, esencialmente se expresa una cantidad, no necesariamente entera, de una cierta unidad, en términos de otra unidad, y que al llevar a cabo tal cambio de unidad, se realizan unitizaciones o normaciones; 2) dichas expresiones de relaciones entre cambios de unidad emergen y permiten la emergencia de formas de variación lineal; lo que induce a proponer un camino de relaciones entre aritmética y álgebra, que posibilita el logro de mejores aprendizajes, utilizando ideas culturalmente sedimentadas involucradas en los procesos de unitización y normación.

Como se ha mencionado, y desde las evidencias aquí presentadas, se puede afirmar que cuando los estudiantes participan en ambientes en los cuales se reconoce la diversidad y se privilegia la comunicación y la interacción en la resolución de problemas, emergen diversas formas de pensar, de proceder, de expresar que no sólo resultan eficaces sino generalizables y potentes, de hecho, son posibles de relacionar con producciones matemáticas de antiguas y nuevas culturas. Esto permite cuestionar el hecho que, aún en el presente, en contextos escolares se pretenda privilegiar formas únicas para el trabajo matemático escolar. Si bien, desde los referentes curriculares (MEN, 1998), se promueve el reconocimiento de la diferencia, de la importancia de formas alternativas de organización curricular, se requiere de formas de organización que no sólo acojan estos referentes sino que promuevan y potencien la diversidad. Es decir, que posibiliten otras formas de hacer y de ser de los niños y jóvenes en la actividad matemática. En este sentido, se pone en discusión la influencia de no reconocer la diversidad en la acción curricular en la restricción de posibilidades de desarrollo del pensamiento aritmético algebraico de nuestros estudiantes.

Referencias

Aaboe, A. (1964). Matemáticas: episodios históricos desde Babilonia hasta Ptolomeo. (A. Linares, Trad.) Cali: Norma.

Alfa III. (2013). Orientaciones específicas para la incorporación de tecnología en procesos de formación de profesores de ciencias naturales, lenguaje y comunicación, y matemáticas en contextos de diversidad para el diseño de secuencias de enseñanza aprendizaje. Valparaíso: Ediciones Universitarias de Valparaíso. Recuperado de: http://www.dri.pucv.cl/wp-content/uploads/2013/04/Libro-Red-Alternativa.pdf

Butto, C y Rojano, T. (2004). Introducción temprana al pensamiento algebraico: abordaje basado en la geometría. Educación matemática, 16 (1), 113-148.

Butto, C y Rojano, T. (2010). Pensamiento algebraico temprano: el papel del entorno Logo. Educación Matemática, 22(3), 55-86

D’Amore, B. (2006). Didáctica de la matemática. (A. Balderas, Trad.). Bogotá: Magisterio.

Delgado, M., Olaya, L. y Velásquez, M. (2005). Procesos de unitización y normación en problemas de razón y proporción. Trabajo de grado inédito. Universidad Distrital Francisco José de Caldas, Bogotá.

Enfedaque, J. (1990). De los números a las letras. Summa, 5, 23-33.

Euclides (1991). Elementos I-IV. (M. Puertas, Trad.). (Original escrito 300 a. d. n.e.). Madrid: Gredos

Euclides (1994). Elementos V-IX. (M. Puertas, Trad.). (Original escrito 300 a. d. n.e.). Madrid: Gredos

Euclides (1996). Elementos X-XIII. (M. Puertas, Trad.). (Original escrito 300 a. d. n.e.). Madrid: Gredos

Fischbein, E., Deri, M., Nello, M. and Marino, M. (1985). The role of implicit models in solving verbal problems in multiplication and division. Journal for research in mathematics education. 16, 1, 3-17.

Glasersfeld, V. (1981). An attentional model for the conceptual construction of units and number. Journal for Research in Mathematics Education, 12, 83–94.

González, F., Martín-Louches, M. y Silván, E. (2010). Prehistoria de la matemática y mente moderna: pensamiento matemático y recursividad en el Paleolítico franco-cantábrico. Dynamis, 30, 167-195.

Harel, G., Behr, M., Post, T. and Lesh, R. (1994). The impact of the number type on the solution of multiplication and division problems. In G. Harel and J. Cofrey (Ed.). The development of multiplicative reasoning in the learning of mathematics. New York: State University of New York.

Lakoff, G. and Núñez, R. (2000). Where mathematics comes from. How the embodied mind brings mathematics into being. New York: Basic Books.

Kieran, C. (1992). The learning and teaching of school algebra. In D. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning. New York: Macmillan.

Küchemann, D. (1980). The meanings children give to the letters in generalised arithmetic. In W. Archenhold, R. Drive, A. Orton, and C. Wood-Robinson (Eds.), Cognitive development research in science and mathematics. Leeds, UK: University of Leeds

Lamon, S. (1994). Proportional reasoning. Unitizing and Norming. In G. Harel and J. Cofrey (Eds.), The development of multiplicative reasoning in the learning of mathematics. New York: State University of New York.

Maza, C. (s.f.). Matemáticas en Egipto. Acceso: abril de 2008. Recuperado de: http://www.personal.us.es/cmaza/egipto

Mescud (2006). El pensamiento multiplicativo. Una mirada a su densidad y complejización en el aula. Informe final de investigación. COLCIENCIAS-IDEP y Universidad Distrital Francisco José de Caldas (Cód. 1130-11-14040).

Mora, O. y Romero, J. (2004). ¿Multiplicación y división "o" cambio de unidad? En P. Rojas (Ed.), Memorias del Sexto Encuentro Colombiano de Matemática Educativa. Bogotá: ASOCOLME. Recuperado de: http://www.asocolme.org/

Mora, O., Romero, J., Bonilla y M., Rojas, P. (2006). Modelos MADA y Regla de tres: complementos inconexos funcionales. 210-213. In S, Sbaragli (Ed.). La Matematica e la sua Didattica: Vent’anni di impegno. Roma (Italia): Carocci Faber.

Narvaez, D. y Urrutia, E. (2005). La Construcción de Esquemas Splitting; un experimento de enseñanza. Trabajo de grado inédita. Universidad Distrital Francisco José de Caldas. Bogotá D. C.

Pérez, J. (1987). Diálogos aritmética, práctica y especulativa. Acceso: abril 10 de 2008. Recuperado de: http://campus-virtual.uprrp.edu/postgrau/activitats/tutormates/37/webs/ajudes/inversi%F3n.pdf

Puig, L. (1998). Componentes de una historia del álgebra. El texto de Al-Khwarizmi restaurado. En F. Hitt (Ed.), Investigaciones en Matemática Educativa II. México: Iberoamérica. Acceso: marzo 03 de 2008. Recuperado de: http://www.uv.es/~didmat/luis/mexico96revisado03.pdf

Radford, L. (2002). Algebra as tekhne: artefacts, symbols and equations in the classroom. Mediterranean Journal for Research in Mathematics Education, 1 (1), 31-56.

Rojas, P., Romero, J., Mora, L., Bonilla, M., Rodríguez, J. y Castillo, E. (2011). La multiplicación como cambio de unidad: Estrategias para promover su aprendizaje. Bogotá: Universidad Distrital.

Rojas, P., Rodríguez, J., Romero, C., Castillo, E. y Mora O. (1997). La Transición aritmética-álgebra. 1 Ed. Bogotá: Universidad Distrital.

Romero, J. (2002). La recursión como modeladora de situaciones. Revista científica, 4, 91-98.

Romero, J. y Rojas, P. (2011). Un caso de toma de conciencia de la indeterminancia; 192-195. In S. Sbaragli (Ed.), La Matematica e la sua Didattica: Quarant’anni di impegno. Bologna (Italia): Pitagora.

Romero, J. y Rojas, P. (2007). Estrategias para promover el aprendizaje de la multiplicación como cambio de unidad. En G. García (Ed.), Memorias del 8º Encuentro Colombiano de Matemática Educativa. Bogotá: ASOCOLME-Universidad del Valle. Recuperado de: http://www.asocolme.org/

Romero, J., Bonilla, M. y Rojas, P. (2011). Razonamiento Matemático y Algo-ritmos: Una Mirada desde los Elementos de Euclides. En G. García (Ed.), Memorias del 12º Encuentro Colombiano de Matemática Educativa. Armenia. Colombia. Recuperado de: http://www.asocolme.org/

Schliemann, A., Carraher, D. and Brizuela, B. (2007). Bringing out the algebraic character of arithmetic: from children's ideas to classroom practice. Mahwah, N.J.: Lawrence Erlbaum.

Steffe, L. (1994). Children´s multiplying and dividing schemes: An overview. In Harel and Cofrey (Ed.), The development of multiplicative reasoning in the learning of mathematics. New York: State University of New York. Vega, L. (1991). Introducción. En Euclides. Elementos I-IV (M. Puertas, Trad.). Madrid: Gredos.