DOI:
https://doi.org/10.14483/23448393.11673Published:
2017-09-12Issue:
Vol. 22 No. 3 (2017): September - DecemberSection:
Electric EngineeringAplicación de Costos de Incertidumbre Analíticos de Energía Solar, Eólica y Vehículos Eléctricos en el Despacho Óptimo de Potencia
Application of Analytical Uncertainty Costs of Solar,Wind and Electric Vehicles in Optimal Power Dispatch
Keywords:
costo de incertidumbre, despacho económico, energía renovable (es).Keywords:
economic dispatch, renewable energy, uncertainty cost (en).References
J. Arévalo, F. Santos and S. Rivera, Uncertainty Cost Functions for Solar Photovoltaic Generation, Wind Energy Generation and Plug-In Electric Vehicles: Mathematical Expected Value and Verification by Monte Carlo Simulation. International Journal of Power and Energy Conversion. 2017. [En línea]. Disponible en: http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijpec
H. Kamankesh, V. Agelidis and A. Kavousi-Fard, “Optimal Scheduling of Renewable Micro-Grids Considering Plug-In Hybrid Electric Vehicle Charging Demand”. Energy, 100, 285–297, 2016.
B. C. Gu, Z. M. Chen, T. Y. Jiv, L. L. Zhang, Q. H.Wu, M. S. Li and J. H. Huang, “Quasi-Monte Carlo Simulation Based Economic Dispatch With Wind Power Integrated”. IEEE Innovative Smart Grid Technologies – Asia (ISGT-Asia), 264–269, Nov., 2016.
H. Huang, C. Y. Chung, K. W. Chan and H. Chen, “Quasi-Monte Carlo Based Probabilistic Small Signal Stability Analysis for Power Systems With Plug-In Electric Vehicle and Wind Power Integration”. IEEE Transactions on Power Systems, 28(3), 3335–3343, Aug., 2013.
J. Hetzer, D. C. Yu and K. Bhattarai, “An Economic Dispatch Model Incorporating Wind Power”. IEEE Transactions on Energy Conversion, 23(2), 603–611, June 2008.
J. Zhao, F. Wen, Z. Y. Dong, Y. Xue and K. P. Wong, “Optimal Dispatch of Electric Vehicles and Wind Power Using Enhanced Particle Swarm Optimization”. IEEE Transactions on Industrial Informatics, 8(4):889–899, Nov., 2012.
I. Erlich, K. Lee, J. Rueda and S. Wildenhues, “Competition on Application Of Modern Heuristic Optimization Algorithms For Solving Optimal Power Flow Problems”. Working Group on Modern Heuristic Optimization (WGMHO)Under the IEEE PES Analytic Methods in Power Systems (AMPS) Committee, February 2014.
M. I. Ennes and A. L. Diniz, “A General Equivalent Thermal Cost Function For Economic Dispatch Problems”. 2012 IEEE Power and Energy Society General Meeting, pages 1–6, July, 2012.
R. S.Wibowo, F. F. Utama, D. F. U. Putra and N. K. Aryani, Unit Commitment With Non-Smooth Generation Cost Function Using Binary Particle Swarm Optimization. In 2016 International Seminar on Intelligent Technology and Its Applications (ISITIA), pages 571–576, July 2016.
J. Bastidas, C. Ramos and E. Franco, Modeling And Parameter Calculation of Photovoltaic Fields in Irregular Weather Conditions. Revista Ingeniería, 17(1), 37–48, Junio, 2012.
T. Chang, “Investigation on Frequency Distribution of Global Radiation Using Different Probability Density Functions”. International Journal of Applied Science and Engineering, 8(2), 99–107, 2010.
S. Surender Reddy, P. R. Bijwe and A. R. Abhyankar, “Real-time Economic Dispatch Considering Renewable Power Generation Variability and Uncertainty Over Scheduling Period”. IEEE Systems Journal, 9(4), 1440–1451, Dec., 2015.
C. Ramos, A. Saavedra and E. Arango, “Distributed Maximum Power Point Tracking in Wind Micro-Grids”. Revista Ingeniería, 17(1), 5–13, Junio 2012.
J. Ceballos, E. Caicedo and S. Ospina, “Una propuesta metodológica para dimensionar el impacto de los vehículos eléctricos sobre la red eléctrica”. Revista Ingeniería, 21(2), 154–175, Agosto, 2016.
W. Group, “Common format for exchange of solved load flow data”. IEEE Transactions on Power Apparatus and Systems, PAS-92(6), 1916–1925, Nov, 1973.
NASA Athmospheric Science Data Center, Surface Meteorology and Solar Energy: Retscreen Data. 2017. [En línea]. Disponible en: https: //eosweb.larc.nasa.gov/cgi-bin/sse/retscreen.cgi
IDEAM [Instituto de Hidrología Meteorología y Estudios Ambientales]. Atlas interactivo del viento de Colombia. 2015. [En línea]. Disponible en: http://www.ideam.gov.co/
UPME [Unidad de Planeación Minero Energética], Integración de las energías renovables no convencionales en Colombia. 2017. [En línea]. Disponible en: http://www.upme.gov.co/Estudios/2015/Integracion_Energias_Renovables/INTEGRACION_ENERGIAS_RENOVANLES_WEB.pdf
C. D. Charalambous and N. U. Ahmed, “Centralized Versus Decentralized Optimization of Distributed Stochastic Differential Decision Systems With Different Information Structures-Part I: A General Theory”. IEEE Transactions on Automatic Control, 62(3),1194–1209, March, 2017.
R. D. Zimmerman, C. E. Murillo-Sanchez and R. J. Thomas, “Matpower: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education”. IEEE Transactions on Power Systems, 26(1), 12–19, Feb., 2011.
C. Zhao and R. Jiang, “Distributionally Robust Contingency-Constrained Unit Commitment. IEEE Transactions on Power Systems”. PP(99),1–1, 2017.
H. Ye, Y. Ge, M. Shahidehpour and Z. Li, “Uncertainty Marginal Price, Transmission Reserve, And Day-Ahead Market Clearing with Robust Unit Commitment”. IEEE Transactions on Power Systems, 32(3), 1782–1795, May, 2017.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Application of Analytical Uncertainty Costs of Solar, Wind and Electric Vehicles in Optimal Power Dispatch
Aplicación de Costos de Incertidumbre Analíticos de Energ ía Solar, Eólica y Vehículos Eléctricos en el Despacho Óptimo de Potencia
Juan Arévalo
Universidad Nacional de Colombia,
jucarevalobo@unal.edu.co
Fabian Santos
Universidad Nacional de Colombia,
fsantosb@unal.edu.co
Sergio Rivera
Universidad Nacional de Colombia,
srriverar@unal.edu.co
Recibido: 08/03/2016. Modificado: 05/06/2017. Aceptado: 07/07/2017.
Abstract
Context: Currently, renewable energy sources are playing an important role in counteracting the environmental impact of traditional energy sources. For this reason, system operators must have analytical tools that allow them to incorporate these new forms of energy. In electrical power systems, when incorporating renewable resources such as photovoltaic solar generation, wind power generation or electric vehicles, uncertainty is introduced due to the stochasticity of primary resources.
Method: Uncertainty costs are proposed that incorporate the injected power variability of the main sources of renewable energy (solar and wind) and the consumed power (electric vehicles). Variability is considered by the probability distributions of the primary sources of renewable energy (solar irradiation and wind speed).
Results: The main result of this research is the application of analytical costs of uncertainty. In this way it is possible to modify the cost function of a traditional economic dispatch. Additionally, it is proposed to solve the problem with a heuristic optimization method of economic dispatch of active-reactive power. Finally, a comparison is made with the operating cost of the system without the incorporation of renewable energies.
Conclusions: The proposed model in this article is a potential decision-making tool that power system operators may consider in the operation of the system. The tool is capable of considering the uncertainties of the primary sources of renewable energy. The probability distribution of the primary source forecast is assumed to be known. An opportunity in order to extend the model is to study its applicability to dynamic time horizons, contemplating the constraints of the unit commitment problem.
Keywords: Economic dispatch, Renewable energy, Uncertainty cost.
Language: Spanish
Resumen
Contexto: Actualmente las fuentes de energía renovables están jugando un importante rol para contrarestar el impacto ambiental de las fuentes de energía tradicional. Por esto, los operadores del sistema deben contar con herramientas de análisis que le permitan incorporar estas nuevas formas de energía. En los sistemas eléctricos de potencia que incorporan recursos renovables y vehículos el éctricos, se introduce incertidumbre debido a la estocasticidad de los recursos primarios y los patrones de conducción de los vehículos.
Método: Para las incertidumbres se ˜ naladas, se proponen costos de incertidumbre que incorporan la variabilidad de potencia inyectada de las principales fuentes de energía renovable (solar y eólica) y la potencia consumida (vehículos el éctricos). La variabilidad es considerada mediante las distribuciones de probabilidad de las fuentes primarias de la energía renovable (irradiación solar y velocidad del viento).
Resultados: El principal resultado de esta investigación es la aplicación de los costos analíticos de incertidumbre. De esta manera es posible modificar la función de costos de un despacho economico tradicional. Adicionalmente se propone solucionar el problema con un m étodo de optimización heurística de despachoóptimo de potencia activa-reactiva. Finalmente, se realiza una comparación con el costo de operación del sistema sin la incorporación de energías renovables.
Conclusiones: El modelo propuesto en este artículo constituye una posible alternativa de toma de decisiones que los operadores de los sistemas de potencia pueden considerar en la operación del sistema que es capaz de considerar las incertidumbres de las fuentes primarias de la energía renovable. Para ello se supone conocida la distribución de probabilidad del pronóstico de la fuente primaria. Como oportunidad de extensión de este estudio se destaca su aplicabilidad a horizontes de tiempo dinámicos, contemplando las restricciones propias de la comisión de unidades.
Palabras clave: Costo de incertidumbre, Despacho económico, Energía renovable.
Idioma: Español
1. Introducción
Cuando se incorporan recursos renovables como la generación solar fotovoltaica, generación con energía eólica o vehículos eléctricos, se introduce incertidumbre en cuanto a la disponibilidad de potencia en el sistema, debido a la estocasticidad de los recursos primarios [1]. Dicha incertidumbre es indeseada en la programación del despacho de energía y se identifica como una de las barreras que ha impedido la alta penetración de los recursos renovables en los sistemas de generación.Con el proposito de asignar un costo a la incertidumbre presentada en los recursos renovables, tradicionalmente se han utilizando simulaciones de Montecarlo [2]–[4]. Si bien tales simulaciones dan resultados que consideran la variabilidad de las fuentes primarias de energía (irradiación solar y velocidad del viento), implican gran número de escenarios a simular [4]. A fin de disminuir el número de escenarios a simular se requiere que los costos de incertidumbre sean modelados con una expresión analítica. En el documento [5] se presenta una propuesta de costos de incertidumbre desarrollada con base en modelos probabilísticos del comportamiento de la velocidad del viento. En [6] se extiende la modelación anterior a vehículos eléctricos. En [1] se desarrolla en detalle la modelación analítica de costos de incertidumbre para el comportamiento de la velocidad del viento y los patrones de manejo de los vehículos eléctricos; ademas se extiende la modelación a sistemas de generación fotovoltaica, modelando la probabilidad de distribución de la irradiación solar. De esta manera, la propuesta de costos de incertidumbre tiene la finalidad de aumentar la penetración de los recursos renovables en los sistemas de generación, ya que es una herramienta de planeación del sistema con renovables, sin afectar la disponibilidad de potencia en la demanda y brindando una solución económicamente viable en el despacho económico.
Los costos de incertidumbre requieren modelos probabilísticos de las fuentes primaria de generación renovable, así, en este trabajo se plantean modelos probabil ísticos en ubicaciones geográficas del territorio colombiano para generación solar fotovoltaica y generación eólica. Los nodos del sistema con renovables se consideran en puntos estratégicos con alto potencial de irradiancia solar para la generación fotovoltaica y puntos con velocidades de viento altas y constantes para la generación con energía eólica. De esta manera se plantea realizar el despachoóptimo de potencia activa-reactiva para un sistema de potencia que incorpora fuentes de generación renovable, modelados con funciones de costos de incertidumbre. Estos costos de incertidumbre son ecuaciones analíticas no polinómicas ( [1]) en función de la potencia programada para los nodos de generación renovable, luego son introducidos como costos de generación en un sistema de potencia que contiene nodos con generación convencional modelados con funciones de costos polinómicas tradicionales.
El despachoóptimo de potencia busca minimizar la función de costo total de generación del sistema, que para el presente caso es una función no polinómica y no convexa, ya que se consideran los costos de incertidumbre anal íticos. Debido a las propiedades de este problema de optimización (función objetivo no convexa, con restricciones no lineales correspondientes a un sistema de ecuaciones algebraicas para el flujo de potencia) se plantea solucionar el problema con optimización heurística. La otra razón de esta decisión, es que en la formulación del problema se plantean elementos de maniobra (taps de transformadores y capacitores shunt) como variables de decisión discretas. Se decidió implementar el algoritmo de optimización heurístico Differential Evolutionary Particle Swarm Optimization (DEEPSO, por sus siglas en inglés) aplicado al sistema de potencia con fuentes renovables modeladas con funciones de costos de incertidumbre. Tal algoritmo fue el que ganó la competencia internacional IEEE “Application of Modern Heuristic Optimization Algorithms for Solving Optimal Power Flow Problems” de la Power & Energy Society (PES por su siglas en inglés) [7]. No obstante se pueden utilizar otras técnicas heurísticas.
Este artículo esta estructurado de la siguiente manera: inicialmente se exponen la formulación matemática de los costos involucrados en la función de costos a minimizar en el despachoóptimo de potencia en la seguna sección. En la tercera sección se describen las funciones de costos de incertidumbre para cada fuente renovable a implementar. En la cuarta sección se realiza la descripción del sistema de potencia dentro de cual se introducen los nodos con generación renovable, allí se pretende solucionar el problema de despacho económico. En la quinta sección se describe el algoritmo de optimización heurístico implementado para realizar la simulación del despachoóptimo de potencia y finalmente se presentan el análisis de resultados y conclusiones.
2. Planteamiento matemático de función de costos a minimizar
En esta sección se realiza el planteamiento matemático de los costos involucrados en la función de costos totales de generación en un sistema que modela los nodos renovables con la propuesta de costos de incertidumbre. Para ello se proponen unos costos de penalización, con esta definición se proceden a definir los costos de incertidumbre, se muestra los costos polinómicos de los generadores tradicionales y finalmente se plantea la función objetivo de costo total de generación.
2.1. Costos de penalización
Los costos de penalización son propuestos en [1], [5], los cuales son una adición a los costos operativos de generación de energía y se producen cuando dentro del despacho se programa una potencia Ws,i la cual subestima o sobrestima la potencia disponible Wav,i en un nodo con recursos renovables.
2.1.1. Costos por subestimar
Son costos de penalización generados cuando la potencia programada Ws,i es menor que la potencia disponible Wav,i en un recurso renovable.
De esta forma se puede definir una función de costos debidos a subestimar la potencia disponible, como:
La función de costos (2) asocia un coeficiente de penalización cu,i por subestimar, el cual debe ser definido por el operador del sistema. Este coeficiente (cu,i ) corresponde al costo por utilizar la diferencia entre la potencia disponible y la potencia programada (que es el valor de inyección que más le conviene a la red) en otra actividad, como almacenamiento de energía s í existe disponible, en vez de utilizarla directamente en la red.
2.1.1. Costos por sobrestimar
Son costos de penalización generados cuando la potencia programada Ws,i es mayor que la potencia disponible Wav,i en un recurso renovable.
De esta forma se puede definir una función de costos debidos a sobrestimar la potencia disponible, como:
La función de costos (4) asocia un coeficiente de penalización co,i por sobrestimar, el cual debe ser definido por el operador del sistema. Este coeficiente (co,i ) corresponde al costo por adquirir la diferencia entre la potencia programada y la potencia disponible, como generadores diesel si existen disponibles en el nodo de generación renovable, de tal manera que se inyecte lo que mas le convenga a la red.
2.2. Costos de incertidumbre
Los costos de incertidumbre se definen como el valor esperado de las funciones de costos de penalización por subestimar (2) y por sobrestimar (4), las expresiones analíticas de costos de incertidumbre aplicados a generación fotovoltaica, eólica y vehículos eléctricos conectados a red se muestran en la sección 3.
2.3. Costos polinómicos
Los generadores de energía convencionales térmicos se modelan por medio de una función de costos polinómica comúnmente de orden dos [8], proveniente de la curva de costo del combustible, de la siguiente forma:
Adicionalmente, los operadores de red de sistemas de los diferentes países pueden tener sus propias funciones de costo para los generadores convencionales que se pueden expresar en forma de polinomios [9].
2.4. Costo total de generación
La función de costos totales de generación del sistema, a minimizar en el nuevo problema de despacho económico con función objetivo no convexa, se describe de la forma:
donde:Nc es el número total de generadores convencionales.
NPV es el número total de generadores fotovoltaicos.
Nw es el número total de generadores eólicos.
Ne es el número total de nodos con vehículos conectados.
Pc,s,i es la potencia programada en el generador convencional i.
WPV,s,i es la potencia programada en el generador fotovoltaico i.
Ww,s,i es la potencia programada en el generador eólico i.
Pe,s,i es la potencia programada en el nodo con conexión de vehículos i.
WPV,i es la potencia disponible en el generador fotovoltaico i.
Ww,i es la potencia disponible en el generador eólico i.
Pe,i es la potencia disponible en el nodo con conexión de vehículos i.
Cc,i es la función de costos del generador convencional i.
CPV,u,i es la función de costos por subestimar del generador fotovoltaico i.
CPV,o,i es la función de costos por sobrestimar del generador fotovoltaico i.
Cw,u,i es la función de costos por subestimar del generador eólico i.
Cw,o,i es la función de costos por sobrestimar del generador eólico i.
Ce,u,i es la función de costos por subestimar del nodo con conexión de vehículos i.
Ce,o,i es la función de costos por sobrestimar del nodo con conexión de vehículos i.
En (6) se puede ver que la función de costo total incluye los costos de generación con agentes convencionales y la propuesta de costos de incertidumbre por subestimar y sobrestimar lo disponible en las fuentes renovables; además se omiten los costos de operación directos (o propios de generación) para los agentes renovables, lo cuales no se toman en cuenta dentro de este estudio ya que se considera que el recurso primario es gratis (sol y viento).
3. Costos de incertidumbre: generación solar, eólica y cargas activas (vehículos eléctricos)
En esta sección se describen las funciones de costos de incertidumbre para casos particulares de generación solar, generación con energía eólica y vehículos eléctricos conectados a la red. Inicialmente se desarrollan los modelos probabilísticos de la potencia disponible en estos recursos.
3.1. Descripción de fuentes de energía renovable
Como se define en la sección 2, los costos de incertidumbre son el valor esperado de los costos de penalización, y dado que los costos de penalización son función de la potencia disponible Wav;i en el recurso renovable, se debe realizar el modelo probabilístico de la energ ía primaria para cada recurso primario y luego hallar su expresión en términos de la potencia disponible.
a) Energía solar
Función de distribución de probabilidad solar: el recurso primario de la energía solar fotovoltaica es la irradiancia ( [10]), la cual es dependiente de la ubicación geográfica de los paneles. Varias investigaciones se han hecho para hallar la distribución de probabilidad de la irradiancia, como la implementada en [11], en donde una de las funciones de distribución de probabilidad es la Log-normal:
donde:
fG(G) es la función de densidad de probabilidad lognormal.
G es la irradiancia solar.
λ es la media de la distribución Log-normal.
β es la desviación estándar de la distribución Log-nomal.
- Potencia de un panel solar fotovoltaico: la potencia que se desarrolla en un panel
fotovoltaico se puede expresar como [12]:
donde:
WPV(G) es la potencia fotovoltaica generada como función de la irradiancia.
G es la irradiancia solar.
Gr es la irradiancia estándar en el ambiente.
Rc es un valor de irradiancia de referencia.
WPVr es la potencia nominal de salida de la celda fotovoltaica.
Como se observa en la ecuación (8), el panel convierte radiación en potencia de forma cuadrática hasta un punto Rc en el que la expresión comienza a ser lineal.
b) Energía eólica
- Función de distribución de probabilidad del viento: la variable que define la energ ía eólica es la velocidad del viento, que para diferentes ubicaciones geográficas presenta variados comportamientos, sin embargo, en artículos como [5], [13] se ha mostrado que el viento tiene una distribución de probabilidad Weibull, cuyos parámetros dependen de la ubicación geográfica:
- Potencia de un generador eólico: la potencia generada en función del viento en una turbina eólica está dada por [5]:
donde:
fv(v) es la función de densidad de probabilidad para la velocidad del viento.
v es la velocidad del viento.
c(m/s)factor de escala en un lugar geográfico. Típicamente entre 5-8 [5].
k factor de forma que también depende de la ubicación geográfica, no tiene dimensiones. Típicamente entre 1-3 [5].
Tomando el factor de forma k como 2 y el factor de escala c como √2σ se tiene la distribución Rayleigh:
donde:
Ww(v) es la potencia eólica generada en función de la velocidad del viento.
v es la velocidad del viento.
vi velocidad de viento de corte inferior del aerogenerador.
vr velocidad de viento nominal del aerogenerador.
vo velocidad de viento de corte superior del aerogenerador.
Wr es la potencia nominal del aerogenerador.
Además, en (11) se definen las constantes:
c) Energía de veh ículos eléctricos conectados a la red
El uso de carros eléctricos tiene un comportamiento estocástico, dependiente del patrón de conducción de estos vehículos ( [14]), y por lo tanto el estado de carga y descarga de sus baterías también lo es. Una de las variables que define la energía disponible en bater ías de carros eléctricos, es la distancia que se recorre con el mismo, en [4] se propone una distribución normal para la distancia recorrida en un vehículo eléctrico:
donde:fD(D) es la función de densidad de probabilidad de la distancia recorrida por un vehículo eléctrico.
D distancia recorrida por el vehículo eléctrico.
μ es la media de la distribución.
φ es la desviación estándar de la distribución. El comportamiento normal de la distancia recorrida se ve reflejado en la forma de carga y descarga de las baterías de los veh ículos eléctricos. Por tanto la potencia disponible Pe en carros eléctricos se puede definir como:
Donde: fpe(Pe) es la función de densidad de probabilidad de la potencia disponible en baterías de vehículos eléctricos.Se debe mencionar que (13) puede tomar valores de potencia negativos, caso para el cual las bater ías le inyectan potencia a la red.
3.2. Formulas analíticas de costos de incertidumbre
De acuerdo con desarrollo detallado por los autores de este artículo en [1], las funciones analíticas de costos de incertidumbre para las fuentes generación solar fotovoltaica, generación con energía eólica y vehículos eléctricos conectados a red, después de desarrollar las integrales correspondientes (proceso presentado en [1]), son:- Energía solar fotovoltaica: para el caso de energía solar fotovoltáica, la fórmula de costo de incertidumbre contempla cuatro partes: dos para el caso subestimado, y dos para el caso sobreestimado.
- Energía eólica: la fórmula de costos de incertidumbre contempla dos partes, una subestimada y otra sobrestimada.
- Energía de vehículos eléctricos: la fórmula de costos de incertidumbre contempla dos partes, una subestimada y otra sobrestimada.
a) Caso subestimado.
b) Caso sobrestimado.
a) Caso subestimado.
b) Caso sobrestimado.
a) Caso subestimado.
b) Caso sobrestimado.
4. Descripción del sistema eléctrico de potencia de prueba
En esta sección se presenta la descripción del sistema de potencia, el cual es una versión simplificada del sistema IEEE-118 tomado de [15], donde se incluyen nodos con generación renovable modelados para zonas del territorio colombiano. En la tabla I se muestra la composición general del sistema.
El sistema tiene una potencia base de 100MW , tensión base de 318kV , una capacidad de generación instalada de 8,205MW y una demanda total de 4,242MW , en la tabla II se muestra la capacidad instalada según el tipo de generación.Como se muestra en la tabla II, el 14 % de la capacidad instalada del sistema corresponde a energías de origen renovable y el 86 % a energías de origen convencional, lo que para el caso colombiano actual se puede considerar como alta penetración de energías renovables.
4.1. Descripción de nodos con generación fotovoltaica
Para establecer el comportamiento probabilístico de la irradiancia solar modelada con una distribución Log-normal (sección 3), se toman valores de irradiancia media y desviación estándar tomados de datos de la NASA [16], para cinco coordenadas geográficas especificas del territorio colombiano con potencial solar según [17] (Figura 1). En la tabla III se muestran los resultados de este proceso.
En la tabla III:
β es la desviación estándar de la distribución Log-normal,
λ es la media de la distribución Log-normal,
Gr es el valor nominal de la irradiancia en el entorno geográfico,
Rc es un valor de irradiancia de referencia,
Con base en los resultados obtenidos en la tabla III se plantean las especificaciones de los nodos fotovoltaicos descritas en la tabla IV.
En la tabla IV:
WPVr potencia activa nominal del recurso fotovoltaico.
WPV,∞ máxima potencia de salida.
cPV,u,i costo de penalización debido a subestimar.
cPV,o,i costo de penalización debido a sobrestimar.
4.2. Descripción de nodos con generación eólica
Para establecer el comportamiento probabilístico de la velocidad de viento modelado con una distribución Rayleigh (sección 3), se toma el estadístico de valor medio de velocidad de viento a una altura de 10m suministrado por la UPME [18], para dos coordenadas geográficas especificas de la zona norte de Colombia, luego se calcula el parámetro de escala de la distribución Rayleigh &sigmna;. En la tabla V se muestran los resultados de este proceso para dos puntos con potencial eólico según [17].
En la tabla V:
σ es el parámetro de escala Rayleigh.
vi es la velocidad de viento de corte inferior del aerogenerador.
vr es la velocidad de viento nominal del aerogenerador.
vo es la velocidad de viento de saturación del aerogenerador.
Con base en los resultados obtenidos en la tabla V se plantean las especificaciones de los nodos eólicos descritas en la tabla VI.
Donde en la tabla VI representan:
Ww,r potencia nominal del nodo eólico.
Ww,∞ potencia máxima entregada por el nodo eólico.
ρ constante líneal.
κ constante independiente.
cw,u,i costo de penalización debido a subestimar.
cw,o,i costo de penalización debido a sobrestimar.
4.3. Descripción de nodos con conexión de vehículos eléctricos
La capacidad de potencia agregada de los nodos con vehículos eléctricos conectados a la red se distribuye de forma normal (sección 3) durante el periodo pico del día, en la tabla VII se describen los nodos con conexión de vehículos.
En la tabla VII:μ potencia media del nodo con conexión de vehículos.
φ desviación estándar.
We,max potencia mínima del nodo con conexión de vehículos.
We,min potencia máxima del nodo con conexión de vehículos.
Ce,u,i costo de penalización debido a subestimar.
Ce,o,i costo de penalización debido a sobrestimar.
5. Algoritmo de optimización para el despacho económico
Se busca realizar el despachoóptimo de potencia activa y reactiva minimizando la función de costo total de generación (6) aplicando el algoritmo heurístico de optimización DEEPSO implementado en la competencia internacional IEEE-PES Application of Modern Heuristic Optimization Algorithms for Solving Optimal Power Flow Problems [7].
Se decidió utilizar heurística, debido a que la función objetivo al incluir los costos de incertidumbre presentados en la sección 3 es no convexa. Adicionalmente, el problema tiene una serie de variables de decisión continuas y discretas que hacen intratable el problema con solvers convencionales de optimización (como GAMS o CPLEX) en lo que se refiere a tiempos de solución y convergencia. Los algoritmos de optimización heurística son desarrollos basados en el comportamiento de procesos naturales, se utilizan comúnmente en problemas de optimización considerados de alta complejidad [19]. Para el caso de sistemas eléctricos de potencia, los procesos de optimización heurística presentan un potencial importante en la búsqueda de solucionar problemas de operación y planeamiento del sistema gracias a su potencial para resolver complejidades matemáticas inherentes relacionadas con alta dimensionalidad, no linealidad, no convexidad, multimodalidad y discontinuidad de los espacios de búsqueda [7].
El algoritmo de optimización involucra 130 variables de decisión continuas y discretas definidas de la forma:
- Continuas (107 en total): 42 representan la potencia activa despachada por los agentes convencionales (excluyendo el nodo slack), cinco son de la potencia activa despachada por los generadores fotovoltaicos, dos son de la potencia activa despachada por los agentes eólicos, cuatro son de la potencia activa en los nodos con conexión de vehículos, 54 variables relacionadas con la magnitud de la tensión en los nodos de generación, las cuales siguen los rangos mínimos y máximos vming,i = 0;95 p.u y vmaxg,i = 1;05 p.u respectivamente.
- Discretas (23 en total): nueve representan el radio de Tap de transformación con mínimo y máximo de Tmink = 0,9 y Tmaxk= 1,1 respectivamente y catorce variables discretas binarias asociadas a los dispositivos de compensación.
En la figura 2 se muestra el diagrama de flujo que sigue el algoritmo de optimización DEEPSO.
La población inicial y la población actualizada de la estrategia de búsqueda del algoritmo se refieren a las 130 variables de decisión sujetas a valores máximos y mínimos de potencia activa generada, tensión en los nodos PQ, Taps de transformación y dispositivos de compensación.
Para la solución en cada flujo de potencia se implementa la herramienta Matpower [20] empleando el modelo típico de análisis en estado estático para sistemas de potencia, luego la evaluación de la función objetivo consiste en determinar el valor de la función de costos de generación Ctotal (ecuación (6)). La función de aptitudes se expresa en (22), la cual es la adición de la función objetivo Ctotal (ecuación (6)) y una función de penalización (PF) expresada en (23).
La función de aptitudes toma en cuenta las limitaciones de generación de potencia activa en el nodo slack Pslack , la limitación de generación de potencia reactiva en los nodos de generación Qg,i, la limitación de magnitud de la tensión en los nodos de carga vload,i y la restricción de flujo de potencia en cada línea de transmisión sl,ρ es un factor de penalización fijado en 1E + 7. NB es el número de nodos de carga del sistema y Nl es el número de ramas del sistema.
El diagrama de flujo se programa en 100.000 iteraciones para finalmente obtener la solución correspondiente al mejor valor de de la función de aptitudes. En esta formulación se asume que todas las unidades de generación (convencionales y renovables) se despachan siempre. Es decir, se soluciona el problema en un intervalo de tiempo de operación del sistema. Esta suposición es válida si previamente se ha corrido un problema de despacho dinámico (Unit Commitment) donde se han definido qué unidades están disponible para el intervalo de tiempo bajo estudio [21], [22].
6. Análisis de resultados
A continuación se presentan los resultados de simulación obtenidos para el sistema con inclusión de nodos generación renovable descrito en la sección 4 y se realiza una comparación con los resultados obtenidos para el mismo sistema sin nodos de generación renovable descrito en el estudio [7].
6.1. Sistema con energías renovables
Se obtienen resultados de 31 ejecuciones del algoritmo de optimización donde cada ejecución implica 100000 iteraciones, con 130 variables de decisión (sección 5).
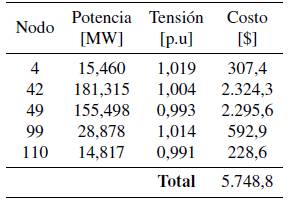
- Nodos fotovoltaicos: como se mencionó previamente, se tienen cinco nodos con generadores solares, nodos 4, 42, 49, 99 y 110. Después de realizada la optimizacón heurística, en la tabla III se muestran los resultados de magnitud de tensión y potencia despachada para los nodos con generación fotovoltaica, junto con el costo total de incertidumbre asociado.
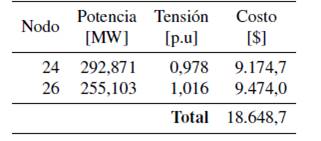
- Nodos eólicos: se tienen dos nodos con generadores eólicos, nodos 24 y 26. Después de realizada la optimizacón heurística, en la tabla IX se muestran los resultados de magnitud de tensión y potencia despachada para los nodos con generación eólica, junto con el costo total de incertidumbre asociado.
- Nodos con conexión de vehículos: se tienen cuatro nodos con conexión de vehículos eléctricos, nodos 59, 80, 90 y 116. Después de realizada la optimización heurística, en la tabla X se muestran los resultados de magnitud de tensión y potencia despachada para los nodos con conexión de vehículos eléctricos, junto con el costo total de incertidumbre asociado.
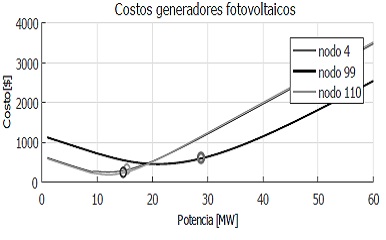
En la figura 3 se muestra la curva de costo de incertidumbre en función de la potencia para los nodos con generación solar. Se puede ver que los nodos 42 y 49 despachan potencias mayores a su potencia nominal (140MW) y menores a su potencia máxima (200MW), los nodos 4,99 y 110 despachan potencias menores a su potencia nominal (40MW) y menores a su potencia máxima (60MW).
En la figura 4 se muestra la curva de costo de incertidumbre en función de la potencia para los nodos con generación eólica. Se puede ver que los nodos 24 y 26 despachan potencias mayores a su potencia nominal (250MW) y menores a su potencia máxima (300MW).
En la figura 5 se muestra la curva de costo de incertidumbre en función de la potencia para los nodos con conexión de vehículos. Se puede ver que los nodos 59, 80, 90 y 166 despachan potencias mayores que su potencia nominal (6,54MW) y menores que su potencia máxima (13,6MW).
Finalmente en la tabla XI se presentan los resultados para generación con energía renovable: Solar, eólica y carros eléctricos. Para los nodos con generación renovable el valor de potencia despachada es fijo para un periodo de tiempo que depende de la resolución del modelo probabilístico, que para este caso es de una hora. Este valor de potencia despachada tiene asociados costos de incertidumbre, lo que quiere decir que no toda la potencia disponible en el recurso es despachada (por subestimar) o que se acude a otra fuente para suplir la demanda (por sobrestimar), en este sentido se consigue no introducir incertidumbre en el despacho gracias a que se mantienen valores de potencia programada para los recursos renovables, con lo cual pueden ingresar de forma competitiva en el mercado eléctrico.
6.2. Sistema sin energías renovables
Para tener un punto de comparación del costo del sistema al considerar energías renovables, se simula el mismo algoritmo de optimización pero considerando sólo con generadores convencionales, es decir, costos cuadráticos de operación para los generadores, descritos de la forma: a.Ws,i2 + b.Ws,i + d, en donde Ws,i es la potencia que se programa al generador i.
Como se mencionó en el la sección 2, el costo de generación depende del tipo de tecnología, lo que quiere decir, que se van a tener diferentes funciones de costo. La comparación se va a hacer en los nodos que tienen instalada energía renovable, se va a mirar la potencia que se programa en estos cuando tienen funciones de costo cuadráticas, y de esta forma ver el impacto de la penetración de energías renovables en el costo y particularmente cuando un bus tiene energ ía convencional y cuando no. Los once nodos renovables corresponden a once nodos con energía convencional, las cuales tienen once funciones de costo que se discriminan en cinco tipos:
1. Función de costo tipo 1: c(Ws,i) = 0,01 . Ws,i2 + 40 . Ws,i
2. Función de costo tipo 2: c(Ws,i) = 0,0318471 . Ws,i2 + 20 . Ws,i
3. Función de costo tipo 3: c(Ws,i) = 0,0490196 . Ws,i2 + 20 . Ws,i
4. Función de costo tipo 4: c(Ws,i) = 0,0645161 . Ws,i2 + 20 . Ws,i
5. Función de costo tipo 5: c(Ws,i) = 0,0209644 . Ws,i2 + 20 . Ws,i
Los nodos 4, 24, 42, 90, 99, 110 y 116 tienen función de costo tipo 1. El nodo 26 tipo 2, el nodo 49 tipo 3, el nodo 59 tipo 4 y el nodo 80 tipo 5. Después de simular el algoritmo de optimización heurística considerando solo energ ía convencional, se encuentran las potencias que se programan a cada bus, dichas potencias y su respectiva función de costo se muestra en la figura 6 para los nodos tipo 1 y en la figura 7 para los nodos tipo 2, 3, 4 y 5.
Como se observa en las figuras 6 y 7, las restricciones del sistema hacen que los generadores que tienen la misma función de costo tengan diferente potencia programada, y su despacho obedece a una optimización de costos. En la tabla XI se muestran los resultados para estos once nodos, ahora convencionales.
A partir de estos resultados, se calculan las diferencias entre los dos casos considerados: con energías renovables y con generación tradicional. Los cuales se muestran en la tabla XII.
En los resultados presentados se puede ver que los nodos con más costos fueron los generadores eólicos, lo cual puede estar asociado a que el coeficiente de costos eólicos por sobrestimar cw,o,i = 70, es 1,5 veces mayor que el costo fotovoltaico por sobrestimar cPV,o,i = 46 y 3,5 veces mayor que el costo por sobrestimar de nodos con conexión de vehículos ce,o,i = 46, también el coeficiente de costos eólicos por subestimar cw,u,i = 140, es 1,8 veces mayor que el costo fotovoltaico por subestimar cPV,u,i = 76 y 3,5 veces mayor que el costo por subestimar de nodos con conexión de vehículos ce,u,i = 40.
7. Conclusiones
El presente artículo propone una herramienta para los operadores de red de sistemas de potencia con penetración de energía renovable. La herramienta utiliza costos de incertidumbre, de esta manera, se tiene un criterio para realizar el despachoóptimo de potencia activa y reactiva, en sistemas que incorporan tanto fuentes de energía convencional como renovables. As í, los costos de incertidumbre modelan mediante una función analítica la incertidumbre en las fuentes primarias. De este modo se permite el ingreso de los elementos de energía renovable de forma competitiva en la programación del despacho de potencia.
Los sistemas de potencia son desarrollados en un entorno económico donde cantidades de potencia son programadas, y es necesario que los valores de las potencias sean suministrados de forma confiable, de otra forma son generados costos de penalización debidos a sobrestimar y subestimar la potencia disponible (para recursos renovables). Como se observa en la tabla XII, para los coeficientes de penalización (cu,i y co,i) tomados, la operación del sistema es más económica con alta penetración de energías renovables. De esta manera, la precisión en la estimación de los costos de incertidumbre permite la optimización de los recursos de generación, en este sentido se estima la cantidad de irradiancia solar, velocidad de viento y potencia en veh ículos eléctricos, haciendo menos dependiente el sistema de potencia de los recursos tradicionales sin afectar la confiabilidad del despacho.
Referencias
[1] J. Arévalo, F. Santos and S. Rivera, Uncertainty Cost Functions for Solar Photovoltaic Generation, Wind Energy Generation and Plug-In Electric Vehicles: Mathematical Expected Value and Verification by Monte Carlo Simulation. International Journal of Power and Energy Conversion. 2017.
[En línea]. Disponible en: http://www.inderscience.com/info/ingeneral/forthcoming.php?jcode=ijpec 325, 326, 327, 331, 332
[2] H. Kamankesh, V. Agelidis and A. Kavousi-Fard, "Optimal Scheduling of Renewable Micro-Grids Considering Plug-In Hybrid Electric Vehicle Charging Demand". Energy, 100, 285–297, 2016. 325
[3] B. C. Gu, Z. M. Chen, T. Y. Jiv, L. L. Zhang, Q. H.Wu, M. S. Li and J. H. Huang, "Quasi-Monte Carlo Simulation Based Economic Dispatch With Wind Power Integrated". IEEE Innovative Smart Grid Technologies – Asia (ISGTAsia), 264–269, Nov., 2016. 325
[4] H. Huang, C. Y. Chung, K. W. Chan and H. Chen, "Quasi-Monte Carlo Based Probabilistic Small Signal Stability Analysis for Power Systems With Plug-In Electric Vehicle and Wind Power Integration". IEEE Transactions on Power Systems, 28(3), 3335–3343, Aug., 2013. 325, 331
[5] J. Hetzer, D. C. Yu and K. Bhattarai, "An Economic Dispatch Model Incorporating Wind Power". IEEE Transactions on Energy Conversion, 23(2), 603–611, June 2008. 325, 327, 330
[6] J. Zhao, F. Wen, Z. Y. Dong, Y. Xue and K. P. Wong, "Optimal Dispatch of Electric Vehicles and Wind Power Using Enhanced Particle Swarm Optimization". IEEE Transactions on Industrial Informatics, 8(4):889–899, Nov., 2012. 325
[7] I. Erlich, K. Lee, J. Rueda and S. Wildenhues, "Competition on Application Of Modern Heuristic Optimization Algorithms For Solving Optimal Power Flow Problems". Working Group on Modern Heuristic Optimization (WGMHO)Under the IEEE PES Analytic Methods in Power Systems (AMPS) Committee, February 2014. 326, 337, 339
[8] M. I. Ennes and A. L. Diniz, "A General Equivalent Thermal Cost Function For Economic Dispatch Problems". 2012 IEEE Power and Energy Society General Meeting, pages 1–6, July, 2012. 328
[9] R. S.Wibowo, F. F. Utama, D. F. U. Putra and N. K. Aryani, "Unit Commitment With Non-Smooth Generation Cost Function Using Binary Particle Swarm Optimization". In 2016 International Seminar on Intelligent Technology and Its Applications (ISITIA), pages 571–576, July 2016. 328
[10] J. Bastidas, C. Ramos and E. Franco, "Modeling And Parameter Calculation of Photovoltaic Fields in Irregular Weather Conditions". Revista Ingeniería, 17(1), 37–48, Junio, 2012. 329
[11] T. Chang, "Investigation on Frequency Distribution of Global Radiation Using Different Probability Density Functions". International Journal of Applied Science and Engineering, 8(2), 99–107, 2010. 329
[12] S. Surender Reddy, P. R. Bijwe and A. R. Abhyankar, "Real-time Economic Dispatch Considering Renewable Power Generation Variability and Uncertainty Over Scheduling Period". IEEE Systems Journal, 9(4), 1440–1451, Dec., 2015. 330
[13] C. Ramos, A. Saavedra and E. Arango, "Distributed Maximum Power Point Tracking in Wind Micro-Grids". Revista Ingeniería, 17(1), 5–13, Junio 2012. 330
[14] J. Ceballos, E. Caicedo and S. Ospina, "Una propuesta metodológica para dimensionar el impacto de los vehículos eléctricos sobre la red eléctrica". Revista Ingeniería, 21(2), 154–175, Agosto, 2016. 331
[15] W. Group, "Common format for exchange of solved load flow data". IEEE Transactions on Power Apparatus and Systems, PAS-92(6), 1916–1925, Nov, 1973. 334
[16] NASA Athmospheric Science Data Center, Surface Meteorology and Solar Energy: Retscreen Data. 2017.
[En línea]. Disponible en: https: //eosweb.larc.nasa.gov/cgi-bin/sse/retscreen.cgi 334, 335
[17] IDEAM [Instituto de Hidrología Meteorología y Estudios Ambientales]. Atlas interactivo del viento de Colombia. 2015. [En línea]. Disponible en: http://www.ideam.gov.co/ 334, 336
[18] UPME [Unidad de Planeación Minero Energética], Integración de las energías renovables no convencionales en Colombia. 2017. [En línea]. Disponible en: http://www.upme.gov.co/Estudios/2015/Integracion Energias Renovables/INTEGRACION ENERGIAS RENOV ANLES WEB.pdf 336
[19] C. D. Charalambous and N. U. Ahmed, "Centralized Versus Decentralized Optimization of Distributed Stochastic Differential Decision Systems With Different Information Structures-Part I: A General Theory". IEEE Transactions on Automatic Control, 62(3),1194–1209, March, 2017. 337
[20] R. D. Zimmerman, C. E. Murillo-Sanchez and R. J. Thomas, "Matpower: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education". IEEE Transactions on Power Systems, 26(1), 12–19, Feb., 2011. 338
[21] C. Zhao and R. Jiang, "Distributionally Robust Contingency-Constrained Unit Commitment. IEEE Transactions on Power Systems". PP(99),1–1, 2017. 339
[22] H. Ye, Y. Ge, M. Shahidehpour and Z. Li, "Uncertainty Marginal Price, Transmission Reserve, And Day-Ahead Market Clearing with Robust Unit Commitment". IEEE Transactions on Power Systems, 32(3), 1782–1795, May, 2017. 339
Recibido: 8 de marzo de 2017; Revisión recibida: 5 de junio de 2017; Aceptado: 7 de julio de 2017
Resumen
Contexto:
Actualmente las fuentes de energía renovables están jugando un importante rol para contrarrestar el impacto ambiental de las fuentes de energía tradicional. Por esto, los operadores del sistema deben contar con herramientas de análisis que le permitan incorporar estas nuevas formas de energía. En los sistemas eléctricos de potencia que incorporan recursos renovables y vehículos eléctricos, se in troduce incertidumbre debido a la estocasticidad de los recursos primarios y los patrones de conducción de los vehículos.
Método:
Para las incertidumbres señaladas, se proponen costos de incertidumbre que incorporan la variabilidad de potencia inyectada de las principales fuentes de energía renovable (solar y eólica) y la potencia consumida (vehículos eléctricos). La variabilidad es considerada mediante las distribuciones de probabilidad de las fuentes primarias de la energía renovable (irradiación solar y velocidad del viento).
Resultados:
El principal resultado de esta investigación es la aplicación de los costos analíticos de incertidumbre. De esta manera es posible modificar la función de costos de un despacho económico tradicional. Adicionalmente se propone solucionar el problema con un método de optimización heurística de despacho (óptimo de potencia activa-reactiva. Finalmente, se realiza una comparación con el costo de operación del sistema sin la incorporación de energías renovables.
Conclusiones:
El modelo propuesto en este artículo constituye una posible alternativa de toma de decisiones que los operadores de los sistemas de potencia pueden considerar en la operación del sistema que es capaz de considerar las incertidumbres de las fuentes primarias de la energía renovable. Para ello se supone conocida la distribución de probabilidad del pronóstico de la fuente primaria. Como oportunidad de extensión de este estudio se destaca su aplicabilidad a horizontes de tiempo dinámicos, contemplando las restricciones propias de la comisión de unidades.
Palabras clave:
Costo de incertidumbre, Despacho económico, Energía renovable., Idioma: Español.Abstract
Context:
Currently, renewable energy sources are playing an important role in counteracting the environmental impact of traditional energy sources. For this reason, system operators must have analytical tools that allow them to incorporate these new forms of energy. In electrical power systems, when incorporating renewable resources such as photovoltaic solar generation, wind power generation or electric vehicles, uncertainty is introduced due to the stochasticity of primary resources.
Method:
Uncertainty costs are proposed that incorporate the injected power variability of the main sources of renewable energy (solar and wind) and the consumed power (electric vehicles). Variability is considered by the probability distributions of the primary sources of renewable energy (solar irradiation and wind speed).
Results:
The main result of this research is the application of analytical costs of uncertainty. In this way it is possible to modify the cost function of a traditional economic dispatch. Additionally, it is proposed to solve the problem with a heuristic optimization method of economic dispatch of active-reactive power. Finally, a comparison is made with the operating cost of the system without the incorporation of renewable energies.
Conclusions:
The proposed model in this article is a potential decision-making tool that power system operators may consider in the operation of the system. The tool is capable of considering the uncertainties of the primary sources of renewable energy. The probability distribution of the primary source forecast is assumed to be known. An opportunity in order to extend the model is to study its applicability to dynamic time horizons, contemplating the constraints of the unit commitment problem.
Keywords:
Economic dispatch, Renewable energy, Uncertainty cost, Language: Spanish..Introducción
Cuando se incorporan recursos renovables como la generación solar fotovoltaica, generación con energía eólica o vehículos eléctricos, se introduce incertidumbre en cuanto a la disponibilidad de potencia en el sistema, debido a la estocasticidad de los recursos primarios [1]. Dicha incertidumbre es indeseada en la programación del despacho de energía y se identifica como una de las barreras que ha impedido la alta penetración de los recursos renovables en los sistemas de generación.
Con el propósito de asignar un costo a la incertidumbre presentada en los recursos renovables, tradicionalmente se han utilizado simulaciones de Montecarlo [2] -[4]. Si bien tales simulaciones dan resultados que consideran la variabilidad de las fuentes primarias de energía (irradiación solar y velocidad del viento), implican gran número de escenarios a simular [4]. A fin de disminuir el número de escenarios a simular se requiere que los costos de incertidumbre sean modelados con una expresión analítica. En el documento [5] se presenta una propuesta de costos de incertidumbre desarrollada con base en modelos probabilísticos del comportamiento de la velocidad del viento. En [6] se extiende la modelación anterior a vehículos eléctricos. En [1] se desarrolla en detalle la modelación analítica de costos de incertidumbre para el comportamiento de la velocidad del viento y los patrones de manejo de los vehículos eléctricos; además se extiende la modelación a sistemas de generación fotovoltaica, modelando la probabilidad de distribución de la irradiación solar. De esta manera, la propuesta de costos de incertidumbre tiene la finalidad de aumentar la penetración de los recursos renovables en los sistemas de generación, ya que es una herramienta de planeación del sistema con renovables, sin afectar la disponibilidad de potencia en la demanda y brindando una solución económicamente viable en el despacho económico.
Los costos de incertidumbre requieren modelos probabilísticos de las fuentes primaria de generación renovable, así, en este trabajo se plantean modelos probabilísticos en ubicaciones geográficas del territorio colombiano para generación solar fotovoltaica y generación eólica. Los nodos del sistema con renovables se consideran en puntos estratégicos con alto potencial de irradiancia so lar para la generación fotovoltaica y puntos con velocidades de viento altas y constantes para la generación con energía eólica. De esta manera se plantea realizar el despacho óptimo de potencia activa-reactiva para un sistema de potencia que incorpora fuentes de generación renovable, mo delados con funciones de costos de incertidumbre. Estos costos de incertidumbre son ecuaciones analíticas no polinómicas ([1]) en función de la potencia programada para los nodos de generación renovable, luego son introducidos como costos de generación en un sistema de potencia que contiene nodos con generación convencional modelados con funciones de costos polinómicas tra dicionales.
El despacho «óptimo de potencia busca minimizar la función de costo total de generación del sis tema, que para el presente caso es una función no polinómica y no convexa, ya que se consideran los costos de incertidumbre analíticos. Debido a las propiedades de este problema de optimización (función objetivo no convexa, con restricciones no lineales correspondientes a un sistema de ecuaciones algebraicas para el flujo de potencia) se plantea solucionar el problema con optimización heurística. La otra razón de esta decisión, es que en la formulación del problema se plantean elementos de maniobra (taps de transformadores y capacitores shunt) como variables de decisión discretas. Se decidió implementar el algoritmo de optimización heurístico Differential Evolutionary Particle Swarm Optimization (DEEPSO, por sus siglas en inglés) aplicado al sistema de potencia con fuentes renovables modeladas con funciones de costos de incertidumbre. Tal algoritmo fue el que gano la competencia internacional IEEE “Application of Modern Heuristic Optimization Al- gorithms for Solving Optimal Power Flow Problems” de la Power & Energy Society (PES por su siglas en inglés) [7]. No obstante se pueden utilizar otras técnicas heurísticas.
Este artículo está estructurado de la siguiente manera: inicialmente se exponen la formulación matemática de los costos involucrados en la función de costos a minimizar en el despacho óptimo de potencia en la segunda sección. En la tercera sección se describen las funciones de costos de incer tidumbre para cada fuente renovable a implementar. En la cuarta sección se realiza la descripción del sistema de potencia dentro de cual se introducen los nodos con generación renovable, allí se pretende solucionar el problema de despacho económico. En la quinta sección se describe el algo ritmo de optimización heurístico implementado para realizar la simulación del despacho óptimo de potencia y finalmente se presentan el análisis de resultados y conclusiones.
Planteamiento matemático de función de costos a minimizar
En esta sección se realiza el planteamiento matemático de los costos involucrados en la función de costos totales de generación en un sistema que modela los nodos renovables con la propuesta de costos de incertidumbre. Para ello se proponen unos costos de penalización, con esta defini ción se proceden a definir los costos de incertidumbre, se muestra los costos polinómicos de los generadores tradicionales y finalmente se plantea la función objetivo de costo total de generación.
2.1. Costos de penalización
Los costos de penalización son propuestos en [1], [5], los cuales son una adición a los costos operativos de generación de energía y se producen cuando dentro del despacho se programa una potencia Ws¡i la cual subestima o sobrestima la potencia disponible Wav,i en un nodo con recursos renovables.
2.1.1. Costos por subestimar
Son costos de penalización generados cuando la potencia programada Ws,i es menor que la potencia disponible Wav,i en un recurso renovable.

De esta forma se puede definir una función de costos debidos a subestimar la potencia disponible, como:
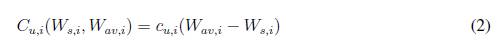
La función de costos (2) asocia un coeficiente de penalización cu,i por subestimar, el cual debe ser definido por el operador del sistema. Este coeficiente (cu,i) corresponde al costo por utilizar la diferencia entre la potencia disponible y la potencia programada (que es el valor de inyección que más le conviene a la red) en otra actividad, como almacenamiento de energía sí existe disponible, en vez de utilizarla directamente en la red.
2.1.2. Costos por sobrestimar
Son costos de penalización generados cuando la potencia programada Ws,i es mayor que la po tencia disponible Wav,i en un recurso renovable.

De esta forma se puede definir una función de costos debidos a sobrestimar la potencia disponible, como:
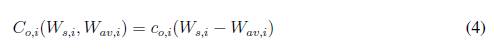
La función de costos (4) asocia un coeficiente de penalización c0,i por sobrestimar, el cual debe ser definido por el operador del sistema. Este coeficiente (c0,i) corresponde al costo por adquirir la diferencia entre la potencia programada y la potencia disponible, como generadores diesel si existen disponibles en el nodo de generación renovable, de tal manera que se inyecte lo que más le convenga a la red.
2.2. Costos de incertidumbre
Los costos de incertidumbre se definen como el valor esperado de las funciones de costos de penalización por subestimar (2) y por sobrestimar (4), las expresiones analíticas de costos de in certidumbre aplicados a generación fotovoltaica, eólica y vehículos eléctricos conectados a red se muestran en la sección 3.
2.3. Costos polinómicos
Los generadores de energía convencionales térmicos se modelan por medio de una función de costos polinómica comúnmente de orden dos [8], proveniente de la curva de costo del combustible, de la siguiente forma:

Adicionalmente, los operadores de red de sistemas de los diferentes países pueden tener sus propias funciones de costo para los generadores convencionales que se pueden expresar en forma de polinomios [9].
2.4. Costo total de generación
La función de costos totales de generación del sistema, a minimizar en el nuevo problema de despacho económico con función objetivo no convexa, se describe de la forma:
dónde:
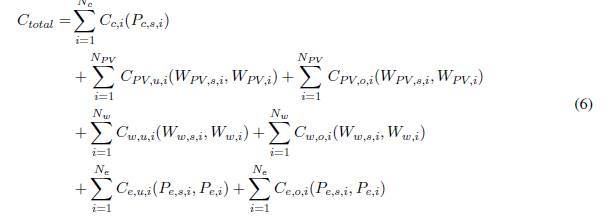
Nc es el número total de generadores convencionales.
Npv es el número total de generadores fotovoltaicos.
Nw es el número total de generadores eólicos.
Ne es el número total de nodos con vehículos conectados.
Pc,s,i es la potencia programada en el generador convencional i.
WpVt8ti es la potencia programada en el generador fotovoltaico i.
Wwsi es la potencia programada en el generador eólico i.
Pe,s,i es la potencia programada en el nodo con conexión de vehículos i.
Wpví es la potencia disponible en el generador fotovoltaico i.
Ww,i es la potencia disponible en el generador eólico i.
Pe,i es la potencia disponible en el nodo con conexión de vehículos i.
Cc,i es la función de costos del generador convencional i.
Cpv,u,í es la función de costos por subestimar del generador fotovoltaico i.
Cpv,o,i es la función de costos por sobrestimar del generador fotovoltaico i.
Cw,u,i es la función de costos por subestimar del generador eólico i.
Cw,o,i es la función de costos por sobrestimar del generador eólico i.
Ce,u,i es la función de costos por subestimar del nodo con conexión de vehículos i.
Ce,o,i es la función de costos por sobrestimar del nodo con conexión de vehículos i.
En (6) se puede ver que la función de costo total incluye los costos de generación con agentes convencionales y la propuesta de costos de incertidumbre por subestimar y sobrestimar lo disponible en las fuentes renovables; además se omiten los costos de operación directos (o propios de generación) para los agentes renovables, lo cuales no se toman en cuenta dentro de este estudio ya que se considera que el recurso primario es gratis (sol y viento).
3. Costos de incertidumbre: generación solar, eólica y cargas activas (vehículos eléctricos)
En esta sección se describen las funciones de costos de incertidumbre para casos particulares de generación solar, generación con energía eólica y vehículos eléctricos conectados a la red. Inicialmente se desarrollan los modelos probabilísticos de la potencia disponible en estos recursos.
3.1. Descripción de fuentes de energía renovable
Como se define en la sección 2, los costos de incertidumbre son el valor esperado de los costos de penalización, y dado que los costos de penalización son función de la potencia disponible Wav,i en el recurso renovable, se debe realizar el modelo probabilístico de la energía primaria para cada recurso primario y luego hallar su expresión en términos de la potencia disponible.
a) Energía solar
■ Función de distribución de probabilidad solar: el recurso primario de la energía solar fotovoltaica es la irradiancia [10], la cual es dependiente de la ubicación geográfica de los paneles. Varias investigaciones se han hecho para hallar la distribución de probabilidad de la irradiancia, como la implementada en [11], en donde una de las funciones de distribución de probabilidad es la Log-normal:
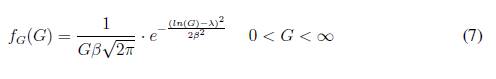
donde:
fG(G) es la función de densidad de probabilidad lognormal.
G es la irradiancia solar.
/ es la media de la distribución Log-normal.
β es la desviación estándar de la distribución Log-nomal.
■ Potencia de un panel solar fotovoltaico: la potencia que se desarrolla en un panel fotovoltaico se puede expresar como [12]:
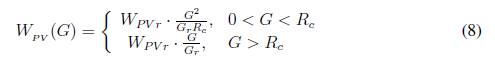
dónde:
WPV (G) es la potencia fotovoltaica generada como función de la irradiancia.
G es la irradiancia solar.
Gres la irradiancia estándar en el ambiente.
Rc es un valor de irradiancia de referencia.
WpVr es la potencia nominal de salida de la celda fotovoltaica.
Como se observa en la ecuación (8), el panel convierte radiación en potencia de forma cuadrática hasta un punto Rc en el que la expresión comienza a ser lineal.
b) Energía eólica
■ Función de distribución de probabilidad del viento: la variable que define la energía eólica es la velocidad del viento, que para diferentes ubicaciones geográficas presenta variados comportamientos, sin embargo, en artículos como [5], [13] se ha mostrado que el viento tiene una distribución de probabilidad Weibull, cuyos parámetros dependen de la ubicación geográfica:
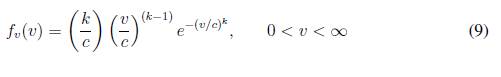
dónde:
fv (v) es la función de densidad de probabilidad para la velocidad del viento.
v es la velocidad del viento.
/factor de escala en un lugar geográfico. Típicamente entre 5-8 (5).
K factor de forma que también depende de la ubicación geográfica, no tiene dimensiones. Típicamente entre 1-3 (5).
Tomando el factor de forma k como 2 y el factor de escala c como se tiene la distribución Rayleigh:
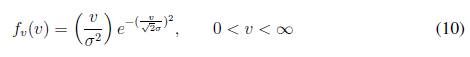
■ Potencia de un generador eólico: la potencia generada en función del viento en una turbina eólica está dada por [5]:
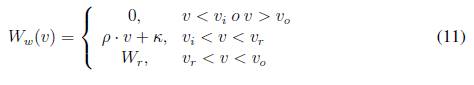
donde:
Ww (v) es la potencia eólica generada en función de la velocidad del viento.
v es la velocidad del viento.
Vj velocidad de viento de corte inferior del aerogenerador.
vrvelocidad de viento nominal del aerogenerador.
vovelocidad de viento de corte superior del aerogenerador.
Wr es la potencia nominal del aerogenerador.
Además, en [11] se definen las constantes: 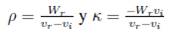
c) Energía de vehículos eléctricos conectados a la red
■ El uso de carros eléctricos tiene un comportamiento estocástico, dependiente del patrón de conducción de estos vehículos [14], y por lo tanto el estado de carga y descarga de sus baterías también lo es. Una de las variables que define la energía disponible en baterías de carros eléctricos, es la distancia que se recorre con el mismo, en [4] se propone una distribución normal para la distancia recorrida en un vehículo eléctrico:
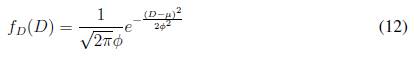
dónde:
fD (D) es la función de densidad de probabilidad de la distancia recorrida por un vehículo eléctrico.
D distancia recorrida por el vehículo eléctrico.
µ es la media de la distribución.
Φ es la desviación estándar de la distribución.
El comportamiento normal de la distancia recorrida se ve reflejado en la forma de carga y descarga de las baterías de los vehículos eléctricos. Por tanto la potencia disponible Pe en carros eléctricos se puede definir como:
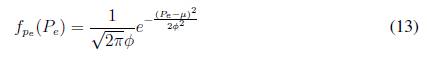
Dónde:
fpe(Pe) es la función de densidad de probabilidad de la potencia disponible en baterías de vehículos eléctricos.
Se debe mencionar que [13] puede tomar valores de potencia negativos, caso para el cual las baterías le inyectan potencia a la red.
3.2. Formulas analíticas de costos de incertidumbre
De acuerdo con desarrollo detallado por los autores de este artículo en [1], las funciones analíticas de costos de incertidumbre para las fuentes generación solar fotovoltaica, generación con energía eólica y vehículos eléctricos conectados a red, después de desarrollar las integrales correspondientes (proceso presentado en [1]), son:
■ Energía solar fotovoltaica: para el caso de energía solar fotovoltaica, la fórmula de costo de incertidumbre contempla cuatro partes: dos para el caso subestimado, y dos para el caso sobreestimado.
a) Caso subestimado.
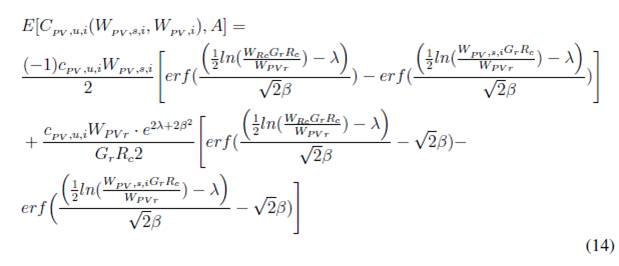
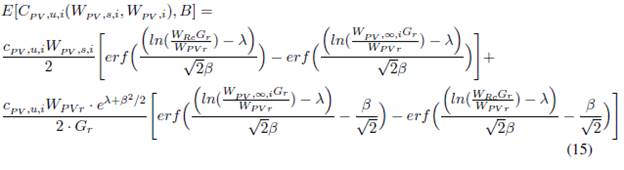
b) Caso sobrestimado.
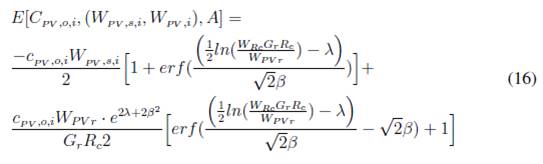
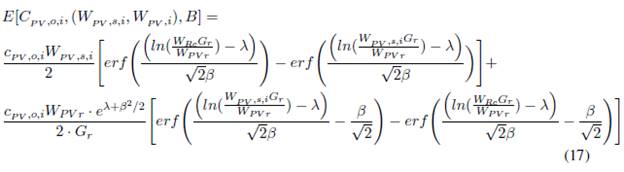
■ Energía eólica: la fórmula de costos de incertidumbre contempla dos partes, una subestimada y otra sobrestimada.
a) Caso subestimado.
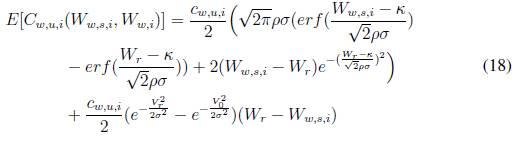
b) Caso sobrestimado.
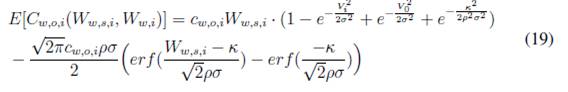
■ Energía de vehículos eléctricos: la fórmula de costos de incertidumbre contempla dos partes, una subestimada y otra sobrestimada.
a) Caso subestimado.
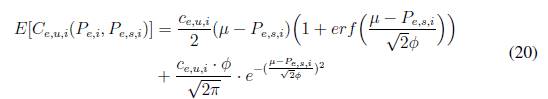
b) Caso sobrestimado.
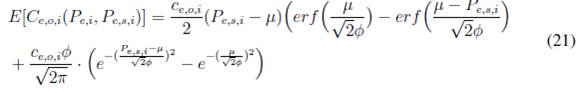
4. Descripción del sistema eléctrico de potencia de prueba
En esta sección se presenta la descripción del sistema de potencia, el cual es una versión simplificada del sistema IEEE-118 tomado de [15], donde se incluyen nodos con generación renovable modelados para zonas del territorio colombiano. En la tabla I se muestra la composición general del sistema.
Tabla I: Composición de sistema IEEE 118
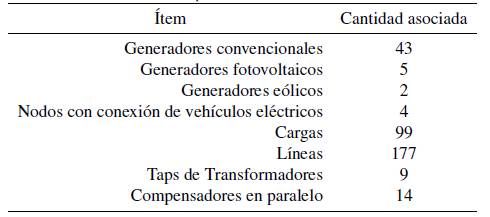
El sistema tiene una potencia base de 100MW, tensión base de 318kV, una capacidad de generación instalada de 8,205MW y una demanda total de 4,242MW, en la tabla II se muestra la capacidad instalada según el tipo de generación.
Tabla II: Capacidad de generación por recursos

Como se muestra en la tabla II, el 14 % de la capacidad instalada del sistema corresponde a energías de origen renovable y el 86 % a energías de origen convencional, lo que para el caso colombiano actual se puede considerar como alta penetración de energías renovables.
4.1. Descripción de nodos con generación fotovoltaica
Para establecer el comportamiento probabilístico de la irradiación solar modelada con una distribución Log-normal (sección 3), se toman valores de irradiancia media y desviación estándar tomados de datos de la NASA [16], para cinco coordenadas geográficas especificas del territorio colombiano con potencial solar según [17] [Figura 1]. En la tabla III se muestran los resultados de este proceso.
En la tabla III:
β es la desviación estándar de la distribución Log-normal,
λ es la media de la distribución Log-normal,
Gr es el valor nominal de la irradiancia en el entorno geográfico,
Rc es un valor de irradiancia de referencia,
Tabla III: Descripción probabilística de nodos con generación fotovoltaica (16)
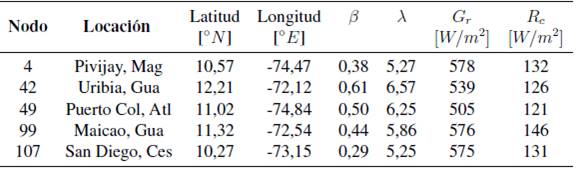
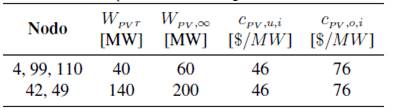
Con base en los resultados obtenidos en la tabla III se plantean las especificaciones de los nodos fotovoltaicos descritas en la tabla IV.
En la tabla IV:
WPVr potencia activa nominal del recurso fotovoltaico.
WPV,∞ máxima potencia de salida.
cPV,u,i costo de penalización debido a subestimar.
cPV,o,i costo de penalización debido a sobrestimar.
Figura 1: Ubicacién geografica de nodos con generacion eolica (azul), nodos con generacién solar fotovoltaica (amarillo) y nodos con fuentes solar y eolica (naranja).
Tabla IV: Descripción de nodos con generación fotovoltaica
4.2. Descripción de nodos con generación eólica
Para establecer el comportamiento probabilístico de la velocidad de viento modelado con una distribución Rayleigh (sección 3), se toma el estadístico de valor medio de velocidad de viento a una altura de 10m suministrado por la UPME [18], para dos coordenadas geográficas específicas de la zona norte de Colombia, luego se calcula el parámetro de escala de la distribución Rayleigh a. En la tabla V se muestran los resultados de este proceso para dos puntos con potencial eólico según [17].
Tabla V: Descripción probabilística de nodos con generación Eólica [18]

En la tabla V:
σ es el parámetro de escala Rayleigh.
vi es la velocidad de viento de corte inferior del aerogenerador.
vr es la velocidad de viento nominal del aerogenerador.
vo es la velocidad de viento de saturación del aerogenerador.
Con base en los resultados obtenidos en la tabla V se plantean las especificaciones de los nodos eólicos descritas en la tabla VI.
Tabla VI: Descripción de nodos con generación Eólica
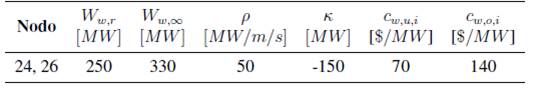
Donde en la tabla VI representan:
Ww,r potencia nominal del nodo eólico.
Ww,∞ potencia máxima entregada por el nodo eólico.
ρ constante lineal.
k constante independiente.
cw,u,i costo de penalización debido a subestimar.
cw,o,i costo de penalización debido a sobrestimar.
4.3 Descripción de nodos con conexión de vehículos eléctricos
La capacidad de potencia agregada de los nodos con vehículos eléctricos conectados a la red se distribuye de forma normal (sección 3) durante el periodo pico del día, en la tabla VII se describen los nodos con conexión de vehículos.
Tabla VII: Descripción de nodos con conexión de vehículos eléctricos

En la tabla VI:
µ potencia media del nodo con conexión de vehículos.
Φ desviación estándar.
We,max potencia mínima del nodo con conexión de vehículos.
We,min potencia máxima del nodo con conexión de vehículos.
Ce,u,i costo de penalización debido a subestimar.
Ce,o,i costo de penalización debido a sobrestimar.
5. Algoritmo de optimización para el despacho económico
Se busca realizar el despacho óptimo de potencia activa y reactiva minimizando la función de costo total de generación [6] aplicando el algoritmo heurístico de optimización DEEPSO implementado en la competencia internacional IEEE-PES Application of Modern Heuristic Optimization Algorithms for Solving Optimal Power Flow Problems [7].
Se decidió utilizar heurística, debido a que la función objetivo al incluir los costos de incertidumbre presentados en la sección 3 es no convexa. Adicionalmente, el problema tiene una serie de variables de decisión continuas y discretas que hacen intratable el problema con solvers convencionales de optimización (como GAMS o CPLEX) en lo que se refiere a tiempos de solución y convergencia. Los algoritmos de optimización heurística son desarrollos basados en el comportamiento de procesos naturales, se utilizan comúnmente en problemas de optimización considerados de alta complejidad [19]. Para el caso de sistemas eléctricas de potencia, los procesos de optimización heurística presentan un potencial importante en la búsqueda de solucionar problemas de operación y planeamiento del sistema gracias a su potencial para resolver complejidades matemáticas inherentes relacionadas con alta dimensionalidad, no linealidad, no convexidad, multimodalidad y discontinuidad de los espacios de búsqueda [7].
El algoritmo de optimización involucra 130 variables de decisión continuas y discretas definidas de la forma:
■ Continuas (107 en total): 42 representan la potencia activa despachada por los agentes convencionales (excluyendo el nodo slack), cinco son de la potencia activa despachada por los generadores fotovoltaicos, dos son de la potencia activa despachada por los agentes eólicos, cuatro son de la potencia activa en los nodos con conexión de vehículos, 54 variables relacionadas con la magnitud de la tensión en los nodos de generación, las cuales siguen los rangos mínimos y máximos 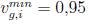 p.u y
p.u y 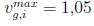 p.u respectivamente.
p.u respectivamente.
Figura 2: Diagrama de flujo del algoritmo heurístico.
■ Discretas (23 en total): nueve representan el radio de Tap de transformación con mínimo y máximo de 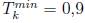 y
y 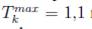 respectivamente y catorce variables discretas binarias asociadas a los dispositivos de compensación.
respectivamente y catorce variables discretas binarias asociadas a los dispositivos de compensación.
En la figura 2 se muestra el diagrama de flujo que sigue el algoritmo de optimización DEEPSO.
La población inicial y la población actualizada de la estrategia de búsqueda del algoritmo se refieren a las 130 variables de decisión sujetas a valores máximos y mínimos de potencia activa generada, tensión en los nodos PQ, Taps de transformación y dispositivos de compensación.
Para la solución en cada flujo de potencia se implementa la herramienta Manpower (20) empleando el modelo típico de análisis en estado estático para sistemas de potencia, luego la evaluación de la función objetivo consiste en determinar el valor de la función de costos de generación Ctotal [ecuación (6)]. La función de aptitudes se expresa en [22], la cual es la adición de la función objetivo Ctotal [ecuación (6)] y una función de penalización (PF) expresada en [23].

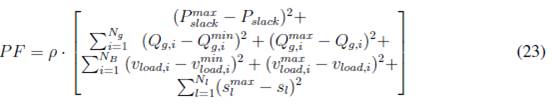
La función de aptitudes toma en cuenta las limitaciones de generación de potencia activa en el nodo slack Pslack, la limitación de generación de potencia reactiva en los nodos de generación Qgi, la limitación de magnitud de la tensión en los nodos de carga vloadti y la restricción de flujo de potencia en cada línea de transmisión sl, p es un factor de penalización fijado en 1E + 7. NB es el número de nodos de carga del sistema y Nl es el número de ramas del sistema.
El diagrama de flujo se programa en 100.000 iteraciones para finalmente obtener la solución correspondiente al mejor valor de la función de aptitudes.
En esta formulación se asume que todas las unidades de generación (convencionales y renovables) se despachan siempre. Es decir, se soluciona el problema en un intervalo de tiempo de operación del sistema. Esta suposición es válida si previamente se ha corrido un problema de despacho dinámico (Unit Commitment) donde se han definido que unidades están disponible para el intervalo de tiempo bajo estudio [21], [22].
6. Análisis de resultados
A continuación se presentan los resultados de simulación obtenidos para el sistema con inclusión de nodos generación renovable descrito en la sección 4 y se realiza una comparación con los resultados obtenidos para el mismo sistema sin nodos de generación renovable descrito en el estudio [7].
6.1. Sistema con energías renovables
Se obtienen resultados de 31 ejecuciones del algoritmo de optimización donde cada ejecución implica 100000 iteraciones, con 130 variables de decisión (sección 5).
■ Nodos fotovoltaicos: como se mencionó previamente, se tienen cinco nodos con generadores solares, nodos 4, 42, 49, 99 y 110. Después de realizada la optimización heurística, en la tabla VIII se muestran los resultados de magnitud de tensión y potencia despachada para los nodos con generación fotovoltaica, junto con el costo total de incertidumbre asociado.
En la figura 3 se muestra la curva de costo de incertidumbre en función de la potencia para los nodos con generación solar. Se puede ver que los nodos 42 y 49 despachan potencias mayores a su potencia nominal (140MW) y menores a su potencia máxima (200MW), los nodos 4, 99 y 110 despachan potencias menores a su potencia nominal (40MW) y menores a su potencia máxima (60MW).
Tabla VIII: Resultados de simulación en nodos fotovoltaicos
■ Nodos etílicos: se tienen dos nodos con generadores eólicos, nodos 24 y 26. Después de realizada la optimización heurística, en la tabla IX se muestran los resultados de magnitud de tensión y potencia despachada para los nodos con generación eólica, junto con el costo total de incertidumbre asociado.
Figura 3: Curva de costos en función de la potencia programada para los nodos con generación fotovoltaica.
Tabla IX: Resultados de simulación en nodos eólicos
En la figura 4 se muestra la curva de costo de incertidumbre en función de la potencia para los nodos con generación eólica. Se puede ver que los nodos 24 y 26 despachan potencias mayores a su potencia nominal (250MW) y menores a su potencia máxima (300MW).
■ Nodos con conexión de vehículos: se tienen cuatro nodos con conexion de vehículos eléctricos, nodos 59, 80, 90 y 116. Después de realizada la optimización heurística, en la tabla X se muestran los resultados de magnitud de tensión y potencia despachada para los nodos con conexión de vehículos eléctricos, junto con el costo total de incertidumbre asociado.
En la figura 5 se muestra la curva de costo de incertidumbre en función de la potencia para los nodos con conexión de vehículos. Se puede ver que los nodos 59, 80, 90 y 166 despachan potencias mayores que su potencia nominal (6,54MW) y menores que su potencia máxima (13,6MW).
Figura 4: Curva de costos en función de la potencia programada para los nodos con generación eólica.
Finalmente, en la tabla XI se presentan los resultados para generación con energía renovable: Solar, eólica y carros eléctricos. Para los nodos con generación renovable el valor de potencia despachada es fijo para un periodo de tiempo que depende de la resolución del modelo probabilístico, que para este caso es de una hora. Este valor de potencia despachada tiene asociados costos de incertidumbre, lo que quiere decir que no toda la potencia disponible en el recurso es despachada (por subestimar) o que se acude a otra fuente para suplir la demanda (por sobrestimar), en este sentido se consigue no introducir incertidumbre en el despacho gracias a que se mantienen valores de potencia programada para los recursos renovables, con lo cual pueden ingresar de forma competitiva en el mercado eléctrico.
Tabla X: Resultados de simulación en nodos con conexión de vehículos
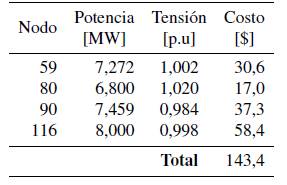
Figura 5: Curva de costos en función de la potencia programada para los nodos con conexión de vehículos.
Tabla XI: Resultados programación casos generadores renovables y convencionales
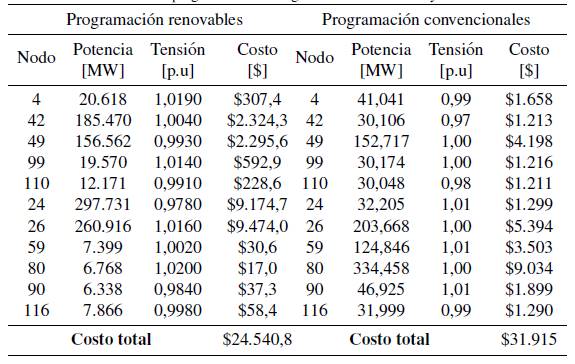
6.2. Sistema sin energías renovables
Para tener un punto de comparación del costo del sistema al considerar energías renovables, se simula el mismo algoritmo de optimización pero considerando solo con generadores convencionales, es decir, costos cuadráticos de operación para los generadores, descritos de la forma: 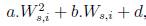 , en donde Ws,i es la potencia que se programa al generador i.
, en donde Ws,i es la potencia que se programa al generador i.
Figura 6: Curva de costos de operación generadores convencionales tipo 1 en función de la potencia programada, en nodos que anteriormente eran renovables.
Como se mencioné en el la sección 2, el costo de generación depende del tipo de tecnología, lo que quiere decir, que se van a tener diferentes funciones de costo. La comparación se va a hacer en los nodos que tienen instalada energía renovable, se va a mirar la potencia que se programa en estos cuando tienen funciones de costo cuadráticas, y de esta forma ver el impacto de la penetración de energías renovables en el costo y particularmente cuando un bus tiene energía convencional y cuando no. Los once nodos renovables corresponden a once nodos con energía convencional, las cuales tienen once funciones de costo que se discriminan en cinco tipos:
-
Función de costo tipo 1: /
-
Función de costo tipo 2: /
-
Función de costo tipo 3: /
-
Función de costo tipo 4: /
-
Función de costo tipo 5: /
Los nodos 4, 24, 42, 90, 99, 110 y 116 tienen función de costo tipo 1. El nodo 26 tipo 2, el nodo 49 tipo 3, el nodo 59 tipo 4 y el nodo 80 tipo 5. Después de simular el algoritmo de optimización heurística considerando solo energía convencional, se encuentran las potencias que se programan a cada bus, dichas potencias y su respectiva función de costo se muestra en la figura 6 para los nodos tipo 1 y en la figura 7 para los nodos tipo 2, 3, 4 y 5.
Figura 7: Curva de costos de operación generadores convencionales tipo 2, 3, 4, 5 en función de la potencia programada, en nodos que anteriormente eran renovables.
Como se observa en las figuras 6 y 7, las restricciones del sistema hacen que los generadores que tienen la misma función de costo tengan diferente potencia programada, y su despacho obedece a una optimización de costos. En la tabla XI se muestran los resultados para estos once nodos, ahora convencionales.
A partir de estos resultados, se calculan las diferencias entre los dos casos considerados: con energías renovables y con generación tradicional. Los cuales se muestran en la tabla XII.
Tabla XII: Comparación de resultados sistemas con y sin generación renovable

En los resultados presentados se puede ver que los nodos con más costos fueron los generadores eólicos, lo cual puede estar asociado a que el coeficiente de costos eólicos por sobrestimar cw,o,i = 70, es 1,5 veces mayor que el costo fotovoltaico por sobrestimar cPV,o,i = 46 y 3,5 veces mayor que el costo por sobrestimar de nodos con conexión de vehículos ce,o,i = 46, también el coeficiente de costos eólicos por subestimar cw,u,i = 140, es 1,8 veces mayor que el costo fotovoltaico por subestimar cPV,u,i = 76 y 3,5 veces mayor que el costo por subestimar de nodos con conexión de vehículos ce,u,i = 40.
7. Conclusiones
El presente artículo propone una herramienta para los operadores de red de sistemas de potencia con penetración de energía renovable. La herramienta utiliza costos de incertidumbre, de esta manera, se tiene un criterio para realizar el despacho óptimo de potencia activa y reactiva, en sistemas que incorporan tanto fuentes de energía convencional como renovables. Así, los costos de incertidumbre modelan mediante una función analítica la incertidumbre en las fuentes primarias. De este modo se permite el ingreso de los elementos de energía renovable de forma competitiva en la programación del despacho de potencia.
Los sistemas de potencia son desarrollados en un entorno económico donde cantidades de potencia son programadas, y es necesario que los valores de las potencias sean suministrados de forma confiable, de otra forma son generados costos de penalización debidos a sobrestimar y subestimar la potencia disponible (para recursos renovables). Como se observa en la tabla XII, para los coeficientes de penalización (cu,i y co,i) tomados, la operación del sistema es más económica con alta penetración de energías renovables. De esta manera, la precisión en la estimación de los costos de incertidumbre permite la optimización de los recursos de generación, en este sentido se estima la cantidad de irradiancia solar, velocidad de viento y potencia en vehículos eléctricos, haciendo menos dependiente el sistema de potencia de los recursos tradicionales sin afectar la confiabilidad del despacho.
Referencias
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.

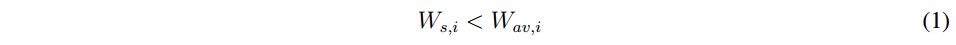
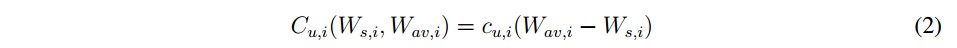
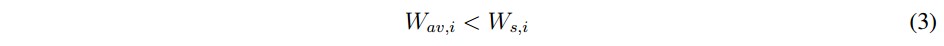
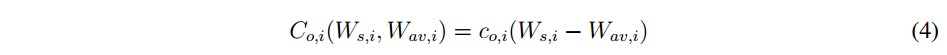
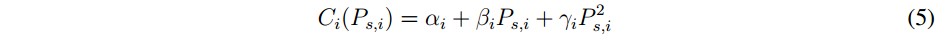
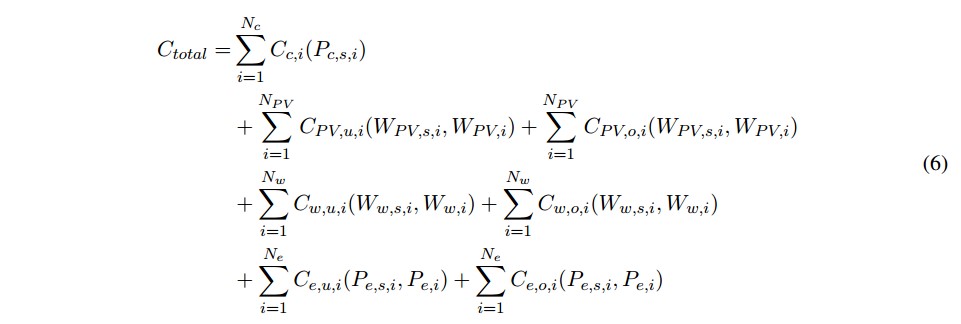
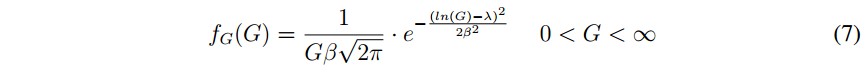
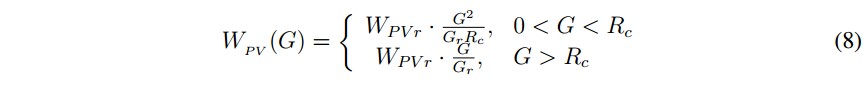
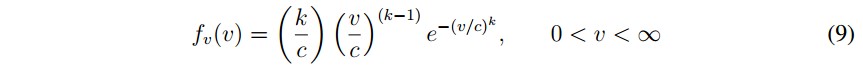
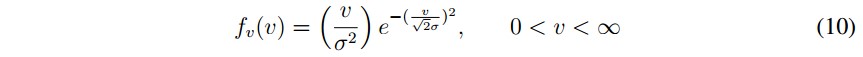
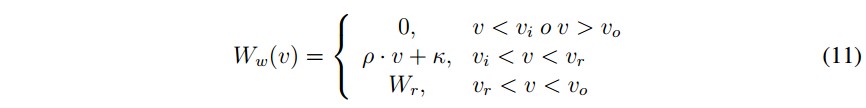
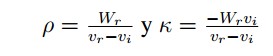
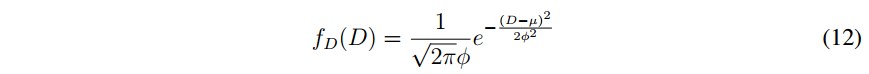
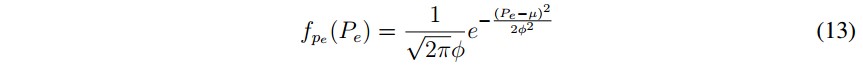
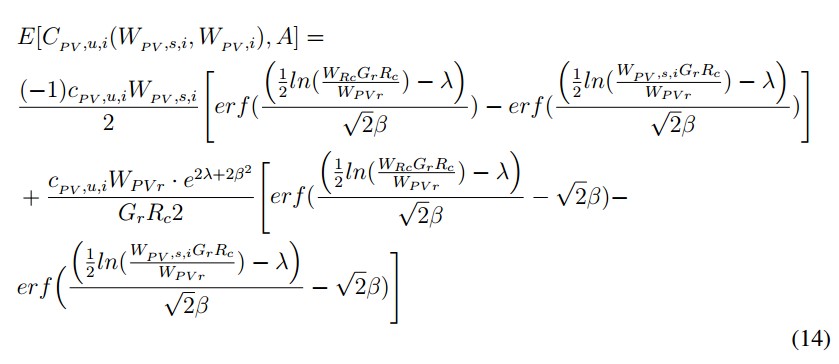
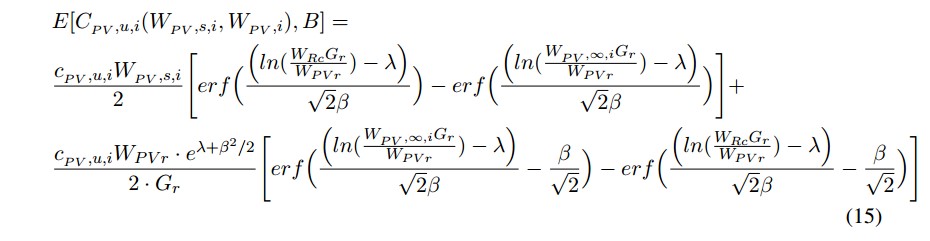
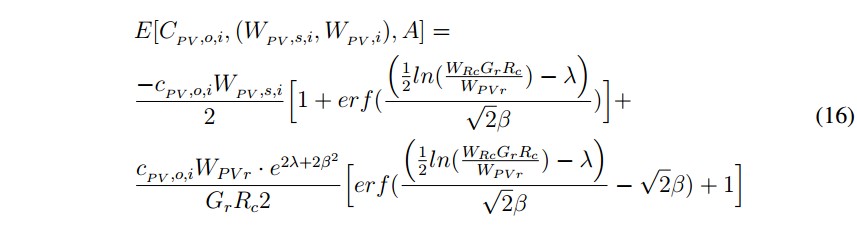
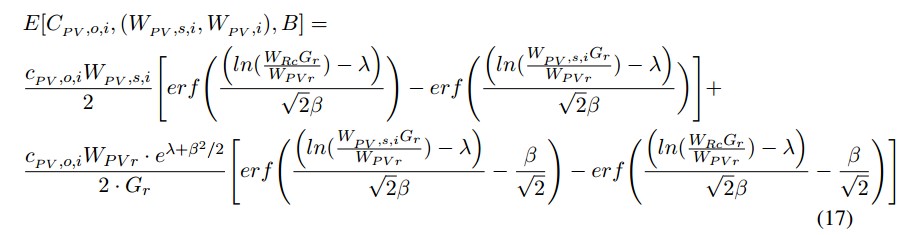
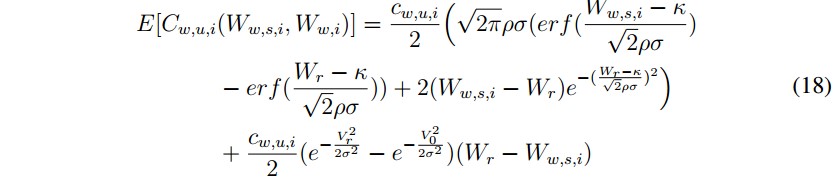
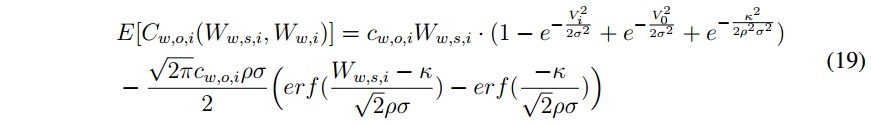
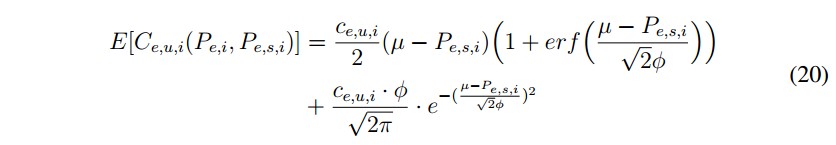
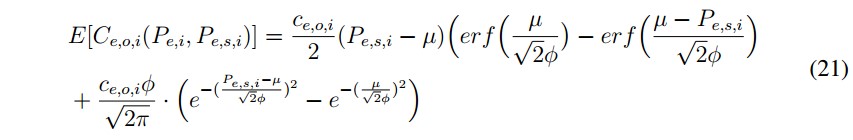


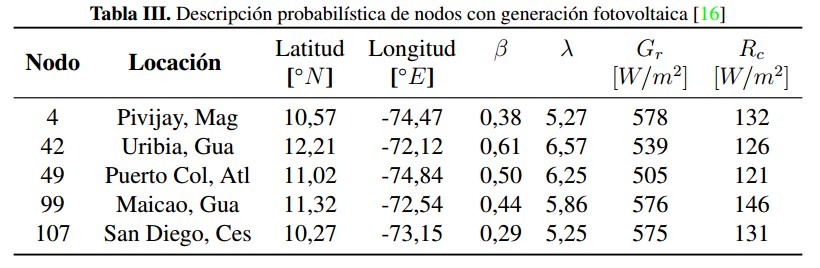
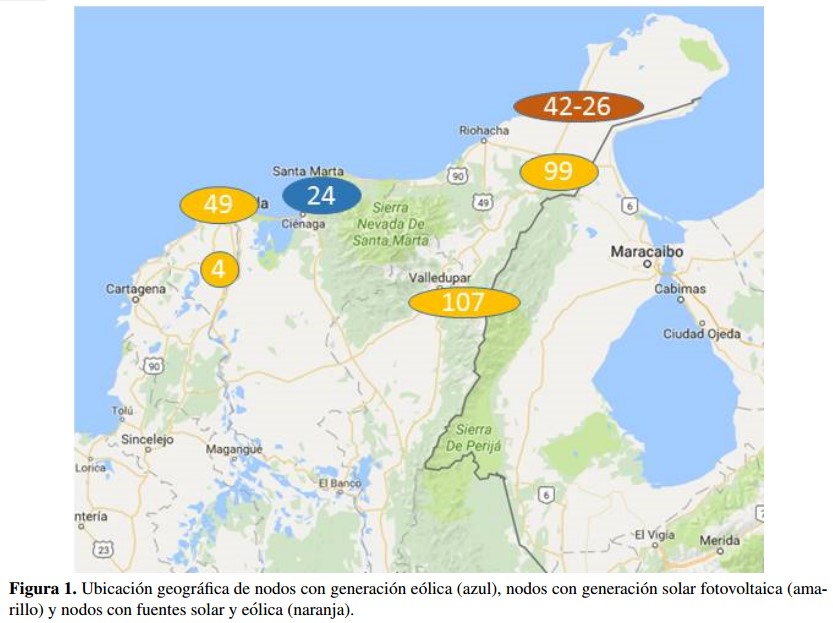
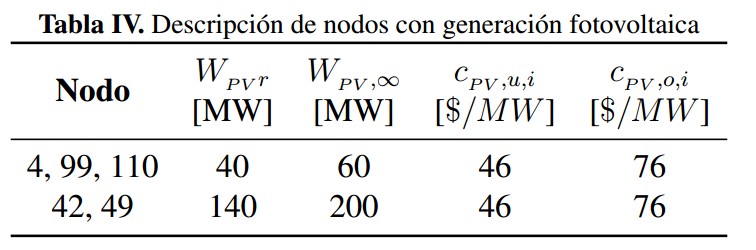
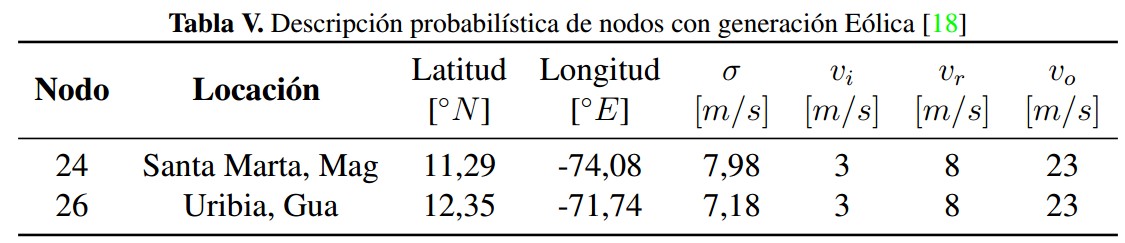


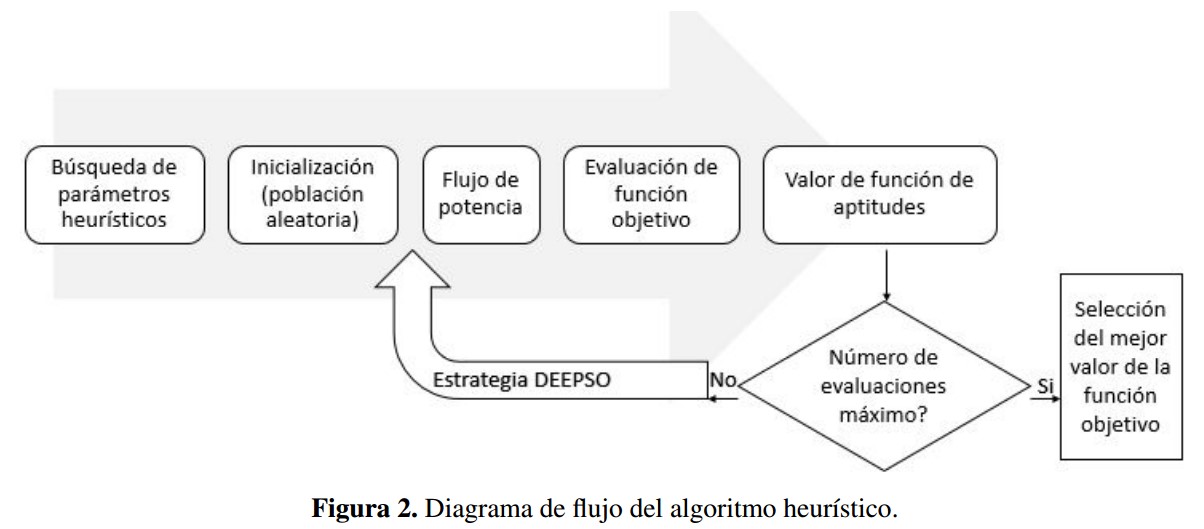
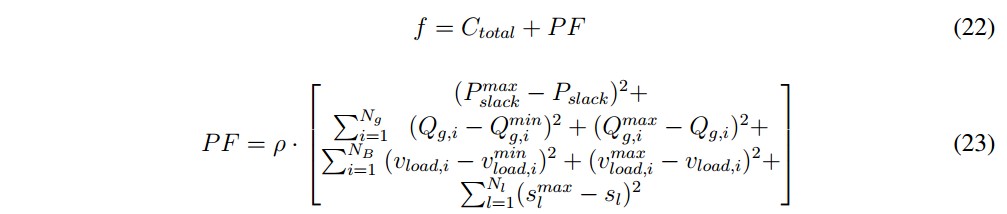
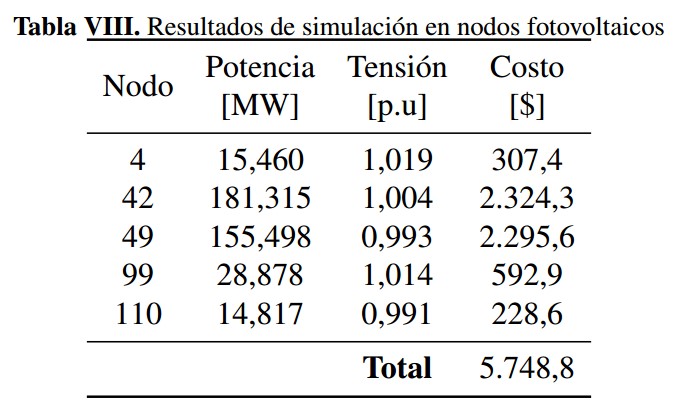
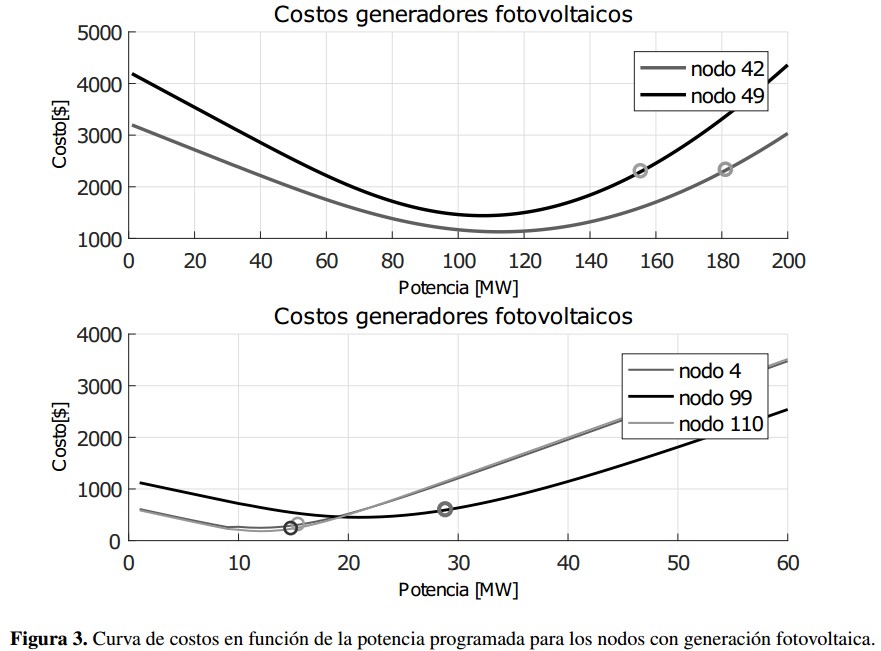
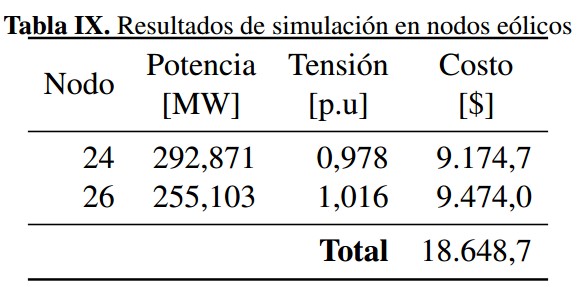
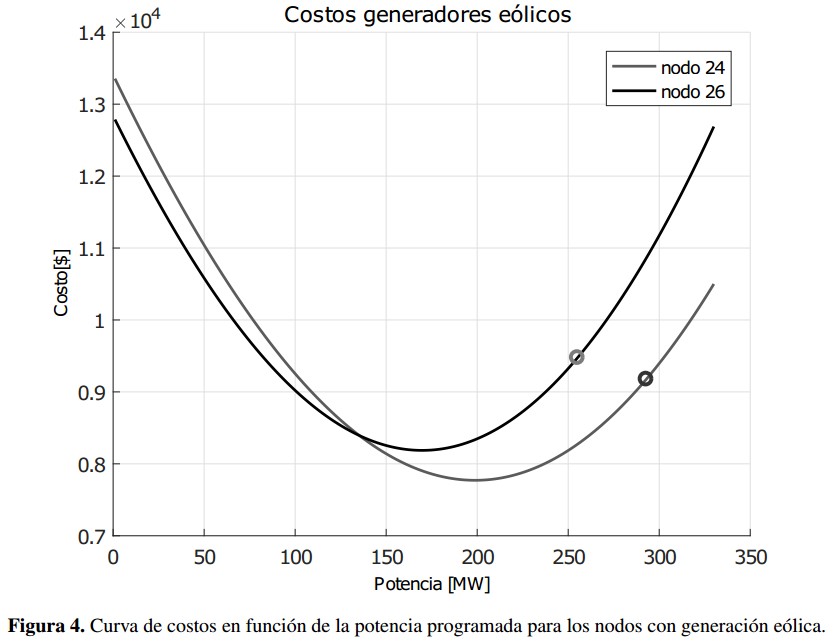
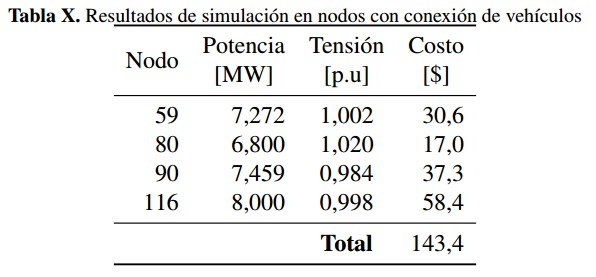
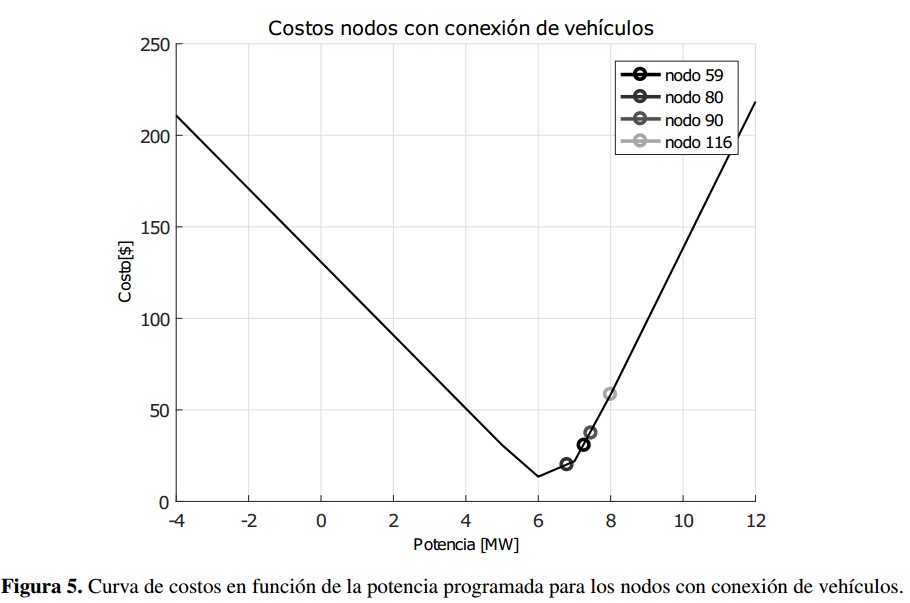
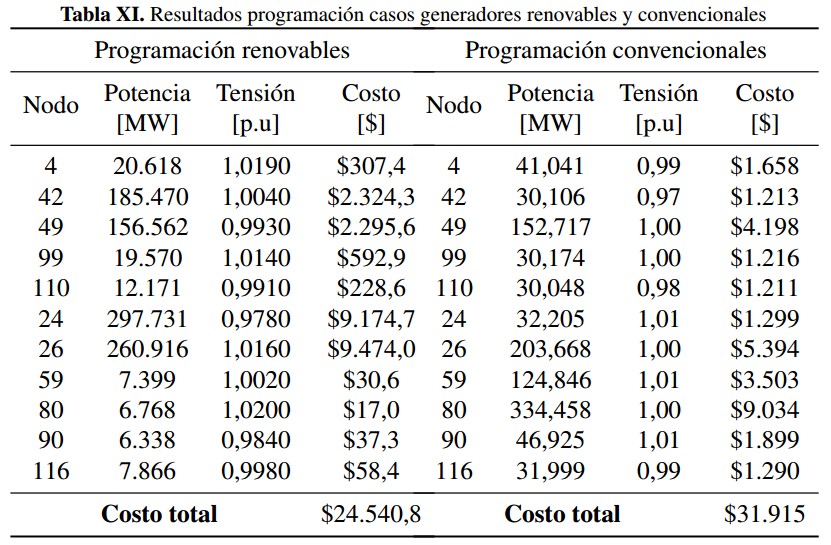
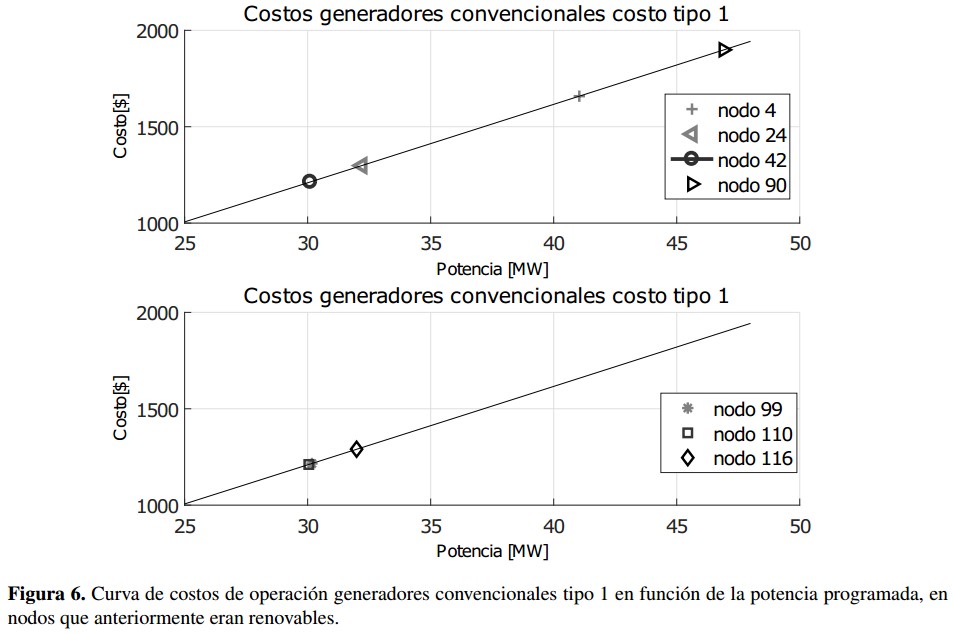
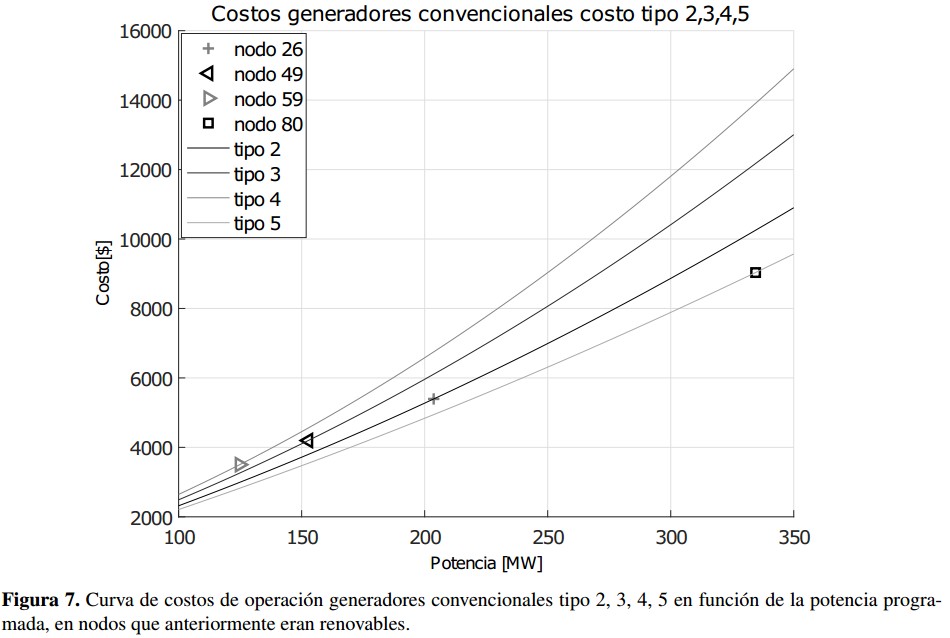
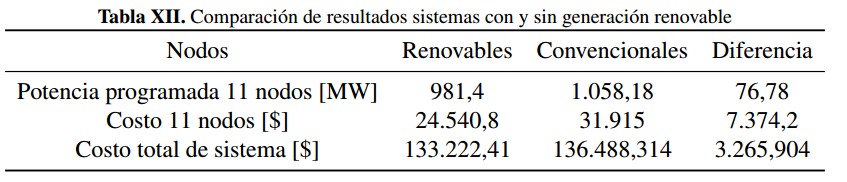
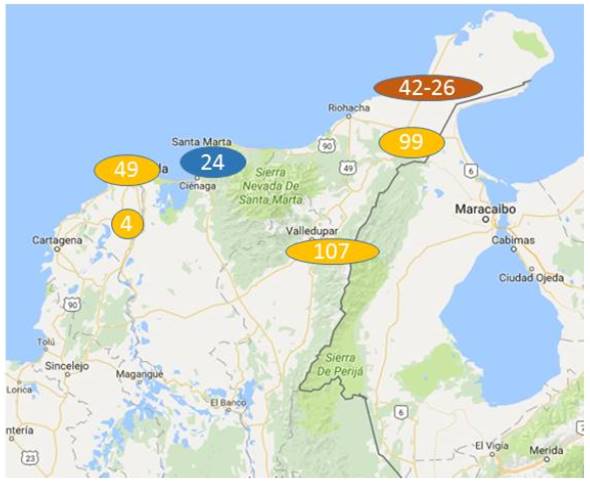
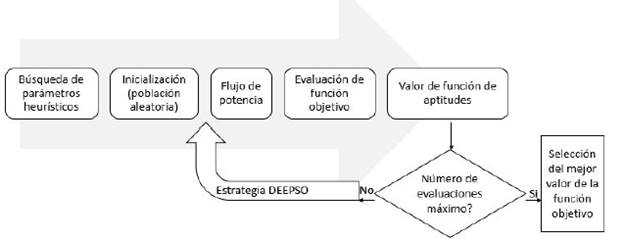
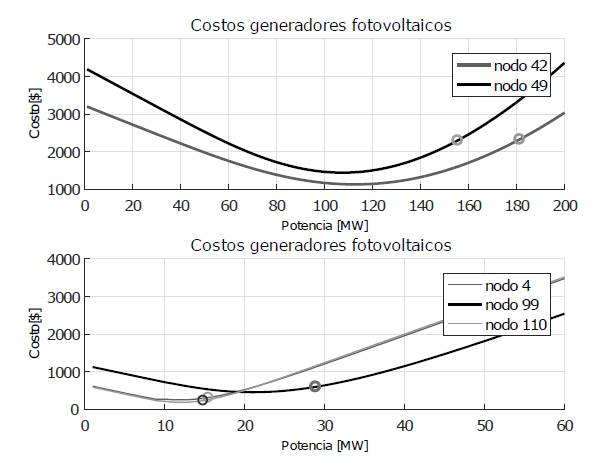
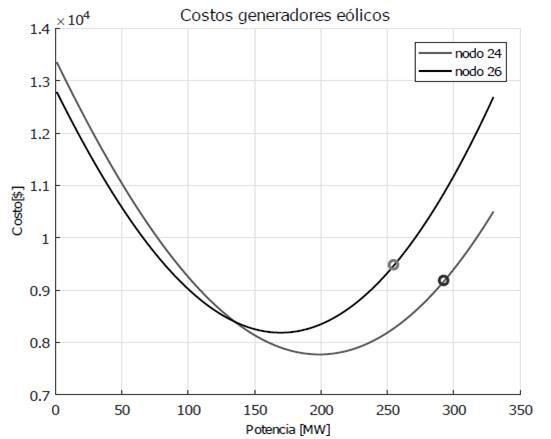
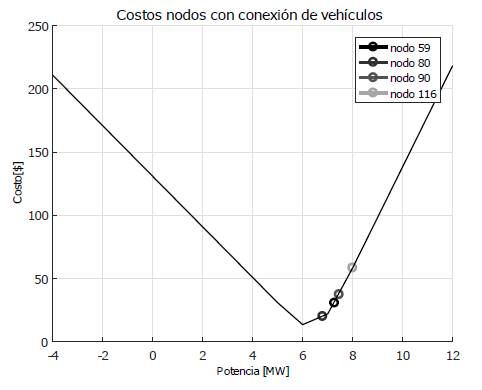
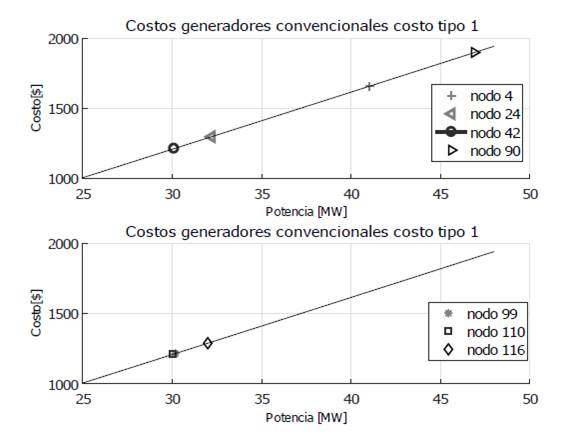
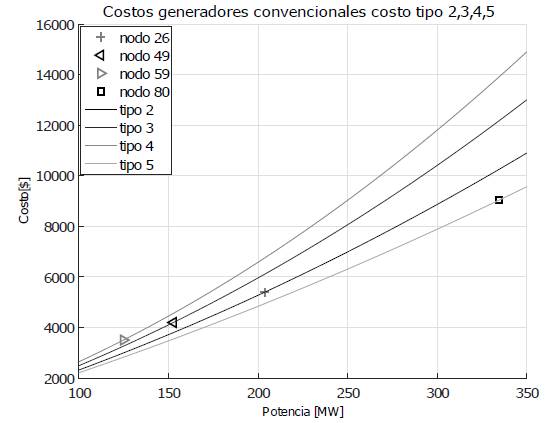


2.jpg)