Parametrización de modelo de circuito equivalente de polarización dual de una celda de ion Litio utilizando la técnica de optimización por enjambre de partículas modificada.

Introducción

Los sistemas de almacenamiento de energía (ESS por su sigla en inglés) se han convertido en un amplio campo de investigación debido a que son elementos importantes en las microrredes de generación de energía aisladas ¹ y las tecnologías de movilidad eléctrica (vehículos, motocicletas, trenes, entre otros) ², las cuales apuntan a la minimización del uso de los combustibles fósiles.

Dentro de los ESS, las baterías son los elementos más utilizados siendo la combinación ion litio la más prometedora actualmente, debido a su alta densidad de potencia y de energía. Para poder analizar el comportamiento de las baterías en las diferentes aplicaciones, típicamente se utiliza una metodología basada en simulación, donde se analizan las características principales como voltaje con base en el comportamiento electroquímico ³, corriente de la batería, estado de carga (SoC por su sigla en inglés) ⁴ y estado de salud (SoH por su sigla en inglés) ⁵. Obtener un modelo que describa el comportamiento físico que gobierna la operación de las baterías permite generar, bajo simulación, un análisis más preciso de cómo responden las baterías a diferentes escenarios de uso y una confiabilidad alta al momento de validar los conceptos bajo pruebas experimentales. Los modelos de baterías encontrados en la literatura se pueden clasificar en modelos empíricos, modelos abstractos, modelos electroquímicos y combinaciones ^{6), (7) y (8}. Una fuente de voltaje con energía infinita de carga/descarga es la manera más fácil de modelar una batería ⁹, sin embargo, no es una aproximación muy exacta al comportamiento de una batería ya que no se incluyen las dinámicas de carga y descarga (Fig. 1a). La dependencia del voltaje de circuito abierto en función del SoC se presenta en ¹⁰, donde el voltaje de una celda completamente cargada es mayor al de una celda descargada (Fig. 1b). La polarización se refiere a cualquier desviación del voltaje en los terminales de la celda debido al paso de corriente. Para incluir el efecto de polarización en la celda se incluye a esta fuente de voltaje una resistencia en serie ², la cual describe que el voltaje en los terminales de la celda cae por debajo del voltaje de circuito abierto cuando la celda es descargada y aumenta por encima del voltaje de circuito abierto cuando la celda está siendo cargada (Fig. 1c). La variación de voltaje debida a la polarización es un proceso que se genera lentamente con el tiempo a medida que la corriente sale o ingresa a la celda e igualmente decae lentamente con el tiempo cuando la celda se encuentra en reposo después de interrumpir la corriente de carga o descarga. Este efecto es conocido como difusión, el cual es aproximado incluyendo uno o más paralelos de resistor - capacitor a los circuitos anteriores como se puede ver en la Fig. 1d, entre más paralelos se agreguen al circuito se mejorará la precisión en el comportamiento esperado, sin embargo, la complejidad es aumentada considerablemente; lo más recomendado es utilizar uno o dos paralelos ^{11), (12}. Otro tipo de efectos como la respuesta en frecuencia (modelo Randles) y la histéresis son modelados y presentados en ¹³ y ¹⁴. Cada uno de estos parámetros adicionados al modelo dependen de la tecnología, referencia de batería y SoH, debido a esto es posible obtener un modelo aproximado para las condiciones de operación de una batería específica, para lo cual hay que encontrar el valor de estos parámetros. La estimación de los parámetros del modelo en función del SoC se puede realizar usando diferentes métodos basados en modelos, los cuales en tiempo real cuentan con una gran robustez y precisión, debido a que tienen una gran adaptabilidad y buen rendimiento, pero se requiere de un modelo muy fiel de la batería y un alto costo en el cálculo de los datos ¹⁵.

Figura 1: Circuitos equivalentes para modelado de baterías encontrados en la Literatura

Para parametrizar estos valores se han utilizado algunas técnicas de optimización cuya función objetivo más común es un error cuadrático medio entre el voltaje del modelo y el voltaje de la batería real frente a la misma excitación de corriente. En ¹⁶⁾ comparan la eficiencia de un algoritmo de optimización por enjambre de partículas (PSO por su sigla en inglés), un algoritmo genético y un PSO mejorado para encontrar los parámetros de modelo de Thévenin con un circuito RC. Otros autores proponen utilizar filtro de Kalman extendido ²⁰ para predecir el estado actual del sistema no lineal, estimando el SoC de la batería con un error aproximado del 3 %. En ²¹,se usa el conteo de Coulomb (CC) unificado con filtro de Kalman de punto sigma (SPKF) para evaluar diferentes parámetros en los cuales se destacan: la tolerancia a la señal ruidosa, la capacidad de recuperación de una distorsión intencional del SoC, así como la comparación de la precisión de la estimación, esto con el fin de analizar tiempo de ejecución de cada método. Algunos trabajos utilizados en la literatura para otros campos también han sido probados para la estimación del SoC, tales como mínimos cuadrados y diseño central compuesto propuesto en ²², redes neuronales presentado en ²³ y filtro de Kalman extendido con covarianza modificada (MVEKF) a diferentes temperaturas evaluado en ²⁴. Dentro de los retos de esta metodología está encontrar los valores de los parámetros del modelo generando una mayor exactitud y bajos tiempos de cómputo. Para el modelo de polarización dual es necesario encontrar el valor de los seis componentes del modelo para cada SoC diferente (100 %, . . ., 0 %), el cual es típicamente abordado como un solo problema, donde el algoritmo busca encontrar los 66 parámetros al mismo tiempo, lo cual arroja tiempos de convergencia y tolerancias por encima de los rangos esperados. Como contribución de este trabajo, se presenta una metodología para la parametrización de un modelo de polarización dual de una batería utilizando PSO, que se basa en una fragmentación del problema global de la búsqueda de los parámetros del modelo en pequeñas subsecciones buscando mejorar la precisión y el tiempo de convergencia del algoritmo. La metodología es comparada con la metodología estándar encontrada en la literatura utilizando el mismo algoritmo PSO, donde se presenta la disminución en los tiempos de convergencia y tolerancia. Finalmente, como trabajos futuros se plantea la comparación del uso de la metodología utilizando diferentes algoritmos de optimización metaheurísticos.

Este trabajo se encuentra organizado de la siguiente manera: en la segunda sección se presentan los materiales y métodos utilizados (base de datos, modelo de polarización dual, algoritmo PSO y función objetivo), en la tercera sección se presentan los resultados y finalmente las conclusiones y los trabajos futuros.

Materiales y métodos

En este trabajo se busca modelar la celda de ion litio 18650, que tiene un voltaje de 3,7 V con una capacidad de 27.600 mAh. Este tipo de celdas son muy utilizadas para construir baterías con mayores capacidades con configuraciones serie y paralelo ²⁵. Para modelar el comportamiento de esta batería se utilizará el modelo de polarización dual, el cual permite simular características de polarización, descarga/carga de la batería, dependencia del voltaje frente a la magnitud y sentido de la corriente. Debido a la naturaleza del espacio de búsqueda del problema se ha seleccionado un algoritmo metaheurístico con buena capacidad de exploración y explotación. A continuación, se describen la base de datos utilizada, el modelo de polarización dual, el algoritmo PSO, la función objetivo y finalmente la metodología propuesta.

Base de datos de la batería

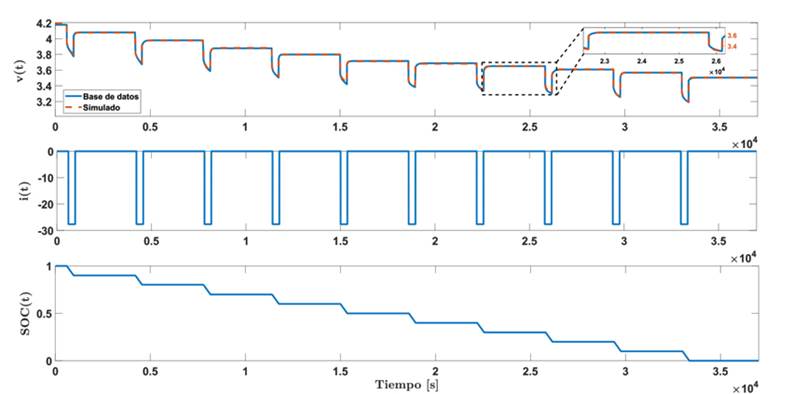
Para este trabajo se utiliza la base de datos Randomized Battery Usage Data Set de la NASA ²⁶, la cual contiene una recopilación de pruebas eléctricas aplicadas sobre baterías de ion litio, que constan de perfiles de carga aleatorios y perfiles de carga con referencia, brindadas de forma gratuita para generar investigación en torno al modelado de baterías. La Fig. 2 muestra una de las curvas encontradas en la base de datos, que consiste en descargar a la batería con pulsos de corriente de 0,1 C por 0,1 horas (6 minutos), seguidos por periodos de relajación de 0,9 horas (54 minutos) con corriente cero.

Figura 2: Curva del voltaje de una celda entregada por Randomized Battery Usage Data Set de la NASA 26

Estas pruebas permiten evaluar los cambios transitorios del voltaje en los terminales de la batería en función de la corriente, el proceso de difusión del circuito equivalente y observar su funcionamiento a diferentes valores de SoC. La secuencia de pulsos se realiza en un solo punto de funcionamiento con respecto a temperatura, corriente y condiciones SoH.

Modelo de polarización dual

El modelo de polarización dual puede considerarse una extensión del modelo Thévenin. Este modelo, ilustrado en la Fig. 3, considera un bloque R-C adicional en serie al circuito presentado en la Fig. 1d con el objetivo de mejorar la precisión en la respuesta del modelo, donde Em representa el voltaje de circuito abierto, la resistencia R1 la polarización electroquímica, R2 la polarización de concentración y R0 la resistencia óhmica. Los capacitores C1 y C2 representan la respuesta transitoria de la transferencia de potencia desde y hacia la batería e i(t) es la corriente de carga y descarga de la batería. El voltaje en los terminales de este circuito esta descrito por la Ec. (1) .

Figura 3: Modelo de polarización dual

Las corrientes en R1 y R2 más la corriente de su respectivo capacitor en paralelo son iguales a i(t). Adicionalmente, sabiendo que ic = Cvc(t) se obtiene la Ec. (2)

Adicionalmente, reemplazando la Ec. (3) que describe el voltaje en los capacitores, en la Ec. (2) , se obtiene la Ec. (5) .

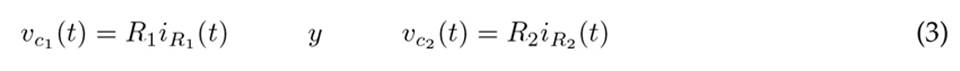
Finalmente, utilizando la Ec. (5) se pueden despejar las derivadas de corriente en las resistencias, presentadas en (5) y (6).

Estas ecuaciones pueden ser convertidas a forma discreta como se presenta en ¹⁰⁾ con el objetivo de simular el comportamiento del circuito para variaciones en la corriente de carga o descarga.

Algoritmo PSO

El algoritmo PSO (Particle Swarm Optimization) es una técnica de optimización metaheurística desarrollada por James Kennedy y Russell C. Eberhart en 1995 ²⁷, la cual tienen la capacidad de trabajar con funciones multimodales, con restricciones y tareas multiobjetivo. El PSO inicia con una creación de una población aleatoria de un número de “i” de partículas, a la cuales es asignada igualmente de forma aleatoria una velocidad con la cual recorrerán el espacio de búsqueda. El movimiento de las partículas está definido por el cambio de los argumentos de entrada que permiten modificar la función objetivo, donde la cantidad de argumentos definirá la dimensión “n” del espacio de búsqueda. Para cada uno de los puntos recorridos por cada partícula se evalúa la función objetivo y la mejor evaluación de la función es almacenada en la función Pm . Adicionalmente, la mejor evaluación de todo el conjunto de partículas es almacenada en la variable Gm. El movimiento de cada partícula en cada iteración del algoritmo se realiza en función de Pm y Gm.

Las composiciones que dominan el movimiento de cada partícula se muestran en la Fig. 4, donde el vector de color verde representa la ubicación de exploración de la partícula, que se calcula a partir de su experiencia particular (mejor posición que ha evaluado la partícula) y de la experiencia global (mejor posición que ha evaluado todo el enjambre). Para lograr este cálculo, cada partícula comparte información con el resto del enjambre de cierta manera durante su exploración y explotación. Entonces cada partícula actualiza su dirección de vuelo basada en su propia mejor experiencia exploratoria local (Pm) y la mejor experiencia global (Gm) de acuerdo con las Ec. (7) y (8) :

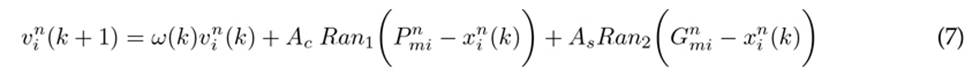
Figura 4: Esquematización del algoritmo PSO para dos dimensiones

Donde para cada nth dimensión de la partícula i, xn i

(k + 1) y x n i (k) representan la posición actual y previa y v n i (k + 1) y v n i (k) denotan la velocidad actual y previa respectivamente. ω(k) es el peso de inercia, Ac y AS son la tasa de aprendizaje cognitivo y social, finalmente Ran1 y Ran2 son números aleatorios con distribución uniforme que comprende los valores entre 0 y 1. Una versión local del PSO modifica el seguimiento global de las partículas por una topología de vecindad, donde cada partícula se direcciona hacia la mejor solución de la vecindad ²⁸.

Función objetivo

El objetivo del algoritmo es encontrar los valores de los elementos del modelo de polarización dual que presenten el comportamiento más cercano a la curva representada en la Fig. 2 para la misma excitación de corriente, cuya metodología es llamada modelo inverso. El proceso de la metodología es esquematizado en la Fig. 5, donde el objetivo es encontrar los argumentos que minimizan la función ε expresada en la Ec. (9) , la cual es el error cuadrático medio (RMSE) donde v(t)m es el voltaje en los terminales de la celda obtenidos a partir del modelo y v(t)BD es el voltaje en los terminales de la celda medidos y entregados por la base de datos.

Figura 5: Algoritmo para encontrar los argumentos del modelo que minimizan el error RMSE

Para lograr esto se ejecutan los siguientes pasos: i) se inicializan los argumentos del modelo dentro del espacio de búsqueda, ii) se evalúa el modelo con estos parámetros y se obtiene la respuesta v(t)m, iii) se evalúa la Ec. (9) , iv) si el error ε es menor al valor esperado se finaliza el algoritmo, de lo contrario se procede al siguiente paso, v) se itera una vez el algoritmo PSO, si el número de iteraciones es menor al valor máximo seleccionado se finaliza el algoritmo, de lo contrario se repite el algoritmo desde el paso ii) hasta que alguna de las condiciones de finalización se cumpla.

Metodología propuesta

Encontrar un solo valor de los elementos para todo el comportamiento de la curva experimental arroja errores altos de aproximación del modelo, debido a esto se debe encontrar un valor diferente para cada uno de los parámetros en función del SoC. Como estrategia para lograr este proceso se propone dividir el problema en diferentes casos para cada uno de los SoC de los que se tenga información disponible. De esta forma se obtendrá un conjunto de valores diferentes {Em, R1, C1, R2, C2} para cada SoC o subsección de la curva como se puede ver en la Fig. 6.

Figura 6: División del problema en casos diferentes

Para el primer caso, las partículas son ubicadas aleatoriamente por el espacio de búsqueda, una vez el algoritmo converge, los valores de los parámetros encontrados son almacenados. Del segundo caso en adelante, los valores Pm y Gm del caso anterior son utilizados como experiencia previa para la asignación de las posiciones iniciales de las partículas con el objetivo de acelerar la convergencia en los demás casos y de esta forma disminuir el tiempo total de parametrización del modelo. Para realizar la distribución inicial de las partículas para el caso 2 en adelante se utiliza la expresión ⁽¹⁰⁾.

Finalmente, los valores encontrados de cada caso se agrupan en una tabla para ser probados en conjunto y analizar la precisión de toda la solución propuesta.

Resultados

Como parámetros para el algoritmo PSO se utilizaron las tasas de aprendizaje, inercia, tolerancia e iteraciones máximas mostradas en la Tabla I. Las iteraciones máximas son utilizadas como criterio de parada del algoritmo si no se ha alcanzado la tolerancia mínima esperada.

En la Tabla II se presentan los límites superiores e inferiores para los parámetros del modelo, dentro de los cuales el algoritmo PSO debe buscar los valores indicados para ajustar la curva de la simulación con la curva real de la base de datos.

Inicialmente se utiliza el PSO con el método típico encontrado en la literatura, el cual es un problema de 66 dimensiones (seis parámetros para cada SoC). El algoritmo es ejecutado utilizando 15, 30 y 60 partículas, se repite cinco veces para cada selección de partículas. Los mejores resultados para cada selección se presentan en la Tabla III. Se puede notar que para las tres soluciones se alcanza el número de iteraciones máximas, además al aumentar el número de partículas se reduce el error obtenido, pero igualmente se aumenta el tiempo de ejecución debido a que más partículas conlleva a un número mayor de ejecuciones del modelo.

Posteriormente, el modelo es parametrizado utilizando el método propuesto, para el cual se usaron diferentes partículas, desde 10 hasta 32, con incrementos de dos, con cinco ejecuciones para cada número de partículas seleccionado. La Fig. 7 presenta los resultados obtenidos, la primera gráfica muestra el promedio de iteraciones para cada selección de partículas y en las dos gráficas inferiores se ve el tiempo de convergencia en minutos y el error cuadrático medio mínimo logrado respectivamente.

Figura 7: Resultados de la parametrización del modelo de polarización dual utilizando el método propuesto

A partir de estas dos últimas gráficas se puede encontrar que el menor tiempo de convergencia promedio de 11,15 minutos se obtiene con 10 partículas, con un valor medio para el RMSE de 1,8e-4. El mayor tiempo de convergencia es obtenido con 32 partículas de 33,3 minutos y un valor RMSE medio de 0,803e-4.

Adicionalmente, se puede observar que debido a que el algoritmo PSO es una técnica metaheurística, el comportamiento del tiempo de convergencia y el error no son iguales para cada ejecución del código, lo que conlleva a obtener que para algunas cantidades de partículas las desviaciones estándares sean más altas que otras. Buscando obtener un excelente compromiso entre el tiempo de convergencia y precisión se seleccionaron 15 partículas y se ejecutó nuevamente el algoritmo, a partir del cual se encontraron los 66 valores que permiten que el modelo de la batería tenga una dinámica muy cercana a la dinámica obtenida en la curva experimental, la cual se puede ver en la Fig. 8 donde se obtiene un RMSE del 0,0001.

Figura 8: Voltaje de salida del modelo parametrizado

En la Fig. 9 se puede observar la variación de los seis parámetros del modelo {Em, R0, R1, C1, R2 y C2} respectivamente en función del estado de carga (SoC), los cuales son los elementos que conforman el modelo circuital de la batería de ion de litio.

Figura 9: Valores encontrados para los parámetros del modelo en función del estado de carga (a)Em vs SoC, (b) R0 vs SoC, (c) R1 vs SoC (d) C1 vs SoC (e) R2 vs SoC (f) C2 vs SoC

Conclusiones

En este trabajo se ha desarrollado una metodología para mejorar los tiempos de parametrización de un modelo de polarización dual de una batería de litio utilizando el algoritmo PSO.

La metodología se centra en dividir el problema en diferentes casos de optimización donde el caso anterior permite generar una distribución de las partículas del algoritmo PSO con base en la experiencia del caso anterior delimitando el espacio inicial de lanzamiento de las partículas, lo que permite una reducción en el tiempo de convergencia del algoritmo. Esta metodología puede ser probada con otro tipo de algoritmos y verificar su efectividad para acelerar el tiempo que puede usarse en la parametrización de cualquier tipo de batería que quiera modelarse y probarse bajo un ambiente seguro de simulación. Este modelo puede ser utilizado para modelar el rendimiento de carga de la batería utilizando un modelo de circuito equivalente para aplicaciones que necesitan el almacenamiento de energía eléctrica como las microrredes y los vehículos híbridos y eléctricos. Los resultados sugieren que el código desarrollado puede usarse con confianza para la extracción de los parámetros de la batería necesarios en un modelo de polarización dual y otros con menor complejidad para una gran variedad de baterías de diferentes tamaños, capacidades y materiales.

Como continuación de este trabajo para futuros eventos, se plantea el desarrollo de la técnica propuesta con otros algoritmos de optimización o la combinación de estos, con el fin de comparar la mejora en los tiempos de respuesta presentados en dicho trabajo. Además, se deja abierto el uso del método planteado con modelos de baterías más complejos presentados en la literatura.