VISIÓN DE CASO

Visión Electrónica, 2012-12-01 Volumen:6, Año:2 pág: 126–133

---

OBTENCIÓN DE MÁXIMA TRANSFERENCIA DE POTENCIA A UNA CARGA ELÉCTRICA POR MÉTODOS DE OPTIMIZACIÓN

OBTAINING MAXIMUM POWER TRANSFER FOR AN ELECTRICAL LOAD THROUGH OPTIMIZATION METHODS

Fery P. Rodríguez M.

Licenciada en Física Universidad Distrital Francisco José de Caldas. Ingeniera Electricista de la Universidad Nacional de Colombia. Especialista en Docencia Universitaria Universidad Militar Nueva Granada. Aspirante a MSc. en Ingeniería Universidad Libre de Colombia. Docente Ocasional de la Universidad Distrital Francisco José de Caldas. Correo electrónico: fery.rodriguez@unimilitar. edu.co.

Álvaro Rogelio T.

Ingeniero Electromecánico de la UPTC Duitama. Especialista en Docencia Universitaria de la Universidad Militar Nueva Granada. Aspirante a MSc. en Ingeniería de la Universidad Libre de Colombia. Docente Cátedra en la Universidad Distrital Francisco José de Caldas. Correo electrónico: alvaro.torres@ unimilitar.edu.co

Harold Vacca G.

Licenciado en Matemáticas de la Universidad Distrital. Especialista en Ingeniería de Software Universidad Distrital y MSc. en Matemática aplicada de la Universidad EAFIT. Director del grupo de investigación SciBas, docente de Planta en la Universidad Distrital Francisco José de Caldas.hvacca@ udistrital.edu.co.

RESUMEN

El presente artículo presenta el análisis de datos en una carga eléctrica para obtener la optimización del valor de la carga eléctrica que permita la máxima transferencia de potencia de un circuito a la carga, modelado mediante un equivalente de thévenin. Para el estudio se tomaron datos experimentales en un circuito para el cual la carga varía mediante un potenciómetro que se instala a un circuito considerado como caja negra, con lo que se encontraron unos datos experimentales de potencia en la carga en función de la resistencia de carga. Al tomar datos experimentales se tiene presente ubicar una condición de optimización de tres puntos, es decir, una concavidad encerrada por tres datos experimentales, para empezar un método de optimización por sección dorada o por método polinomial de Powell.

Palabras clave

Optimización, carga eléctrica, potencia eléctrica, equivalente circuital.

Abstract

This article presents the analysis of data on an electrical charge for maximizing the value of electric charge to allow for maximum power transfer circuit connected to the load, modeled by a Thévenin equivalent. To study experimental data were taken in a circuit to which the load varies by a potentiometer that is installed on a circuit considered as a black box, finding experimental data on the load power as a function of load resistance. By taking experimental data has provided this place a three-point optimization, when a concavity is enclosed by three experimental data to begin an optimization method of golden section and method of Powell.

Key Words

Optimization, electric charge, electric power, equivalent circuital.

---

Introducción

El optimizar un sistema permite que se aprovechen de la mejor manera los recursos, se reduzcan costos y se logre una mejor efectividad en el funcionamiento de dicho sistema. Para el caso de análisis de circuitos, cuando es posible variar la condición de carga eléctrica instalada entre terminales a un circuito real, es de gran importancia tener pleno conocimiento sobre cuál debe ser el valor de dicha carga para que se logre la mayor transferencia de energía en una determinada unidad de tiempo.

Supóngase que se necesita hacer solo un análisis parcial de un circuito; probablemente solo es necesario calcular la corriente, el voltaje y la potencia entregados a una carga en especial por el resto del circuito al que se encuentra conectada, el cual puede constar de un gran número de fuentes y resistores; o quizás se desea calcular la respuesta para diferentes valores de la resistencia de carga.

Entonces, el Teorema de Thévenin dice que es posible sustituir todo, excepto el resistor de carga, por un circuito equivalente que consista en solo una fuente independiente de voltaje en serie con un resistor [1]. Es así como uno de los principales usos del Teorema de Thévenin [2] es la sustitución de una gran parte de una red, a menudo una parte complicada y que no es de interés inmediato, por un equivalente muy simple (figura 1).

Figura1. Caja negra de la red o circuito fijo instalado a la carga

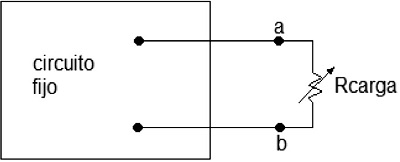
Fuente: elaboración propia.

El nuevo y más simple circuito (figura 2) permite llevar a cabo cálculos rápidos del voltaje, la corriente o la potencia que el circuito original es capaz de entregar a la carga; también ayuda a elegir el mejor valor para esta resistencia de carga en términos de máximo aprovechamiento de la potencia entregada por el resto del circuito a esta [3].

Figura 2. Equivalente de Thévenin representativo, conectado a la carga

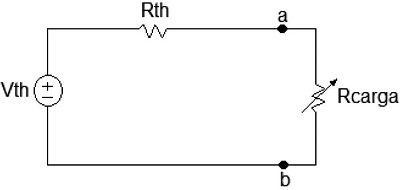
Fuente: elaboración propia.

El equivalente de Thévenin de un circuito con fuentes de voltaje o corriente independientes conectadas a una carga en terminales a-b se puede hallar de dos formas: el voltaje Thévenin es el voltaje quitando la carga y evaluando así el voltaje en terminales a-b. El voltaje evaluado de esta forma es el llamado “voltaje de circuito abierto” (Vca) en a-b y será el voltaje de Thévenin del equivalente. Por otro lado, unir terminales en a-b con un corto circuito y verificar la corriente que circula en el conductor que une a-b llamada corriente de corto circuito (Icc) [2]

El equivalente Thévenin tendrá resistencia Thévenin calculada por 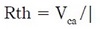(1)

        (1)

Y voltaje de Thévenin Vca dado en 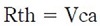(2)

        (2)

2. Procedimiento

Para evaluar y optimizar la potencia entregada a una carga eléctrica instalada a un circuito en los terminales a-b se escogió el circuito mostrado en la siguiente figura:

Figura 3. Circuito de estudio instalado en laboratorio

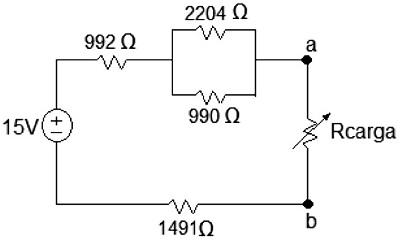
Fuente: elaboración propia.

Figura 4. Fotografía del montaje realizado en el laboratorio

Fuente: elaboración propia.

Para encontrar la carga óptima instalada en a-b (que el circuito instalado a la carga le entregase la máxima potencia [4]) se conectó el circuito en protoboard y como carga se instaló un potenciómetro con rango de 0-5 KO, el cual fue variando, y se tomaron datos de corriente y resistencia de potenciómetro para obtener una tabla como la mostrada anteriormente, evaluando con los datos la potencia en la carga (tabla 1).

Tabla 1. Datos experimentales del circuito

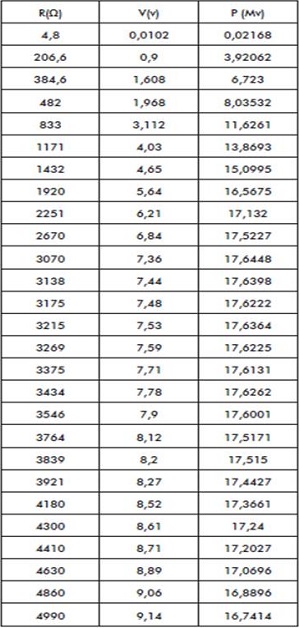
Fuente: elaboración propia.

Para las mediciones se empleó un multímetro de gama Extech TM 320, fuente D.C. de rango 0-30 V; 2,5 A . En la figura 4 se puede ver el montaje realizado en el laboratorio.

El comportamiento de los datos se puede visualizar en la figura 5.

Figura 5. Resultados experimentales de resistencia de carga vs. potencia

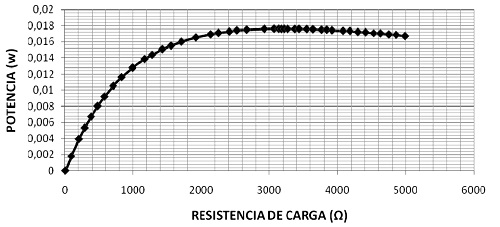
Fuente: elaboración propia.

Al realizar el circuito equivalente Thévenin se obtiene el siguiente circuito de la figura 6.

Figura 6. Equivalente de Thévenin conectado a la carga instalada en a-b

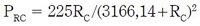
Fuente: elaboración propia.

Al evaluar la potencia entregada a Rc en función de Rc se encuentra que la función está dada por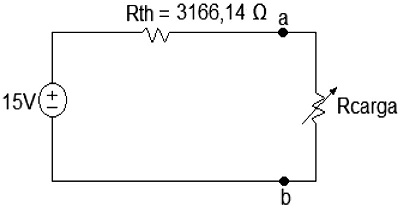 (3):

        (3)

Por el teorema de máxima transferencia de potencia “Una fuente de voltaje independiente en serie con una resistencia RS entregan una potencia máxima a aquella resistencia de carga Rc para la cual Rc=RS” [3].

Este teorema coincide con el análisis de la función PRC, en la cual un punto crítico de la función está dado para 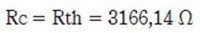(4)

        (4)

3. Propuesta

Para encontrar la carga en la cual la potencia transferida a la carga es máxima, es posible aplicar óptimo de la función PRC que se encuentra en el mínimo de -PRC, por corolario de teorema de optimización [5].

Cuando se emplea el método de optimización por sección dorada [6] se requiere el criterio de tres puntos, y el de convergencia con el número áureo 1,61803, para obtener las iteraciones a partir de intervalo con extremos de intervalo de tres puntos, de esta manera se lleva al óptimo.

Realizando programación de este método con recurso computacional Matlab® se obtiene:

Sección dorada

        

Figura 7. Resultado óptimo de potencia transferida en función de Rc por método de sección dorada

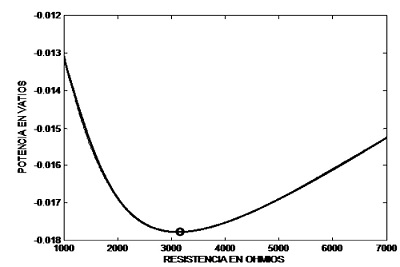
Fuente: elaboración propia.

Por método de Powell

        

Figura 8. Resultado óptimo de potencia transferida en función de Rc por método de Powell

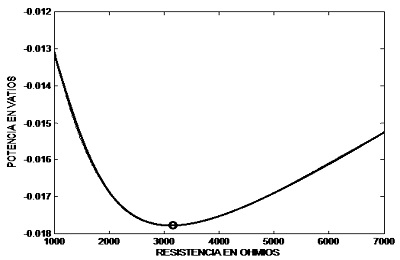
Fuente: elaboración propia.

4. Conclusiones

1. Una aplicación de los métodos de optimización se encuentra en la optimización de la potencia transferida a una resistencia de carga eléctrica, instalada a un circuito que puede representarse por un equivalente Thévenin; así, se verifica que la potencia máxima se logra cuando la resistencia Thévenin y la resistencia de carga son iguales, como lo indica el teorema de máxima transferencia de potencia eléctrica.
2. Los métodos de optimización son aplicables en diferentes áreas de la ingeniería, como es el caso de los circuitos eléctricos, para verificar óptimos de eficiencia energética a la salida de una red, respecto de la energía de entrada que en ocasiones es fija.
3. La utilización de métodos de optimización de sección dorada y de polinomial de Powell requiere el cumplimiento de las condiciones de entrada necesarias para el método aplicado, en este caso el criterio de los tres puntos.

Reconocimientos

Los autores reconocen al grupo de investigación SciBas por la orientación teórica de los métodos de optimización y su implementación computacional.

Referencias

1. A. M. Sommariva, A maximum power transfer theorem for DC linear twoports, Brescia: Dipt. Di Electtronica per l'Automazione, 2002.
2. R. C. Dorf, Teoremas de thévenin y norton. Circuitos. México: Universidad de California, 1995.
3. J. Bonet-Dalmau, P. Pala–Schonwalder, An ultrasound-based laboratory experience to illustrate the maximum power transfer theorem. Manresa: Dept. of Signal Theor & Commun., Tech. University of Catalonia (UPC), 2008.
4. W. H. Hayt y J. E. Kemmerly, Máxima transferencia de potencia en circuitos eléctricos. Análisis de circuitos en ingeniería. California: Universidad de California, 1988.
5. A. D. Belegundu, T. R. Chandrupatla, Optimization concepts and applications in engineering. New York: Prentice Hall, 1999.
6. S. Chapra y R. Canaole. Método de optimización por sección dorada. Métodos Numéricos para Ingenieros. 5ª edición, Bogotá, Colombia, Mc Graw Hill, 2007.

---

Creation date: Diciembre de 2012