VISIÓN DE CASO

Visión Electrónica, 2012-06-01 Volumen:6, Año:1 pág: 98–103

ESTUDIO CON ANÁLISIS POR ELEMENTOS FINITOS DE SISTEMAS ANÁLOGOS CIRCUITALES EN FÍSICA

STUDY WITH FINITE ELEMENT ANALYSIS OF ANALOG CIRCUIT SYSTEMS IN PHYSIC

Fery P. Rodríguez

Licenciado en Física, Ingeniera Electricista, Especialista en ocencia Universitaria, M.Sc. (c) en Ingeniería. Lugar de trabajo: Universidad istrital Francisco José de Caldas. Correo: fery. rodriguez@unimilitar. edu.co

Álvaro R. Torres

Ingeniero Electromecánico, Esp. en ocencia Universitaria, M.Sc.(c) en Ingeniería. Lugar de trabajo: Universidad istrital Francisco José de Caldas. Correo: alvaro. torres@unimilitar. edu.co

Harold Vacca G.

Licenciado en Matemáticas, Especialista en Ingeniería de Software, Universidad istrital Francisco José de Caldas.M.Sc. En Matemática aplicada, Universidad EAFIT, Colombia. irector Grupo de investigación SciBas. Lugar de trabajo: Universidad istrital Francisco José de Caldas. Correo: hvacca@udistrital. edu.co

RESUMEN

Este artículo plantea un desarrollo didáctico de solución de tres sistemas análogos circuitales: eléctricos, magnéticos y térmicos, los cuales presentan una correspondencia estructural y funcional en términos de las ecuaciones que rigen sus dominios. El conocimiento y manejo de un dominio puede servir como soporte para facilitar la enseÑanza y aprendizaje de un dominio nuevo, llamado blanco [1], que comparte estructuras o ecuaciones semejantes del comportamiento de los mismos, por lo que sus respuestas físicas se resuelven con el mismo método; en este caso, con el de elementos finitos [2].

Análogos didácticos, elementos finitos, estructuras en serie, dominios, nodos.

Abstract

This article presents a didactic development of three systems solution circuital analogs such as electric, magnetic and thermal which present a structural and functional correspondence in terms of the equations that govern their domains. The knowledge and use of a domain can serve as a support to facilitate teaching and learning a new domain called white [1], which share similar structures and equations of their behavior, thus, their physical responses resolve with same method, as in this case may be finite elements [2].

Analog teaching, FEM serial structures, domains, nodes.

Introducción

Al momento de abordar problemas de física referentes a formas que tienen diferentes dominios estructurales, pero que satisfacen ecuaciones matemáticas análogas, es decir, ecuaciones que al intercambiar términos de cada dominio resultan ser simétricas para una ecuación general, las leyes físicas que rigen estos sistemas son las mismas en esta simetría, y las soluciones del comportamiento que presentan se obtienen transponiendo términos en los diferentes campos de trabajo.

Puede utilizarse el recurso didáctico de analogías [1] para explicar los contenidos y facilitar el proceso de aprendizaje de nuevos conceptos de una manera comprensible para los alumnos, en razón a que la analogía guía a los alumnos en la construcción de un modelo mental inicial basado en la estructura de una temática familiar o conocida (dominio análogo) hacia una temática menos conocida (dominio blanco) [3]. El objetivo es que el estudiante trate de asimilar un objeto nuevo a uno preexistente. El ideal del docente sería, con estos parámetros, encontrar un análogo óptimo para cada temática del campo curricular.

Bajo la premisa de que el estudiante conoce el dominio análogo [4], se encuentran tres campos que se pueden abordar con analogías, si el estudiante conoce uno de ellos, como son: el eléctrico, magnético y térmico. Las ecuaciones que rigen estos campos parten del concepto genérico de resistencia, además de compartir los conceptos físicos de conservación de la energía, conservación de la masa y conservación de la carga eléctrica.

El empleo de analogías facilita la solución de los sistemas, toda vez que, aunque traten dominios diferentes, son aplicables tanto al dominio análogo como al dominio blanco [3].

En los sistemas mencionados, ellos pueden resolverse por sistemas de ecuaciones de las leyes de conservación y por resistencia equivalente. El objetivo de este documento es presentar la aplicación del método del elemento finito que se ha venido utilizando para la solución del modelo térmico unidireccional en la solución de voltajes a lo largo de un hilo conductor, empleando como material de referencia valores de potencial eléctrico en la frontera conocidos.

Este tipo de analogías permite obtener resultados de una forma alterna al método tradicional de solución; además, con ellas se puede encontrar un método de solución por elementos finitos en respuesta con régimen permanente, aplicable específicamente cuando se requieren respuestas en mallas finas de los elementos o estructuras en cada caso, como son:

1. Hilo conductor con una diferencia de potencial eléctrico entre extremos.
2. Barra compuesta por materiales soldados con diferencia de potencial térmico entre extremos.
3. Ventana magnética con una bobina enrollada en la misma y corriente circulante i por espira.

Descripción de las variables

En un hilo conductor como el de la Figura 1 se tiene que la resistencia eléctrica es

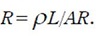
Figura 1. Hilo conductor.

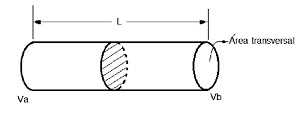
Además, satisface equivalentes resistivos en serie y en paralelo:

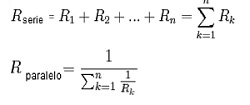
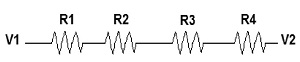
Si el conductor se secciona en cuatro resistencias eléctricas, el equivalente de circuito es:

Cumple la ley de Ohm:

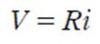. Y satisface ley de voltajes de Kirchhoff.

En un lazo cerrado

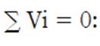
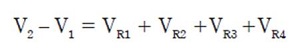
En una barra con secciones sólidas soldadas entre sí e igual sección transversal (Figura 2):

La resistencia térmica es

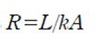
Satisface

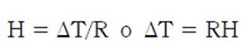
Figura 2. Paredes adyacentes.

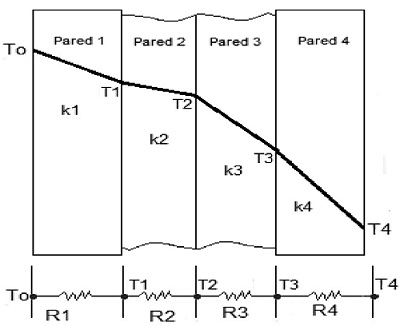
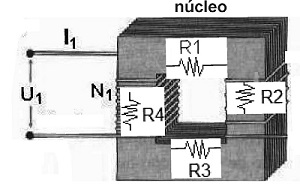
Figura 3. Ventana magnética con alimentación de fuerza magnetomotriz.

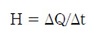
Además cumple ley de potenciales térmicos

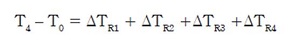
En una malla magnética como la de la figura 3 se tiene, según ley de Ampere sobre el lazo magnético [5], que:

La resistencia magnética, llamada reluctancia, es

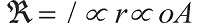
Satisface la ecuación

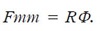. Donde

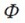es el flujo magnético que se establece en la ventana en

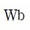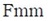, es la fuerza magnetomotriz o excitación magnética del sistema y es

La reluctancia equivalente es la suma de reluctancias de cada barra de la ventana. Se encuentra, entonces, que hay analogías resumibles en cada uno de los campos, como muestra la Tabla 1.

Tabla 1. Paralelo por estructura relacional de ecuaciones entre los campos térmico, eléctrico y magnético.

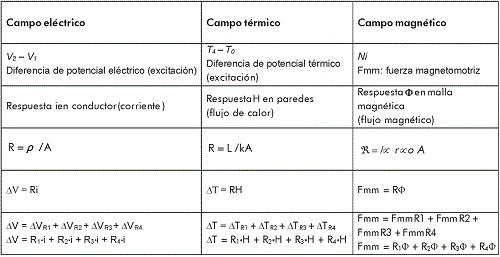
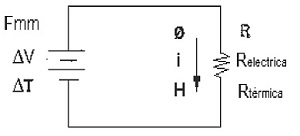
Así, para este caso, en cada campo el modelo de circuito equivalente es simplificable al mostrado en la Figura 4, donde cumple la ecuación general de equivalente en cada campo.

Figura 4. Estructura circuital equivalente.

Procedimiento

Para cada uno de los sistemas mencionados se tiene una condición problema similar y es la división de la estructura en tramos, para los cuales se busca evaluar el potencial eléctrico, térmico o de fuerza magnetomotriz, según el caso, dadas unas condiciones de caracterización de materiales, geometría y excitación energética en los extremos o fronteras de la estructura. Los datos experimentales se tomaron para uno de los tres casos, para lo cual se seleccionó el hilo conductor.

Campo eléctrico en un hilo conductor

Un hilo conductor de Constantan ,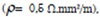

diámetro de 0,44 mm, se alimentó con una diferencia de potencial eléctrico de 1,46 Voltios. Se midió el potencial eléctrico cada 0,05 m a partir de la frontera de alimentación de mayor potencial hasta la frontera de menor potencial. La medición se hizo con un multímetro marca Fluke, calibrador y tornillo micrométrico, y se obtuvieron los valores mostrados en la Tabla 2.

Tabla 2. Valores experimentales de potencial eléctrico en frontera por tramo.

Figura 5. Puntos de voltaje en función de corriente.

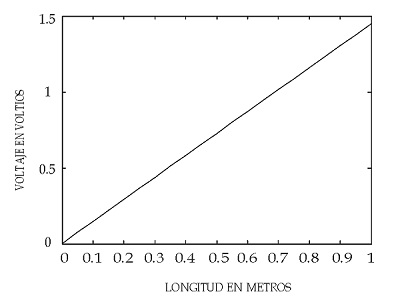
La Figura 5 muestra los puntos representados en la Tabla 1 medidos en el experimento.

Por fitting en Matlab® se obtiene la pendiente m = 1,4452 y b = 0,0037, con lo cual se ajustan los datos a la gráfica y se obtiene la Figura 6:

Figura 6. Resultado de fitting en Matlab® con datos experimentales.

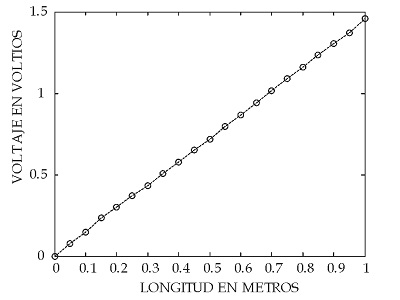
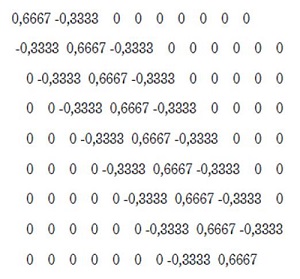
Para la solución por elementos finitos y herramienta computacional Matlab®, tomando los tramos seleccionados como referencia, se obtiene la matriz de rigidez de la estructura[ 6].

1. MATRIZ DE RIGIDEZ:

           

2. VECTOR DE FRONTERAS POR ELEMENTOS FINITOS:

           

3. VECTOR DE RESPUESTAS DE VOLTAJES POR ELEMENTOS FINITOS:

           

En la Figura 7 se muestran los resultados por elementos finitos del voltaje en función de la longitud frontera del conductor.

Figura 7. Voltajes en función de la longitud del conductor obtenidos por elementos finitos.

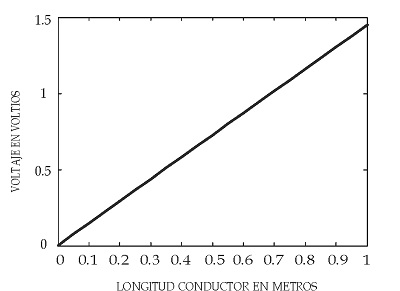
Conclusiones

Se puede corroborar en los resultados experimentales obtenidos que el método del elemento finito que se utiliza normalmente en el modelo de transferencia de calor por conducción, de Fourier, funciona muy bien para el modelo análogo del voltaje para un hilo conductor, [8].

El uso de analogías en la enseÑanza [8], particularmente de las ciencias, se puede extender a temáticas del currículo de las ciencias en Ingeniería, ya que permite abordar temas no conocidos a partir de bases conocidas por el estudiante y prever sus posibles dificultades, tarea que será más eficaz si el docente sabe escoger los dominios para la analogía – más familiar– y el blanco –menos conocido–. Es el caso de los sistemas eléctrico, térmico y magnético, cuyas ecuaciones de comportamiento físico son análogas y, por tanto, pueden inducir a conectar tales sistemas, relacionándolos y promoviendo la formación integral de conceptos que son básicos en ingeniería.

Es así como, dada la analogía presentada, y debido a que los métodos de solución son iguales también poseen soluciones simétricas para las variables análogas. En la solución del caso de estudio es posible aplicar, además, elementos finitos, que se hacen imprescindibles cuando se requieren datos para tramos con malla cada vez más fina.

Referencias

1. L. E. Richland y I. M. McDonough, “Learning by analogy”. Contemporary Educational
Psychology, 35, enero 2010.
2. Chandrupatla, “Elemento finito en ingeniería”, 2 ed. México: Pearson, 1999.
3. M. R. Otero, “Cómo usar analogías en Física”, Revista Iberoamericana de Educación 14(2), ,pp.179-187, agosto de 1997.
4. V. Sarina, I. K. Namukasa. “Toronto District School Board, Faculty of Education” . Ontario Canadá, 2010.
5. S. J. Chapman, “Máquinas eléctricas”, 3 ed. Bogotá: McGraw-Hill, 2000.
6. R. Burden y D. J. Faires, “Análisis numérico”, 1 ed. México: Interamericana, 1988.
7. W. H. Hayt. “Teoría electromagnética”, 2 ed. México: McGraw Hill, 1999.
8. A. E. Felipe y S. C. Gallarreta, “Aportes para la utilización de analogías en la enseÑanza de las ciencias”, Revista Iberoamericana de Educación, Vol. 6, número 37, 9 p., febrero 2006.