VISÓN HISTÓRICA

Visión Electrónica, 2013-06-01 Volumen:7, Año:1

VISÓN HISTÓRICA

JOHANN KARL AUGUST RADON: el nómada académico precursor matemático de la tomografía

Nació en Tetschen –cerca de Bohemia, en la actual República Checa, entonces parte del Imperio Austro-Húngaro–, el 16 de diciembre de 1887 y falleció en Viena el 25 de mayo de 1956. Estudió Matemáticas en la Universidad de Viena en 1905, con maestros de la talla de Hans Hahn, Wilhelm Wirtinger, Franz Mertens, entre otros. Sin embargo, fue con Gustav von Escherich –uno de los primeros austriacos en difundir los rigurosos fundamentos del Análisis Funcional de Weierstrass– que se inclinó por el cálculo variacional, tema de su tesis doctoral en 1910 titulada Sobre el mínimo de la integral 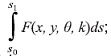; que se ocupa de las condiciones suficientes para su cálculo cuando aparecen derivadas de orden superior en los integrandos.

En 1913 apareció su célebre Teoría y aplicación de las funciones absolutamente aditivas, que trata de ecuaciones integrales, lineales y formas bilineales en diversas variables como un caso especial. Allí, combinó de manera original teorías de integración de Stieltjes, Lebesgue y Hellinger, por lo que logró generalizar la teoría de integración a la teoría de la medida, incluso llegando a considerar, tal vez de forma inconsciente, que una función Lebesgue integrable puede ser discontinua en todo punto; incluso, no necesita de un contexto topológico para ser introducida, pues solo precisa de un conjunto, una estructura de 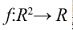-algebra y una medida.

En abril de 1917, durante su estancia en la Universidad Tecnológica de Viena, año en el que tuvo su primera hija –quien falleció casi de inmediato y marcó un trágico precedente ya que de su progenie, cuatro hijos, solo la última le sobrevivió y siguió el sendero de las Matemáticas–, en una reunión de la Sociedad Real de Física y Matemática de Sajonia, publicada bajo el título Sobre la definición de funciones por sus integrales a lo largo de ciertos planos, presentó la solución del problema inverso de cómo determinar una función de dos variables a partir de sus integrales de línea o, lo que es igual, enunció la transformada de Radon como la que mapea una función 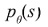en el conjunto de sus proyecciones 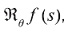. Dicha transformada, denotada como 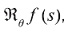, se expresa en términos de la distribución delta Dirac como:

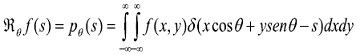
Como consecuencia de lo anterior, para reconstruir una imagen 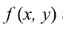a partir de las proyecciones será necesario invertir la transformada de Radon. Estos principios, reconocidos solo a finales de la década del sesenta, explican uno de los desarrollos tecnológicos más impresionantes del siglo XX: la imagenología médica, que previene, diagnostica y trata patologías o traumas, observando el interior del cuerpo humano de manera precisa y segura, menos invasiva si se compara con una cirugía. La expresión tecnológica de dicha matemática es lo que se conoce hoy como Tomografía Computarizada, temática por la que Cormack (1924-1998) y Hounsfield (1919-2004) obtuvieron el premio Nobel en 1979; los Tomógrafos siguen su sofisticada marcha de última generación en el siglo XXI.

Radon continuó su errante vida académica de 1919 a 1947 en Hamburgo, Viena, Greifswald, Erlangen, Breslau, –ciudad polaca sitiada y bombardeada por Rusia en la segunda Guerra Mundial–, y brevemente en Innsbruck. Por último, se instaló de nuevo en la Universidad de Viena, donde permaneció el resto de su vida ejerciendo como decano y luego como rector, desde 1954 hasta su muerte. Radon fue miembro de la Academia de Ciencias de Austria, presidente de la Sección de Matemática y Física, y se desempeñó como presidente de la Sociedad Matemática de Austria; siempre con el interés de divulgar sus logros, por ejemplo a través de las revistas especializadas como la que fundó con el nombre de Monatshefte für Mathematik.

Pero la mejor muestra de su temple radicó en que ejerció la docencia universitaria, de alto nivel, en los múltiples lugares en que vivió; padeció penurias aplastantes en dos brutales Guerras Mundiales, que superó estoicamente y con cuerda para tener fresco el espíritu de su gusto por el arte y la literatura, bien pudo ser un talentoso cantante barítono, con talla de cantante de ópera, un hábil navegante o músico de jerarquía en la ejecución del laúd o el violín. Por todo lo anterior, será recordado como reconstructor de la escena matemática austriaca, enhiesto ante semejantes condiciones históricas.

En 2003, la Academia de Ciencias de Austria inauguró el Instituto de Matemática Computacional y Aplicada, que actualmente promueve el papel de las matemáticas en la ciencia, la industria y la sociedad. Es decir, tareas que se corresponden con el impacto del modelo de Johann Radon en los logros tecnológicos de la bioingeniería actual y futura, significado que lejos está de la facilidad.

Harold Vacca G.