DOI:
https://doi.org/10.14483/22484728.800Publicado:
2008-12-02Número:
Vol. 2 Núm. 2 (2008)Sección:
Visión de ContextoLos conjuntos borrosos, modelación cualitativa de la realidad en ingeniería
Fuzzy Sets, Qualitative Modeling Of The Reality In Engineering
Palabras clave:
Incertidumbre, conjunto borroso, nociones, relaciones, aplicaciones. (es).Palabras clave:
Uncertainty, Set Fuzzy, notions, relationship, applications. (en).Descargas
Referencias
Ballester L, y Colom A. Cañellas.( 2006). "Lógica difusa: Una nueva epistemología para las Ciencias de la Educación", en Revista de Educación No. 340. Universidid de las Islas Baleares: Área de Teoría e Historia de la Educación.
Beliakov,Gleg. theorical básic of a fuzzy expert system for medical diagnostics. uniandes: Santafé de Bogotá , 1.994.
Bordogna, G. y Pasi, G. (2000). "Application of fuzzy set theory to extend boolean information retrieval. In Soft Computing in Information Retrieval: techniques and applications".
Braunstingl, R, Mujika, J. y J.P. Uribe. (1995). "A wall, following robot with a fuzzy logic controller optimized by a genetic algorithrn". En Proceedings of the International Joint Conference of the Fourth IEEE Intérnational Conference on Fuzzy Systems and the Second International Fuzzy Engineering Symposium, tomo 5, págs. 77-82
Cariñena, P. (2003). "Un modelo de reglas temporales borrosas para el razonamiento sobre sistemas dinámicos". Santiago de Compostela: Tesis doctoral.
Kaufmann, Arnold. Introduction to the theory of fuzy subsets. Academie press: New York, 1.975. vol. 1. Kaufmann, a.; Gupta, m.m. (1985). "Introduction to Fuzzy Arithmetic". New York.: Van Nostrand Reinhold.
Klir, George j. fuzzy sets uncertainty and information. prentice-hall: New York, 1.988.
Kruse,r. J, Gebhardt, F. Kiawonn. Foundations of Fuzzy Systems. Jhon Wiley & sons, 1994. ISBN 0-471-94243 X.
López Martínez. C. (2004). "Aplicación de la Lógica Difusa en Robótica". Madrid, España: Programa de Doctorado: Diseño, Análisis y Aplicaciones de Sistemas Inteligentes.UB, España.
Mariño Sarmiento, Rafael, teoría de conjuntos. Universidad nacional de Colombia: Santafé de Bogotá, 1.978.
Martín F., Matellán V., Barrera P., Localización basada en logica difusa y filtros de Kalman para robots con patas. Grupo de Robótica, Universidad Rey Juan Carlos, Madrid, 2004.
Muñoz Quevedo, José Maria. Introducción a la teoría de conjuntos. Universidad Nacional de Colómbia: Santa fe de Bogotá, 1.983.
Rairán, A. D. (2007). "Implementación de uñ controlador Difuso para la regulación de posición de un cilíndrico hidráulico lineal". Bogotá D: C. Tecnura No 19 pp. 18 -- 28.
Zadeh, :Lotfi . Advances in fuzzy set theory and aplications. Acadernic press: -New York, 1.978.
Fuzzy sets and their áplications to cognitive and, decision proCbsses.
Academie preás:- New York, 1.975.
Linear system theory: the átate space approach. Mc-Graw Hill: New York, 1.969. System theory; Mc-Graw hill: New York,4.969.
Infografia
http://www.lpa.co.uk/fht htmhttp://www.hyperlogic.com
http://www.ortech-engr.com/fuzzy/togai.html.
http://décsai.ugnes/difuspdsoftware/software_pscar95.html
http://www.fuzzy-logie.comiffitzy_logic__110.html
Recursos de Software Asociado:
Fuzzy Logic 2.0 -,- Requiere Matemática
PAI (Programa para Automatización Inteligénte) creado con el software LabWindows/CVITM y validado para ser utilizado en ambientes universitarios o industriales.
UNFUZZY L2 Software para el Análisis, Diseño, SiMulación e Implerhentación deSisterilas de Lógica Difusa.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visión de Contexto
Visión Electrónica, 2008-05-00 nro:2 pág:98-108
LOS CONJUNTOS BORROSOS, MODELACIÓN CUALITATIVA DE LA REALIDAD EN INGENIERÍA
FUZZY SETS, QUALITATIVE MQDELING OF THE REALITY IN ENGINEERING
Jaime Francisco Pantoja Benavides
Licenciado en Matemáticas, Universidad Distrital Francisco José De Caldas, Especialista en Estadística de la Universidad Nacional de Colombia, vinculado al grupo "Robótica Móvil Autónoma ROMA de la (UDFJDC) reconocido por COLCIENCIAS, como investigador auxiliar. Docente adscrito a la Facultad Tecnológica de la Universidad Distrital Francisco José de Caldas. jfpantojab@udistrital. edu.co
Harold Vacca González
Lic. En Matemáticas de la Universidad Distrital, Especialista en Ingeniería del Software de la misma Universidad. Coinvestigador del grupo UDINEX reconocido por Centro de Investigaciones de la Universidad Distrital CIDC. Docente adscrito a la Facultad Tecnológica. de la Universidad Distrital Francisco José de Caldas. hvacca@udistrital.edu. co
Resumen
El artículo hace explícitas una serie de ideas, con ejemplos y gráficos, que le permitarán al lector asimilar un giro en el enfoque aplicativo de la Teoría de Conjuntos Clásica hacia los Conjuntos Borrosos con la extensión de nociones de inclusión, unión, intersección, complemento, relación, etc. Este nuevo marco formal, permite el tratamiento y la manipulación de la incertidumbre en el ámbito de modelación de numerosos fenómenos, particularmente de Control. Sea esta una motivación adicional para inducir la incorporación del tema en los currículos de tecnología e ingeniería, a partir del estudio sistemático de situaciones problema de la Electrónica, el Control y las Telecomunicaciones.
Palabras clave
Incertidumbre, Conjunto borroso, nociones, relaciones, aplicaciones.
Abstract
This paper presents a set of clear ideas through examples and graphs to allow the reader to assimilate a change in the approach of the Theory of Sets, emphasizing the importance of Fuzzy Sets extending the notions of inclusion, intersection, complement, relationship, etc. as normal frame to permit the treatment and manipulation of the uncertainty in the ambit of a number of phenomena, particularly in Control. This is an additional motivation to induce the incorporation of this subject into the curricula of both, technology and engineering, through the systematic study of typical problems in Electronics, Control, and telecommunications.
Key Words
Uncertainty, Set Fuzzy, notions, relationships, applications
Introducción
La idea básica que subyace al desarrollo de la ciencia es la búsqueda de la verdad; pero en la mayoría de las concepciones desarrolladas por los académicos de todas las épocas se supone una intrínseca dicotomía entre verdadero y falso. Matemáticamente hablando, esta oposición implica la validez de dos leyes fundamentales: toda proposición es verdadera o falsa y no cabe otra posibilidad; y ninguna proposición es verdadera y falsa simultáneamente. Ello, generó una serie de paradojas e insatisfacciones que le dieron paso a la necesidad de superar esta estricta bivalencia veritativa de la lógica clásica.
Filosóficamente, hasta que aparece la concepción de la falsabilidad Popperiana, una teoría será verdadera si es satisfactoria para describir un dominio dado de la realidad, y en la lógica, Luckasiewicz, en 1920, propuso tres valores veritativos para las proposiciones: verdadero, falso e indeterminado. Es decir, se hizo necesario un replanteamiento radical de los conceptos clásicos de verdad y falsedad, Sustituyéndolos por el concepto de vaguedad o borrosidad, dentro de los cuales la verdad y/o falsedad no son más que casos extremos. Por borrosidad entendemos el hecho de que una proposición pueda ser parcialmente verdadera y parcialmente falsa de forma simultánea. Es decir, se deben involucrar nuevas nociones como el uso de variables lingüísticas, algoritmos, cuantificadores y predicados de carácter difuso; para decidir sobre la realidad, dando origen así a una lógica polivalente [2], generatriz de la Teoría de Conjuntos Borrosos. Según Lotfi Zadeh (Pionero de la teoría de conjuntos borrosos) al abordar el estudio de fenómenos y a medida que la complejidad de un sistema aumenta, nuestra capacidad de realizar formulaciones precisas y significativas sobre su comportamiento disminuye hasta que se alcanza un umbral por debajo del cual la precisión y la relevancia se convierten en características mutuamente excluyentes. [14]. Éste es el "principio de incompatibilidad".
En ingeniería, donde frecuentemente el pensamiento dinámico intenta formular simbólicamente sistemas mentales, la incompatibibilidad de las variaciones en los fenómenos implica el arte de modelar en la presencia de grados de incertidumbre, es decir, producir modelos matemáticos que simulen ciertos subprocesos que ocurren en la realidad; poniéndolos a prueba, ajustándolos, comparándolos y generalizándolos o descartándolos, con esta reciente tecnología socialmente disponible de los conjuntos borrosos.
1. Noción de Conjunto Borroso
El proceso por el cual se determina si los elementos del conjunto referencial X son o no miembros de un conjunto, puede definirse por una función característica. Para un conjunto dado A, esta función asigna un valor μA (x) a cada tal que:
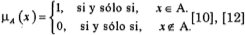
Así, la función envía los elementos del conjunto referencial al conjunto cuyos elementos son O o 1. Esto puede indicarse por μA: →{0,1},. Esta función puede generalizarse, de tal forma que los valores asignados a los elementos del conjunto referencial caigan dentro de un rango específico, e indiquen el grado de pertenencia de estos elementos con respecto al conjunto en cuestión. Los valores más grandes denotan más altos grados de pertenencia al conjunto. Tal función se llama función de pertenencia o de membresía [13], y el conjunto definido por ella se llama conjunto borroso. [6], [14].
Figura 1. Función de pertenencia "Valores cercanos a cero"
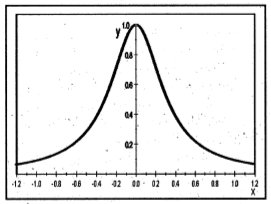
Definición 1. Un conjunto borroso  en un espacio de puntos X, es una clase de eventos con un continuo grado de pertenencia y se caracteriza por una función de pertenencia μÂ(x) , la cual asocia a cada punto de X un número real en el intervalo [0,1], es decir μÂ(x) X→[0.1]. [12]
Por ejemplo se puede definir una posible función de pertenencia para el conjunto borroso de números cercanos a cero, como [7]:
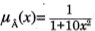 (1)
(1)
Usando esta función, se puede determinar el grado de pertenencia de cada número real en este conjunto borroso, que significa el grado en el cual ese número es cercano a cero, es decir, al número 1.2 se le asigna un grado de 0.055, al número 1 un grado de 0.09, al número 0.25 un grado de 0.62 y al número O un grado de 1.
2. Conceptos básicos de conjuntos borrosos
Aquí se trataran extensiones y generalizaciones de los conceptos básicos de conjuntos clásicos [10], [12], y otros únicos para el marco de conjuntos borrosos. Para ilustrar algunos de los conceptos, se consideran los grados de pertenencia de los elementos de un conjunto referencial en cuatro conjuntos borrosos diferentes, como se muestra en la tabla 1. Aquí, el conjunto referencial clásico X de edades, que se ha seleccionado, es como se muestra en (2). Y los conjuntos borrosos nominados: niño, adulto, jóven y viejo conceptos vagos o del lenguaje cotidiano, son cuatro de los elementos del conjunto potencia que consta, de todos los subconjuntos borrosos posibles de X y se denota ℘(x) análogo al concepto de conjunto potencia ℘(x) la teoría de conjuntos clásica, formado por todos los posible subconjuntos de X [6]:
(X)={5,10,20,30,40;50,60,70,80} (2)
Tabla 1. Conjuntos borrosos
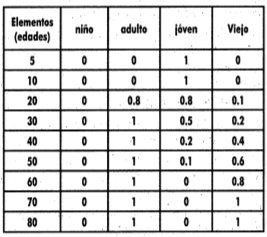
El soporte de un conjunto difuso  en el conjunto referencial X, es el conjunto clásico que contiene todos los elementos de X que tiene grado de pertenencia diferente a O en Â. Esto es, los soportes de los conjuntos borrosos en X se obtienen por la función 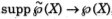 , donde
, donde
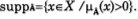 .
.
Por ejemplo, en la tabla 1, el soporte del conjunto borroso jóven es el conjunto supp, (jóven)={5,10,20,30,40,50}. Un conjunto borroso vacío tiene un soporte vacío, como el conjunto borroso niño, supp (niño)=1 }
Sea xi un elemento del soporte (finito) del conjunto borroso  , y,  su grado de pertenencia en Â, entonces,  se escribe como  = μ1 / X1 + μ2 / X2 + ••• + μn / Xn donde / se emplea para unir los elementos del soporte con sus grados de pertenencia en Â. Para el caso en el cual un conjunto borroso &Acir;se define sobre un conjunto referencial que es finito y contable, podemos describir
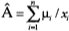 (3)
(3)
Análogamente, cuando X es un intervalo de números reales, un conjunto borroso A se escribe a menudo de la forma
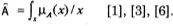 (4)
(4)
La altura de un conjunto borroso es el grado de pertenencia más grande ostentado por cualquier elemento en ese conjunto. Un conjunto borroso se llama normalizado [2], [6], cuando al menos uno de sus elementos ostenta el grado de pertenencia máximo posible. Si por ejemplo, los grados de pertenencia caen en el intervalo cerrado [0,1], entonces, al menos un elemento debe tener el grado de pertenencia de 1 para que el conjunto difuso sea considerado normalizado. Claramente, esto también implica que la altura del conjunto borroso es 1. Los tres conjuntos borrosos: adulto, jóven y viejo, de la tabla 1., al igual que el definido en la Figura 1, son normalizados.
Un α– corte, [2], [6], de un conjunto borroso  es un conjunto clásico Âα que contiene todos los electos del conjunto referencial X, que tiene un grado de pertenencia en  mayor o igual al valor especificado de α. Esto es, Âα = {x∈ X / μA (x) ≥α}, el valor α puede escogerse arbitrariamente, pero se toma a menudo de los valores de los grados de pertenencia que aparecen en el conjunto borroso en consideración. Por ejemplo, para α =0.2, el α– corte del conjunto borroso jóven, de la Tabla 1., es el conjunto clásico, jóven0.2 = {5, 10,20,30,40}:

Obsérvese, que el conjunto de todos los α– cortes de cualquier conjunto borroso sobre X, es una familia de subconjuntos de X. El conjunto de todos los niveles α∈[0,1], que representan distintos α– cortes de un conjunto borroso dado Â, se llama conjunto nivel en  [2], [6]. Formalmente ∧A = {α / μA, (x)= α para x ∈ X} donde denota el conjunto nivel del conjunto ÂA definido sobre X.
La cardinalidad escalar, [2], [6], de un conjunto borroso Â, definido sobre algún conjunto referencial finito X, es la sumatoria de los grados de pertenencia de todos los elementos de X en Â. Así,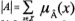 de esta manera, la cardinaLidad escalar del conjunto borroso viejo de la tabla 1. Es:
de esta manera, la cardinaLidad escalar del conjunto borroso viejo de la tabla 1. Es:
|viejo|=0+0.1+0.2+0.4+0.6+0.8+1+1=4.1, y la cardinalidad del conjunto borroso niño es 0.
La cardinalidad borrosa se define más como un número difuso que como un número real, como es el caso de la cardinalidad escalar. Cuando un conjunto borroso  tiene un soporte finito, su cardinalidad difusa |Ã| es un conjunto borroso (número borroso (3)), definido sobre los naturales, cuya función de pertenencia está dada por 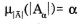 para todo α∈∧A.
para todo α∈∧A.
La cardinalidad difusa del conjunto difuso viejo de la tabla 1. Es:

Si el grado de pertenencia de cada elemento de un conjunto borroso  es menor o igual que el grado de pertenencia de cada elemento de un conjunto difuso  [6], [4]. En otras palabras
[6], [4]. En otras palabras 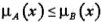 para cada x ∈ X
para cada x ∈ X
El conjunto borroso viejo, en la tabla 1, es un sulbconjünto del conjunto borroso adulto, ya que cada elemento en el conjunto referencial cumple con: μviejo (x) ≤ μ adulto (x).
Los conjuntos borrosos  y  se dicen iguales si
se dicen iguales si 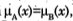 para todo x ∈ X denotado  =
para todo x ∈ X denotado  =  . si los conjuntos borrosos Â
. si los conjuntos borrosos   no son iguales porque
no son iguales porque
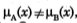 , para algún x ∈ X , denotado  ≠
, para algún x ∈ X , denotado  ≠ 
El conjunto borroso  se llama subconjunto propio del conjunto borroso  cuando A en un subconjunto de
cuando A en un subconjunto de  y los dos conjuntos son diferentes, esto es,
y los dos conjuntos son diferentes, esto es, 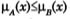 para cada
para cada
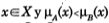 para almenos, un x ∈X así Â ⊆
para almenos, un x ∈X así  ⊆  y  ≠
y  ≠ 
Se mencionó que el conjunto borroso viejo de la tabla 1 es un subconjunto borroso del conjunto borroso adulto y que estos dos conjuntos borrosos no son iguales, por consiguiente, viejo es un subconjunto propio de adulto.
Cuando los grados de pertenencia caen en el intervalo cerrado [0,1], se denota el complemento borroso,[2], [6], [7], con respecto al conjunto referencial X por à y se define μ Ã(x) = 1− μ A, (x) para cada x ∈ X.
Así, si un elemento tiene grado de pertenencia de 0.8 en un conjunto A, su grado de pertenencia en à será 0.2.
La unión de dos conjuntos  y  es un conjunto borroso  ∪
es un conjunto borroso  ∪  , tal que:
, tal que:
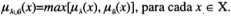
Así que, el grado de pertenencia de cada elemento del conjunto universal en à ∪  es el grado de pertenencia en Â; o el grado de pertenencia en
es el grado de pertenencia en Â; o el grado de pertenencia en  , el que sea mayor entre los dos. De lo cual se concluye que los conjuntos borrosos Â; y
, el que sea mayor entre los dos. De lo cual se concluye que los conjuntos borrosos Â; y  son subconjuntos del conjunto borroso Â; ∪
son subconjuntos del conjunto borroso Â; ∪  , [6], [7] y [14].
, [6], [7] y [14].
Por ejemplo, sean los jóven y viejo de la tabla 1, se obtiene el siguiente conjunto borroso: jóven ∪ viejo = 1/5+1/10+0.8/20+ 0.5/30+0.4/40+0.6/50+0.8/60+1/70+1/80
La intersección de conjuntos borrosos  y es un conjunto borroso  ∩
es un conjunto borroso  ∩ 
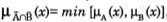 para cada x ∈ X.
para cada x ∈ X.
Aquí, el grado de pertenencia de cada elemento del conjunto universal en Â∩ es el grado de pertenencia más pequeño de cada uno de los grados de pertenencia en  y en
es el grado de pertenencia más pequeño de cada uno de los grados de pertenencia en  y en  . Como es de esperarse, el conjunto borroso Â∩
. Como es de esperarse, el conjunto borroso Â∩ es un subconjunto tanto de  como de
es un subconjunto tanto de  como de  .
.
Por ejemplo, sean los conjuntos joven y viejo de la tabla 1, se obtiene el siguiente conjunto borroso: jóven ∩ viejo = 1/5+1/10+0.8/20+ 0.5/0/10+0.1/20+0.2/30+0.2/30+0.2/40+0.1/ 50+0/60+0/70+0/80
Estas formulaciones originales de complemento, unión e intersección borrosa actúan de forma análoga a los correspondientes operadores de conjuntos clásicos, cuando los grados de pertenencia están restringidos a los valores O y 1.
Un principio básico que permite la generalización de conceptos matemáticos clásicos al marco borroso, se conoce como el principio de extensión. Este brinda el medio para que cualquier función f que aplica puntos x1, x2,...,xn del conjunto clásico X en el conjunto clásico Y; se generalice, tal que aplique subconjuntos borrosos de X en Y. Formalmente, dada una función f que aplica puntos de X en puntos de Y, para cualquier conjunto borroso  ∈ ℘ donde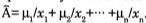 . El principio de extensión indica que:
. El principio de extensión indica que:
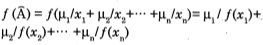
Si más de un elemento de X es enviado por f al mismo elemento y ∈ Y, entonces, el máximo de los grados de pertenencia de estos elementos en el conjunto difuso Â, se escoge como el grado de pertenencia para Y en f (Â). Si ningún elemento x ∈ Y se aplica en
Como una ilustración simple del uso de este principio, suponga que f es una función que envía pares ordenados de X1{a,b,c} y X2 ={x,y} en Y={p,q,r}. Sea f, especificada por la siguiente matriz:
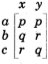
Sea Â1 un conjunto borroso sobre X1 y sea  un conjunto borroso definido sobre X2 tales que: A1 = 0.8 /a+0.9 /b+0.6 /6, y A2= 0.6 /x+1 /y.
Los grados de pertenencia de p, q y r en el conjunto difuso B= f(A1, A2) ∈ ℘ (Y), pueden ser calculados a partir del principio de extensión como sigue:
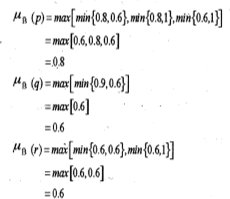 (5)
(5)
3. Relaciones difusas
Las nociones de gráfica, correspondencia y relación juegan un papel importante en las aplicaciones de la matemática, por ejemplo, el concepto de clase de equivalencia (en conjuntos clásicos, [12], [10]). Este, será reemplazado por una semejanza fuerte y más apta para representar algunas situaciones menos precisas, pero que se encuentran más frecuentemente. El ingeniero investigador, considerará esta opción, para medir la igualdad de ciertos objetos presentes en fenómenos, hasta cierta propiedad de incertidumbre, propicia para fenómenos complejos.
Definición 2. Una relación borrosa es un conjunto borroso definido sobre el producto cartesiano de conjuntos ordinarios X1, X2,...,Xn, donde las n-uplas (x1,x2,...,xn) pueden tener grados diferentes de pertenencia en la relación. Este grado de pertenencia es representado usualmente por un número real contenido en el intervalo cerrado [0,1] e indica la relación presente entre los elementos de la n-uplas, [6], [7], [14].
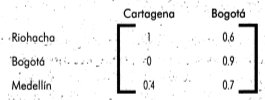
Ejemplo Sea ℜ una relación borrosa entre dos conjuntos, X ={Bogotá, Cartagena}, y Y={Rioacha, Bogotá, Medellín},que representa el concepto de relación "muy lejos". Esta relación puede escribirse:

Cuya matriz de pertenencia se muestra en la tabla 2
tabla 2. Matriz de pertenencia
3.1. Relaciones binarias
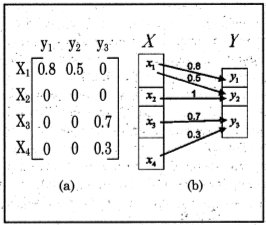
Definición 3. A toda relación entre dos conjuntos X e Y se le denomina binaria. Esta se denota por ℜ(X, Y)(4) y para su representación, se puede acudir a una matriz de pertenencia o a un diagrama sagital, como las mostradas en la figura 2.
Figura 2. Ejemplo de representación de una relación binaria borrosa:
(a) Matriz de pertenencia; (b) Diagrama sagital
3.1.1. Relaciones binarias sobre un conjunto único
Así como se definió una relación binaria entre dos conjuntos diferentes, también es posible hacer una definición análoga entre los elementos de un mismo conjunto X. Dicha relación puede denotarse por ℜ(X,X).
Una relación ℜ(X,X) puede también ser expresada como las relaciones binarias generales (diagramas sagitales, matrices). Sin embargo, se pueden representar convenientemente por medio de diagramas simples que cumplan con las siguientes condiciones:
- Cada elemento del conjunto X se representa por un único nodo.
- Las conexiones dirigidas entre nodos indican pares de elementos de X con grado de pertenencia en ℜ diferente de cero.
- Cada conexión en el diagrama se denomina por el grado de pertenencia actual del par correspondiente en ℜ.
Figura 3. Formas de representación de una relación borrosa ℜ(X,X)
(a) Diagrama sagital; (b) Diagrama simple; (c) Matriz de pertenencia; (d) Tabla
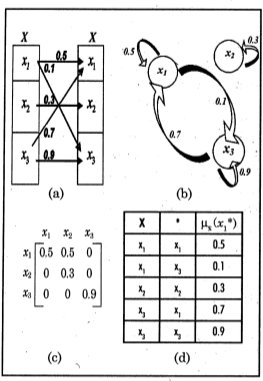
En la figura 3, se describe una relación ℜ(X,X), definida sobre X={x1,x2,x3}, en sus diferentes formas de representación, [6], [7], [14].
Definición 4. Una relación clásica ℜ(X,X) es reflexiva, si y sólo si, (x, x) ∈ ℜ para todo x∈X. Una relación borrosa ℜ(X,X) es reflexiva, si y sólo si, μ ℜ(x, x) = 1 para todo x∈X. En cada una de las teorías, si éste no es caso para algún x∈X, entonces, la relación se llama irreflexiva.
Definición 5. Una relación clásica ℜ(XX) es simétrica, si y sólo si, (x,y) ∈ ℜ se tiene también (y,x) ∈ ℜ, para todo x,y ∈X. Si este no es caso para cada x, y ∈ X, entonces, la relación se llama asimétrica. Si (x, y) ∈ ℜ ó (y,x) ∈ ℜ, siempre que x≠y, entonces la relación se llama estrictamente antisimétrica.
Análogamente, para la teoría borrosa, ℜ(X,X) es simétrica, si y sólo si, μℜ (x,y) = μℜ x), para todo x, y ∈X .
Definición 6. En la teoría clásica, ℜ(X,X) es transitiva si y solo si (x,z) ∈ ℜR siempre que (x,y) ∈ ℜ y (y, z) ∈ ℜ, para al menos un y∈X. Una relación que no satisface esta propiedad se llama no transitiva.
Si se trabaja en la teoría borrosa, ℜ(X,X) es transitiva (más específicamente transitiva max-min) si y sólo si, μ ℜ(x,z)>max min[μℜ(x,y), μℜ (y, z)],[1], se satisface para cada par (x,z)∈ ℜ(X,X) . Si no se cumple la anterior inecuación para alguno de los miembros de X, se llamará no transitiva(5).
Ejemplo. Dada ℜ una relación borrosa definida sobre el conjunto de colegios, que representa el concepto "muy cerca", ella cumple:
- Relación reflexiva. Ya que se puede asumir que un colegio está "muy cerca" de si mismo (por ejemplo, a un grado de 1).
- Relación simétrica. Si un colegio X está "muy cerca" de un colegio Y, entonces, Y está ciertamente "muy cerca" al colegio X (al mismo grado).
- Relación no transitiva. Si el colegio X está "muy cerca" al colegio Y, por ejemplo a un grado de 0.6, y el colegio Y está "muy cerca" al colegio Z, a algún grado, digamos 0.6, es posible (aunque no necesario), que X esté "muy cerca" al colegio Z a un grado más pequeño, por ejemplo 0.4, [6], [7].
4. Aplicaciones
El uso de conjuntos borrosos en el área de control fue una de las primeras aplicaciones prácticas del paradigma, [8]. Debido a su naturaleza cualitativa; es posible utilizar controladores sobre diferentes plataformas sin realizar muchos cambios. Los resultados de investigación, se aprecian en control de ascensores (Toshiba), sistemas de diagnóstico de golf (Maruman Golf), video cámaras (Sony/Canon), lavadoras (Matsushita), aspiradoras (Matsushita), calentadores de agua (Matsushita), aire acondicionado (Mitsubishi), inversiones (Yamaichi Securities), etc. Igualmente, utilizando modelos no lineales aproximados para la regulación de posición de dispositivos, se han planteado intuitivamente conjuntos borrosos como error y velocidad... Junto a ello, la adquisición de datos en tiempo real utilizando Software como Lab View enlazado por Script con la simulación del controlador borroso a través del Toolbox de Matlab®, v. [13], facilita, cuando se conocen los universos de entrada (error, velocidad, etc.) y salida (voltajes, presiones, etc); la selección de funciones de pertenencia ( triangulares, trapezoidales, sigmoideas); los métodos (Mamdani o Su geno), y las relaciones.
La teoría de conjuntos borrosos también ha demostrado recientemente ser una herramienta especialmente útil en la investigación en robótica, dada la presencia de incertidumbre en el conocimiento que se tiene del entorno del móvil, en dos sentidos: observar la imprecisión debida a la dificultad de caracterizar una medida en un valor concreto (conjunto Crisp) y la recurrente falta de evidencia, debida al conocimiento incompleto [9]. Es posible entonces medir de esta nueva manera: la auto-localización, los Comportamientos (evitar obstáculos fijos, seguir un contorno, evitar obstáculos móviles, cruzar puertas, seguir una trayectoria, empujar o cargar un objeto, etc., v [4]), las Geometrías, las Topologías, la Navegación, la percepción y el aprendizaje, y [11].
Desde lo particular, un problema básico en robótica es la planificación de los movimientos para resolver alguna tarea ya especificada, y el control del robot mientras ejecuta las órdenes necesarias para lograr unos objetivos. Para una máquina, la clasificación de rostros, datos médicos o reconocimiento de letras son tareas difíciles, más que para un ser humano, y necesita del aprendizaje de estructuras borrosas, donde el asunto consiste en adaptar los parámetros de un sistema, en este caso artificial, para obtener la respuesta deseada, [9]. Para ello basta modelar: los Comportamientos a través del Diseño de Comportamientos, Coordinación. de Comportamientos, Fusión de comportamientos, y Arbitraje de comportamientos. La Geometría y la Topología, a través de la constitución de regiones denominadas segmentos difusos de posibilidad, que definen las fronteras de un espacio georeferenciado, v. [11](6). La Navegación, desde la información recogida a través de los conjuntos borrosos se representa la incertidumbre en la localización real de los objetos al ejecutar un conjunto de reglas de inferencia borrasy defuzzificar los resultados. La Percepción a través de la detección de características del entorno (luz del ambiente, complejidad del entorno) mediante un sistema de visión, por ejemplo, una cámara de video de cuyo producto se trata la imagen en tiempo real. El Aprendizaje sobre una población de reglas borrosas, por el cual se aprenden a coordinar los comportamientos produciendo meta-reglas difusas que determinan el contexto en el que será activado cada comportamiento [11].
Referencias bibliográficas
- Ballester L, y Colom A. Cañellas.( 2006). "Lógica difusa: Una nueva epistemología para las Ciencias de la Educación", en Revista de Educación No. 340. Universidid de las Islas Baleares: Área de Teoría e Historia de la Educación.
- Beliakov, Gleg. theorical básic of a fuzzy expert system for medical diagnostics. uniandes: Santafé de Bogotá, 1.994.
- Bordogna, G. y Pasi, G. (2000). "Application of fuzzy set theory to extend boolean information retrieval. In Soft Computing in Information Retrieval: techniques and applications".
- Braunstingl, R, Mujika, J. y J.P. Uribe. (1995). "A wall, following robot with a fuzzy logic controller optimized by a genetic algorithrn". En Proceedings of the International Joint Conference of the Fourth IEEE Intérnational Conference on Fuzzy Systems and the Second International Fuzzy Engineering Symposium, tomo 5, págs. 77-82
- Cariñena, P. (2003). "Un modelo de reglas temporales borrosas para el razonamiento sobre sistemas dinámicos". Santiago de Compostela: Tesis doctoral.
- Kaufmann, Arnold. Introduction to the theory of fuzy subsets. Academie press: New York, 1.975. vol. 1. Kaufmann, a.; Gupta, m.m. (1985). "Introduction to Fuzzy Arithmetic". New York.: Van Nostrand Reinhold.
- Klir, George j. fuzzy sets uncertainty and information. prentice-hall: New York, 1.988.
- Kruse,r. J, Gebhardt, F. Kiawonn. Foundations of Fuzzy Systems. Jhon Wiley & sons, 1994. ISBN 0-471-94243 X.
- López Martínez. C. (2004). "Aplicación de la Lógica Difusa en Robótica". Madrid, España: Programa de Doctorado: Diseño, Análisis y Aplicaciones de Sistemas Inteligentes. UB, España.
- Mariño Sarmiento, Rafael, teoría de conjuntos. Universidad nacional de Colombia: Santafé de Bogotá, 1.978.
- Martín F., Matellán V., Barrera P., Localización basada en logica difusa y filtros de Kalman para robots con patas. Grupo de Robótica, Universidad Rey Juan Carlos, Madrid, 2004.
- Muñoz Quevedo, José Maria. Introducción a la teoría de conjuntos. Universidad Nacional de Colombia: Santa fe de Bogotá, 1.983.
- Rairán, A. D. (2007). "Implementación de un controlador Difuso para la regulación de posición de un cilíndrico hidráulico lineal". Bogotá D: C. Tecnura No 19 pp. 18-28.
- Zadeh, Lotfi. Advances in fuzzy set theory and aplications. Acadernic press: New York, 1.978.
- Zadeh, lotfi. Fuzzy sets and their aplications to cognitive and, decision processes. Academie preas:- New York, 1.975.
- Zadeh, Lotfi. Linear system theory: the atate space approach. Mc-Graw Hill: New York, 1.969. System theory; Mc-Graw hill: New York,4.969.
Infografía
- http://www.lpa.co.uk/fht htmhttp://www.hyperlogic.com
- http://www.ortech-engr.com/fuzzy/togai.html .
- http://décsai.ugnes/difuspdsoftware/software_pscar95.html
- http://www.fuzzy-logie.comiffitzy_logic__110.html
- Recursos de Software Asociado
- Fuzzy Logic 2.0 -Requiere Matemática-.
- PAI (Programa para Automatización Inteligénte) creado con el software LabWindows/CVI TM y validado para ser utilizado en ambientes universitarios o industriales.
- UNFUZZY L2 Software para el Análisis, Diseño, SiMulación e Implementación de sistemas de Lógica Difusa.
Notas
(3)El concepto de "número borroso" es el fundamento de la "aritmética borrosa", que puede ser examinada como una extensión de intervalo aritmético, [4], [3]. Entre otras aplicaciones, los números borrosos son esenciales para la expresión de los cardinales borrosos y consecuentemente los cuantificadores borrosos. La aritmética borrosa es un instrumento básico para relacionar los cuantificadores borrosos con la aproximación al razonamiento, esto es también una base para el desarrollo para un cálculo difuso [I]. Para una ampliación solamente sobre este tema ver [5].
(4) El símbolo ℜ se usa como xℜy cuando (x,y) ∈ ℜ(x,y); para las relaciones difusas se escribirá w/xℜy cuando μℜ(x,Y)= w.
(5) Las nociones de relación borrosa, basada en la composición maxmin fue propuesta e investigada inicialmente por Sánchez [ 1976] y luego por Prevot [1981] y , Drewniak Czogalo, Drewniak y Pedryez [1982] para conjuntos finitos.
(6) En este artículo, dividen el campo de acción del robot utilizando celdas que contienen información sobre la probabilidad de que el robot esté en esa. celda, e información sobre cual es el rango de orientaciones más probables para el robot. Para ello se valen de un trapezoide difuso, definido por la n-upla (0,p,a, h,b), cuyas, variables son referidas a la geometría del trapezoide; e iterativamente se dan pasos de predicción y de actualización.
Creation date:

.png)




.jpg)





