DOI:
https://doi.org/10.14483/23448350.12679Published:
09/01/2018Issue:
Vol. 33 No. 3 (2018): September-December 2018Section:
Science and EngineeringAncho de banda en superficies selectivas en frecuencia tipo cruz de dipolo
Bandwidth in Cross Dipole Frequency Selective Surfaces
Keywords:
ancho de banda, método de las matrices en cascada, modelo de circuito equivalente, superficies selectivas en frecuencia (es).Keywords:
bandwidth, equivalent circuit model, frequency selective surfaces, matrix cascading method (en).Downloads
References
Balanis, C. A. (2011). Frequency Selective Screens. En T. Cwik (ed.), Modern Antenna Handbook (pp. 779-828). Nueva York: Wiley.
Callaghan, P., Parker, E. A. y Langley, R. J. (1991). Influence of supporting dielectric layers on the transmission properties of frequency selective surfaces. IEE Proceedings H Microwaves, Antennas and Propagation IET, 138(5), 448-454.
https://doi.org/10.1049/ip-h-2.1991.0075
Campos, A. L. P. S., Moreira, R. C. O. y Trindade, J. I. (2009). A comparison between the equivalent circuit model and moment method to analyze FSS. Proceedings of IEEE International Conference Microwave and Optoelectronics (IMOC). Belem, Brazil.
https://doi.org/10.1109/IMOC.2009.5427477
Celozzi, S., Lovat, G. y Araneo R. (2008). Frequency Selective Surfaces. Electromagnetic Shielding (pp. 219-240). Nueva York: Wiley.
https://doi.org/10.1002/9780470268483.ch10
Costa, F., Monorchio, A. y Manara, G. (2012). Efficient analysis of frequency-selective surfaces by a simple equivalent-circuit model. IEEE Antennas and Propagation Magazine, 54(4), 35-48.
https://doi.org/10.1109/MAP.2012.6309153
Ferreira, D., Calderinha, R., Cuinas, I. y Fernandes, T. (2015). Square loop and slot frequency selective surfaces study for equivalent circuit model optimization. IEEE Transactions on Antennas and Propagation, 63(9), 3947-3955.
https://doi.org/10.1109/TAP.2015.2444420
Luukkonen, O., Simovski, C. y Granet, G. (2008). Simple and accurate analytical model of planar grids and high-impedance surfaces comprising metal strips or patches. IEEE Transactions on Antennas and Propagation, 56(6), 1624-1632.
https://doi.org/10.1109/TAP.2008.923327
Marcuvitz, N. (1951). Waveguide Handbook. Nueva York: McGraw-Hill.
Mackay, A., Sanz-Izquierdo, B. y Parker, E. A. (2014). Evolution of frequency selective surfaces. Forum of Electromagnetic Research Methods and Applications Technologies, 2(8), 1-7.
Munk, B. A. (2005). General Overview, Frequency selective surfaces: Theory and Design. Nueva York: Wiley.
Rodriguez, M. y Carpes, Jr. W. (2015). Numerical model of the effective permittivity for square-loop frequency selective surfaces. IEEE Transactions on Magnetics, 51(3), 1-4.
https://doi.org/10.1109/TMAG.2014.2368782
Rodriguez, M. y Carpes, Jr. W. (2016). Particle swarm optimization for square loop frequency selective surfaces considering a model of dielectric effective permitivity. COMPEL. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 35(5), 1643-1655.
https://doi.org/10.1108/COMPEL-10-2015-0362
Rodriguez, M. y Carpes, Jr. W. (2017). Bandwidth for the equivalent Circuit Model in Square-loop frequency selective surfaces. IEEE Transactions on Antennas and Propagation, 65(11), 5932-5939.
https://doi.org/10.1109/TAP.2017.2754418
Sanz, J. (2012). Frequency Selective Surfaces for Terahertz applications (tesis de posdoctorado). Escuela de Ingienería, Universidad de Edinburgo, Edinburgo, Escocia.
Singh, D., Kumar, A., Meena, S. y Agarwala, V. (2012). Analysis of frequency selective surfaces for radar absorbing materials. Progress in Electromagnetic Research, 38, 297-314.
https://doi.org/10.2528/PIERB11121601
Sung, H. H. (2006). Frequency Selective wallpaper for mitigating indoor wireless interference. (tesis de posdoctorado). Departamento de Ingeniería Eléctrica y Electrónica, Universidad de Auckland, Auckland, Nueva Zelanda.
Wang, Z. L., Hashimoto, K., Shinohara, N. y Matsumoto, H. (1999). Frequency-selective surface for microwave power transmission. IEEE Transactions on Microwave Theory and Techniques, 4(10), 2039-2042.
https://doi.org/10.1109/22.795083
Wu, T. K. (1995) Fundamentals of Periodic Structures. Frequency selective surface and grid array. Nueva York: Wiley.
Yilmaz, A. E. y Kuzuoglu, M. (2009). Design of the square loop frequency selective surfaces with particles swarm optimization via the equivalent circuit model. Radioengineering, 18(2), 95-102.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de octubre de 2017; Aceptado: de julio de 2018
Resumen
A continuación, se presentan los resultados de la implementación del modelo de circuito equivalente (MCE) acoplado con el método de las matrices en cascada (MMC) para la determinación del ancho de banda en superficies selectivas en frecuencia (SSF) tipo cruz de dipolo. Lo modelos de permitividad efectiva del dieléctrico en SSF facilitan determinar el efecto del material aislante usado como soporte de los elementos resonantes, en relación con la frecuencia de resonancia y el ancho de banda de la superficie selectiva, como función del espesor del material dieléctrico. Sin embargo, en este tipo de enfoque el soporte aislante es considerado como dieléctrico delgado y, por lo tanto, es modelado como un parámetro de tipo concentrado. Esta consideración puede llevar a resultados no adecuados en el cálculo del ancho de banda de la superficie selectiva para soportes dieléctricos gruesos. La principal novedad de este artículo es la implementación del MCE conjuntamente con el MMC, con el objetivo de determinar la respuesta en frecuencia de la superficie selectiva cruz de dipolo para cualquier espesor y configuración del material dieléctrico. Los resultados obtenidos son comparados con los generados por el software de simulación electromagnética basado en el método de elementos finitos (Ansys-HFSS). Es de resaltar el bajo tiempo computacional, así como la exactitud aceptable obtenida con el enfoque propuesto.
Palabras clave:
ancho de banda, método de las matrices en cascada, modelo de circuito equivalente, superficies selectivas en frecuencia.Abstract
This paper presents the implementation outcomes of the Equivalent Circuit Model (ECM) acting in conjunction with the Matrix Cascading Method (MCM) for bandwidth calculation in cross dipole Frequency Selective Surfaces (FSSs). Dielectric layers are used as a support of resonant elements in FSSs. Models of effective permittivity of the dielectric layers in FSSs allow to determine the effect of the material used as insulating support of the resonant elements, in relation to the resonant frequency and bandwidth, as a function of the thickness of the dielectric material. However, in this approach, the insulating support is considered as thin dielectric, and therefore, it is modeled as a lumped parameter. This consideration may lead to unsuitable results in calculating the bandwidth for thick dielectric supports. The novelty of the paper is the implementation of the Equivalent Circuit Model together with the Matrix Cascading Method to determine the frequency response of the cross dipole selective surface for any dielectric thickness and configuration. It is notable the low computational time as well as the acceptable accuracy obtained with the proposed approach, compared to Ansys-HFSS simulations.
Keywords:
bandwidth, equivalent circuit model, frequency selective surfaces, matrix cascading method.Resumo
O artigo versa sobre a implementação do Modelo do Circuito Equivalente (MCE) implementado junto com o Método das Matrizes em Cascata (MMC) para a determinação da largura de banda em Superfícies Seletivas em Frequência (SSF) do tipo cruz de dipolo. Modelos de permissividade efetiva do dielétrico em SSF permitem determinar o efeito do material usado como suporte dos elementos ressonantes na frequência de ressonância e na largura de banda como função da espessura do material dielétrico. No entanto, neste tipo de abordagem, o suporte dielétrico é considerado como parâmetro concentrado. Esta consideração pode levar a resultados inadequados no cálculo da largura de banda da superfície seletiva para suportes dielétricos espessos. A originalidade do artigo tem a ver com a implementação do Modelo de Circuito Equivalente junto com o Método das Matrizes em Cascata para determinar a resposta em frequência da superfície seletiva para qualquer espessura e configuração dielétrica. É importante ressaltar o baixo tempo computacional, obtendo adicionalmente uma acurácia aceitável com a abordagem proposta, em comparação com simulações implementadas no Ansys - HFSS.
Palavras-chaves:
superfícies seletivas em frequência, modelo do circuito equivalente, largura de banda, método das matrizes em cascata.Introducción
Las superficies selectivas en frecuencia (SSF) son dispositivos electromagnéticos que permiten, de forma selectiva, controlar la propagación de radiación electromagnética. Específicamente, son superficies que presentan comportamiento de filtro electromagnético en relación con la radiación incidente sobre ellas. Esta característica permite su uso extensivo en áreas como la industrial, militar y científica, y en un rango en el espectro electromagnético que se extiende desde las microondas hasta el infrarrojo (Balanis, 2011). Actualmente, las SSF se encuentran en aplicaciones asociadas a la protección contra interferencias electromagnéticas, blindaje electromagnético, absorbedores electromagnéticos, control de propagación de señales electromagnéticas tipo WLAN (wireless local area network), telefonía celular o televisión digital, entre otras (Wu, 1995; Munk, 2005; Sung, 2006; Celozzi, Lovat y Araneo, 2008; Balanis, 2011).
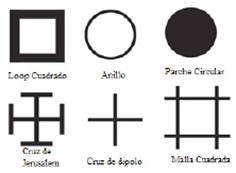
De acuerdo con la respuesta en frecuencia de la superficie selectiva, es decir, la forma específica de los coeficientes de transmisión y reflexión como función de la frecuencia, se puede clasificar su respuesta como pasa altos, pasa bajos, pasa banda y rechaza banda (Sung, 2006). En forma general, las SSF se construyen con elementos metálicos de diferentes formas dispuestos sobre superficies aislantes o con ranuras en superficies metálicas de formas diversas. La figura 1 muestra algunos de los elementos resonantes comúnmente utilizados en las aplicaciones mencionadas. Los elementos de las SSF forman un patrón periódico en una estructura de tipo bidimensional. Por lo tanto, al definir la menor parte de la estructura que, periódicamente repetida en el espacio forma la estructura periódica completa, es posible definir la “celda unitaria” de la SSF.
Figura 1: Elementos resonantes en SSF y denominaciones. En color negro, material conductor
La importancia de la celda unitaria radica en que sirve de base para algunos métodos numéricos de análisis de SSF, como el método de los elementos finitos (FEM) o el método de los momentos (MoM). La principal desventaja de estos métodos es el alto costo computacional involucrado (Celozzi et al., 2008; Costa, Monorchio y Manara, 2012). Así fue como el Modelo de Circuito Equivalente (MCE) surgió como una alternativa de análisis hace aproximadamente 50 años (Mackay, Sanz-Izquierdo y Parker, 2014), pues su principal ventaja es su bajo costo computacional junto con una exactitud aceptable comparado con los métodos mencionados (Campos, Moreira y Trindade, 2009; Wang, Hashimoto, Shinohara y Matsumoto, 1999). Sin embargo, una de las principales limitaciones del MCE es la modelización de los efectos del material dieléctrico usado como soporte de los elementos de la superficie selectiva (Wu, 1995); específicamente, sus efectos en la frecuencia de resonancia y el ancho de banda.
Trabajos recientes procuran resolver esta limitación usando modelos de permitividad efectiva del dieléctrico para la SSF tipo loop cuadrado (Rodríguez y Carpes, 2015; Ferreira, Calderinha, Cuinas y Fernandes, 2015; Rodríguez y Carpes, 2017). En el presente trabajo, el MCE y el MMC son empleados en conjunto para determinar el comportamiento de la frecuencia de resonancia y el ancho de banda de la superficie selectiva tipo cruz de dipolo, para cualquier espesor del material dieléctrico. Es de resaltar el bajo tiempo computacional y la exactitud aceptable obtenida con la metodología desarrollada comparado con simulaciones implementadas en el software electromagnético basado en el método de elementos finitos Ansys-HFSS.
Metodología
El MCE, en el cual el dieléctrico es considerado como parámetro concentrado, y el MCE actuando en forma conjunta con el Método de Matrices en Cascada (MMC), en el que el dieléctrico es considerado como parámetro distribuido, son implementados computacionalmente para determinar la respuesta en frecuencia de la superficie selectiva cruz de dipolo, en incidencia normal, a través de un código de programa desarrollado en el software Matlab. Por otro lado, y con fines de comparación, es usado el módulo Floquet Ports del programa para análisis electromagnético Ansys-HFSS para la determinación de la respuesta en frecuencia de la superficie selectiva. A continuación, se realiza una descripción del MCE, el MMC y del módulo Floquet Ports del Ansys-HFSS.
Modelo de circuito equivalente
El MCE es uno de los métodos más simples y eficientes para el análisis de SSF, pues permite, a partir de un modelización básica, encontrar la respuesta en frecuencia de una superficie selectiva; en particular, sus coeficientes de transmisión y reflexión ante la incidencia de ondas transversales electromagnéticas (TEM). Es importante resaltar que su potencial es limitado, pues en su concepción es considerada una aproximación de tipo cuasi-estático (Costa et al., 2012), para la cual, el periodo de repetición espacial de la superficie selectiva debe ser mucho menor que la longitud de onda a la frecuencia de operación. Lo anterior permite especificar la impedancia de la superficie selectiva como un circuito de parámetros concentrados. Los resultados del MCE son aceptables teniendo en cuenta el bajo costo computacional involucrado, así como la exactitud aceptable de los resultados obtenidos comparados con software de simulación electromagnética full-wave (Campos et al., 2009).
En Singh, Kumar, Meena y Agarwala (2012) son presentados algunos circuitos equivalentes para diferentes tipos de SSF, con una o varias resonancias. En la figura 2 se presenta la SSF del tipo cruz de dipolo, cuya respuesta en frecuencia corresponde a rechaza banda. Adicionalmente, se muestra el elemento resonante y su circuito equivalente usado para el análisis electromagnético a través de MCE.
Figura 2: a. SSF tipo cruz de dipolo; b. elemento resonante cruz de dipolo; c. circuito equivalente para análisis electromagnético. Z0 corresponde a la impedancia característica del espacio libre.
Para determinar los parámetros inductivo y capacitivo del circuito equivalente mostrado en la figura 2 c, pueden usarse varias metodologías. En la primera, estos parámetros son extraídos de resultados de simulaciones electromagnéticas full-wave a partir del coeficiente de reflexión de la superficie periódica, tal como es referenciado en Costa et al. (2012). Usando procesos de escalamiento es posible obtener los valores de los parámetros inductivo y capacitivo para otras dimensiones de la superficie selectiva y, por tanto, para otras frecuencias de resonancia (Costa et al., 2012). Otras metodologías proponen expresiones analíticas para la determinación de la impedancia o la admitancia de la superficie periódica (Luukkonen, Simovski y Granet, 2008), o también son usadas modificaciones de las ecuaciones propuestas por Marcuvitz (1951) para rejillas de tipo periódico.
Independientemente del tipo de procedimiento usado para la obtención de los parámetros inductivo y capacitivo de la superficie periódica, la magnitud de los coeficientes de transmisión 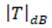 y reflexión
y reflexión 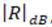 , para el modelo presentado en la figura 2c, en decibelios, se especifican como:
, para el modelo presentado en la figura 2c, en decibelios, se especifican como:
En las ecuaciones 1y 2, 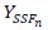 corresponde a la admitancia normalizada de la superficie selectiva, definida como:
corresponde a la admitancia normalizada de la superficie selectiva, definida como:
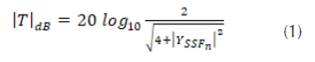
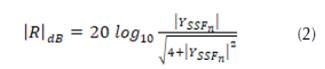
En la ecuación 3, Y0 corresponde a la admitancia característica del espacio libre, YSSF es la admitancia de la superficie selectiva, X y B corresponden a la admitancia inductiva y a la susceptancia capacitiva normalizadas de la superficie selectiva, respectivamente. En la condición resonante, X=1/B, y por lo tanto, la impedancia normalizada de la superficie selectiva, ZSSFn, será igual a cero y la admitancia normalizada de la superficie selectiva 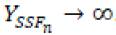 Por lo tanto, la magnitud de los coeficientes de reflexión
Por lo tanto, la magnitud de los coeficientes de reflexión 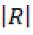 y transmisión
y transmisión 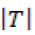 serán respectivamente:
serán respectivamente:
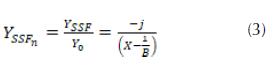
La condición especificada en la ecuación 4 acontece a una única frecuencia, conocida como la frecuencia de resonancia de la superficie periódica, y en esta condición la onda electromagnética es totalmente reflejada por la superficie periódica y su transmisión es nula. A diferencia de la metodología empleada en Rodríguez y Carpes (2017), en la cual para la determinación de admitancia inductiva y susceptancia capacitiva normalizadas de la superficie selectiva fueron usadas las ecuaciones modificadas de Marcuvitz para la superficie selectiva tipo loop cuadrado. Se tiene en cuenta que, según Sung (2006), es posible expresar la admitancia inductiva y susceptancia capacitiva normalizadas de la superficie selectiva como:
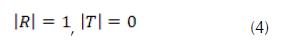

En la ecuación 6, ε eff corresponde a la permitividad efectiva del dieléctrico. Como fue mencionado, una de las limitaciones del MCE es la modelización de los efectos del material dieléctrico usado como soporte de los elementos de las SSF. En Rodríguez y Carpes (2015) es propuesta una formulación para la determinación de la permitividad efectiva del dieléctrico de la superficie selectiva tipo loop cuadrado como función de los parámetros geométricos y los relacionados con el material dieléctrico como son el espesor, permitividad relativa y configuración. En la literatura especializada no se reporta una relación de este tipo para la superficie selectiva del tipo cruz de dipolo. Sin embrago, en Costa et al. (2012) es propuesta una formulación para considerar los efectos del dieléctrico en el comportamiento de la superficie selectiva con permitividad relativa ε r en SSF, como se muestra a continuación:

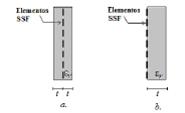
En la ecuación 7, el factor N depende la geometría específica del elemento resonante y de la relación, en una celda unitaria, de la superficie metálica con respecto a la superficie de la celda. El espesor de la capa dieléctrica es especificado por el parámetro t y p está asociado al periodo de repetición espacial de la celda unitaria. El valor asintótico de la permitividad efectiva, ε rh , depende de la configuración del dieléctrico y es definido como ε r para la configuración de doble cara y (ε r +1)/2 para la configuración de cara simple. La figura 3 muestra estas dos configuraciones del dieléctrico en SSF.
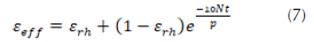
Figura 3: Configuraciones del dieléctrico en SSF. a. doble cara; b. cara simple.
Para SSF del tipo rechaza banda, el ancho de banda se define con un nivel de -10 dB (Celozzi et al., 2008) y porcentualmente es definido como:
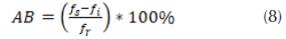
Donde fs y fi corresponden a las frecuencias superior e inferior asociadas a un nivel de -10 dB en el coeficiente de transmisión, respectivamente; y fr corresponde a la frecuencia de resonancia de la superficie selectiva. Múltiples reflexiones en las fronteras del dieléctrico alteran el ancho de banda de la superficie selectiva (Callaghan, Parker y Langley, 1991) y, por lo tanto, esta modelización está fuera del alcance del MCE. El MCE es adecuado para espesores totales del dieléctrico inferiores a 0.1λ m , donde λ m corresponde a la longitud de onda en el material dieléctrico. El soporte aislante es considerado, en este caso, como parámetro concentrado.
Si el espesor total del dieléctrico es un múltiplo de λ m /2, las múltiples reflexiones en las fronteras del material dieléctrico alteran de modo significativo el ancho de banda de las SSF (Sanz, 2012). Este efecto puede ser considerado usando el MCE en conjunto con el Método de las Matrices en Cascada (MMC). El soporte aislante es considerado, en este caso, como parámetro distribuido.
Método de las matrices en cascada (MMC)
El MMC es una técnica que permite encontrar la respuesta de un dispositivo formado por la conexión en cascada de estructuras individuales a través de la multiplicación, en forma matricial, de sus parámetros ABCD. La ecuación 9muestra los componentes de la matriz ABCD para el soporte dieléctrico, de espesor t, el cual es considerado libre de pérdidas y en incidencia normal (Marcuvitz, 1951).
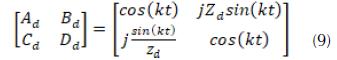
En la ecuación 9, el número de onda y la impedancia característica del dieléctrico están definidas como:
En la ecuación 10, corresponde a la frecuencia y es la velocidad de la luz en el espacio libre. Por otro lado, la matriz ABCD de la SSF es determinada como:
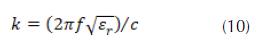

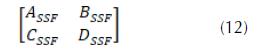
Las ecuaciones 13a la 16 muestran los componentes de la matriz ABCD de la superficie selectiva (Marcuvitz, 1951):


En la ecuación 15, corresponde a la admitancia de la superficie selectiva. Las matrices ABCD de la estructura completa para las configuraciones de dieléctrico de doble cara (dieléctrico-SSF-dieléctrico) y de cara simple (dieléctrico-SSF) son, respectivamente:

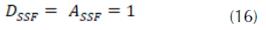
A partir de los parámetros ABCD obtenidos de acuerdo con las ecuaciones 17 y 18, es posible obtener los coeficientes de reflexión (R) y transmisión (T) de la estructura completa, como es mostrado a continuación (Marcuvitz, 1951):
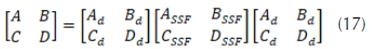
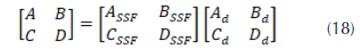
En las ecuaciones 19 y 20, corresponde a la impedancia característica del espacio libre.
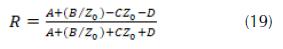
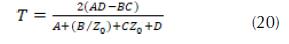
Software de simulación electromagnética
Como fue mencionado, el módulo Floquet Ports del software de simulación electromagnética full-wave basado en el FEM Ansys-HFSS es usado para comparar los resultados obtenidos en el MCE, así como también en la implementación computacional conjunta del MCE y el MMC.
El módulo Floquet Ports del Ansys-HFSS permite simular el comportamiento de SSF mediante el uso de una celda unitaria de la superficie y considerando la periodicidad espacial de la estructura mediante el uso de condiciones de frontera periódica. Para la solución del problema numérico, es decir, la determinación de la respuesta en frecuencia de los coeficientes de transmisión y reflexión de la estructura periódica, el programa usa un refinamiento iterativo, o sea, un incremento en el número de elementos de la malla en regiones en las que el error es alto, proceso que es conocido como análisis adaptativo. En cada uno de los pasos del refinamiento son determinados los parámetros S de la superficie selectiva y son comparados con su valor en el paso inmediatamente anterior, generando un cambio en los parámetros S y, por lo tanto, un cambio entre refinamientos de la malla, conocido como ΔS.
Como criterio para detener el proceso de refinamiento de la malla, el programa presenta dos opciones. La primera, asociada con un número específico de refinamientos de la malla y, por otro lado, un valor pre-definido en el ΔS. Como criterio para detener el proceso no fue usado un número específico de refinamientos, pues no es posible conocer previamente el valor del ΔS para el número de refinamientos especificado. De la misma forma, no fue usado un valor pre-definido en el ΔS dada su alta inestabilidad en el proceso de refinamiento, conclusión producto de los muchos casos de simulación considerados. Finalmente, el criterio usado fue una estabilización en el valor del ΔS (del orden de 0.002), el cual es alcanzado para un número de refinamientos de la malla del orden de 15. Para el método de enmallado, el programa escoge automáticamente entre dos opciones: enmallado clásico y enmallado TAU. Los criterios usados por el programa para escoger el método de enmallado son un balance entre los siguientes aspectos: fiabilidad, velocidad, tamaño y características del diseño.
Resultados
La figura 4 muestra la geometría de la superficie selectiva seleccionada, la cual se encuentra referenciada en Costa et al. (2012). Es importante resaltar que, con fines de comparación, se tienen en cuenta para la respuesta en frecuencia en los tres métodos considerados, es decir, el ECM, ECM + MMC y el Ansys-HFSS, las mismas frecuencias máxima, mínima, así como el incremento en frecuencia Δf.
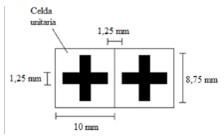
Figura 4: Parámetros geométricos de la superficie selectiva tipo cruz de dipolo.
En Costa et al. (2012), para la condición free-standing (sin dieléctrico) la inductancia, capacitancia y factor N especificados para la superficie selectiva son 4.368 nH, 20 fF y 1.8, respectivamente. La admitancia inductiva y susceptancia capacitiva normalizadas de la superficie selectiva son determinadas usando los valores referenciados para la inductancia y capacitancia a través de las ecuaciones 5 y 6 , respectivamente. La configuración especificada para el dieléctrico es de doble cara, la permitividad relativa del mismo es ε r = 5 y es considerado libre de pérdidas y, como fue mencionado, N = 1.8. Estas consideraciones, y adicionalmente las características geométricas presentadas en la figura 4, permiten determinar el valor de la permitividad efectiva según la ecuación 7. Respecto del material conductor componente de la superficie selectiva, se consideró igualmente libre de pérdidas. Para el Ansys-HFSS es implementada una celda unitaria, como se muestra en la figura 4, con condiciones de frontera periódica y son usados para el conjunto de simulaciones planteadas y en las condiciones especificadas en el numeral 2.3, un número de elementos (tetraedros) entre (40-50) × 103.
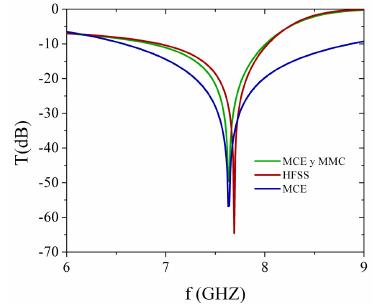
La figura 5 muestra la respuesta en frecuencia de la magnitud, en decibelios, del coeficiente de transmisión para un espesor de t = 2.8 mm para el MCE, como también para el MCE en conjunto con el MMC. Adicionalmente, son mostrados los resultados del Ansys-HFSS.
Figura 5: Magnitud del coeficiente de transmisión para el MCE, MCE + MMC y HFSS. Espesor de t = 2.8 mm y εr = 5.
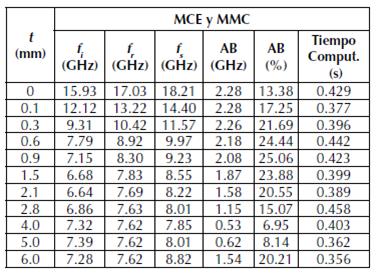
De los resultados mostrados en la figura 5, se puede concluir que para los tres métodos considerados, es decir, el MCE, MCE + MMC y Ansys-HFSS, la frecuencia de resonancia no presenta diferencias significativas. Lo anterior debido a que esta no se ve afectada por las múltiples reflexiones en las fronteras del dieléctrico. Por otro lado, con respecto a la respuesta en frecuencia, y en particular el ancho de banda, son claras las diferencias entre el MCE (en la cual el dieléctrico es considerado como parámetro concentrado) y el MCE + MMC y el Ansys-HFSS (en el que el dieléctrico es considerado como parámetro distribuido). Es importante resaltar el ajuste aceptable en la respuesta en frecuencia entre el MCE + MMC y el Ansys-HFSS. Las tablas 1, 2 y 3 consolidan los resultados del coeficiente de transmisión para espesores desde t = 0 hasta t = 6.0 mm para el MCE, el MCE en conjunto con el MMC y el Ansys-HFSS. Se muestran las frecuencias de resonancia ( fr ) y las frecuencias tanto superior ( fs ) como inferior ( fi ), correspondientes a -10 dB. A partir de estos valores es determinado el ancho de banda (GHz) y el ancho de banda porcentual, según la ecuación 8. Además, es mostrado el tiempo computacional empleado por los métodos referenciados.
Fuente: elaboración propia de los autores.
Tabla 1: Resultados MCE.
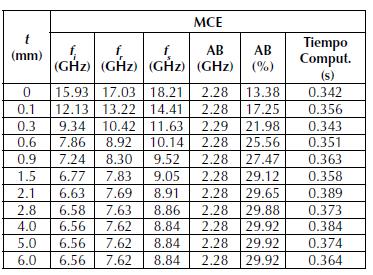
Fuente: elaboración propia de los autores.
Tabla 2: Resultados MCE y MMC.
Fuente: elaboración propia de los autores.
Tabla 3: Resultados Ansys HFSS.
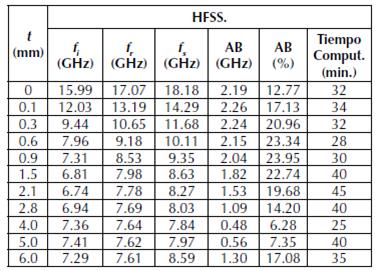
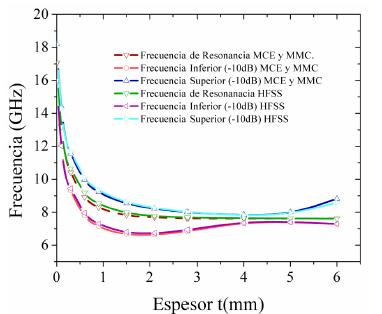
La figura 6 muestra los resultados consolidados de las tablas 2 y 3, en cuanto a las frecuencias de resonancia ( fr ) y las frecuencias superior ( fs ) e inferior ( fi ) correspondientes a -10 dB, para el MCE en conjunto con el MMC así como para el Ansys-HFSS.
Figura 6: Frecuencia de resonancia (fr) y las frecuencias superior (fs) e inferior (fi) correspondientes a -10 dB, para el MCE y MMC y para el HFSS.
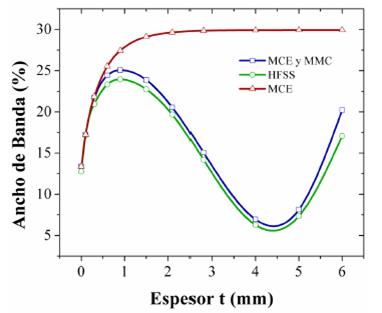
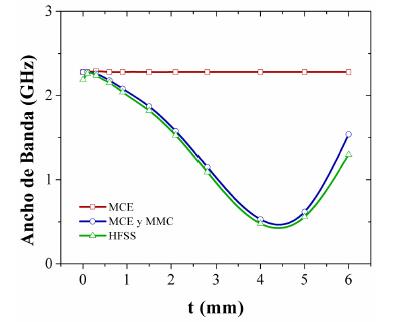
La figuras 7 y 8 muestran de forma gráfica los resultados consolidados de las tablas 1, 2 y 3 en cuanto al ancho de banda y el ancho de banda porcentual, para el MCE en conjunto con el MMC y para el Ansys-HFSS.
Figura 7: Ancho de banda porcentual para MCE, MCE y MMC, HFSS.
Figura 8: Ancho de banda para MCE, MCE + MMC y HFSS.
Los resultados consolidados, producto de la implementación del ECM, ECM + MMC y el Ansys-HFSS en el análisis de la superficie selectiva tipo cruz de dipolo mostrados en las figuras 7 y 8, permiten resaltar las limitaciones del MCE en la determinación de la respuesta en frecuencia de la superficie selectiva al considerar el dieléctrico como parámetro concentrado independientemente de su espesor. Por otro lado, las figura 6, 7 y 8 muestran las ventajas de la implementación computacional conjunta del MCE y el MMC, traducidas en su bajo costo computacional y exactitud aceptable comparado con el Ansys-HFSS.
Conclusiones
En este artículo se presentan los resultados de la implementación del MCE en conjunto con el MMC para la determinación de la respuesta en frecuencia de SSF tipo cruz de dipolo, como función del espesor del soporte dieléctrico. La exactitud aceptable y el bajo tiempo computacional son los aspectos más relevantes para destacar. En este sentido, la diferencia porcentual en la determinación del ancho de banda entre el método implementado (MCE y MMC) y Ansys-HFSS, tomado como referencia, no es superior al 20%. De igual manera, se resalta el bajo tiempo computacional, especificado en las tablas 2 y 3, empleado por el método implementado (MCE y MMC), comparado con el Ansys-HFSS. Los dos aspectos considerados, es decir, exactitud aceptable y bajo tiempo computacional, no implican que el método de análisis basado en elementos finitos pueda ser sustituido por el método implementado. Es de resaltar que el MCE es considerada en su concepción como una aproximación de tipo cuasi-estático, por lo que su rango de análisis en frecuencia es limitado; adicionalmente, el Ansys-HFSS tiene disponibles muchas más variables de análisis electromagnético. Sin embargo, las características más relevantes del MCE en conjunto con el MMC, es decir, su exactitud aceptable y su bajo tiempo computacional, son una ventaja cuando se tienen un número importante de simulaciones a realizar; por ejemplo, cuando es usado en procesos de optimización (Yilmaz y Kuzuoglu, 2009; Rodríguez y Carpes, 2016).
Por otro lado, y en relación con los resultados de las figuras 7 y 8, es de resaltar los resultados del MCE, comparados con el MCE en conjunto con el MMC y los resultados del Ansys-HFSS. Como se puede concluir, el MCE permite reproducir el comportamiento del ancho de banda solamente para espesores pequeños del material dieléctrico, es decir, cuando el dieléctrico se comporta como parámetro concentrado.
Los efectos de los parámetros geométricos de la superficie selectiva cruz de dipolo en el ancho de banda no son considerados en el análisis presentado. Sin embargo, la herramienta desarrollada permite realizar este tipo de estudios paramétricos para cualquier superficie selectiva con resonancia simple a partir de los valores de inductancia y capacitancia de la superficie y del modelo de permitividad efectiva del dieléctrico.
Actualmente trabajamos en la implementación del método incluyendo la variable angular y la polarización de la onda electromagnética para diferentes tipos de SSF, así como en procesos de síntesis de SSF, usando métodos de optimización y aplicado a SSF con dieléctricos gruesos.
Referencias
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.