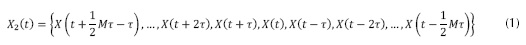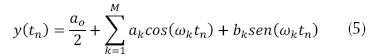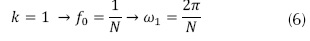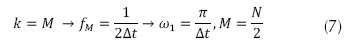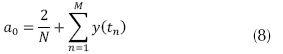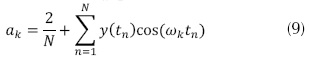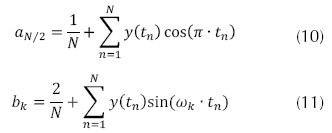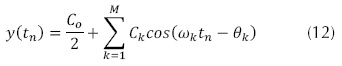Identificación de patrones de variabilidad climática a partir de análisis de componentes principales, Fourier y clúster k-medias

doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.4.a04

Identificación de patrones de variabilidad climática a partir de análisis de componentes principales, Fourier y clúster k-medias

Identifying patterns of climate variability from principal component analysis - PCA, Fourier y k-means clustering.

Juan Gabriel Rueda Bayona¹, Cindy Judith Elles Pérez², Edgar Humberto Sánchez Cotte³, Ángel León González Ariza⁴, Germán Daniel Rivillas Ospina⁵

¹ Ingeniero civil, magíster en Ingeniería � Recursos Hidráulicos, tecnólogo en Oceanografía, candidato a doctor en Ingeniería Civil, Universidad del Norte, Barranquilla, Colombia. Contacto: jgrueda@uninorte.edu.co
² Ingeniera química, candidata a doctor en Ingeniería Civil, Universidad del Norte, Barranquilla, Colombia. Contacto: ellesc@uninorte.edu.co
³ Ingeniero civil, magíster en Ingeniería Civil, estudiante de Doctorado en Ingeniería Civil en la Universidad del Norte, Barranquilla, docente de planta, Universidad Distrital Francisco José de Caldas, Bogotá D. C. Contacto: esanchez@udistrital.edu.co
⁴ Ingeniero industrial, doctor en Ingeniería Industrial, docente investigador, Universidad del Norte, Barranquilla, Colombia. Contacto: agonzale@uninorte.edu.co
⁵ Ingeniero civil, máster en Ingeniería, doctor en Ingeniería. Profesor, asistente Departamento de Ingeniería Civil y Ambiental. Universidad del Norte, Barranquilla, Colombia. Contacto: grivillas@uninorte.edu.co

Fecha de recepción: 17 de febrero de 2016 Fecha de aceptación: 10 de septiembre de 2016

Cómo citar: Rueda-Bayona, J.G.; Elles-Pérez, C.J.; Sánchez, E.H.; González, A.L. y Rivillas-Ospina, G.D. (2016). Identificación de patrones de variabilidad climática a partir de análisis de componentes principales, Fourier y clúster k-medias. Revista Tecnura, 20(50), 55-68. doi: 10.14483/udistrital.jour.tecnura.2016.4.a04

RESUMEN

Contexto: Una investigación mediante el Análisis de Componentes Principales (APC) se llevó a cabo para identificar la variabilidad y los patrones climáticos de dos importantes ciudades del Caribe Colombiano.

Método: Para el desarrollo de este trabajo se empleó información satelital de resolución temporal trihoraria de 35 años (1980-2014) y se efectuó escalamiento espacial mediante información in situ para dos ciudades en Colombia (Cartagena y Barraquilla).

Resultados: Los resultados de correlación superiores al 80% permitieron efectuar un adecuado ajuste para el análisis de información de velocidad de viento y temperatura ambiente. Para cada una de las 4 series de tiempo se construyó una matriz de empotramiento y de desfase con el objetivo de aplicar análisis de componentes principales o conocido también como análisis espectral singular. Fueron identificados los componentes principales cuya representatividad es inmediatamente superior al 70% para la temperatura y para el viento en ambas ciudades. Se efectuó un análisis de Fourier a la velocidad del viento y la temperatura y se detectaron modos de oscilación similares a los modos de oscilación (componentes principales) detectados mediante el APC.

Conclusiones: Se encontró una variabilidad diurna para temperatura, y variabilidad diurna del viento para la ciudad de Cartagena, explicada por las brisas de mar y de tierra. Adicionalmente se encontró variabilidad trimestral asociada a las oscilaciones Maden Julian, variabilidades semestrales, anuales, y variabilidad de 6 años relacionada con el fenómeno del Niño. Finalmente mediante análisis de clúster se identificaron dos patrones climáticos en las zonas de estudio.

Palabras clave: Clima, Temperatura, Velocidad del viento, Componentes Principales, Fourier. Clúster.

ABSTRACT

Context: Is achieved a research through Principal Component Analysis (PCA) for determining the variability and climate patterns of two important cities in the Colombia Caribbean.

Method: This research used satellite data with three hourly resolution contained in a 35 year data set (1980 to 2014), and a spatial scaling was performed using information related to Cartagena and Barranquilla cities, located in the north of Colombia.

Results: The correlation results, above 80 %, show an appropriate adjustment for the information analysis of wind speed and temperature. Time lag matrixes were built for the time series with the aim of applying the Principal Component Analysis (PCA), known as Singular Spectrum Analysis. The main components were identified, which represent more than 70% of the temperature and the wind data in both cities. A Fourier analysis for the wind speed and the temperature allowed identifying similar oscillation modes (main components) detected by the PCA.

Conclusions: Sea and land breezes explain the identified diurnal temperature and wind speed variability in Cartagena. Additionally were observe a quarterly variability associated with fluctuations Maden Julian, semiannual, annual, and 6-year variability associated with ENSO. Finally, the cluster analysis allowed the identification of two-climate pattern in the study area.

Keywords: Climate, Temperature, Wind speed, Principal Components, Fourier, Cluster.

INTRODUCCIÓN

Los procesos físicos que se dan en la atmósfera presentan un carácter dinámico, aleatorio y de diferente naturaleza, lo que los convierte en fenómenos complejos de comprender y cuantificar. Para estudiar los efectos que en los sistemas ambientales y la infraestructura producen dichos procesos, es necesario caracterizar en detalle los cambios que se dan en las variables atmosféricas a diferentes escalas. En ingeniería es muy importante caracterizar las componentes de viento, precipitación, oleaje y caudal para el diseño de infraestructura hidráulica o para la definición de sistemas de gestión de riesgo. Para el pronóstico de estas variables se emplean comúnmente modelos estocásticos que permiten obtener con base en series de tiempo conocidas, el comportamiento futuro de los parámetros físicos evaluados en una localidad específica. El empleo de modelos numéricos estructurados a partir de métodos numéricos o estadísticos para estudiar el clima en distintas escalas, se ha evidenciado en diversos estudios de investigación.

Skittides y Früh (2014) emplean el análisis de componentes principales (ACP) para estimar los campos de viento, basados en el comportamiento de los procesos físicos en el pasado para predecir eventos futuros de naturaleza dinámica. El potencial de esta técnica se basa en la capacidad de pronosticar el error probable que será obtenido y en efectuar pronósticos a partir de un conjunto de eventos pasados de características similares, lo que permite generar series sintéticas de gran precisión en el instante que la información es generada.

Rojo-Hernández y Carvajal-Serna (2010) estudiaron la dinámica no lineal de los caudales de los ríos de Colombia utilizando un modelo periódico de predicción basado en el análisis espectral singular (AES), el cual deriva su funcionamiento en los métodos ACP. El estudio se enfocó en estudiar los ciclos que influyen sobre la dinámica de las series de caudales a partir del empleo ACP, mediante la aplicación de regresiones lineales múltiples, bien sobre componentes principales o mediante componentes reconstruidas, e involucrando variables climáticas macrorrezagadas en el tiempo.

Carvajal y Marco (2004) llevaron a cabo un estudio de ACP a 50 estaciones de precipitación mensual y 8 de caudal, con el fin de verificar la asociación entre variables macroclimáticas relacionadas con el fenómeno ENSO (El Niño Oscilación del Sur) y la hidrometeorología del Valle del Cauca (Colombia). Encontraron que al emplear esta metodología en la modelación de la precipitación y el caudal se obtiene un mejor ajuste de los modelos regresivos.

En la investigación realizada por Giraldo, León y Gómez (2013) se empleó el método K-medias (K-means) para inicializar algoritmos particionales aplicados al proceso de minería de flujo de datos.

Los investigadores Plazas-Nossa y Torres (2014) combinaron la técnica de PCA y Fourier con el objetivo de pronosticar series de tiempo obtenidas mediante la técnica de espectrotometría UV-Vis. Los autores recomendaron efectuar los análisis de los rangos de los espectros UV y Vis de manera independiente, facilitando así la identificación de los componentes principales y los armónicos fundamentales.

Miao et al. (2015) utilizaron en conjunto el método K-medias tradicional con el método spectral clustering (SC), dando como resultado el método SKC (spectralanalysis-basado K-means clustering. Mo y Ghil (1988) hacen uso de un método de análisis de clúster modificado para identificar patrones espaciales de flujo del viento en el planeta, y su interacción. Skapa et al. (2012) utilizan el agrupamiento K-medias para identificar los fenómenos climáticos que tienen efectos sobre la propagación de las ondas de radio en telecomunicaciones móviles, y a su vez centran su trabajo en analizar los parámetros meteorológicos importantes como los resultados de K-medias. Kumar et al. (2012) aplicaron funciones de densidad de probabilidad en conjunto con el método de K-medias para predecir el clima en Quinland.

Frecuentemente la información climática disponible para la realización de investigaciones y estudios de ingeniería a escala local es limitada. Por lo general, se disponen de estaciones climatológicas cercanas para inferir sobre el comportamiento local de las variables atmosféricas, lo que puede conllevar establecer patrones de variabilidad climática no asociados a las condiciones esperadas. Adicionalmente, las estaciones cercanas al área de estudio poseen registros de información, con series de tiempo menores a 10 años, limitando así identificar modos de oscilación climáticos superiores al tiempo de medición in situ de las estaciones. Otra limitación observada en las estaciones climatológicas, son los vacíos de información generados principalmente por fallas en los instrumentos de medición, dando como resultado a que se afecte la calidad de los estudios.

Las limitaciones para la realización de estudios climatológicos locales se han reducido con el avance de los sistemas de teledetección con aplicación meteorológica, la evolución de los modelos numéricos, y el mejoramiento de las técnicas de análisis de información numérica satelital. Con base en lo anterior, la aplicación conjunta de información medida y modelada, se conoce como reanálisis, la cual es una técnica de asimilación de datos para la creación de conjunto de datos climáticos de alta resolución espacial y temporal.

Con base en las consideraciones anteriores, el presente trabajo identifica patrones de comportamiento de velocidad del viento y temperatura en localidades donde la disponibilidad de información es limitada. Se empleó información de reanálisis localmente ajustada con información in situ, y se estudió la variabilidad climática mediante análisis de componentes principales, Fourier y clúster K-medias.

METODOLOGÍA

Manejo de la información

Como paso previo a la aplicación de los métodos numéricos y estadísticos de modelación y análisis, se efectuó asimilación de información de reanálisis perteneciente a la base de datos NCEP North American Regional Reanalysis NARR (NOAA, 2015). La asimilación pretende escalar información satelital a los puntos de estudio, mediante análisis de regresión lineal a una serie de tiempo trihoraria de 30 años (NARR); como información in situ de referencia para la asimilación, se empleó información horaria de 2013 y 2014 de las estaciones climáticas ubicadas en los aeropuertos de Barranquilla y Cartagena (Ideam, 2016).

Pronóstico basado en análisis de componentes principales

Una forma de entender la dinámica de las series de tiempo climatológicas es a través del análisis espectral singular (AES), que en términos generales es la aplicación del análisis de componentes principales (ACP) a series de tiempo rezagadas (Elsner y Tsonis, 2013). El tratamiento de los datos se hace mediante la aplicación del teorema de Takens (1980), para la construcción de una matriz de retrasos. La matriz se construye a partir de un vector de retrasos con dimensión M, representando la ventana de tiempo escogida para la modelación de los datos, (ecuación (1)) (Skitties y Früh, 2014).

De esta forma, la matriz de retraso queda con las siguientes dimensiones para N_d datos de la serie de tiempo.

Filas: 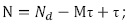Columnas: M.

El análisis de componentes principales se hace obteniendo la matriz de varianza-covarianza para la matriz de retrasos, a través de los eigenvalores y los eigenvectores de acuerdo con la ecuación (2).

Donde A es la matriz de varianza-covarianza, e_i los eigenvectores, que representan la contribución de cada variable a la señal original y l_i los eigenvalores, que expresan la variabilidad asociada a cada eigenvector.

La reconstrucción de la señal original se puede lograr al proyectar los eigenvalores sobre la matriz de datos originales X(t) mediante la ecuación (3).

Donde Y_i(t) son los componentes principales asociados a cada eigenvector e_i. Al final, mediante la ecuación (4) se puede reconstruir la señal como la sumatoria de los Y_i(t) (García-Cabrejo y Moreno-Sánchez, 2006).

El análisis de componentes principales se logró mediante la aplicación de los supuestos teóricos anteriormente mencionados. Primero, se obtuvo la matriz de retrasos para valores de ventana M de 3 días, 1 mes, 6 meses, 1 año y 6 años, con el fin de determinar la ventana de tiempo que ofrecía un mejor ajuste de los datos. Segundo, se obtuvieron los eigenvectores y los eigenvalores según la ecuación (3) y con los eigenvalores, se extrajo información acerca de la varianza acumulada explicada por los eigenvectores.

Seguidamente, se determinó el número de eigenvectores necesarios para modelar los datos, sin incluir ruido en el modelo, esto se hizo teniendo en cuenta que los eigenvectores explicaran más del 70 % de la variabilidad total del sistema. Se proyectaron todos los eigenvectores sobre la serie de datos original, tanto para la temperatura como para la velocidad del viento de Barranquilla y Cartagena respectivamente, para espacios de tiempo de 25 años y luego se modelaron de 3 días, 1 mes, 6 meses, 1 año y 6 años para observar patrones de oscilación y relacionarlos con fenómenos naturales. Por último se realizó la sumatoria de los componentes encontrados según la ecuación (4). El ajuste de la señal proyectada con los datos originales de la serie de tiempo se midió por medio del cálculo del coeficiente de correlación.

Pronóstico basado en análisis de fourier

En líneas generales el análisis de Fourier consiste en descomponer series de tiempo, en un conjunto de ondas regulares con fase, amplitud y periodo definido, a través de funciones seno y coseno. Debido a que la variabilidad climática representa las oscilaciones o cambios de patrón recurrente de variables atmosféricas, se decidió emplear la técnica de Fourier, considerando el método mínimos cuadrados elaborado por Dronkers y Schonfeld (1959).

Para el presente estudio, la velocidad del viento y la temperatura se aproximan entonces, a la suma de esas ondas regulares (ecuación (5)).

Donde,

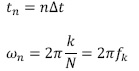
Δt: intervalo de muestreo o de registro.

N: número de observaciones de nuestra serie de tiempo.

k: es el armónico.

ω_n: es la frecuencia del k-ésimo armónico en radianes.

M: número de armónicos a determinar.

La frecuencia mínima a partir de los registros de medición o de las observaciones se calcula utilizando la ecuación (6).

La frecuencia máxima de las mediciones se calcula utilizando la ecuación (7).

Cumpliéndose que:

Los coeficientes de Fourier se calculan utilizando las ecuaciones (8) - (11)

La señal obtenida, se construyó mediante la ecuación (12).

Los coeficientes C_k y θ_k se obtiene mediante la ecuación (13) y ecuación (14).

Identificación de patrones de asociación bivariado mediante análisis de cluster k-medias

En busca de identificar si existen patrones de agrupación entre la velocidad del viento y la temperatura ambiente para cada una de las dos ciudades, se efectuó un análisis de clúster mediante el método del k-medias (k-means clustering), y para determinar el número de grupos de una manera cuantitativa, se empleó el método de identificación de silueta (silhouette).

El análisis de clúster (conglomerados) es una técnica multivariante que busca agrupar elementos (o variables), tratando de lograr la máxima homogeneidad posible en cada grupo y marcadas diferencias entre ellos; se puede combinar con otras técnicas como el ACP, y de esta forma reducir el volumen de los datos correlacionados, en un número de componentes principales representativos no correlacionados, y posteriormente hacer un análisis clúster sobre los componentes obtenidos.

La técnica de análisis de clúster puede ser de tipo jerárquico o no jerárquico, y para la presente investigación se empleó el análisis de tipo no jerárquico conocido como la metodología de K-medias. En esta metodología se seleccionan unos valores considerados base de cada conglomerado, para agrupar en torno a ellos todos los elementos que se encuentren en una determinada distancia (distancia euclidiana). Se toman los k primeros casos como grupos unitarios y se asignan el resto de casos a los grupos con el centroide más próximo, después de cada asignación se recalculan los centroides y se vuelven a asignar los individuos al centroide más próximo; iterando hasta que ningún individuo cambie de grupo cuando se haga la reasignación, de forma que tenga un comportamiento convergente. El tamaño del grupo o del conglomerado puede ser definido con base a la distancia euclidiana entre elementos (ecuación (15)).

RESULTADOS

Manejo de la información

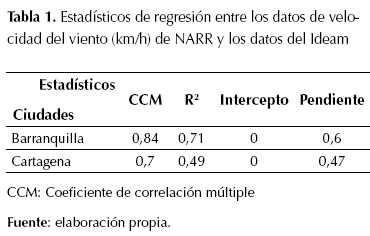
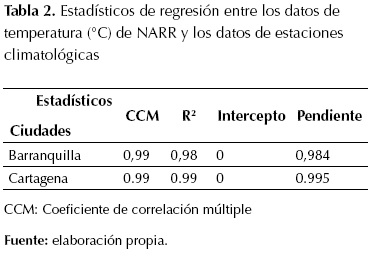
Las tablas 1 y 2 presentan el ajuste de los datos NARR, junto con los de las estaciones climatológicas del Ideam. A partir de los estadísticos de regresión para los datos de velocidad del viento y de temperatura de las ciudades de Barranquilla y Cartagena, se infirió que el ajuste era adecuado, y permitía establecer una interpolación para obtener la información trihoraria desde enero 1 de 1980 hasta diciembre 31 de 2014, de las series de tiempo bajo estudio.

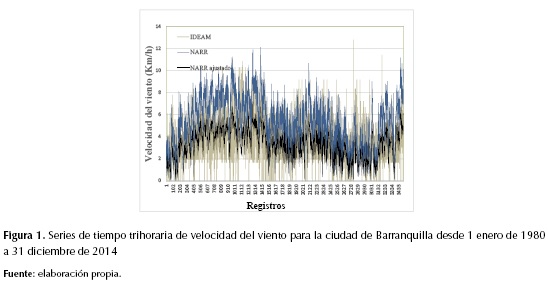
La figura 1 presenta, a manera de ilustración, las series de tiempo trihorarias de los datos tomados de NARR y los del Ideam, junto con los NARR ajustados según el modelo obtenido para la velocidad del viento en Barranquilla, Colombia.

Pronóstico basado en ACP

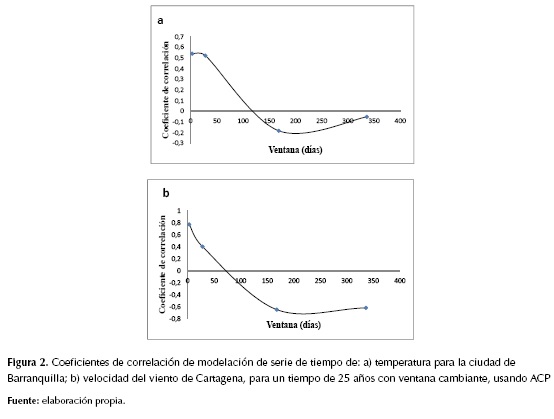
La escogencia del tamaño de la ventana se realizó a partir del coeficiente de correlación del modelo obtenido por ACP; en la figura 2, se puede observar que a medida que se aumentó el tamaño de la ventana para los datos de temperatura y velocidad del viento de Barranquilla y Cartagena respectivamente, el coeficiente de correlación se disminuyó de manera significativa.

El gráfico de sedimentación en el cual se muestran los eigenvalores l_i, o autovalores, se presenta en la figura 3 de aquí podemos observar que a partir de cierto número de componentes los autovalores permanecen constantes.

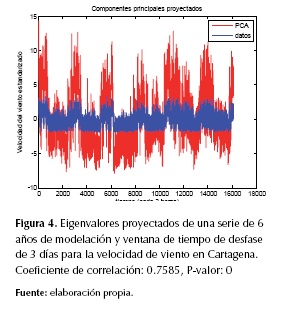
Finalmente, al proyectar los eigenvalores escogidos sobre la serie original se obtuvo el pronóstico a 25 años de velocidad del viento para la ciudad de Cartagena, con cambio de ventana de 3 días. En la figura 4 se exhibe la comparación de la proyección lograda con la serie original.

Pronóstico basado en análisis de Fourier

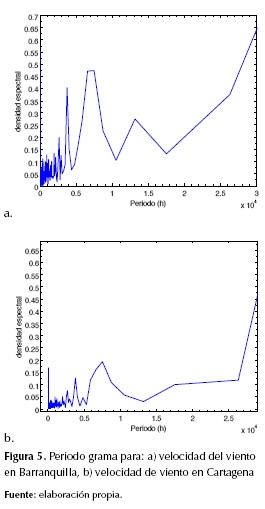
Con base en el periodograma (figura 5) de la velocidad del viento para la ciudad de Barranquilla y Cartagena, se identificaron ciclos de variabilidad de 8, 12, 24 horas; 81, 109,5, 156,41, 312,87 días; 2 años. Estos ciclos de oscilación se asocian a la variabilidad natural del parámetro, donde el ciclo de 6 años se encuentra relacionado con el fenómeno de El Niño.

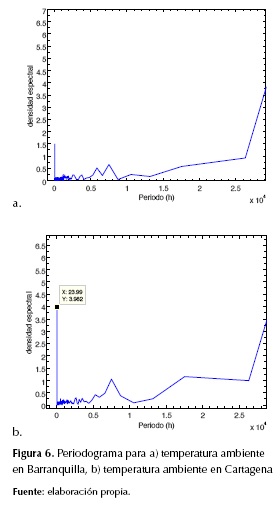
Inspeccionando los resultados de análisis espectral para temperatura ambiente (figura 6) se identificaron ciclos de variabilidad de 24 horas, 109,5 días, 312,87 días, 2 años y 6 años. Estos ciclos de oscilación se asociaron a la variabilidad natural del parámetro, donde el ciclo de 6 años esté posiblemente relacionado con el fenómeno de El Niño.

Los modos de oscilación natural para la ciudad de Barranquilla (figuras 5 y 6) fueron similares a los de Cartagena, en donde se observó un ciclo diurno, cuasitrimestral, anual, de 2 y 6 años. El ciclo cuasitrimestral puede estar asociado a los cambios de estación relacionados con los solsticios y equinoccios.

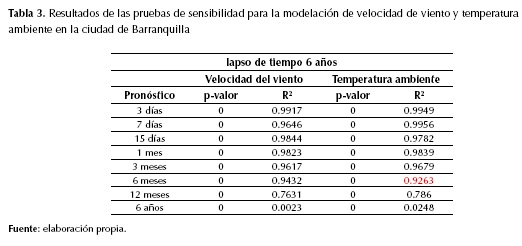
Se efectuaron las pruebas de sensibilidad mediante la variación del lapso de tiempo del conjunto de datos al cual se le efectuó el análisis de Fourier, y la variación del tiempo de modelación para las dos ciudades, obteniéndose modelos muy similares. Efectuadas las pruebas se encontró que para la ciudad de Barranquilla, se obtuvo un modelo de Fourier para el pronóstico del viento empleando una serie de tiempo trihoraria la cual debe tener un lapso de 6 años. A partir de lo anterior se obtuvo al comparar los resultados del modelo con la información satelital ajustada, un coeficiente de determinación de 0,9432 y un p-valor significativo de 0 (tabla 3).

Los resultados de la prueba de sensibilidad del modelo de Fourier construido indicaron que se puede modelar velocidad del viento y temperatura ambiente para la ciudad de Cartagena y Barranquilla hasta 6 meses según el coeficiente de determinación de 0,93 con p-valor significativo de 0 (tabla 3).

Con respecto a la temperatura se obtuvo un modelo de Fourier de temperatura para pronosticar cada 3 horas hasta 6 meses (figura 7). El momodelo de Fourier de temperatura para pronosticar cada 3 horas hasta 6 meses (figura 7). El modelo fue validado con los datos de satélite ajustado, y se obtuvo un coeficiente de determinación de 0,93 con p-valor significativo de 0.

Agrupamiento mediante k-medias

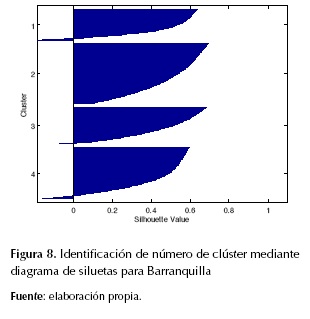
Con el objeto de identificar patrones de asociación de las variables atmosféricas, se efectuó el análisis de conglomerados. El número de grupos puede ser inspeccionado mediante el diagrama de siluetas (figura 8).

Las siluetas deben ser iguales o mayores a 0,6, de lo contrario, nos indican que los grupos no están correctamente diferenciados. Con base en los resultados en esta investigación, fue posible identificar dos grupos o clúster de asociación entre la temperatura ambiente y el viento para la ciudad de Barranquilla y Cartagena (figura 8).

A partir de la agrupación no jerárquica de clús-ter (k-medias) vista en la figura 9, se encontró que para la ciudad de Barranquilla se presentan dos patrones característicos del clima, siendo el primero de temperaturas de 25 °C y velocidad de viento de 3,5 m/s, y el segundo de 31 °C y velocidad de viento de 3,6 m/s, donde los rangos de viento y temperatura ambiente se encontraron entre 2,7 -4,7 m/s y 20-39 °C.

Los resultados de agrupación no jerárquica de clúster para la ciudad de Cartagena, evidenciaron dos patrones característicos del clima, donde el primero indicó temperaturas de 26 °C y velocidad de viento de 2 m/s, y el segundo de 29 °C y velocidad de viento de 2,2 m/s, donde los rangos de viento y temperatura ambiente se encontraron entre 0-6 m/s y 20-35 °C.

Discusión

La ventana de tiempo escogida para realizar el ACP fue de 3 días, ya que esta presentó un mejor ajuste de los datos y mayores coeficientes de correlación tanto para la temperatura como para la velocidad del viento de las ciudades de Barranqui-lla y Cartagena.

Para la temperatura de Barranquilla (figura 3a) solo fue necesaria la inclusión de siete autovalo-res, y para la velocidad del viento en Cartagena cuatro (los cuales explicaron el 70 % de la variabilidad de sistema); la inclusión de más componentes introduciría ruido en la predicción.

El ACP permitió replicar el comportamiento oscilatorio de la serie de tiempo; sin embargo, la amplitud de la señal proyectada es menor que la de la serie original, lo que indica que es necesario el uso de otra técnica en conjunto para lograr un mejor ajuste, que para la presente investigación se seleccionó un análisis de Fourier.

Con los análisis de Fourier, fue posible identificar patrones de variabilidad climática esperados, donde el ciclo diurno fue el de mayor densidad espectral para las dos ciudades y los dos parámetros. Las pruebas de sensibilidad, las cuales se efectuaron para conjunto de datos de tamaño de 1 y 6 años, se encontraron que a medida que aumenta el tamaño del lapso de tiempo, la técnica incrementa la identificación de los modos de oscilación natural. Para Barranquilla, el mejor modelo de viento mediante Fourier para la velocidad de viento y temperatura, requirió de 6 años del conjunto de información, con capacidad de pronosticar hasta de 6 meses. Con respecto a la ciudad de Cartagena, se requirió de un conjunto de datos de 6 años de duración, obteniéndose un modelo de Fourier con capacidad para modelar de manera trihoraria hasta 3 meses velocidad de viento, y 6 meses temperatura ambiente.

Los patrones de clima obtenidos mediante el análisis de clúster permitieron identificar que, para la ciudad de Barranquilla, con la forma esférica de agrupación los datos se asocian a una distribución normal conjunta, tomando como las medias los valores de los centroides de cada clúster. Para Cartagena, el comportamiento de agrupación denotó que mayores velocidades de viento se presentan con respecto a Barranquilla principalmente cuando se registran 27 °C. Se encontró que las más bajas temperaturas tienen cierto grado de asociación con velocidad de viento inferior a 2 m/s donde se registraron valores de temperatura mínimos de 20 °C y atípicos alrededor de 10 °C.

CONCLUSIONES Y RECOMENDACIONES

La asimilación de datos de reanálisis, mediante el ajuste con información in situ de estaciones climatológicas, permitió construir una serie de tiempo de 30 años con intervalos trihorarios. Las series de tiempo construidas fueron posteriormente analizadas mediante ACP, Fourier y K-medias.

El análisis de componentes principales (ACP) permitió a través de las matrices de varianza de las series de tiempo, identificar modos de oscilación contenidos en los autovalores. Los autovectores calculados mediante AES permitieron modelar con un alto grado de correlación, 25 años de velocidad del viento para la ciudad de Cartagena, con cambio de ventana de 3 días. Si bien el método AES pudo representar el periodo y la fase de la señal atmosférica, tuvo limitaciones en la amplitud de la misma. Lo anterior evidenció una debilidad en la técnica cuando se trata de obtener pronósticos con una ventana de tiempo grande.

Mediante el análisis de Fourier fue posible identificar patrones de variabilidad en diversas escalas, de las cuales se pueden mencionar la diaria, mensual, trimestral, semestral, anual, 2 años y 6 años, las cuales pueden estar asociadas a eventos climáticos locales y de orden regional como el fenómeno de El Niño. El modelo fue construido y validado con resultados estadísticos significativos, los cuales permiten emplear el modelo de Fourier para pronosticar temperatura ambiente y velocidad de viento en las localidades de estudio, hasta un lapso de tiempo de 6 meses. Con la técnica de clúster fue posible identificar dos patrones climáticos en las localidades de estudio, donde a través del centroide de cada clúster se reconocieron condiciones medias de temperatura y velocidad de viento.

En términos generales, fue posible emplear información de reanálisis, escalada espacialmente hasta las ciudades de Barranquilla y Cartagena, y validar el modelo mediante el empleo de información de estaciones climatológicas de resolución horaria. A través de ajustes de regresión fue posible ajustar la información de reanálisis, y con este se emplearon las técnicas de APC-AES, Fourier y K-medias, para identificar los principales modos de oscilación y agrupamiento de cada parámetro meteorológico. A partir de los modos de oscilación calculados mediante Fourier, se construyeron 4 modelos con capacidad de pronósticos de resolución trihoraria y de horizonte de pronóstico de 6 meses.

AGRADECIMIENTOS

Los autores agradecen a la Universidad del Norte por el apoyo financiero a través de las becas de doctorado UN-OJ-2013-22058 y UN-OJ-2013-22022, y al Departamento de Ingeniería Civil y Ambiental por el apoyo académico y administrativo.

REFERENCIAS BIBLIOGRÁFICAS

Carvajal, Y. y Marco, J.B. (2004). Análisis de variabilidad de datos medioambientales aplicando funciones ortogonales empíricas o componentes principales. Ingeniería de Recursos Naturales y del Ambiente, 1(2), 4-12.

Dronkers, J.J. y Schonfeld, J.C. (1955). Tidal computations in shallow water:. Am. Sot. Civil Engineers Proc. Hydraulics Div. A. Waalewijn (81, No. 714,49 p.).

Elsner, J.B. y Tsonis, A.A. (2013). Singular Spectrum Analysis: a new tool in time series analysis. Nueva York: Springer Science & Business Media.

García-Cabrejo, O. y Moreno-Sánchez, G. (2006). Sobre la utilización del análisis de fourier, análisis espectral singular y redes neuronales artificiales en estratigrafía. Parte 1: Teoría y caso sintético. Geología Colombiana, 31.

Giraldo, F.; León, E. y Gómez, J. (2013). Caracterización de flujos de datos usando algoritmos de agrupamiento. Revista Tecnura, 17(37), 153-166.

Instituto de Hidrología, Meteorología y Estudios Ambientales (Ideam) (2016). Recuperado el 05 de 02 de 2016, de: http://www.ideam.gov.co.

Kumar, A.; Sinha, R.; Bhattacherjee, V.; Verma, D. y Sin-gh, S. (2012). Modeling using K-means clustering algorithm. Recent Advances in Information Technology (RAIT), 1st International Conference.

Kumar, V.; Steinbach, M.; Tan, P.; Klooster, S.; Potter, C. y Torregrosa, A. (2001). Mining scientific data: Discovery of patterns in the global climate system. Joint Statistical Meeting.

Miao, C.; Chen, J.; Liu, J. y Su, H. (2015). An improved Markov chain model for hour-ahead wind speed prediction. Control Conference (CCC), 2015 34th Chinese.

Mo, K. y Ghil, M. (1988). Cluster analysis of multiple planetary flow regimes. Journal of Geophysical Research: Atmospheres, 93, 10927-10952.

NOAA (10 de octubre de 2015). Earth System Research Laboratory. Recuperado el 11 de mayo de 2016, de: http://www.esrl.noaa.gov/psd/data/gridded/data.narr.html.

Plazas-Nossa, L. y Torres, A. (2014). PCA/DFT como herramienta de pronóstico para series temporales de absorbancia registradas mediante captores UV-Vis en sistemas de saneamiento urbano. Revista Tecnura, 19(44), 47-57.

Rojo-Hernández, J.D. y Carvajal-Serna, L.F. (2010). Predicción no lineal de caudales utilizando variables macroclimáticas y análisis espectral singular. Tecnología y Ciencias del Agua, 1 (4), 59-73.

Skapa, J.; Dvorsky, M.; Michalek, L.; Sebesta, R. y Blaha, P. (2012). K-mean clustering and correlation analy-sis in recognition of weather impact on radio signal. Telecommunications and Signal Processing (TSP), 35th International Conference.

Skittides, C. y Fr�h, W. (2014). Wind forecasting using principal component analysis. Renewable Energy, 69, 365-374.

Takens, F. (1980). Detecting strange attractors in turbulence. Warwick: Springer, 1980.