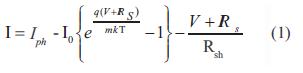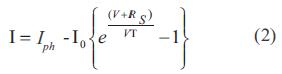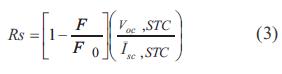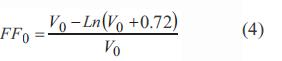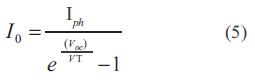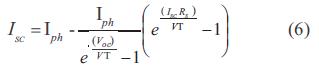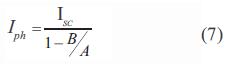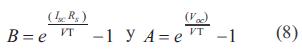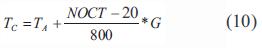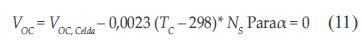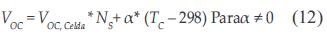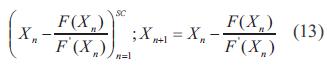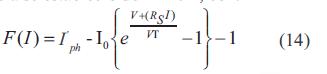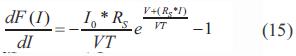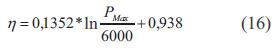Modelo de un sistema fotovoltaico interconectado

Modelo de un sistema fotovoltaico interconectado

Model of a grid connected photovoltaic system

Johann Alexander Hernández Mora¹, César Leonardo Trujillo Rodríguez², William Andrés Vallejo Lozada³

¹Ingeniero Electricista, Magíster en Ingeniería Eléctrica, Doctor en Ingeniería Eléctrica. Docente Asistente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: jahernandezm@udistrital.edu.co
²Ingeniero Electrónico, Magíster en Ingeniería Eléctrica, Doctor en Ingeniería Electrónica. Docente Asociado de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: cltrujillo@udistrital.edu.co
³Químico, Doctor en Química. Docente de la Facultad de Ciencias Básicas de la Universidad del Atlántico. Barranquilla, Colombia. Contacto: wavallejol@uniatlantico.edu.co

Fecha de recepción: 30 de agosto de 2012 Fecha de aceptación: 27 de noviembre de 2012

Resumen

En este artículo se presenta un modelo para predecir el comportamiento de un sistema fotovoltaico conectado a la red, el cual puede ser implementado ya sea en un software de programación común o en uno de simulación de sistemas eléctricos comercial. El modelo desarrollado tiene en cuenta los parámetros de entrada que influyen en el comportamiento del módulo fotovoltaico, como la radiación y la temperatura ambiente; además, involucra las diferentes partes que componen el sistema como los módulos fotovoltaicos (con sus respectivas características eléctricas y físicas), la conexión de estos para formar el generador, y el tipo de inversor. Este modelo ha sido verificado por medio de la comparación de su comportamiento con los resultados medidos en un sistema instalado en la Universidad Nacional de Colombia de 3,6 KWp, el cual hace parte de los dos primeros prototipos de generación fotovoltaica interconectada a la red en el país.

Palabras clave: sistema fotovoltaico interconectado, temperatura, radiación.

Abstract

This work presents a model to predict the performance of a grid connected photovoltaic system; this model can be implemented either in common programming software or in simulator oficommercial electric system. The model takes into account the input parameters that determinates its performance, such as radiation and temperature, the model incorporates different components of the photovoltaic's modules and their electrical and physical characteristics, furthermore the connections to become the generator and the investors. This model has been checked against a real grid connected PV system (3,6KWp) located at the Universidad Nacional de Colombia which is part of the first two prototypes ofirid connected PV system in the country.

Key words: grid-connected photovoltaic system, temperature, radiation.

1. Introducción

La masificación de las fuentes de energías limpias en los sistemas eléctricos, y la urgencia de remplazar las fuentes convencionales de energía, han creado la necesidad de estudiar el impacto que tendrían estos sistemas al conectarlos con la red eléctrica para satisfacer la demanda de energía. En el caso de los sistemas fotovoltaicos interconectados, se sabe que, dependiendo de la ubicación de estos sistemas dentro de un sistema, de la capacidad instalada y de la operación del sistema de distribución, se pueden obtener impactos positivos o negativos en la calidad de potencia que se le entrega al usuario [1].

El presente trabajo desarrolla una metodología para determinar el modelo del sistema FV, que integre todos sus componentes, y que pueda ser utilizada en un simulador de sistemas eléctricos para posteriores estudios que permitan determinar los impactos anteriormente mencionados. Dicha metodología fue realizada bajo una aplicación desarrollada en Matlab y en el software de sistemas eléctricos DIgSILENT. Sin embargo, esta puede ser probada en cualquier lenguaje de programación básico. El modelo matemático ha sido contrastado con datos reales obtenidos a través de un sistema fotovoltaico interconectado a la red, instalado en la Universidad Nacional de Colombia.

2. Modelo Del Sistema

La figura 1 muestra un esquema de un sistema fotovoltaico interconectado (SFVI) a la red y los elementos que lo componen.

El SFVI está compuesto por las siguientes unidades básicas:

• Generador FV, conformado por los módulos fotovoltaicos y su correspondiente estructura de soporte.
• El acondicionador de potencia, responsable de adaptar las características de la energía producida por el generador (DC a tensión variable) a las requeridas por la red eléctrica (AC a 120 o 208 V), también llamado convertidor DC/AC o inversor.
• El panel general de servicios, o punto de acople común (PCC - point oficommoncoupling), donde se encuentran las protecciones, o conjunto de elementos y medidas adoptadas para garantizar la seguridad del propio SFVI y la de la red eléctrica.
• El contador bidireccional de energía AC, el cual registra no solo la energía que se consume de la red, sino la que se podría estar entregando al sistema interconectado en un instante dado.
• La carga, formada por todas aquellas aplicaciones que demandan energía eléctrica para su funcionamiento.
• La red eléctrica convencional.

La herramienta desarrollada integra los componentes que participan activamente en la generación de potencia en el SFVI.

2.1 Modelo matemático del módulo fotovoltaico

La mayoría de los módulos fotovoltaicos, en la actualidad, están hechos de silicio. Lo anterior se debe a que este es un material semiconductor de gran abundancia en la corteza terrestre y actualmente es uno de los elementos más utilizados por la industria microelectrónica y computacional, lo que ha permitido su amplia masificación. Esto ha facilitado el desarrollo de métodos de síntesis y manufactura de obleas de silicio, material primario para la fabricación de módulos solares.

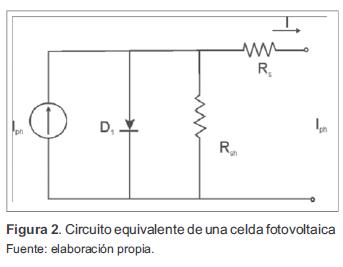
Un módulo estándar de silicio está conformado por celdas solares interconectadas en serie o en paralelo, por medio de una rejilla metálica. Cada celda solar presenta en la oscuridad un funcionamiento similar al de un diodo, y bajo la incidencia de luz se genera una corriente eléctrica como consecuencia de la generación y separación de portadores de carga en la interface de la juntura p/n de la celda solar. En la figura 2, se muestra el circuito equivalente de una celda solar fotovoltaica real típica: en el diagrama se representan las pérdidas causadas por la resistencia óhmica presente en los materiales semiconductores y los contactos eléctricos por medio de una resistencia serie (RS); las fugas de corriente en el volumen del dispositivo son representadas por medio de una resistencia paralela (RSh) [2].

El comportamiento de una celda solar es representado por la ecuación (1):

Donde Iph representa la corriente fotogenerada, Io representa la corriente de saturación del diodo, m es el factor de idealidad del diodo, R_S es la resistencia en serie, R_sh es la resistencia en paralelo, K corresponde a la constante de Boltzman, T es la temperatura absoluta de la celda y q es la carga elemental.

La experiencia comercial ha demostrado que el valor de la resistencia R_shes muy superior al valor del numerador (V + IR_S) haciendo que el tercer factor de la la ecuación (1) pueda despreciarse [3]. Adicionalmente, el factor de idealidad para celdas de silicio es m≈1 y el término kT/q se conoce como voltaje termodinámico VT. Tomando todo lo anterior, la la ecuación (1) se reduce la ecuación (2):

Un parámetro que no entrega el fabricante es el valor de R_S, y es común obtener el valor de R_S con una relación empírica obtenida por Green [5]:

Donde FF es el factor de llenado que suministra el fabricante y FFo es un factor de llenado ideal del dispositivo, cuando se supone R_S=0. El valor de FFo se puede calcular mediante la siguiente ecuación:

Donde V₀ se define como la relación entre el voltaje de circuito abierto (V_OC) y el voltaje termodinámico VT. La corriente fotogenerada Iph e Io de la la ecuación (2), a condiciones ambientales estándares (irradiación [G_X] igual a 1000 w/m² y temperatura ambiente igual a 25 °C), se puede expresar en función de V_OC y la corriente de corto circuito (I_SC).

En circuito abierto, I = 0, V = V_OC

En corto circuito, I = I_SC, V = 0

Donde:

Debido a que la corriente fotogenerada (I_ph) es directamente proporcional a la irradiación solar (G_X), la corriente fotogenerada a condiciones ambientales estándares (determinada por la ecuación (7) deberá tomar en cuenta esta dependencia. El nuevo valor de I_ph se determina segúnla ecuación (9)

Asimismo, se tiene en cuenta la temperatura ambiente para determinar la operación de las celdas que componen el módulo, ya que esta incide ligeramente en la tensión de circuito abierto y en su eficiencia. La temperatura de la celda (T_C) se determina teniendo en cuenta la temperatura ambiente (Ta) en el momento de operación y el NOCT (temperatura de operación nominal de la celda) entregado por el fabricante.

La tensión de circuito abierto se encuentra en función de la temperatura de operación de la celda y está determinada por un factor alfa entregado por el fabricante. Si dicho valor no lo entrega el fabricante se asume alfa igual a cero.

Donde N_S es el número de celdas conectadas en serie y V_OC es la tensión de circuito abierto del módulo. Las dos incógnitas que determinan la potencia de generación de los módulos (I_SC y V_OC) que se encuentran en la ecuación (2), generan una ecuación trascendente. Para dar solución a esta ecuación, se acudió a un análisis numérico por medio del método de Newton-Raphson [6] para encontrar una aproximación de las raíces de la solución. Para este caso, se tomó como punto inicial la corriente foto generada a temperatura ambiente (I_ph') y una vez seleccionado el punto inicial se desarrolló la siguiente sucesión ecuación (13):

La convergencia del método dependerá de qué tan pequeño se desee que sea el error. En este caso, la tolerancia se estableció de 1 x 10^-10, con:

En el método desarrollado, se hace un barrido de la tensión desde cero hasta la tensión de circuito abierto y, de esta forma, se pueden encontrar los valores de corriente para cada uno de los valores de tensión. Se identifican así las parejas de Tensión-Corriente y es posible determinar cuál es el punto de máxima potencia (P_MAX). Este procedimiento se hace para una de las celdas y una vez establecidas las parejas de Tensión-Corriente, estos valores se deben multiplicar por el número de celdas conectadas en serie y en paralelo respectivamente para encontrar los valores correspondientes al Módulo FV.

2.2 Pérdidas por conexión en el generador y eficiencia del inversor

Para completar el modelo matemático del Generador FV, se deben determinar las pérdidas que existen en las conexiones de los módulos fotovoltaicos y la eficiencia del inversor. Para tal fin, se utilizaron los datos medidos por un generador FV instalado en la Universidad Nacional, monitoreado por el Grupo de Materiales Semiconductores y Energía Solar (MS&ES) [7].

Para determinar las pérdidas por conexión en los módulos FV, se tuvieron en cuenta los días con radiación máxima, radiación mínima y radiación media a las 12 hora meridiano, considerando que esta es la hora en la que se alcanza la máxima generación. Lo anterior para cada uno de los 12 meses del 2009, ya que correspondía al año más completo en cuanto a mediciones se refere. Una vez establecidos los 36 días, se tomaron los valores de potencia generada cada 2 minutos, a lo largo de cada uno de estos días, para ser comparados con la potencia generada en el modelo desarrollado bajo la radiación solar y temperatura presentes en los 36 días.

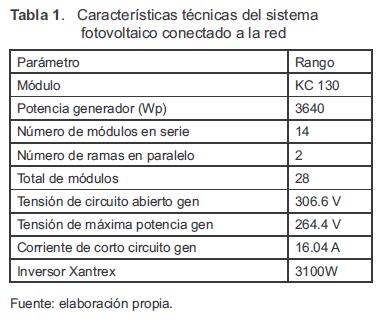
El modelo desarrollado fue verificado con el sistema fotovoltaico interconectado de potencia nominal de generador de 3640 Wp (compuesto por módulos Kyocera, instalado en la Universidad Nacional en Bogotá, Colombia.

La tabla 1 muestra las características del sistema utilizado.

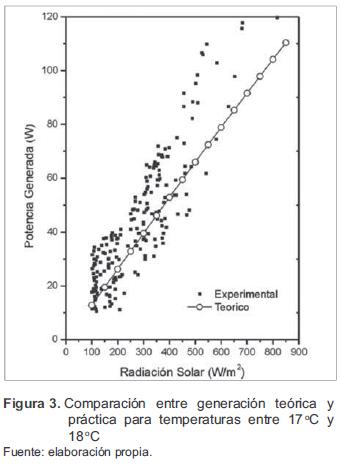
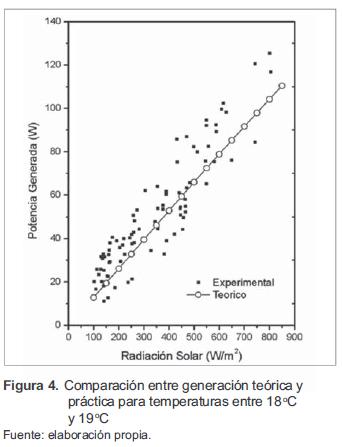
En las figuras 3 y 4 se muestran algunas de las comparaciones entre la potencia generada medida y la potencia generada simulada. Los valores de radiación menores a 100 w/m² se despreciaron, debido a que esos valores se encuentran por debajo de las horas de brillo solar (valor mínimo a partir del cual se dice que el sol brilla). Luego de comparar el comportamiento del generador FV simulado con los valores medidos, se estimó que las pérdidas por conexión de los módulos corresponden al 9.17 % de la potencia generada. Estas pérdidas son consecuencia de las resistencias propias de los materiales semiconductores y los contactos eléctricos, así como también del desgaste que se va presentando en los mismos elementos.

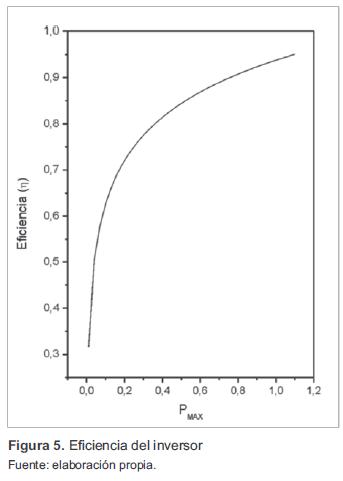
La eficiencia del inversor se calculó luego de comparar los valores medidos de la potencia AC con los valores de la potencia DC, encontrando que la relación entre la potencia DC y la eficiencia del inversor presenta un comportamiento logarítmico ecuación (16) mostrado en la figura 5. Esta ecuación puede ser utilizada para cualquier valor de potencia de entrada de inversor.

3. Resultados Y Discusión

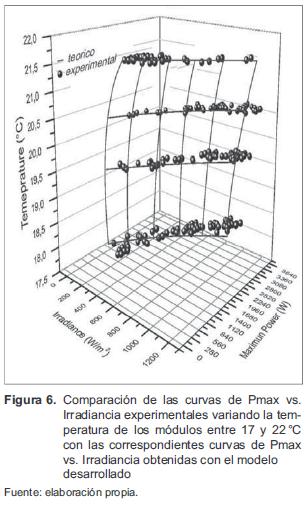
Se realizaron pruebas de campo a diferentes valores de radiación y temperatura ambiente mediante un sistema de adquisición de datos desarrollado con instrumentación virtual [7]. La figura 6 muestra de manera tridimensional el comportamiento de la potencia máxima del generador en función con la radiación y la temperatura ambiente. Además de las medidas experimentales, se presenta la potencia máxima que generaría el módulo de forma teórica, calculada mediante el modelo desarrollado, el cual se programó en Matlab, pero que puede ser desarrollado bajo cualquier plataforma de programación.

Además de obtener la potencia máxima de salida en un sistema FV interconectado, el algoritmo desarrollado puede ser integrado en un simulador especializado en flujos de carga eléctricos que permita hacer aplicaciones por parte del usuario, y así poder extender los análisis a estudios eléctricos como flujos de carga en una red con presencia de generación distribuida de origen fotovoltaica. Para este propósito, se ha implementado el modelo dentro del programa de cálculo PowerFactory, desarrollado por DIgSILENT, el cual es una herramienta diseñada para el análisis de sistemas eléctricos de potencia. La precisión y validez de los resultados obtenidos con este paquete, han sido confirmadas en un gran número de implementaciones, por organizaciones dedicadas a la planeación y operación de sistemas de potencia. Las funciones integradas permiten desarrollar flujos de carga, cálculos de corto circuito, análisis de armónicos, coordinación de protecciones, cálculos de estabilidad, entre otros. PowerFactory permite, a través de DIgSILENT Programming Language (DPL), la automatización de procesos. Gracias a su interfaz desarrollada, es posible crear rutinas personalizadas, ya que permite cálculos iterativos, llamar subrutinas y objetos del Power-Factory, y hacer uso de expresiones matemáticas, entre otras [8].

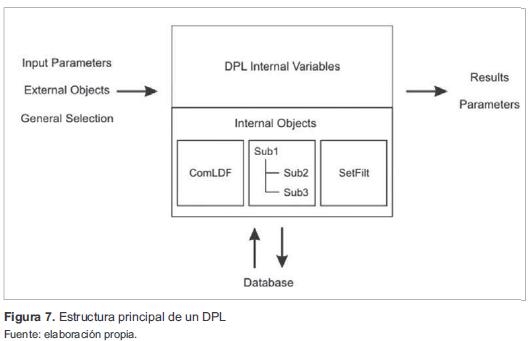
En un análisis de flujo de carga, un sistema FV se puede simular como un nodo de carga de potencia constante P-Q (con un factor de potencia conocido, que en la mayoría de la veces es de valor 1) con valor de potencia consumida equivalente negativa, la cual representa la potencia máxima de salida del generador [9] - [14]. Para la presente aplicación, el algoritmo mencionado se integró como una librería DPL, en la cual los parámetros de entrada variables son la radiación y la temperatura ambiente, los fijos son las características propias del generador, como el número total de módulos, las conexiones entre sí y el tipo de inversor, y el valor de salida es la potencia máxima del generador. Todo este conjunto integrado (DPL del sistema FV-Carga de potencia negativa) representa, entonces, el sistema fotovoltaico interconectado SFVI para ser utilizado en cualquier aplicación de PowerFactory. En la figura 7 se observa la estructura de un DPL [8].

4. Conclusiones

El programa desarrollado para calcular los principales parámetros que caracterizan el comportamiento de un sistema fotovoltaico interconectado, reproduce de forma adecuada su funcionamiento en condiciones normales de operación, las cuales, en la mayoría de las veces, son distintas a las condiciones estándar. Este instrumento es una herramienta muy útil para el diseño de sistemas fotovoltaicos ya que estos suelen hacerse en muchas ocasiones sin tener en cuenta las correcciones por temperatura presente en el lugar de la instalación.

Una vez seleccionado el modelo matemático del módulo FV, se realizó una aproximación de las pérdidas causadas por las conexiones en serie y paralelo de dicho módulo, además de establecer la eficiencia del inversor. Dicha aproximación se comprobó con datos reales de generación. Asimismo, se comprobó que este modelo se puede utilizar con cualquier lenguaje de programación, lo que facilita la inclusión de los generadores FV en programas especializados de sistemas eléctricos que no los tengan incluidos dentro de sus librerías.

Referencias

[1] N. Srisaen and A. Sangswang, "Effects of PV Grid-Connected System Location on a Distribution System", in IEEE Asia Pacific Conference on Circuits and Systems, Dec. 2006.

[2] T. Markvart and L. Castañer, Practical Handbook of Photovoltaics: Fundamentals and Applications, Oxford: Elsevier, 2003.

[3] M. C. Alonso García and J.L. Balenzategui, Estimation of photovoltaic module yearly temperature and performance based on Nominal Operation Cell Temperature calculations, Renewable Energy, Oxford: Elsevier, 2004.

[4] D.A. Neamen, Semiconductor Physics and Devices.McGraw Hill, New York, 1997.

[5] M.A. Green, Solar cells. Operating principles, Technology and System Applications, New Jersey: Prentice-Hall, 1982.

[6] A.A. Samarski, Introducción a los métodos numéricos, Moscú: Editorial Mir, 1986.

[7] N. Forero, J. Hernández and G. Gordillo, "Development of a monitoring system for a PV solar plant", in Energy Conversion and Management, January 2006.

[8] DIgSILENT Group, Powerfactory 14.0 user´s manual, Gomaringen, Germany: DIgSILENT GmbH, July 2010.

[9] L.M. Ayompe, A. Duffy, S.J. McCormack and M. Conlon.Validated real-time energy models for small-scale grid-connected PVsystems, Energy, July 2010.

[10]Syafi, M.N. Khalid and A. Mamdouh, "Grid-Connected Photovoltaic Models for Three-Phase Load Flow Analysis", in IEEE International Conference on Power and Energy (PECon2010), Nov 29 - Dec 1, 2010.

[11] M. Djarallah and B. Azoui, "Grid Connected Interactive Photovoltaic Power FlowAnalysis: A Technique for System Operation Comprehension and Sizing", in 41st International Universities Power Engineering Conference, 2006, UPEC ‘06.

[12] Wang Yi-Bo, Wu Chun-Sheng, Liao Hua and Xu Hong-Hua, "Steady-state model and power fow analysis ofirid-connected photovoltaic power system", in 2008 IEEE international conference on industrial technology (IEEE ICIT 2008).

[13] F. Delfino, R. Procopio, M. Rossi, and G. Ronda, "Integration of large-size photovoltaic systems into the distribution grids: a p-q chart approach to assess reactive support capability", in Renewable Power Generation, IET. 2010, pp. 329-340.

[14] V, Jukka Paatero and D. Peter Lund, "Effects of large-scale photovoltaic power integrationon electricity distribution networks", Renewable Energy, vol. 32, Issue 2, February 2007.