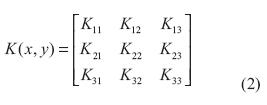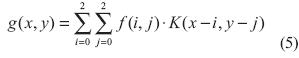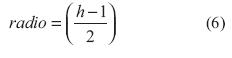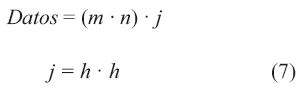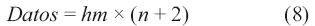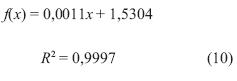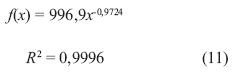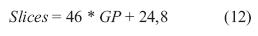Procesamiento paralelo en FPGA para convolución de imágenes usando Matlab

Procesamiento paralelo en FPGA para convolución de imágenes usando Matlab

Parallel processing on FPGA for image convolution using Matlab

Diego Armando Giral Ramirez¹, Ricardo Romero Romero², Fernando Martínez Santa³

¹Ingeniero eléctrico, estudiante de Maestría en Ingeniería Eléctrica, Universidad de los Andes, Bogotá, Colombia. Contacto: da.giral10@uniandes.edu.co
²Ingeniero eléctrico, Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: rromeror@udistrital.edu.co
³Ingeniero eléctrico, magíster en Ingeniera Electrónica y de Computadores, docente de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: fmartinezs@udistrital.edu.co.

Fecha de recepción: 15 de febrero del 2014-Fecha de aceptación: 15 de agosto del 2014

Clasificación del artículo: Investigación
Financiamiento: Universidad Distrital Francisco José de Caldas

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.1.a09

Resumen

Este artículo describe el diseño de dos arquitecturas para un filtro de convolución de imágenes, que mediante Hardware cosimulation del toolbox de Matlab Xilinx System Generator son implementadas en una FPGA Xilinx Spartan 3AN. El proyecto nace con el propósito de evaluar el rendimiento del procesamiento paralelo de imágenes con respecto al procesamiento en serie. Inicialmente se realiza el diseño y la implementación en hardware de las dos arquitecturas. Después, a partir de la medición de variables específicas, se selecciona la mejor arquitectura como alternativa de paralelización. Haciendo uso de las herramientas que brinda el toolbox, se evalúa la relación entre grado de paralelismo, tiempos de ejecución y recursos hardware utilizados. Finalmente, y entre las conclusiones más importantes, se obtiene que el tiempo de procesamiento de la imagen es reducido notablemente a medida que aumenta su grado de paralelización.

Palabras clave: arreglos de compuertas programables, convolución, grado de paralelismo, cosimulación de hardware, Xilinx System Generator.

Abstract

This paper shows the design of two convolution image filter architectures, which use Hardware cosimulation through Xilinx System Generator Matlab toolbox to be implemented in a Xilinx Spartan 3AN FPGA. The purpose of the project is to evaluate the performance of parallel image processing versus the serial one. Initially the design and hardware implementation of the two architectures are performed, after, from the measurement of specific variables the best architecture is selected as an alternative for parallelization, using the tools provided by the toolbox evaluates the relationship between the degree of parallelism, execution times and hardware resources used , and finally among the most important conclusions are obtained that the processing time of the image is significantly reduced with increasing the degree of parallelization of the image.

Keywords: convolution, degree of parallelization, field programmable gate array, hardware cosimulation, Xilinx System Generator.

Introducción

El origen del procesamiento digital de imágenes, por el alto nivel de procesamiento que estas requieren, se encuentra directamente relacionado con el desarrollo y la evolución de las computadoras. La mayoría de filtros para imágenes que enfocan, desenfocan, realzan bordes y detectan bordes, entre otras, utilizan la convolución como operación matemática. El procesamiento de imágenes es un área de investigación muy extensa con un gran número de aplicaciones en múltiples campos como: las ciencias exactas, la medicina, la ingeniería (eléctrica, mecánica, automotriz, civil, etc.), la navegación aeronáutica, la navegación marítima, entre otras; sin embargo, presenta problemas en su implementación por la velocidad de procesamiento y los tiempos de desarrollo (Gonzales y Woods, 2002).

El diseño de algoritmos para múltiples aplicaciones, tradicionalmente se fundamenta en procesos seriales, que requieren la culminación de una instrucción para la ejecución de la siguiente. El procesamiento en paralelo como técnica de programación permite ejecutar de manera simultánea varias instrucciones, resolviendo a bajo costo y de manera eficiente los inconvenientes que surgen en problemas específicos con la programación en serie y los problemas de implementación y tiempos de desarrollo en el procesamiento de imágenes (Rodríguez Pérez, 2010; Garces Socarras, 2012).

Las FPGA (Field Programmable Gate Array) son dispositivos compuestos por bloques lógicos que permiten ser reprogramados a voluntad del usuario. Los lenguajes de programación para FPGA más utilizados, entre otros, son: VHDL, ABEL y Verilog. Su objetivo es acelerar el proceso del diseño; sin embargo, hoy existe software que permite realizar la programación de este tipo de dispositivos, sin necesidad de tener un conocimiento exhaustivo de algún lenguaje de descripción de hardware, como por ejemplo Matlab y LabView, que son programas de uso frecuente por sus amplias herramientas (Boemo Scalvinoni, 2005; López Vallejo, 2004; Sánchez Élez, 2014).

Metodología

El diseño de la arquitectura y la implementación se ejecuta en cuatro etapas: en la primera se selecciona la herramienta de trabajo, en la segunda se realiza el estudio de la etapa de preprocesamiento, procesamiento y posprocesamiento basado en el análisis matemático, en la tercera se diseña la arquitectura y en la cuarta se implementa y se obtienen las respectivas métricas de evaluación.

Xilinx System Generator

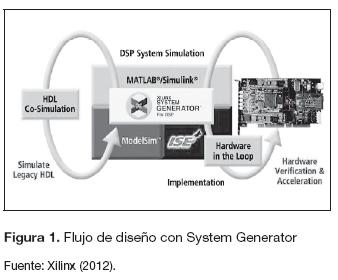
Xilinx System Generator cuenta con la posibilidad de realizar cosimulaciones, esta herramienta permite utilizar la FPGA como unidad de procesamiento, con señales de entrada y salida desde Matlab (figura 1) (Xilinx, 2012; Raygoza, Ortega, Cabrerae Ibarra, 2009).

Adicionalmente a la cosimulación y entre muchas más herramientas, el toolbox cuenta el con el "Xilinx Mcode", que permite incorporar códigos basados en funciones de Matlab. El bloque traduce los M-code en un equivalente de lenguajes de descripción de hardware (Verilog/VHDL). Cuando se realiza la implementación en la tarjeta, el bloque admite un subconjunto limitado de instrucciones de Matlab, pero son instrucciones suficientes para implementar funciones aritméticas, máquinas de estados finitos y lógica de control. El segundo bloque: "Resource Estimator" proporciona una estimación de los recursos que requiere la FPGA para implementar el diseño creado en Simulink. En la etapa de diseño y medición se profundizará en detalle sobre estos bloques (Xilinx, 2012; Moctezuma, Sánchez, Álvarez y Sánchez, 2007).

Preprocesamiento, procesamiento y posprocesamiento

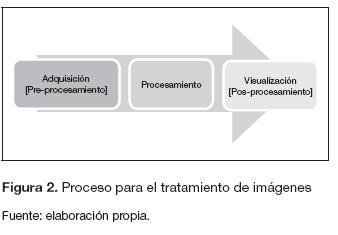
La base del diseño de la arquitectura son las etapas del procesamiento digital de imágenes. El proceso se clasifica en tres etapas: adquisición, procesamiento y visualización. La figura 2 muestra el flujo de las tres etapas (Gonzales y Woods, 2002).

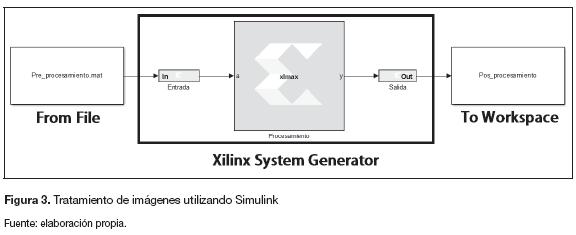
Con el propósito de obtener la mejor arquitectura basada en resultados comparativos se realizan dos diseños con el mismo filtro. La diferencia se encuentra en la cantidad de datos que llegan a la etapa de procesamiento. El preprocesamiento y el posprocesamiento para ambos diseños se realizan directamente con los bloques de Simulink, mientras que el procesamiento será con la librería de Xilinx System Generator (figura 3).

Las entradas y las salidas de la arquitectura dependen directamente del procesamiento. Por este motivo, el diseño general de la arquitectura parte de la segunda etapa de la figura 2.

Procesamiento. El diseño de la etapa de procesamiento se realiza de acuerdo con el filtro de convolución que se va a implementar. Se considera f(x,y) como una imagen de m*n píxeles (ecuación (1)), donde cada uno de los elementos que componen la matriz representa un pixel de la imagen (Garces Socarrás, 2012; Forero Vargas y Arias Cruz, 2001; Rodríguez Cruz, Rivero Flores y Castillo Atoche, 2006).

La matriz de convolución o matriz kernel K(x,y) puede tomar cualquier tamaño dependiendo del filtro que se desee aplicar. Para el desarrollo de este trabajo se utiliza un kernel de 3 x 3 (ecuación (2)).

A fin de aplicar convolución a los bordes de la imagen, es necesario proporcionarle un marco que no altere la imagen. La ecuación (3) muestra el marco de ceros adicional que se agrega a la matriz f(x,y), modificando el tamaño de f(x,y) a (m+2)*(n+2) pixeles.

La convolución se define matemáticamente para modelos bidimensionales a partir de la ecuación (4), donde g(x,y) representa el resultado de convolución entre la imagenf(x,y) de (m+2)*(n+2) pixeles y un kernel de tamaño h^xh (Forero Vargas y Arias Cruz, 2001; Rodríguez Escudero , 2013).

Para el caso particular cuando h = 3 (ecuación (2)), la ecuación (4) se transforma en la expresión descrita en la ecuación (5) (Rodríguez Escudero, 2013).

La ecuación (5) se traduce en la sumatoria de la multiplicación de todos lo pixeles de la imagen con el correspondiente valor del coeficiente de kernel. Finalmente, se obtiene una imagen procesada en todos los puntos de la imagen original menos en el marco de ceros adicionado (Garces Socarras, 2012; Rodríguez Cruz, Rivero Flores y Castillo Atoche, 2006).

El procesamiento de imágenes con convolución trabaja a partir del radio de los pixeles circundantes al pixel (x,y), el radio se determina a partir de la ecuación (6) (Garces Socarrás, 2012; Rodríguez Cruz, Rivero Floresy Castillo Atoche, 2006).

Remplazando en la ecuación (6) el valor de h=3, se obtiene que el radio=1 para la arquitectura que se va a implementar.

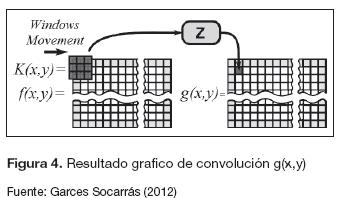
En la figura 4 se presenta de forma gráfica el resultado de convolución g(x,y) entre la imagen f(x,y) de (m+2)*(n+2) pixeles y un kernel de tamaño 3*3 con radio=1.

A partir de la figura 4 es claro que para un kernel de 3*3 el bloque de convolución debe procesar 9 datos al mismo tiempo, este criterio es la base del diseño de la etapa de preprocesamiento.

Preprocesamiento. Como se muestra en la figura 3, el preprocesamiento se realiza llamando un archivo *.mat creado desde el workspace de Mat-lab. La conexión entre el preprocesamiento y el procesamiento se realiza a partir del "Xilinx Gateway In". Este bloque realiza la conversión del dato de Simulink a datos de tipo booleano, punto fijo o coma flotante, sin signo o con complemento A2; es la puerta de enlace entre los bloques de Si-mulink y los bloques de Xilinx System Generator. Cuando se realiza la implementación en hardware de la arquitectura, cada "Xilinx Gateway In" define las entradas en el lenguaje de descripción de hardware, y por lo tanto en la FPGA (Garces Socarrás, 2012; Xilinx, 2012).

Sin embargo, el "Xilinx Gateway In" recibe únicamente datos de tipo integer, single o doublé; no recibe arreglo de datos (Garces Socarras, 2012; Xilinx, 2012), por lo tanto, no es posible que los nueve datos de la figura 4 se entreguen al bloque de procesamiento en forma matricial; sin embargo, se pueden usar múltiples entradas que permitan construir el arreglo de datos en forma de un vector columna de nueve elementos, donde cada dato representa el pixel circundante al pixel (x,y) de f(x,y).

La etapa de preprocesamiento consiste en diseñar el algoritmo que permita entregarle en forma de vector y de manera lógica los datos al bloque de procesamiento.

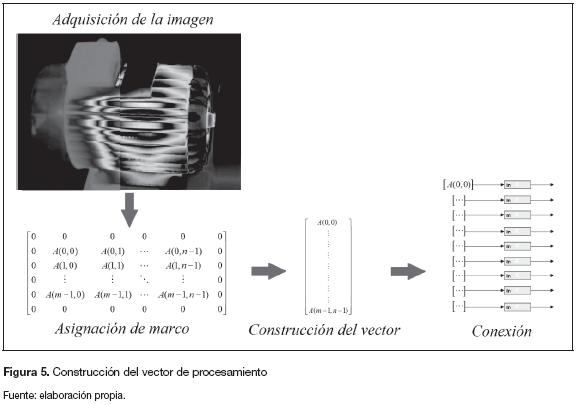
La figura 5 presenta las cuatro partes que intervienen en el algoritmo de preprocesamiento:

• Adquisición de la imagen: se lee la imagen a color desde una ruta específica y se convierte a escala de grises para que el procesamiento se realice sobre una única matriz.
• Asignación de marco: se enmarca con ceros la matriz de la imagen.
• Construcción del vector: se convierte la matriz en un vector. Este tiene una construcción específica la cual hará que tenga datos repetidos; es la primera diferencia entre arquitecturas.
• Conexión: se realiza la conexión entre el pre-procesamiento y el procesamiento.

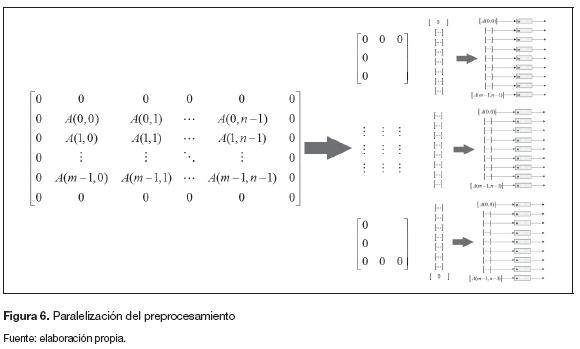
El preprocesamiento tiene una etapa adicional a las que se muestran en la figura 5, se encuentra ubicada entre la segunda y la tercera parte y consiste en dividir la matriz principal en pequeñas submatrices (figura 6). El objetivo es paralelizar la arquitectura tantas veces como sea posible en la verificación de hardware. El número de veces que se pueda dividir en pequeñas submatrices se define como grado de paralelismo y es uno de los datos que se espera determinar a partir de las co-simulaciones.

Posprocesamiento. El posprocesamiento es la etapa encargada de construir la matriz de datos g(x,y). A diferencia del preprocesamiento trabaja con un único dato de entrada y es el resultado de la convolución entre los nueve datos de la matriz f(x,y) y la matriz kernel de 3*3. El algoritmo de posprocesamiento tiene la misma estructura para las dos arquitecturas.

Como se muestra en la figura 3, el posprocesamiento se realiza llevando los datos de salida del Xilinx System Generator al workspace de Matlab. Al igual que en el preprocesamiento, la conexión entre el procesamiento y el posprocesamiento se realiza a partir del "Xilinx Gateway Out", este bloque realiza la conversión del dato de Xilinx System Generator a datos de tipo integer, single o doublé de Simulink (Garces Socarras, 2012; Xilinx, 2012).

Cuando se realiza la división de la matriz f(x,y) en submatrices (figura 7), el algoritmo de posprocesamiento debe además unificar los resultados de cada subprocesamiento para reconstruir nuevamente la imagen en una sola matriz.

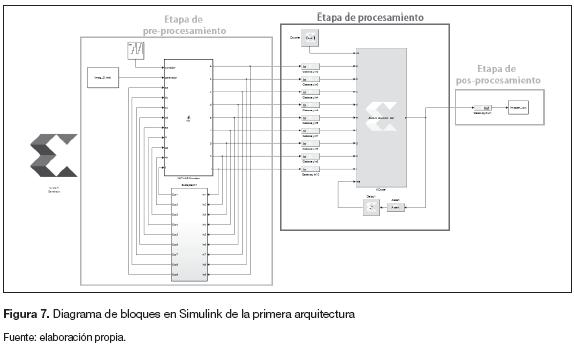
Primera arquitectura (memoria para nueve datos). La figura 7 muestra el diagrama de bloques en Simulink de las tres etapas de la arquitectura.

Preprocesamiento. Como se observa en la figura 7, el preprocesamiento le entrega a la nueva etapa de procesamiento datos de entrada, el principio de funcionamiento consiste en posicionar cada elemento del vector a partir de un contador ascendente entre 0 y 8.

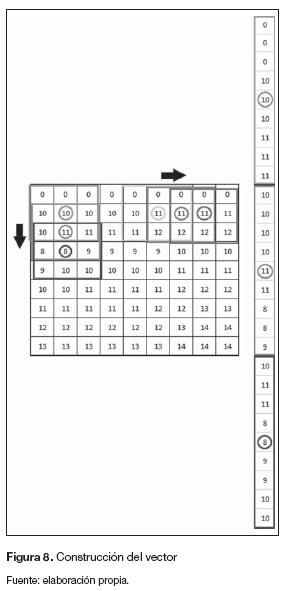
El objetivo es que el bloque de procesamiento realice la operación de convolución únicamente cuando los nueve datos estén posicionados, para mantener los datos hasta que se cumpla esta condición el bloque de preprocesamiento retroalimenta sus salidas. El vector se construye a partir del radio de los pixeles circundantes al pixel (x,y), como se muestra en la figura 8.

Para determinar el tamaño del vector se utiliza la ecuación (7), la cantidad de datos que envía esta arquitectura es j veces mayor que la imagen original.

Donde

m: cantidad de filas de la imagen
n: cantidad de columna de la imagen
h: filas o columnas de la matriz kernel.

Procesamiento

La etapa de preprocesamiento se implementa mediante el bloque Mcode del toolbox de Xilinx System Generator, cuenta con once entradas, una para el contador que permite posicionar cada dato, nueve para los datos que se van a procesar y la última para mantener el dato retroalimentado la salida.

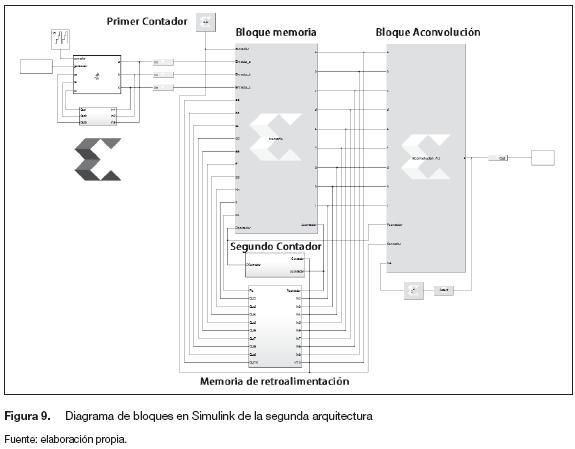
Segunda arquitectura (memoria con corrimiento). La construcción de la segunda arquitectura, además de comparar resultados, se diseña con el objetivo de reducir la cantidad de datos que se van a procesar. La figura 9 muestra el diagrama de bloques en Simulink de las tres etapas de la arquitectura.

Preprocesamiento. A diferencia del primer diseño, la etapa de preprocesamiento se encarga únicamente de posicionar tres datos con el contador ascendente. La construcción del vector de nueve datos se diseña para que sea realizada en la etapa de procesamiento (figura 9). Para esta arquitectura se incorporan tres bloques adicionales.

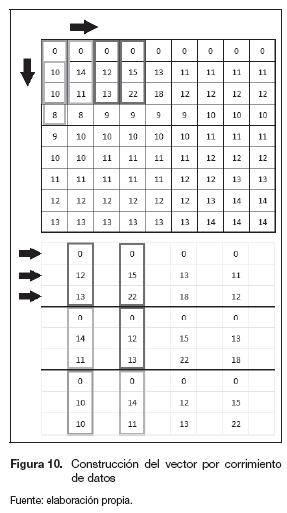
Procesamiento. Para la construcción del vector de nueve datos, la arquitectura realiza un corrimiento de posición de los tres datos entregados por la etapa de preprocesamiento, este corrimiento se realiza hasta que se acumulen la totalidad de los datos necesarios para hacer la convolución. En la figura 10 se presenta un ejemplo de la manera en que se realiza el corrimiento.

Para determinar el tamaño del vector que equivale a la cantidad de datos que se van a enviar a la etapa de procesamiento, se utiliza la ecuación (8).

Donde

m: cantidad de filas de la imagen
n: cantidad de columnas de la imagen
h: filas o columnas de la matriz kernel.

En la demostración descrita en la ecuación (9) se determina que la segunda arquitectura reduce la cantidad de datos que se van a procesar, para cualquier valor de m y n el resultado de la ecuación (8) siempre es menor que el resultado de la ecuación (7).

Sea:

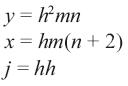
Probar que x < y

Si y = ax, si a > 1, significa que x < y Entonces:

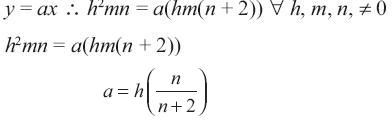
Como n εN, entonces

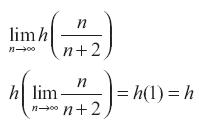
Luego a = h cuando n→∞

Se concluye que a > 1 si h > 1 (9)

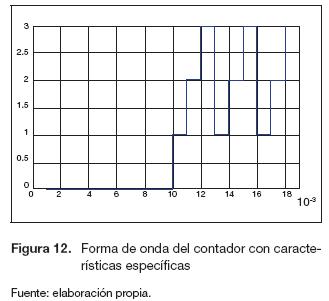
El bloque de memoria (figura 9) encargado de realizar el corrimiento dispone de tres sistemas adicionales: un bloque de memorias para la retroalimentación (se implementa para mantener los datos) y dos contadores, el primero es un contador libre ascendente que inicia en cero y se utiliza para posicionar los primeros nueve datos, en tanto que el segundo contador (figura 12) tiene dos características específicas.

• Debe iniciar el conteo después de que se posicionan los primeros nueves datos.
• Después de ser activado debe contar de cero a tres una sola vez, luego debe contar de uno a tres.

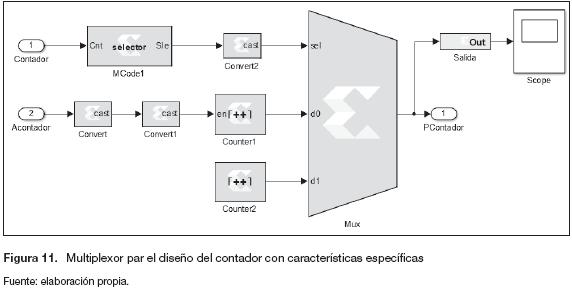
Para poder cumplir con las características específicas se implementa un multiplexor (figura 11) con dos entradas (d0, di), la señal de control (sel) se programa mediante un bloque "Xilinx Mco-de" y las entradas son dos contadores adicionales (Counter 1, Counter 2), uno que cuenta de cero a tres y el otro que lo hace de uno a tres.

En la figura 12 se muestra la señal obtenida del diagrama de bloques de la figura 11.

Implementación

La implementación de las arquitecturas se realiza en dos partes, la primera consiste en realizar la comprobación mediante la simulación (directamente sobre software), y en la segunda se compila el algoritmo para que genere el bloque de cosimulación y poder correr la arquitectura en la FPGA.

En ambos casos los ajustes se deben realizar sobre el "System Generator Token", que es el panel de control principal del toolbox que se utiliza para configurar los parámetros del sistema y de la tarjeta. Todos los modelos de Simulink que contengan blockset de Xilinx deben contener este panel de control para poder simular (Xilinx, 2012).

Simulación por software. Realizados los ajustes del "System Generator Token" se realiza la simulación de las arquitecturas, como cualquier otro modelo realizado en Simulink. Con esta simulación se identifican y solucionan errores y, además, se puede verificar que la arquitectura cumpla con los objetivos esperados.

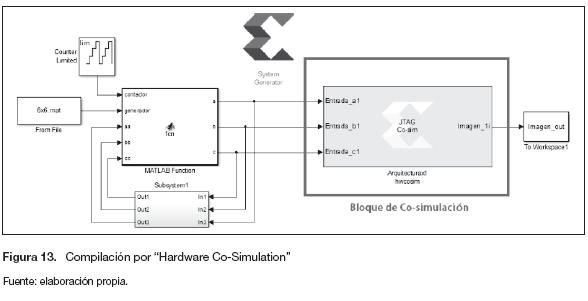
Implementación en FPGA. La tarjeta sobre la cual se implementa la arquitectura es una Xilinx Spartan 3AN - XC3S700AN. Para utilizar la FPGA como unidad de procesamiento, se debe crear el bloque de cosimulación. Cuando se genere la compilación para "Hardware Co-Simulation" con la configuración de la referencia de la tarjeta que se va a utilizar, Matlab genera el archivo de configuración bitstream, el cual es asociado a un nuevo bloque. En la figura 13 se muestra la segunda arquitectura con el bloque de cosimulación. Como se puede observar, toda la etapa de procesamiento de la figura 9 es remplazada por el bloque de cosimulación (Xilinx, 2012).

Cuando el modelo de la figura 13 se simula en Simulink, los resultados son calculados en hardware y son regresados a la computadora por medio de la conexión JTAG. Esto permite probar el diseño a nivel hardware, pero corriendo la simulación desde Simulink.

Para la simulación de las arquitecturas con los bloques de cosimulación, es necesario que Matlab responda rápidamente. Además, debe trabajar por encima de los servicios de primer y segundo plano que ejecute el sistema operativo en el momento de la simulación, y esto se logra dándole prioridad de tiempo real en el administrador de tareas de Windows.

Timing and power analysis. Adicionalmente a la compilación "Hardware Co-Simulation", el "System Generator Token" cuenta con un análisis de tiempo y potencia llamado "Timing and Power Analysis", que permite a los diseñadores analizar los requerimientos de potencia-energía y las frecuencias de reloj máximas. Esta herramienta se utiliza para determinar los tiempos según las frecuencias de reloj máximo y poder concluir según los resultados obtenidos (Xilinx, 2012).

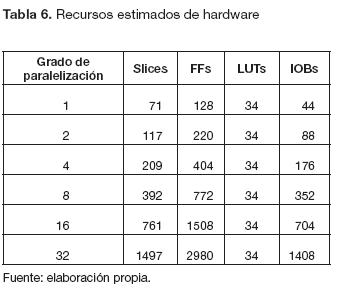
Recursos de hardware. A fin de estimar los recursos que requiere la FPGA para implementar el diseño de la arquitectura creado en Simulink, se utiliza el bloque "Xilinx Resource Estimator". La estimación de estos recursos se realiza para siete campos: slices (generalmente compuestos por dos flipflops, dos LUTs, algunos multiplexores y una pequeña lógica de control), lookuptables (LUTs), flipflops (FFs), bloques de memoria (BRAM), multiplicadores 18x18, buffers tri-estado y puertos de entrada/salida (IOBs) (Xilinx, 2012;Moc-tezuma Eugenio y Torres Huitzil, 2006).

Análisis de resultados

Terminada la etapa de diseño de las arquitecturas se realizan las respectivas pruebas de funcionamiento. Estas consisten en:

1. Generación de la imagen aplicando un filtro específico de convolución a partir de la simulación de las arquitecturas diseñadas.
2. Estimación de los tiempos de comunicación entre la FPGA y el software de desarrollo.
3. Comparación de los tiempos promedios del procesamiento en paralelo de la imagen en la FPGA corriendo la simulación desde Simu-link para las dos arquitecturas diseñadas.
4. Establecer el grado de paralelismo de la arquitectura seleccionada. Se realiza la comparación del rendimiento del procesamiento paralelo vs. el procesamiento en serie.
5. Analizar la relación entre el grado de paralelismo y la cantidad de recursos hardware utilizados en la implementación de la arquitectura.

Debido a que la implementación de las arquitecturas depende de la relación software (Matlab) hardware (FPGA), es importante mencionar que las respectivas pruebas de funcionamiento y mediciones se realizaron sobre un computador Intel(R) Core (TM) i5-2450M CPU 2,50 GHz (4 CPU), con memoria ram de 6 GB.

Generación de la imagen aplicando un filtro de convolución

Para verificar el funcionamiento de las arquitecturas diseñadas como alternativa de paralelización, se realiza una comparación de las imágenes resultantes entre las dos arquitecturas y un script. La figura 14 muestra una imagen termográfica de un motor eléctrico en funcionamiento, esta es la imagen que se va a procesar en las dos arquitecturas y con la cual se realizará el análisis comparativo. Se utiliza el filtro de convolución de realce y la imagen se convierte a escala de grises con el objetivo de procesar una única matriz.

Los resultados de la imagen procesada por la primera y por la segunda arquitectura se muestran en la figura 15 (a) y (b), respectivamente.

La comparación se realiza a partir de la matriz de datos de cada una de las imágenes, utilizando la instrucción isequal (A,B) de Matlab (Math Works, 2013). Si el resultado es cero las matrices A y B son diferentes, pero sí es uno las dos matrices son iguales. El resultado de la comparación entre las figuras 15 (a) y 15 (b) fue de uno, lo cual indica que las dos arquitecturas están funcionando y son capaces de aplicar filtros de convolución. Es importante resaltar que las dos arquitecturas están en la capacidad de aplicar cualquier filtro de convolución siempre que el kernel sea de 3x3. Para realizar la comparación entre arquitecturas y el script se selecciona la matriz de la figura 15 (b), el resultado obtenido también fue de uno.

Medición de los tiempos de comunicación

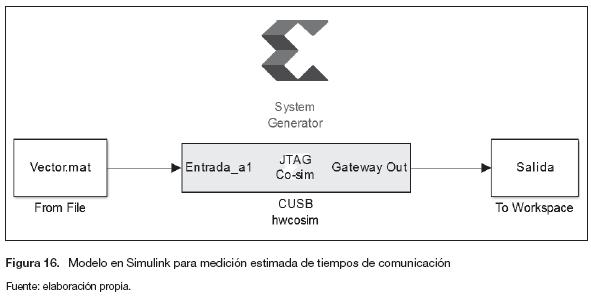
Para realizar una medición estimada de los tiempos de comunicación, se implementa una metodología que incluye un diseño adicional, el cual permite enviar diferentes cantidades de datos sin ningún tipo de procesamiento (figura 16).

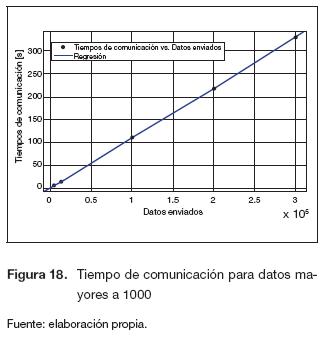
El modelo de la figura 16 envía un tren de 2ⁿ datos, donde n es un número natural. La medición de los tiempos se realiza utilizando las instrucciones tic toc de Matlab, a partir de los datos medidos se construyen las figuras 17 y 18.

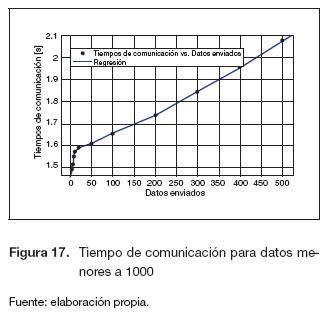
En la figura 17 se observa una mayor pendiente para valores menores a 50, debido a que hay una mayor concentración de puntos, además se observa una variación no considerable en el tiempo que varía entre 1 y 1,6 [s]. Para datos mayores a 50 se presenta un comportamiento lineal en aumento, con una variación pequeña en el tiempo pero mayor al rango anterior. En la figura 18 se muestra que para una mayor cantidad de datos, el tiempo de comunicación aumenta. La ecuación (10) describe el comportamiento de esta figura.

La ecuación (10) permitirá estimar el tiempo de comunicación y establecer un parámetro de medición de los tiempos de implementación de las arquitecturas.

Comparación de los tiempos promedios del procesamiento

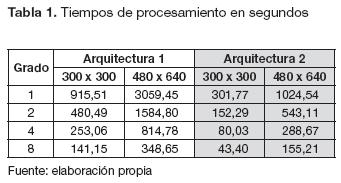
En la tabla 1 se muestra la comparación de los tiempos promedios del grado de paralelismo de la imagen en la FPGA, utilizando las dos arquitecturas y para dos tamaños de imágenes diferentes: una de 300 x 300 y otra de 480 x 640 pixeles. En la arquitectura 2 se obtiene una mayor eficiencia, en razón de la considerable disminución del tiempo de procesamiento de la imagen, casi a la tercera parte del tiempo utilizado por la arquitectura 1. Este resultado era de esperarse, debido la demostración realizada en la ecuación (9).

A partir de los resultados de la tabla 1, la arquitectura 2 fue escogida para continuar con la investigación. Se aumentó el grado de paralelización utilizando la imagen de tamaño 480 x 640 pixeles, puesto que es un tamaño estándar.

Grado de paralelismo y comparación del rendimiento del procesamiento

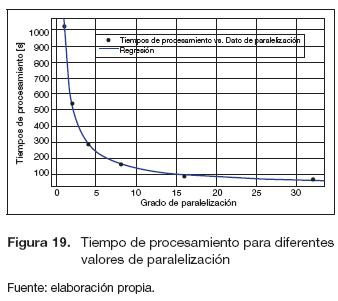
Grado de paralelismo. En la figura 19 se presentan los resultados del tiempo del procesamiento para diferentes valores de paralelización, se observa un comportamiento exponencial decreciente el cual evidencia que existe una reducción en el tiempo de procesamiento a medida que aumenta el grado de paralelización de la imagen. Cabe anotar que solo fue posible llegar hasta el grado de paralelización 32, debido a que Matlab no permitió generar la compilación del bloque de cosi-mulación para un valor mayor.

La ecuación (11) describe la curva de la figura 22 con una correlación de 0,9996.

Procesamiento serie y paralelo. La comparación entre el procesamiento en serie y en paralelo se realiza por dos métodos diferentes.

Primer método. La medición del tiempo total se realiza haciendo uso de la instrucción de Matlab tic toc, desde que se entregan los datos a la etapa de procesamiento hasta la construcción del vector de salida, teniendo en cuenta la comunicación con la FPGA.

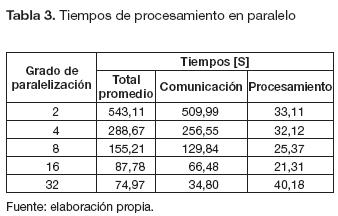
De los resultados obtenidos se construyen las tablas 2 y 3, las cuales contienen el tiempo total promedio medido. En las dos tablas la columna "Comunicación" contiene el tiempo estimado de comunicación que se demoran los datos en pasar del software al hardware. Estos datos se obtienen aplicando las ecuaciones (8) y (10); la columna "Procesamiento" se obtiene al restarle al "Total promedio" la columna de "Comunicación".

En los valores mostrados en las tablas 2 y 3 se observa que el tiempo de procesamiento fue menor en el serial si se compara con los diferentes grados de paralelización, aunque el tiempo total del proceso fue mayor en el serial que en los de paralelización.

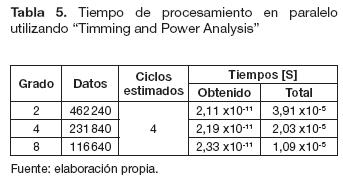
Segundo método. Se utiliza la herramienta "Timing and Power Analysis", la cual permite obtener para un ciclo de reloj, el tiempo que tarda un dato en recorrer la etapa de procesamiento de la arquitectura cuando el diseño es implementado en la FPGA.

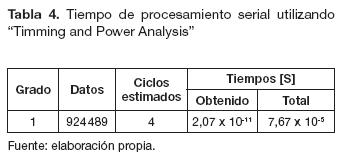
Si se implementaran las etapas de preprocesamiento, procesamiento y posprocesamiento directamente sobre la FPGA, se requeriría más de un ciclo de reloj para procesar un solo pixel. Se estima que si se utilizara la memoria RAM de la tarjeta para almacenar la imagen en forma de vector, se requeriría un ciclo de reloj para ubicar el pixel almacenado, un segundo ciclo para leer el pixel, un tercero para ubicar la posición de memoria donde se va guardar el pixel procesado, y un cuarto ciclo para la escritura sobre la memoria que almacena la imagen final. Debido a que la convolución es combinacional y no secuencial, no se necesita un ciclo de reloj para el procesamiento del pixel, por lo tanto, se estima un total de cuatro ciclos de reloj para procesar un solo dato.

Los tiempos obtenidos para un solo ciclo son los que se muestran en la columna "Obtenido" de las tablas 4 y 5, este valor al ser multiplicado por el número de datos calculados utilizando la ecuación (8) y los cuatro ciclos estimados, permite determinar el tiempo total de procesamiento (columna de las tablas 4 y 5 llamada "Total").

En las tablas 4 y 5 se observa que el tiempo obtenido en el procesamiento serial es menor que los tiempos en el procesamiento paralelo; sin embargo, los tiempos totales son menores para el procesamiento en paralelo. Es importante aclarar que dicha herramienta no permitió obtener los tiempos de los grados de paralelismo 16 y 32.

Procesamiento software y hardware. Adicionalmente a la comparación efectuada con los dos métodos para el procesamiento serie y paralelo, se mide el tiempo de un código M que realiza la convolución de imágenes utilizando la instrucción conv2 (Math Works, 2013).El resultado obtenido se compara con los tiempos calculados a partir del "Timming and Power Analysis".

El tiempo promedio medido mediante la instrucción tic toc para el código M creado fue de t = 197,8x10^-5[s]. Comparando el tiempo t con los datos de la columna "Total" de la tablas 4 y 5, se puede determinar que los tiempos obtenidos mediante el análisis del "Timming and Power Analysis" son menores que el tiempo promedio medido para el código M. Este resultado se obtiene para todos los grados de paralelismo y además para el modelo serial.

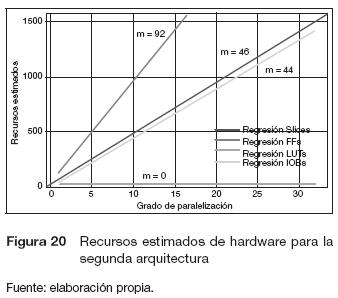
Cantidad de recursos hardware. En la tabla 7 se muestran los datos obtenidos para los recursos estimados de la FPGA si la segunda arquitectura se implementa en hardware, a partir de los datos de la tabla 6 se obtiene las curvas de la figura 20, produciendo tendencias lineales en aumento para el casos de los recursos Slices, FFs, y IOBs y constante para el caso de LUTs.

Teniendo en cuenta que los slices están compuestos por dos flipflops y dos LUT, el análisis se puede realizar directamente sobre este recurso. La ecuación (12) describe el comportamiento de los slices según el grado de paralelización (GP).

La ficha técnica de la FPGA Spartan 3AN XC3S700AN indica que la tarjeta cuenta con un total de 5888 slices.

Trabajo futuro

Además de las herramientas utilizadas de Xilinx System Generator para la elaboración de este proyecto, el toolbox cuenta con múltiples recursos adicionales, pero que en algunos casos están limitados a la tarjeta. Una propuesta para un trabajo futuro sería implementar la segunda arquitectura diseñada en una tarjeta más robusta, que permita realizar otro tipo de estrategia aparte de la cosi-mulación. Hoy existen en el mercado una serie de FPGA de la familia de Xilinx que trabajan con un protocolo de comunicación diferentes al JTAG para la comunicación con Matlab, el propósito de estos protocolos adicionales es poder simular arquitecturas desde Metlab con verificación en hardware en tiempo real.

Para este proyecto se implemento un algoritmo que permite paralelizarse (convolución); sin embargo, existen múltiples algoritmos para el procesamiento digital de imágenes que no pueden ser paralelizados. Una propuesta para un trabajo futuro sería diseñar e implementar este tipo de algoritmos mediante Xilinx System Generator; por ejemplo, el de esqueletización. El objetivo sería poder realizar un análisis comparativo entre un algoritmo no paralelizable y uno paralelizable.

Conclusiones

La convolución es un filtro utilizado para el procesamiento de imágenes que no depende de resultados anteriores, es decir, que con independencia de las veces en que se divida la imagen, el algoritmo de convolución va a funcionar; por lo tanto, la convolución es un algoritmo paralelizable.

El grado de paralelismo tiene un comportamiento exponencial decreciente en función del tiempo de procesamiento, este comportamiento indica que existe un rango hasta donde es viable paralelizar. Aunque los tiempos seguirán disminuyendo, la reducción no será tan notable como en los primeros grados de paralelización.

Se plantea una metodología para estimar los tiempos de comunicación a través de una arquitectura adicional, donde se obtuvo que los tiempos estimados de comunicación en la paralelización de la imagen son menores que en el serial; sin embargo, la diferencia entre el tiempo total y el de comunicación muestra que el tiempo de procesamiento es menor en el serial que en el paralelo, lo cual indica que la forma en la que se está estimando el tiempo de comunicación no es correcta. Este método no es útil para medir.

Con respecto al tiempo t = 197,8x10⁵,medido para el código M creado a partir de la instrucción conv2, la razón entre t y el tiempo medido con el "Timming and Power Analysis" aumentan a medida que los tiempos totales de las tablas 4 y 5 disminuyen; es decir, que los tiempos del "Timming and Power Analysis" son inversamente proporcionales a dicha razón, la relación para el procesamiento en serie es de 25 y para los grados de paralelización 2, 4 y 8 es de 51, 97 y 181, respectivamente.

Los mejores tiempos de procesamiento se obtuvieron cuando se utilizó la herramienta "Timming and Power Analysis". Los tiempos medidos para las cosimualciones no alcanzaron valores tan bajos, debido al tiempo de comunicación que requieren para enviar la información a la FPGA.

Debido a las restricciones del System Generator, el máximo grado de paralelización que se pudo cosimular fue de 32 para una imagen estándar de 480 x 640, para el cual se usó un recurso estimado de 1497 slices; sin embargo, si la limitante no fueran las restricciones del software, sino la cantidad de recursos de la tarjeta, el máximo grado de paralelización que se podría obtener sería de 80. No se puede obtener una paralelización de 128, debido a que superaría los recursos en aproximadamente 24,8 slices.

En los recursos estimados en el proceso de paralelización de la imagen se observan tendencias lineales a medida que aumenta el grado de paralelización, de las cuales se obtiene una mayor pendiente en los FF de un valor m = 92, y una menor de m = 44 para los IOB. Además de una pendiente igual a 0 para los LUT, lo cual muestra que sin importar el grado de paralelización, dicho recurso se mantendrá constante.

Referencias

Boemo Scalvinoni, E. (2005). Estado del arte de la tecnología FPGA. Recuperado de http://www.inti.gob.ar/electronicaeinformatica/instrumen-tacion/utic/publicaciones/cuadernilloUE/CT_Microelectronica17_FPGA.pdf.

Electrical Professional Service (2013). Termografía infrarroja. Recuperado de http://www.epspan.com/.

Escalante Ramírez, B. (2006). Procesamiento digital de imágenes. Apuntes de clase de la Universidad Nacional Autónoma de México, Distrito Federal, México.

Forero Vargas, M. G. y Arias Cruz, E. A. (2001). Estudio del efecto de las máscaras de con-volución en imágenes mediante el uso de la transformada de Fourier. Revista de Ingeniería e Investigación, 48, 46-51.

Garces Socarrás, L. M. (2012). Aceleración de algoritmos mediante hardware reconfigurable. La Habana: CUJAE.

Gonzales, R. y Woods, R. (2002). Digital Image Proccesing. Estados Unidos: Prentice Hall.

López Vallejo, M. (2004). FPGA: Nociones básicas e implementación. Recuperado de http://www.lsi.die.upm.es/~marisa/docencia/fpga_a2_2004.pdf.

Math Works (2013). Image Processing Toolbox. Recuperado de http://www.mathworks.com/help/images/index.html.

Moctezuma Eugenio, J. C. y Torres Huitzil, C. (2006). Estudio sobre la implementación de redes neuronales artificiales usando xi- linx system generator. Puebla, México: Departamento de Ciencias Computacionales, Universidad Autónoma de Puebla, Mexico.

Moctezuma, J. C., Sánchez, S., Álvarez, R. y Sánchez, A. (2007). Architecture for Filtering Images Using Xilinx System Generator. International Journal of Mathematics and Computers in Simulation, 1 (2), 101-107.

Raygoza, J., Ortega, S., Cabrera, H. y Ibarra, F. (2009). Prototipado y verificación de un sistema de procesamiento de audio en FPGAs mediante hardware in the loop. XXIV Congreso de Instrumentación SOMI. México.

Rodríguez Cruz, C., Rivero Flores, R. y Castillo Atoche, A. (2006). Procesamiento de imágenes con Xilinx System Generator. Primer Congreso Internacional de Sistemas de Computacionales y Electrónicos (CIS- CE). México.

Rodríguez Escudero, A. A. (2013). Convolución bidimensional. Recuperado de http://digitimagen.blogspot.com/2013/04/convolucion-bidimensional.html.

Rodríguez Pérez, J. F. (2010). Programación MATLAB en paralelo sobre clúster computacional: evaluación de prestaciones (tesis de grado en ingeniería). Universidad Politécnica de Cartagena, España.

Sánchez Élez, M. (2014). Introducción a la programación en VHDL. Recuperado de http://eprints.ucm.es/26200/1/intro_VHDL.pdf.

Electrical Professional Service (2013). Termografía infrarroja. Recuperado de http://www.epspan.com/.

Xilinx (2012). Xilinx System Generator for DSP User's Guide. Recuperado de http://www.xilinx.com/support/documentation/sw_manuals/xilinx14_1/sysgen_user.pdf.