Proceso agroindustrial de la producción de panela

Proceso agroinsdustrial de la producción de la panela

Agribusiness production process of panela

Roger Andrés Ordoñez Lugo¹, Fernando Martínez Santa², Hugo Reinel García Bernal³

¹ Tecnólogo en Electricidad. Asistente de operaciones de Halliburton. Houston, Estados Unidos. Contacto: rogerordonez@gmail.com
² Ingeniero en Control Electrónico e Instrumentación, magíster en Ingeniería Electrónica y Computadores. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: fmartinezs@udistrital.edu.co
³ Ingeniero Agrónomo, magister en Ingeniería Agrónoma. Investigador de CORPOICA. Bogotá, Colombia. Contacto: hugogarciab@yahoo.es

Fecha de recepción: 17 de septiembre de 2011 Fecha de aceptación: 16 de octubre de 2012

Resumen

El modelamiento en Matlab de un sistema de evaporación de múltiple efecto para la producción de panela está dirigido a toda la gente interesada en el control de procesos agroindustriales, específicamente a los productores de panela, con el fin de brindar una contribución al desarrollo tecnológico de esta agroindustria, sin embargo es importante resaltar que para el entendimiento de este documento se requieren conocimientos de control y termodinámica. El modelo matemático desarrollado está dividido dos diferentes procesos involucrados en la obtención del producto final (panela): a) el control de la concentración de azúcar y b) el control de nivel en los efectos del evaporador. A lo largo del documento el análisis está enfocado a que estos dos sistemas sugieran el controlador ideal para la operación del evaporador.

Palabras clave: Concentración, Control, Evaporación, Panela, Termodinámica.

Abstract

The multiple effect evaporation system modeling in Matlab is aimed at all the people who could be interested in control processes in regard to the agronomy feld, looking for an important contribution to this important industry. In order to have a properly understanding about this current research project, it is necessary to have a previous knowledge in engineering that has to do with control and thermodynamic. The mathematical modeling is divided in two different and indispensable processes involved in the development of a final product (panela): a) sugar concentration control and b) level control in the multiple effect evaporation system. All along the document, an analysis is stated about these systems suggesting a controller, which is ideal to come into a proper operation.

Key words: Concentration, Control, Evaporation, Panela, Thermodynamic.

1. Introducción

En la actualidad, el proceso panelero es realizado mediante una evaporación abierta generando desventajas energéticas, de recursos naturales y de productividad; es por esto que es necesario realizar un cambio tecnológico debido a la baja competitividad existente de los pequeños y medianos productores. Frente a este cambio de tecnológica se presenta una negativa por parte de los productores, esta actitud genera una desventaja competitiva frente a los mercados internacionales y poca tecnificación del proceso panelero, es por esto, que se plantea el modelamiento de un sistema de evaporación de múltiple efecto en cual tiene involucrado tecnologías no utilizadas como lo es el vapor en sistemas cerrados, el ahorro energético y termodinámica que se encuentra inmersas en el sistema [1].

2. Metodología

2.1 Modelamiento matemático

Las variables que intervienen en el proceso son [2], [3]:

• Caudal de entrada a cada efecto
• Presión en cada efecto
• Temperatura en cada efecto
• Área de intercambio de cada efecto
• Altura de cada efecto
• Coeficientes globales de transferencia de calor en cada efecto
• Entalpías de vaporización
• Volumen de cada efecto

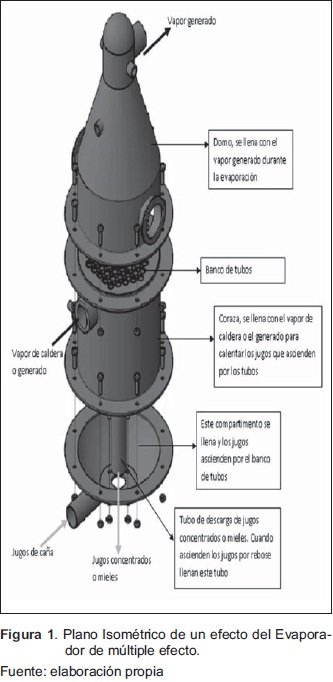
En la Figura 1 se muestra un plano isométrico de un efecto del Evaporador de múltiple efecto.

Para realizar el modelamiento del sistema de evaporación de múltiple efecto se tomaron condiciones ideales tales como:

• La no pérdida de calor al ambiente
• El no desgaste de la tubería a través del tiempo
• La no presencia de incrustaciones
• La no pérdida de caída de presión en los efectos
• La no formación de espuma en los jugos de caña durante la evaporación.

Además de esto se tuvieron en cuenta datos de las variables tomados experimentalmente y calculados previamente.

Conociendo el funcionamiento y las diferentes variables en un proceso de evaporación de múltiple efecto se realizó el Modelamiento del sistema con el fin de proponer un controlador óptimo para su funcionamiento, para realizar esto se empleó la matemática pertinente que se involucra y se modeló en un software apto para este tipo de problemas como lo es Matlab versión 2009A.

De acuerdo a los fenómenos involucrados en la evaporación de múltiple efecto se decidió controlar dos aspectos importantes para su correcto funcionamiento [4].

• Control de concentración de azúcar en cada efecto. (°Brix)
• Control de nivel en cada efecto.

2.2 Control de Concentración de Azúcar en Cada Efecto (°Brix)

Variables de entrada y salida: Las variables que de entrada y salida para el modelamiento del sistema de concentración de azúcar son las siguientes.

• Variable de entrada: Temperatura en cada efecto intercambiador (°C)
• Variable de salida: Concentración en cada uno de los efectos (°Brix)

Modelamiento: Para poder realizar un control en la concentración se debe tener en cuenta la química que actúa en cada uno de los efectos. La concentración de azúcar de una sustancia determina qué porcentaje de esta es azúcar, esta medida se determina a través de los grados Brix. Para concentrar una sustancia, que en este caso son jugos de caña, se realiza una evaporación de los mismos de tal manera que al evaporarlos se reduce el porcentaje de agua y de otras sustancias que se convierten en vapor quedando los jugos de caña más concentrados [1], [5].

2.3 Control de Nivel en Cada Efecto

Variables de entrada y salida: Las variables que de entrada y salida para el modelamiento del sistema de control de nivel son las siguientes.

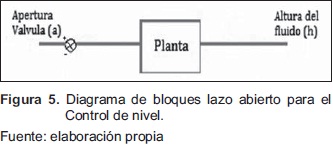
• Variable de entrada: % apertura de válvula (a)
• Variable de salida: Nivel en cada efecto (h)

Modelamiento: El análisis de nivel se realiza a partir de un balance simple de flujos que intervienen y caídas de presión entre cada uno de los efectos, partiendo de la ecuación de la capacitancia hidráulica e inductancia hidráulica y tomando como referencia los diferentes fujos, resistencias y presiones que actúan en el sistema, por consiguiente son dimensionalmente correctos para las operaciones entre ellos [6].

2.4 Modelamiento en lazo abierto y lazo cerrado

El diagrama de lazo abierto del sistema representa todos los elementos que actúan en el sistema en serie, mientras que el diagrama en lazo cerrado representa una retroalimentación de la respuesta en la entrada con el fin de disminuir el error y tener un propio control [7].

2.4.1 Diagrama de Bloques para el Control de Concentración de Azúcar

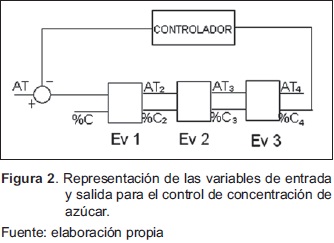
En la Figura 2 se representan las variables para el control de concentración de azúcar.

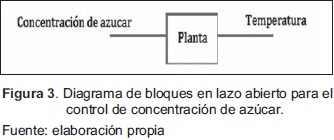
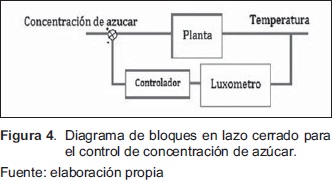
En la Figura 3 y Figura 4 se muestran los diagramas de bloques para el control de concentración de azúcar.

2.4.2 Diagrama de Bloques para el Control de Nivel

Diagrama de bloques en lazo abierto y cerrado: En la Figura 5 y Figura 6 se muestran los diagramas de bloques en lazo abierto y cerrado respectivamente

3. Resultados

3.1 Funciones de transferencia para los diferentes sistemas

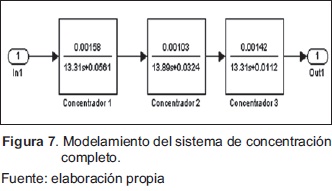
Concentración de Jugos: Luego de tener las 3 Funciones de Transferencia (FT), Figura 7, y aplicando técnicas de reducción de bloques se obtiene la función de transferencia del sistema de concentración de azúcar de tercer orden:

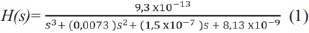
Control de Nivel: Luego de analizar las ecuaciones del sistema de control de nivel, se decidió hacer un análisis general del sistema incluyendo los 3 efectos donde se realiza la evaporación obteniendo una FT de 1 orden como se muestra a continuación.

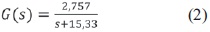
3.2 Simulación en lazo abierto

Simulación en lazo abierto del sistema de concentración de azúcar: El sistema en lazo abierto (Figura 8) muestra una estabilidad del sistema en aproximadamente 6000 seg (1,6 h) lo cual indica que el modelamiento realizado se aproxima a la realidad puesto que el sistema en práctica genera una estabilidad en 1 hora.

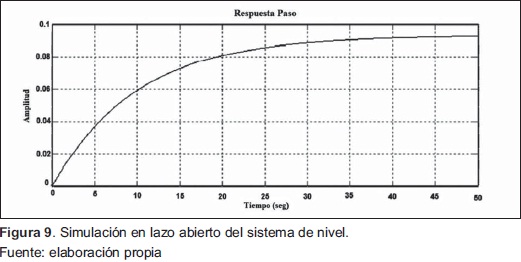
Simulación en Lazo Abierto del Sistema de Nivel: La simulación del sistema de control de nivel en lazo abierto (Figrua 9) muestra una estabilidad cerca a los 30 seg, debido a que el sistema fue analizado de manera general.

3.3 Estabilidad del sistema

Estabilidad del sistema de concentración de azúcar: Luego de utilizar el la técnica de root locus en Matlab, el sistema de concentración de azúcar posee tres polos al lado izquierdo del plano lo cual indica que el sistema posee un comportamiento estable, a pesar de esto dos de los tres polos tiene una tendencia a la inestabilidad, por este motivo es que se planteó un controlador con el fin de lograr una estabilidad del sistema, es decir, que la tendencia de los polos sea a la estabilidad, para esto utilizó la técnica de rltool en Matlab, incluyendo ceros en el sistema para que los polos tengan una tendencia hacia estos.

3.4 Estabilidad del sistema de control de nivel

De acuerdo a FT del sistema de control de nivel, el sistema posee una estabilidad debido a que el único polo que el sistema tiene se encuentra en el lado derecho del sistema y además este tiene una tendencia hacia el infinito, por consiguiente se planteó un control proporcional.

3.5 Diseño del controlador

Para el diseño del controlador se decidieron parámetros como lo fueron: el máximo sobreimpulso del sistema y el tiempo de estabilización del mismo, los tiempos de estabilización se quiere reducir queriendo una estabilidad en un tiempo menor a una hora como lo es en el caso real, el máximo sobre impulso será determinado con un 10%,

• Máximo sobre impulso. (Mp) = 10%
• Tiempo de estabilización = menor a 1 hora (3600 seg)

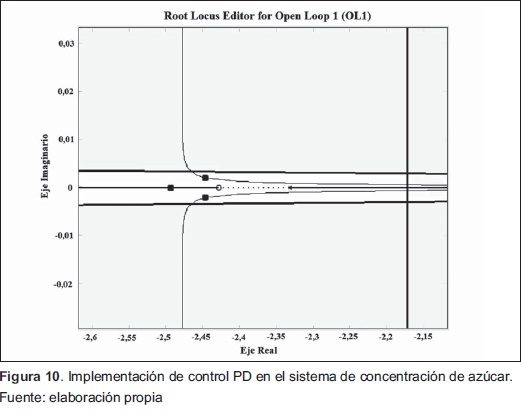
En la Figura 10 se muestra la implementación del Control Proporcional Derivativo (PD) en el sistema de control de azúcar.

4. Conclusiones

Como resultado del modelo obtenido se debieron tener en cuenta la dinámica del fuido entre los evaporadores. El fujo del jugo para el contenedor es constante y por lo tanto es el punto de partida para el modelamiento, además de esto se debe tener en cuenta la diferencia de presión entre los evapora-dores, el área del evaporador y como variable de salida se tiene la válvula de entrada al siguiente evaporador. Para poseer un modelo más real se debe tener en cuenta el cambio de densidad que se da mientras el jugo fuye un evaporador a otro.

Los efectos termodinámicos para el control de nivel no fueron tomados en cuenta, en el caso de ser tenidos en cuenta se debería tener un diferencial adicional de densidad del fuido, haciendo esto, se tendría ecuaciones diferenciales de segundo grado para cada evaporador.

El diferencia depresión entre cada evaporador permite que el jugo se transporte desde el evaporador que posee una mayor presión hacia el de una menor presión, permitiendo la dinámica del fuido, además de esto las presiones disminuyen con el fin de lograr un punto de ebullición a una menor temperatura en el siguiente efecto.

El sistema de concentración de azúcar se modeló bajo un ambiente ideal en donde no fueron consideradas las pérdidas del propio sistema como lo son desgaste de tubos por el tiempo, pérdidas calóricas con el ambiente, diferencia de concentración en los jugos de entradas y un sin número de características que se presenta en el sistema real.

Es necesario realizar una tecnificación en todas las industrias paneleras en Colombia puesto que hoy en día no se ha realizado ningún avance tecnológico en el 90% de los trapiches ubicados alrededor del territorio colombiano.

Los sistemas de control de nivel y de concentración fueron analizados de manera diferente pero los dos se relacionan en el funcionamiento, si no se controla el nivel en cada cuerpo de evaporación, la concentración puede ser inadecuada puesto que en cada cuerpo de evaporación se podría tener más o menos líquido con el mismo calor de transferencia [8], [9].

En el momento de realizar la evaporación en cada uno de los cuerpos se produce un efecto de espuma propia del jugo de caña, es necesario escoger de manera selectiva los sensores de nivel con el fin de no generar falsas alarmas que puedan perjudicar el sistema.

5. Agradecimientos

Este trabajo hace parte y fue financiado a través del proyecto "Desarrollo de un sistema de evaporación y concentración de jugos de múltiple efecto para mejorar la eficiencia térmica y la productividad y disminuir el impacto ambiental en la producción de panela" ejecutado por la Corporación colombiana de Investigación Agropecuaria-CORPOICA y financiado por el Ministerio de Agricultura y Desarrollo Rural.

Referencias

[1] K. M. Nielsen, T. S. Pedersen y J. F. D. Nielsen, Simulation and control of a multiple effect evaporator, Control '96, UKACC International Conference on (Conf. Publ. No. 427), 2, pp. 1166-1171, Exeter-UK, 2 al 5 de Septiembre, 1996.

[2] A. Zdravkovic, S. Turajlic y N. Marsenic, Fuzzy PI control algorithm for the multiple effect evaporation station, in Proceedings of the third IEEE conference on control applications, 1, pp. 677-682, 24 al 26 de Agosto, 1994.

[3] E. Duran, "Determinación de la eficiencia energética de un sistema de evaporación de múltiple efecto empleado en la concentración de jugos de caña panelera". Trabajo de grado, Fundación Universidad de América - CORPOICA, Bogotá-Colombia, 2010.

[4] H. R. García, A. C. Peña, y R. A. López, "Desarrollo de un sistema de evaporación y concentración de jugos de múltiple efecto para mejorar la eficiencia térmica y la productividad y disminuir el impacto ambiental en la producción de panela: tercer Informe de Avance del proyecto", CORPOICA, Bogotá-Colombia, 2009.

[5] Á. A. Ruiz, y H. Álvarez, Escalamiento de Procesos Químicos y Bioquímicos basado en un Modelo Fenomenológico. Información Tecnológica: 22(6), pp. 33-52, 2011.

[6] W. Chatrattanawuth, N. Suksariwattanagul, T. Benjanarasuth and J. Ngamwiwit, Fuzzy I-PD Controller for Level Control, SICEICASE, 2006. International Joint Conference, pp. 5649-5652, 18 al 21 de Octubre, 2006.

[7] J. M. Blanco, y F. Peña, Incremento de la Eficiencia en Centrales Termoeléctricas por Aprovechamiento de los Gases de la Combustión, Información Tecnológica: 22(4), pp. 15-22, 2011.

[8] A. C. Borbón, R. E. Cabanillas y J. B. Pérez, Modelación y Simulación de la Transferencia de Calor en Muros de Bloque de Concreto Hueco. Información Tecnológica: 21(3), pp. 27-38, 2010.

[9] M. M. Rahman y G. W. Soon, An experimental study on condensation and evaporation heat transfer and pressure drop in microfin copper tubes, Energy and Environment, 2009. ICEE 2009. 3rd International Conference on, pp. 104-109, 7 al 8 de Diciembre, 2009.