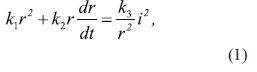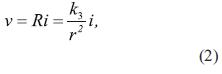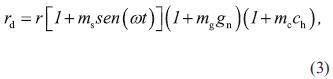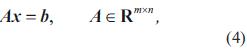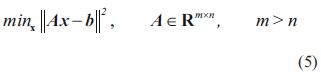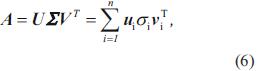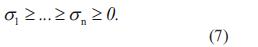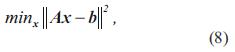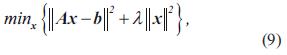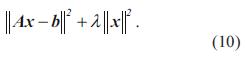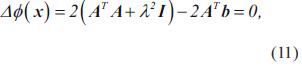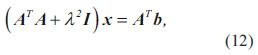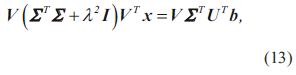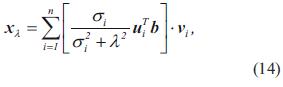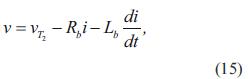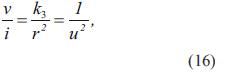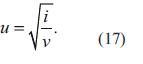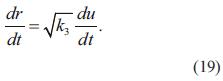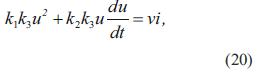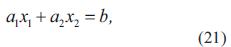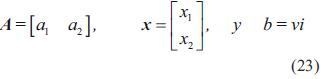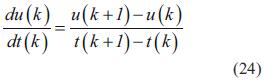DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2013.3.a04Published:
2013-07-01Issue:
Vol. 17 No. 37 (2013): July - SeptemberSection:
ResearchRegularización de Tikhonov para estimar los parámetros de un modelo de un horno de arco
Keywords:
armónicos, horno de arco, modelo dinámico, regularización de Tikhonov. (es).Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Regularización de Tikhonov para estimar los parámetros de un modelo de un horno de arco
Parameter estimation for an electric arc furnace model using Tikhonov regularization
Jesser James Marulanda Durango1, Alfonso Alzate Gómez2, Christian David Sepúlveda Londoño3, Mauricio Holguín Londoño4
1Ingeniero Electricista. Docente Auxiliar de la Universidad Tecnológica de Pereira. Pereira,
Colombia. Contacto: jjmarulanda@utp.edu.co
2Ingeniero Electricista, Magíster en Ingeniería Eléctrica. Docente de la Universidad Tecnológica
de Pereira. Pereira, Colombia. Contacto: alalzate@utp.edu.co
3Ingeniero Electricista. Investigador de la Universidad Tecnológica de Pereira. Pereira, chrisdavis1205@utp.edu.co
4Ingeniero Electricista, Magíster en Ingeniería Eléctrica. Docente Asistente de la Universidad
Tecnológica de Pereira. Pereira, Colombia. Contacto: mau.hol@utp.edu.co
Fecha de recepción: 3 de agosto de 2012 Fecha de aceptación: 21 de mayo de 2013
Resumen
Este documento presenta una metodología para estimar los parámetros de un modelo de un horno de arco eléctrico usando regularización de Tikhonov. La regularización de Tikhonov es uno de los métodos de regularización usado más comúnmente. El modelo de horno de arco utilizado considera la naturaleza no lineal y altamente variable que exhibe este tipo de carga. Se ha utilizado el toolbox Regularization Tools desarrollado para Matlab que permite determinar el valor del vector de parámetros estimados de norma mínima.
Los resultados obtenidos en simulación del modelo del horno de arco implementado en PSCAD son comparados con mediciones reales tomadas en la etapa más crítica de la operación del horno. Se muestra cómo el comportamiento del modelo del horno de arco con un ajuste apropiado de los parámetros, captura en un alto porcentaje las formas de onda de los voltajes trifásicos de fase en el secundario del transformador que energiza los electrodos; además, se obtienen corrientes de línea eficaces de arco eléctrico con errores no mayores al 2,8 % del valor real.
Palabras clave: armónicos, horno de arco, modelo dinámico, regularización de Tikhonov.
Abstract
In this paper, we present a methodology for estimating the parameters of a model for an electrical arc furnace by using Tikhonov regularization. Tikhonov regularization is one of the most widely employed methods for regularization. The model proposed for an electrical arc furnace takes into account the highly nonlinear and time varying characteristic of this type of load. We use Regularization Tools (an open-source Matlab toolbox) to determine the value of an estimated-parameter vector with smaller norms.
Results obtained through simulation of the model in PSCAD are compared to real measurements taken during the furnace's most critical operating point. We present models for the electrical arc furnace with appropriate parameter tuning, capturing the real three-phase voltage at the secondary of a furnace transformer with great detail. Results show a maximum error of 2,8 % when line current's root mean square error is applied.
Key words: harmonics, arc furnace, dynamic models, Tikhonov regularization.
1. Introducción
El horno de arco eléctrico provee un medio relativamente simple para la fusión de metales y es usado en la producción de aluminio, cobre, plomo, acero de alta pureza y otros metales. Sin embargo, en los sistemas eléctricos de potencia se considera como una fuente generadora de fluctuaciones de voltaje, produciendo parpadeo oficker en el nodo conexión común PCC (Point of Common Coupling) y en otros barrajes aledaños. El ficker origina molestias visuales en las instalaciones de iluminación y depende básicamente de la frecuencia y amplitud [1] de las fluctuaciones de la amplitud de la forma de onda del voltaje. Además de generar fluctuaciones de tensión, los hornos de arco son fuentes de armónicos de corriente por la naturaleza no lineal del arco eléctrico, estableciendo condiciones indeseables de operación en los equipos conectados a la red y en las instalaciones de usuarios aledaños.
Operadores de red y usuarios industriales que cuenten con este tipo de carga son conocedores de estos inconvenientes y deben generar estrategias para su atenuación. Por tanto, obtener la respuesta en el tiempo de este tipo de carga se vuelve una tarea importante para evaluar soluciones partiendo de un marco de referencia técnico y económico de sistemas de compensación, desde la instalación de reactores en serie, hasta la inclusión de sistemas más complejos como el compensador estático de reactivos SVC y el compensador estático síncrono D-STATCOM.
Varios modelos matemáticos se han propuesto en la literatura para el horno de arco eléctrico. En [2], se modela el arco eléctrico usando una ecuación diferencial no lineal entre el voltaje y la corriente del arco eléctrico a partir del principio de la conservación de la energía, donde la característica simulada voltaje - corriente del arco eléctrico tiene gran similitud con la característica voltaje - corriente real. Sin embargo, el modelo no considera las fluctuaciones de baja frecuencia en las amplitudes de las formas de onda de los voltajes y corrientes observadas en barrajes aledaños al punto de conexión de los hornos de arco.
Un modelo que considera las fluctuaciones en las formas de onda de voltajes y corrientes se presenta en [3], en donde usando el modelo determinista descrito en [2] se obtienen las formas de onda para el voltaje y la corriente del arco. Posterior a esto, con el oscilador de Chua se genera una señal caótica de baja frecuencia que se utiliza para modular en amplitud el voltaje del arco eléctrico; los resultados obtenidos del índice de severidad de ficker de corta duración o Pst obtenidos con el planteamiento anterior, son mayores a 1, donde los parámetros del modelo se asumen conocidos.
En [3], los parámetros que definen la dinámica del arco eléctrico se sintonizan de forma heurística, con base en mediciones reales de Pst o en la potencia nominal del horno. En [4] se presenta una metodología para estimar los parámetros del modelo a partir de mediciones reales de voltaje, usando el toolbox SystemI dentification de Matlab. Un algoritmo para estimar los parámetros del modelo presentado en [3] se muestra en [5], donde se ajustan los parámetros del modelo para estimar el Pst de una nueva instalación, con base en un análisis estadístico de mediciones reales de Pst de instalaciones similares.
En este documento se presenta una metodología para estimar los parámetros del modelo de horno de arco presentado en [6] usando regularización de Tikhonov [7]. El ajuste de los parámetros se realiza mediante manipulación matemática del modelo descrito por la ecuación diferencial no lineal de [2], para obtener una ecuación lineal equivalente de los parámetros del modelo. La sintonización de los parámetros se ha realizado con señales muestreadas de las formas de onda de los voltajes de fase y las corrientes del arco eléctrico en el secundario del transformador que energiza los electrodos del horno, a una frecuencia de muestreo de 2335 muestras por segundo, tomadas al inicio del ciclo de fusión [8].
El modelo del horno de arco se ha desarrollado en el programa PSCAD, y se ha utilizado el toolbox Regularization Tools [7] desarrollado para Matlab, para determinar el vector de los parámetros de norma mínima. La validación del modelo es realizada comparando inicialmente los valores eficaces de las señales simuladas y reales. Luego, se compara el espectro armónico de las formas de onda de las corrientes de arco reales y simuladas. Se muestra también una comparación del nivel instantáneo de ficker IFL (Instantaneous Flicker Level), de las formas de onda de los voltajes reales y simulados. Por último, se presentan las conclusiones de la investigación.
2. Fundamentos
2.1 Circuito eléctrico de potencia del horno de arco
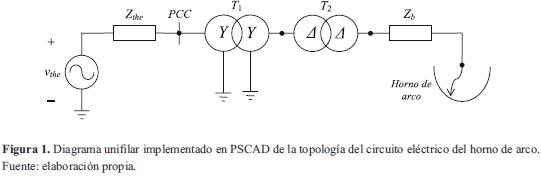
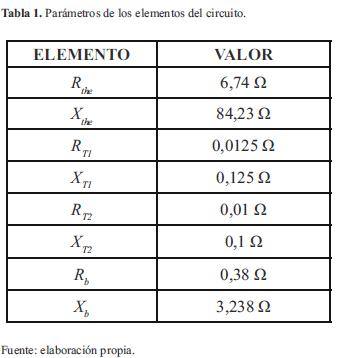
El circuito eléctrico que conecta el horno de arco se basa en la topología descrita en [9]. La figura 1 presenta el modelo de circuito uniflar realizado en el programa PSCAD, que consta de los siguientes elementos principales: una fuente trifásica de voltaje ideal denominada vthe configurada con un voltaje línea a línea de 115 kV y una frecuencia de 50 Hz. En serie a esta fuente de voltaje se encuentra la impedancia Zthe que modela la impedancia de cortocircuito en el punto de acoplamiento común, también conocida como impedancia de Thevenin, Zthe consiste en una impedancia serie RL, donde los valores de R y L se han determinado a partir de una potencia de cortocircuito de 1 962,167 MVAen el punto de acoplamiento común PCC, una relación de X/R igual a 9,896 y un voltaje base de 115 kV.
El circuito eléctrico presenta dos transformadores de potencia denominados T1 y T2. El transformador T1 tiene una relación de transformación de 110/20 kV y una potencia nominal de 80 MVA, conexión YY. El transformador T2 tiene una relación de transformación de 20/0,7 kV, potencia aparente nominal de 83 MVA, conexión ΔΔ.
El modelo del circuito de baja tensión que considera los cables de conexión y los electrodos, se representa por una impedancia serie tipo RL denominada como Zb. Los valores de Zb se han ajustado usando los valores típicos reportados en [9]. Los parámetros Rb y Xb de los distintos elementos del circuito se indican en la tabla 1.
2.2 Modelado del horno de arco
Diferentes modelos de horno de arco han sido presentados en la literatura especializada utilizando planteamientos deterministas y estocásticos. En [10], el comportamiento dinámico de la longitud del arco eléctrico se plantea de dos maneras, cada una de ellas considerada de forma independiente. Inicialmente, se plantea una variación sinusoidal de la longitud del arco con una frecuencia definida dentro del rango de mayor sensibilidad de ficker. Luego, se utiliza una señal aleatoria con un ancho de banda dentro del rango 4-14 Hz, para representar la dinámica de la longitud del arco eléctrico, siendo esta última aproximación la que mejor se asemeja a la dinámica real [11].
En años recientes, se ha probado que las fluctuaciones de voltaje y potencia de los hornos de arco son de naturaleza caótica y modelos basados en este planteamiento se describen en [12] y [13]. Cabe destacar que hasta el momento no se cuenta con un modelo que describa perfectamente las mediciones observadas, sin embargo estos capturan las características esenciales y la tendencia que presenta este tipo de carga.
El modelo que se utiliza en este artículo se basa en el modelo presentado en [6]. Este modelo se desarrolla en dos partes, en la primera etapa se considera un comportamiento determinista del arco eléctrico que conduce a formas de onda de voltajes y corrientes estacionarias, capturando la naturaleza no lineal del fenómeno del arco eléctrico; en la segunda etapa se modela la naturaleza variable de la longitud del arco eléctrico a través de la modulación de amplitud del radio del arco con tres señales de baja frecuencia: una señal sinusoidal, una señal caótica generada con el oscilador de Chua [14][15], y una señal aleatoria con distribución de probabilidad Gaussiana.
2.2.1 Comportamiento determinista del arco eléctrico
El comportamiento determinista del arco eléctrico se obtiene usando el modelo de arco representado por la ecuación diferencial no lineal derivada en [2], basada en el principio de la conservación de la energía.
Donde r es el radio del arco, i es la corriente instantánea del arco y k n (n = 1,2,3) son las constantes de proporcionalidad del modelo. El voltaje instantáneo del arco v, se determina a partir de la ecuación (2).
Donde v es el voltaje instantáneo del arco y R es la resistencia del arco eléctrico. Este modelo es capaz de representar con buen grado de detalle el comportamiento del arco en un circuito monofásico y puede ser utilizado en simulación para obtener los arcos eléctricos entre los electrodos de un horno trifásico.
2.2.2 Dinámica del arco eléctrico
La naturaleza variable de la longitud del arco eléctrico se refleja en el modelo introduciendo un comportamiento de tipo determinista, aleatorio y caótico al arco del radio eléctrico r en forma simultánea. Tomando como variables de entrada del modelo las corrientes de fase de cada arco eléctrico, el radio del arco r se determina con la ecuación (1) para cada una de las fases. Esta variable se modula en amplitud simultáneamente con tres señales: una sinusoidal, una aleatoria con distribución de probabilidad Gaussiana y una caótica con frecuencia dentro del rango 3-25 Hz generada con el oscilador de Chua [14] [15].
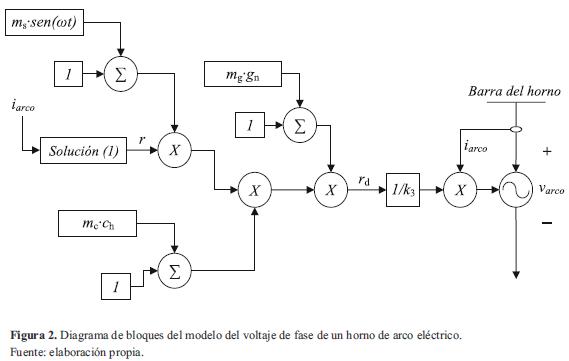
Después de añadir el comportamiento aperiódico y aleatorio al modelo, se determinan con la Ec. los voltajes de arco instantáneos en cada una de las fases, y se incluyen en el circuito eléctrico de potencia usando fuentes controladas de voltaje. El diagrama de bloques simplificado del modelo se muestra en la figura 2 y se describe matemáticamente con la ecuación (3).
Donde ω es la frecuencia angular de la variación sinusoidal del voltaje del arco eléctrico. m s, m g y m c son los factores de modulación de amplitud sinusoidal, aleatorio y caótico respectivamente, gn es una señal aleatoria con distribución de probabilidad normal y ch es una señal caótica en la banda de frecuencias de 3-25 Hz.
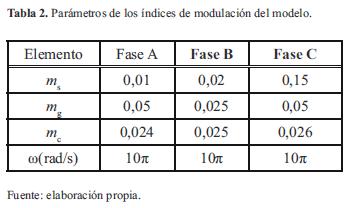
Para ajustar el factor de modulación m s, y la frecuencia de modulación ω, se requieren mediciones reales de voltajes y corrientes del arco eléctrico para cada fase [16]. Con relación a los índices de modulación m g y m c, se han seleccionado valores diferentes para cada una de las fases con el objetivo de introducir desbalances en las corrientes trifásicas del horno de arco, y sus valores son proporcionales al Pst medido en el secundario del transformador T2. En la tabla 2 se muestran los valores de los índices de modulación.
2.3 Problemas mal condicionados
Un problema "mal condicionado" es aquel cuya solución no es única, o no es una función continua de los datos, es decir, si una variación pequeña de los datos genera una gran variabilidad en su solución [7]. Una manifestación típica de un problema mal condicionado son los sistemas lineales y los problemas de mínimos cuadrados lineales que surgen a partir de la discretización de un problema mal condicionado. Considerando un sistema lineal de ecuaciones descrito por la ecuación (4).
y el problema de mínimos cuadrados lineales
Se dice que son problemas mal condicionados si los siguientes dos criterios se cumplen: los valores singulares de la matriz A decaen gradualmente a cero y la relación entre el mayor valor singular y el menor valor singular de la matriz A es suficientemente grande. En un problema mal condicionado, los métodos estándar del álgebra lineal para solucionar la ecuación (4) , o la ecuación (5), como la factorización LU (Lower Upper) o Cholesky no son fácilmente aplicables, por lo que es necesario aplicar un método de regularización para determinar la solución [7].
2.3.1 Descomposición en valores singulares
Considerando la matriz rectangular A , con m≥n. La descomposición en valores singulares de la matriz A se presenta en la ecuación (6),
Donde U = (u1,…, u n) y V = (v1,…, v n) son matrices con columnas ortonormales, UTU = VTV = I n, y Σ es una matriz diagonal, es decir, Σ = diag(σ1,•, σn) con elementos no negativos ordenados en forma descendente,
Los números σi son los valores singulares de la matriz A, mientras que los vectores ui y vi son los vectores propios de A. De las ecuaciones ATA = V Σ2VT y AAT = UΣ2UT, se observa que la descomposición en valores singulares se encuentra relacionada con la descomposición en valores propios de las matrices simétricas positivas y semidefinidas positivas ATA y AAT. Esto demuestra que la descomposición en valores singulares es única para una matriz A dada, excepto para vectores singulares asociados con múltiples valores singulares [7].
2.3.2 Regularización de Tikhonov
Considerando el problema descrito en la ecuación (4), se pretende encontrar la solución de norma mínima de la ecuación (4), es decir
Se coloca una restricción a la minimización
Donde el término de regularización l controla el tamaño de x mientras se minimiza la función. En efecto,
Resolviendo para el producto interior de la ecuación (10), y derivando sobre el funcional, se obtiene
Por lo tanto
Aplicando descomposición de valores singulares sobre la matriz A, y remplazando en la ecuación (12), se encuentra que
Donde V es una matriz con columnas ortonormales y Σ es una matriz diagonal cuyos elementos σi son los valores singulares de la matriz A. Por manipulación algebraica, se llega a una solución para x
Donde ui son los componentes del vector propio, U, b es el vector de salidas del modelo (datos conocidos) y vi son los componentes del vector propio V.
3. Metodología
3.1 Base de datos
Los datos utilizados para estimar los parámetros k n (n = 1,2,3) del modelo del horno de arco, se indican en [8], y consisten en mediciones de los voltajes de fase en el secundario del transformador T2 y las corrientes del arco eléctrico durante 5 ciclos de 50 Hz, con una frecuencia de muestreo de 2048 muestras por segundo, por lo que es necesario determinar inicialmente el voltaje del arco en cada fase, de acuerdo a los requisitos de la ecuación (2).
3.2 Estimación de los parámetros del modelo
En esta sección se muestra una metodología para estimar los parámetros k1, k2 y k3 del modelo matemático del horno de arco dado por la ecuación (1), con base en mediciones reales. Para este trabajo se tienen muestras de las formas de onda de los voltajes de fase en el secundario del transformador T2 y las corrientes del arco eléctrico. El voltaje instantáneo del arco v en cada fase, se obtiene a partir de la corriente del arco i de su fase respectiva y el voltaje de fase en el secundario del transformador T2 como:
Donde Rb y Lb corresponden a los parámetros de la impedancia del circuito de baja tensión Zb del horno de arco, tal como se indican en la tabla 1. Antes de realizar la estimación de parámetros usando regularización de Tikhonov, se transforma la ecuación (1) a un modelo de regresión lineal. En efecto, a partir de la ecuación (2), se define la variable u como:
El arco del radio r, en función de u, se determina usando la ecuación (16), tomando la raíz positiva:
Debido a que en la ecuación (1) se requiere la derivada de r con respecto al tiempo, esta se determina derivando la ecuación (18) con respecto al tiempo, resultando en:
Remplazando la ecuación (18) y la ecuación (19) en la ecuación (1), se obtiene
Realizando las siguientes sustituciones en la ecuación (20), a1 = u2, a2 = u(du/dt), x1 = k1 k3, x2 = k2k3, b = vi, se obtiene una ecuación lineal para el cálculo de los coeficientes x1 y x2
Que se puede expresar en forma vectorial para un único dato de voltaje y corriente como
Donde,
Para 253 datos de voltaje y corriente por fase, A es una matriz de dimensiones 253x2, x es un vector de dimensiones 2x1, y b es un vector de dimensiones 1x253. El cálculo de la derivada de u con respecto al tiempo se puede realizar de diferentes maneras, por ejemplo, utilizando la definición de la derivada de una variable discreta o expresando la variable u como una combinación lineal de funciones base para realizar su derivada de manera analítica. En este trabajo, se determina la derivada de u con respecto al tiempo usando la definición de la derivada de una variable discreta, como se indica en la ecuación (24).
Luego de obtener una ecuación lineal equivalente del modelo del horno de arco, se busca una solución para x, usando regularización de Tikhonov con la ecuación (14). En la tabla 3 se muestra el algoritmo para determinar los parámetros del modelo del horno de arco.
Se utilizó la función tikhonov del toolbox REGULARIZATION TOOLS desarrollado para Matlab, para la solución numérica de la ecuación (14), con un valor de λ de 1e-5.
4. Resultados
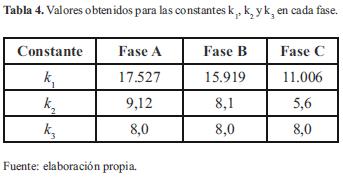
En esta sección se presentan los resultados obtenidos en simulación del modelo del horno de arco y se comparan estos resultados con mediciones reales. Se realizaron simulaciones con el sistema mostrado en la figura 1. En la tabla 4, se muestran los resultados obtenidos para las constantes k n en las tres fases.
De acuerdo con los resultados obtenidos en el algoritmo para las constantes kn, se realizó la simulación en PSCAD del modelo del horno de arco.
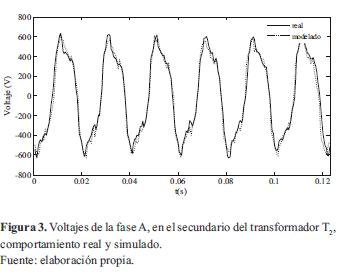
Las formas de onda del voltaje de la fase A en el secundario del transformador T2, reales y simuladas, se muestran en la figura 3. En esta figura se observa que el modelo del horno de arco captura la naturaleza no lineal de los voltajes reales; además, con los valores obtenidos de las constantes, se presentan niveles de voltajes similares a los valores reales.
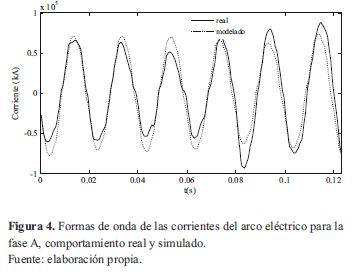
Una comparación similar se ha realizado para las formas de onda de las corrientes. En la figura 4, se muestran las corrientes del arco eléctrico real y simulado para la fase A.
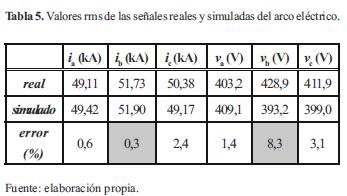
Se determinó el valor eficaz de las formas de onda de tensión y corriente para cada una de las fases, y en cada caso se compararon los resultados de simulación con el respectivo valor eficaz de las señales reales. Los resultados se muestran en la tabla 5.
El porcentaje de error se ha calculado con la ecuación (25), que muestra el error mínimo de estimación con respecto al valor real.
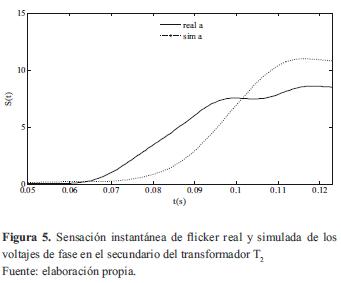
El nivel instantáneo de ficker S(t), es una medida de la cantidad de sensación de ficker producida por alguna fuctuación de tensión. Este parámetro tiene en cuenta la sensibilidad del ojo humano respecto a la frecuencia de cambios de la luminosidad de una lámpara incandescente [17]. La figura 5, muestra la evolución del nivel instantáneo de ficker producido por las fluctuaciones de tensión de la fase A obtenidas con el modelo y con los datos reales. Se observa cómo la evolución en el tiempo guarda cierta similitud. Se requiere de un método de estimación de los parámetros de la segunda fase del modelo para reducir las diferencias que se presentan.
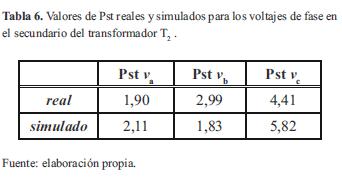
Para determinar el valor del Pst de los voltajes de fase en el secundario del transformador T2, se ha utilizado el ficker-meter, basado en el estándar IEC-61000-4-15 [17]. En la tabla 6, se muestra una comparación de los valores de Pst de los voltajes de fase reales y simulados.
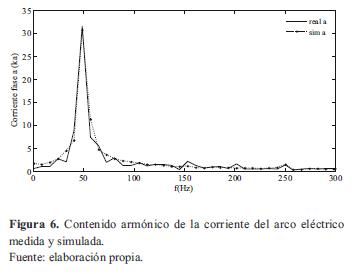
Debido a que el horno de arco es por naturaleza una fuente de armónicos, el modelo debe de reproducir en forma cercana los armónicos generados por el arco. La figura 6 muestra el espectro armónico de las corrientes del arco medida y simulada para la fase A.
Las dos curvas presentan un comportamiento similar, produciendo componentes interarmónicos y componentes armónicos de orden par e impar. Resultados similares se obtuvieron para las corrientes de las demás fases.
5. Conclusiones
La comparación de los resultados obtenidos a partir de las simulaciones realizadas con los datos reales, permite inferir que el modelo implementado refleja el comportamiento caótico y aleatorio de la carga y valida su inclusión en los problemas que se van a analizar en la red de distribución.
Basados en los resultados obtenidos, se puede concluir que la estimación de los parámetros de la primera etapa del modelo del horno de arco usando regularización de Tikhonov entrega resultados aproximados a las mediciones reales, soportado con un error máximo de 2,4 % en el valor eficaz de las corrientes y un error máximo de 8,3 % en el valor eficaz de tensión.
Referencias
[1] L. Tang, S. Kolluri, and M. McGranaghan, "Voltage fiker prediction for two simulta neously ac arc furnace", IEEE Transactions on Power Delivery, vol. 12, no. 2, pp. 985-992, April 1997.
[2] E. Acha, A. Semlyen, and N. Rajakovic, "A harmonic domain computational package for nonlinear problems and its application to electric arcs", IEEE Transactions on Power Delivery, vol. 5, no. 3, pp. 1390-1397, July 1990.
[3] O. Ozgun and A. Abur, "Flicker study using a novel arc furnace model", IEEE Transactions on power delivery, vol. 17, no. 4, pp. 1158-1163, Oct. 2002.
[4] R. Collantes and T. Gómez, "Identification and modelling of a three phase arc furnace for voltage disturbance simulation", IEEE Transactions on Power Delivery, vol. 12, no. 4, pp. 1812-1817, Oct. 1997.
[5] M. Fabiano, Z. Assis, C. Peixoto, and D. Goncalves, "An integrated model for the study of ficker compensation in electrical networks", Electrical Power Systems Research, no. 80, pp. 1299-1305, June 2010.
[6] A. Alzate, J. Marulanda, and M. Escobar, "Electric arc furnace modeling for power quality analysis", in IEEE Andescon Conference, Bogotá, septiembre 2010.
[7] C. Hansen, Regularization tools. A Matlab package for analysis and solution of discrete ill posed problemes, University of Denmark, Lyngby, reporte march 2008.
[8] E. Cano and E. Tacca, Arc furnace modeling in ATP-EMTP, in International conference on power system transients, Montreal, Canada, june 2005.
[9] J. Trageser, "Power usage and electrical circuit analysis for electric arc furnace", IEEE transactions on industry applications, vol. IA-16, no. 2, pp. 277-284, March -April 1980.
[10] G. Montanari, M. Loggini, A. Cavallini, L. Pitti, and D. Zaninelli, "Arc furnace model for the study of ficker compensation in electrical networks", IEEE Transactions on Power Delivery, vol. 9, no. 4, pp. 2026-2036, Oct. 1994.
[11] G. Manchur, "Development of a model for predicting ficker from electric arc furnace", IEEE Transactions on Power Delivery, vol. 7, no. 1, pp. 416-426, January 1992.
[12] E. O'Neill, G. Heydt, E. Kostelich, S. Ven-kata, and A. Sundaram, "Nonlinear deterministic modeling of highly varying loads", IEEE Transactions on Power Delivery, vol. 14, no. 2, pp. 537-542, April 1999.
[13] G. Carpinelli, F. Iacovane, A. Russo, and P. Varilone, "Chaos-based modeling of DC arc furnace for power quality issues", IEEE Transactions on power delivery, vol. 19, no. 4, pp. 1869-1876, October 2004.
[14] M. Kennedy, "Three steps to Chaos-Part I: Evolution", IEEE Transactions on circuit and systems-I:Fundamental, theory and applications, vol. 40, no. 10, pp. 640-665, October 1993.
[15] M. Kennedy, "Three steps to chaos-Part II: A chua's circuit primer", IEEE Transactions on circuit and systems-I:Fundamental, theory and applications, vol. 40, no. 10, pp. 657-674, October 1993.
[16] R. Horton, A. Haskew, and R. Burch, "A time-domain ac electric arc furnace model for ficker planning studies", IEEE Transactions on Power Delivery, vol. 24, no. 3, pp. 1450-1457, July 2009.
[17] IEC, "Electromagnetic compatibility (EMC). Part 4. Testing and measurements techniques. Section 15: Flickermeter-Functional and design specifications", CEI/IEC, International Standard CEI/IEC 61000-415, 1997.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.