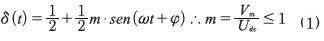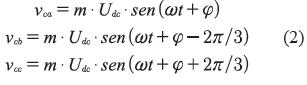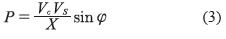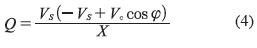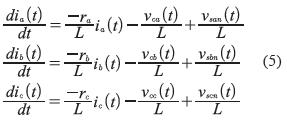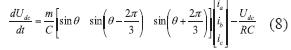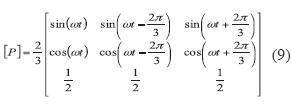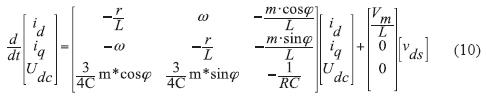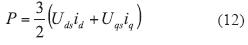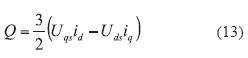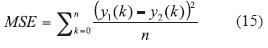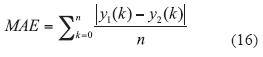DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2014.2.a04Published:
2014-04-01Issue:
Vol. 18 No. 40 (2014): April - JuneSection:
ResearchDiseño e implementación de controladores lineales para regulación del bus DC en convertidores VSC para HVDC
Design and implementation of linear controllers for VSC based HVDC DC bus regulation
Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Diseño e implementación de controladores lineales para regulación del bus DC en convertidores VSC para HVDC
Design and implementation of linear controllers for VSC based HVDC DC bus regulation
Carlos Alberto Hidalgo Mora1, Nelson Leonardo Díaz Aldana2, César Leonardo Trujillo Rodríguez3
1Ingeniero Electrónico de la Universidad Distrital, Asistente de Investigación del grupo LIFAE de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: carlosalbertohm@gmail.com
2Ingeniero Electrónico, Magíster en Automatización Industrial. Docente Asistente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: nldiaza@udistrital.edu.co
3Ingeniero Electrónico, Magíster en Ingeniería Eléctrica, Doctor en Ingeniería Electrónica. Docente Asociado de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: cltrujillo@udistrital.edu.co
Fecha de recepción: 10 de marzo de 2013 Fecha de aceptación: 27 de agosto de 2013
Clasificación del artículo: investigación
Financiamiento: Universidad Distrital Francisco José de Caldas
Resumen
Durante las últimas dos décadas se ha innovado y desarrollado tecnologías en los sistemas de transmisión en corriente continua. El desarrollo tecnológico en equipos y componentes electrónicos de potencia ha permitido la flexibilidad y modularidad de interconexiones de varios sistemas en corriente alterna y corriente continua. En este sentido, la tecnología de sistemas de transmisión de alta tensión en corriente continua, a base de convertidores a fuente de tensión, aparece como una opción tecnológica de amplio desarrollo gracias a la facilidad y flexibilidad que ofrece en el control del flujo de potencia activa y reactiva entre sistemas de diferentes características. Por lo tanto, para una correcta operación del sistema de transmisión en alta tensión en corriente continua, se requiere una regulación del voltaje en el bus de corriente continua y el flujo de potencia reactiva entre la subestación rectificadora y la red de corriente alterna con el cual se interconecta. En el presente artículo se establecen metodologías para el modelado, identificación y diseño de controladores para la regulación del bus de corriente continua y el flujo de potencia reactiva en un convertidor a fuente de voltaje operando como rectificador. Adicionalmente, se abordan técnicas de control por realimentación de estados aplicadas al convertidor a fuente de voltaje. Por último, se presentan resultados prácticos obtenidos de la implementación de un prototipo de convertidor en conjunto con los controladores diseñados.
Palabras clave: flujo de potencia, linealización, realimentación de estados, VSC.
Abstract
During last two decades, several technologies have developed and improved the high voltage direct current systems. The technological growth in power electronics converters has led to increase flexibility and modularity for interconnections of alternating current and direct current systems. In this sense, high voltage direct current system based on voltage source converters appear as feasible and flexible technology when active and reactive power flow have to be regulated between different power grids. Therefore, for an adequate operation, one of the major challenges is to regulate the direct current voltage and the reactive power flow between the alternating current system and the voltage source converter at the rectifier station. In this document, several methodologies will be explored for modeling, identifying, and designing controllers to regulate the direct current voltage at the common bus, and reactive power flow. In particular, linear techniques such as feedback states are used for the design of controllers. Finally, practical results will be presented on a physical voltage source converter prototype.
Key words: Feedback State Control, Linearization, Power Flow Control, VSC.
Introducción
El incremento en los sistemas de transmisión de energía, la integración de fuentes alternativas de energía y la interconexión de redes de corriente alterna (AC) con diferentes características, han creado la necesidad de tener sistemas de interconexión más eficientes y flexibles (Bahrman y Johnson, 2007). En este sentido, los sistemas HVDC (High Voltage Direct Current) aparecen como una opción tecnológica con altas ventajas comparativas respecto a las convencionales tecnologías de transmisión e interconexión en AC (Bahrman y Johnson, 2007).
Los sistemas HVDC se basan en arreglos de convertidores electrónicos conmutados que, mediante un proceso de doble conversión, corriente alterna a corriente directa (DC) AC/DC (rectificación) y DC/AC (inversión), permiten una fácil interconexión de redes con incompatibilidad de frecuencias, e incluso con diferencias de fase y modos de operación (Song, Zheng, Ruomei Li y Zhou, 2005). Una de las tecnologías de amplio desarrollo desde la década de los años noventa, es la de conversores a fuente de voltaje (VSC). Los VSC, son convertidores electrónicos compuestos por dispositivos semiconductores conmutables y, por lo tanto, es posible tener control sobre el encendido y el apagado de cada dispositivo semiconductor que compone el convertidor (Song, Zheng, Ruomei Li y Zhou, 2005; Sood, 2004). Como consecuencia, es posible la generación de corrientes y tensiones adecuadas que permitan un control rápido e independiente sobre los flujos de potencia activa y reactiva con la red AC (Sood, 2004).
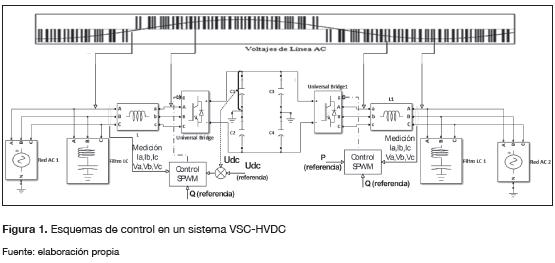
Un sistema VSC-HVDC básico está compuesto por dos convertidores VSC, los cuales se componen típicamente de IGBT conmutados a alta frecuencia, un reactor inductivo que enlaza el convertidor a la red AC y filtros pasivos para los componentes de alta frecuencia, producto de la conmutación (Song, Zheng, Ruomei Li y Zhou, 2005). En la figura 1 se muestra el esquema básico de un sistema VSC-HVDC en el cual uno de los convertidores se encarga de la regulación del flujo de potencia activa y el otro de la regulación del bus DC (Song, Zheng, Ruomei Li y Zhou, 2005). Por esta razón, la regulación adecuada del bus DC resulta fundamental para asegurar una correcta operación de todo el sistema de interconexión.
Este documento presenta el análisis y diseño de controladores para la estación rectificadora de un sistema VSC-HVDC. Dicha estación tiene como principal objetivo garantizar la regulación del voltaje DC y el control del flujo de potencia reactiva entre el sistema AC y el conversor VSC. Además, se obtienen los modelos dinámicos del VSC conectado a red, necesarios para el diseño de controladores. Luego, se presenta el diseño de controladores mediante realimentación de estados y los respectivos resultados obtenidos, tanto en las simulaciones como en el prototipo construido.
Metodología
Modelo dinámico y análisis del VSC conectado a red
Los convertidores VSC se componen de un puente trifásico de IGBT, filtros sintonizados para eliminar armónicos debido a la conmutación en alta frecuencia del SPWM -típicamente entre 1Khz a 2 Khz-, condensadores de almacenamiento que permiten realizar el enlace DC y reactores inductivos que permiten el flujo de potencias entre el VSC y el sistema AC, como se muestra en la figura 1 (Trujillo, Velasco, Guarnizo y Díaz, 2011).
El VSC puede generar una tensión sinusoidal a la frecuencia de la red a la cual se va interconectar a partir de una técnica de modulación SPWM en el cual el ciclo útil variable (δ(t)) se establece mediante la expresión de la ecuación (1) (Trujillo, Velasco, Guarnizo y Díaz, 2011; Peña y Trujillo, 2006).
En la ecuación (1), m representa el índice de modulación; φ es el ángulo de fase de la señal generada; Udc representa la tensión DC por polo; Vm en el valor máximo de la señal AC de la red en su componente fundamental -para este caso 60hz-. Finalmente, luego de un filtrado adecuado de los componentes de alta frecuencia, la tensión generada por fase se puede expresar a partir de la ecuación (2).
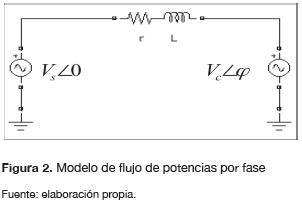
Considerando únicamente los componentes fundamentales de la tensión generada por el inversor, el sistema interconectado se puede representar como se muestra en la figura 2, donde Vs y Vc corresponden a los valores eficaces de tensión por cada fase en la red AC y en el conversor VSC respectivamente (Gengyin, Ming, Jie, Guangkai y Haifeng, 2004).
El flujo de potencias se puede aproximar a partir del análisis del circuito de la figura 2. Por lo tanto, el flujo de potencia activa (P) y potencia reactiva (Q), por fase, se presentan en las ecuaciones (3) y (4), en donde X representa la reactancia del inductor y φ es el ángulo de desfase del conversor VSC con respecto a la red AC (Diaz, Barbosa y Trujillo, 2007).
Las ecuaciones (3) y (4) muestran que el flujo de potencia activa depende principalmente del ángulo de desfase φ y, por su parte, el flujo de potencia reactiva depende del valor eficaz de la componente fundamental de la tensión generada por el VSC. Por otra parte, es necesario tener presente que para obtener la potencia activa y reactiva en el sistema trifásico se debe multiplicar por tres los valores de P y Q.
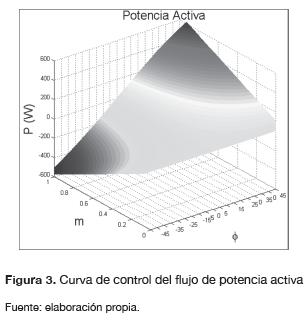
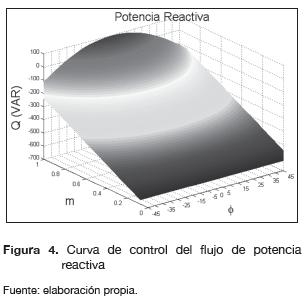
La figura 3 permite evidenciar que para el flujo de potencia activa, el ángulo de desfase (φ) presenta un mayor peso de control que el índice de modulación (m). De igual manera, en la figura 4 se muestra que en el flujo de potencia reactiva el índice de modulación (m) tiene mayor peso que la variable (φ). Como consecuencia, se puede decir que es posible controlar de forma independiente el flujo de potencia activa mediante ajustes del ángulo de desfase y la potencia reactiva mediante ajustes del índice de modulación.
Basado en el modelo de flujo de potencias y las leyes de Kirchhoff de voltaje y corriente sobre el circuito de la figura 2 se pueden obtener las ecuaciones que modelan el sistema para cada una de las fases, como se muestra en la ecuación (5).
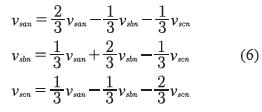
Teniendo en cuenta que en caso de no existir conexión entre el neutro de la carga y el neutro del convertidor, aparecerán componentes de tensión de secuencia cero entre los dos puntos centrales de la carga y el convertidor cuando se presenten desbalances en el sistema (Bose, 2002). Entonces, las tensiones de fase referenciadas al neutro del enlace DC se deben expresar como se muestra en la ecuación (6).
Reemplazando los sistemas de ecuaciones (2) y (6) en el modelo descrito en la ecuación (5) se obtiene un modelo dinámico no lineal variante en el tiempo, el cual permite describir el comportamiento del sistema trifásico. Dicho modelo únicamente considera los componentes fundamentales para representar la interconexión de la red AC con la estación rectificadora y se expresa como se muestra en la ecuación (7).
Donde θ=ωt+φ. Es importante aclarar que si se desea obtener el modelo en la estación inversora, los signos de las matrices en los voltajes del conversor y en los de la fuente AC cambian de signo (Gengyin, Ming, Ming y Chengyong, 2007).
Por su parte, el modelo de la tensión DC se obtiene a partir de las funciones de conmutación del convertidor, las corrientes de línea y la potencia que se va a transferir a la carga de la estación tal y como se presenta en la ecuación (8) (Guibin y Zheng, 2001).
De los modelos de las ecuaciones (7) y (8), se aprecia que el flujo de potencia y la tensión del bus DC, dependen directamente de las variables de control -ángulo de desfase e índice de modulación-. Adicionalmente, los modelos obtenidos son no lineales y variantes en el tiempo, por lo que se hace necesario desarrollar modelos que eliminen la variable temporal o recurrir a técnicas de identificación que permitan obtener modelos lineales e invariantes en el tiempo (LTI) para el diseño de controladores.
Modelo del VSC por espacio de estados
La obtención analítica de un modelo matemático LTI que represente de forma adecuada un sistema VSC-HVDC, requiere la eliminación de la variable temporal presente en los modelos anteriormente descritos. Usualmente, es necesario recurrir a herramientas computacionales de identificación que utilizan los modelos no lineales del VSC conectado a red como un sistema de caja negra con sus respectivas entradas y salidas (Trujillo, Velasco, Guarnizo y Díaz, 2011). Este proceso de identificación puede retrasar el proceso de diseño en el caso de no contar con herramientas de identificación adecuadas.
Para eliminar la dependencia temporal de los modelos de las ecuaciones (7) y (8) se propone el uso de la transformación de Park, la cual es básicamente una transformación lineal de un sistema de marco de referencia temporal (abc) a uno de referencia síncrona (dq0) (Bose, 2002). Para realizar la transformación se define la matriz, no singular, [P] que se presenta en la ecuación (9) de tal forma que el sistema transformado será B=PA. En este caso, A representa el sistema de ecuaciones (7) y (8) y B el sistema en coordenadas dq0.
Aplicando la matriz de transformación en los modelos de las ecuaciones (7) y (8), se obtiene el modelo no lineal del VSC por espacio de estados que se presentan en la ecuación (10), donde las variables de estado son (Udc, Id, Iq). Es de destacar que este modelo ya es invariante en el tiempo.
Donde Vm es la tensión máxima de la red AC y Uds, Uqs, U0s se describen en la ecuación (11).
Bajo el sistema de referencia síncrono las expresiones de potencias activa y reactiva se describen en las ecuaciones (12) y (13).
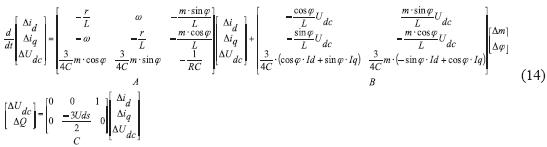
Sin embargo, para el diseño de los controladores por realimentación de estados, se requiere contar con un modelo lineal además de una invariante en el tiempo. Se procede entonces a la linealización del modelo de la ecuación (10) mediante la aproximación de Taylor (Chen, 1999; Astrom y Murray, 2010). Dicho modelo se linealiza para las condiciones de operación nominales las cuales se mencionan a continuación: Udc = 195V; P = 300W; Q = 0VAR; m=0.88; id=1.1813 A; iq = 0A; φ = -9.1°. Finalmente, el modelo linealizado se presenta en la ecuación (14).
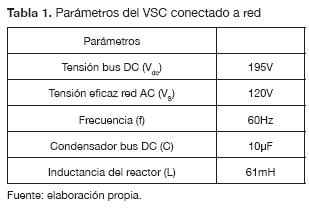
El modelo de la ecuación (14) es un modelo genérico lineal e invariante en el tiempo, cuya principal ventaja es que se encuentra en términos de los principales parámetros de VSC y de la red AC por interconectar. Por este motivo, el diseño de controladores utilizando en este modelo resulta simple. En la tabla 1 se presentan los principales parámetros del sistema diseñado.
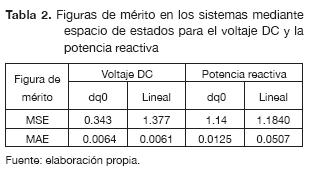
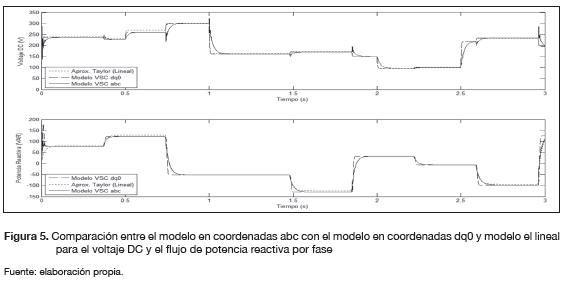
Los modelos por espacio de estados en el sistema de coordenadas dq0 y el modelo lineal fueron comparados respecto al modelo de coordenadas abc utilizando figuras mérito tales como: MAE (Mean Absolute Error), MSE (Mean Square Error), como se muestra en las ecuaciones (15) y (16).
Los resultados se presentan en la tabla 2, donde se aprecia un alto grado de aproximación en los modelos. Adicionalmente, en la figura 5, se presenta la respuesta en el tiempo de los tres modelos en la cual se evidencia que, en estado estacionario, el comportamiento de los modelos es similar, esto se puede verificar de forma cuantitativa con la figura de mérito MAE.
Adicionalmente, en las respuestas de estado transitorio se presentan las mayores diferencias en error entre los modelos con respecto al modelo en coordenadas abc, razón por la cual los valores en las figuras de mérito MSE, en la gran mayoría, se encuentran por encima de 1. Sin embargo, el porcentaje de similitud entre los dos modelos con el modelo dinámico del conversor VSC es alto y por ello se consideran apropiados para representar el VSC conectado a red y suficientes para el diseño del controlador.
La mayor ventaja de usar el modelo lineal del VSC es que este no requiere el uso de herramientas de identificación ante diferentes condiciones. Para ser precisos, este es un modelo general que se puede aplicar incluso ante cambios en los parámetros del sistema lo cual facilita el diseño y ajuste de los controladores lineales.
Control por realimentación de estados del VSC
La mayoría de las técnicas de diseño en la teoría de control moderna utilizan la configuración de la realimentación de estado, es decir que en lugar de emplear configuraciones fijas en trayectorias directas, el control se realiza a partir de variables de estado (Chen, 1999; Astrom y Murray, 2010).
La metodología de diseño de control por realimentación de estados consiste en utilizar los modelos por espacio de estados de la ecuación (13), asignando los polos de acuerdo con una respuesta deseada. Para este caso particular, se determinan como criterios de diseño en la tensión del bus DC (Mp=2 %, ts = 10 ms) y en el flujo de potencia activa (Mp = 0 %, ts = 15 ms). Donde, ts equivale al tiempo de establecimiento deseado y Mp equivale al porcentaje de sobrepaso máximo permitido en la respuesta del sistema.
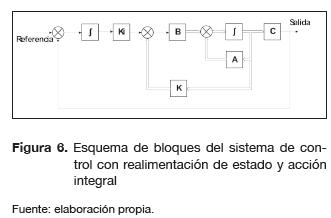
La técnica de control moderna escogida consistió en una realimentación de estados con acción integral, debido a que el sistema presenta dos entradas y dos variables de salida. Los análisis desarrollados demostraron que es posible un control independiente para el bus DC mediante la variable de control (Δφ) y para el flujo de potencia reactiva Q mediante la variable de control (Δm) (Trujillo, Velasco, Guarnizo y Díaz, 2011; Díaz, Barbosa y Trujillo, 2007). Adicionalmente, las variaciones de carga y de las dos entradas se pueden considerar como perturbaciones en el sistema que deben afectar las entradas del SPWM, con esto se justifica la adición de la acción integral en el VSC, tanto para el bus DC como para el flujo de potencia reactiva. En la figura 6 se presenta el esquema básico de un controlador por realimentación de estados y acción integral.
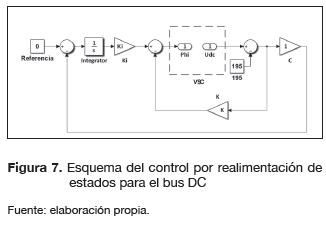
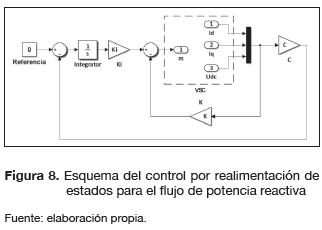
Se diseñaron dos controladores por realimentación de estados: el primero, basado en la condiciones de (Mp) y (ts) descritas anteriormente; el segundo, es un control óptimo cuadrático (LQR) con el cual se busca minimizar el coste de energía en las variables de control (Astrom y Murray, 2010). La técnica de sintonización utilizada es la de asignación de polos, aproximando la respuesta del sistema a la de un sistema de segundo orden mediante la correcta selección de los polos dominantes que aseguren los valores deseados de Mp y Ts (Astrom y Murray, 2010). Para el control de voltaje DC se realimenta únicamente la variable de estado Udc. Se usó un controlador vectorial con acción integral para asegurar error cero y seguimiento de referencias ante perturbaciones en el sistema -variaciones en la potencia activa y el índice de modulación-. La figura 7 muestra el esquema del controlador utilizado para la regulación del bus DC. Por otro lado, para regular el flujo de potencia reactiva, es necesario realimentar las tres variables de estado del sistema id, iq y Udc. El esquema del controlador usado para la regulación del flujo de potencia reactiva se muestra en la figura 8.
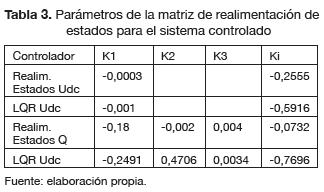
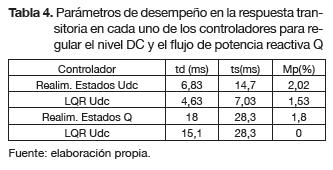
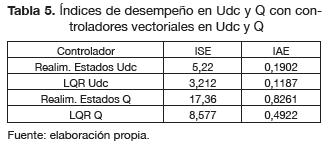
En la tabla 3 se presentan los parámetros de la matriz de realimentación de estados K para cada uno de los controladores diseñados. Adicionalmente, en la tabla 4 se presenta una comparación del desempeño de los controladores diseñados incluyendo el parámetro (td = tiempo de levantamiento). Por último, se hace la evaluación del sistema controlado mediante índices de desempeño tales como: ISE -integral de error cuadrático- e IAE -integral de error absoluto-, la cual se presenta en la tabla 5.
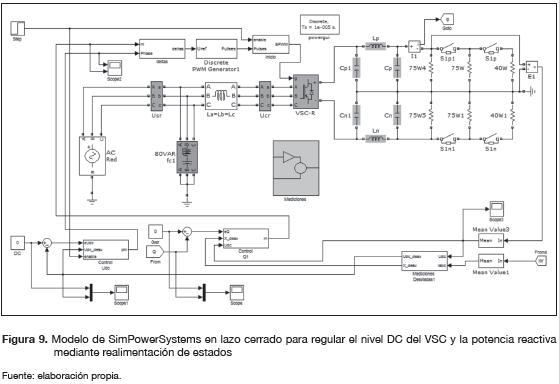
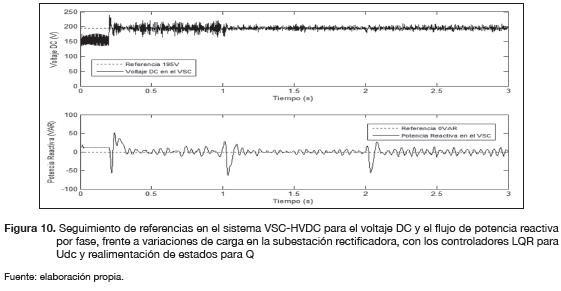
De las tablas 4 y 5 se observa que el control LQR es el de mejor desempeño, tanto en la respuesta transitoria como en estado estacionario, el ISE disminuye y lo cual indica que el sistema responde más rápido. Los resultados y el seguimiento de referencias en las variables del sistema VSC-HVDC para el rectificador se simularon en Sim-PowerSystems de MATLAB, como se muestra en la figura 9. La simulación se realizó considerando el caso en el cual la red AC debe transferir potencia activa al enlace DC bajo condiciones de carga de: 150W, 300W y 380W con una tensión DC regulada en 195V por polo. Los resultados se muestran en la figura 10.
En la figura 10, el mejor desempeño de los controladores por realimentación de estados se encuentra cerca del punto de operación nominal, es decir, cerca de 300 W y 380 W, como se observa en los periodos (1 s-2 s) y (2 s-3 s), respectivamente. Cuando el sistema se aleja de las condiciones nominales para las cuales fue diseñado, su desempeño se deteriora como se observa en la primera parte de la figura 10 en la tensión DC.
Resultados experimentales
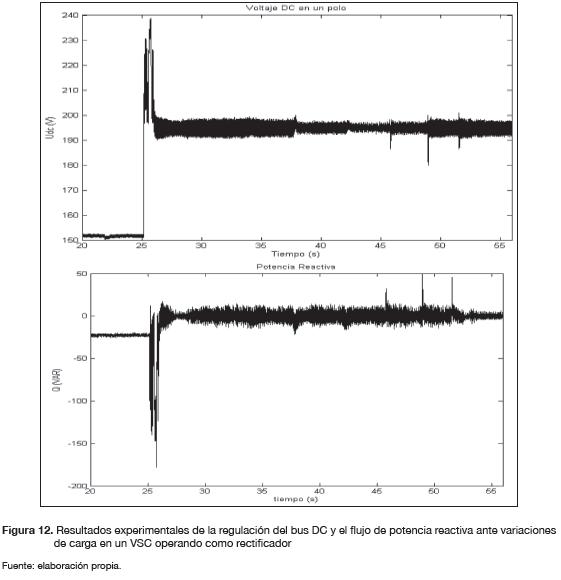
Con el fin de verificar experimentalmente el desempeño de los controladores, se establecieron variaciones de carga entre 255 W y 390 W en el VSC. De esta forma, se observó el comportamiento del conversor en la regulación de la tensión DC y el flujo de potencia reactiva. En la figura 11 se muestra una imagen del convertidor VSC implementado.
En la figura 12 se presenta la respuesta real del sistema implementado. En dicha figura se observa que la tensión DC tiene un sobre impulso al comienzo, esto sucede cuando se habilita la regulación del sistema VSC-HVDC. Las oscilaciones en la regulación del bus DC disminuyen cuando hay variaciones de carga, al igual que ocurre en la regulación de la potencia reactiva. El mejor desempeño del sistema se presenta cerca del punto de operación nominal para el cual fue diseñado el VSC. Mediante un instrumento de medición como el PQA824 (analizador de calidad de potencia) se obtuvieron los resultados que se presentan en la tabla 6 bajo operación en estado estacionario. En la figura 12 se puede ver que la tensión en el bus DC al igual que el flujo de potencia reactiva logran ser reguladas a pesar de las variaciones en la carga.
El factor de potencia se encuentra en 0,97 debido a los armónicos producidos por la conmutación de los IGBT en alta frecuencia (1800 hz y 3600 hz). Es importante resaltar que los modelos sobre los cuales fueron diseñados los controladores no tenían en cuenta los componentes de alta frecuencia. Sin embargo, los valores obtenidos para componentes reactivos a la frecuencia fundamental muestran un desempeño aceptable en el control para regular el flujo de potencia reactiva.
En los resultados presentados en la figura 12 se aprecian niveles importantes de ruido en las salidas. Esto se debe a la conmutación de los IGBT en altas frecuencias y la transmisión de datos al sistema computacional. Sin embargo, se puede apreciar el seguimiento alrededor del valor medio de la tensión DC (195V) y el valor medio del flujo de potencia reactiva (0VAR). Este tipo de oscilaciones son altamente comunes en sistemas de potencia, debido a la interacción de todos los componentes electrónicos, sobre todo cuando se realizan altas transferencias de potencia (Paserba, 2007).
Conclusiones
El modelo obtenido por espacio de estados es un modelo genérico que permite el diseño directo de controladores por realimentación de estados a partir de los parámetros básicos de diseño del VSC y del sistema a interconectar. Adicionalmente, su mayor ventaja radica en que no es necesario realizar una identificación del sistema usando herramientas computacionales.
A pesar que los conversores VSC sean sistemas no lineales acoplados, es posible, desarrollar controladores lineales para regular el voltaje DC y el flujo de potencia reactiva en la estación rectificadora de forma independiente. De la misma forma, sería posible un control independiente de los flujos de potencia activa y reactiva en la estación inversora de un sistema HVDC.
El control por realimentación de estados permite la regulación de procesos de múltiples entradas y salidas como los que se presentan en los sistemas HVDC-VSC. Además de las ventajas mencionadas, su fácil metodología en el diseño y facilidades en la sintonización mediante reguladores LQR, abren la posibilidad para que este tipo de técnicas de control se consideren en la planeación, diseño e implementación de controladores para los sistemas VSC-HVDC.
Referencias
Bahrman, M. P. & Johnson, B. K. (2007). The ABCs of HVDC transmission technologies. IEEE Power and Energy Magazine, 5 (2),32-44.
Song, R., Zheng, C., Ruomei Li, L. & Zhou, X. (agosto, 2005). VSCs based HVDC and its control strategy. Transmission and Distribution Conference and Exhibition: Asia and Pacific. Dalian, China.
Sood, V. K. (2004). HVDC and FACT's controllers: Applications of static converters in power systems. Nueva York, USA: Springer.
Trujillo, C. L., Velasco, D., Guarnizo, J. G. & Díaz, N. (2011). Design and implementation of a VSC for interconnection with power grids, using the method of identification the system through state space for the calculation of controllers. Applied Energy, 88 (9), 3169-3175.
Peña, R. y Trujillo, C. L. (2006). Análisis y simulación de VSCs con modulación PWM para uso en redes HVDC. Revista Ingeniería Universidad Distrital Francisco José de Caldas, 11 (2), 30-39.
Gengyin, L., Ming, Z., Jie, H.,Guangkai, L. & Haifeng, L. (2004, nov.) Power flow calculation of power systems incorporating VSC-HVDC. International Conference on Power System Technology, Singapore, Singapore.
Diaz, N. L., Barbosa, F. H. & Trujillo, C. L. (2007, sep.). Analysis and Design of a Nonlinear Fuzzy Controller Applied to a VSC to Control the Active and Reactive Power Flow. Electronics, Robotics and Automotive Mechanics Conference, Cuernavaca, México.
Bose, B. K. (2002). Modern power electronics and AC drivers. Nueva York: Prentice Hall.
Gengyin, L., Ming, Y., Ming, Z. & Chengyong, Z. (2007, jun.). Decoupling Control for Mul-titerminal VSC-HVDC Based Wind Farm Interconnection. IEEE Power Engineering Society General Meeting, Tampa, USA.
Guibin, Z. & Zheng, X. (2001, ene.). Steady-state model for VSC based HVDC and its controller design. IEEE Power Engineering Society Winter Meeting, Columbus, USA.
Chen, C. T. (1999). Linear System Theory and Design. Nueva York: Oxford University Press.
Astrom, K. J. & Murray, R.M. (2010). Feedback Systems: An Introduction for Scientists and Engineers. California: Caltech BOOK.
Paserba, J. (2007). Robust control in power systems [Book Reviews]. IEEE Power and Energy Magazine, 5 (5), 79-81.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.