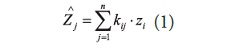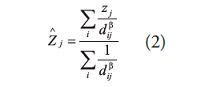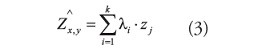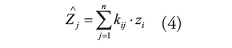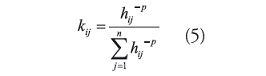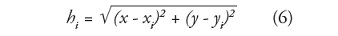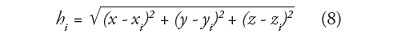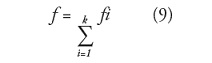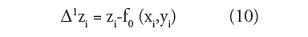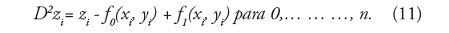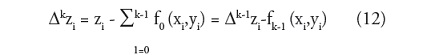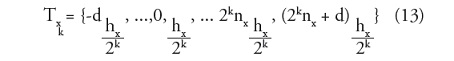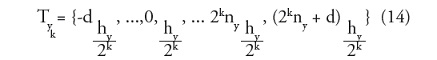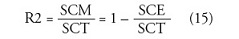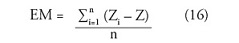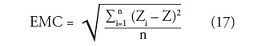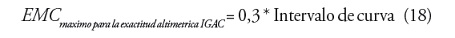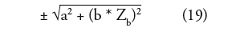Modelos digitales batimétricos generados por métodos de interpolación IDW, KRIGING, SHEPARD y B-SPLINE en el Archipiélago de Islas del Rosario

MODELOS DIGITALES BATIMÉTRICOS GENERADOS POR MÉTODOS DE INTERPOLACIÓN IDW, KRIGING, SHEPARD Y B-SPLINE EN EL ARCHIPIÉLAGO DE ISLAS DEL ROSARIO

BATHYMETRIC DIGITAL MODELS GENERATED BY INTERPOLATION METHODS IDW, KRIGING, SHEPARD AND B-SPLINE IN THE ARCHIPELAGO OF ROSARIO ISLANDS

Denisse Scarly Alvarez Osorio¹, Jhon Camilo Matiz Leon², Andres Cardenas Contreras³

¹Ministerio de Ambiente Vivienda y Desarrollo Territorial (MAVDT skarly.alvarez@gmail.com

² Instituto Geografico Agustin Codazzi (IGAC)ing.camilo.matiz@gmail.com

³Universidad Distrital “Francisco José de Caldas” acardenas@udistrital.edu.co

Recibido: 29/07/2011 - Aceptado: 21/09/2011

RESUMEN

La Armada Nacional, en su buque ARC Providencia, cuenta con el magnetómetro G-882, con el cual se obtuvieron los datos de profundidad del lecho marino de la falla Rocha inferida en islas del Rosario, puntos que fueron representados por métodos de interpolación geoestadisticos como el IDW, Kriging, Shepard y B-Spline, que generaron los modelos digitales batimetricos correspondientes, basados en las correcciones asociadas a las mareas y alturas elipsoidales. Partiendo de ello, se evaluó que el fondo marino no influye de una forma sustancial en la bondad de ajuste del modelo generado, de ahí que fue preciso identificar los diversos cambios del relieve submarino para escoger los datos necesarios en la representación del modelo batimétrico y así realizar la selección del mejor método a través de la evaluación y comparación del error medio cuadrático (EMC), y evaluar la calidad del modelo, a través de los criterios de calidad de validación cruzada, la exactitud altimétrica y la incertidumbre total vertical.

El resultado del estudio permitió establecer la confiabilidad del magnetómetro G-882, como herramienta admisible para representar las profundidades marinas.

Palabras clave: batimetría, exactitud altimétrica, geoestadistica, incertidumbre total vertical, métodos de interpolación, validación cruzada.

ABSTRACT

The National navy´s ship providence ARC has the G-882 magnetometer, from which extracted data from the seafloor depth of the fault inferred Rocha Rosario islands, points were represented by geostatistical interpolation methods such as IDW, Kriging, Shepard and B-Spline that generated the corresponding Bathymetric Digital Models based on the corrections associated with the tides and ellipsoidal heights. On this basis, it was assessed that the seafloor is not a substantial influence on the goodness of fit of the model generated, hence it was necessary to identify the various changes of undersea to choose the necessary data on the bathymetric model representation and so the selection of the best method through the assessment and comparison of Root Mean Squared (EMC), the criteria of quality and cross validation, accuracy and uncertainty total altimeter vertical.

The result of the study allowed to establish the reliability of G-882 magnetometer as a tool to represent the allowable depths.

Key words: Bathymetry, altimetry accuracy, geostatistics, vertical total uncertainty, interpolation methods, cross-validation.

INTRODUCCIÓN

Los levantamientos hidrográficos han experimentando cambios fundamentales en la obtención de la información debido al avance tecnológico en los sistemas de medición, como por ejemplo los sistemas multihaz acústicos y laser aerotransportados, que proporcionan cobertura y medición casi total del fondo marino, en comparación con muestreos hechos por perfiles batimetricos. Así, la selección de datos se encuentra condicionada directamente a la distribución y densidad de los mismos, los cuales son tomados a través de las sondas monohaz, multihaz y sondas de barrido lateral, estas últimas se usan para definir aéreas que requieren más detalle y exactitud, representando en los levantamientos batimetricos la obtención del posicionamiento vertical (Z) y el posicionamiento horizontal (X,Y) a través del Global Positioning System (GPS), que es realizado in situ y de forma concreta para cada punto, estando el modelo limitado por su escala y software empleado, donde el resultado del modelo digital batimétrico (MDB) para la misma área puede variar según los parámetros de control seleccionados que permitan establecer el cálculo del error entre el modelo generado y la superficie real.

En el procesamiento de datos de la profundidad del mar se deben tener en cuenta las correcciones por mareas y alturas elipsoidales que afectan el posicionamiento vertical y horizontal de las muestras obtenidas, para una posterior representación espacial. Para la interpolación de este tipo de datos que contienen el atributo altitud se implementaron los métodos convencionales geoestadisticos IDW, Kriging, Shepard y B-Spline, aplicando el error medio cuadrático y criterios de calidad como la validación cruzada, la exactitud altimétrica y la incertidumbre total vertical en la generación y selección del mejor MDB, el cual fue interpolado por el método B-Spline, arrojando una representación de la superficie del lecho marino mas “fiel” a la realidad.

Batimetría

La batimetría se define como el “estudio de las profundidades oceánicas, lacustres y corrientes de agua continuas como ríos, mediante el trazado de mapas de isobatas” (Real Academia de la Lengua Española, 2001); sin embargo, algunos autores la definen como ciencia y otros como una técnica de medición que facilita la obtención de valores de profundidad del agua, ya sea marina, lacustre o fluvial, determinando la topografía del fondo subacuático.

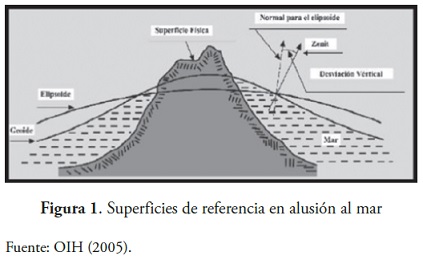
La batimetría requiere la elección de un sistema de referencia que precise y defina la ubicación de un punto en el plano x, y, z (Martínez y Sánchez, 2005), donde de la verdadera cota del punto levantado se determina a partir diferentes correcciones que permiten reducir los sondeos al datum o cota de referencia.

Los levantamientos batimetricos se diferencian de los terrestres porque los primeros no cuentan con una estabilidad para los instrumentos durante la observación, ni tampoco para estacionar una y otra vez en un determinado punto debido al movimiento de la masa de agua. Por esta razón, el avance de la tecnología en las metodologías, técnicas e instrumentos para la determinación de la profundidad del lecho marino han facilitado que las mediciones sean mas precisas y fundamentales para el desarrollo de estudios batimetricos.

En la actualidad se cuenta con los sistemas de haz simple provenientes de los sonares militares, que se han venido desarrollando hasta los sistemas acústicos multihaz (MBES) y los sistemas laser aerotransportados (ALS), que proporcionan una mayor precisión en la medición de la profundidad y una cobertura total del fondo marino. Estos avances han proporcionado una calidad de datos aceptable para la representación de los MDB, siendo la ecosonda multihaz la herramienta insignia del país para la toma de datos batimetricos y el magnetómetro G-882 (Geometrics, 2005) el instrumento ideal para la toma de datos del campo magnético terrestre, dado que posee un altímetro en su sensor, el cual registra la profundidad del lecho marino, instrumentos utilizados para este proyecto.

CORRECCIONES DE COTA

El termino marea se conoce como el cambio periódico y alternativo de ascenso y descenso que posee el nivel del agua producido por distintos fenómenos tales como fuerzas gravitacionales, presión atmosférica o efectos locales en los niveles de agua los cuales, dependiendo de si hay una acción acumulativa de fuerzas, se produce una pleamar o marea alta o, por el contrario, cuando existe un alejamiento compensando de las aguas, se produce lo que se conoce como bajamar o marea baja.

El datum de nivel de agua es un plano local de elevación que se aplica solamente en el área especifica donde se han hecho las mediciones de nivel del agua. Bien sea de marea o no debido a esta, es permanentemente referido a la tierra al nivelar el medidor del nivel de agua a una red local de marcas de nivelación (OHI 2005).

Teniendo en cuenta lo anterior, y debido a que no existe estabilidad en la masa acuática que permita determinar fácilmente la verdadera cota de la superficie subacuática, se hace imprescindible realizar correcciones como la de mareas o la de alturas, que tienen por objeto establecer una corrección, la cual se aplica a los datos de profundidad y con ello se obtiene el valor real de la misma.

MODELO DIGITAL BATIMÉTRICO (MDB)

Un modelo es considerado como una abstracción aproximada que busca la simplicidad de la realidad y se establece mediante la aplicación de unos supuestos, los cuales determinan qué tipo de propiedades son relevantes (Felicisimo-Perez, 1994), que en el caso de los MDB es la profundidad. Esta variable continua, y distribuida espacialmente mediante un conjunto de datos, es la distancia que se encuentra entre el nivel medio del mar y el fondo acuático, que permite establecer la topografía de las profundidades marinas.

Este tipo de modelos se describen como una función bivariable continua P = f(x, y), donde P es la profundidad en un punto de coordenadas (x, y).

MÉTODOS DE PREDICCIÓN ESPACIAL

Los métodos de predicción espacial se fundamentan en el procedimiento que permite calcular el valor de una variable y su posición a partir de valores muestreados de la misma variable en otras posiciones del espacio, a través de algoritmos matemáticos que facilitan el cálculo de los mismos. En el presente estudio se trabajaron como métodos de predicción espacial los métodos IDW, Kriging, Shepard y el B-Spline, con el objeto de predecir aéreas sin información.

MÉTODO PONDERACIÓN DE LA DISTANCIA INVERSA (IDW )

El IDW se fundamenta en asignar pesos a los datos muestreados que van a ser interpolados para determinar el dato central en función inversa a la distancia que los separa (Giraldo-Henao, 2003). La formula general es:

Donde Zj es el valor estimado para el punto j, n , el numero de puntos necesarios para la interpolación, zj el valor en el punto i-esimo y kj el peso asociado al dato i en el calculo del nodo j. Los pesos k varían entre 0 y 1 para cada dato y la suma total de ellos es la unidad. La función de proporcionalidad entre el peso y la distancia se muestra en la siguiente fórmula:

Siendo la fórmula del peso un exponente de ponderación que controla la forma en la que el peso asignado al dato disminuye con la distancia, es decir, que si el exponente o la potencia van disminuyendo los pesos asignados serán menores, por el contrario, si la potencia aumenta la diferencia en los pesos será mayor (Droj, 2008).

MÉTODO KRIGING

Este método de interpolación define la altitud como una variable regionalizada, suponiendo que funciones de correlación espacial pueden explicar en su totalidad o parcialmente la variación espacial de esta, que es la variable estimada que se va a representar a través de funciones homogéneas que se deducen de toda el área de análisis, es decir, los valores próximos de z (Giraldo-Henao, 2003).

Estas funciones homogéneas son derivadas teniendo en cuenta la distancia d que existe entre los datos medidos a través de la semivarianza, analizando así la correlación espacial entre ellos en función de d y estimando una media ponderada:

Donde un conjunto de k datos se sitúan en torno del punto interpolado y l representa los pesos asignados a cada uno de ellos. La ventaja del método es el criterio de asignar a cada dato su valor ponderado junto a la asignación de un valor de error a cada punto interpolado, lo que permite aplicar criterios estadísticos brindando una buena definición del área de análisis.

Los supuestos estimados en este tipo de métodos suponen que la altitud en un punto este determinada por los valores de los puntos mas próximos distribuidos a distancias variables, y que en función de ellas habrá una mayor o menor inferencia.

MÉTODO SHEPARD

El método de Shepard utiliza el método de distancia inversa a través de mínimos cuadrados ponderados, dado que su uso elimina o reduce el “ojo de buey”, que son contornos generados dentro del modelo. La ecuación utilizada en este método es la siguiente:

Donde Z_j es el valor estimado para el punto j,n j , n el número de puntos necesarios para la interpolación, Z_i el valor en el punto i-esimo, y k_ij el peso asociado al dato i en el cálculo del nodo j. La ecuación del peso es:

Donde P es un numero real positivo arbitrario, llamado el exponente de ponderación, que controla la forma en la que el peso asignado al dato disminuye con la distancia, donde generalmente se deja el 2 como valor predeterminado, aunque este puede ser modificado; h_ij es la distancia desde el punto de dispersión hasta el punto de interpolación, donde la suma de pesos sea igual a la unidad (Gordon y Wixon, 1978).

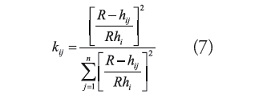
Aunque la función de peso arriba indicada es la forma clásica de la función de peso en la interpolación de la distancia inversa ponderada, a partir de ella se deduce la siguiente ecuación:

Donde h_ij es la distancia desde el punto de interpolación para esparcir el punto interpolado, R es la distancia desde el punto de interpolación hasta el punto de dispersión mas distante, y n es el número total de puntos de dispersión. Esta ecuación se ha encontrado para dar resultados superiores a la ecuación clásica.

En tres dimensiones (x, y, z) el método de las ecuaciones de Shepard es idéntico a las ecuaciones en dos dimensiones (x, y), solo que se le adiciona la coordenada z, la cual es la variable altura (h) por interpolar, y se calcula de la siguiente forma:

Donde (x, y, z) son las coordenadas del punto de interpolación y (xi_i, y_i, z_i) son las coordenadas de cada punto de dispersión.

MÉTODO B-SPLINE

Al ingresar un conjunto de datos dispersos al algoritmo, el método arroja como resultado un tensor producto de las superficies B-Spline, siendo estos algoritmos los esquemas básicos B-Spline.

Los algoritmos de una aproximación B-Spline (BS – por sus siglas en ingles) generan una compensación existente entre la “forma” suavizada y la precisión de la función de aproximación. Para superar dicha compensación, los algoritmos de aproximación multinivel B-Spline (MBA – por sus siglas en ingles) son introducidos en la ejecución del método (Lee et al., 1997). El algoritmo hace uso de una jerarquía de control de latices para generar una secuencia de funciones f _i ) y la función final de aproximación f, que es definida como la suma de las funciones f_i).

Para optimizar este proceso, el refinamiento B-Spline es usado para reducir la suma de estas funciones dentro de una función B-Spline equivalente. El algoritmo MBA sirve de resultado como una aproximación inicial suave fo → ΔoP = P definido en el control latice menos “refinado” Φ0 = Φ, aplicando el algoritmo MBA. Para continuar hacia el nivel mas “fino”, la primera aproximación posible deja grandes discrepancias en los puntos (datos) en P, en particular f0 deja una desviación:

El siguiente control latice mas fino F₁, el que se utiliza para obtener la función f₁ aproxima las diferencias a Δ1P = {(xi,yi,Δ1zi)}.

Entonces, la suma de f₀ + f₁ produce una menor desviación para cada (x_i, y_i) en

En general, para cada nivel k en la jerarquía, el punto de ajuste Δ^k P = {(x_i, |y_i,Δ^k z_i)} es aproximado por una función fk definida sobre el control de latices F_k, donde:

Y D₀, z_i, = z_i,. Este proceso empieza desde el latice menos refinado f₀, y continua incrementalmente hacia el latice mas fino f_k, con el conjunto de vectores nodos son definidos por las siguientes ecuaciones:

La función final de aproximación f es definida como la suma de las funciones. Debido al sistema de jerarquías que maneja el método B-Spline para generar las funciones mas aproximadas a la función de ajuste de la superficie, se obtiene una aproximación desde la curva de interpolación B-Spline mas “rugosa y dura” para representar la superficie hasta la más fina de las funciones de interpolación para representar la suavidad de la misma. Mientras la jerarquía avanza de nivel, el control latice aplicado por cada multinivel, suaviza e interpola el conjunto de puntos que componen la superficie generando una representación aproximada de la realidad. En los modelos digitales batimetricos, el algoritmo se comporta de tal manera que cada ajuste Dkzi que se realiza a cada punto interpolado, permite que dicho control aplicado a la distancia entre datos sea lo suficientemente pequeño con relación a la distribución de los datos, debido a que cada nivel jerárquicamente posicionado “suaviza” o “robustece” cada red de datos interpolada por el método B-Spline (Lee et al. 2005).

METODOLOGÍA

Área de estudio

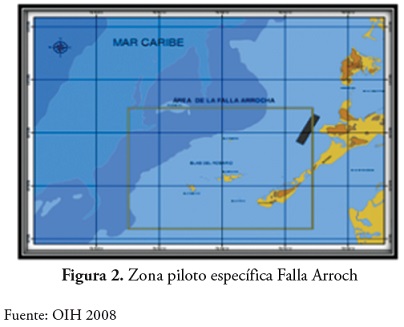
El área de estudio corresponde a la zona continental del norte de Colombia (Zona UTM 18 norte), departamento de Bolívar, Cartagena, ubicada en el archipiélago de Islas del Rosario, en el sector cercano a Punta Gigante, sobre la Falla Rocha inferida, entre las coordenadas 10°06’30” N y 10°16’30” N de latitud y 75°52’00” W 75°38’00” W de longitud, la cual cubre una área de 5 km2 de lecho marino.

Adquisición de los datos

La adquisición de la información comienza bajo el proyecto de investigación denominado “Metodología de adquisición y procesamiento de datos geomagnéticos marinos”, en un convenio interadministrativo entre el Centro de Investigaciones Oceanográficas e Hidrográficas de la Armada Nacional y la Universidad Distrital “Francisco José de Caldas”, que permitió adquirir los datos con el magnetómetro G-882, sobre la plataforma ARC providencia, buque que posee la infraestructura para realizar este tipo de tareas científico-marinas.

El magnetómetro G-882, equipo diseñado para detectar anomalías del campo magnético (generadas por cuerpos que posean material de hierro), recibe los datos geográficos con el GPS doble frecuencia que posee el buque para detectar en tiempo real la medición en posición. Los datos tomados por el magnetómetro son enviados a través de un cable a una botella telemétrica garantizando que la información sea grabada en tiempo real; la información se envía a un modem para que la codifique y luego la grabe en un computador para su posterior procesamiento e interpretación, mediante el software MagLog Magnetometer Logging (Geometrics, 2005).

De la información adquirida se seleccionaron como atributos primordiales para generar las correcciones y los modelos batimetricos la longitud, latitud, fecha, hora, profundidad (profundidad del magnetómetro, medida desde el winche que lo sostiene hasta el magnetómetro), altura (altura del magnetómetro con respecto al lecho marino) y altura GPS (altura medida GPS, conocida como la altura elipsoidal h del punto capturado por el magnetómetro).

Tratamiento de los datos

El magnetómetro G-882 tomo inicialmente 174.830 puntos; al ser evaluados con estadística descriptiva se percibió la presencia de datos atípicos que infirieron directamente en la normalidad de la variable. La desviación estándar dio como resultado 99,5, la varianza 9901,62, una Kurtosis de 29595,6, el dato mínimo fue de -47,0 m y el máximo alcanza aproximadamente 25,4, corroborando este ultimo que fueron datos arrojados por el sensor como un error del mismo en la medición.

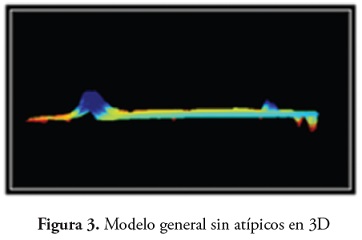
Al proceder con la eliminación de los atípicos se suprimieron aquellos datos no representativos para el área de estudio, pues el terreno se caracterizo por poseer una tendencia plana, excepto en dos aéreas que hacen que los datos con menor profundidad sean considerados como atípicos, lo que implica una cuidadosa eliminación de los mismos. Al ser evaluada nuevamente la tabla de datos sin los atípicos, mediante estadística descriptiva, la distribución no fue normal; sin embargo, fue esta base de datos la que se utilizo para el proyecto, que incluyo un total de 171.854 datos (Figura 3).

De este modo, se generaron los diferentes modelos con los 171.854 datos, a través de diversos métodos de interpolación, sin embargo, al ser la base de datos tan grande, se decidió trabajar al tiempo con una de 17.181 datos, es decir, casi el 10% de los datos originales, con el objetivo de percibir si existiría algún mejoramiento o empeoramiento en el resultado de los métodos de interpolación.

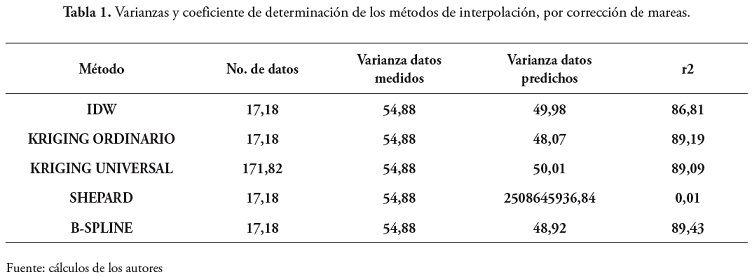
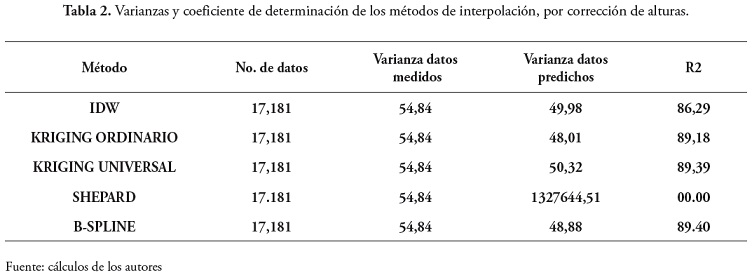
Para el estudio se aplicaron las correcciones tanto de mareas y de alturas a los datos de profundidad, con el objeto de verificar cuales diferencias se podrían establecer entre las mismas y así discernir que corrección fue mejor o mas aceptable para nuestro caso de estudio. En consecuencia, los datos resultantes de cada corrección fueron la base para aplicar los métodos de interpolación como los IDW, Kriging, Shapard y B-Spline, que permitieron generar los modelos correspondientes y establecer la particularidades o semejanzas de los mismos.

RESULTADOS

Evaluación de la calidad del MDB La calidad constituye la aptitud de uso de un producto o la utilidad del mismo para satisfacer una necesidad (Corrales y Martínez 2000), la cual esta medida por la diferencia entre los datos existentes y los verdaderos, a esto se le conoce como error.

A fin de evaluar la exactitud vertical, esta se hace por separado para establecer elevaciones precisas; esta situación se torna un poco más complicada para verificar la batimetría de un área debido a su naturaleza por la dificultad para gestionar un levantamiento devaluatorio y sus costos. De manera que la forma como se evaluó los MDB, fue con los 1500 datos tomados por la ecosonda multihaz que fueron adquiridos simultáneamente con los datos magnéticos en campo. Además, se utilizaron los criterios de validación cruzada, evaluación de la exactitud altimétrica e incertidumbre total vertical (TVU).

Validación cruzada Al generar los diferentes modelos digitales batimetricos por los métodos de interpolación, mas adelante descritos, con la base de datos final, se determino el mejor modelo de cada método a partir del coeficiente de determinación (R2) o validación cruzada, que permite evaluar la correlación de cada modelo con el fenómeno, a través de la siguiente ecuación:

Como resultado de este parámetro, en las tablas 1 y 2 se relacionan los modelos por correcciones de marea y altura, donde el mejor modelo por corrección de marea fue el IDW con un R² = 86,81, y por corrección de alturas fue el B-Spline con un R² = 86,40.

Evaluación de la exactitud altimétrica En busca del mejor modelo que represente el fondo marino fue necesario comparar la diferencia de la información del modelo interpolado con el de la ecosonda, el cual fue considerado como el modelo que representaba la realidad de la batimetría del lecho marino del área de estudio; de manera que a partir del error medio cuadrático (EMC) se evaluó la precipicio de los mismos, dado que este caracteriza las propiedades espaciales como la rugosidad, característica fundamental en los modelos digitales de terreno y, en este caso, de los MMDB; el EMC se describe según la siguiente formula.

Donde z_i es la profundidad estimada por los métodos de interpolación y z es la profundidad ya determinada.

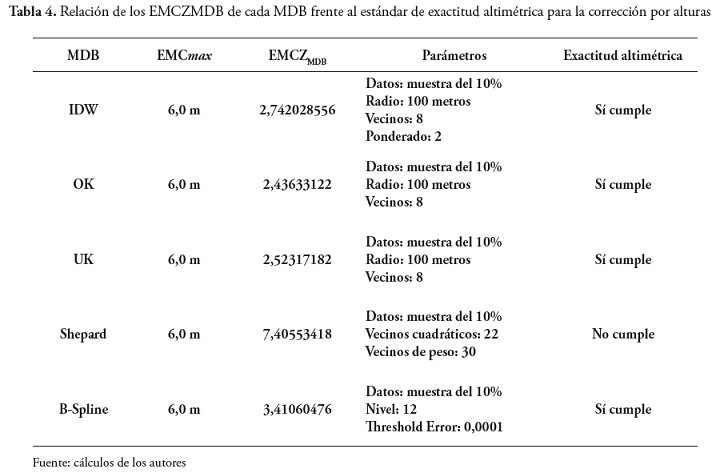
Posteriormente, se realizo un análisis de los EMCZ_b para determinar si los mapas batimetricos finales cumplían con los requisitos mínimos de exactitud altimétrica según los estándares del IGAC, mediante la siguiente relación:

Para la escala de los productos finales (escala 1:20.000) las curvas de nivel y batimétricas se definieron cada 20 metros, para el caso de estudio, quedando un EMC_max = 6,0 m.

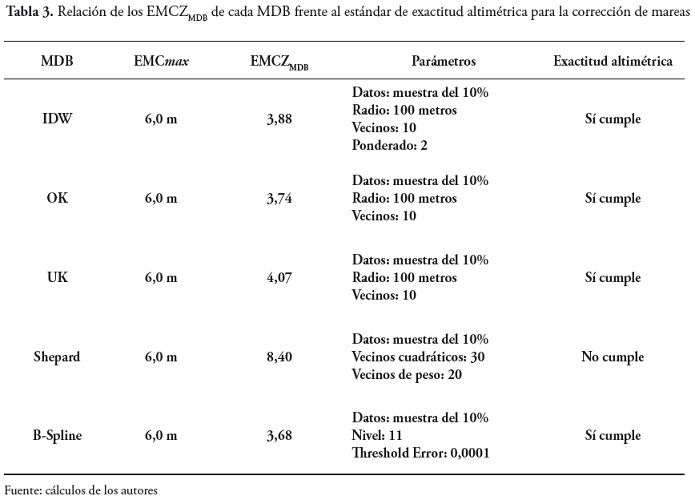
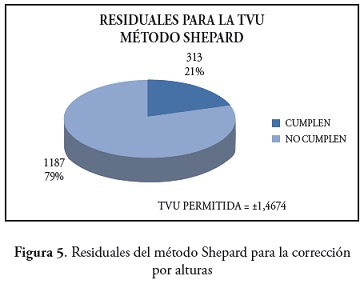
En las tablas 3 y 4se muestran los resultados de la exactitud altimétrica para cada uno de los modelos con su respectiva corrección, en donde se establece que para las dos correcciones el método Shepard es el único que no cumple con el parámetro de la exactitud altimétrica.

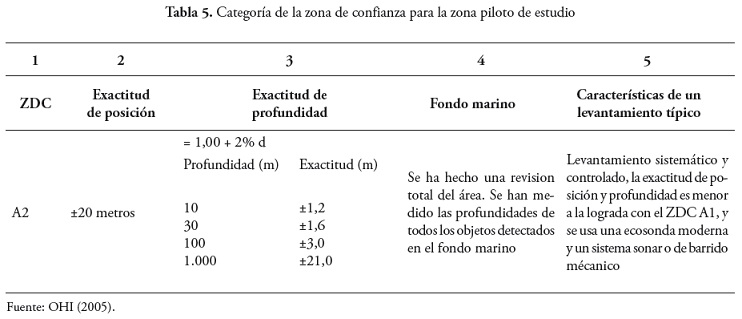
Incertidumbre total vertical (TVU). Este criterio de evaluación se aplica a los datos geográficos adquiridos en campo (datos crudos), los cuales no se encuentran exentos de errores, ya que estos pueden presentarse desde la captura, el procesamiento y la representación de los datos. La Organización Internacional de Hidrografía (OIH) desarrollo como método para clasificar los datos batimetricos las zonas de confianza (ZDC), las cuales identifican varios niveles de confianza, donde se establece que: “la exactitud de la posición y de la profundidad especificada por cada ZDC se refiere a los errores contenidos en la representación final del sondaje que incluye no solo los errores del levantamiento sino también cualquier otro error introducido en el proceso de producción de la carta” (OHI, 2005). Para nuestro caso la ZDC se clasifico dentro de la categoría A2 (tabla 5).

La incertidumbre vertical se entiende como aquella de las profundidades reducidas, debido a esto se suman todos los errores cometidos en la determinación de la profundidad para conseguir la incertidumbre total vertical (TVU) con un 95% de confianza, que según la OHI (2005) se expresa de la siguiente manera:

Donde a representa la parte de la incertidumbre que no varia con la profundidad, b es un coeficiente que representa la parte de la incertidumbre que varia con la profundidad Z_b es la profundidad. a y b son constantes determinadas por los estándares de la OIH según el orden del levantamiento.

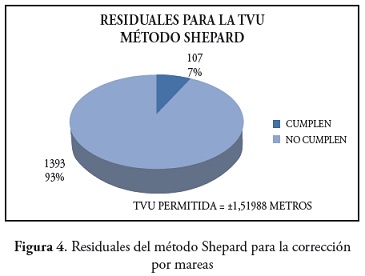
Para este parámetro los resultados establecieron que el método Shepard es el que menos datos incluye dentro del intervalo mostrado en las tablas, pues en la corrección por mareas el 93% de los datos no se incluyen dentro del intervalo y en la corrección de alturas el porcentaje es del 79% indicando la alta concentración de errores en la interpolación de los valores calculados para la superficie modelada por este método.

CONCLUSIONES

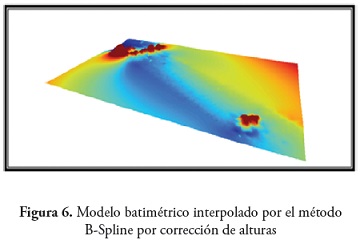
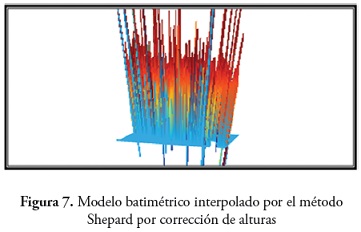
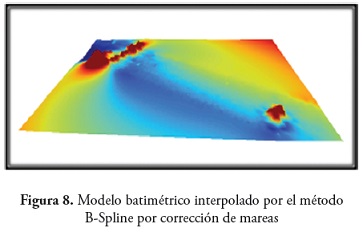
Al evaluar la calidad de los MDB generados por cada método y para cada una de las correcciones tanto por mareas como por alturas, los criterios de la validación cruzada o coeficiente de determinación R2, error medio cuadrático (EMC), estándar de calidad mínimo e incertidumbre total vertical (TVU), además de comprobar visualmente la superficie interpolada que más se ajusto a la realidad, establecieron que el método B-Spline cumplió con estos parámetros en las dos correcciones a pesar de la extrapolación que realiza (figura 6) y (figura 8) . Contrario a lo que sucedió con el método Shepard, lo que se ratifico en la interpolación de la superficie de los dos métodos (figura 7) y (figura 9)

Al ser evaluada la base de datos total por cada uno de los métodos se percibió que no había una buena ajustabilidad de la superficie a la realidad, de manera que al tomarse el 10% de la muestra (17.181 datos) para evaluar que tanto mejoraban los resultados, se observo una clara diferencia en los resultados obtenidos corroborando la influencia que la densidad de puntos ejerce en el requerimiento computacional y estudio de la superficie. Por ello, los métodos en general modelaron de mejor manera la superficie con la muestra mas pequeña.

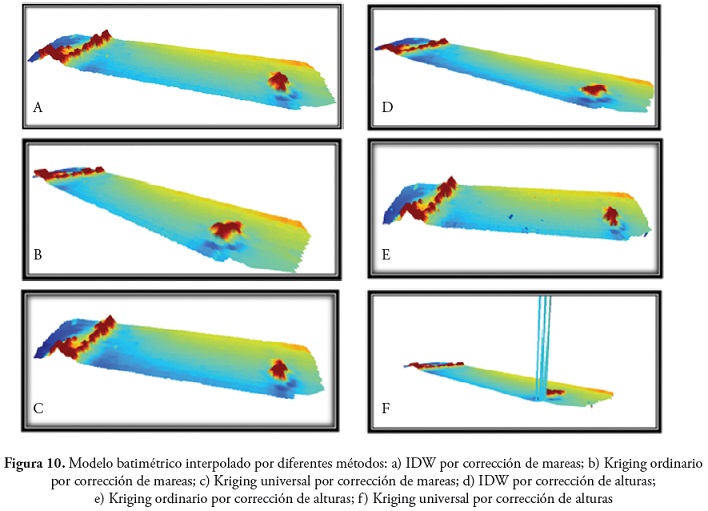
El visualizar el resultado de los modelos generados por el método B-Spline (figura 6) y (figura 8), IDW (figuras 10 a y d), Kriging Ordinario (figura 10 b y e) y Kriging Universal (figuras 10 c y f), por cada corrección nos permitió establecer que los métodos convencionales geoestadisticos se convierten en una poderosa herramienta para la estimación de superficies interpoladas a partir de los datos del magnetómetro G-882 debido a su portabilidad, reducción de costos, fácil accesibilidad e interoperabilidad en el formato de datos capturados y el uso interdisciplinar del sensor para fines diferentes al magnetismo terrestre.

Referencias bibliográficas

1. Corrales, C. C. y Martínez, S. A. (2000). Calidad de datos y propagación de errores en la elaboración de modelos digitales de elevación (propuesta metodológica). Bogotá: Universidad Distrital “Francisco José de Caldas”.
2. Droj, G. (2008). Improving the Accuracy of Digital Terrain Models. Vol. LIII. Babes-Bolyai: Studia Universitatea.
3. Felicisimo-Perez, A. M. (1994). Modelos digitales del terreno: introducción y aplicaciones a las ciencias ambientales. Oviedo: Universidad de Oviedo.
4. Geometrics (2005). Operation Manual: G-882 Cesium Marine Magnetometer Data Sheet. California: Geometrics Inc.
5. Giraldo-Henao, Ra. (2003). Introducción a la Geoestadistica. Teoría y aplicación. Bogotá: Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de Estadística.
6. Gordon, W. J. y Wixon, J. A. (1978). Shepard´s method of “metric interpolation” to bivariate and multivariate interpolation. Mathematics of Computation, 32 (141), 253-264.
7. Lee, B. G., Lee, J. J. y Kwon, K. R. (2005). Quasi-interpolants based multilevel B-Spline surface reconstruction from scattered data. Singapore: Universal; International Conference on Computational Science and Its Applications.
8. Lee, S., Wolberg, G. y Shin, S. Y. (1997). Scattered data interpolation with multilevel B-Splines. IEEE Transactions on Visualization and Computer Graphics, 3 (3), 228-244.
9. Martínez, W. y Sánchez, L. (2005). Hacia un nuevo sistema vertical de referencia en Colombia. Bogota-Munich: Instituto Geografico Agustin Codazzi (IGAC). Organización Hidrográfica Internacional (OHI) (2005).
10. Manual de Hidrografía. Mónaco: Bureau Hidrográfico Internacional, Principado de Mónaco.