DOI:
https://doi.org/10.14483/23448350.11948Publicado:
09/01/2017Número:
Vol. 30 Núm. 3 (2017): Septiembre-Diciembre 2017Sección:
Educación CientíficaAnálisis de problemas en estadística y probabilidad en libros de texto de segundo año de educación secundaria
An analysis of problems in statistics and probability in second year educational text books
Palabras clave:
análisis de texto, tipos de problemas, estadística, probabilidad (es).Palabras clave:
text analysis, types of problems, statistics and probability (en).Descargas
Referencias
Batanero, C. (2000). Significado y comprensión de las medidas de tendencia central. Uno, 25, 41-58.
Batanero, C., Contreras, J. y Arteaga, P. (2011). El currículo de estadística en la enseñanza obligatoria. EM-TEIA Revista de Educaçao Matematica e Tecnologica Iberoamericana, 2(2).
Ceballos, J. y Blanco, L. (2008). Análisis de los problemas de los libros de texto de Matemáticas para alumnos de 12 a 14 años de edad de España y de Chile en relación con los contenidos de proporcionalidad. Publicaciones, 38, 63-88.
Cid, E. (2009). Matemática 2º Medio. Texto para el estudiante, 3era ed. Santiago: Cal y Canto Eds.
Del Valle, M. (1997). Requerimientos de cambios en la formación de profesores de matemática en Chile. En R. Olfos y H. González (eds.), Alternativas para la formación de profesores de matemática (pp. 116-126). La Serena, Chile: Edición conjunta de la Sociedad Chilena de Educación Matemática y el Departamento de Matemática de la Universidad de la Serena.
Díaz-Levicoy, D. y Roa, R. (2014). Análisis de actividades sobre probabilidad en libros de texto para un curso de básica chilena. Revista chilena de educación científica, 13(1), 9-19.
Díaz. V. y Poblete, A. (2001). Contextualizando tipos de problemas matemáticos en el aula. Números. Revista de didáctica de las matemáticas, 45, 33-41.
Escolano, A. (2009). El manual escolar y la cultura profesional de los docentes. Tendencias pedagógicas, 14, 169-180.
Estrella, S. (2008). Medidas de tendencia central en la enseñanza básica en Chile. Análisis de un texto de séptimo básico. Rechiem. Revista chilena de educación matemática, 4(1), 20-32.
Fernández, P., Caballero, P. y Fernández, J. (2013). ¿Yerra el niño o yerra el libro de matemáticas? Números, 83, 131-148.
Fernández, E. y Mejía, M. (2010). Análisis de textos escolares para el diseño de situaciones de enseñanza. En G. García (ed.), Memoria 11° encuentro colombiano de matemática educativa (pp. 61-68). Bogotá: Asociación Colombiana de Matemática Educativa.
Ferrater, J. (1993). Diccionario de filosofía abreviado. Argentina: Editorial Sudamericana.
Ferreira, M. y Mayorga, L. (2010). Propuesta para la evaluación de los libros de texto de matemática de todos los niveles educativos. Revista ciencias de la educación, 20(35). Valencia.
Franklin, C. et al. (2007). Guidelines for assessment and instruction in statistics education (GAISE) report: A pre K-12 curriculum framework. Alexandria, VA: American Statistical Association.
Gal, I. (2002). Adult's statistical literacy. Meanings, components, responsibilities. International Statistical Review, 70(1), 1-25. https://doi.org/10.1111/j.1751-5823.2002.tb00336.x
Garfield, J. y Ben-Zvi, D. (2008). Developing students’ statistical reasoning: Connecting research and teaching. Nueva York: Springer.
Giaconi, V. y Varas, L. (9 de octubre de 2010). Estudio reveló que los textos de matemáticas no enseñan a los escolares a razonar. La Nación, p. 24.
Gil, E. y Ben-Zvi, D. (2011). Explanations and context in the emergence of students' informal inferential reasoning. Mathematical Thinking and Learning, 13(1-2), 87-108. https://doi.org/10.1080/10986065.2011.538295
Hernández, R., Fernández, C. y Baptista, P. (2006). Metodología de la investigación. México D. F.: McGraw Hill.
Icaza, L. (15 de noviembre de 2008). ¿En qué medida los textos escolares de matemática ayudan a que las personas sean más reflexivas en la vida cotidiana? Recuperado de: http://www.educarchile.cl/ech/pro/app/detalle?id=206547
Krulik, S. y Rudnik, K. (1980). Problem solving in school mathematics. Year Book. Reston, VA: NCTM.
López, F. (2002). El análisis de contenido como método de investigación. Revista de Educación, 4, 167-179.
Ministerio de Educación de Chile (Mineduc). (1999). Objetivos fundamentales y contenidos mínimos obligatorios de la educación básica. Decreto 240. Santiago de Chile: Mineduc.
Mineduc. (2009). Fundamentación del ajuste a los marcos curriculares vigentes de educación básica y media. Santiago de Chile: Mineduc.
Mineduc. (2012). Bases curriculares 2012. Matemática, Educación Básica. Santiago de Chile: Mineduc. Recuperado de: http://ww2.educarchile.cl/UserFiles/P0001/File/curriculum_al_dia/bases_matematica_2012.pdf
Mineduc. (2013). Bases curriculares, 7° básico 2° Medio. Santiago de Chile: Mineduc, Unidad de Curriculum y Evaluación.
National Council of Teachers of Mathematics (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Pólya, G. (1962). Mathematical discovery. On Understanding, Learning and Teaching Problem Solving. Nueva York: John Wiley & Sons.
Rico, L. (2006). Marco teórico de evaluación en Pisa sobre matemáticas y resolución de problemas. Revista de educación, número extraordinario, 275-294.
Sánchez, N. (2012). Análisis del texto de Educación Matemática entregado por el Mineduc utilizado en segundo año de enseñanza secundaria en el periodo 2007-2011. Tesis de magíster no publicada, Departamento de Matemática y Estadística, Universidad de la Frontera, Temuco, Chile.
Sandín, M. P. (2003). Investigación cualitativa en educación. fundamentos y tradiciones. Madrid: McGraw-Hill.
Schrock, C. (2000). Problem Solving-What Is It? Journal of School Improvement, 1(2), Fal./Winter.
Schoenfeld, A. (1992). Learning to think mathematically: Problem Solving, Metacognition, and sense making in Mathematics. En D.A.
Grouws (ed.), Handbook of Research on Mathematics Teaching and Learning. Reston, VA: NCTM.
Vidal, R. (2010). El libro de texto de matemáticas en Chile en el último siglo 1910–2010. Cuadernos de educación Nº 27, Facultad de Educación, Universidad Alberto Hurtado. Recuperado de: http://mailing.uahurtado.cl/cuaderno_educacion_27/pdf/articulo_adjunto_27.pdf
Zañartu, M., Darrigrandi, F. y Ramos, M. (2007). Texto para el estudiante Matemática 2° Educación Media (1ª edición). Santiago de Chile: Santillana del Pacífico S.A. de Ediciones.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: de mayo de 2017; Aceptado: de agosto de 2017
Resumen
La sociedad demanda hoy día que todo ciudadano logre desarrollar la capacidad de interpretar y cuestionar distintos fenómenos presentes en tablas, gráficos y datos; estas capacidades deben desarrollarse de forma progresiva desde los primeros años de educación. Para ello, también se hace necesario que los recursos apunten al desarrollo de estas, como por ejemplo el libro de texto de matemáticas. El siguiente trabajo tiene por objetivo analizar los tipos de problemas propuestos en dos libros de texto de matemática de segundo año de enseñanza secundaria, en el eje temático de estadística y probabilidad. Ambos textos fueron aquellos que se licitaron y distribuyeron gratuitamente y responden a dos periodos curriculares distintos: 1) aquel en que estaban vigentes las antiguas bases curriculares; y 2) el otro donde se implementaron las bases curriculares actuales. El uso del libro de texto escolar por estudiantes y profesores asume la premisa de que las diversas tareas propuestas deben tender a la resolución de problemas. La investigación se llevó a cabo por medio de una metodología cualitativa a través del análisis de contenido. Se usaron las categorías teóricas propuestas por Díaz y Poblete (2001). Dentro de los resultados encontrados se identifica mayormente problemas de tipo rutinarios que sirven para mecanizar procesos; los problemas no rutinarios o de contexto real aparecen en muy pocos casos.
Palabras clave:
análisis de texto, tipos de problemas, estadística, probabilidad.Abstract
At present society demands that every citizen manage to develop the capacity to interpret and question different phenomena present in tables, graphs and data, capacities that must be developed progressively from the earliest years of education. For this, it is also necessary that the resources point to the development of these skills, such as the textbook of Mathematics. The objective of the present work is to analyze the types of problems proposed in two Secondary Mathematics textbooks in the thematic area of Statistics and Probability. Both texts were those that were tendered and distributed free of charge and respond to two different curricular periods: 1) the one in which the old curriculum bases were in force and the other 2) when the current curricula were implemented. The use of the school textbook book by students and teachers assumes the premise that the various tasks proposed should tend to solve problems. The research was carried out through a qualitative methodology through content analysis. The theoretical categories proposed by Díaz and Poblete (2001) were used. Among the results found most routine problems are identified that serve to mechanize processes; The non-routine problems or real context, appear in very few cases.
Keywords:
text analysis, types of problems, statistics, probability.Resumo
Atualmente, a sociedade exige que todos os cidadãos consigam desenvolver a capacidade de interpretar e questionar diferentes fenômenos presentes em tabelas, gráficos e dados, capacidades que devem ser desenvolvidas progressivamente desde os primeiros anos de educação. Para isso, também é necessário que os recursos apontem para o desenvolvimento dessas habilidades, como o livro de Matemática. O objetivo do presente trabalho é analisar os tipos de problemas propostos em dois livros didáticos de Matemática Secundária na área temática de Estatística e Probabilidade. Ambos os textos foram aqueles que foram oferecidos e distribuídos gratuitamente e respondem a dois períodos curriculares diferentes: 1) aquele em que as antigas bases curriculares estavam em vigor e a outra 2) quando os currículos atuais foram implementados. O uso do livro de livros escolares por estudantes e professores assume a premissa de que as várias tarefas propostas tendem a resolver problemas. A pesquisa foi realizada através de uma metodologia qualitativa através da análise de conteúdo. As categorias teóricas propostas por Díaz e Poblete (2001) foram utilizadas. Entre os resultados encontrados, identificam-se a maioria dos problemas de rotina que servem para mecanizar processos; Os problemas não rotineiros ou o contexto real, aparecem em poucos casos.
Palavras-chaves:
análise de texto, tipos de problemas, estatística, probabilidade.Introducción
La estadística como disciplina escolar se ha insertado de forma gradual y ha mostrado un gran desarrollo, tanto a nivel de contenidos como de recursos para su enseñanza. Dentro de los recursos que forman parte en el proceso de aprendizaje de los estudiantes aparece el libro de texto, el cual se ajusta a las normativas de licitación que exige el Ministerio de Educación de Chile (de aquí en adelante Mineduc) para cada año en curso.
La nueva base curricular de matemáticas, dentro de sus cuatro ejes temáticos, define el de estadística y probabilidad como uno de los más relevantes dentro del proceso de enseñanza y aprendizaje, principalmente por las relaciones que es posible establecer con otras áreas del conocimiento y respondiendo “a la necesidad de que todos los y todas las estudiantes aprendan a realizar análisis, inferencias y obtengan información a partir de datos estadísticos” (Mineduc, 2013, p. 100). Los múltiples elementos relacionados con la estadística en diversos medios de comunicación, tanto escritos como audiovisuales, ponen en evidencia la importancia de profundizar en la enseñanza de estas ramas de las matemáticas para desenvolverse en la actual sociedad.
De esta forma, para propiciar un proceso de enseñanza en el eje temático de estadística y probabilidad, se hace necesario disponer de recursos de aprendizaje que permitan mostrar las ideas, conceptos y ejemplos de forma variada. En particular, los artefactos tecnológicos muchas permiten ver desde una perspectiva real los fenómenos aleatorios que se pretenden estudiar, por ejemplo, Fathom y TinkerPlots son relevantes para las necesidades que declaran desarrollar la base curricular de matemáticas en el nivel secundario (Franklin et al., 2007). A pesar de esto, el recurso utilizado por excelencia, en la mayoría de los casos, es el libro de texto. Se convierte así en el recurso de base sugerida, del cual se pueden analizar, estructurar y desarrollar secuencias de aprendizaje coherentes con los programas curriculares.
Algunas investigaciones (Escolano, 2009; Díaz-Levicoy y Roa, 2014; Ceballos y Blanco, 2008; Fernández y Mejía, 2010), centradas en libro de texto en el eje de estadística y probabilidad, han dado cuenta de las inconsistencias en los tipos de tareas, problemas y las estructuras que presentan los libros de textos. Por ejemplo, las diferencias que muestran en relación a los tipos de problemas que presentan, algunos hacen mayor énfasis en problemas de tipo mecanicista y otros dan prioridad situaciones más aplicadas a la experimentación o menos rutinarias, es decir, aquellos más orientados hacia la resolución de problemas.
El material utilizado para la presente investigación corresponde a libros licitados y distribuidos de manera gratuita por el Ministerio de Educación a establecimientos de dependencia municipal y particular subvencionada. Este recurso debe cumplir los requerimientos mínimos de calidad. Un texto se dice que es de calidad si cumple con los normativos legales, ministeriales, de directrices y es ajustado a los estudiantes en su aprendizaje (Vidal, 2010).
En este trabajo se presenta una tipología de problemas que permite clasificar y analizar los problemas de acuerdo a los datos y su estructura, en dos libros de texto; uno de ellos, utilizado antes de la reforma curricular y el otro usado posterior a esta.
Problemas y resolución de problemas: una caracterización
Dentro de las causas que problematizan la enseñanza de las matemáticas escolares se encuentra aquellas relacionadas con ajustes en los programas de estudio, la falta de profundidad en los contenidos escolares, unas matemáticas vacías de contexto o en algunos casos, ficticios. Los tipos de actividades que proponen los libros de texto deben propender a la promoción de nuevas y novedosas actividades. Para Krulik y Rudnik (1980), un problema es un escenario donde los resolutores necesitan encontrar una solución, en la cual no conocen los medios o caminos lógicos para obtenerla.
En relación con lo anterior, Mineduc afirma que “la enseñanza deberá contribuir a un mejor desempeño de las personas en la vida diaria a través de […] resolver problemas cotidianos del ámbito familiar social y laboral” (1999, p. 47).
Varios investigadores se han interesado por la resolución de problemas, dando una connotación para el desarrollo de competencias matemáticas en los estudiantes. Esta es entendida como “la capacidad de los individuos para formular, emplear e interpretar la matemática en distintos contextos” (Mineduc, 2013, p. 12). En este sentido, el papel que juega la resolución de problemas para el desarrollo de estas competencias es relevante, pues permite “buscar formas conscientes de acción y apropiadas para lograr un objetivo claramente concebido pero no alcanzable de forma inmediata” (Polya, 1962, p. 117). Por su parte, Schrock (2000) plantea que un problema debe tener tres criterios que permitan clasificarlo como tal: 1) el alumno debe aceptar que estará implicado en el problema; 2) debe tener cierto grado de obstrucción y no poseer un método para solucionar de inmediato el problema; y 3) debe explorar activamente el problema en busca de una solución.
Las situaciones problemas no necesariamente se circunscriben a la adecuación de un ejercicio en un contexto; en este sentido, Schoenfeld (1992) plantea que los términos de problemas y resolución de problemas a menudo presentan diferentes significados y estas interpretaciones en la literatura dificultan la interpretación. Por ejemplo, Schoenfeld (1983, citado en Schoenfeld, 1992) propone una serie de categorías en función de los objetivos que pueda perseguir algún curso basado en las respuestas de resolución de problemas: 1) entrenar a estudiantes en pensamiento creativo o el desarrollo de competencias para la resolución de problemas (basado en estrategias heurísticas); 2) permitir a los profesores potenciar la instrucción con situaciones que no necesariamente sean limitadas para los estudiantes; 3) aprender técnicas estándares de dominios particulares, además de permitir la posibilidad de la modelación matemática; y 4) entregar nuevas aproximaciones remediales en matemáticas (herramientas básicas) para tratar de inducir un pensamiento crítico o herramientas de razonamiento analítico.
Del Valle (1997) plantea que es necesario reconocer que la resolución de problemas es parte integral de una alfabetización matemática; y esta es entendida como la capacidad para analizar razonar y comunicar eficazmente, cuando enuncian, formulan y resuelven problemas en diferentes contextos (Rico, 2006). Se da en el contexto de un conjunto de nuevas exigencias planteadas por el avance de la sociedad, la cual reclama aprendizajes significativos y destrezas intelectuales de orden más elevado que las que actualmente se propician.
Como parte necesaria del conocimiento para alcanzar dicha alfabetización matemática (en el sentido de Rico, 2006), Sánchez (2012) plantea que se hace necesario no descuidar los aspectos formales en la enseñanza de la matemática, en tanto brinda un soporte en la adquisición del conocimiento matemático, construyendo y reconstruyendo unas matemáticas con sentido crítico y reflexivo en la apropiación del saber matemático.
Hoy en día la resolución de problemas es el foco en la enseñanza de las Matemáticas […], da al estudiante la ocasión de enfrentarse a situaciones desafiantes que requieren, para su resolución, variadas estrategias, poner en juego contraejemplos y comprobar soluciones en el contexto del problema para validar sus respuestas. (Mineduc, 2012)
Hacia una cultura estadística
Hasta hace algunos años no se apreciaba un mayor interés en la investigación sobre la enseñanza y aprendizaje de la estadística. Hoy en día el interés en esta área ha suscitado mayor preocupación en el tema, considerando la gran cantidad de información que aparece en distintos medios y que debe ser comprendida por todo ciudadano. Los enfoques actuales que proponen diversos programas de estudio es que la estadística debe estar enfocada en el análisis de datos, de dónde y cómo surgen, donde los estudiantes tengan los espacios para experimentar con estos, elaborar, proponer y hacer preguntas de investigación, justificando la forma en que se seleccionan los datos y la importancia que tiene el tamaño de la muestra que se toma para hacer predicciones a la población (Batanero, Contreras y Arteaga, 2011).
El eje temático de Estadística y probabilidad en segundo año de educación secundaria es incorporado para implementar el uso de modelos en el razonamiento en situaciones de incertidumbre. Este se propone desarrollar conceptos y técnicas propias de la estadística y la teoría de probabilidades que permitan realizar inferencias a partir de información de naturaleza estadística y distinguir entre los fenómenos aleatorios y deterministas (Mineduc, 2009).
La estadística debe ser incorporada en contextos específicos en función de los aprendizajes y diversidad de estudiantes. Debe emerger un desarrollo de aspectos esenciales asociados a la variabilidad, el muestreo, replicabilidad, tamaño muestral, etc., de manera que surja la necesidad utilitaria que debe tener el análisis de datos al servicio de diversos fenómenos. Esta disciplina no debe verse como un conjunto acabado de técnicas y cálculos estadísticos que den información aislada de la población, se debe considerar que la extracción de datos tiene un contexto natural y legitimado (Garfield y Ben-Zvi, 2008; Gil y Ben-Zvi, 2011).
A fin de cuentas, se debe proporcionar una comprensión simple de los fenómenos sociales y culturales, proporcionando aspectos esenciales para cultura estadística, la cual facilite dos componente interrelacionados: 1) capacidad para interpretar y evaluar críticamente la información estadística, los argumentos apoyados en datos o los fenómenos estocásticos que las personas pueden encontrar en diversos contextos, incluyendo los medios de comunicación, pero no limitándose a ellos; y 2) capacidad para discutir y comunicar sus opiniones respecto a tales informaciones cuando sea relevante (Gal, 2002, pp. 2-3).
De los aspectos que ofrece la cultura estadística en la sociedad actual para su comprensión, el uso de tecnología digital toma un sitio privilegiado, así como el papel de la evaluación y la investigación va en creciente aumento con el fin de contribuir y mejorar la educación en estadística. Se parte de la reflexión y los aportes que tanto estadísticos y educadores pueden brindarse mutuamente (Batanero, 2000). Del mismo modo, el creciente interés por la enseñanza de la estadística y sus diversos enfoques, tanto formales como informales, plantea la necesidad de formar a ciudadanos capaces para comprender las ideas y conceptos elementales que son la base de la estadística.
La estadística en el currículo escolar
El conocimiento que se pone en juego y la formación de estudiantes en temas relacionados con estadística, por una parte, debe ser profundo y, por otro lado, ajustado a la relación sobre los significados que se le deben atribuir. Se debe considerar en la enseñanza procesos intuitivos de los estudiantes, que en progresión deben ser formalizados en ideas más abstractas e interconectadas, lo que permitiría adquirir una comprensión global de los fenómenos en estudio.
La estructura del sistema escolar chileno considera tres niveles educativos, estos son:
-
Nivel preescolar.
-
Nivel primario (o nivel básico). Este comprende dos ciclos de enseñanza: 1) primer ciclo, que cubre desde 1° a 4° y 2) segundo ciclo, que comprende de 5° a 8° de enseñanza primaria.
-
Nivel secundario (o nivel medio). Este comprende dos ciclos específicos: 1) el primero que incluye los primeros dos grados de enseñanza secundaria obligatoria (plan común) y, 2) el segundo ciclo, que incluye el 3° y 4° de enseñanza secundaria. Este último ciclo permite escoger por cursos optativos, dependiendo de la orientación de cada estudiante. Estas orientaciones, por lo general son humanista y científica.
El eje temático de estadística y probabilidad es incluido desde el nivel preescolar, transitando hasta 4to grado de educación secundaria. Los contenidos que propone la base curricular de matemáticas buscan desarrollar en todos los estudiantes capacidad para registrar, clasificar y leer información dispuesta en tablas y gráficos, y que se inicien en temas relacionados con la probabilidad. En la tabla 1 se muestran los objetivos de aprendizaje para 2do grado de educación secundaria.
Fuente: Mineduc (2013, p. 138)
Tabla 1: Interfaz de explicación. Histograma con los votos del vecindario.

Curricularmente, a nivel nacional, se han introducido desde los niveles iniciales de escolaridad elementos que incluyen el tratamiento de actividades para comprender fenómenos aleatorios, brindando al estudiante situaciones para que experimenten, analicen y discutan información en estos contextos (Estrella, 2008).
Importancia de analizar los libros de texto
En la actualidad existe diversidad de recursos de aprendizaje en educación escolar, que van desde los tradicionales cuadernos y lápices hasta una variedad de recursos provenientes de las tecnologías digitales (softwares educativos, applet en internet, tablets, simuladores estadísticos, entre otros), los cuales son utilizados como mediadores en la comprensión de los diversos fenómenos de estudio. Finalmente, como recurso casi irremplazable del sistema escolar, destaca el libro de texto, el cual es usado como recurso tanto para planificar lecciones de clases por profesores y como guía de apoyo para los estudiantes.
Siendo este el recurso más utilizado, es importante saber si estos: ¿toman en consideración aquellos temas relevantes que deben aprender los estudiantes en cada nivel educativo?, ¿responden a las necesidades y demandas de los variados contextos socioculturales?, ¿el orden que predomina en la organización del libro de texto es idónea para que los estudiantes construyan su propio conocimiento?, ¿proponen actividades que ayuden a profundizar en los contenidos estudiados? (Fernández, Caballero y Fernández, 2013)
De este modo, es lógico destacar la importancia que tiene el libro de texto de matemáticas para el desarrollo de los aprendizajes; merece que tanto el educador como los estudiantes tengan un material educativo que pueda ser utilizado de manera eficaz, dentro y fuera del aula de clase, para lo cual se requiere una permanente evaluación por parte de los docentes y entes autorizados (Ferreira y Mayorga, 2010).
Como forma de dar sustento a la importancia que tiene el libro de texto escolar, Icaza (2008) menciona que se potencien las capacidades reflexivas de los alumnos, no solo debe presentar situaciones de aplicabilidad inmediata, sino que debe proponer situaciones en que la solución implica interpretar, modelar y finalmente escoger debidamente las herramientas matemáticas adecuadas.
En esta misma línea, un buen libro de texto escolar ofrecerá oportunidades a los estudiantes de resolver problemas que requieran seleccionar la información relevante, ensayar diversas estrategias para resolverlos y de hacerse preguntas acerca de la solución obtenida (Giaconi y Varas, 2010).
Metodología
El presente trabajo centra su interés en analizar los tipos de problemas presentes en dos libros de texto del estudiante de 2° de enseñanza secundaria en los años 2009 y 2011.
Se consideraron estos dos como casos de análisis por ser distribuidos antes y después de la implementación de los ajustes curriculares. Se seleccionaron, por una parte, considerando que responden a periodos de ajustes curriculares distintos. Estos libros de texto son aquellos de mayor distribución, pues se usan en instituciones educativas de carácter público y además en aquellos de carácter particular subvencionado (es decir, que reciben recursos del Estado y por parte privada) y que cumplían con las propuestas curriculares del Ministerio de Educación vigentes para el ambos años (2009 y 2011). Además, otro criterio de selección es que ambos libros de texto siguieron las normativas vigentes de la base curricular de matemáticas en este nivel.
La base curricular de matemáticas (Mineduc, 2013) acentúa el desarrollo de la resolución de problemas como elemento articulador para desarrollar el pensamiento matemático. Además, la base curricular de matemáticas (Mineduc, 2013, p. 107), plantea que se deben desarrollar cuatro habilidades: 1) la resolución de problemas, 2) argumentación y comunicación, 3) modelación y, 4) representación, las que son transversales a todos los ejes temáticos del programa de estudio de matemáticas y permiten desarrollar el pensamiento matemático.
Los textos son distribuidos por el Mineduc de forma gratuita y fueron aprobados por medio de un proceso de licitación, cumpliendo con la exigencia y propuesta curricular que son reflejo de los planes de estudio y los objetivos que estos persiguen para el aprendizaje de los estudiantes.
Los dos textos seleccionados fueron:
-
Texto A: Cid, E. (2009). Matemática 2º Medio. Texto para el estudiante, 3era ed. Santiago: Cal y Canto Eds.
-
Texto B: Zañartu, M., Darrigrandi, F. y Ramos, M. (2011). Matemática 2º Educación Media. Texto del estudiante, 4ta ed. Santiago: Santillana del Pacífico S.A.
Diseño y enfoque y muestra
La presente investigación tiene un enfoque cualitativo. En palabras de Sandín, este tipo de investigación “es una actividad sistemática orientada a la comprensión en profundidad de fenómenos educativos y sociales, a la transformación de prácticas y escenarios socioeducativos, a la toma de decisiones y también hacia el descubrimiento y desarrollo de un cuerpo organizado de conocimiento” (2003, p. 276). El método de investigación es el análisis de contenido, ya que es una forma viable para el análisis de documentos como los libros de texto (López, 2002).
El nivel del estudio es descriptivo, pues se busca la precisión de lo que se pretende observar (Ferrater, 1993) y se realiza un muestreo no probabilístico intencional (Hernández, Fernández y Baptista, 2006).
Por medio de este enfoque, se analiza y describen los tipos de problemas presentes en relación con el eje temático de estadística y probabilidad en el libro de texto de Matemática de 2do grado de educación secundaria.
Unidad de análisis del libro de texto
El presente artículo muestra los resultados finales de investigación al haber comparados los dos libros de texto. Para el análisis se realiza una revisión global del libro de texto, en relación con tipos de problemas y características de los mismos en la unidad de estadística y probabilidad. El análisis se realiza por medio de las características definidas de las categorías teóricas elaboradas por Díaz y Poblete (2001) (tabla 2).
Tabla 2: Clasificación de los problemas según su estructura.

Resultados
Los resultados se dividen en dos secciones distintas, así se hace visible la distinción y claridad de los resultados mostrados (en Chile los libros de texto se dividen en unidades de aprendizaje) en ambos libros de texto. En primer lugar, se esbozan los resultados que dan cuenta de la estructura del texto para ambos periodos curriculares y, por otro lado, los resultados sobre el análisis de los problemas que proponen los libros de texto en la unidad de aprendizaje probabilidad y estadística.
Análisis global de la estructura de los libros de texto en la unidad de estadística y probabilidad
El libro de Cid (2009) es licitado antes de la implementación de los ajustes curriculares. Este texto solo incluía temas relacionados con el tópico de probabilidades; estos estaban centrados en el cálculo de probabilidad desde un punto de vista clásico (equiprobabilidad). En este periodo académico aún no se consideraba el tópico de estadística descriptiva en los programas de estudio. Estos tópicos se impartían en tercer y cuarto año de enseñanza secundaria.
Con relación al libro de Zañartu, Darrigrandi y Ramos (2011), este se licitó e implementó con los ajustes curriculares posteriores al año 2009.
Este libro de texto incluye en la unidad de estadística y probabilidades temas como: cálculo de probabilidades desde un punto de vista clásico y algunos casos de eventos compuestos, estadística descriptiva (construcción de gráficos, tablas de frecuencia) y medidas de variabilidad y tendencia central.
Los problemas que se consideraron en este libro de texto (Zañartu, Darrigrandi y Ramos, 2011) fueron aquellos que se proponían a los estudiantes para su resolución, es decir, trabajos grupales y estrategias para presentar y exponer propuestas a soluciones de problemas y discusión.
Con base en lo anterior, los resultados se analizan con respecto a cada unidad (estadística y probabilidad), en general y a cada tópico en caso particular en ambos libros de texto.
Con respecto a la unidad estadística y probabilidad
Texto A
Cid, E. (2009). Matemática 2º Medio. Texto para el estudiante, (3 ed.), Santiago: Cal y Canto, Eds.
El total de problemas que propone el libro de texto A son 106. De estos, hay problemas de profundización, de ejercitación, de selección múltiple y de análisis y la mayoría son de tipo rutinarios (figura 1).
Figura 1: Ejemplo de problema de naturaleza no rutinaria.
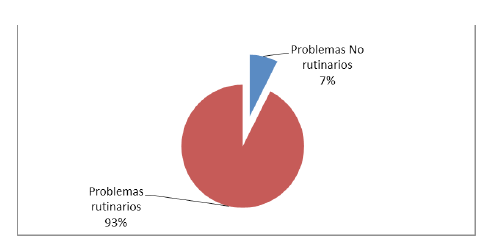
De estos 106 problemas que presenta el libro de texto, ocho son de naturaleza no rutinaria (7,54 %) (figura 2).
Figura 2: Proporción de problemas propuestos en el libro de texto A.
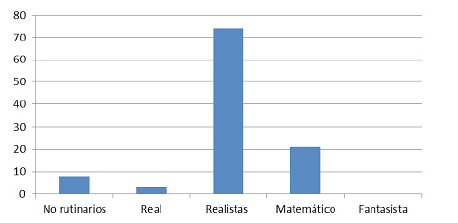
De los problemas de naturaleza rutinaria, tres son de contexto real (2,83%) (figura 3), 74 son de contexto realista (69,8%) y 21 son de contexto matemáticos puros (19.8%). Esto evidencia que la mayoría de los problemas que se presentan en el texto son de situaciones que requieren alguna operacionalización matemática asociada a algún contexto “amigable” o conocido por los estudiantes. Problemas de contexto fantasista no se encuentran presentes en el texto (figura 4).
Figura 3.: Ejemplo de problema de naturaleza rutinaria de contexto real.
Figura 4: Clasificación de problemas según naturaleza y contexto para la unidad de aprendizaje de estadística y probabilidad.
Texto B
El total de problemas que se proponen en este libro de texto es de 173, de los cuales 65 (37.6%) corresponde al tópico de tratamiento de la información (estadística, gráficos, medidas de variabilidad y tendencia central y posición). Los restantes 108 problemas (62.4%), corresponden a temas relacionados con probabilidades (nociones de conjunto, técnicas de conteo y probabilidades).
La unidad de aprendizaje de estadística y probabilidad presenta seis (9.2%) problemas de naturaleza no rutinaria, cuatro problemas de contexto real, 28 (43.1%) problemas de contexto realista y 27 (41.5%) (figura 5) problemas de contexto puramente matemático. No se presentan problemas de contexto fantasista.
Figura 5: Ejemplo de problema de naturaleza rutinaria de contexto realista.
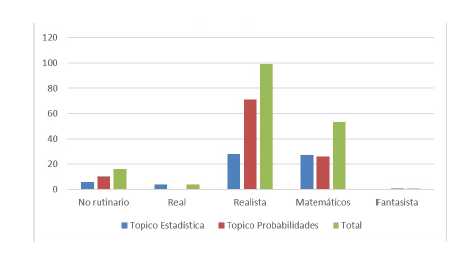
En relación con el tema de cálculo de probabilidades y el total de problemas en este tópico (108), se presentan 10 problemas (9,3%) de naturaleza no rutinaria, 71 problemas (65,7%) de contexto realista y 26 problemas (24,1%) de contexto puramente matemático (figura 6), los problemas de contexto real no aparecen y se propone solo un problema fantasista (0,9%).
Al considerar la unidad de aprendizaje de estadística y probabilidad en su forma general, con relación a la totalidad de problemas que se presentan (173), se tiene que 16 (9,2%) son de naturaleza no rutinaria y cuatro (2,3%) son de contexto real, 99 (57,2%) son de contexto realista, 53 (30,6%) de contexto matemático puro y se presenta solo un (0,6%) problema de tipo fantasista (figura 7).
Figura 6: Ejemplo de problema de naturaleza rutinaria de contexto puramente matemático.
Figura 7. : Clasificación de problemas según naturaleza y contexto para el tópico de estadística, probabilidades y en relación con el total.
La figura 7 entrega una visión comparada de la cantidad de problemas en cada tópico (análisis de información y probabilidades) con respecto al total presentado en la unidad en el libro de texto B. Se aprecia que los problemas que más aparecen en este libro de texto son los realistas en ambos tópicos. Los que menos se proponen son problemas de tipo real y, en menor cuantía, los no rutinarios y fantasistas (figura 8).
Figura 8: Ejemplo de problema de naturaleza rutinaria de contexto fantasista.
Los problemas realistas, en general, son aquellos que aparecen con mayor reiteración en pruebas como Simce, (Sistema de medición de la calidad educativa) en el contexto nacional y, en internacionales como Pisa (Programme for International Student Assessment) o TIMSS (Trends in International Mathematics and Science Study).
Ambos libros de texto siguen líneas de acción como las anteriores, con el fin que los estudiantes logren, por una parte, desarrollar habilidades para la resolución de problemas y, por otra, aunque se presenta en una menor cantidad de casos, la capacidad para poder plantear problemas en diversos contextos. Se hace necesario propender a propuestas en libros de texto de problemas que converjan en la construcción de situaciones reales y procesos, donde haya espacios de interacción, discusión, planteamiento de soluciones y validez de las mismas en los contextos de la resolución de problemas. La idea es lograr potenciar y hacer tangible un empoderamiento del saber estadístico.
Conclusiones
Con base en los resultados encontrados al llevar a cabo el análisis de los libros de texto, quedan de manifiesto algunos aspectos que pueden ser mejorados en futuras elaboraciones de texto de Matemática. Tomando en consideración que lo que se pretende es una construcción participativa de estudiantes, para transitar desde del conocimiento a un estatus de saber. Este saber debe permitir a los estudiantes tomar el conocimiento adquirido y que tenga una utilidad, es decir, una función. Este es el sentido al que debe propender un recurso tan usado como el libro de texto.
Queda de manifiesto que hay una excesiva propuesta de problemas de contexto matemático, por encima de aquellos problemas orientados a la resolución de problemas y, más aún, en problemas de tipo no rutinarios. Esto considerando que el texto utilizado en el año 2011 (con ajuste curricular en los programas de estudio) aumenta la cantidad de problemas de este tipo con respecto al texto utilizado en el año 2009.
No se aprecia gran variedad de situaciones y contextos necesarios para desarrollar tareas matemáticas implícitas en su ejecución. Esto debido a que la cantidad de problemas que se proponen para desarrollar competencias matemáticas de análisis (argumentar, representar, resolver problemas y modelar) son escasos. La mayoría de estos son problemas de tipo real. No se evidencian problemas de naturaleza no rutinaria, que son aquellos que permitirían a los estudiantes desarrollar de forma sistemática y analítica una alfabetización matemática (Rico, 2006).
La unidad de aprendizaje de estadística y probabilidad analizada del libro texto usado en el año 2011 (que es aquel que siguió los nuevos ajustes curriculares debido a los desfases en comparación a estándares internacionales como NCTM, 2000) no muestra mayor incorporación de problemas de contexto real comparado con el libro de texto usado en el año 2009. En lo que respecta a problemas de contexto realista, el texto A incorpora considerablemente más ejercicios de este tipo realista, en comparación al texto B, lo que muestra una contradicción en relación con las nuevas competencias a desarrollar. De la misma forma, hay un incremento de los problemas de contexto matemático en el texto usado en el año 2009 en contraste a los incluidos en el texto usado en el año 2011.
Finalmente, la investigación en el área de análisis de libros texto pretende ser un aporte para posteriores planeaciones, diseños y elaboraciones de los mismos, pero desde enfoques innovadores como lo es el de resolución de problemas matemáticos. Para ello es necesario que se consideren los resultados de investigación que provienen de las matemáticas y, en particular, del campo de la didáctica de la estadística y la probabilidad. Con esto se pretende apoyar a profesores y estudiantes con recursos idóneos y actualizados a la sociedad para orientar los procesos de enseñanza y aprendizaje.
Por otro lado, se recomienda que el libro de texto de matemática del estudiante, en sus futuras licitaciones, incorpore alguna(s) sección(es) dentro de cada uno de los tópicos en la unidad de Estadística y Probabilidad como actividades de indagación y exploración estadística, utilizando conocimientos previos en el proceso de aprendizaje. La construcción de conocimiento estadístico fortalecería la idea de un trabajo de manera formal como es el caso de probabilidades teóricas, siendo los casos más desarrollados el lanzamiento de una moneda (o dos), el lanzamiento de dados o juegos de naipes. Justamente, estas actividades son las que brindan espacios de experimentación, análisis, discusión y no uso de excesiva formalización y matematización de la estadística en la enseñanza a nivel escolar.
Referencias
Licencia
El (los) autor(es) al enviar su artículo a la Revista Científica certifica que su manuscrito no ha sido, ni será presentado ni publicado en ninguna otra revista científica.
Dentro de las políticas editoriales establecidas para la Revista Científica en ninguna etapa del proceso editorial se establecen costos, el envío de artículos, la edición, publicación y posterior descarga de los contenidos es de manera gratuita dado que la revista es una publicación académica sin ánimo de lucro.