DOI:
https://doi.org/10.14483/23448350.12257Publicado:
01/01/2018Número:
Vol. 31 Núm. 1 (2018): Enero-Abril 2018Sección:
Educación CientíficaAspectos matemáticos que amplían la noción de notación científica en el área de física de educación media general
Mathematical aspects that extend the notion of scientific notation in the area of Physics of General Middle Education
Palabras clave:
significant numbers, physics, didactic guide, scientific notation, order of magnitude (en).Palabras clave:
Cifras significativas, Física, Guía didáctica, Notación científica, Orden de magnitud (es).Descargas
Referencias
Álvarez, J. (2009). Física. Caracas: Fundación Editorial Salesiana.
Brett, E. y Suarez, W. (2009). Teoría y práctica de física de tercer Año. Caracas: Discolar S.A.
Briceño Valero, J. M. y García Oropeza, L. (2012). El lenguaje matemático como competencia necesaria para la enseñanza y aprendizaje de la física. En E. Badillo Jiménez, El desarrollo de competencias en la clase de ciencias y matemáticas. Mérida, Venezuela: Fondo Editorial Mario Briceño Iragorri.
De Pro, A. (septiembre de 2003). Algunas reflexiones sobre la enseñanza de la física y de la química. Educar en el 2000, 12-17. Recuperado de https://www.educarm.es/documents/246424/461834/3reflexiones.pdf/a00305ef-90c1-4457-b13e-966f6aaa97b3
Duschl, R. (1995). Perspectivas epistemológicas sobre el cambio conceptual: implicaciones para la práctica educativa. Comunicación, lenguaje y educación, 25, 107-125. https://doi.org/10.1174/021470395321337857
Florez, R. (1994). Hacia una pedagogía del conocimiento. Bogotá: McGraw Hill.
Lobo, H., Gutiérrez, G., Briceño, J., Rosario, J., Villarreal, M. y Caceres, J. (2005). Mecánica. Mérida, Venezuela: Editorial Codepre.
Rodríguez, A. (2002). Historia de las Matemáticas: Arquímedes El Genio de Siracusa.
Rodríguez, M. (2011). La matemática y su relación con las ciencias como recurso pedagógico. Números, 77, 35-49.
Stracuzzi, S. P. y Pestana, F. M. (2006). Metodología de la investigación cuantitativa. Caracas: Fedupel.
United Nations Educational, Scientific and Cultural Organization (Unesco). (1981). Manual de la Unesco para la enseñanza de las ciencias. París: Unesco.
Upel. (2011). Manual de Trabajos de grado de especialización y maestría y tesis doctorales. Caracas: Fedupel.
Zabalza Beraza, M. (2004). Guía para la planificación didáctica de la docencia universitaria en el marco del EEES. Documento de trabajo. La Coruña. España: Universidad de Santiago de Compostela.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: de junio de 2017; Aceptado: de noviembre de 2017
Resumen
Para este trabajo se diseñó una propuesta didáctica constructivista en donde los estudiantes del tercer año de educación media general puedan adquirir un aprendizaje significativo en el uso de la notación científica. El tipo de investigación utilizado se encuentra entre los proyectos factibles con un diseño de campo no experimental. Para la recolección de datos se utilizó una encuesta aplicada a 43 estudiantes de la asignatura de física del tercer año del liceo Rosario Almarza, en Trujillo, Venezuela. Los análisis de los resultados indicaron que estos presentan deficiencias en cuanto a las cifras significativas y orden magnitud, los cuales son aspectos matemáticos esenciales para la comprensión y el uso de la notación científica en la física; también resaltaron la necesidad de implementar otras estrategias de enseñanza y aprendizaje, como lo es una serie de actividades complementarias para el docente en el aula o el estudiante. Con estos resultados, se procedió a realizar una guía didáctica usando los aspectos matemáticos conocidos y diversas actividades lúdicas para ampliar la noción y uso de la notación científica.
Palabras clave:
cifras significativas, física, guía didáctica, notación científica, orden de magnitud.Abstract
For this work, a constructivist didactic proposal was designed in which the students of the third year of General Media Education can acquire a significant learning in the use of Scientific Notation. The type of research used is among feasible projects with a non-experimental field design. For data collection, the survey technique was used, which was applied to 43 students of the Physics subject of the third year of the Liceo Rosario Almarza Trujillo-Venezuela. The analysis of the results indicated that they present deficiencies in terms of significant numbers and order magnitude, which are essential mathematical aspects for the understanding and use of Scientific Notation in the area of Physics, as well as highlighting the need for Implement other teaching and learning strategies, such as a series of complementary activities for the teacher in the classroom or the student. In view of these results, a didactic guide was carried out using the known mathematical aspects and various ludic activities to extend the notion and use of scientific notation.
Keywords:
significant numbers, physics, didactic guide, scientific notation, order of magnitude.Resumo
Para este trabalho, se busque uma proposta didáctica construtiva em donde os estudantes do terceiro ano de Educação Mídia Geral ganha um aprendito significativo no uso da Notação Científica. O tipo de investigação utilizado se encontra entre os projectos factibles com um design de campo sem experimentação. Para a recolecção de dados, utilizou a técnica da pesquisa aplicada a 43 estudantes da categoria de Física do terceiro ano do Liceo "Rosario Almarza" Trujillo-Venezuela. Os análises dos resultados indicam que são apresentadas em más de 10.000 significados e ordenadas, os quais são matemáticos essenciais para a compreensão e o uso da Notação Científica na área da Física, assim como também ressaltaron a necessidade de Implementar outras estratégias de ensino e aprendizagem, como é uma série de atividades complementares para o docente na fila do estudante. Em Vista a estes resultados, se procede a realizar uma guia didáctica usando os problemas matemáticos conhecidos e diversas atividades lúdicas para ampliar a noção e uso da notação científica
Palavras-chaves:
algarismos significativos, física, tutorial, notação científica, ordem de grandeza.Introducción
El estudio de la física y las matemáticas han jugado un papel muy importante para la interpretación de los fenómenos naturales y sociales, por lo que tienen un rol muy significante en la formación del estudiante de educación media general en Venezuela.
El estudio de la física no se trata solo de ecuaciones matemáticas, es también una comprensión correcta de principios y leyes que el estudiante adquiere para poderlos aplicar en distintas situaciones. Para ello es necesario que el docente implemente estrategias que sean acordes a las deficiencias de los estudiantes, pues no es suficiente la consulta bibliográfica de un texto de ciencias para dichas debilidades en el aprendizaje de la física. Cabe agregar que el estudio de los fenómenos naturales por parte de la física comienza con la estimación y medida de magnitudes, lo que hace tener una relación íntima con las matemáticas.
Como se ha señalado anteriormente, las matemáticas son fundamentales para la comprensión de la física. En el caso de la notación científica, es una herramienta matemática usada en la física para poder expresar cantidades tan grandes y/o pequeñas que solo pueden ser medidas dentro de cierto límite de error; como, por ejemplo, la distancia del universo o la masa de un protón. Sin embargo, se ha observado que cuando el estudiante esta frente a un cálculo de dichas magnitudes presentan dificultades para asirse de los conocimientos matemáticos.
Lo anterior conduce hacia la promoción didáctica de estrategias para fortalecer la notación científica, como un enlace entre la matemática y la física. Muchos han sido los esfuerzos por crear y promover proyectos de aprendizaje que involucren la interdisciplinaridad de las ciencias. Así pues, la guía didáctica que se propone en esta investigación surge como una alternativa para aportar soluciones positivas tanto al docente como al estudiantado.
Marco Referencial
Para Arquímedes, el manejo de la notación científica en tiempos remotos probablemente pudo haberle aportado una mayor simplicidad para crear sus grandes inventos, ya que para ese tiempo no existía una tecnología tan sofisticada como la que gozamos actualmente.
Según Rodríguez, haciendo referencia a Arquímedes, expresa lo siguiente:
[…] Pero intentaré demostraros por medio de puntos geométricos que seréis capaces de seguir, que los números nombrados por mi… algunos exceden no sólo al número de la masa de arena igual en magnitud a la de la Tierra llena de la forma descrita, sino al de la masa igual en magnitud al Universo. (2002, p. 241)
Con base en lo anterior, lo que le pudo haber proporcionado una ventaja a Arquímedes para sus inventos probablemente fue el uso de la notación científica, ya que esta representa una forma de interactuar e interpretar problemas cotidianos y fenómenos naturales que ocurren a nuestro alrededor de forma matematizada. Hoy día los estudiantes de física de educación media general cuentan con esta herramienta matemática, lo cual facilita el proceso del par enseñanza y aprendizaje de las ciencias naturales.
Por lo tanto, esta investigación se propone conectar las ideas matemáticas, específicamente la notación científica con el área de física, de tal modo que el estudiante observe estas ciencias fácticas como un todo integrado y pueda tener un aprendizaje creativo y productivo, así como una actitud científica ante la vida. Para lograr tal fin, se ha diseñado una guía de estudio con un enfoque constructivista.
El modelo constructivista en el análisis de las dimensiones
El constructivismo parte de que el aprendizaje nunca puede ser independiente de quien aprende; no puede simplemente transferirse de una persona a otra como el símil de un vaso que llena al otro. El modelo constructivista indica que cada ser humano debe concatenar ideas y estructuras que tengan un significado personal, siempre y cuando tenga el deseo de aprender. Es por ello que el enfoque constructivista de la enseñanza exige, en primer lugar, conocer las ideas previas, es decir, el esquema conceptual de los estudiantes. De allí la importancia del uso de la pregunta, pero no una pregunta cualquiera que induce respuestas estereotipadas y la cual presupone la respuesta correcta, sino aquellas preguntas que conducen a la reflexión sobre el entorno y estimular la creación de modelos que permitan dar explicación a su mundo.
A esto se suman docentes con un enfoque constructivista que confían en las capacidades de sus estudiantes para encontrar respuestas a las preguntas y soluciones a los problemas, por tanto, fomenta la autonomía moral y cognitiva. Enseña a partir de problemas que tienen significado y por ello hace diagnósticos de los problemas, necesidades, intereses y recursos tanto de los estudiantes como del entorno. Florez (1994, p. 238) Duschl (1995, p. 110) proponen a los docentes algunas sugerencias o principios para potenciar la enseñanza constructivista:
-
Partir del nivel de desarrollo del estudiante.
-
Asegurar la construcción de un aprendizaje significativo.
-
La necesidad de que los estudiantes realicen aprendizajes significativos por sí solos.
-
La exigencia de que los estudiantes modifiquen sus esquemas de conocimiento.
-
Y que los estudiantes realicen una intensa actividad creativa e intelectual.
La matemática como herramienta para la física
Las matemáticas juegan un papel importante en el desarrollo y enseñanzas de las ciencias, como se ha venido desarrollando hasta ahora, guarda una estrecha relación especialmente con la comprensión de la Física. Sin embargo, en el proceso académico enseñanza-aprendizaje, en algunas ocasiones, se realizan de forman tan abstracta que alejan la ciencia formal de los intereses reales de los estudiantes.
Para la enseñanza de la matemática en el área de física, química y biología se debe aplicar un nuevo enfoque donde el estudiante pueda aplicar dichos conocimientos a su vida diaria. En relación con esto, Rodríguez expresa que:
[...] para que los estudiantes descubran sus propias ideas matemáticas, es menester asumir la postura inicial de mostrar la relación matemática-cotidianidad, porque alienta en primer lugar al estudiante a dejar su predisposición inicial, y verla como inalcanzable y, en segundo lugar, aprecian su verdadero valor y utilidad al relacionarla con los problemas del mundo y de su cotidianidad. (2011, p. 39)
Existen relaciones de la matemática con la física, la computación, la biología, la música, la química, las ciencias sociales y otros; no obstante, sin exagerar demasiado, se podría afirmar que la mayor parte del desarrollo de la matemática en los últimos tres siglos tiene origen y motivación en el deseo de resolver situaciones derivadas de planteamientos físicos-matemáticos. De allí la importancia que tiene el enfocar los aspectos matemáticos tales como cifras significativas, orden de magnitud y notación científica para la comprensión y resolución de problemas en física de tercer año de educación media general.
Aspectos matemáticos como cifras significativas, orden magnitud presentes en la notación científica
Estos dos aspectos de carácter matemático se pueden explicar a nivel físico, para que los estudiantes lo puedan comprender en un nivel concreto y luego visualizarlo a un nivel abstracto. En el caso de las cifras significativas, muchos de los números que se manejan en la ciencia son el resultado de una medida y, por lo tanto, solo se conocen con cierta incertidumbre experimental. La magnitud de esta incertidumbre, que depende de la habilidad del científico y del aparato utilizado, frecuentemente solo puede estimarse. Considere la longitud de un bolígrafo medido con una regla graduada. El resultado se podría expresar de la siguiente manera:
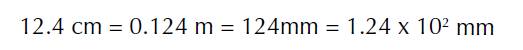
La medida anterior tiene tres (3) cifras significativas
Cuando se realizan cálculos aproximados o comparaciones se suele redondear un número hasta la potencia de 10 más próxima, tal número recibe el nombre de orden de magnitud. Por ejemplo, si una longitud es 100 veces mayor que otra se dice que es dos órdenes de magnitud mayor. Cuando dos números tienen aproximadamente el mismo valor, se dice que son del mismo orden de magnitud. En física es muy importante manejar los órdenes de magnitud, ya que nos permiten representar y comparar de una forma simplificada las distintas magnitudes físicas.
Ahora bien, estos dos términos explicados anteriormente son indispensables para trabajar con notación científica que Briceño Valero y García Oropeza (2012, p. 118) definen como “un medio de indicar y mantener un seguimiento de la coma decimal en un número”. Es muy frecuente el uso de la notación científica (también denominada notación exponencial) en la física, ya que ella permite simplificar algunas medidas que son extremadamente grandes o muy pequeñas y por tanto difíciles de manejar.
Un aspecto importante que debe quedar claro para el alumno es que un número expresado en notación científica está compuesto por dos factores: el primer factor es un número que tiene una cifra entera (de 0 a 9) y una parte decimal, mientras que el segundo factor es una potencia de 10, con exponente positivo si se trata de una cantidad muy grande o con exponente negativo si es una cantidad muy pequeña.
Véase mejor con los siguientes ejemplos:
-
La masa de un electrón es de aproximadamente 0.000 000 000 000 000 000 000 000 000 9 gramos, expresado en notación científica quedaría de la siguiente manera: 9x10-28 gramos.
-
El año-Luz es la distancia que recorre la luz en un año y equivale aproximadamente a 9 500 000 000 000 kilómetros. En notación científica equivale a 9.5x1012 km.
Guía didáctica como estrategia para el aprendizaje de la notación científica
Una guía didáctica es considerada como un instrumento impreso que generalmente se entrega al estudiante al principio de un curso, lapso o año escolar. Esta contiene todos los elementos indicativos para que el estudiante pueda realizar los estudios necesarios y así lograr los objetivos de aprendizaje de un contenido específico. Asimismo, tal vez le ayude a comprender qué relación significativa puede existir entre un libro de texto y la vida diaria.
La guía de estudio que se diseñó en esta investigación ha permitido suavizar las dificultades generales de los estudiantes, las cuales han sido diagnosticadas mediante instrumentos de recolección de datos, mostrando una estructura muy flexible para los estudiantes de física de tercer año de educación media general. Las actividades le permitirán interaccionar con lo recibido en clase, para luego ser evaluados según sus componentes y habilidades.
Metodología
El propósito de este trabajo fue valorar los procesos didácticos de un grupo de estudiantes de tercer año de educación media general en la asignatura de física, para luego proponer estrategias acordes a las necesidades presentadas por los mismos. En este sentido, este estudio forma parte de una investigación tipo factible con diseño de campo no experimental. Entendiéndose un proyecto factible como un estudio “que consiste en la investigación, elaboración y desarrollo de una propuesta de un modelo operativo viable para solucionar problemas, requerimientos o necesidades de organizaciones o grupos sociales” (Upel, 2011, p. 21); y el diseño de campo no experimental, el que se realiza sin manipular las variables.
La muestra estuvo compuesta por un grupo de 43 estudiantes del liceo Rosario Almarza, del municipio de Trujillo del estado Trujillo, en Venezuela. De igual manera, para Stracuzzi y Pestana, la muestra “representa un subconjunto de la población, accesible y limitado...” (2006, p. 116). Como la población es relativamente pequeña, la muestra es la cantidad de estudiantes que comprende la población en total. En este caso son las dos secciones de la asignatura de física de dicha institución con un total de 43 estudiantes.
Por otro lado, para evitar sesgos entre lo que lo que se investiga y aquello que realmente se quiere investigar, se utilizó la técnica de validación del juicio del experto, la cual consiste en entregarles a tres o cinco expertos un ejemplar del instrumento a aplicar, con su respectiva matriz de respuestas, acompañado de los objetivos de investigación y luego de su evaluación y realización de sugerencias (si las hay), ejecutarlo. Para el caso presente, la evaluación del instrumento estuvo a cargo de los Magister en Ciencias Oswaldo Linares, Ermelinda Azuaje y María Castro, quienes son especialistas en metodología, pedagogía y matemática, respectivamente, todos ellos profesores activos de la Universidad de Los Andes en Trujillo, Venezuela.
El cuestionario que se utilizó estaba compuesto por 12 ítems agrupadas en cuatro dimensiones. A continuación, se describen cada una:
-
Nivel declarativo: capacidad de reconocer los elementos matemáticos asociados a la notación científica como la potenciación y sus propiedades.
-
Nivel operativo: capacidad de demostrar el proceso para resolver un ejercicio a través de herramientas matemáticas como suma y resta de potencias, identificación de cifras significativas y orden de magnitud, entre otros.
-
Nivel explicativo: capacidad de aplicar sus conocimientos de notación científica para la resolución de problemas prácticos de la vida real, como expresar la distancia entre dos ciudades, el tamaño de una molécula, cantidad de letras en un libro, entre otros.
-
Nivel didáctico: capacidad del docente para diseñar, organizar y poner en práctica un conjunto de estrategias de enseñanza y actividades de aprendizaje, como las guías didácticas, mapas conceptuales, V de Gowin, entre otros.
La escala de respuesta fue entre 0 y 100%, donde las respuestas que tiende a 100% se consideran muy satisfactoria y las nada satisfactoria las que se acercaban a 0%.
La siguiente tabla , muestra los ítems con sus respuestas y dimensiones
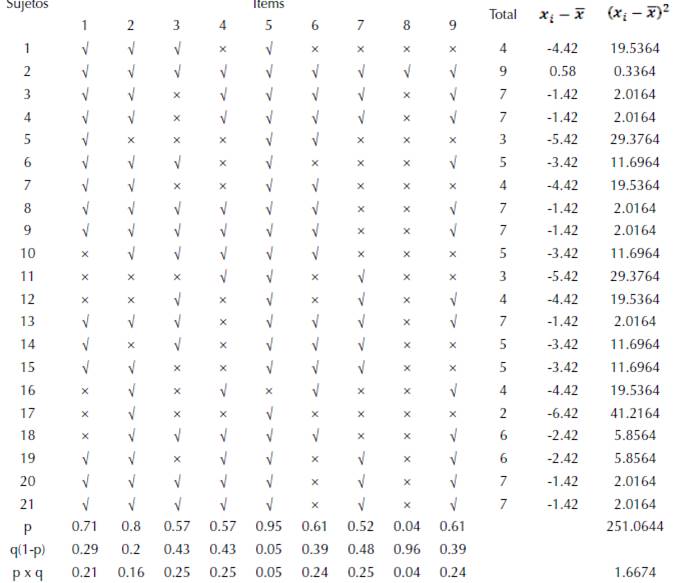
Así mismo, Stracuzzi y Pestana (2006) aseguran que la confiabilidad es la “ausencia de error aleatorio en un instrumento de recolección de datos”. Para calcular la confiabilidad del instrumento aplicado se utilizó el método K-R20, el cual procede de la siguiente forma: en primer lugar, para cada ítem se computa p, que es la proporción de sujetos que pasaron un ítem sobre el total de sujetos; luego, se computa q, que es igual a 1 - p; se multiplica p x q; y finalmente se suman todos los valores de p x q. El resultado obtenido es la sumatoria de la varianza individual de los ítems, o sea, Σp x q. En segundo lugar, se calcula la varianza total de la distribución de calificaciones (Vt); y, en tercer lugar, se aplica la fórmula correspondiente.
El modelo de Kuder-Richardson es aplicable en las pruebas de ítems dicotómicos en los cuales existen respuestas correctas e incorrectas, como las aplicadas en el cuestionario en cuestión.
Para calcular la confiabilidad, se aplicó una prueba piloto en una de las secciones del tercer año de educación media general y, puesto que el resultado fue favorable, se aplicó a la segunda sección. En la tabla 1 se observa el procedimiento para calcular la confiabilidad.
Fuente: Godoy (2011).
Tabla 1: Valoración de respuestas del instrumento aplicado.
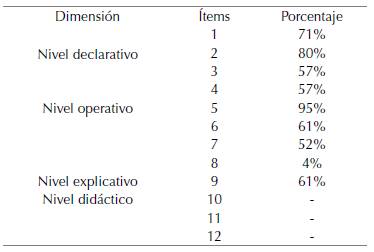
Tenemos el coeficiente de confiabilidad de la siguiente manera:
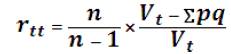
Tenemos que n=9 representa el número de ítems que contiene el instrumento.
La varianza total de la prueba queda determinada por la siguiente formula:
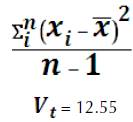
Para ello, fue necesario calcular la media aritmética:
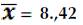
Sustituyendo todos los valores anteriores, tenemos que la confiablidad es:
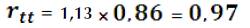
A mayor valor de 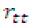 , mayor confiabilidad. El mayor valor teórico de
, mayor confiabilidad. El mayor valor teórico de 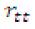 es 1 y, en general, 0.80 se considera un valor aceptable. Como se puede observar, la
es 1 y, en general, 0.80 se considera un valor aceptable. Como se puede observar, la  . Este resultado indica que existe una correlación “muy alta”, lo cual equivale a decir que el instrumento analizado es altamente confiable.
. Este resultado indica que existe una correlación “muy alta”, lo cual equivale a decir que el instrumento analizado es altamente confiable.
Fuente: Godoy (2011).
Tabla 2: Confiabilidad del instrumento.
Resultados
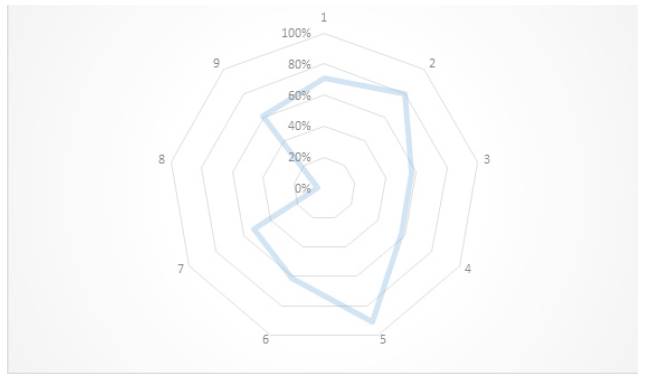
La figura 1 ilustra el porcentaje promedio de los nueve ítems valoradas por los estudiantes de la asignatura de física del liceo Rosario Almarza.
Figura 1: Porcentaje promedio de las respuestas en cada item.
El porcentaje promedio de la muestra fue del 52%, lo que denota una valoración moderadamente satisfactoria. La figura 1 presenta los ítems en el orden antes mencionado, las primeras cuatro corresponden a la dimensión Nivel declarativo, las siguientes al Nivel operativo y así respectivamente.
Lo que estos resultados arrojan de los ítems (6, 7 y 8) es que los estudiantes reflejan poca operatividad en:
-
Las cifras significativas, lo cual puede producir confusión a la hora de expresar un número en notación científica. Como lo expresan Brett y Suarez (2009), al indicar que generalmente las medidas realizadas en laboratorio, los dígitos serán significativos cuando están dados por la apreciación del instrumento.
-
Orden de magnitud, la cual consiste precisamente en representar cantidades en potencia de 10 más cercana al valor real de un número según Lobo et al. (2005). Con esta falta de operatividad, el estudiante no aprovechará las bondades que ofrece la notación científica de comparar cantidades muy grande y/o pequeñas de forma rápida y precisa.
Seguidamente, de los ítems (3 y 4) los estudiantes medianamente reflejan un nivel declarativo en:
-
Reconocer condiciones mínimas para expresar un número en Notación Científica, ya que según Álvarez (2009, p. 11), las cantidades en notación científica se expresan por medio de un número natural entre 1 y 9, seguido de algunos decimales a conveniencia y multiplicado por una potencia de base 10.
-
Aceptar que los factores parte entera y literal, son factores importantes de la notación científica, que depende tanto del signo como del valor del exponente, que según (Álvarez, 2009, p. 13) el exponente de la potencia de 10 representa el número de cifras (lugares) que debe correrse la coma decimal hacia la derecha o izquierda, si el exponente es positivo o negativo respectivamente.
Por otro lado, el ítem que podría calificarse como mínima aceptable (por su importancia) es de la dimensión Nivel didáctico. Esto denota la capacidad del estudiante en aplicar la notación científica en situaciones reales o a su contexto inmediato, ya que se evidencia poco trabajo imaginativo para relacionar cualquier distancia empleada entre dos objetos y expresarla en notación científica. Es por eso que se hace el esfuerzo de una guía didáctica que propicie el uso de la imaginación en los estudiantes a través de diferentes actividades lúdicas. Afianzado en que “una guía didáctica es un recurso que ponemos en las manos de nuestros estudiantes para que les informe y oriente en su aprendizaje” (Zabalza Beraza, 2004, p. 7).
Conclusiones
Como se pudo apreciar en la presentación de los resultados, los estudiantes encuestados presentan información muy básica con respecto a la notación científica. Su relación con esta es muy abstracta; no existe, para ellos, una aplicabilidad a su quehacer cotidiano, situación que no mejora con otros aspectos matemáticos como las cifras significativas y el orden de magnitud, que de hecho fue el ítem donde los estudiantes presentaron mayor deficiencia. Esto conlleva a pensar que el estudiante tiene una visión bastante errónea de la física, pues tal parece que la considera como una asignatura aislada e independiente.
Con respecto a lo anterior, los investigadores han sopesado la gran importancia de la promoción de estrategias innovadoras y motivantes con enfoques constructivistas en la asignatura de física, especialmente para los estudiantes de tercer año de educación media general, pues es para ellos su primer encuentro formal con esta área de formación y dicha experiencia marcará un hito para el éxito o fracaso en su comprensión y por ende la asimilación de las demás asignaturas afines. Por lo que se hizo hincapié en la promoción de una guía didáctica sobre la notación científica que servirá no solo para tener una mejor fluidez en la resolución de problemas físicos, sino también para la química, biología, astronomía, entre otros.
La guía didáctica titulada Aprendiendo física con el uso la notación científica fue diseñada para combinar aspectos matemáticos como cifras significativas, orden de magnitud y potenciación para el buen uso de la notación científica y, a su vez, ampliar los diferentes enfoques prácticos de esta con la vida cotidiana. Su estructura interna quedó de la siguiente manera: Portada, Índice, Introducción, Justificación, Objetivos, Aspectos teóricos, Actividades lúdicas, Lecturas complementarias y Bibliografía. Está diseñado con un lenguaje sencillo para que el estudiante pueda usarlo con o sin ayuda del docente. Dicha guía didáctica se encuentra alojada en el siguiente blog: https://sites.google.com/site/theorematicas/guiadidactica.
Referencias
Licencia
El (los) autor(es) al enviar su artículo a la Revista Científica certifica que su manuscrito no ha sido, ni será presentado ni publicado en ninguna otra revista científica.
Dentro de las políticas editoriales establecidas para la Revista Científica en ninguna etapa del proceso editorial se establecen costos, el envío de artículos, la edición, publicación y posterior descarga de los contenidos es de manera gratuita dado que la revista es una publicación académica sin ánimo de lucro.