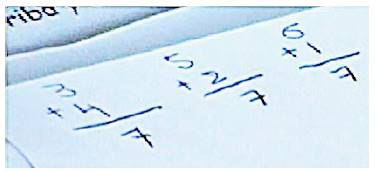DOI:
https://doi.org/10.14483/23448350.13326Published:
09/01/2018Issue:
Vol. 33 No. 3 (2018): September-December 2018Section:
Science EducationComprensión de la probabilidad de jóvenes con discapacidad intelectual
Understanding the probability at young with intellectual disability
Keywords:
discapacidad intelectual, educación especial, matemáticas escolares, probabilidad (es).Downloads
References
Arias, J. R. y Prieto, A. I. (2015). Aprendizaje de los números (del 0 al 9) en alumnos con discapacidad intelectual leve. Revista nacional e internacional de educación inclusiva, 8(1), 42-58.
Correa, Y. y Pulido, E. (2013). Adaptación e implementación de recursos didácticos para la enseñanza de ecuaciones de primer y segundo grado a niños con discapacidad visual en un aula inclusiva. Revista Científica, 17(2), 510-514.
diSessa, A. (2007). An interactional analysis of clinical interviewing. Cognition and Instruction 25(4), 523-565. DOI: https://doi.org/10.1080/07370000701632413
Eisner, E. (1998). El ojo ilustrado. Indagación cualitativa y mejora de la práctica educativa. Barcelona, España: Paidós
Fischbein, E. (1975). The intuitive sources of probabilistic thinking in children. Dordrecht, Holanda: Reidel.
Florian, L. (2010). Special education in an era of inclusion: the end of special education or a new beginning. The Psychology of Education Review, 34 (2), 22-29.
Hacking, I. (1975). The emergence of probability. New York, USA: Cambridge University Press.
Hawkins, A. y Kapadia, R. (1984). Children´s conceptions of probability a psychological and pedagogical review. Educational Studies in Mathematics 15(1), 349-377. DOI: https://doi.org/10.1007/BF00311112
Heitele, D. (1975). An epistemological view on fundamental stochastic ideas. Educational Studies in Mathematics, 6(2), 187-205. DOI: https://doi.org/10.1007/BF00302543
Maturana, H. (2003). Desde la Biología a la Psicología. Buenos Aires, Argentina: Lumen-Editorial Universitaria.
Mevarech, Z. (1983). A deep structure model of students´statistical misconceptions. Educational Studies in Mathematics 14(4), 415-429. DOI: https://doi.org/10.1007/BF00368237
Ojeda, A. M. (1994). Understanding fundamental ideas of probability at pre-university levels (Tesis de Doctorado inédita). King´s College London. UK.
Ojeda, A. M. (2006). Estrategia para un perfil nuevo de docencia: un ensayo en la enseñanza de estocásticos. En E. Filloy (Ed.), Matemática Educativa, treinta años: una mirada fugaz, una mirada externa y comprensiva, una mirada actual (pp. 195-214). México: Santillana.
Ojeda, A. M. (2007). Probabilidad y estadística en Matemática Educativa. Seminario de investigación. Documento interno. Manuscrito no publicado, Cinvestav - IPN, México.
Piaget, J. e Inhelder, B. (1951). La Genèse de l´idée de hasard chez l´enfant. Paris, Francia: Presses Universitaires De France.
Romero, S. y García, I. D. (2013). Educación especial en México. Desafíos de la educación inclusiva. Revista Latinoamericana de Educación Inclusiva 7(2), 77-91.
Steinbring, H. (1989). The interaction between teaching practice and theoretical conceptions. A cooperative model of in-service training in stochastics for mathematics teachers (Grades 5-10). En R. Morris (Ed.) Studies in Mathematics Education. The Teaching of Statistics (pp. 202-214). Paris, Francia: UNESCO.
Steinbring, H. (1991). The concept of chance in everyday teaching: aspects of a social epistemology of mathematical knowledge. Educational Studies in Mathematics 22, 503-522. DOI: https://doi.org/10.1007/BF00312713
Steinbring, H. (2005). The construction of new mathematical knowledge in classroom interaction. Boston, USA: Springer.
Vasilachis, I. (2006). Estrategias de investigación cualitativa. Barcelona, España: Gedisa.
Verdugo, M. A. (1988). La integración personal, social y vocacional de los deficientes psíquicos adolescentes. (Tesis de Doctorado inédita). Universidad Autónoma de Madrid, España.
Vygotski, L. S. (1997). Fundamentos de la defectología. Obras escogidas V. Madrid, España: Visor Dis.
Zazkis, R. y Hazzan, O. (1999). Interviewing in mathematics educations research: Choosing the questions. Journal of Mathematical Behavior, 17(4), 429-439.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de mayo de 2018; Aceptado: de julio de 2018
Resumen
El presente informe hace parte de una investigación más amplia centrada en caracterizar el pensamiento probabilístico de niños con discapacidad. De manera particular, el documento exhibe el uso de esquemas compensatorios relacionados con el pensamiento probabilístico de niños con discapacidad intelectual. La investigación, cualitativa y en curso, se rige por tres ejes rectores: epistemológico, cognitivo y social. Aquí se presentan los resultados de la tercera fase, la cual consistió en la comprensión de las ideas fundamentales de probabilidad, después de su enseñanza, de tres jóvenes (15-17 años) con discapacidad intelectual del tercer grado de secundaria especial, revelada en entrevistas individuales semiestructuradas en cámara Gesell sobre el enfoque frecuencial de la probabilidad. La estrategia consistió en dar a los alumnos el papel de examinador para obtener datos de su comprensión de los conceptos matemáticos incluidos en lo que examinan. Los resultados atañen al uso de la memoria de trabajo, el esquema perceptual visual y la atención para las ideas de espacio muestra, medida de probabilidad y variable aleatoria (de manera cualitativa con las frecuencias absolutas).
Palabras clave:
discapacidad intelectual, educación especial, matemáticas escolares, probabilidad.Abstract
This report is part of a larger investigation that was interested in characterizing the probabilistic thinking of children with disabilities. In particular, the document shows the use of compensatory schemes related to the probabilistic thinking of children with intellectual disabilities. Three guiding axes govern the research, qualitative and ongoing: epistemological, cognitive and social. Here are presented the results of the third phase that concerned the understanding of the fundamental ideas of probability, after teaching, of three young people (15-17 years old) with intellectual disability of the third degree of special secondary, revealed in semi-structured individual interviews in the Gesell camera on the frequency approach of probability. The strategy was to give students the role of examiner to obtain data of their understanding of the mathematical concepts included in what they examine. The results concern the use of working memory, the visual perceptual scheme and the attention for the ideas of sample space, probability measure and random variable (qualitatively with absolute frequencies).
Keywords:
probability, intellectual disability, special education, school mathematics.Resumo
Este relato faz parte de uma investigação maior que se interessou em caracterizar o pensamento probabilístico de crianças com deficiência. Em particular, o documento mostra o uso de esquemas compensatórios relacionados ao pensamento probabilístico de crianças com deficiência intelectual. A pesquisa, qualitativa e em andamento, é regida por três eixos norteadores: epistemológico, cognitivo e social. Apresentam-se aqui os resultados da terceira fase que diziam respeito à compreensão das ideias fundamentais de probabilidade, após o ensino, de três jovens (15-17 anos) com deficiência intelectual do terceiro grau do secundário especial, reveladas em entrevistas individuais semiestruturadas na câmera de Gesell na aproximação de freqüência de probabilidade. A estratégia era dar aos alunos o papel de examinador para obter dados de sua compreensão dos conceitos matemáticos incluídos no que eles examinam. Os resultados dizem respeito ao uso da memória de trabalho, o esquema perceptivo visual e a atenção para as idéias de espaço amostral, medida de probabilidade e variável aleatória (qualitativamente com frequências absolutas).
Palavras-chaves:
probabilidade, deficiência intelectual, educação especial, matemática escolar.Introducción
Ante las demandas internacionales que exigen a los sistemas educativos brindar una educación básica para todos, es necesario indagar sobre los elementos que se requieren para cumplir con tal misión. El que todo ciudadano domine los conocimientos que se marcan como indispensables fomentaría un mejor acceso a la información y sentaría las bases para una sociedad educada.
Con la tendencia a la educación inclusiva (Florian, 2010) es necesario que los docentes de educación especial estén preparados para atender a la diversidad que envuelve su aula. Esta se complica dada la variedad de discapacidades que confluyen en ella, pues los maestros deben acercar los contenidos de la educación básica a los niños con estas características. Como ejemplo de esos, en las matemáticas, se encuentran los temas de probabilidad y de estadística.
Proporcionar al individuo con discapacidad una cultura matemática integral, aquella que incluya temas de probabilidad y de estadística, suministraría elementos para desarrollar una red conceptual en la cual el uso de otros conceptos permita dotarla de otro sentido para los estudiantes.
De manera importante, las disciplinas probabilidad y estadística han marcado la pauta en una diversidad de aplicaciones, de adelantos científicos, tecnológicos e inclusive en tendencias en el arte y la cultura (Ojeda, 2007). Además, si bien los temas de probabilidad y de estadística son los menos tratados en el currículo educativo mexicano, con estos se puede desarrollar un pensamiento crítico, es decir, aquel que se abre a lo posible y es importante en la toma de decisiones.
Por otra parte, Vygotski (1997) ha señalado que en lugar de enfatizar las deficiencias o ausencias la educación debería centrarse en potenciar las características con las que cuenta el individuo. Ello permitiría establecer un marco de referencia que considere los esquemas compensatorios como promotores del pensamiento matemático que el docente debe tener en cuenta en el diseño de actividades de enseñanza para la constitución de las redes conceptuales implicadas por los estocásticos.
En ese sentido, el objetivo de nuestra investigación fue establecer un marco de referencia que permita a los docentes de educación especial plantear actividades para el tratamiento de los estocásticos ante la heterogeneidad de afecciones en una misma aula. Se pretende responder a la interrogante ¿cuáles esquemas compensatorios favorecen el desarrollo del pensamiento probabilístico de niños con discapacidad intelectual? Pues los resultados se orientan a la comprensión que tienen los jóvenes respecto a los conceptos de medida de probabilidad, espacio muestra y variable aleatoria.
Perspectiva teórica
El trabajo de investigación se ajustó a la propuesta de tres ejes rectores (Ojeda, 1994) para la comprensión de ideas fundamentales de estocásticos para los distintos niveles educativos. El eje epistemológico refiere al conocimiento del azar, la probabilidad y la estadística. En el cognitivo interesan los procesos del pensamiento del sujeto relativos al azar y a la probabilidad. Para el eje social interesa la consideración del sujeto en el aula referida al conocimiento de estocásticos. Por la naturaleza del escenario de investigación se incorporaron en el eje cognitivo información sobre los esquemas compensatorios y sobre la discapacidad intelectual.
Eje epistemológico
Heitele (1975) ha propuesto 10 ideas fundamentales de estocásticos como guía para un currículo en espiral. Para el autor, una idea fundamental es “aquella que proporciona al individuo modelos explicativos tan eficientes como sea posible” (p. 188). Argumenta que el tratamiento de las ideas fundamentales debe partir de un plano intuitivo y llegar a un plano formal, de manera que se garantice continuidad en la educación. Las ideas fundamentales de interés para el documento son: medida de probabilidad, espacio muestra y variable aleatoria. En el mismo sentido, es de interés el enfoque frecuencial de la probabilidad (Hacking, 1975), ya que este se refiere a la estimación de la probabilidad de un evento con base en su frecuencia relativa de ocurrencia en una secuencia grande de repeticiones del fenómeno aleatorio, del cual ese evento es un resultado posible. Este es un enfoque a posteriori o empírico (Hawkins y Kapadia, 1984), pues supone la realización de las repeticiones del fenómeno aleatorio.
Eje cognitivo
En su obra sobre las fuentes intuitivas del pensamiento probabilístico, Fischbein (1975) entiende por intuición un conocimiento que se deriva de la experiencia, de recuperación inmediata, sintético, que se extrapola y no es susceptible de análisis. El autor señala que en la formación de intuiciones probabilísticas es necesario considerar lo incierto y conectarlo con la acción por medio de frecuencias relativas; de esta forma se establecerá un comportamiento de la situación aleatoria caracterizado como más probable, menos probable o igualmente probable. La probabilidad es, por tanto, apropiada para el estudio de esas intuiciones. Debido a su enfoque frecuencial, la probabilidad está determinada por la acción y es en la acción u observancia de los fenómenos naturales como se puede desarrollar una base intuitiva.
También son importantes los esquemas compensatorios como procesos que permiten superar una ausencia o limitación de manera que asumen la función inactiva o dañada para el desarrollo del pensamiento del individuo (Vygotski, 1997). Particularmente, la afección de discapacidad intelectual “se caracteriza por limitaciones significativas en el funcionamiento intelectual y en la conducta adaptativa, expresada en las habilidades adaptativas conceptuales, sociales y prácticas” (Verdugo, 1988, p. 8), provoca dificultades en la comunicación y los procesos de adquisición del conocimiento son lentos (Arias y Prieto, 2015).
Eje social
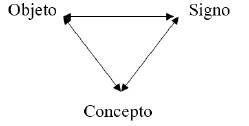
Steinbring (2005) establece una relación entre la naturaleza epistemológica del concepto matemático y su significado socialmente constituido en las interacciones en el aula. El autor argumenta que para la adquisición del concepto es necesaria la interacción entre el contexto de referencia en que se implica al objeto y el signo asociado a este. La constitución resulta de un balance entre las relaciones entre los tres vértices (figura 1), de modo que se pueda deducir el significado del conocimiento matemático. Al objeto se le dota de sentido según el contexto de referencia, y es representado por el signo, de manera que el concepto matemático se construye como una estructura simbólica relacional y se le codifica mediante signos y símbolos que se pueden combinar lógicamente en operaciones matemáticas (Steinbring, 1991).
Figura 1: Triángulo espistemológico.
El objeto “se construye como nuevo conocimiento en una relación matemática” (Steinbring, 1989, p. 155). El signo matemático tiene dos funciones: en la semiótica se le considera como “algo que representa algo más” y “en la epistemológica es un marco de la constitución epistemológica del conocimiento matemático” (Steinbring, 1989, p. 134). Por tanto, el concepto es perfectible, dado que va de las nociones a ideas en estrecha interrelación entre el objeto y el signo.
Metodología
La investigación de tipo cualitativa (Eisner, 1998; Vasilachis, 2006) y en curso1 se desarrolló en tres fases y siguió las directrices del órgano operativo y de la célula de análisis de la enseñanza (Ojeda, 2006). El primero organiza los escenarios en los que se desarrolló la investigación; el segundo conjuga elementos teóricos y aspectos del método para someter a escrutinio los conceptos de probabilidad y estadística.
En la Fase I, documental, se constituyeron los escenarios que albergaron a la investigación y se examinó la propuesta institucional para introducir en la educación básica la probabilidad. La Fase II, de experienciación (Maturana, 2003), se enfocó en la enseñanza de la probabilidad. Se obtuvieron datos para caracterizar el desempeño de los niños en actividades de enseñanza de temas de azar, probabilidad y datos de su uso de esquemas compensatorios. La Fase III, mediante entrevistas individuales semiestructuradas (Zazkis y Hazzan, 1999; diSessa, 2007), profundizó en la comprensión de los niños de las ideas fundamentales de probabilidad después de su enseñanza y en su uso de esquemas compensatorios.
El método empleado fue la entrevista individual semiestructurada. Por entrevista se entiende aquí la interacción entre dos individuos cuando uno le plantea preguntas al otro para alcanzar un objetivo ―el de obtener datos de la comprensión del segundo respecto a una situación o a conceptos implicados en una actividad-. Por lo que es relevante el tipo de comunicación (Zazkis y Hazzan, 1999; diSessa, 2007) posible con cada caso debido al síndrome o afección. Para diSessa (2007), el objetivo de una entrevista es permitir al entrevistado que “exponga de manera natural” (p. 526) su forma de pensar respecto a la situación que se está tratando, mientras que el entrevistador explora diferentes maneras de enmarcar la situación problemática para exhibir el conocimiento del entrevistado.
Una de las estrategias utilizadas en las entrevistas fue la aplicada por Mevarech (1983), que consistió en solicitar a los alumnos que analizaran una tabla de frecuencias en la que se incluían eventos imposibles con ocurrencias registradas. Se plantearon preguntas para saber si los alumnos se percataban de que algunos datos en la tabla eran erróneos. De esa manera, se esperaba que ellos se convirtieran en diagnosticadores de los errores y pusieran en juego el conocimiento adquirido.
Se emplearon criterios de análisis, a saber: situación de referencia, ideas fundamentales de estocásticos, otros conceptos matemáticos, recursos semióticos, términos para referirse a estocásticos (Ojeda, 2006) y esquemas compensatorios. Los instrumentos de recopilación de datos utilizados en la Fase III fueron guiones de entrevista basados en las actividades propuestas en el aula alterna y en el aula normal (Ojeda, 2006) para profundizar en la comprensión de los jóvenes de las ideas de estocásticos implicadas en esas.
Los estudiantes
Los resultados que se presentan en este informe corresponden a la comprensión de ideas fundamentales de probabilidad de tres jóvenes de tercer grado de secundaria especial de un centro de atención múltiple (CAM), espacio (perteneciente a una institución) que ofrece servicios educativos a niños con discapacidad o discapacidad múltiple, o aquellos con trastornos graves del desarrollo, que no pueden ser integrados a la escuela regular, además de pertenecer a la modalidad educativa Educación Especial (Romero y García, 2013). Los casos que se eligieron para entrevista evidenciaron: mejor desempeño que el resto de sus compañeros, tendencia a un pensamiento mítico por manifestar indicios de nociones de espacio muestra. Se eligieron tres casos con discapacidad intelectual: UR, porque manifestó un pensamiento mítico (colocó sus manos a manera de “ruego” de que saliera cierto color) y a JE por tener el mejor desempeño que el resto de sus compañeros del aula. Mientras que a CE se le eligió por su elección de un evento imposible.
Las situaciones para entrevista
Las entrevistas individuales semiestructuradas se realizaron en sesiones de 30 minutos en promedio en el escenario de cámara Gesell, disponible en el CAM. Fueron dos situaciones para entrevista. La primera consistió en presentarle al alumno una tómbola de 12 cm de diámetro, en la cual se introdujeron cinco canicas blancas, dos verdes y una amarilla, todas del mismo tamaño. El estudiante tenía que girar la tómbola y registrar el resultado de la expulsión en hojas blancas. La canica se regresaba a la tómbola para mantener ocho canicas en total.
La segunda situación consistió en analizar una tabla con los registros de uno de los alumnos del tercero de secundaria realizada en La carrera con dados (figura 2). La actividad en el aula consistió en elegir un número del 1 al 13 como corredor en una pista de una tabla de registro. Se lanzaban dos dados ordinarios distinguibles por color, se sumaban los puntos de las caras que quedaban hacia arriba y la suma avanzaba una celda; ganó el número que llegó primero a la meta en la tabla 1.
Figura 2: Hoja de control para entrevista. Tabla de frecuencias de JO.
Fuente: elaboración propia del autor.
Tabla 1: Documentos revisados.
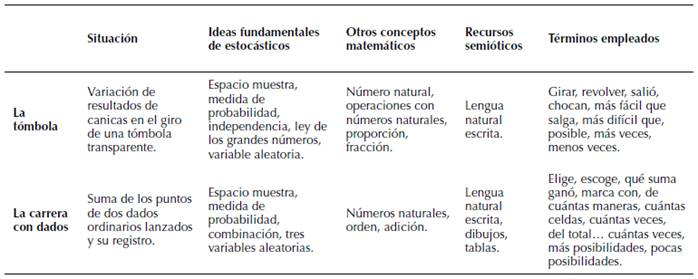
Para la tómbola se apela a la idea de azar con la mezcla aleatoria del contenido producida por los giros de esta. Interesa en este caso el resultado de la canica al cabo de cada giro. En la carrera con dados el fenómeno aleatorio implicaría identificar la variedad de resultados después del lanzamiento de los dos dados ordinarios.
Resultados
De los resultados se obtuvo evidencia de un acercamiento a las ideas de espacio muestra, medida de probabilidad y, de manera cualitativa, de variable aleatoria; así como su correspondiente uso del esquema compensatorio: memoria de trabajo, esquema perceptual visual y la atención. De manera particular, UR en el desarrollo de la entrevista superó el pensamiento mítico que evidenció en el aula. Para JE se corroboró su desempeño hacia las ideas fundamentales de probabilidad y CE se obtuvo evidencia del evento imposible.
Espacio muestra
En la tómbola UR no tuvo dificultad para identificar los posibles resultados y argumentó que era más fácil que salieran las canicas blancas, pues eran cinco, y que la más difícil era la canica amarilla2.
[117] I: A ver, UR, en el siguiente giro ¿qué va a resultar? ¿Qué canica es más fácil que salga?
[118] UR: La blanca [una canica blanca ].
[119] I:¿Por qué?
[120] UR: Mmm… [Pensando]. Porque hay cinco [canicas] blancas, dos verdes y una amarilla.
Se mueven las canicas, mira, hace rato la verde estaba arriba [identifica una posición de una canica] y ahora está debajo de las blancas… las canicas chocan entre ellas.
Lo anterior sugiere un acercamiento a la idea de azar, pues en su respuesta identifica la posición de las canicas al cabo de cada movimiento de la tómbola. Además, el tipo de argumento que emplea sugiere el uso de la memoria de trabajo y la atención, pues pareciera estar atento a lo que se produce en el interior de la tómbola con las canicas.
[145] I: UR, ¿sale la misma canica siempre? Siempre que tú giras la tómbola ¿el resultado es siempre el mismo?
[146] UR: No, se mueven las canicas, mira, hace rato la verde estaba arriba [identifica una posición de una canica] y ahora está debajo de las blancas… las canicas chocan entre ellas.
En la carrera con dados, al preguntarle a CE sobre cuál era la suma que el niño de la tabla había elegido, él respondió que fue la suma “siete porque la marcó” y señaló con el dedo índice el número siete en la salida de la pista de carreras. Cuando se le preguntó a CE si el niño ganó con esa suma respondió “no, porque no llegó a la meta” e identificó la suma que ganó.
[17] I: A ver, CE, el niño eligió el siete [la suma] ¿verdad? ¿El niño ganó?
[18] CE: No [mueve la cabeza].
[19] I: ¿Por qué?
[20] CE: Mmm… No llegó a la meta [la suma].
[21] I: ¿Hasta dónde llegó?
[22] CE: Hasta aquí [señala con el dedo índice el último tache e inicia el conteo], uno, dos, tres, cuatro, cinco, seis, siete.
[23] I: Bien, entonces ¿qué suma ganó?
[24] CE: 10 [la suma].
Al cuestionarle a CE sobre cuál suma era más fácil que resultara después del lanzamiento de los dos dados dijo que la suma siete tenía más posibilidades de ocurrir y escribió otras posibilidades.
[77] I: A ver, CE, si lanzamos dos dados, ¿qué suma es más fácil que salga?
[78] CE: El siete…
[79] I: ¿Por qué?
[80] CE: Mmm… porque “3+4”, “5+2”, “6+1”.
[81] I: A ver escribe [le proporciona una hoja en blanco].
En la figura 3 se puede señalar que CE identifica otras posibilidades que tiene la suma siete para ocurrir. La organización que presenta es a manera del algoritmo tradicional de la adición, pero esta disposición fue propuesta por él. Lo anterior sugiere el uso de la memoria de trabajo, pues recupera las formas en las que se puede obtener el 7.
Figura 3: Posibilidades para la suma siete.
Figura 3. Posibilidades para la suma siete.
Fuente: elaboración propia del autor.
Además, al interrogar si la persona que jugó y registró en la hoja había realizado correctamente el juego él respondió que no porque tenía registros en las casillas de las sumas 1 y 13 y que las sumas posibles eran del 2 al 12. Reconoció que él perdió cuando se desarrolló la actividad en el aula porque eligió la suma 13.
[123] I: A ver, CE, ¿por qué no se puede obtener la suma trece
[124] CE: No [mueve la cabeza], necesitamos seis más siete.
[125] I: ¿Cómo son nuestros dados?
[126] CE: Tenemos uno, dos, tres, cuatro, cinco, seis [puntos]…
[127] I: ¿Entonces? ¿Podemos obtener la suma trece?
[128] CE: No, nada más seis más seis, doce…
Medida de probabilidad
Para la tómbola, UR reconoció que si siguiera girando sería mucho más fácil que a la larga saliera más veces la canica blanca y más difícil que saliera la amarilla. Si bien su justificación refirió a la cantidad mayor de canicas blancas que amarillas, de manera implícita presenta un pensamiento probabilístico, pues parcialmente puso en relación el número de casos posibles con el total de casos. Cuando se le preguntó a JE sobre si el juego era justo respondió: “No, porque la canica amarilla está solita”.
[218] I: …JE, así como tenemos esto [refiriéndose a la tómbola], así como estamos jugando, ¿consideras que el juego es justo? ¿O estamos haciendo trampa?
[219] JE: [Mueve la cabeza como asintiendo].
[220] I: ¿Qué, estamos haciendo trampa?
[221] JE: Sí [sonríe].
[222] I: ¿Por qué? ¿Trampa para quién?
[223] JE: Para el amarillo y para el verde [sonríe], la canica amarilla está solita.
[224] I: ¿Sí? ¿Por qué?
[225] JE: Porque son cinco…
[226] I: ¿Cinco qué?
[227] JE: Cinco blancas, dos verdes y una amarilla [refiere a la cantidad de canicas].
[228] I: Mmm… Entonces, ¿qué se espera a la larga? ¿que salgan más canicas… de qué color?
[229] JE: Blancas…
[230] I: Si te dijeran que debes apostar a un color, para que ganes, ¿a qué color le apostarías?
[231] CE: Al blanco…
Variable aleatoria
Para la tómbola, UR y JE registraron los resultados de cada giro en hojas blancas. JE organizó sus datos a manera de tabla; en la parte superior colocó los posibles resultados, en la parte inferior registraba los resultados efectivos (frecuencias relativas). Lo anterior sugiere un nivel de comprensión superior al de solamente organizarlos en serie de uno en uno. En cambio, UR registró uno por uno los resultados de los 20 giros (frecuencias).
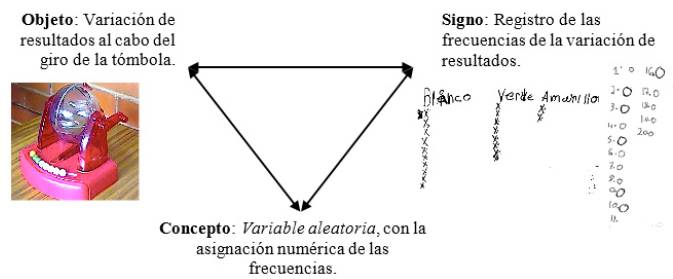
Se argumenta una constitución del concepto matemático variable aleatoria (figura 4), debido a que los estudiantes pudieron identificar la variedad de resultados después de cada giro de la tómbola. Además, señalaron la mezcla de las canicas que se produce en el prototipo. Lo anterior se relacionó con el registro de las frecuencia del resultado de cada canica, uno de estos fue a manera de tabla de doble entrada y el otro correspondió a la sucesión de resultados uno a uno.
Figura 4: Triángulo epistemológico de la variable aleatoria.
Para los casos anteriores, el uso del esquema perceptual visual jugó un papel importante, pues la correspondencia entre la mezcla de las canicas, que se produce cuando la tómbola está en movimiento, acercó a dar argumentos en función al fenómeno aleatorio y no a expresiones del tipo sucede por azar. A lo anterior se le asigna un registro por cada resultado para señalar cuál de las canicas tiene más oportunidades de ocurrir en un número muy grande de extracciones.
Conclusiones
Se corroboró la comprensión de las ideas de espacio muestra, medida de probabilidad y variable aleatoria por parte de JE y UR. Este último, en las actividades en el aula, atribuía el resultado de los eventos de un fenómeno aleatorio a otras causas más que a la probabilidad de cada evento, motivo por el cual fue seleccionado. Las respuestas de UR en las entrevistas consideraban, parcialmente, la probabilidad que tuviera cada evento del fenómeno aleatorio. También tuvo un acercamiento a la idea de azar físico, “interferencia de series causales independientes” (Piaget e Inhelder, 1951, p. 13). En la situación de la tómbola, su respuesta ante la pregunta ¿por qué no salen siempre las mismas canicas? fue “las canicas chocan entre ellas”. Para la respuesta anterior, se apoyó del esquema perceptual visual, según (Steinbring 1991; 2005), la atención se centró en el objeto de la actividad matemática.
Por su parte, el mejor desempeño de JE se mantuvo en las entrevistas. Las situaciones no presentaron mayor dificultad para el estudiante. Fue con el único que, según su producción, se pudo tener un acercamiento a la idea de juego justo. Identificó que en la situación de la tómbola los eventos no tenían la misma probabilidad de ocurrir: “la canica amarilla está solita”. La memoria de trabajo y la atención, jugaron un papel importante en esta actividad, pues recuperaba de manera inmediata las frecuencias de cada uno de los eventos (canica amarilla, canica blanca, canica verde).
CE identificó el evento con mayor probabilidad en la tabla de frecuencias de la carrera con dados y el evento imposible al percatarse que era difícil obtener una suma 13 con dos dados ordinarios. La memoria de trabajo le permitió señalar los eventos imposibles y argumentar otras posibles formas de obtener la suma siete.
JE y UR propusieron una manera de organizar los resultados de las canicas al girar la tómbola. Lo anterior, según Steinbring (2005), exhibe la distinción que los jóvenes realizaron del objeto y del signo para la adquisición del concepto matemático. Es decir, distinguieron la variedad de resultados con la frecuencia de cada categoría para arribar al enfoque frecuencial de la probabilidad.
De todo lo anterior, un acercamiento al pensamiento probabilístico de los niños con discapacidad está en función al tipo de actividades de enseñanza de estocásticos propuestas. Es decir, un marco de referencia para la enseñanza de la probabilidad en educación especial se constituye con la identificación de los esquemas compensatorios según el tipo de afección de que se trate; es decir, el uso de material concreto, físico y llamativo, que permita al niño dotar de sentido a las acciones. Por ejemplo, para el caso con discapacidad visual Correa y Pulido (2013) proponen materiales didácticos manipulativos que propicien una acción reflexiva en el estudiante; dicho de otra forma, es necesario poner en juego el triángulo epistemológico para la adquisición del conocimiento matemático.
Referencias
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.