La espiral de Euler en la montaña rusa

Introducción

Se estudió la curvatura de las posibles trayectorias que seguiría un vehículo en un riel de una atracción mecánica y su relación con la aceleración normal del vehículo para evidenciar los posibles riesgos que tendrían los pasajeros si se unen trayectorias de curvatura diferente. Buscando una trayectoria en la que su curvatura aumente linealmente con el desplazamiento, se deducen las ecuaciones que corresponden a la espiral de Euler. Esta trayectoria es más segura al evitar discontinuidades en la aceleración normal, ya que este tipo de cambios pueden resultar nocivos para los pasajeros (Eager, Pendrill y Reistad, 2016). El análisis también muestra que la curvatura de la espiral de Euler es diferente en cada punto, de tal forma que resulta apropiada para unirla suavemente con otras trayectorias de diferentes curvaturas (Thomas y Finney 2000).

Durante el estudio se observó que la forma de los bucles de las montañas rusas de los parques de diversiones no es circular en su totalidad, sino que presenta una forma de gota invertida (Pendrill, 2005). En algunos casos los bucles tienen una secuencia de espiral de Euler-circunferencia-espiral de Euler. La forma de conectar tramos de diferentes trayectorias de manera suave es uniéndolas en los puntos en los que sean tangentes a la misma recta, de este modo se pudo unir suavemente un segmento recto con una sección de la espiral de Euler y luego con una sección de circunferencia.

Aplicando los conceptos del análisis vectorial a curvas en el espacio en el programa Geogebra, fue posible simular diferentes bucles y hacer una comparación visual con una fotografía de la montaña rusa Doble loop del parque Salitre Mágico de Bogotá. A partir de la comparación, se identificó que la atracción mecánica tiene dos partes de la espiral de Euler conectadas con una sección de circunferencia.

Metodología

El problema a resolver es calcular la curvatura (κ) de la trayectoria en una atracción mecánica para que sea segura cuando los vehículos la recorren.

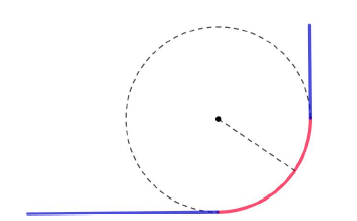
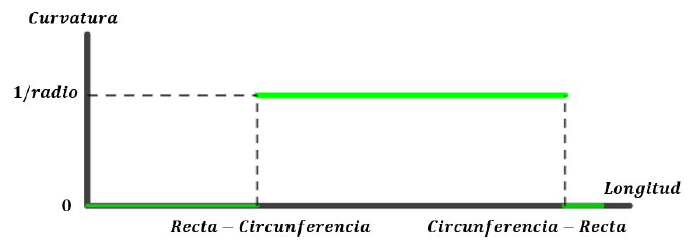
Cuando un vehículo pasa de una recta a un arco de circunferencia experimenta un cambio discontinuo de curvatura, ya que la curvatura de una recta es κ = 0 y la de una circunferencia de radio r es κ = 1/r. También hay un cambio discontinuo cuando pasa de una circunferencia a una recta (figuras 1 y 2).

Figura 1: Segmentos de rectas conectadas a través de un arco de circunferencia.

Figura 2: Curvatura en el recorrido de la curva de la figura 1. Se observan discontinuidades de la curvatura.

Teniendo en cuenta que la aceleración normal y la curvatura son proporcionales, el vehículo intentaría seguir la línea recta si la velocidad es alta. Lo mismo pasaría en un bucle de una montaña rusa.

Por esta razón, se recomienda que en las atracciones mecánicas no haya segmentos de recta conectados con arcos de circunferencia.

Para el caso de la montaña rusa, este trabajo se enfocará en el bucle de la atracción para entender a qué se debe su forma de gota invertida y porqué de esta manera hay mayor seguridad sin dejar de lado la diversión que trae consigo la adrenalina.

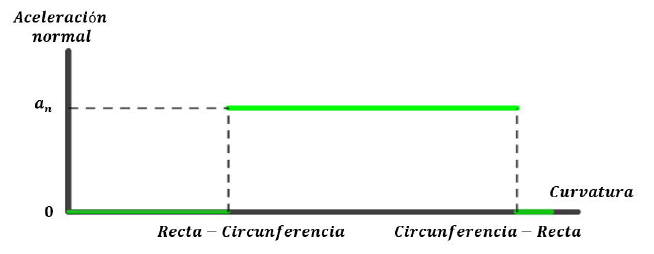
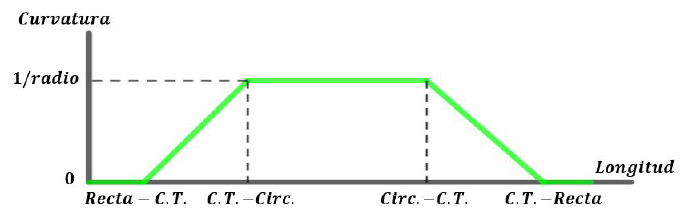
Para solucionar el problema descrito se requiere conectar la recta con la circunferencia a través de una curva de transición con el fin de que la curvatura cambie linealmente, como se ve en figura 3 y 4.

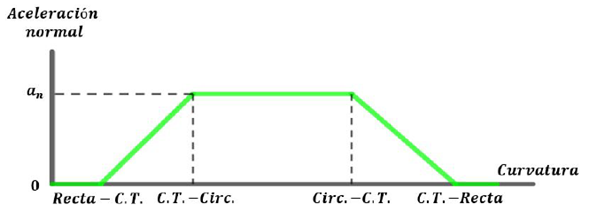
Figura 3: Aceleración normal en el recorrido de la figura 1 a rapidez constante. Donde an es el producto del cuadrado de la velocidad con la curvatura de la circunferencia.

Figura 4: Cambio lineal de la curvatura en la curva de transición

Para un recorrido con rapidez constante se obtiene la siguiente gráfica para la aceleración normal, como se ve en figura 5.

Figura 5: Cambio lineal de la aceleración normal en la curva de transición a una rapidez constante.

Figura 6: Parametrización de la curva de transición.

Para parametrizar dicha curva de transición con la propiedad indicada anteriormente, se fijará como constante a lo largo de la trayectoria el producto de la longitud recorrida con el radio de curvatura en cada punto. A dicha constante se le llamará A²:

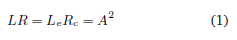
Donde Le es la longitud de la curva y Rc es el radio donde empalma con la circunferencia (Jiménez, 2007). Como R = 1/k se obtiene la curvatura en función de la longitud recorrida:

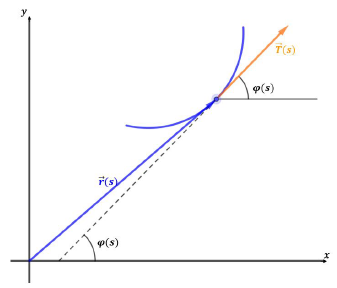
Sea →r (s) = (x(s), y(s)) su representación paramétrica en función del parámetro longitud de arco s y es el ángulo que forma el eje x con el vector tangente unitario→T (s) en el punto r(s) (Blanch, Checa y Marín, 2013).

Por lo tanto, el vector tangente unitario es igual:

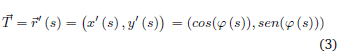
Para parametrizar dicha curva se empieza por evaluar la derivada del vector tangente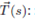

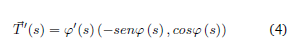
de donde se concluye que la curvatura está dada por:

teniendo en cuenta que κ (s) = s/A2 se obtiene una expresión para el ángulo

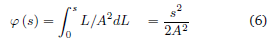
con lo que finalmente se puede parametrizar la curva como

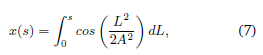
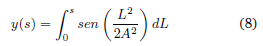
La curva descrita por estas dos ecuaciones coincide con la conocida espiral de Euler, usada clásicamente para solucionar otro tipo de problemas (Blanch, Checa y Marín, 2013; Levien, 2008).

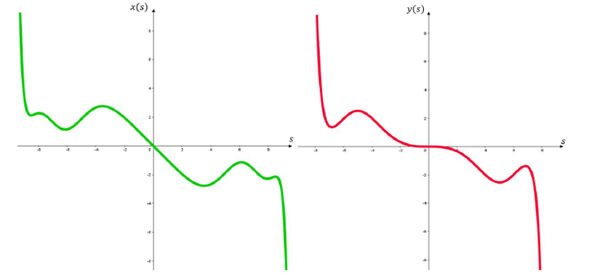
Utilizando series de Taylor para dar una aproximación numérica a la curva descrita por las ecuaciones, donde para x(s) se puede calcular hasta una potencia de grado 20 y para y(s) hasta una potencia de grado 21 y un A=2, el cual solamente cambia la escala de la espiral (Thomas, 2006). Las ecuaciones obtenidas son las siguientes:

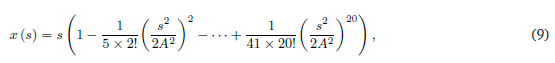
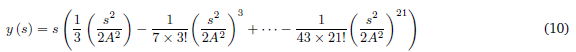
de las cuales se obtiene las gráficas de las figuras 7 y 8.

Figura 7: Gráficas correspondientes a las ecuaciones (9) y (10)

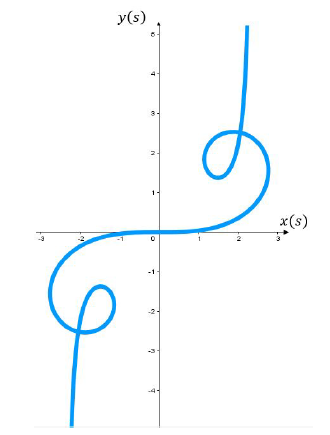
Figura 8:: Aproximación numérica de la Espiral de Euler.

Como las gráficas anteriores son aproximaciones numéricas a las curvas reales podemos ver que en los extremos de cada una tienden a seguir en línea recta debido al error acumulado.

Calculando algunos puntos usando las ecuaciones 7 y 8, en el intervalo de -10 a 10 para s cada 0.1 al graficarlos se puede ver la forma de la espiral y al compararlos con la gráfica anterior se obtiene la gráfica de la figura 9.

Figura 9: Comparación de la curva de la figura 8, curva azul, con los puntos evaluados a través de las ecuaciones 7 y 8, los cuales son los de color morado.

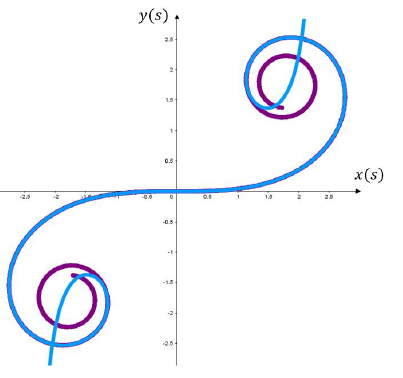
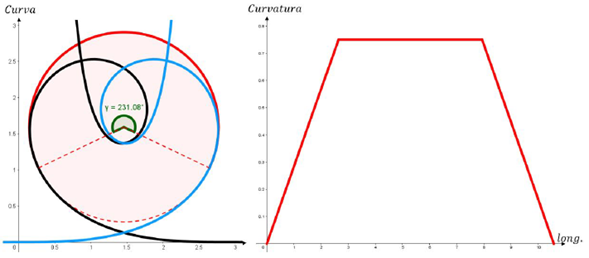
Figura 10: Análisis de la curvatura en el desplazamiento de un posible bucle. Las curvas azul y negra corresponden a una aproximación de la espiral de Euler las cuales son conectadas por el arco de circunferencia rojo de manera suave y se puede ver a la derecha como cambia la curvatura en el recorrido de esta secuencia espiral de Eulercircunferencia-espiral de Euler.

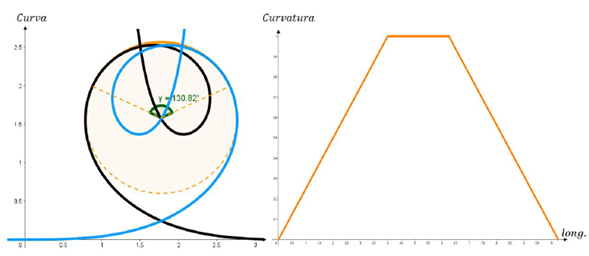
Figura 11: Análisis de la curvatura en el desplazamiento de un posible bucle. Para este caso la longitud del arco de circunferencia es inferior a la anterior gráfica y hay mayor longitud recorrida de espiral de Euler. A la derecha se ve como varía la curvatura en el recorrido de esta curva.

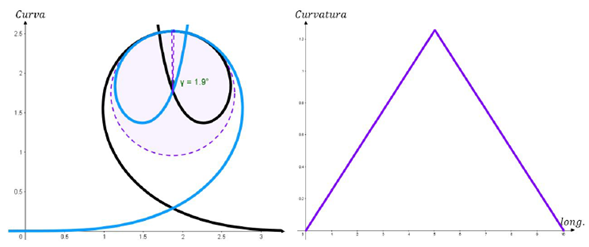
Figura 12: Análisis de la curvatura en el desplazamiento de un posible bucle. Para este caso, la longitud de arco circular es tan reducida que permite conectar casi de manera directa las espirales. A la derecha se ve como varía la curvatura en el recorrido de esta curva.

Como se evidencia en la figura 9, la aproximación numérica es igual hasta cierto punto a la verdadera espiral, pero esa aproximación es lo suficientemente buena para utilizarla como un tramo de la espiral de Euler.

Con esto se encuentra que la curva analizada, descrita por las ecuaciones 7 y 8, es la curva de transición que resuelve el problema de conectar la recta con la circunferencia, como se describe en la figura 4, y permite construir un bucle que modele el de una montaña rusa sin discontinuidades en la curvatura, lo que hace que el recorrido de un vehículo que transita dicha trayectoria sea más seguro.

Para conectar dos curvas de manera suave se deben tener en cuenta los puntos en los que ambas tengan la misma recta tangente; pero, además, donde se tengan la misma curvatura para evitar las discontinuidades de la misma. Las siguientes gráficas son algunos bucles con su respectivo análisis de curvatura versus longitud recorrida, dejando A igual en todos los casos:

Esta caracterización explica la forma de gota invertida para los bucles de la montaña rusa. La trayectoria está formada por una secuencia de una sección de la espiral de Euler, luego una sección de circunferencia para conectar nuevamente con una sección de la espiral de Euler. La figura 13 es una adaptación de los bucles simulados con una imagen de la montaña rusa Doble loop del parque Salitre Mágico en Bogotá.

Figura 13: Montaña rusa Doble loop del parque Salitre Mágico. En esta imagen se evidencia la secuencia espiral de Euler-circunferenciaespiral de Euler que se aproxima a uno de los bucles de esta atracción mecánica. Las curvas azul y negra son dos espirales de Euler y la verde a un arco circunferencia.

En la superposición de la simulación con la fotografía se identifican las partes del bucle que corresponden a la espiral de Euler y las que coinciden con un arco de circunferencia, mostrando que en el diseño de esta atracción mecánica se evitaron los cambios discontinuos en la curvatura de la trayectoria que estarían asociados a cambios no seguros en la aceleración normal del vehículo que recorre la atracción mecánica.

Conclusiones

El análisis de la curvatura en la trayectoria que sigue un vehículo en una atracción mecánica nos lleva a la búsqueda de una sección de curva capaz de unir suavemente trayectorias con diferentes curvaturas. En la espiral de Euler la curvatura cambia linealmente con el desplazamiento, por esto permitió resolver el problema de encontrar una trayectoria de curvatura continua apropiada para modelar los rieles de una atracción mecánica.

En el desarrollo aquí presentado se aborda el problema considerando todas las superficies sobre un mismo plano, lo cual es una aproximación al problema real. En un estudio más minucioso se podrían considerar las trayectorias en el espacio, generando una componente adicional a los vectores tangentes que a su vez harían contribuciones a la curvatura.