Propuesta de enseñanza en Cálculo Vectorial: un acercamiento a la clase invertida

Introducción

La historia del análisis vectorial tiene parte de sus orígenes en los fenómenos físicos. Dicha relación permite inferir que su aprendizaje es fundamental para el futuro ingeniero, ya que con las herramientas que adquiere en este espacio podrá modelar matemáticamente situaciones físicas a través de una representación vectorial.

No obstante, enseñar y aprender sobre cálculo vectorial es un proceso con alto grado de complejidad y abstracción de los objetos matemáticos que allí se estudian; esto implica un pensamiento matemático avanzado que puede suponer un ritmo de aprendizaje diferente para cada estudiante. Por ello, son varias las publicaciones de investigaciones en educación Matemática sobre cómo enseñar cálculo vectorial en el ámbito universitario. Algunas centran su atención en la búsqueda de estrategias didácticas que mejoren y acompañen el proceso de enseñanza y aprendizaje; otras consideran mecanicista y descontextualizada la enseñanza actual de cálculo vectorial, pues aseguran que impide comprender los significados de los objetos matemáticos y su relación directa con otras ciencias, tal como lo describen Costa y Arlego (2011), en su estudio sobre el estado del arte en la enseñanza del cálculo vectorial. Identifican, además, la importancia de acercarse a una enseñanza contextualizada, ligando los conceptos del cálculo con su génesis o adaptándolos a problemas de la Ingeniería o la Física. También, encuentran en el uso de TIC un recurso apropiado a utilizar en los procesos de enseñanza y aprendizaje, pues les permite a los alumnos comprender los conceptos, interpretarlos y vincularlos con otras áreas del conocimiento, alcanzando un aprendizaje significativo.

Como docentes de esta asignatura, en reflexiones sobre nuestra práctica, evidenciamos las dificultades de los estudiantes para tomar un curso de cálculo vectorial debido a la falta de comprensión de objetos matemáticos estudiados en cursos anteriores, el hábito no adquirido de leer matemáticas, la ausencia de motivación intrínseca al abordar el curso, y su pasividad percibida en el desarrollo de la clase donde, usualmente, están a la espera de cada sesión para escribir lo que el profesor explica. A esto podemos añadir el poco o inadecuado uso de herramientas tecnológicas para el desarrollo de las clases; pues con frecuencia los estudiantes hacen uso de software matemáticos únicamente para verificar soluciones o pasos de solución de algún ejercicio algebraico y no como una herramienta que les facilita visualizar y comprender conceptos matemáticos.

Atendiendo a la problemática descrita en la teoría y a partir de nuestra experiencia, identificamos que los estudiantes de Ingeniería, en el curso de cálculo vectorial, no mostraban una mejoría en su rendimiento académico a lo largo del semestre, incluso haciendo uso del material construido durante varios años para apoyar su proceso de aprendizaje.

A partir de una prueba diagnóstica evidenciamos los vacíos conceptuales que los estudiantes tenían de cursos anteriores y su falta de motivación para abordar el curso, viéndolo como un cálculo más, sin importancia para su conocimiento en Ingeniería. Luego de esta reflexión se propuso un desarrollo de clase invertida, o Flipped Classroom, en dos cursos de cálculo vectorial durante el semestre 2018-2.

Elaboramos una propuesta de enseñanza basada en el diseño de herramientas tecnológicas y un libro de texto que apoyan el desarrollo de la clase, teniendo como objetivo evaluar el cambio de un modelo tradicional de enseñanza al modelo de aula invertida desde un punto de vista cuantitativo y cualitativo en el curso de cálculo vectorial. Esto permitió identificar los factores de éxito y fracaso del modelo en el contexto propio de la universidad con 34 estudiantes de Bioingeniería y 27 estudiantes de Ingeniería Ambiental. Se evaluó el aprendizaje en comparación con grupos de semestres anteriores y las percepciones de algunos estudiantes frente a la propuesta.

Marco de referencia

Metodología

La propuesta de aula invertida fue desarrollada en dos cursos: Bioingeniería, con 34 estudiantes, e Ingeniería Ambiental, con 27, durante el segundo semestre de 2018. Se les comunicó a los estudiantes la metodología de clase desde el primer día y la aplicación de la propuesta fue progresiva. A continuación, se describen las herramientas usadas en el desarrollo de la propuesta, que fueron ubicadas por temas en el aula virtual (Moodle) de la universidad.

Prueba diagnóstica: se realizó el primer día de clase de manera presencial, con el fin de evaluar el conocimiento frente a temas relacionados con álgebra lineal y cálculo diferencial e integral. En total se diseñaron y aplicaron 20 preguntas de selección múltiple con única respuesta.

Notas de clase: atendiendo a las necesidades de los estudiantes, y reconociendo los vacíos con los que llegaban al curso de cálculo vectorial, se elaboró en un lenguaje sencillo y detallado un texto guía llamado “Notas de clase”, el cual contiene los procesos algebraicos de los ejemplos desarrollados y los temas enunciados en el Syllabus de los programas de Ingeniería Ambiental y Bioingeniería. Cada capítulo contiene una serie de ejercicios con diferentes niveles de profundidad, y al final un taller de apoyo para preparación del examen, así como un simulacro de este. Cabe resaltar que el uso del texto en el aula de clase comenzó en el primer semestre del año 2018.

Videos: con el apoyo de profesores del Departamento, se realizaron siete videos explicativos de los temas que se consideró requerían más atención por su grado de complejidad, como: superficies cuádricas, funciones vectoriales, límites en varias variables, derivada direccional y gradiente, máximos y mínimos en varias variables, integrales dobles en coordenadas rectangulares y polares e integrales triples en sus diferentes coordenadas.

Cuestionarios en línea: en el aula virtual de la universidad se diseñaron ocho cuestionarios sin límite de intentos, con el fin de que el estudiante se pudiera enfrentar a preguntas tipo examen y evaluara cuánto sabía y cuánto debía reforzar por medio de las clases.

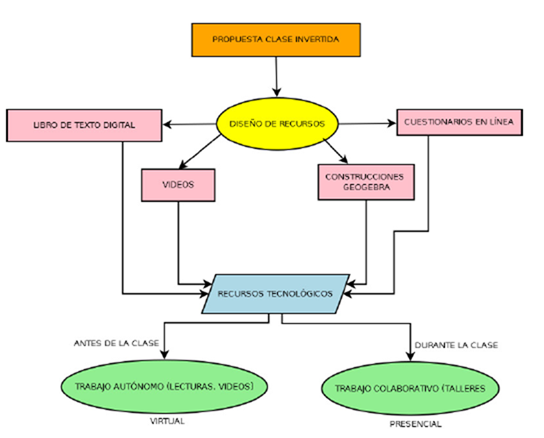
La construcción de las herramientas descritas anteriormente se hizo de manera progresiva durante dos años y fueron empleadas parcialmente durante el primer semestre del año 2018, esto con el fin de identificar aciertos y elementos por mejorar. En la figura 1 se describe el proceso de cómo se usaron para el desarrollo de la propuesta de enseñanza.

Figura 1: Proceso de construcción material de apoyo para el desarrollo de la propuesta de clase invertida

A continuación, se describe cómo fueron los espacios antes y durante las clases presenciales.

Las clases presenciales

Las clases tuvieron lugar en el horario propuesto por la universidad: seis horas a la semana distribuidas en tres sesiones de dos horas aproximadamente. Todas las sesiones y los temas a debatir estaban detallados en Syllabus, así como las actividades a desarrollar. En los encuentros presenciales se reforzaban los conceptos que los estudiantes habían leído en las notas de clase. Sin embargo, en las sesiones de inicio del curso se estableció que menos de la mitad de los estudiantes no habían hecho una lectura previa del tema; por esta razón, en varias ocasiones los alumnos se organizaron en grupos de trabajo para realizarla y luego socializar los conceptos, con el objetivo de reforzar y garantizar la comprensión del tema. Con el tiempo descubrieron la importancia de hacer una lectura previa y, como consecuencia, adquirieron el hábito de leer en matemáticas y asistir a la clase con preguntas relacionadas con los conceptos o procesos de los ejemplos explicados en cualquiera de las herramientas brindadas.

En la tabla 1, se describen algunas actividades efectuadas en las sesiones de clase presenciales. Las primeras que se presentan fueron guiadas completamente por el docente, ya que no había un alto de manejo del software Geogebra.

Tabla 1: Actividades desarrolladas en clase, con el apoyo de Geogebra

Se presentan actividades que requerían un conocimiento básico en el uso de Geogebra por parte de los estudiantes (conocimiento que ya habían adquirido con las actividades mencionadas anteriormente). (Tabla 2).

Tabla 2: Actividades desarrolladas en clase, con el apoyo de Geogebra.

Durante el semestre se realizaron tres exámenes escritos que correspondieron al 50 % de la nota del curso; el 50 % restante fueron pruebas y talleres que debían realizar semanalmente en el espacio de clase. Se dispuso de horarios de tutorías para atender a aquellos estudiantes que requirieran un apoyo en el proceso. Aunque la asistencia no era alta, un 40 % de los estudiantes del curso hicieron uso de este recurso al menos una vez.

Los estudiantes se autoevaluaron en dos momentos; el primero, en el primer corte del semestre (en total son tres), y el otro, al culminar el tercero. Con estas se pretendió concientizar al estudiante sobre sus fortalezas adquiridas en el proceso de aprendizaje y también sobre aquellos elementos que debía mejorar durante el desarrollo del semestre.

Resultados

Para dar cumplimiento al objetivo de evaluar el cambio de un modelo tradicional de enseñanza a un modelo de aula invertida, se analizaron las calificaciones de los estudiantes en cada uno de los tres cortes del semestre.

A continuación, se muestra un comparativo de aprobación de la asignatura durante los semestres 2017-2 al 2018-2.

Como se observa en la figura 2, durante el segundo semestre de 2017, el 68 % de los estudiantes aprobaron la asignatura con una metodología de clase tradicional. Durante el primer semestre de 2018 aprobó el 83 %, teniendo una variación en la metodología cuando se hizo uso del texto guía, que los estudiantes leyeron y con el cual prepararon los exámenes. Cabe destacar que esta propuesta mostró un cambio favorable en el porcentaje de aprobación de la asignatura. En el semestre 2018-2 aprobó el 96 % de los estudiantes con la propuesta de aula invertida, lo que evidencia una disminución significativa en la pérdida de la asignatura en comparación con la metodología de clase tradicional.

Figura 2: Porcentaje de aprobación de la asignatura cálculo vectorial durante los semestres 2017-2 al 2018-2.

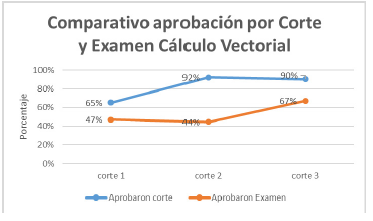
En cuanto al registro de calificaciones durante el semestre (2018-2), se identifica una disminución en la pérdida de los exámenes, lo que implica una adaptación a la metodología propuesta en la clase y un compromiso del estudiante por comprender los temas

Figura 3: Porcentaje de aprobación de cada corte y examen durante el semestre 2018-2 en los cursos de cálculo vectorial en los que se aplicó la propuesta.

El examen que se realiza en el corte tres es acumulativo, es decir, evalúa todos los contenidos estudiados durante el curso. La nota media fue de 3,38, con una desviación de 0,75; la nota mínima fue 2,0 y la nota máxima fue de 4,4. Lo que permite inferir que, aunque no todos aprobaron el examen final, los resultados no están a más de 2 desviaciones estándar.

Por otra parte, se entrevistaron a algunos estudiantes sobre su percepción frente a la propuesta de clase invertida y la utilidad de las herramientas usadas para el desarrollo de esta. En sus respuestas afirmaron que fueron de gran ayuda, destacando los videos y las notas de clase, ya que les permitió avanzar a su propio ritmo de aprendizaje.

A continuación, se presenta una transcripción de dos respuestas dadas por un estudiante de quinto semestre de Ingeniería Electrónica.

• ¿Considera que las notas de clase diseñadas por las profesoras fueron una buena herramienta para el estudio y desarrollo del curso?

Siempre que los estudiantes tengan la motivación sí es un buena herramienta, ya que hay unas personas que se le dificultan unas cosas más que a otras, entonces considero que esas personas lo que necesitan son herramientas y las notas de clase son una buena herramienta para una persona que no está acostumbrada a leer un texto de matemáticas […] Entonces, eso le ayuda a la persona a agarrarle el gusto a las definiciones matemáticas que es un poco lo más complicado […].

• ¿Considera que se debe mejorar la propuesta en algún aspecto? ¿Qué herramientas se podrían seguir diseñando como apoyo para el proceso de aprendizaje?

En general, son muy buenas herramientas. Sin embargo, en las notas de clase considero que hay dos temas que son algo complejos y estaban descritos en un espacio muy pequeño: multiplicadores de Lagrange y el tema de coordenadas esféricas y coordenadas cilíndricas […]. Y… de acuerdo a cosas que se podrían seguir haciendo, es seguir haciendo los videos que se complementan con las notas de clase, porque son muy, muy, muy ─mmm ─ , ayudan muchísimo; tanto antes para preparar la clase, como para después de la clase, para sentar el conocimiento.

Conclusiones

La aplicación de la propuesta en los dos cursos de cálculo vectorial requirió un trabajo estructurado por parte de las docentes, ya que el diseño y elaboración de las herramientas de apoyo a la clase, así como la preparación del cronograma por sesión, exigió tiempo y continuas evaluaciones, con el fin de entregarle a los estudiantes un material que cumpliera con el objetivo de soporte para su proceso de aprendizaje, a través de un lenguaje sencillo, pero sin perder la profundidad matemática que los temas requieren.

El curso tuvo ganancias agregadas como el alcance de un estudio autónomo, la profundización del conocimiento y la organización del tiempo por parte del estudiante, adquirida a partir de la necesidad de preparar las sesiones presenciales con antelación y, por supuesto, la notoria disminución en la pérdida de la asignatura.

Se evidencia a través de las entrevistas semiestructuradas el impacto positivo de los recursos diseñados para que el estudiante pudiera aprender a su ritmo. En cuanto a las clases presenciales, otorgaron un alto valor al trabajo en equipo, así como al papel del docente como apoyo en la solución de dudas y profundización del tema.

Fueron más provechosos los espacios presenciales de lo que usualmente se percibe en las clases con una metodología tradicional.

Las herramientas utilizadas para aplicar el modelo de aula invertida permitieron en algunas ocasiones que los estudiantes se adelantaran en los temas debido a salidas de campo o ausencias de clase, lo cual es difícil en una clase de enseñanza tradicional.

El éxito de la aplicación del modelo de aula invertida requiere de tres elementos fundamentales: estudiantes dispuestos al cambio, docentes capacitados en el uso de herramientas tecnológicas y aptos para diseñar la propuesta igualmente, así como el apoyo institucional que facilite tiempos para la elaboración de esta y un espacio virtual para organizarlas.

La realización de una herramienta estandarizada para evaluar el modelo de aula invertida podría ser otra fase del proyecto de investigación y tener un impacto positivo mostrando el alcance que pueden tener los estudiantes en cursos posteriores, al haber tenido la experiencia de participación en el curso en contraste con aquellos que no la han tenido.

Los resultados obtenidos a partir de la investigación sugieren que la implementación del modelo de aula invertida obedece a un cambio importante que va más allá de cómo se distribuye el tiempo dentro y fuera de la clase. Por ello, este tipo de investigaciones podría proponerse como un proyecto institucional, que permita tener registro de lo sucedido e implementando mejoras de forma continua.