Diseño y validación de rúbrica para la evaluación de modelación matemática en alumnos de secundaria

Introducción

Hace más de cuatro décadas la modelación matemática comenzó a tomar relevancia. Hoy en día, hay un interés por promoverla alrededor del mundo (Borromeo, 2013). Huang (2012) afirma que esta importancia se fue robusteciendo debido a que la manera tradicional de la enseñanza de las matemáticas ha llevado a que los alumnos la consideren como una materia aburrida, abstracta y apartada del mundo real. Además, establece que, debido a ase concepción negativa, investigadores sobre la educación sugieren que en esta disciplina se incorporen problemas reales para relacionar el mundo de las matemáticas y el real con la modelación.

El estilo convencional con el que se enseñan las matemáticas en la educación superior también parece tener efectos adversos. De acuerdo con Nourallah y Farzad (2012), a los graduados de las carreras de ingeniería se les dificulta ejercer una profesión práctica y aplicada cuando el estilo de enseñanza con el que aprendieron matemáticas fue tradicional. Ejemplos de esta afirmación se encuentran en la mayoría de los cursos de ecuaciones diferenciales en las carreras de ingeniería, pues estos ofrecen a los estudiantes procedimientos analíticos que permiten responder a problemas matemáticos puros. Los conocimientos adquiridos no son suficientes para lograr una formación con la cual los futuros profesionales puedan resolver problemas del mundo real y específicos de la profesión que estudiaron (Rodríguez y Quiroz, 2016).

Según estas investigaciones, el papel que tienen las matemáticas en el aula y en el campo laboral parece estar disociado (Sepúlveda et al., 2020; Rendón-Mesa et al., 2016; Rosa y Orey, 2010). Las características que se observan en los problemas cotidianos y los problemas laborales son muy diferentes a los problemas que abordan las matemáticas escolares y, por lo mismo, no son adecuadas para facilitar la solución de problemas en el entorno laboral (Pertamawati y Retnowati, 2019). Según Wake (2014), el problema de los graduados en su ambiente laboral radica en que hay una diferencia esencial entre dichos papeles: en el ambiente escolar las matemáticas son el objeto de estudio y en el trabajo del profesional son una herramienta que permite al profesional realizar su actividad laboral.

En los últimos años la modelación matemática ha tomado un papel importante puesto que investigadores en el mundo se preguntan qué tan preparados están los estudiantes para resolver problemas cotidianos más allá de la escuela (Ciltas e Isik, 2013). Incluir la modelación en el aula podría formar personas altamente alfabetizadas en la enseñanza de las matemáticas a partir de relacionar esta con el mundo real (Maabb et al., 2019; Huincahue et al., 2018; Erbas et al., 2014). La modelación en la educación básica es un medio para que los alumnos mejoren la comprensión de conceptos matemáticos y puedan descubrir la función de las matemáticas, la cual es servir como herramienta para interpretar la realidad (Jung et al., 2019; Shabhari y Peled, 2017). Además, modelar situaciones del mundo real involucra a los estudiantes con procesos sociales, matemáticos y comunicativos, lo que les da una amplia gama de posibilidades de aprendizaje y les motiva a aprender matemáticas (Daher y Shahbari, 2015).

Estudios recientes demuestran que los beneficios de la modelación matemática se dan a lo largo de los diferentes niveles escolares. Tal es el caso de la investigación realizada por Shabhari y Peled (2017), quienes revisaron una forma en que el modelado se puede integrar en el programa curricular de la escuela primaria a través de actividades enfocadas en el concepto de fracción. El objetivo principal del estudio fue observar las oportunidades de aprendizaje creadas por las actividades de modelado para estudiantes de sexto grado. Los hallazgos muestran que los alumnos utilizaron su conocimiento conceptual y de procedimiento sobre las fracciones en la construcción de modelos matemáticos para las situaciones dadas. Algunos estudiantes también fueron capaces de generalizar el modelo de fracción y transferirlo a una nueva situación problemática. Las actividades revelaron además las dificultades en el conocimiento de las fracciones, algunas de las cuales fueron superadas en el proceso de organización del problema.

Schukajlow et al. (2015) estudiaron a alumnos alemanes de noveno grado de tres diferentes escuelas trabajando en cada una con un grupo de control y uno experimental. Esto con la intención de probar los efectos de un instrumento estratégico llamado plan de solución, el cual consiste en guiar paso a paso la solución de actividades de modelación matemática. En el grupo experimental en que se aplicó el instrumento se encontró un aumento significativo en las estrategias de organización, elaboración, ensayo y planificación. También se observó que los estudiantes asumieron una actitud de autonomía para hacer el diagnóstico de las dificultades de resolución de problemas.

Se han encontrado estudios con participantes de nivel universitario en los que se busca determinar el impacto del modelado matemático en un grupo experimental en contraste con un grupo de control en el que las clases impartidas fueron de manera convencional (Cozcher, 2017; Doerr et al., 2014; Nourallah y Farzad, 2012). Los investigadores evidenciaron que el efecto principal para el enfoque instruccional fue estadísticamente significativo y concluyeron que la modelación representa una ayuda valiosa para el aprendizaje del estudiante. Los alumnos se benefician de iniciar con situaciones o problemas contextuales relevantes y avanzar hacia resultados generalizados e ideas matemáticas formales. También hay investigaciones sobre los bloqueos y obstáculos que los alumnos pueden experimentar en el modelado (Rodríguez, 2019; Plaza, 2016; Huang, 2012).

Incluso cuando la modelación matemática es considerada como esencial en los programas escolares, esta no se aplica a profundidad en muchos países. Hay muy poca modelación en el aula cotidiana y en su mayoría es tratada como matemáticas sin contexto o como problemas razonados, esto significa que hay una brecha entre la teoría educativa y la práctica en el aula (Kurniadi et al., 2020; Arseven, 2015).

La razón por la que existe una diferencia entre los programas y las prácticas educativas es que los docentes tienen dificultades para trabajar con la modelación matemática (Tropper et al., 2015). Los investigadores aseguran que si los profesores aprenden la teoría de la modelación matemática en la universidad y trabajan en el diseño de modelos no deberán tener problemas al iniciar su práctica docente. Es decir, los docentes deben capacitarse para dominar el tema. Estas conclusiones coinciden con investigaciones en las cuales se estudia a futuros profesores de matemáticas que participan en un curso de modelación matemática a la vez que trabajan con alumnos en actividades de modelado.

Yenmez et al. (2017) estudiaron cómo evoluciona el conocimiento de los maestros con respecto a la creación de criterios de valoración para evaluar en los alumnos el modelado matemático mediante un programa basado en el ciclo de lecciones desde la perspectiva del modelaje. El proceso que llevaron a cabo las docentes se basó en sesiones en donde mostraron sus modelos de enseñanza y aprendizaje con la planeación de clases para sus estudiantes probándolas a través de su implementación y observación en el aula. Los investigadores encontraron que al inicio del estudio las profesoras pensaban que para cada actividad de modelación matemática debería haber diferentes criterios de evaluación. Sin embargo, durante el proceso se dieron cuenta de que los alumnos pasaban por procesos de modelación casi iguales independientemente de los temas con los que trabajaban. Además, los investigadores concluyeron que los criterios de evaluación claros son importantes en el proceso de la modelación matemática debido a que el aprendizaje es más eficaz cuando los propios practicantes tienen una comprensión de la capacidad para medir sus logros.

El estudio realizado por Zeytun et al. (2017) tuvo como participantes a 19 futuros profesores de matemáticas que ingresaron a un curso de modelación durante un semestre. Los resultados revelaron que los procesos de modelado de los futuros profesores constan de cinco etapas: comprender la tarea, diseñar un plan de solución, ejecutar el plan, interpretar y verificar el modelo y presentar el modelo. Trabajando en las tareas de modelado con un enfoque orientado a resultados, los futuros maestros pasaron por un proceso de modelado de ciclo único y no buscaron un mejor modelo al reflexionar y mejorar sus modelos. Ante dificultades en un punto del proceso de solución, en ocasiones ignoraron las variables más importantes o hicieron suposiciones que respaldaron sus respuestas intuitivas para poder llegar a una solución; en otros casos, consideraron válidas sus soluciones sin necesidad de verificación adicional. Los investigadores concluyeron que los programas de formación de profesores de matemáticas y programas de matemáticas deben contar con cursos de modelización matemática para mejorar las competencias en este aspecto. El ejercicio de modelado matemático también puede permitir a los alumnos tener una mejor comprensión de los conceptos matemáticos.

Según Jacobs y Durandt (2017), los profesores de matemáticas de preservicio deben estar involucrados en los desafíos que plantea el modelado matemático durante su formación para mejorar su conocimiento pedagógico y de contenido, a la vez que fortalecen gradualmente sus disposiciones y, en especial, su confianza. Así lo reveló el estudio que llevaron a cabo a través de una encuesta aplicada a 50 maestros de preservicio de matemáticas de tercer año sobre sus actitudes hacia la modelización después de la implementación de un curso de modelado.

Considerando la importancia de la aplicación de la modelación matemática en la enseñanza de las matemáticas, Shahbari y Tabach (2016) investigaron los efectos de cómo los profesores afrontan las actividades de modelado en el desarrollo de sus habilidades para identificar ciclos de modelado. La investigación se realizó con 34 profesores en ejercicio que cursan estudios de maestría. Los datos fueron recolectados de dos informes y una reflexión proporcionada por los participantes sobre una actividad de modelado. El primer informe se presentó antes de que los propios participantes se ocuparan de las actividades de modelado; mientras que el segundo informe y la reflexión se presentaron después de su participación en las actividades de modelado. Los hallazgos muestran que antes de participar en la actividad la mayoría de los profesores describieron la participación de los estudiantes en la actividad de modelado como un proceso lineal. Los maestros participantes notaron el modelo matemático final y los resultados matemáticos obtenidos de su aplicación, pero la mayoría de ellos ignoraron los resultados realistas, el proceso de validación y la naturaleza cíclica del avance del modelo matemático. Sin embargo, después de que los profesores participaron en actividades de modelado como aprendices sus informes indicaron que la mayoría pudo reconocer todas las fases de modelado y distinguir los procesos cíclicos del progreso de los modelos matemáticos. Además, según los análisis de las reflexiones, los profesores participantes son conscientes de los cambios en sus descripciones.

El uso de la modelación matemática es importante para los estudiantes en la solución de problemas. Por lo que el conocimiento y experiencia de la modelación de los profesores y futuros profesores es indispensable (Hapizah y Mulyono, 2020). La práctica efectiva de la modelación en el aula es desafiante para los docentes, por lo que la calidad de las experiencias de aprendizaje de los alumnos dependerá de la calidad de la formación que los profesores puedan ofrecer. Según Sahin et al. (2019), para que los docentes puedan dar una enseñanza de calidad a través de la modelación deben contar con las competencias de: conocer el propósito e importancia del modelado matemático y las propiedades del modelado matemático, diferenciarlo de los problemas tradicionales, diseñar y aplicar actividades de modelado matemático y realizar evaluaciones.

Considerando que la evaluación del uso de la modelación matemática es pertinente para la enseñanza de las matemáticas, este estudio tiene como objetivo proponer una rúbrica que pueda evaluar el nivel de modelación matemática de alumnos del último grado de secundaria (cuando trabajan en la solución de problemas de manera individual). La rúbrica puede ser una herramienta muy útil para los profesores de matemáticas de educación secundaria, pues su aplicación permite identificar la habilidad de los estudiantes en modelación matemática y diagnosticar las fases de esta.

Modelación matemática

De acuerdo con Brito-Vanilla et al. (2011), un modelo es una representación de la realidad. Por ello se puede decir que la modelación matemática intenta caracterizar una parte de la realidad a través de las matemáticas. También, afirman que los modelos matemáticos representan los elementos de mayor importancia del problema. Estos relacionan la teoría matemática y el mundo cotidiano, por lo que pueden tomarse como una valiosa opción didáctica con pensamiento crítico y sistémico, lo cual es prioridad en la formación de ingenieros (Plaza, 2017).

La modelación no es un tema nuevo, pues se ha investigado por más de 40 años. Y a pesar de que el término modelación matemática es utilizado en diferentes partes del mundo, existe controversia entre expertos en el tema. Estas surgen de diferentes perspectivas teóricas desde las cuales se aborda la modelación matemática (Borromeo, 2013). Una clasificación de estas perspectivas teóricas es la de Kaiser y Srirman que clasifican a la modelación en seis categorías (Borromeo, 2013). En la tabla 1, se puede observar esta clasificación de las perspectivas de la modelación matemática de Kaiser y Srirman (2006) que se utiliza actualmente, las relaciones con perspectivas matemáticas anteriores y sus antecedentes. Cabe mencionar que la perspectiva de modelación cognitiva la consideran como una metaperspectiva y fue la última que se agregó a la clasificación.

Tabla 1: Clasificación de las perspectivas de la modelación matemática

Fuente: Kaiser y Sriraman (2006, p. 304).

Una aplicación matemática se realiza siempre que hay un propósito para aplicar las matemáticas para afrontar algún aspecto del mundo extramatemático, es decir, el mundo real (Niss et al., 2007). En ocasiones cuando se habla de modelo y modelación se cree que significan lo mismo. Sin embargo, el modelo es el resultado de la modelización, la cual representa un proceso (Dundar et al., 2012) y existe un consenso de que el modelado es un proceso no lineal, un ciclo de modelado matemático es una forma de describirlo (Czocher, 2017).

Blum y Borromeo (2009) utilizan en sus estudios un ciclo de modelación de siete pasos: construir, simplificar y estructurar, matematizar (calculando y resolviendo ecuaciones), trabajar matemáticamente, interpretar, validar y haciendo una presentación. En este ciclo el alumno debe comprender el problema que se presenta y tomar lo relevante para solucionarlo a partir de la simplificación, estructuración y precisión. Al traducir el problema a un modelo matemático se deberá trabajar con cálculos o resolución de ecuaciones para tener un resultado que más adelante se pueda interpretar en el mundo real. Por último, se deberá validar este resultado para poder exponerlo. Este ciclo de modelación se puede observar en la figura 1.

Figura 1: Ciclo de modelación.

Fuente: Blum y Bomorreo (2009), p. 49.

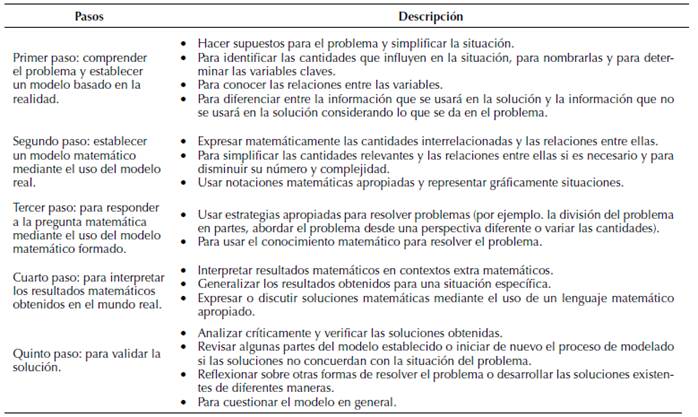
Entre los objetivos de la enseñanza de las matemáticas se encuentra el que los alumnos desarrollen el pensamiento matemático, de tal manera que puedan interpretar situaciones y crear soluciones para el problema que se les presenta. El modelo matemático es una ecuación, una fórmula, una expresión matemática que representa las características más significativas de una situación problemática. Por lo tanto, la modelación matemática será el proceso en el cual se desarrolla el modelo matemático (Dundar et al., 2012). Blum y Kaiser (2016, p. 9) presentan las habilidades que están asociadas a la modelación matemática en cada uno de sus pasos; estos se muestran en la tabla 2.

Tabla 2: Habilidades implicadas en cada paso de la modelación matemática.

Fuente: elaboración propia.

Según Houston (2006), p. 247, la modelación matemática es un proceso que por lo general se da en siete fases, que son:

1. Especificar el problema verdadero.

2. Crear el modelo matemático.

3. Especificar el problema matemático.

4. Resolver los problemas de matemáticas.

5. Interpretar las soluciones matemáticas.

6. Validar el modelo.

7. Revisar y reportar.

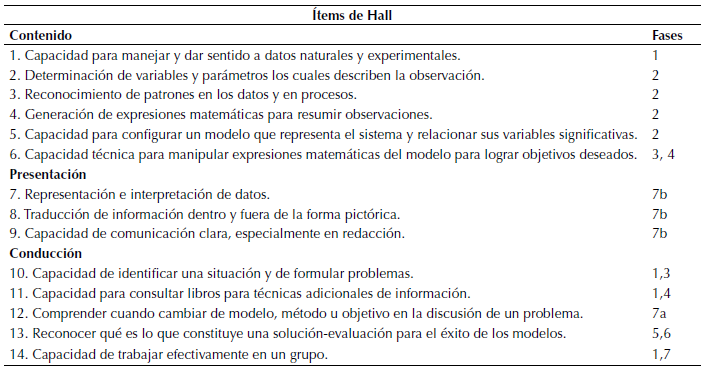
El interés por evaluar la modelación matemática se inició en la década de 1980. Hall establece tres grupos de habilidades para evaluar la modelación (citado en Houston, 2006). El primero es el grupo de contenido, el cual recoge los aspectos técnicos del modelado; el segundo, es el de presentación, que tiene que ver con la escritura del proyecto; y el tercer grupo, conducción, se relaciona con la originalidad y la gestión. La tabla 3 muestra los grupos de evaluación y la fase que le corresponde.

Tabla 3: Ítems y mapeo de las fases de Hall

Fuente: Houston (2006), p. 249.

La Organización para la Cooperación y el Desarrollo Económico (OCDE) creó en 1997 el Programa para la Evaluación Internacional de los Alumnos (Pisa por sus siglas en inglés) con la intención de contar con pruebas comparables en el mundo en relación con el desempeño de los alumnos. El objetivo de la OCDE fue ofrecer a los países miembros información sobre el resultado de los sistemas educativos mediante la medición del logro de los alumnos dentro de un marco internacional, con la intención de que cada país pueda tomar decisiones sobre sus objetivos educativos, considerando las habilidades que son de gran importancia para la vida adulta (OCDE, 2013).

Para el programa Pisa el ciclo de la modelación matemática es el núcleo para comprender cómo los estudiantes solucionan problemas de manera activa. En la prueba que se aplica a los estudiantes, por lo general, llevan a cabo algunas fases del ciclo de modelación, dependiendo de la información de los ítems. Así como el ciclo es considerado no lineal, los participantes van de un proceso a otros para revisar y validar sus conclusiones en la resolución de problemas. En la figura 2 se puede observar el ciclo de modelación matemática en el cual se centra Pisa. En el presente trabajo la modelación matemática se entiende como el proceso cíclico en el cual,un problema del mundo real es simplificado para resolverlo, interpretarlo y validarlo.

Figura 2: Modelo de la alfabetización matemática en la práctica.

Fuente: OCDE (2013)

Metodología

Para medir el nivel de modelación matemática en alumnos de secundaria, se diseñó una rúbrica basada en las fases del ciclo de la modelación. De acuerdo con la revisión de literatura, el proceso de la modelación matemática es cíclico. Sin embargo, en todas las tareas o actividades, aunque sean diferentes, se considera que se puede observar las mismas fases. Teniendo en cuenta lo anterior, la rúbrica puede utilizarse para cualquier problema que se plantee a los alumnos de manera individual. Por lo general, se recomienda trabajar la estrategia de modelación matemática en colaboración, no obstante, hay momentos en el aula en los que el alumno debe hacerlo por su cuenta. Este instrumento es, precisamente, para cuando se trabaja de manera individual.

Con el objetivo de validar la rúbrica diseñada se construyó una prueba con problemas que se obtuvieron de ítems liberados de Pisa. Sin embargo, se agregaron preguntas en cada problema para poder tener información de las fases de la modelación matemática. En este apartado se describen los participantes del estudio, así como el diseño y aplicación de la rúbrica y de la prueba.

Participantes

Participaron 61 alumnos de tercero de secundaria repartidos en dos grupos de un colegio del sur de la ciudad de Monterrey, Nuevo León, México. De ellos, 18 alumnos se eligieron aleatoriamente para aplicarles la prueba piloto. La prueba a gran escala se aplicó a los 43 alumnos restantes. De estos alumnos 22 son mujeres y 21 son varones. Con respecto a las edades, cinco alumnos (12 %) tienen 13 años, 33 alumnos (76 %) tienen 14 y cinco alumnos (12 %) tienen 15 años.

Diseño de instrumento

Gatica-Lara y Uribarren-Berrueta establecen que las rúbricas “son guías precisas que valoran los aprendizajes y productos realizados. Son tablas que desglosan los niveles de desempeño de los estudiantes en un aspecto determinado, con criterios específicos sobre rendimiento” (2013, p. 62). El diseño de la rúbrica en este estudio se basa en las fases propuestas por los trabajos especializados en modelación matemática en la revisión de literatura; específicamente en Blum y Borromeo (2009), Blum y Kaiser (1997), Hall (2006) y OCDE (2013). En estas fases los indicadores se diseñaron de acuerdo con aquellas actividades observables en la prueba que se aplicó a los alumnos considerando que el trabajo es individual. A partir de estos supuestos se establecieron cuatro fases o dimensiones de la modelación matemática: formulación, resolución, interpretación y validación.

Con respecto a las fases de modelación matemática, la fase de resolución cuenta con tres indicadores y las tres fases restantes tienen dos indicadores cada una. A su vez los indicadores tienen cuatro niveles para su medición donde 1 es el valor mínimo y 4 es el valor máximo. La rúbrica con indicadores y niveles de medición para evaluar los problemas para cada fase, se muestran en la tabla 4.

Tabla 4: Rúbrica de las fases con indicadores y niveles de medición

Fuente: elaboración propia.

La rúbrica se utilizó para evaluar cuatro problemas de una prueba creada a partir de ítems diseñados por Pisa y que fueron liberados para el público en general. Se eligió este tipo de problemas ya que en estas pruebas que se aplica a los estudiantes, por lo general, se realizan algunas fases del ciclo de modelación, dependiendo de la información de los ítems. Además, se agregaron preguntas para observar qué podían hacer los estudiantes en las diferentes fases y así evaluarlos con la rúbrica.

La figura 3 muestra un ejemplo de un problema contenido en la prueba y uno de sus incisos. En este problema se puede observar la indicación: “Describe el problema que se te ha pedido resolver demostrando tu comprensión de él”; su información permite evaluar la fase de formulación de la rúbrica que se diseñó con el primer indicador. La prueba se conforma de 24 incisos en total que permitieron evaluar cada una de las fases o dimensiones de la modelación matemática. A cada fase le corresponden seis incisos.

Figura 3: Ejemplo de un problema de la prueba con ítems de Pisa

Fuente: elaboración propia

Validación y confiabilidad de la rúbrica

La validación de la rúbrica se hizo en dos etapas. La primera consistió en la revisión de la redacción y niveles de intensidad por dos expertos. La segunda etapa se realizó mediante un juicio por tres expertos. Cada uno de ellos, por separado, evaluó cada inciso de la prueba con la rúbrica diseñada para ello. Se calculó el coeficiente de Kappa para medir la concordancia entre los expertos.

Con respecto a la prueba, se realizó una prueba piloto con 18 alumnos de tercero de secundaria, la cual duró alrededor de 50 minutos. Una vez que se aplicó a los alumnos, se hicieron cambios para mejorar la calidad de la información que se recabó del resto de los 43 alumnos. Se tomó la decisión de omitir uno de los problemas debido a que era un poco confuso para los alumnos. Por otro lado, la omisión del problema pudo disminuir el tiempo de aplicación de la prueba, esto con la intención de que los alumnos no se cansaran y disminuyera el interés por contestar la prueba. Además, se mejoró la redacción de algunos incisos de acuerdo con las dudas que los alumnos expresaron durante la prueba piloto. En relación con la confiabilidad de la rúbrica, se calculó el coeficiente de Chronbach de cada uno de los datos de los tres expertos que evaluaron la prueba y se eligieron los datos con el valor más alto. Los resultados se presentan en el siguiente apartado.

Resultados

Con los datos obtenidos de la aplicación de la prueba a los 43 alumnos de tercero de secundaria se calculó la media, la desviación estándar y el sesgo de cada reactivo y de la puntuación total. En la tabla 5 se muestran los datos agrupados por cada una de las cuatro fases de la modelación matemática con las que cuenta la rúbrica.

Tabla 5: Medidas de tendencia central

Fuente: elaboración propia.

En relación con los datos obtenidos de las medidas de tendencia central, se puede observar que, en general, los alumnos se encuentran en un nivel elemental. No obstante, la fase de formulación es aquella que cuenta con la media más alta de las cuatro fases. Además, los valores de los sesgos son negativos, a excepción del reactivo 10 (que es cero); por lo tanto, se puede afirmar que es la fase de mayor fortaleza de los alumnos. En el caso de la fase de resolución los reactivos con las medias más bajas son los 5 y 20, estos corresponden a realizar cálculos y resolver el modelo matemático. Esto permite concluir que hay un área de oportunidad en los conocimientos de la disciplina.

Con respecto a la validación del instrumento, se calculó el coeficiente de Kappa para cada reactivo. Este coeficiente refleja la fuerza de la concordancia entre dos o más observadores, puede tomar valores entre -1 y +1, cuanto más cercano a +1 mayor es el grado de concordancia inter-observador (Cerda y Villarroel, 2008). Quero (2010) afirma que valores mayores de 0 indican que hay concordancia leve (0,01-0,20), aceptable (0,21-0,40), moderada (0,41-0,60), considerable (0,61-0,80) o casi perfecta (0,81-1,00). Los resultados de cada reactivo que van de 0,511 a 0,883 reflejan una concordancia moderada para algunos de los reactivos y considerable para otros del instrumento; por lo que se puede afirmar que hay una concordancia buena del instrumento. La tabla 6 muestra los valores para cada reactivo de las fases.

Tabla 6: Coeficiente de Kappa de los reactivos de las fases

Fuente: elaboración propia.

Para cada grupo de datos de los evaluadores se calculó el coeficiente de Cronbach para medir la fiabilidad de la prueba. El coeficiente Cronbach se determinar al calcular la correlación de cada reactivo o ítem con cada uno de los otros, resultando una gran cantidad de coeficientes de correlación. El valor de α es el promedio de todos los coeficientes de correlación, su valor oscila entre 0 y 1, cuanto más se acerque el coeficiente a 0 mayor error habrá en la medición (Quero, 2010). Los resultados son: para los datos del evaluador 1, el coeficiente fue de 0.86; para los datos de los evaluadores 2 y 3 el coeficiente fue de 0,88. Los valores obtenidos permiten considerar que el instrumento de la rúbrica es confiable.

Conclusiones

La modelación matemática, según la revisión de literatura, es una estrategia que se ha enfatizado como un enfoque educativo en todos los niveles escolares, desde nivel básico hasta universitario (Kurniadi et al., 2020). Actualmente, el papel de la modelación matemática en el aprendizaje de las matemáticas tiene gran importancia ya que ayuda a los estudiantes a comprender el mundo real, fomenta la motivación de los alumnos a desarrollar un pensamiento más competente y los lleva a descubrir estrategias para resolver problemas, entre otras cosas (Hapizah y Mulyono, 2020).

La modelación es un proceso iterativo en el cual, a través de modelos matemáticos se resuelven problemas de la vida cotidiana. Es una práctica que se espera que todos los estudiantes desarrollen y es el docente quien tiene un papel primordial y desafiante para lograr el desarrollo de esta competencia en sus alumnos (Jung et al., 2019).

De acuerdo con la revisión de literatura, la modelación implica un trabajo de evaluación por parte del maestro que requiere que conozca y haya experimentado la modelación para que esta evaluación sea de calidad (Sahin et al., 2019).

Además, requiere de mayor trabajo por parte del docente ya que es necesario el diseño de actividades para que los alumnos experimenten con la modelación matemática. En ocasiones puede ser difícil lograr el diseño de actividades que se centren en situaciones cotidianas a las cuales pueden enfrentarse sus alumnos (Yemenz et al., 2018). La rúbrica presentada puede apoyar al profesor a reconocer en qué nivel se encuentra de manera individual sus estudiantes y encontrar áreas de oportunidad del grupo al analizar los puntajes medios de cada fase. De tal manera que esta información pueda ayudar a encaminar los esfuerzos por reforzar estas debilidades de manera más oportuna y específica.

Por último, es importante considerar que cuando se trabaja en colaboración los indicadores de la rúbrica pueden aumentar, por lo que se deja la invitación para trabajar en el diseño de rúbricas para actividades de modelación para grupos de estudiantes. El diseño de estas actividades es necesario para el desarrollo de habilidades de la modelación matemática; por ello, se sugiere diseñar y programar las actividades antes de iniciar el ciclo escolar. En la programación se pueden planear actividades interdisciplinarias de tal manera que otras asignaturas puedan participar en el diseño de proyectos transversales.