DOI:
https://doi.org/10.14483/23448350.20549Publicado:
05/15/2023Número:
Vol. 47 Núm. 2 (2023): Mayo-Agosto 2023Sección:
ArtículosModelo matemático para la dinámica de la tuberculosis considerando latentes de bajo riesgo
Mathematical Model for the Dynamics of Tuberculosis Considering Low-Risk Latents
Palabras clave:
mathematical modeling, optimal control, qualitative analysisy, numerical simulations, control methodology (en).Palabras clave:
Modelamiento matemático, control óptimo, análisis cualitativo, simulaciones numéricas, metodología de control (es).Descargas
Referencias
Así Vamos en Salud. (2019). Tasa de Mortalidad por Tuberculosis - Georeferenciado. https://www.asivamosensalud.org/indicadores/enfermedades-transmisibles/tasa-de-mortalidad-por-tuberculosis-georeferenciado
Baltussen, R., Floyd, K., Dye, C. (2005). Cost effectiveness analysis of strategies for tuberculosis control in developing countries. BMJ, 331(7529), e1364. https://doi.org/10.1136/bmj.38645.660093.68 DOI: https://doi.org/10.1136/bmj.38645.660093.68
Banderas, J. E. (2023). Casos de tuberculosis han venido en aumento en Cali. Caracol Radio. https://caracol.com.co/2023/03/27/casos-de-tuberculosis-han-venido-en-aumento-en-cali/#:~:text=Los%20casos%20presentados%20en%20Cali,tasa%20de%209%2C9%20casos
Blower, S. M., McLean, A. R., Porco, T. C., Small, P. M., Hopewell, P. C., Sanchez, M. A., Moss, A. R. (1995). The intrinsic transmission dynamics of tuberculosis epidemics. Nature Medicine, 1(8), 815-821. https://doi.org/10.1038/nm0895-815 DOI: https://doi.org/10.1038/nm0895-815
Blower, S. M., Small, P. M., Hopewell, P. C. (1996). Control strategies for tuberculosis epidemics: New models for old problems. Science, 273(5274), 497-500. https://doi.org/10.1126/science.273.5274.497 DOI: https://doi.org/10.1126/science.273.5274.497
Bhunu, C. P., Garira, W., Mukandavire, Z., Zimba, M. (2008). Tuberculosis transmission model with chemoprophylaxis and treatment. Bulletin of Mathematical Biology, 70(4), 1163-1191. https://doi.org/10.1007/s11538-008-9295-4 DOI: https://doi.org/10.1007/s11538-008-9295-4
Cali Cómo Vamos. (s.f.). Cali Cómo Vamos | Estadísticas Cali. https://www.calicomovamos.org.co/
Castillo-Chávez, C., Feng, Z. (1997). To treat or not to treat: The case of tuberculosis. Journal of Mathematical Biology, 35(6), 629-656. https://doi.org/10.1007/s002850050069 DOI: https://doi.org/10.1007/s002850050069
Castillo-Chávez, C., Song, B. (2004). Dynamical Models of Tuberculosis and Their Applications. Mathematical Biosciences and Engineering, 1(2), 361-404. https://doi.org/10.3934/mbe.2004.1.361 DOI: https://doi.org/10.3934/mbe.2004.1.361
Chitnis, N., Hyman, J. M., Cushing, J. M. (2008). Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bulletin of Mathematical Biology, 70(5), 1272-1296. https://doi.org/10.1007/s11538-008-9299-0 DOI: https://doi.org/10.1007/s11538-008-9299-0
Choi, S., Jung, E. (2014). Optimal tuberculosis prevention and control strategy from a mathematical model based on real data. Bulletin of Mathematical Biology, 76(7), 1566-1589. https://doi.org/10.1007/s11538-014-9962-6 DOI: https://doi.org/10.1007/s11538-014-9962-6
Cohen, T., Murray, M. (2004). Modeling epidemics of multidrug-resistant M. tuberculosis of heterogeneous fitness. Nature Medicine, 10(10), 1117-1121. https://doi.org/10.1038/nm1110 DOI: https://doi.org/10.1038/nm1110
Córdoba, C., Buriticá, P. A., Pacheco, R., Mancilla, A., Valderrama-Aguirre, A., Bergonzoli, G. (2020). Risk factors associated with pulmonary tuberculosis relapses in Cali, Colombia. Biomédica, 40(Supp. 1), 102-112. https://doi.org/10.7705/biomedica.5061 DOI: https://doi.org/10.7705/biomedica.5061
DANE. (2019a). Estadísticas vitales de nacimientos y defunciones. https://www.dane.gov.co/index.php/estadisticas-por-tema/salud/nacimientos-y-defunciones
DANE. (2019b). Resultados Censo Nacional de Población y Vivienda 2018. https://www.dane.gov.co/files/censo2018/informacion-tecnica/presentaciones-territorio/190711-CNPV-presentacion-valle.pdf
Hethcote, H. W. (2000). The mathematics of infectious diseases. SIAM Review, 42(4), 599-653. https://doi.org/10.1137/s0036144500371907 DOI: https://doi.org/10.1137/S0036144500371907
Lahey, T., von Reyn, C. F. (2016). Mycobacterium bovis. BCG and new vaccines for the prevention of tuberculosis. Microbiology Spectrum, 4(5), e3. https://doi.org/10.1128/microbiolspec.tnmi7-0003-2016 DOI: https://doi.org/10.1128/microbiolspec.TNMI7-0003-2016
La Salle, J. P. (1976). The stability of dynamical systems. Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9781611970432 DOI: https://doi.org/10.1137/1.9781611970432
Lenhart, S., Workman, J. T. (2007). Optimal control applied to biological models. Crc Press. https://doi.org/10.1201/9781420011418 DOI: https://doi.org/10.1201/9781420011418
Mao, K. X., Zhen, C. X., Lu, H. Y., Dan, Q., Ming, M. X., Zhang, C. Y., Hu, X. B., Dan, J. H. (2003). Protective effect of vaccination of Bacille Calmette-Guerin on children. Chinese Journal of Contemporary Pediatrics, 5, 325-326.
Martcheva, M. (2015). An introduction to mathematical epidemiology. Springer. https://doi.org/10.1007/978-1-4899-7612-3 DOI: https://doi.org/10.1007/978-1-4899-7612-3_1
MinSalud. (2020a). Resolución 227 de 2020. https://www.minsalud.gov.co/Normatividad_Nuevo/Resoluci%C3%B3n%20No.%20227%20de%202020.pdf
MinSalud. (2020b). Informe de evento tuberculosis año 2021. https://www.minsalud.gov.co/sites/rid/Lists/BibliotecaDigital/RIDE/VS/PP/ET/comportamiento-tuberculosis-2020.pdf
MinSalud. (s.f.). ¿Qué es tuberculosis (TB)? https://www.minsalud.gov.co/salud/publica/PET/Paginas/Tuberculosis.aspx
Rodrigues, P., Gomes, M. G. M., Rebelo, C. (2007). Drug resistance in tuberculosis – A reinfection model. Theoretical Population Biology, 71(2), 196-212. https://doi.org/10.1016/j.tpb.2006.10.004 DOI: https://doi.org/10.1016/j.tpb.2006.10.004
Sanchez, M. A., Blower, S. M. (1997). Uncertainty and sensitivity analysis of the basic reproductive rate: Tuberculosis as an example. American Journal of Epidemiology, 145(12), 1127-1137. https://doi.org/10.1093/oxfordjournals.aje.a009076 DOI: https://doi.org/10.1093/oxfordjournals.aje.a009076
Secretaría de Salud Valle del Cauca. (2019). Base de datos pacientes con Tuberculosis, Cali Valle.
Sepúlveda, L. S. (2015). Optimisation et contrôle viable de modèles épidémiologiques de dengue. https://cermics.enpc.fr/cermics-theses/2015/2015/sepulveda.pdf
Sepúlveda, L. S., Vasilieva, O. (2016). Optimal control approach to dengue reduction and prevention in Cali, Colombia. Mathematical Methods in the Applied Sciences, 39(18), 5475-5496. https://doi.org/10.1002/mma.3932 DOI: https://doi.org/10.1002/mma.3932
van den Driessche, P., Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 180(1-2), 29-48. https://doi.org/10.1016/s0025-5564(02)00108-6 DOI: https://doi.org/10.1016/S0025-5564(02)00108-6
World Health Organization. (2022a). Tuberculosis. https://www.who.int/es/news-room/facts-in-pictures/detail/tuberculosis
World Health Organization. (2022b). Aumenta la morbimortalidad por tuberculosis durante la pandemia de COVID-19. https://www.who.int/es/news/item/27-10-2022-tuberculosis-deaths-and-disease-increase-during-the-covid-19-pandemic
Yang, Y., Tang, S., Ren, X., Zhao, H., Guo, C. (2016). Global stability and optimal control for a tuberculosis model with vaccination and treatment. Discrete and Continuous Dynamical Systems - Series B, 21(3), 1009-1022. https://doi.org/10.3934/dcdsb.2016.21.1009 DOI: https://doi.org/10.3934/dcdsb.2016.21.1009
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: de febrero de 2023; Aceptado: de mayo de 2023
Resumen
En este trabajo plantea un modelo para la dinámica de la tuberculosis, el cual considera la población latente de bajo riesgo con el objetivo de evaluar la importancia de incluirla en el modelo y determinar si es necesario tratarla y/o controlarla. Para ello, se realizó un análisis cualitativo, determinando qué parámetros tienen mayor relevancia en la transmisión inicial de la enfermedad y calculando cuál es el número promedio de nuevas infecciones producidas por un individuo infeccioso. Se formuló y resolvió numéricamente un problema de control óptimo, en el cual se busca minimizar tanto los infectados como los costos económicos que estos impliquen la implementación de los controles en la dinámica de la tuberculosis planteada. Se utilizaron simulaciones numéricas para analizar los efectos de implementar los controles obtenidos. Por último, se realizaron simulaciones para Cali (Colombia), estableciendo una metodología para el diseño de estrategias de control para reducir la transmisión de la tuberculosis en la ciudad.
Palabras clave:
análisis cualitativo, control óptimo, metodología de control, modelado matemático, simulaciones numéricas, tuberculosis..Abstract
This work proposes a model for the dynamics of tuberculosis, which considers a latent low-risk population, with the aim of evaluating the importance of including it in the model and determining whether it is necessary to treat and/or control it. To this effect, a qualitative analysis of the model was carried out, determining which parameters are most relevant in the initial transmission of the disease and calculating the average number of new infections produced by an infectious individual. An optimal control problem was formulated and numerically solved, which seeks to minimize both the infected and the economic costs generated by the implementation of controls in the proposed dynamics of tuberculosis. Numerical simulations were used to analyze the effects of implementing the controls obtained. Finally, simulations are carried out for Cali (Colombia), establishing a methodology for the design of control strategies aimed at reducing the transmission of tuberculosis in the city.
Keywords:
control methodology, mathematical modeling, numerical simulations, optimal control, qualitative analysis, tuberculosis..Resumo
Neste artigo, ele propõe um modelo para a dinâmica da tuberculose, que considera a população latente de baixo risco para avaliar a importância de incluí-la no modelo e determinar se é necessário tratá-la e/ou controlá-la. Para isso, foi realizada uma análise qualitativa, determinando quais parâmetros são mais relevantes na transmissão inicial da doença e calculando o número médio de novas infecções produzidas por um indivíduo infectante. Um problema de controle ótimo foi formulado e resolvido numericamente, no qual se busca minimizar tanto os infectados quanto os custos econômicos que estes implicam na implementação dos controles na dinâmica da tuberculose levantada. Simulações numéricas foram utilizadas para analisar os efeitos da implementação dos controles obtidos. Finalmente, foram realizadas simulações para Cali (Colômbia), estabelecendo uma metodologia para o desenho de estratégias de controle para reduzir a transmissão da tuberculose na cidade.
Palavras-chaves:
análise qualitativa, controle ótimo, metodologia de controle, modelagem matemática, simulações numéricas, tuberculose.Introducción
La tuberculosis (o TB, como se le conoce en inglés) es causada por Mycobacterium tuberculosis, una bacteria que casi siempre afecta los pulmones. Se trata de una enfermedad curable y prevenible. En todo el mundo, la TB es la principal causa de muerte por un único agente infeccioso (por encima del SIDA). Un total de 1.6 millones de personas murieron de tuberculosis en 2021 (entre ellas 187 000 personas con VIH) (World Health Organization, 2022b). Se calcula que un tercio de la población mundial está infectada por el bacilo de la TB (World Health Organization, 2022b).
A principios del 2023, el observatorio Cali Cómo vamos informó que Cali es el tercer territorio con más casos de TB en Colombia (Cali Cómo Vamos, s.f.). Banderas (2023) indica que los casos presentados en Cali, según las estadísticas de la secretaría de Salud para el segundo período epidemiológico de 2023 son 241 casos. La tendencia ha sido al alza en los últimos años, en 2022 se presentaron 8 casos por cada 100 mil habitantes y hasta febrero de 2023 se registraba una tasa de 9.9 casos.
Los modelos matemáticos son una herramienta importante para analizar la propagación y el control de enfermedades infecciosas (Hethcote, 2000). Estos modelos ayudan a comprender cualitativamente el problema y derivan, en muchos casos, en caminos que ayudan prevenir enfermedades. El modelado matemático, aparte de ser muy eficaz, es de muy bajo costo, ya que su implementación no involucra la manipulación de sustancias químicas, farmacéuticas u orgánicas.
Se han realizado varios estudios sobre el modelado de la transmisión de la TB con diferentes estrategias de prevención y control, tales como la vacunación, el tratamiento, la cuarentena y el aislamiento (Blower et al., 1996; Castillo-Chávez y Feng, 1997). Yang et al. (2016) tuvieron en cuenta una combinación de métodos de control. Formularon un modelo con vacunación y tratamiento, concluyendo que estas estrategias son efectivas para reducir la transmisión de la TB.
En Choi y Jung (2014) se introdujo una clase denominada latentes de bajo riesgo, la cual agrupa a los individuos latentes que no progresan a TB infecciosa y los individuos recuperados (naturalmente o por tratamiento).
En este trabajo se combinan los compartimentos usados en los trabajos de Yang et al. (2016) y Choi y Jung (2014), con el fin de plantear un modelo que ayude a explorar la dinámica de la tuberculosis, teniendo en cuenta a la población latente de bajo riesgo y evaluando la importancia de considerar y/o tratar a dicha población.
Metodología
Se plantea un modelo SELITV, denotado así por las iniciales de sus compartimentos poblacionales, para la dinámica de la TB que incluye población latente de bajo riesgo. Se realiza un análisis cualitativo que consiste en calcular el número reproductivo básico asociado al modelo, así como los puntos de equilibrio, y se determina la estabilidad de estos últimos. Después, se formula un problema de control óptimo mediante la extensión del sistema del modelo, incluyendo dos funciones de control: vacunación y tratamiento. Luego, se demuestra la existencia de los controles óptimos del problema y se los caracteriza mediante la aplicación del principio de máximo de Pontryagin para controles acotados (Lenhart y Workman, 2007). Se utilizan herramientas computacionales y la teoría de control óptimo para analizar y plantear posibles estrategias para reducir la epidemia de TB, teniendo en cuenta los costos asociados a la infección y la aplicación de los controles. Por último, se realizan simulaciones para Cali (Colombia), estableciendo una metodología para el diseño de estrategias de control para reducir la transmisión de la TB en la ciudad.
Resultados
La población total se divide en seis compartimentos: susceptibles (S), latentes de alto riesgo (E), latentes de bajo riesgo (L), infecciosos (I), tratados (T) y vacunados (V). El diagrama de flujo entre compartimientos se presenta esquemáticamente en la Figura 1.
Figura 1: Esquema del modelo SELITV de la dinámica de la transmisión de la tuberculosis.
Las Tablas 1 y 2 describen, respectivamente, las variables y los parámetros que se manejan en el modelo SELITV.
Tabla 1: Variables del modelo SELITV

Tabla 2: Parámetros del modelo SELITV

Sean
 La Figura 1 se puede representar con el siguiente sistema de ecuaciones diferenciales ordinarias:
La Figura 1 se puede representar con el siguiente sistema de ecuaciones diferenciales ordinarias:

Demostración (idea)
Basta demostrar que el cambio de las trayectorias solución del Sistema (1) apunta hacia el interior de la región Ω o está sobre la frontera de la misma cuando se toma desde algún punto de los hiperplanos que la limitan.
Análisis cualitativo del modelo
Número reproductivo básico
Epidemiológicamente, el número reproductivo básico representa el número promedio de casos secundarios que producirá un individuo infectado en una población totalmente susceptible durante su periodo infeccioso. Para calcular el número reproductivo básico correspondiente al modelo, se siguen los lineamientos presentados por van den Driessche y Watmough (2002).
En este modelo, el número reproductivo básico es
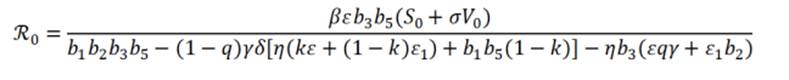
Puntos de equilibrio
Teorema 2
Si
 el Sistema (1) tiene un equilibrio libre de enfermedad
el Sistema (1) tiene un equilibrio libre de enfermedad
 además de /, el Sistema (1) también tiene un equilibrio positivo
además de /, el Sistema (1) también tiene un equilibrio positivo

Notación para el Teorema 2

están determinados por:

Demostración (idea)
Los puntos de equilibrio son las soluciones constantes del Sistema (1). Para calcularlos, se iguala cada ecuación del Sistema (1) a cero y se resuelve el sistema de ecuaciones resultante.
Estabilidad global de los equilibrios
Teorema 3
Para el Sistema (1), el equilibrio libre de enfermedad
 es globalmente asintóticamente estable sobre el conjunto Ω si
es globalmente asintóticamente estable sobre el conjunto Ω si
 . El equilibrio endémico
. El equilibrio endémico
 es globalmente asintóticamente estable sobre el conjunto Ω si
es globalmente asintóticamente estable sobre el conjunto Ω si
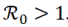 .
.
Demostración (idea)
Se usan funciones de Lyapunov y el principio de invarianza de La Salle (1976).
Problema de control óptimo
Se definen como variables exógenas aquellas que dependen del tiempo y que no dependen de ninguna variable del Modelo (1). Para ello, se denota con u 1 (t) la variable de control que indica la proporción de recién nacidos que se deben vacunar y con u 2 (t) la variable de control que indica la proporción del tratamiento que debe ser exitosa. Por lo tanto, al introducir los dos controles anteriores, el Modelo (1) queda de la siguiente manera:

con condiciones iniciales

donde
 son dos funciones reales continuas a trozos.
son dos funciones reales continuas a trozos.
Ahora, se plantea el problema de control óptimo introduciendo los dos controles mencionados anteriormente. El objetivo es minimizar el número de infectados y el costo de la aplicación de dichos controles. De acuerdo con la literatura sobre el costo de epidemias (Sepúlveda, 2015) y los costos asociados a la infección (Sepúlveda y Vasilieva, 2016), para los costos de los infecciosos se toma una función lineal y, para los costos de cada control, una función cuadrática.
Sean B
1
, B
2,
B
3,
B
4,
C
1 Y
C
2
constantes no negativas y
 el tiempo máximo de intervención. El problema de control óptimo resultante es el siguiente:
el tiempo máximo de intervención. El problema de control óptimo resultante es el siguiente:
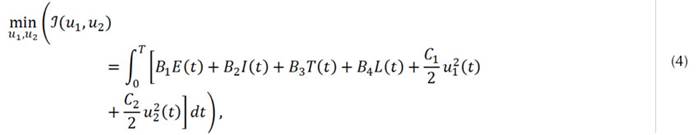
sujeto al Sistema (2) y las Condiciones Iniciales (3), donde B 1 , B 2, B 3, B 4, C 1 Y C 2 representan las prioridades de la meta planteada en el funcional objetivo.
Existencia de controles óptimos
Teorema 4
Cuando
 , existen controles óptimos
, existen controles óptimos
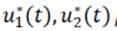 para el Problema (4).
para el Problema (4).
Demostración (idea)
Se demuestra que se satisfacen las hipótesis del Teorema 9.1 de (Martcheva, 2015).
Caracterización de los controles
Teorema 5

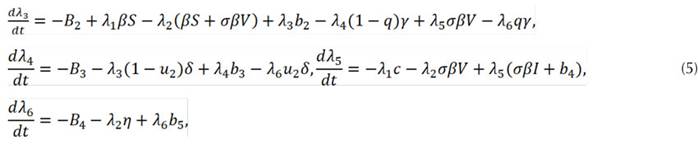
con condiciones de transversalidad

Además, se pueden caracterizar y así:


Demostración
El resultado se desprende de la aplicación directa de una versión del Principio del Máximo de Pontryagin para controles acotados (Lenhart y Workman, 2007). El Hamiltoniano
 para el Problema (4) está dado por
para el Problema (4) está dado por

Las ecuaciones adjuntas están dadas por

que son las Ecuaciones (5) y satisfacen las condiciones de transversalidad
 , que son las Condiciones (6). Finalmente, las condiciones de optimalidad establecen que
, que son las Condiciones (6). Finalmente, las condiciones de optimalidad establecen que
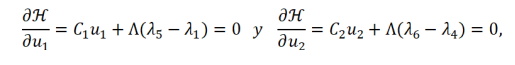
para los controles óptimos
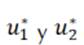 y en el interior del conjunto de definición de los controles, y esta condición se simplifica en las Ecuaciones (7) y (8), teniendo en cuenta los límites de la definición de los controles.
y en el interior del conjunto de definición de los controles, y esta condición se simplifica en las Ecuaciones (7) y (8), teniendo en cuenta los límites de la definición de los controles.
Simulaciones numéricas
Las simulaciones numéricas se realizaron en la plataforma MATLAB. Para resolver numéricamente el Problema de Control Óptimo (4), se usan el método del barrido hacia adelante y hacia atrás y la teoría de control óptimo (Lenhart and Workman, 2007). A continuación, se presenta un esbozo del algoritmo:
-
Paso 1: Se toma un valor inicial para los controles.
-
Paso 2: Usando las Condiciones Iniciales (3) y los valores para los controles, se resuelve el Sistema (2), de las variables de estado hacia adelante en el tiempo, teniendo en cuenta las condiciones de optimalidad.
-
Paso 3: Usando las Condiciones de Transversalidad (6) y los valores para los controles y las variables de estado encontrados anteriormente, se resuelve el Sistema (5), de las variables adjuntas hacia atrás en el tiempo, usando las condiciones de optimalidad.
-
Paso 4: Se actualizan los controles, sustituyendo los nuevos valores para las variables de estado y adjuntas dentro de la caracterización del control óptimo. Se obtienen los nuevos valores para los controles.
-
Paso 5: Se comprueba la convergencia. Si los valores de los controles en los pasos 1 y 4 difieren muy poco, se detiene el proceso; de lo contrario, se regresa al paso 2.
Para resolver los Sistemas (2) y (5), se usa el método de Runge-Kutta de cuarto orden.
Con el propósito de realizar comparaciones con el modelo de Yang et al. (2016), se toman los parámetros que se usaron en las simulaciones de dicho modelo y, a falta de datos, algunos valores de parámetros se asumen dentro de rangos realistas (ver Tabla 3). Para el control u 1 (t), que indica la proporción de recién nacidos que se deben vacunar, se toma como límite inferior 0 y como límite superior 1. Para el control u 2 (t) que indica la proporción de tratamiento que debe ser exitosa, se toma como límite inferior 0 y como límite superior 0.75, ya que, en la realidad, el tratamiento no tiene un éxito en el 100 % de los casos. Para los pesos del funcional objetivo, se toman B1 = 1,B2 = 1000,B3 = 2000, C1 = 103 y C2 = 106 como en Yang et al. (2016). Por último, se realizan simulaciones para Cali, estableciendo un método para diseñar estrategias de control para reducir la transmisión de la TB en la ciudad.
Tabla 3: Valores de los parámetros

Comparaciones y estrategias
Para esta primera simulación, se tomó el peso B 4 , el peso asociado a disminuir la población latente de bajo riesgo, con un valor de 0, en aras de comparar los resultados con los de Yang et al. (2016). Más adelante, se variaría el peso B 4 para conocer el efecto de involucrar la población latente de bajo riesgo.
Las condiciones iniciales se asumieron así:

y las simulaciones se realizaron para un periodo de 20 años.
La Figura 2 presenta el modelo estudiado por Yang et al. (2016) con y sin control. A su vez, la Figura 3muestra el modelo SELITV con y sin control.
Figura 2: Modelo de Yang et al. (2016) con y sin control.
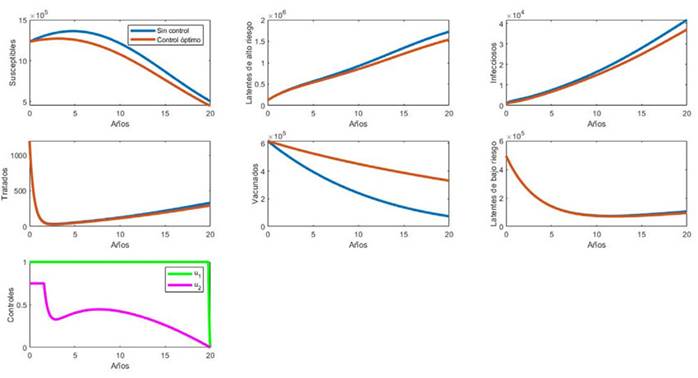
Figura 3: Modelo (1) con y sin control óptimo.
Se observa que el resultado del problema de control óptimo es similar al resultado obtenido por Yang et al. (2016): se debe vacunar al total de los recién nacidos durante casi todo el tiempo de intervención, y la fracción de tratamiento exitoso debe ser la máxima posible durante los primeros años. Esta última va disminuyendo gradualmente, para mantenerse casi constante en 0.5 desde el año 5 hasta casi finalizar el periodo de intervención.
Acto seguido, se varió el peso B4 para conocer el efecto de considerar la población latente de bajo riesgo en el modelo.
En la Figura 4 se observa que, si B4 = 0, 10 o 100, es decir, si se quiere minimizar la población latente de bajo riesgo (con prioridades bajas), los resultados del problema de control óptimo son los mismos -las curvas se superponen y por eso no se distinguen en las gráficas. El cambio, se observa que, cuando B4 = 1000, es decir, si hay mayor interés en minimizar la población latente de bajo riesgo, el resultado indica que no se deben tener tratamientos exitosos durante más de 15 años, lo cual no es deseable en la realidad.
Figura 4: Control óptimo para el Modelo (1) minimizando la población latente de bajo riesgo.
Asimismo, en la Figura 5 se observa que, si se toma B4 = -10 o -100, es decir, si se quiere maximizar la población latente de bajo riesgo, los resultados del problema de control óptimo son los mismos del caso B4 = 0. Entretanto, si B4 = -1000, es decir, si hay mayor interés en maximizar a la población latente de bajo riesgo, el resultado del problema de control óptimo indica que no se deben vacunar recién nacidos durante más de 15 años, lo cual aumentaría la población infectada. Con esto se concluye que no hay que gastar esfuerzos en controlar la población latente de bajo riesgo. Es por ello que, en las siguientes simulaciones, se tomó el valor de B4 = 0.
Figura 5: Control óptimo para el Modelo (1) maximizando la población latente de bajo riesgo.
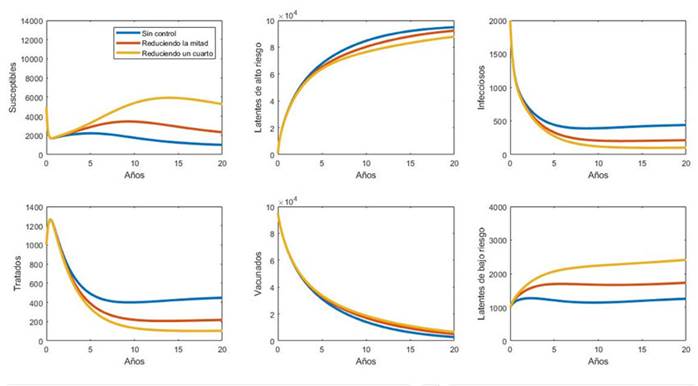
En este modelo, al introducir el nuevo compartimento de los latentes de bajo riesgo, se introdujo también un nuevo parámetro: la tasa de recaída η. Esto, en aras de examinar el efecto de disminuir los parámetros η y ε en la dinámica sin control. Para ello, se realizó una simulación en la cual estos parámetros se redujeron a la mitad y a una cuarta parte con respecto a los valores de la dinámica sin control. El resultado se muestra en la Figura 6.
Figura 6: Efecto de reducir los parámetros y en la Dinámica (1).
Se encontró que, si se reducen los parámetros η y ε al mismo tiempo, se obtiene un mejor resultado en la dinámica sin control, reduciendo la población latente de bajo riesgo, los infecciosos y los tratados, esto es, con resultados similares a los obtenidos en el problema de control óptimo.
Simulaciones para Cali
Por último, se utilizó el modelo SELITV para la ciudad de Cali (Colombia). En la Tabla 4 se presentan los valores de los parámetros. Los parámetros σ y c son tomados de la literatura, q es asumido ε1 ? 5ε, (Choi y Jung, 2014), α2 es el valor para Colombia y los demás parámetros son valores para la ciudad de Cali. Para los pesos del funcional objetivo se tomó B1= 10, B2 = 100 y B4 = 0, como lo sugiere el análisis anterior. Para esta primera simulación, se tomó B3, el peso asociado a disminuir la población tratada, con un valor de 0. Después se variaría el peso B3 para determinar si es necesario o no disminuir la población tratada. Para los costos de los controles, se asumió C1= 103 y C2 = 106. Con esto se estableció una metodología para determinar estrategias de control de la TB en Cali. Para llevarlas a la práctica, es necesario ajustar c1 y c2 a las condiciones de la ciudad.
Tabla 4: Valores de los parámetros para Cali

Las condiciones iniciales se asumieron así:
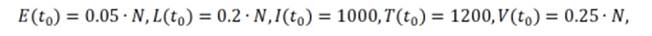
donde N= 2.470.852 es el número de habitantes de Cali en el año 2019. Es decir, se consideró que, inicialmente, el 25 % de la población inicial era latente (de bajo y alto riesgo) (World Health Organization, 2022a), había 1000 personas con tuberculosis activa (Minsalud, 2020b), por cada infeccioso había 1.2 personas en tratamiento (Secretaría de Salud Valle del Cauca, 2019) y el 25 % de la población aún poseía la inmunidad de la vacuna (población menor a 10 años) (DANE, 2019b). Las simulaciones se realizaron para un periodo de 20 años. La Figura 7 muestra el modelo SELITV para Cali con y sin control.
Figura 7: Modelo SELITV para Cali con y sin control, minimizando la población latente de alto riesgo y los individuos infecciosos.
El resultado del problema de control óptimo indica que se debe vacunar al total (todos los recién nacidos en cada instante de tiempo) de los recién nacidos durante todo el tiempo de intervención, así como la fracción (curva rosada) de tratamiento que debe ser exitoso durante el periodo de intervención para lograr disminuir la población latente de alto riesgo y los individuos infecciosos, como se plantea en el funcional objetivo, (es decir que al inicio el 75 % de tratamientos deben ser exitosos y estos van disminuyendo a medida que pasa el tiempo, luego se establecen alrededor del 40 % y estos decrecen con el tiempo).
Para conocer el efecto de disminuir la población tratada, se varió el peso B3, como lo muestra la Figura 8.
Figura 8: Modelo SELITV para Cali con y sin control, minimizando la población tratada.
Se observa que, si B3 = 0, 10 o 100, es decir, si se quiere minimizar la población tratada (con prioridades bajas), los resultados del problema de control óptimo son los mismos -las curvas se superponen y por eso no se distinguen en las gráficas. El cambio, cuando B3 toma valores muy grandes (e.g., B3 = 10 000), es decir, si hay mayor interés en minimizar la población tratada, el resultado indica que, durante todo el periodo de intervención, además de vacunar al total de los recién nacidos, la fracción de tratamientos exitosos debe ser la máxima posible. Esto implica más gastos en tratamiento, pero los resultados en la dinámica son muy parecidos a los obtenidos cuando B3 = 0, 10 o 100.
Conclusiones
Se observa que, si se incluye la población de latentes de bajo riesgo en la dinámica de Yang et al. (2016), las estrategias de vacunación y tratamiento siguen siendo las mismas para reducir la transmisión de la tuberculosis.
Si se logra reducir la velocidad de infección de los latentes de alto riesgo, en conjunto con la tasa de recaída, se pueden lograr resultados parecidos a los alcanzados con vacunación y tratamiento exitosos, es decir, se reduce la población latente de alto riesgo, los infecciosos y los tratados. Se sabe que un tratamiento exitoso requiere muchos esfuerzos médicos y económicos. Por lo tanto, una alternativa para reducir la propagación de la tuberculosis es disminuir la velocidad de infección de los latentes de alto riesgo, identificando y tratando la tuberculosis latente, así como prevenir las recaídas en la población latente de bajo riesgo, completando las dos fases del tratamiento de tuberculosis y realizando seguimiento a estas personas durante al menos el primer año posterior a la finalización del tratamiento.
Este trabajo muestra la importancia de introducir la población latente de bajo riesgo en la dinámica de la tuberculosis, pues esto ayuda a estudiar esta dinámica de una forma más próxima a la realidad. Además, se determina que, dado que no representan un riesgo para la población, no hay necesidad de disminuir ni maximizar la población latente de bajo riesgo.
Se realizaron simulaciones para Cali con el modelo SELITV, y se concluyó que no es necesario disminuir la población tratada; tratar de disminuirla solo aumentaría gastos, y estos Con este trabajo, se establece una metodología para el diseño de estrategias de control para reducir la transmisión de la TB en Cali, las cuales, para ser implementadas en la práctica, requieren la determinación de los costos C1 y C2 así como el ajuste de algunos parámetros de acuerdo con la población de estudio.
Acknowledgements
Agradecimientos
Este trabajo fue financiado parcialmente por Minciencias, en el marco del proyecto de investigación CI. 71243: Métodos matemáticos para seguimiento, análisis y control de la tuberculosis en Cali.
Referencias
Licencia
Derechos de autor 2023 Tatiana Girón-Carabalí, Juddy-Heliana Arias-Castro, Héctor-Jairo Martínez-Romero

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
El (los) autor(es) al enviar su artículo a la Revista Científica certifica que su manuscrito no ha sido, ni será presentado ni publicado en ninguna otra revista científica.
Dentro de las políticas editoriales establecidas para la Revista Científica en ninguna etapa del proceso editorial se establecen costos, el envío de artículos, la edición, publicación y posterior descarga de los contenidos es de manera gratuita dado que la revista es una publicación académica sin ánimo de lucro.