DOI:
https://doi.org/10.14483/23448350.20680Published:
02/01/2024Issue:
Vol. 49 No. 1 (2024): January-April 2024Section:
Research ArticlesUn nuevo teorema geométrico y su aplicación en la construcción de conjeturas a través de un ambiente de geometría dinámica
A New Geometric Theorem and its Application in Conjecture Construction through a Dynamic Geometry Environment
Keywords:
ambiente de geometría dinámica, arrastre, conjeturas, enseñanza de la geometría (es).Keywords:
conjecture, drag, dynamic geometry environment, teaching geometry (en).Downloads
References
Abrate, R. S., Delgado, G. I., Pochulu, M. D. (2006). Caracterización de las actividades de Geometría que proponen los textos de Matemática. Revista Iberoamericana de Educación, 39(1), e1. https://doi.org/10.35362/rie3912598 DOI: https://doi.org/10.35362/rie3912598
Afonso Martín, M. C. (2003). Los niveles de pensamiento geométrico de Van Hiele: Un estudio con profesores en ejercicio [Tesis Doctoral, Universidad de La Laguna].
Arzarello, F., Micheletti, C., Olivero, F., Paola, D., Robutti, O. (1998). A model for analysing the transition to formal proofs in geometry. En A. Olivier & K. Newstead (Eds.), Proceedings of PME22 (pp. 24-31). University of Bristol. https://hdl.handle.net/1983/136e3582-c7ec-4b66-81d7-12273034eb9f
Arzarello, F., Olivero, F., Paola, D., Robutti, O. (2002). A cognitive analysis of dragging practises in Cabri environments. Zentralblatt Für Didaktik Der Mathematik, 34(3), 66-72. https://doi.org/10.1007/BF02655708 DOI: https://doi.org/10.1007/BF02655708
Baccaglini-Frank, A. (2019). Dragging, instrumented abduction and evidence, in processes of conjecture generation in a dynamic geometry environment. ZDM, 51(5), 779-791. https://doi.org/10.1007/s11858-019-01046-8 DOI: https://doi.org/10.1007/s11858-019-01046-8
Baccaglini-Frank, A., Mariotti, M. A. (2010). Generating conjectures in dynamic geometry: The maintaining dragging model. International Journal of Computers for Mathematical Learning, 15(3), 225-253. https://doi.org/10.1007/s10758-010-9169-3 DOI: https://doi.org/10.1007/s10758-010-9169-3
Cobb, P., Jackson, K., Dunlap, C. (2017). Conducting design studies to investigate and support mathematics students’ and teachers’ learning. En NCTM (Eds.), Compendium for Research in Mathematics Education (pp. 208-233). NCTM.
De Benito Crosetti, B., Salinas Ibáñez, J. M. (2016). La investigación basada en diseño en tecnología educativa. Revista Interuniversitaria de Investigación En Tecnología Educativa, 0, 44-59. https://doi.org/10.6018/riite2016/260631 DOI: https://doi.org/10.6018/riite2016/260631
Benítez Mojica, D., Santos-Trigo, M. (2006). Identifying and supporting mathematical Conjectures through the use of dynamic software, Research Reports Abr-Dri Editors: Jarmila Novotná. 2, Proceedings of PME 30 (pp. 29–136).
Bonelo, Y., Leung, A., Benitez, D., Marmolejo, G. (2022). Control structure in dynamic geometry exploration [Manuscrito presentado para publicación].
Camargo Uribe, L. (2019). Estrategias cualitativas de investigación en educación matemática. https://conferencia.ciaem-redumate.org/index.php/xvciaem/xv/paper/viewFile/1061/568
Cañadas, M. C., Piquet, J. D., Figueiras, L., Reid, D. A., Yevdokimov, O. (2008). Perspectivas teóricas en el proceso de elaboración de conjeturas e implicaciones para la práctica: tipos y pasos. Enseñanza de las Ciencias. Revista de investigación y experiencias didácticas, 26(3), e3. https://doi.org/10.5565/rev/ensciencias.3753 DOI: https://doi.org/10.5565/rev/ensciencias.3753
Gempeler, M. E. A., Leal, J. E. F. (2017). Enseñando geometría con tecnología digital: una propuesta desde la teoría de las situaciones didácticas. Universidad Distrital Francisco José de Caldas. https://doi.org/10.14483/9789585434462 DOI: https://doi.org/10.14483/9789585434462
Leung, A., Baccaglini-Frank, A., Mariotti, M. A. (2013). Discernment of invariants in dynamic geometry environments. Educational Studies in Mathematics, 84(3), 439-460. https://doi.org/10.1007/s10649-013-9492-4 DOI: https://doi.org/10.1007/s10649-013-9492-4
Leung, A., Bolite-Frant, J. (2015). Designing mathematics tasks: The role of tools. En A. Watson & M. Ohtani (Eds.), Task Design In Mathematics Education: An ICMI study 22 (pp. 191-225). Springer International Publishing. https://doi.org/10.1007/978-3-319-09629-2_6 DOI: https://doi.org/10.1007/978-3-319-09629-2_6
López-Real, F., Leung, A. (2006). Dragging as a conceptual tool in dynamic geometry environments. International Journal of Mathematical Education in Science and Technology, 37(6), 665-679. https://doi.org/10.1080/00207390600712539 DOI: https://doi.org/10.1080/00207390600712539
Marrades, R., Gutiérrez, Á. (2000). Proofs produced by secondary school students learning geometry in a dynamic computer environment. Educational Studies in Mathematics, 44(1), 87-125. https://doi.org/10.1023/A:1012785106627 DOI: https://doi.org/10.1023/A:1012785106627
Mason, J., Burton, L., Stacey, K. (2010). Thinking mathematically (2nd ed.). Pearson Education Limited.
Ministerio de Educación Nacional (1998). Lineamientos Curriculares de Matemáticas. Cooperativa Editorial Magisterio. https://www.mineducacion.gov.co/1621/articles-89869_archivo_pdf9.pdf
Miragliotta, E., Baccaglini-Frank, A. (2017). Visuo-spatial abilities and geometry: A first proposal of a theoretical framework for interpreting processes of visualization. https://hal.science/hal-01950545
Monroy Guzmán, L. A. (2023). Formas de razonamiento que muestran estudiantes de primer año de ingeniería en la resolución de problemas del álgebra lineal con medios digitales [Tesis doctoral, Universidad del Valle].
Moreno Armella, L. (2002). Instrumentos matemáticos computacionales. En Ministerio de Educación Nacional, Dirección de Calidad de la Educación Preescolar, Básica y Media (Eds.), Proyecto: Incorporación de Nuevas Tecnologías al currículo de Matemáticas de la educación media de Colombia (pp. 81-86). Editorial MEN.
Romero López, D., De Benito Crosetti, B. (2020). Diseño de una propuesta didáctica para el uso de simuladores virtuales en la rama sanitaria de formación profesional. Revista Interuniversitaria de Investigación en Tecnología Educativa, 8, e383431. https://doi.org/10.6018/riite.383431 DOI: https://doi.org/10.6018/riite.383431
Samper, C., Perry, P., Camargo, L., Molina, Ó., Echeverry, A. (2010). Geometría dinámica: su contribución a la comprensión de condicionales de la forma si-entonces. Educación Matemática, 22(3), 119-142.
Santos-Trigo, M. (2023). Trends and developments of mathematical problem-solving research to update and support the use of digital technologies in post-confinement learning spaces. En T. L. Toh, M. Santos-Trigo, P. H. Chua, N. A. Abdullah, & D. Zhang (Eds.), Problem Posing and Problem Solving in Mathematics Education: International Research and Practice Trends (pp. 7-32). Springer Nature. https://doi.org/10.1007/978-981-99-7205-0_2 DOI: https://doi.org/10.1007/978-981-99-7205-0_2
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: de abril de 2023; Aceptado: de diciembre de 2023
Resumen
Este artículo presenta un nuevo resultado de geometría euclidiana que involucra los baricentros de un triángulo y los triángulos formados modificando un vértice del triángulo anterior por su reflexión axial con respecto a una recta dada. Estos baricentros son colineales, y la recta que los contiene es perpendicular a la recta inicial sobre la cual se consideraron las reflexiones axiales. Adicionalmente, se suministra una generalización del teorema mencionado para cuadriláteros y se detallan las demostraciones formales de ambos resultados. Esto se presenta siguiendo los pasos para la construcción de conjeturas de Benítez Mojica y Santos-Trigo, utilizando ambientes de geometría dinámica que se puedan emplear en experiencias futuras en cursos de geometría euclidiana con ayuda de nuevas tecnologías.
Palabras clave:
ambiente de geometría dinámica, arrastre, conjeturas, enseñanza de la geometría.Abstract
This article presents a new result in Euclidean geometry involving the centroids of a triangle and the triangles formed by modifying one vertex of the preceding one through its axial reflection with respect to a given line. These centroids are collinear, and the line containing them is perpendicular to the initial one considered for the axial reflections. Additionally, a generalization of the aforementioned theorem for quadrilaterals is provided, and the formal proofs of both results are detailed. This is presented following the steps for the construction of conjectures by Benítez Mojica and Santos-Trigo, using dynamic geometry environments that can be employed in future experiences in Euclidean geometry courses with the aid of new technologies.
Keywords:
conjecture, drag, dynamic geometry environment, teaching geometry.Resumo
Este artigo apresenta um novo resultado em geometria euclidiana envolvendo os baricentros de um triângulo e os triângulos formados pela modificação de um vértice do triângulo anterior pela sua reflexão axial em relação a uma dada reta. Estes baricentros são colineares e a reta que os contém é perpendicular à reta inicial sobre a qual foram consideradas as reflexões axiais. Além disso, é fornecida uma generalização do teorema acima para quadriláteros e são dadas provas formais de ambos os resultados. A apresentação é feita seguindo os passos para a construção de conjecturas de Benítez Mojica e Santos-Trigo, utilizando ambientes de geometria dinâmica que podem ser usados em futuras experiências em cursos de geometria euclidiana com o auxílio das novas tecnologias.
Palavras-chaves:
ambiente de geometria dinâmica, arrastrar, conjecturas, ensino de geometria.Introducción
La educación matemática atiende diversos desafíos que se pueden abordar desde la enseñanza y/o el aprendizaje de las matemáticas y todas las posibles relaciones profesor-saber-estudiante (triángulo didáctico) que emerjan, más aún si se considera el medio entre ellos.
Particularmente en la enseñanza de la geometría se han abordado métodos diferentes al del estudio memorístico y mecánico de definiciones, propiedades y construcciones descontextualizadas, cuyo fin se limita a la aritmetización y resolución automática de problemas que no contribuyen al desarrollo del pensamiento geométrico del estudiante (Abrate et al., 2006; Afonso Martín, 2003; Benítez Mojica & Santos-Trigo, 2006; Gempeler & Leal, 2017; Ministerio de Educación Nacional, 1998; Samper et al., 2010). La enseñanza de la geometría debe fortalecer la intuición y la argumentación del estudiante, no solo limitarse a la presentación de contenidos. Es por esto que es ideal favorecer un ambiente en el aula donde los estudiantes puedan comunicar sus ideas, formular preguntas, usar múltiples representaciones, hacer conjeturas, establecer estrategias de resolución de problemas y formular contraejemplos. Lo anterior permite ver que la geometría no es un objeto acabado e inútil y lleva al estudiante a reflexionar sobre su propio aprendizaje de las matemáticas.
La representación de objetos matemáticos es fundamental en el aprendizaje de la geometría. En particular, la regla y el compás son herramientas esenciales para tal fin. Sin embargo, las herramientas computacionales también permiten representar objetos matemáticos y visualizar sus relaciones. Lo anterior muestra cuán importante es detallar otros sistemas de representación geométrica, como lo es el software de geometría dinámica. Este tipo de software se conoce en la literatura especializada como DGE (dynamic geometry environments, o ambientes de geometría dinámica).
Interés de la investigación
Esta investigación se enfoca en documentar el proceso de construcción y formalización de una conjetura geométrica. Su propósito es explicitar los elementos constitutivos y emergentes de este proceso, profundizando, destacando y fomentando la interacción entre el pensamiento geométrico y las herramientas tecnológicas. Lo anterior se hace resaltando la influencia positiva de la tecnología en el proceso cognitivo y creativo de los estudiantes y su aporte a la construcción de conjeturas en el ámbito geométrico.
Santos-Trigo (2023) reflexiona sobre la siguiente pregunta en ambientes de resolución de problemas:
¿Cómo influye el uso de herramientas digitales por parte de profesores y estudiantes en la forma en que razonan y resuelven problemas matemáticos?
Este planteamiento no solo ha llevado a repensar continuamente la conexión entre tecnología y mediación, sino también a las siguientes preguntas:
¿Cómo se enseña a construir una conjetura?
¿Qué elementos debe tener un profesor de matemáticas para enseñar a construir conjeturas?
¿Cuáles son los beneficios y desafíos de utilizar entornos computacionales en la construcción de conjeturas?
¿Qué procesos cognitivos subyacen a la actividad geométrica cuando es promovida por un DGE?
Esta investigación posibilita, desde la didáctica de las matemáticas, una mirada integral a la construcción de conjeturas geométricas, resaltando la importancia de la mediación instrumental, la demostración y los procesos cognitivos relacionados con dicho proceso.
La geometría dinámica como instrumento de aprendizaje
Es importante distinguir entre herramienta e instrumento. Una herramienta está diseñada para un uso específico de trabajo y, desde una perspectiva metacognitiva, una herramienta “no modifica, sino que complementa el pensamiento del estudiante” (Moreno Armella, 2002, p. 85). Entretanto, un instrumento es una herramienta cuyo uso sostenido desarrolla funciones diferentes a las inicialmente diseñadas y contribuye en la generación de cambios de estrategias de solución de problemas y de resignificación en el planteamiento de los mismos. En otras palabras, es el sujeto o usuario del DGE quien adapta la herramienta a sí mismo.
En consonancia con lo anterior, el uso de una herramienta facilita la amplificación de lo que inicialmente podría pasar desapercibido. Al igual que una lupa, esta herramienta permite examinar en detalle lo que se observa a una escala diferente. Por otro lado, el instrumento propicia una reorganización cognitiva, i.e., permite percibir lo que sería imposible sin la ayuda de la herramienta, evocando la imagen de un microscopio, que brinda acceso a un nivel de realidad más profundo y a un conocimiento más amplio (Moreno Armella, 2002).
La geometría dinámica emergente de los entornos computacionales brinda al usuario una realidad matemática en la que los conceptos y construcciones abstractos pueden cosificarse visualmente (Baccaglini-Frank & Mariotti, 2010; López-Real & Leung, 2006). En este sentido, los objetos geométricos se convierten en entidades que un solucionador puede observar y transformar figurativamente. Más aún, proporcionan dominios epistémicos, pues el movimiento, la variación y la retroalimentación visual pueden guiar la identificación de las propiedades geométricas de las figuras (Leung et al., 2013).
Los ambientes de geometría dinámica ayudan a crear situaciones de aprendizaje en las que los estudiantes pueden interactuar de múltiples maneras con las propiedades matemáticas de los objetos a través de representaciones semióticas ejecutables, más cómodamente que en el entorno del lápiz y el papel (Marrades & Gutiérrez, 2000).
El software GeoGebra, por ejemplo, se caracteriza por trabajar con sistemas matemáticos, en este caso un sistema geométrico conformado por objetos (puntos, rectas y polígonos), operaciones (construcciones con regla y compás), transformaciones isométricas en el plano y relaciones (paralelismo, pertenencia y perpendicularidad). También cuenta con una fenomenología propia, que emerge del ambiente dinámico. Los fenómenos que ocurren en la pantalla son el arrastre, el lugar geométrico y la animación, lo que permite ver el proceso de construcción de los objetos geométricos a través del movimiento.
El arrastre (dragging)
En un DGE, la acción que se logra al utilizar el ratón (mouse) del computador para mover un objeto del programa en diferentes direcciones y a diferentes lugares de la pantalla se conoce como arrastre o dragging. El arrastre permite conservar las relaciones geométricas implícitas en la configuración inicial. De esta manera, la naturaleza de las figuras que se hacen en un DGE dista de las de un dibujo hecho a lápiz y papel.
En los entornos de geometría dinámica coexisten dominios de tipo estructural, propios del software, y de tipo fenomenológico. En el primero de estos, un conjunto de objetos base (línea, punto) y las operaciones que se realizan sobre ellos permiten la operación formal del micro-mundo computacional. El segundo vincula los objetos y las operaciones con los fenómenos que se visualizan (e.g., el arrastre). Este último dominio permite una discriminación en relación con las acciones y decisiones que puede tomar un estudiante o un usuario durante el proceso de exploración del micro-mundo computacional.
El arrastre ha sido un elemento fundamental para las investigaciones interesadas en vincular la tecnología computacional a la clase de matemáticas, y se ha tipificado según su uso y objetivo de estudio. En la literatura (Arzarello et al., 2002; Baccaglini-Frank y Mariotti, 2010; Bonelo et al., 2022; López-Real & Leung, 2006) se ha clasificado el uso del arrastre en distintas modalidades, por ejemplo: errante, de mantenimiento, rastro activado y prueba de arrastre (Baccaglini-Frank & Mariotti, 2010).
El arrastre es considerado en la literatura como un instrumento cognitivo emergente del micro-mundo computacional que ofrecen los DGE y como una poderosa herramienta dinámica para la adquisición de conocimiento (López-Real & Leung, 2006), pues un usuario podría interactuar con las representaciones semióticas de los objetos matemáticos y así experimentar la realidad matemática virtual de las mismas.
Se ha podido configurar el uso del arrastre como un modelo que describe algunos procesos cognitivos que pueden ocurrir durante la producción de conjeturas en geometría dinámica y que parecen estar relacionados con modalidades de arrastre específicas (Baccaglini-Frank & Mariotti, 2010).
Macro-construcción
Por defecto, los DGE incluyen herramientas para proyectar en la pantalla nuevos objetos geométricos, generales o de acción. Particularmente en GeoGebra se permite la creación de herramientas propias, que posteriormente pueden emplearse como las del repertorio original e incluso establecerse como un comando más en la barra de entrada. A estas nuevas herramientas se les conoce con el nombre de macro-construcciónes, pues aluden a la ‘construcción de construcciones’ o a la programación de la construcción de un objeto (Benítez Mojica & Santos-Trigo, 2006).
Desde una construcción existente se pueden crear herramientas propias, y para ello hay que tener en cuenta las variables dependientes e independientes en la construcción de un objeto, i.e., los objetos de entrada y salida de la programación deseada.
La construcción de conjeturas en DGE
La construcción de conjeturas ha sido tratada desde distintas perspectivas en cuanto a contextos y tipología (Cañadas et al., 2008; Leung & Bolite-Frant, 2015). Algunos autores asumen la conjetura como una declaración aparentemente razonable, pero cuya verdad no se ha establecido, i.e., no se ha justificado de manera convincente. Por otra parte Mason et al. (2010) tratan de ubicar la conjetura en un estado no terminado en el paso inmediatamente anterior a la demostración. Esto, debido a que, después de lograr dicha demostración, el estado es terminado y la conjetura asume el papel de teorema. Baccaglini-Frank y Mariotti (2010) definen la conjetura como un enunciado condicional, dado que su construcción se da por una premisa que precede a una conclusión.
Construir una conjetura no es trivial, ya sea usando un software o la mente humana. Para ello se precisa un adecuado uso y una comprensión de la lógica matemática, como lo sugieren Samper et al. (2010). Por tanto, la conjeturación se convierte en una de las múltiples formas de aprender y enseñar matemáticas, pues en ella se vislumbran elementos del conjeturador que surgen en el camino a la conjetura, como lo son los procesos cognitivos, las formas argumentativas, los registros de representación, las estructuras y los elementos de control.
Por otra parte, se han realizado investigaciones sobre la producción y/o lo construcción de conjeturas en contextos específicos, como es el caso de la geometría dinámica (Arzarello et al., 1998; Baccaglini-Frank, 2019; Leung et al., 2013) y el de la resolución de problemas (Baccaglini-Frank, 2019; Benítez Mojica & Santos-Trigo, 2006; Miragliotta & Baccaglini-Frank, 2017).
Metodología
Naturaleza y estrategia de la investigación
Esta es una investigación cualitativa en el ámbito de la educación matemática, fundamentada en los principios de la investigación basada en diseño, según lo propuesto por Cobb et al. (2017), de Benito Crosetti y Salinas Ibáñez (2016) y Romero López y de Benito Crosetti (2020). La estrategia investigativa adoptada sigue un enfoque en primera persona, como sugiere Camargo Uribe (2019). Este enfoque implica el estudio directo de un fenómeno investigativo, accedido por sus participantes, con el propósito de capturar y profundizar en los detalles más significativos.
Esto implica que el investigador se convierte en sujeto de su propia investigación, involucrándose en el proceso de recolección y análisis de datos desde su propia perspectiva y experiencia. Al adoptar esta estrategia, el investigador busca explorar y comprender sus propias experiencias en relación con el objeto de estudio, lo que puede ayudar a revelar información y perspectivas nuevas y únicas.
De igual manera, esta metodología promueve la reflexión crítica sobre el proceso de investigación y sobre la propia posición del investigador en relación con el objeto de estudio. Al involucrarse de manera personal en el proceso de investigación, el investigador puede comprender mejor las complejidades y matices del objeto de estudio, así como los efectos que su propia posición y perspectiva puedan tener en los resultados de la investigación.
El objetivo de esta investigación es presentar una actividad que permita la construcción de conjeturas y su formalización para su uso en estudios futuros o como una guía en prácticas pedagógicas.
Este trabajo presenta un nuevo resultado geométrico, el proceso de construcción de una conjetura, su prueba y su extensión. Para ello, se utilizó el DGE GeoGebra. Se vinculan como elementos guía los resultados de la investigación de Benítez Mojica y Santos-Trigo (2006), que describe una secuencia instruccional en la construcción de conjeturas geométricas mediante un DGE, en aras de brindar orientación desde la resolución de problemas.
Esta secuencia permite la identificación de invariantes y propiedades emergentes durante el proceso de configuración de las conjeturas y está estructurada en cinco etapas clave:
-
Identificación visual de la conjetura
-
Puesta a prueba de la conjetura (prueba de arrastre)
-
Construcción de una macro para la verificación de la conjetura
-
Cuantificación y verificación de propiedades para detectar patrones
-
Presentación de argumentos formales para la comprobación de la conjetura
El desarrollo de cada etapa se concretó como actividad de investigación. Se inició con la presentación de un problema y las interrogantes a su alrededor, i.e., la colinealidad de los baricentros de un triángulo. Esta conjetura surgió como resultado de la construcción de una configuración inicial durante las exploraciones propias de uno de los autores de este artículo, después de usar reflexiones axiales de los lados de un triángulo y preguntándose por las propiedades que se obtienen con los puntos notables del triángulo. Después de aplicar la secuencia instruccional mencionada anteriormente, la conjetura fue reafirmada por dos de los autores y extendida a la generalización en el contexto de un paralelogramo. Subsecuentemente, el tercer autor, con formación en matemáticas, demostró los resultados. Esta demostración fue posteriormente presentada en diversos cursos y seminarios.
Actividad de investigación
Se plantea un problema geométrico, con el objetivo de formular una conjetura. La idea es explorar las propiedades y relaciones entre los elementos que conforman la configuración inicial.
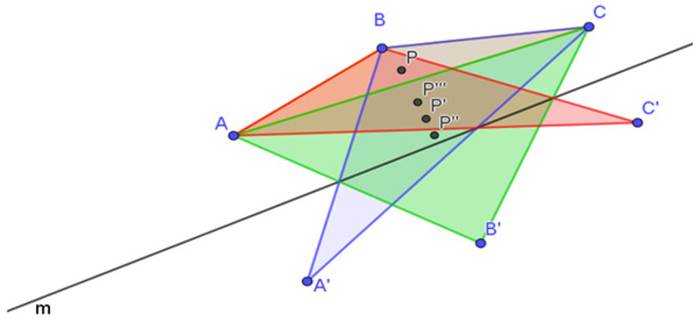
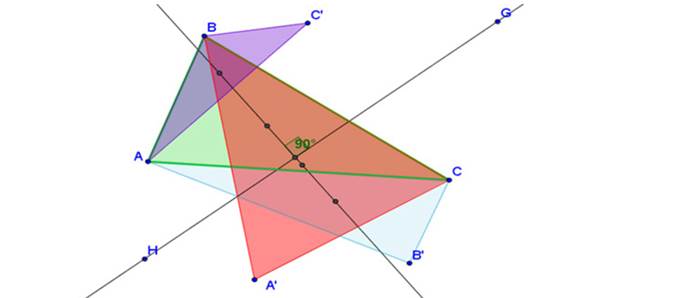
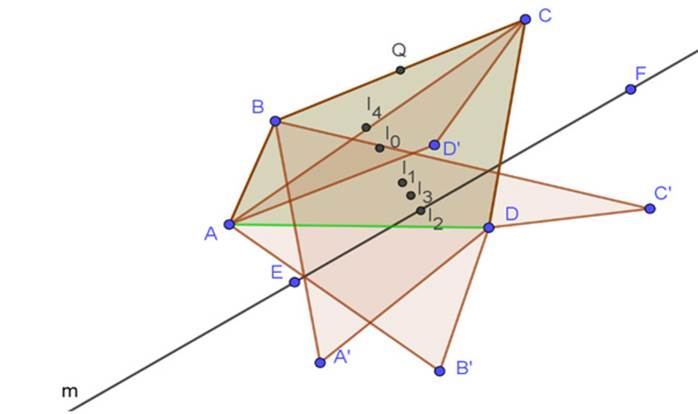
Formulación del problema. Sea ABC un triángulo y sea m una recta cualquiera. Se trazan los puntos A´B´ y C´, simétricos axiales de A, B y C respectivamente, con respecto a la recta m. Se trazan los triángulos ABC´, ACB´ y CBA´. Se construyen los baricentros P, P´, P´´ y P´´´ de los triángulos ABC, CBA´, ACB´ y ABC´ respectivamente, como se muestra en la Figura 1.
Figura 1: Baricentros del triángulo inicial y triángulos simétricos.
Por lo tanto, se plantea la siguiente pregunta: ¿qué propiedades o relaciones se pueden formular sobre los baricentros P, P´, P´´ y P´´´?
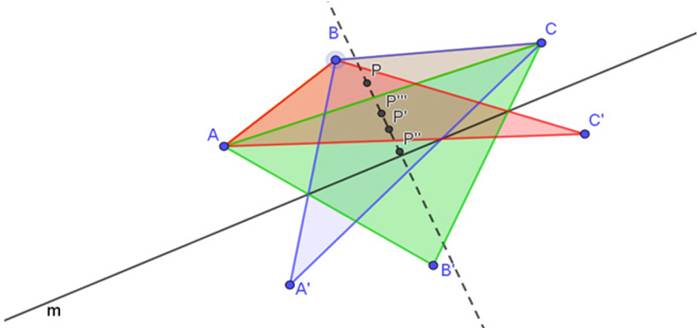
Identificación visual de la conjetura. Una importante característica de GeoGebra es que se pueden hacer construcciones con precisión. Esto resulta en visualizaciones adecuadas de las posibles relaciones entre objetos geométricos, las cuales constituyen el germen de una conjetura. Para el caso particular del problema de estudio, se elaboran un triángulo ABC y una macro-construcción que genera su baricentro. Se trazan los baricentros P, P´, P´´ y P´´´ de los triángulos ABC, CBA´, ACB´ y ABC´. Una vez hechos los trazos, se observa que los cuatro baricentros dan la apariencia de estar alineados, por lo cual se traza una recta por dos de ellos.
Figura 2: Colinealidad de los baricentros
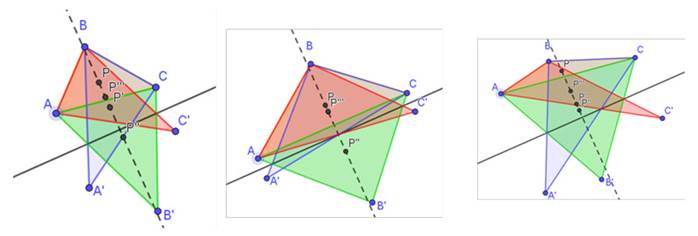
Prueba del arrastre. El dinamismo del ambiente GeoGebra permite verificar si la conjetura falla o se mantiene dentro de una familia de objetos isomórficos. En este caso, se exploró la validez de la conjetura para una familia de triángulos mediante el arrastre.
La prueba del arrastre es recurrente en sistemas de geometría dinámica como GeoGebra. Cuando se dice que los objetos geométricos son isomórficos según la prueba de arrastre, se hace referencia a que, al manipular o arrastrar los puntos o elementos geométricos en la interfaz del software, las propiedades esenciales bajo las cuales fue construida la figura o el objeto se mantienen constantes.
En otras palabras, si dos figuras son isomórficas bajo la prueba del arrastre, esto significa que, al mover, girar o transformar una figura en otra mediante manipulaciones directas en la interfaz y sin cambiar sus propiedades geométricas fundamentales, la esencia de la figura original se mantiene. Esto proporciona una manera dinámica de explorar y comprender las relaciones entre objetos geométricos al interactuar con ellos en tiempo real.
La capacidad de preservar propiedades esenciales durante la manipulación es lo que hace que dos objetos sean considerados isomórficos bajo la prueba del arrastre en un sistema de geometría dinámica. Este enfoque facilita el estudio y la comprensión de conceptos geométricos al permitir a los usuarios experimentar con las formas y sus relaciones de manera interactiva.
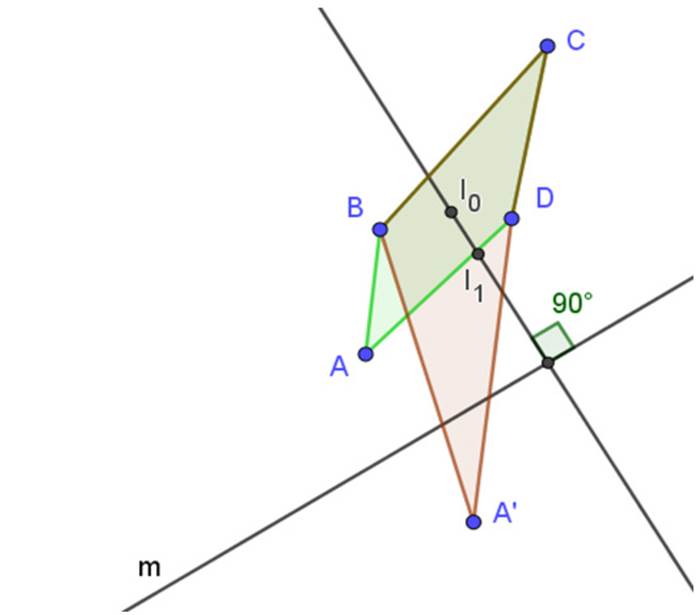
Durante la prueba de arrastre, se encontraron dos aspectos relevantes en la construcción de la conjetura: (i) que la colinealidad de los baricentros se mantiene en los casos explorados y (ii) que la recta de los baricentros parece ser perpendicular con la recta m.
Figura 3: Prueba de arrastre
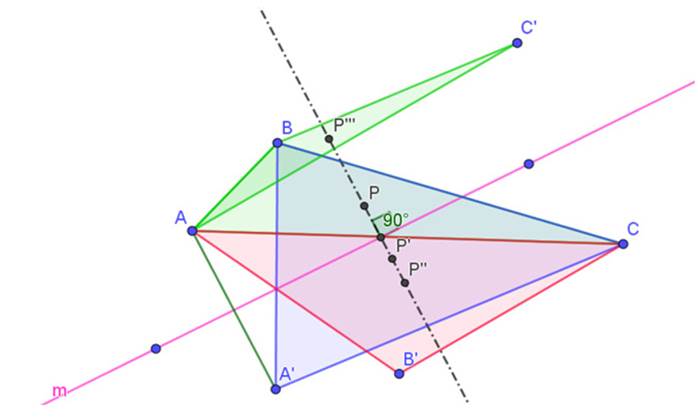
Cuantificar y verificar las propiedades de objetos matemáticos. Hasta este momento, en nuestra exploración muestra un germen de conjetura que emerge de la visualización. La idea es realizar un conjunto de medidas y pruebas para verificar propiedades. Con el software, es fácil cuantificar atributos (pendientes, ángulos, relaciones entre objetos, etc.) de la figura y observar si la conjetura se mantiene desde otro registro de representación. Para este caso particular, se tomaron las siguientes medidas y se verificaron las siguientes propiedades:
-
Se trazó una recta por P y P´ y otra por P y P´´. Posteriormente, se midieron las pendientes de estas dos rectas y se confirmó que eran iguales.
-
Se utilizó la opción de verificación de propiedades entre P´´ y la recta que pasa por P y P´´. El software reportó que el punto P´´ pertenecía a la recta.
-
Se midió el ángulo entre la recta m y la recta de los baricentros. El ángulo siempre era de 90º.
-
Se utilizó la opción de verificación de propiedades para las dos rectas. GeoGebra reportó que las dos rectas eran perpendiculares.
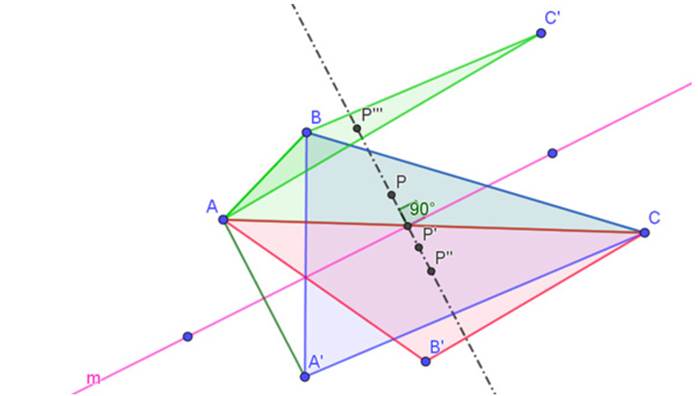
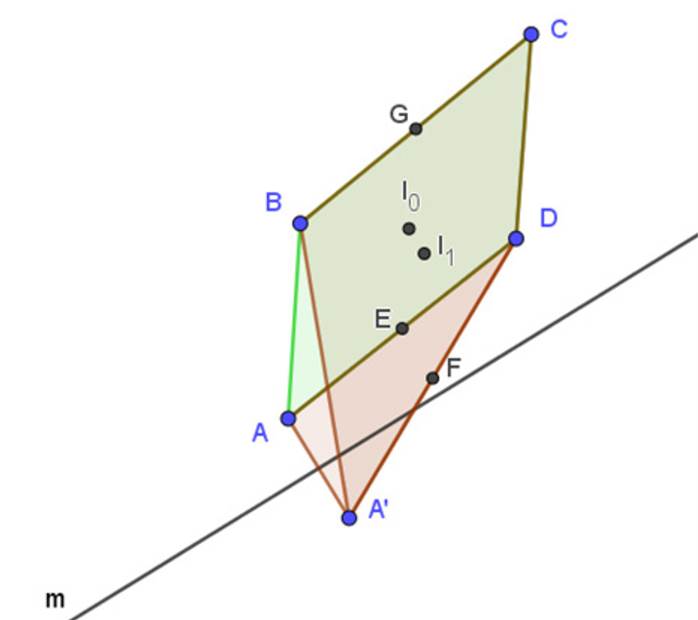
Formulación de la conjetura emergente. Sea ABC un triángulo y sea m una recta cualquiera. Se trazan los puntos A´, B´ y C´, simétricos axiales de A, B y C respectivamente, con respecto a la recta m. Se trazan los triángulos ABC´, ACB´ y CBA´. construimos los baricentros P, P´, P´´ y P´´´ de los triángulos ABC, CBA´, ACB´ y ABC´, respectivamente, como en la Figura 4.
Figura 4: Perpendicularidad entre las rectas
Entonces:
-
Los baricentros P, P´, P´´ y P´´´ de los triángulos ABC, CBA´, ACB´ y ABC, están alineados.
-
La recta que contiene los cuatro baricentros es perpendicular a la recta m.
Construcción de una macro
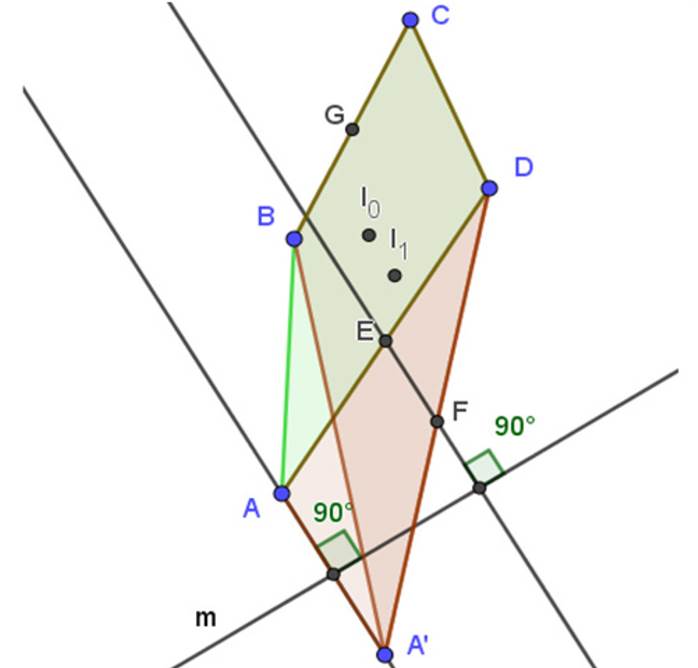
Dado un conjunto de objetos iniciales, se elaboró un conjunto de trazos geométricos hasta obtener los objetos finales. Para cada conjunto de objetos iniciales, un programa o función computacional (denominada macro-construcción) entrega un único conjunto de objetos finales. Para este caso particular, se construyó una macro con las siguientes características:
-
Objetos iniciales: el triángulo ABC y la recta m.
-
Proceso: construir los simétricos axiales de A, B y C con respecto a m. Se trazan los triángulos ABC´, ACB´ y CBA´. Se construyen los baricentros P, P´, P´´ y P´´´ de los triángulos ABC, CBA´, ACB´ y ABC´ respectivamente.
-
Objetos finales: los baricentros P, P´, P´´ y P´´´, la recta que pasa por estos baricentros y el ángulo entre la recta m y la recta que pasa por los baricentros.
En la pantalla de GeoGebra, se observó que, cada vez que se le aplica la macro al triángulo ABC y a la recta m, los objetos finales y la configuración son los siguientes:
Figura 5: Configuración de la macro-construcción
Argumentación formal
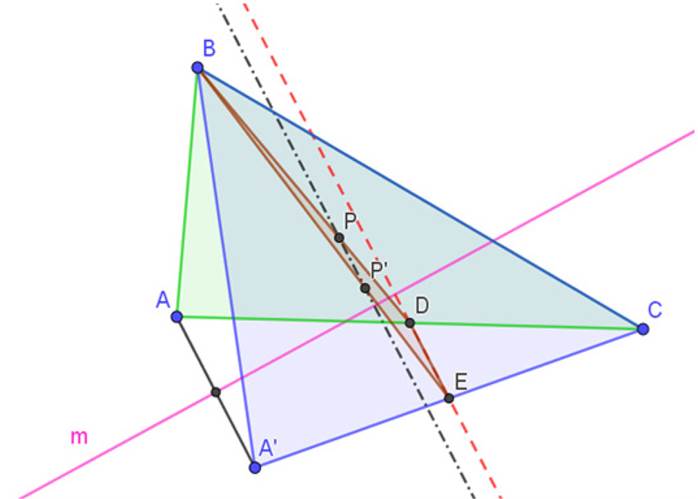
Sea ABC un triángulo y m una recta arbitraria. Sean A', B' y C' reflexiones axiales de A, B y C sobre m respectivamente. Se quiere probar que los baricentros de los triángulos ABC, A'BC, AB'C y ABC' están alineados y que la recta que los contiene es perpendicular a la recta m.
Figura 6: Ideas básicas para construir la prueba formal
Se probará, además, que la recta que contiene el baricentro del triángulo ABC y contiene al baricentro de A'BC es perpendicular a m. Lo anterior es suficiente debido a la unicidad de dicha recta perpendicular. Se podría cambiar A'BC por AB’C y ABC'.
Se denotan con P y P' los baricentros de ABC y A'BC respectivamente. Sean D y E los puntos medios de los segmentos AC y A’C respectivamente. Por la definición del punto A', se tiene que el segmento AA' es perpendicular a la recta m. Considerando el triángulo AB'C, recordando que D y E son puntos medios de AC y A'C y por el teorema de Tales, se sigue que la recta que pasa por D y E es paralela a la que pasa por A y A'. Por tanto, DE es perpendicular a m.
Figura 7: Unicidad de la recta perpendicular
Sean P y P' los baricentros de los triángulos ABC y A'BC. Por la definición del baricentro de un triángulo, se tiene que P y P' son los puntos sobre los segmentos BD y BE respectivamente. Para estos baricentros, PB y P'B miden dos tercios de los segmentos DB y BE. De nuevo, por el teorema de Tales en el triángulo DEB y la proporción entre sus lados, se sigue que la recta que pasa por P y P' es paralela a la recta que pasa por D y E. Dado que esta última es perpendicular a m, se sigue que la recta que pasa por P y P' también lo es, que es lo que se quería probar.
Figura 8: Analogía del razonamiento
Ahora bien, se puede hacer un razonamiento análogo para los baricentros de los triángulos ABC' y AB'C. De aquí se desprende que las rectas PP´, PP´´ y P P´´´ son perpendiculares a m. Sin embargo, por el punto P puede trazarse una sola recta perpendicular a m. Por lo tanto, se puede concluir que:
-
Los baricentros P, P´, P´´ y P´´´ de los cuatro triángulos, están alineados.
-
La recta que contiene los cuatro baricentros es perpendicular a la recta m.
Extensión: el caso de los cuadriláteros
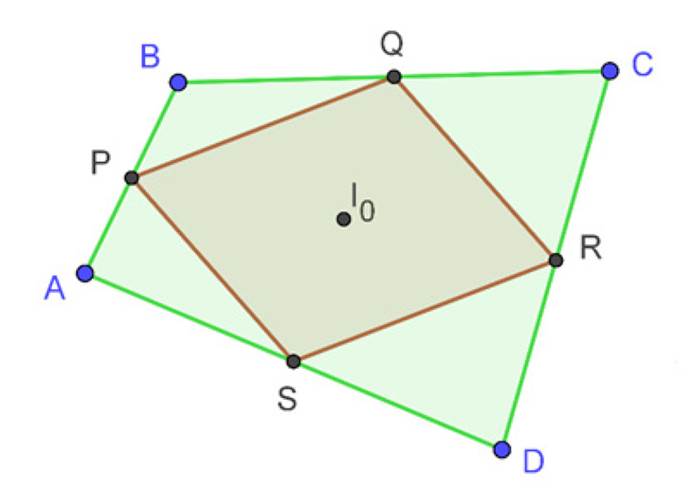
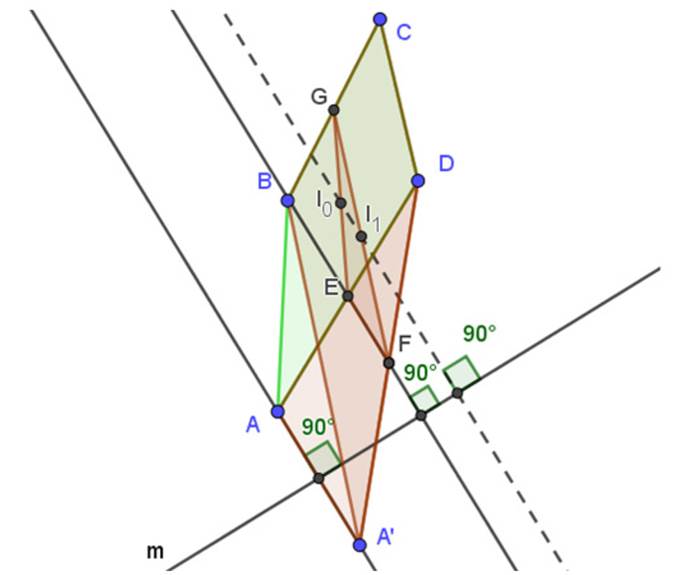
El teorema de alineación de baricentros presentado anteriormente no funciona para otros puntos notables de un triángulo (incentro, circuncentro y ortocentro). Sin embargo, se puede extender este resultado a los baricentros de un cuadrilátero. Para tal fin, se puede considerar ABCD como un cuadrilátero cualquiera. Sean P, Q, R y S los puntos medios de los lados de ABCD. El cuadrilátero PQRS es un paralelogramo. El centro I0 del cuadrilátero EFGH se toma como centro de ABCD.
Figura 9: En búsqueda de una extensión
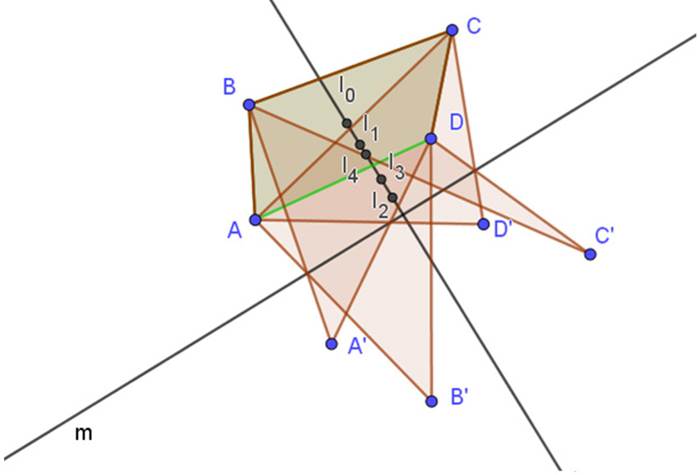
Sean ABCD un cuadrilátero y m una recta arbitraria. Sean A', B', C' y D' reflexiones axiales de A, B, C y D sobre m. Se probará que los centros I0, I1, I2, I3 e I4 de los cuadriláteros ABCD, A'BCD, AB'DC, ABC'D y ABCD' están alineados y que la recta que los contiene es perpendicular a la recta m.
Figura 10: Colinealidad de los baricentros
Se probará que la recta que contiene el centro I0 del cuadrilátero inicial y el centro I1 de A'BCD es perpendicular a m. Lo anterior es suficiente debido a la unicidad de dicha recta perpendicular, se podría cambiar A'BCD por AB’DC, ABC'D y ABCD'.
Figura 11: Perpendicularidad de las rectas
Se denotan con I0 e I1 los centros de ABCD y A'BCD respectivamente. Sean E, F y G los puntos medios de los segmentos AD, A'D y BC. Se traza el triángulo AA'D.
Figura 12: Ideas básicas para la prueba formal
Por la definición del punto A', se tiene que el segmento AA' es perpendicular a la recta m. Considerando el triángulo AA'D, recordando que E y F son puntos medios de A'D y A'D y por el teorema de Tales, se sigue que la recta que pasa por E y F es paralela a la que pasa por A y A'. Por tanto, EF es perpendicular a m.
Figura 13: Aplicación del teorema de Tales
Es preciso recordar que I0 y I1 son los centros de ABCD y A'BCD, por lo que son los puntos medios de los segmentos EG y FG respectivamente. Por el teorema de Tales, en el triángulo EFG, la recta que pasa por P y P' es paralela a la que pasa por E y F. Dado que esta última es perpendicular a m, se sigue que la recta que pasa por I0 y I1 también lo es, que es lo que se quería probar.
Figura 14: Paralelismo y perpendicularidad
De manera análoga, se puede demostrar que las rectas I0I2, I0I3 e I0I4 son perpendiculares a m. Por otra parte, por un punto exterior a una recta, se puede trazar una y solo una perpendicular. Esto implica que los puntos I0, I1, I2, I3 e I4 están alineados.
Figura 15: Analogía del razonamiento
Los hallazgos reportados en esta investigación involucran distintas miradas en cuanto a la educación matemática. Una de ellas es el vínculo entre la tecnología computacional y la resolución de problemas, la generación de conjeturas y los procesos emergentes como formas de razonamiento matemático, lo cual se detalla en el desarrollo de la actividad instrumentada (Monroy, 2023).
En el análisis de la construcción de una conjetura geométrica, y más específicamente en la exploración de la enseñanza de dicho proceso utilizando DGE, se evidencian estructuras de control que influyen de manera determinante en el pensamiento del conjeturador. Estas estructuras de control están estrechamente vinculadas a las decisiones tomadas para llevar a cabo la tarea mencionada, así como a los elementos que podrían influir en el diseño de actividades destinadas a fomentar la conjeturación. Entre estos elementos se destacan los procesos cognitivos subyacentes a la actividad geométrica, tales como la visualización, el razonamiento y la construcción. La interrelación entre estructuras de control y procesos cognitivos proporciona un marco integral para comprender y potenciar la capacidad de conjeturar en el ámbito de la geometría.
Adicionalmente, un elemento clave en la estructura de control son las operaciones cognitivas que emergen durante la actividad estudiada. A continuación, se presentan las operaciones detalladas en la exploración.
Tabla 1: Operaciones visuales dinámicas
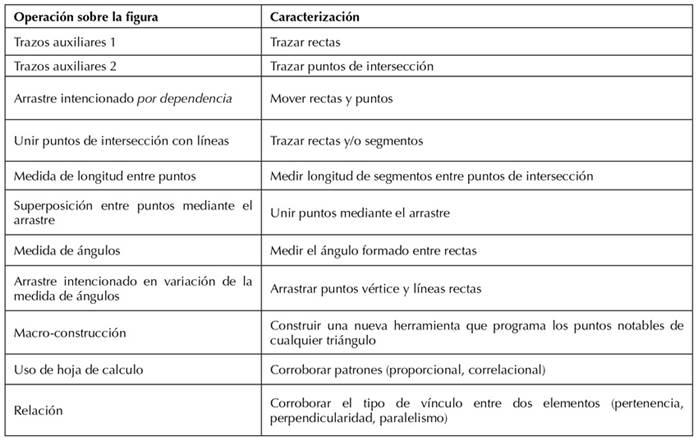
Una operación visual es un tipo de operación cognitiva que se lleva a cabo en el proceso de comprensión y manipulación de figuras geométricas. Estas operaciones se centran en la interpretación y la modificación de las características visuales de las figuras, como lo son su forma, posición, tamaño y orientación.
Las operaciones visuales permiten a los individuos realizar transformaciones mentales en las figuras, lo que les brinda la capacidad de visualizar y comprender las relaciones espaciales y geométricas entre los elementos. Al realizar estas operaciones visuales, los individuos pueden explorar las diferentes configuraciones de las figuras, compararlas y establecer conexiones entre ellas.
Estas operaciones fueron identificadas de acuerdo con el patrón de los datos. Con el uso continuo del DGE, fueron emergiendo unas más que otras como parte del proceso de conjeturación, pero en esencia permitieron materializar lo que se deseaba hacer con la configuración inicial, realizando modificaciones que permitieran llegar a una corroboración o a un posible resultado.
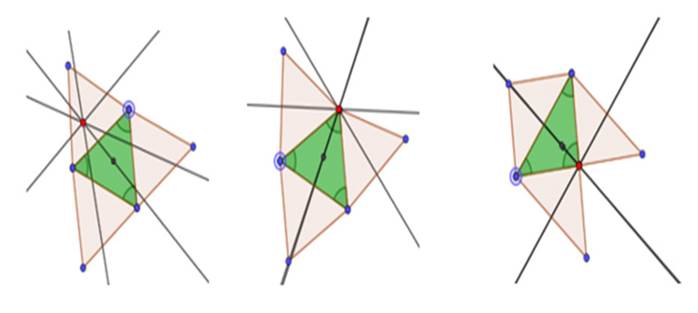
Dado su carácter dinámico, estas operaciones permitieron establecer relaciones entre los elementos de la figura. Una, por ejemplo, fue la de superposición de puntos mediante el arrastre (Figura 16).
Figura 16: Superposición de puntos
Conclusiones
Esta investigación establece una posible ruta para la construcción y el seguimiento de una conjetura en un DGE, reconociendo las implicaciones de estos entornos en el proceso de conjeturación, que involucran la visualización activa y el reconocimiento de las pseudo-realidades que genera el movimiento.
Se presenta un nuevo teorema geométrico que involucra baricentros de triángulos, el cual fue construido directamente en un DGE, en aras de que un estudiante pueda ser guiado a establecer conjeturas a través de la exploración de estas herramientas.
El mismo DGE facilitó la extensión de dicho resultado a cuadriláteros, que se visualizaron a través de elementos constitutivos como el arrastre y la programación de macro-construcciones.
Se suministran las demostraciones matemáticas de los nuevos resultados, y se hace reconocimiento de la herramienta cognitiva de arrastre que ofrece el DGE, cuyo uso se ha documentado como determinante en el discernimiento de invariantes y en la conducción al razonamiento matemático, especialmente en el proceso de generación de conjeturas en geometría.
La exploración del problema planteado abre las puertas a otras investigaciones en el campo de la educación matemática que diseñen e implementen actividades de aprendizaje similares para su integración en un curso de geometría euclidiana. Este enfoque no solo busca ofrecer nuevo contenido, sino también propiciar un cambio de paradigma en la introducción de tecnologías emergentes en la educación matemática. Al asignar a los estudiantes un papel central en la comunicación, la formulación de conjeturas y la reflexión sobre su proceso de aprendizaje en geometría, se aspira a cultivar un ambiente de aprendizaje participativo que contribuya al desarrollo de los procesos centrales del pensamiento matemático. Es esencial destacar que el verdadero impacto de esta integración tecnológica no radica únicamente en la herramienta computacional, sino en la sinergia armónica de diversos componentes, incluyendo la didáctica, la historia, el lenguaje, la filosofía y la epistemología de las matemáticas, en entornos educativos que trasciendan a los métodos tradicionales basados en lápiz y papel.
Se han explorado resultados similares para los ortocentros, circuncentros e incentros, pero no hay colinealidad. En los lugares geométricos que dejan estos puntos, no se han encontrado regularidades. Se han realizado otras exploraciones geométricas mediante extensiones y generalizaciones, lo cual puede dar continuidad al trabajo en esta línea de investigación.
Referencias
License
Copyright (c) 2024 Yonathan Bonelo-Ayala, David Benítez-Mojica, Jhovanny Muñoz-Posso

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.