Firma digital basada en redes (Lattice)

Edilberto José Reyes González

Escuela de Matemáticas, Profesor Asociado Universidad Industrial de Santander.

Juan Gabriel Quintero Peña

Ingeniero de Sistemas UIS - Universidad Industrial de Santander, Magister en Ingeniería, UIS.

Resumen

Se describe la secuencia de pasos necesaria para firmar digitalmente mediante Redes (Lattice) un mensaje, basado en la conjetura computacional de la dificultad que implica el problema de reducción SVP[1] y CVP2[2] . El objetivo es brindar una alternativa al momento de utilizar algoritmos de cifrado de clave pública y firmas digitales.

Palabras Clave:

Criptografía de clave pública, firma digital, funciones Hash, redes (lattice), archivos binarios.

---

INTRODUCCIÓN

La facilidad que brinda la Web a la comunicación entre personas permite disminuir el consumo del papel y aumentar la velocidad de entrega, aunque presenta una dificultad al asociar al mensaje la identidad del usuario. Este inconveniente ocasiona que el intercambio de información se convierta en una actividad insegura debido a que no se tiene certeza de quien remite ni garantía de la no alteración de los datos. Puede darse el caso que un tercero suplante al emisor o altere el mensaje sin que exista alguna forma de validar la integridad de la información, lo cual podría facilitar el fraude informático.

Una solución a esta situación la brinda la criptografía de clave pública, en particular la firma digital.

Una firma digital es una cadena de datos creada a partir de un mensaje (o parte de él), de forma que sea difícil que quién lo envía reniegue la acción (repudio) y que el individuo que recibe pueda asegurar que el emisor es realmente quien dice ser, es decir, el receptor de un Mensaje digital 'pliede.asegurar Cual es el origen del mismo (autenticación). Además, las firmas digitales garantizan la integridad de los datos (no modificación durante la transmisión).

El mecanismo de firma digital por ser de clave pública basa su seguridad en algún problema matemático que proporciona una función de una vía (one-way function) como: factorización de números primos grandes (RSA [3]), curvas elípticas, logaritmos discretos y muchos otros problemas, entre los cuales se encuentra el problema de reducción de redes (lattice).

1. CONCEPTOS DE FIRMA DIGITAL

1.1 Funciones Resumen (Hash)

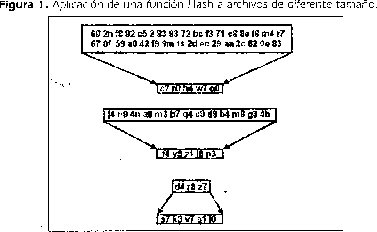
De manera matemática, se puede definir una función resumen (hash functions) como proyecciones de un conjunto, generalmente con un número elevado de elementos, sobre un conjunto de tamaño fijo y mucho más pequeño que el anterior. Al resultado obtenido al aplicar una función resumen se le llama número resumen. En Fig 1 se observa a manera de ejemplo tres casos de aplicación de una función hash.

El resultado de aplicar una función resumen tiene las siguientes características:

• Todos los números resumen generados con un mismo método tienen el mismo tamaño, sea cual sea el texto utilizado como base.

• Dado un texto base, es fácil y rápido (para un computador) calcular su número resumen.

• Es imposible reconstruir el texto base a partir del número resumen.

2. FIRMA DIGITAL

El propósito de una firma es asociar la identidad del firmante con la información registrada en el documento (autenticidad). Las firmas manuscritas permiten realizar esta función pero si el documento es alterado el firmante seguirá avalando la información registrada en él. Las firmas digitales por el contrario permiten asociar la identidad del firmante con el documento avalado y detectar modificaciones del mismo (Integridad).

Una firma digital de un documento es un segmento de información (un grupo de bits) basado en el documento a firmar, la clave del usuario y en una función o esquema de firma.

Las firmas digitales se construyen utilizando criptografía de clave pública, la cual utiliza dos claves, una privada y otra pública. La primera se mantiene en secreto y la segunda se divulga libremente. Para firmar es necesario utilizar la clave privada y para verificar la firma se utiliza la clave pública.

Para que una firma digital producida sea válida debe cumplir:

• Vigencia. Haber sido creada durante el período de vigencia del certificado digital válido del firmante.
• Verificación. Ser debidamente verificada por la referencia a los datos de verificación de firma digital indicados en dicho certificado según el procedimiento de verificación correspondiente.
• Emisión. Que dicho certificado haya sido emitido o reconocido por un certificador licenciado.

Cualquier esquema de firma cuenta con dos partes, la primera se denoMina proceso de firma (similar al cifrado) y la segunda parte proceso de verificación de la firma (similar al descifrado). Existen dos tipos de esquemas sobre firma digital, uno denominado esquema de firma digital con apéndice [4] y el esquema de firma digital con mensaje recuperable.

2.1 Esquema de Firma con Apéndice

2.1.1 Proceso de Firma

a. Se le aplica al mensaje M (mensaje a firmar) una función hash que reduce su longitud a un mensaje H(M) de longitud 128 o 160 bits, dependiendo el tipo de función que aplique, lo cual permite trabajar cualquier archivo como una cadena de longitud constante.

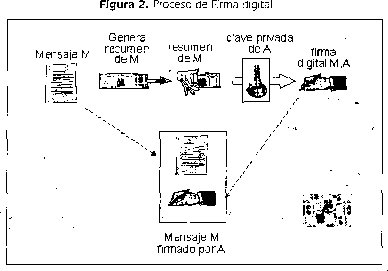
b. I-1(M) se somete también a un proceso de cifrado según el algoritmo aplicado (RSA, DSS) con lo cual se obtiene un número h(M).

c. Se envía el mensaje firmados

2.1.2 Proceso de Verificación

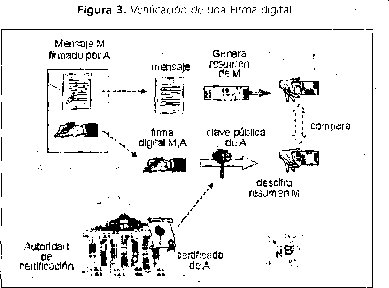
a. Quien recibe s, se supone conoce el mensaje M, aplica la función de verificación que depende de la clave pública de quien se dice propietario del mensaje.

b. Se aplica la función hash al mensaje M y si h (M) = h' entonces acepta la firma.

2.2 Esquema de Firma con Mensaje Recuperable

En este esquema no es necesario conocer el mensaje, luego que la firma es aceptada éste se puede recuperar.

3. REDES Y PROBLEMAS ASOCIADOS

3.1 Redes (Latticess[]5)

Son objetos geométricos usados para resolver muchos problemas en matemáticas y en ciencia de la computación. Se puede describir gráficamente como un conjunto de intersecciones de puntos de una cuadricula regular (pero no necesariamente ortogonal) n dimensional.

Figura 4. Ejemplo de un Lattice en dos dimensiones [6] Definition and Related Problems

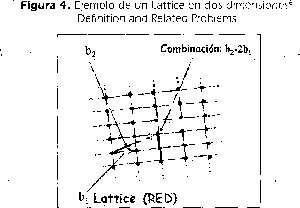
Una definición formal de una Redes:

Dado B = {b₁, b₂,... b_n.) vectores linealmente independientes en 1 m, la Red generada por B es el conjunto de todas las combinaciones lineales con coeficientes enteros de los vectores base.

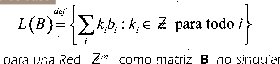
Se toma una base para una Red Z^m como matriz B no singular de n x n , en la cual las columnas son los vectores de la base. De esta forma, la Red generada por es el conjunto

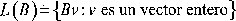
Existen muchas bases para cualquier Red L . Por ejemplo, si el conjunto B = {b₁, b₂,... b_n.) genera alguna Red entonces tomando cualquier vector b_{1 ∈} B y adicionando a él cualquier combinación lineal entera de los otros vectores se obtiene una base diferente para la misma Red. Un hécho importante sobré las Redes es que todas las bases de una Red tienen el mismo determinante. Esto ocurre debido que hay una matriz entera T tal que BT = C y otra matriz T¹ = B tal que CT¹ = B.

Las Redes proporcionan problemas que no pueden ser resueltos en tiempo polinomial (NP-hard) y que permiten crear funciones de una vía o funciones tramposas;, uno de ellos, es el problema del vector más corto (SVP) y otro es el del vector más cercano (CVP) en L (Lattice).

3.2 SVP. Problema del vector más corto[7]

El problernErdel vector más corto (con respecto a [8]) es: dada una Red encontrar un vector no cero en él, tal que la norma del vector sea mínima. En otras palábras, dado >L (B), encontrar

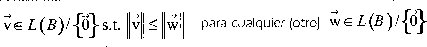
El interés en el problema no es por la solución trivial (el vector cero, el cual tiene la norma más pequeña que cualquier otro vector).

La solución al SVP depende de la norma que se esté usando. Cuando se utilizan bases reducidas el primer vector es aproximadamente el más corto en el Lattice.

3.2 CVP. Problema del vector más cercano

Dada una Red L(B) y un vector objetivo 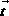encontrar 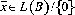tal que sea mínima.

Se simplifica este problema probando encontrar un punto dentro de un cierto paralelepípedo P(B*), donde B* el resultado de aplicar ortogonalización de Gram- Schmidt a B .

El problema se traduce en encontrar un vector entero dentro de 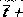P(B*)

4. ESQUEMA DE FIRMA BASADO EN LATTICE [9]

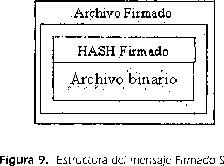
La firma digital con Lattice se le aplica al resumen del archivo, tal como se muestra en Fig 7.

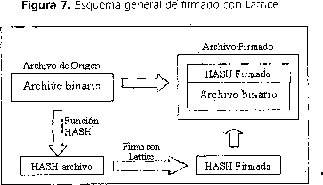
Luego ésta se firma con Lattice obteniendo un resumen firmado. Para poder enviar la información se concatenan el resumen firmado con el archivo binario creando un paquete, buscando que cuando éste llegue a su destino y se verifique la validez de la firma, se pueda extraer el archivo original (binario).

Todo el proceso de firma con Lattice se muestra para el usuario como una elección de archivo fuente, tipo de resumen (MD5 o Shal), clave privad o clave pública y ruta de archivo destino. De manera que la complejidad del problema de los Lattice para firmar archivos queda totalmente oculta para el usuario.

Para firmar archivos con Lattice se requiere contar con un juego de claves, la privada y la pública, las cuales se obtienen de la siguiente manera:

4.1 Generación de Claves

Este proceso se debe realizar para obtener las claves pública (B) y privada (R) , las cuales corresponden a las bases de los Lattices a utilizar en el proceso.

Las bases B y R son representadas por matrices de nxn son las columnas de éstas.

4.1.1 Base Privada

Se empieza a partir de una caja K • I en Zⁿ (pára un número entero k ), y se adiciona un «ruido» a cada uno de los vectores de la caja. En particular, se escoge una matriz

R' que se distribuya uniformemente en 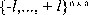y después se calcula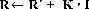

4.1.2 Base Pública

Una vez se tenga la base privada 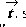se debe escoger la base pública B según una cierta distribución del Lattice L(R) .

La forma de obtener la base pública es: se multiplica R por algunas matrices unimodulares «aleatorias» para obtener aB, particularmente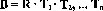

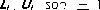Cada una de estas matrices de transformación unimodular se escoge como un producto de un matriz triangular superior y una matriz triangular inferior, T, = L,U, , donde las entradas de la diagonal en las otras entradas de L₁ ,U₁ son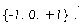

4.2 Esquema De Firma Digital Con Lattice

La firma con Lattice se realiza por medio de dos procesos, uno de firma y otro de verificación. En cada úno de ellos se llevan a cabo proCedimientds que permiten firmar aplicando el problema de reducción de Lattice.

Se propone un esquema de firma con mensaje recuperable.

4.2.1 Proceso de Firma

Requiere conocer el Lattice               (clave pública).

a. Se le aplica al mensaje M (mensaje a firmar) una función Hash que reduce su longitud a un mensaje h(M) de longitud 128 o 160 bits, dependiendo el tipo de función que el usuario escoja (MD5 o SHA-1), lo cual permite trabajar cualquier archivo como una cadena de longitud constante. Esto se hace para garantizar que no ocurrirán alteraciones durante el envío.

b. h(M) se somete a un proceso de cifrado aplicando Lattice.

• Se crea un vector 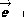(error o ruido) y un vector 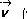(vector de información).

Vector e

Se crea escogiendo valores entre 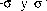de manera aleatoria asignándolos a cada componente del vector, donde a se toma como 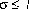Máxima norma de R.

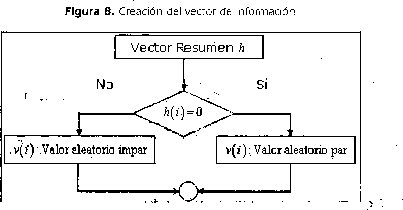
Vector v

A partir del resumen obtenido del archivo h(M) se crea un vector que contiene valores aleatorios pares e impares dependiendo del contenido del mismo.

• Se realiza el cifrado del vector 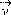obteniendo un vector 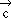mediante la operación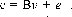

c. Envía el mensaje firmado S

• Proceso de Verificación

Requiere conocer el Lattice R (clave privada).

a. Quien recibe el mensaje firmado S aplica la funCión de verificación que depende de la clave privada de quien se dice propietario del mensaje.

                                                                        

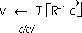
Teniendo en cuenta la definición

                                                                        

Al aplicar la función mostrada anteriormente, lo que se hace es representar a 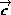como una combinación lineal de las columnas de R y redondear los coeficientes de ésta a los números enteros más cercanos para obtener un punto Lattice. La representación de este punto Lattice como combinación lineal en las columnas de B es el vector .

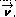b. Luego de recuperado el vector se procede a realizar un proceso de recuperación del resumen almacenado en él, según Fig 10.

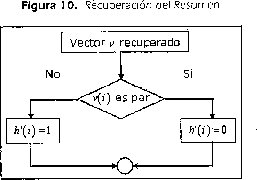
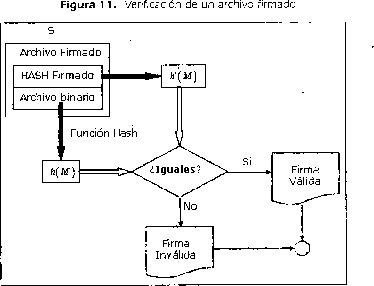
c. Se procede a comparar el resumen recuperado h(M) con el resumen del archivo h(M) contenido en S. Si coinciden, quiere decir que el archivo firmado es válido y puede ser aceptado.

5. BIBLIOGRAFÍA

• [1] AJTAI, Miklos and Dwork, Cynthia. A public key cryptosystem with worst case/ average case equivalente. ACM Symposium on theory of computing. 1997.
• [2] BABA!, L. On Lovász lattice reduction and the nearest lattice point problem. in Combinatorica, vol. 6, 1986, pp. 1-13.
• [3] DWORK, Cynthia. Lattices and Their Application to Cryptography, Stanford University, Spring Quatre. 1998.
• [4] FISCHLIN, Roger and SEIFERT, Jean Pierre. Tensor based trapdoors for CVP and their application to public key cryptography. Goethe university at Frankfurt, Germany, 2000.
• [5] GOLDREICH, Oded, Weizmann Institute of Science, ISRAEL, GOLDWASSER Shafi, HALEVI Shai, MIT, Laboratory . for computer science, Public key cryptosystems from lattice reduction problems. 1997.
• [6] LENSTRA, H.W and LOV'ASZ, L.. Factoring polynomials with rational coefficients. Mathematische Annalen 261, 515-534 (1982).
• [7] LUCENA, Manuel José. Criptografía y seguridad de computadores. Segunda Edición. España, 1999.
• [8] MICCIANO, Daniele. Lattices in cryptography and cryptoanalisys. University of California. San Diego, 1999.
• [9] and GOLDWASSER, Shafi. Complexity of Lattice Problems: a Cr_yptographic Perspective, volume 671 of The Kluwer International Series in Engineering and Computer Science. Kluwer Academic Publishers, Boston, Massachusetts, Mar. 2002.
• [10] RAMI&Oacuxte; AGUIRRE, Jorge. Libro digital de Seguridad Informática y Criptografía. Madrid España 2005.
• [11] SCHNEIER, Bruce. Applied Cryptography : Protocols, algorithms and Source code in C. Editorial John Wiley. New York. 1996. 758.

Notas

1. Problema del vector más corto (Short Vector Problem).
2. Problema del vector más cercano (Closest Vector Problem).
3. RSA. Algoritmo de clave pública creado por Ron Rivest, Adi Shamir, y Leonard Adleman.
4. Ver [7].
5. Ver [8].
6. Tomado de: Lattice. Definition and Related Problems.
7. Ver [9].
8. Es una norma. Por lo general se utiliza la norma euclidiana definida como
9. En adelante el término Lattice se toma como análogo a Red

---