La relación: Matemática-Semiosis-Argumentación, en la elaboración de diseños didácticos

Olga Lucía León C

olleon@udistrital.edu.co

La autora es Doctora en Educación, con énfasis en Educación Matemática de la Universidad del Valle, miembro del Grupo de Investigación interdisciplinaria en Pedagogía del lenguaje y las matemáticas y profesora de planta de la Universidad Distrital Francisco José de Caldas.

Resumen

Este artículo presenta resultados de investigación sobre las relaciones entre los componentes curriculares, cognitivos, comunicativos y matemáticos, que se requieren para los diseños didácticos que buscan la formulación de relaciones geométricas como la pitagórica.

El diseño investigativo general se estructuró desde la ingeniería didáctica. Se presentan aquí los análisis a priori y a posteriori de uno de los talleres del diseño didáctico estructurado [1]. Los dos niveles de análisis comprometen en la dimensión pedagógica, el desarrollo didáctico; y_ en la dimensión matemática, el desarrollo semiótico-argumentativo. De manera que los resultados proporcionan un marco interpretativo de la interacción entre procesos didácticos y desarrollo de conocimiento matemático en un contexto escolar.

Palabras clave:

Didáctica de las matemáticas, análisis de tareas, diseños didácticos, relación pitagórica, semiosis, argumentación en geometría.

Abstract

This article presents results of research on the relations among the mathematical, communicative, cognitive, and curriculum componente, required for the didactic designs looking forward the formulation of geometric relations such as the Pythagoream relation.

The general investigative design was structured since the didactic engineering. The analysis are presented here a priori and a posteriori of one of the workshops of the structured didactic design [2]. The two levels of analysis engage the didactic development in the pedagogical dimension, and the semiotic-argumentative development in the mathematical dimension. Thus the results provide an interpretive framework of the interaction between didactic processes and development of mathematical knowledge in a school context.

The general investigative design was structured since the didactic engineering. The analysis are presented here a priori and a posteriori of one of the workshops of the structured didactic design o . The two levels of analysis engage the didactic development in the pedagogical dimension, and the semiotic-argumentative development in the mathematical dimension. Thus the results provide an interpretive framework of the interaction between didactic processes and development of mathematical knowledge in a school context.

Keywords:

Math teaching, tasks analysis, didactic designs, Pythagoream relation, semiosis, and, argumentative competence in geometry.

1. INTRODUCCIÓN

Dos factores están asociados á este estudio: uno, el reconocimiento de un problema de aprendizaje y de enseñanza situado en un ámbito de desarrollo comunicativo y matemático, vinculado a la construcción significativa de los conocimientos escolares, a través de la argumentación; y dos, la necesidad de desarrollar un saber de tipo didáctico que permita comprender, planear, ejecutar, monitoreary valorar el desarrollo de procesos de aprendizaje escolar relacionados con el aprendizaje de relaciones geométricas.

La investigación pretendió identificar relaciones entre los componentes curriculares, cognitivos, comunicativos y matemáticos, que se requieren para los diseños didácticos que buscan la formulación de relaciones geométricas como la pitagórica.

El diseño investigativo general se estructuró desde la ingeniería didáctica, de manera que en la fase preliminar se determinaron concepciones que circulan en ambientes universitarios sobre la argumentación y la validación que permitieron identificar relaciones entre las dimensiones comunicativa y argumentativa. Estos estudios ya cuentan con resultados publicados en dos libros[3]. El desarrollo de la fase de concepción determinó como resultado la caracterización del ambiente curricular en cuanto a la enseñanza de la geometría y el marco de relaciones teóricas entre representación, argumentación y enseñanza-aprendizaje de la geometría. Estos resultados se presentan como fundamento teórico, tanto del diseño didáctico, como de las categorías de análisis de las tareas en sus niveles macroestructural y microestructural.

En este artículo se presentan los análisis a priori y a posteriori de uno de los talleres del diseño didáctico global. Los dos niveles de análisis comprometen en la dimensión pedagógica, el desarrollo didáctico; y en la dimensión matemática; el desarrollo semiótico-argumentativo. De manera que los resultados proporcionan un marco interpretativo de la interacción entre procesos didácticos y desarrollo de conocimiento matemático en un contexto escolar.

2. ASPECTOS TEÓRICOS DE LA PROPUESTA DIDÁCTICA

Los antecedentes curriculares en cuanto a reformas y textos de apoyo, evidencian la importancia del tema teorema de Pitágoras, durante un siglo (1903-2003) de reformas curriculares y de adecuación de textos a las mismas. Este tema aparece en diversos campos curriculares de la matemática (geometría, aritmética, trigonometría) y como apoyo para el desarrollo de diversos temas (propiedades de las figuras planas, cálculos de longitudes y áreas, relaciones aritméticas entre números, relaciones trigonométricas). Se podría decir que el Teorema de Atágorasse constituye en un componente fundamental que articula diversos campos en el tejido estructural temático curricular que soporta la formación matemática básica de los niños colombianos.

2.1 La relación pitagórica

La comprensión de lo que es una relación requiere considerar diferentes aspectos que sLa relación es un principio activo, en el sentido de que, al aplicarlo a dos o más elementos, produce algo nuevo: una proposición acerca de ellos.

Pero si se contrasta con una operación, una relación parece un principio pasivo, contemplativo, en cuanto que no transforma los elementos (que podríamos llamar «relacionandos») en un nuevo elemento, mientras que la operación sí transforma los elementos (llamados «operandos») en un nuevo elemento (el resultado o producto de la operación).(Vasco, 2005).

En un sentido global de relación, la propoición «La suma de las áreas de los cuadrados sobre los catetos de un triángulo rectángulo es igual al área del cuadrado sobre la hipotenusa [del mismo]» enuncia una relación geométrica entre áreas de figuras, que llamamos «la relación pitagórica». Formulada así: »La suma de los cuadrados sobre los catetos de un triángulo rectángulo es igual al cuadrado sobre la hipotenusa [del mismo]» parece enunciar una relación geométrica entre figuras. Reformulada así: «La suma de los cuadrados de los dos primeros números naturales de una terna o tripla de números es igual al cuadrado del tercero,» enunciaría una relación aritmética entre números naturales. Esta relación aritmética no se cumple para todas las ternas o triplas. En algunas se cumple, como en la terna (3, 4, 5), pero en otras no, como en la terna (4, 5, 6). Si llamamos «ternas pitagóricas» o «ternas rectángulas» a aquéllas en las que sí se cumple, tendríamos otra relación pitagórica, ya no de la geometría, sino de la aritmética, que llamaremos «la relación aritmética pitagórica»: «La suma de los cuadrados de los dos primeros números naturales de una terna o tripla rectangular de números es igual al cuadrado del tercero.»

Si la reformulamos como una relación entre las longitudes de los lados de los triángulos rectángulos, medidas con cualquier unidad, diríamos así: «La suma de las longitudes elevadas al cuadrado de dos de los lados de un triángulo rectángulo es igual a la longitud del tercer lado elevada al cuadrado.» Esta sería uria relación aritmética pitagórica, ya no entre ternas de números de la aritmética natural, sino de la aritmética de los números reales positivos (o en la de los números algebraicos reales y positivos).El hecho de que esa terna siempre defina las longitudes de los tres lados de un triángulo rectángulo es lo que liga la relación aritmética pitagórica con la relación geométrica pitagórica particular; por ello, amerita la demostración de un teorema específico al respecto. La relación pitagórica es una relación ternaria fundamentalmente aditiva, bien entre números: para una terna de números enteros (a, b, c) a² +b² =c² ; bien entre áreas de cuadrados; bien entre cuadrados, o bien entre longitudes de segmentos entre otras.

2.2 La argumentación en el contexto escolar

Las siguientes características del proceso argumentativo se articulan a los procesos educativos estableciendo una relación inmediata con el ambiente escolar.

•En cuanto a su intencionalid ad: «La argumentación es una actividad que siempre trata de modificar un estado de cosas preexistentes» (Perelman & Olbrechts 1989: 105). se presenta aquí un aspecto común entre el discurso epidíctico propio de la argumentación y el discurso educativo por cuanto ambos buscan crear una disposición a la acción con la finalidad de modificar un contexto.

• En cuanto a su objeto:Dos aspectos emergen como objetos fundamentales de la teoría de la argumentación en tanto que cohesionan los demás elementos que la constituyen. En primer lugar está el efecto de la adhesión determinado por el persuadir y convencer.. El segundo lo constituye la interacción y fuerza de los argumentos, dos nociones vinculadas en la producción de un discurso, la primera determina la amplitud y el orden, de la argumentación y la segunda la intensidad de la adhesión y los enlaces utilizados.

• En cuanto a los ro/es de los partic ipantes: Orador y auditorio son los roles asignados en una argumentación. El auditorio se define como el conjunto de aquellos en quienes el orador quiere influir con su argumentación. El desarrollo de la argumentación construye una relación entre orador y auditorio que Perelman & Olbrechts denominan «el contacto intelectual».. Orador y educador pretenden que la intensidad de la adhesión no se limite a la producción de resultados puramente intencionales, sino a desencadenar una acción. En la educación el rol de maestro que tiene el educador, presupone una actitud de confianza en el auditorio, razón por la cual el discurso del educador no precisa partir de tesis que admite el auditorio, para crear una disposición en los oyentes. El segundo, tiene que ver con los roles originados por los procesos de solución de problemas, el prestigio que proviene de obtener una solución que permanece inmodificable a objeciones, consolida otro tipo de educador determinado por el objeto de la argumentación, y que desplaza al maestro en su rol de educador para que eventualmente sea asumido por uno de sus estudiantes. Este segundo aspecto consolida un juego de roles propiciado por el contexto de la argumentación en la solución de problemas en la clase de matemáticas.

• En cuanto a sus métodos: «El uso de la argumentación implica que se ha renunciado a recurrir únicamente a la fuerza, que se atribuye un valor a la adhesión del interlocutor, conseguida con la ayuda de una persuasión razonada» (Perelman & Olbrechts, 1989: 106). Es decir, que el uso de la violencia es contrario a todo proceso argumentativo, como lo es a todo proceso de educación, por cuanto la educación se constituye en la forma como las sociedades forman a sus individuos para la comprensión de los fenómenos que los afectan como pueblos, siendo uno de ellos la autodestrucción de la misma cultura por factores de violencia entre sus integrantes.

Los siguientes factores de desplazamiento, demarcan un tipo de desplazamiento requerido para el desarrollo de la argumentación en matemáticas:

• El auditorio: De una argumentación dirigida a un auditorio heterogéneo a una argumentación dirigida a un auditorio universal que puede ser considerado o bien como un auditorio elite en tanto modelo o un auditorio científico en tanto asimilación voluntaria. «Un auditorio elite sólo encarna al auditorio universal para aquellos que le reconocen este papel de vanguardia y de modelo...Ciertos auditorios especializados se asimilan voluntariamente al auditorio universal como el auditorio científico (Perelman & Olbrechts, 1989: 76).

• El contenido de la argumentación: De una situación argumentativa referida a campos sociales o a polos externos a los mismos campos, a una situación argumentativa referida a campos científicos determinados por procesos de solución de problemas. «Se arriesga menos simplificando y deformando la situación en la cual se efectúa el proceso argumentativo al considerar que es un caso particular aunque muy importante aquel al que la prueba de la verdad o de la probabilidad de una tesis puede administrarse en el interior de un campo formal, científico o técnicamente circunscrito de común acuerdo con todos los interlocutores» (Perelman & Olbrechts, 1989: 93).

• El orador: De un orador que procura crear uná comunión en torno a ciertos valores a un orador que no teme a la contradicción, que erige como valor universal o verdad eterna lo que ha adquirido consistencia por la unanimidad social. «en la demostración, el orador se hace educádor» (Perelman & Olbrechts, 1989:100).

• Las técnicas: De una técnica de enlace cuasilógica como la de la incompatibilidad a una técnica lógica como la contradicción o la inconsistencia.

• El tipo de argumento:De argumentos basados en la estructura de lo real a argumentos basados en las estructuras de las teorías, como el argumento demostrativo.

• El tipo de lenguaje: Del uso privilegiado de un lenguaje natural al uso de un lenguaje formal. Este es uno de los aspectos del desplazamiento que sitúa la demostración en límite de la argumentación, por cuanto en el razonamiento no formal que privilegia la lengua natural el encadenamiento no es restrictivo y deja lugares para el desacuerdo. Mientras que en el razonamiento formal que privilegia el uso de los lenguajes formales el encadenamiento es restrictivo según condiciones del sistema, se trata de eliminar la posibilidad de proposiciones contradictorias.

• El tipo de dialogo: De un diálogo erístico que tiene por objeto dominar al adversario, a un diálogo habitual cuyo fin es persuadir para determinar una acción inmediata o futura. Y de estos dos tipos de diálogo a un diálogo heurístico en el que el interlocutor es una encarnación del auditorio universal.

Por lo anterior la argumentación se convierte en una forma de organización de los procesos cognitivos de los estudiantes, los factores de desplazamiento de una argumentación no matemática a una matemática, exigen el desarrollo de procesos de razonamiento.

La caracterización del razonamiento, está dada por procesos que realiza el sujeto en los que, a partir de informaciones previas se intenta pasar a nuevas formas de información. Esta caracterización le confiere dos dimensiones al razonamiento: en primer lugar, el hecho de ser una forma de pensamiento determinada por un tipo de operación cognitiva especial: la inferencia. Y en segundo lugar, el estar ligado al uso de un lenguaje que lo caracteriza, como un tipo de organización discursiva. La forma como se produce una inferencia constituye lo que denominaremos un paso de razonamiento y es un aspecto local en la producción discursiva. Estos pasos de razonamiento están determinados por un genero discursivo que les confiere uná forma de producción y organización textual, como el genero pedagógico (Martínez, 2004).

2.3 El registro figural y la emergencia de los razonamientos

La utilización de la figura, bien sea para representar una situación geométrica, o para hacer aparecer en cada objeto posibles reláciones con otros objetos, o para explorar o anticipar resultados, genera rapidez y economía de aprehensión de una situación Duval (1999)y justifica además la importancia que las matemáticas asignan al rol de las figuras. Se han identificado dos requerimientos específicos que debe llenar la figura para que represente un objeto matemático. El primero, que sea una configuración; es decir, ser una unión o una fusión de diferentes géstales que se relacionan y que a su vez caracterizan la configuración (condición visual). El segundo, es el de anclar (fijar - asegurar) en un enunciado algunas propiedades representadas por la gestal esta ancla discursiva lleva a la entrada matemática en la configuración.

Las dos condiciones anteriores llevan a considerar la necesidad de, por lo menos, dos tipos de registros: el de la figura y el de la lengua natural. Duval (1999) señala como un problema para el aprendizaje de la geometría, la falsa proximidad entre los tratamientos matemáticos pertinentes y los que espontáneamente se practican en uno de los dos registros, así como la necesidad de coordinación entre los tratamientos que provienen de registros figurales y tos que provienen de registros discursivos. De allí la necesidad de establecer criterios de distinción entre los tratamientos espontáneos y los matemáticos pertinentes y, en consecuencia, de precisar los diferentes tratamientos matemáticos pertinentes en el registro de las figuras geométricas. Todo lo anterior lleva a establecer las unidades constitutivas del registro figural, los tipos de articulación de las mismas en una figura y posibilidades de modificación de figuras.

Duval (1999) señala como unidades elementales del registro de las figuras Geométricas, las que se obtienen por el cruce de las variables visuales cualitativas (de forma, tamaño, orientación, granulación, color) y la variable de dimensión. Para esta caracterización se usa la variable visual forma por considerarse que las otras variables, aunque son pertinentes en un gráfico, no los son en una figura geométrica. En estos términos, la figura representa una situación geométrica «si la significación de ciertas unidades figurales y de algunas de sus relaciones están explícitamente fijadas de entrada» (Duval, 1999:159).

3. EL ANÁLISIS A PRIORI Y EL DISE˜O DIDÁCTICO

La construcción de la propuesta didáctica esta determinada por un análisis de género discursivo en el que se inscriben las tareas, y sus variables macroestructurales como el contexto, el modo de organización de la interacción y la intencionalidad para la situación de comunicación. La consolidación del diseño queda determinada por el análisis de las variables microestructurales vinculadas a los componentes matemático semiótico y argumentativo.

La noción de tarea que se construye desde el modelo de investigación de la ingeniería didáctica investigación, se constituye como un sistema propuesto para el desarrollo de los aprendizajes de los estudiantes, que se articula en los niveles macro (curricular y didáctico) y micro (de la interacción con el conocimiento y con los interlocutores del aula), niveles que se han de tener en cuenta en los respectivos análisis.

3.1 El género pedagógico y sus variables macroestructurales

Contexto escolar

La tarea se sitúa, desde el nivel macro, en el género discursivo pedagógico y, más específicamente en la relación enseñanza-aprendizaje. Esto se refleja en el diseño didáctico elaborado para toda la secuencia de talleres. El diseño se realizó bajo una estructuración didáctica paulatina que se informó con los resultados del momento de investigación acción. Se consideran entonces los focos identificados teóricamente en las fases del análisis preliminar. Además, se orientó a la construcción de una situación argumentativa en matemáticas que propendiera por la realización efectiva de las relaciones iniciales determinadas en los requerimientos didácticos. Como efecto de todo el proceso anterior, se consolidó un diseño delimitado por los siguientes tipos de identificación:

• Identificación del espacio escolar: La actividad se dirige a estudiantes de décimo grado de educación media, de un colegio del Distrito Capital. La propuesta se constituye en , una experiencia fuera del currículo regular, pero que soporta la formación correspondiente al grado décimo.

• Identificación del objeto curricular: La relación pitagórica en su sentido geométrico. De los tres sentidos identificados teóricamente para esta relación, se privilegia el geométrico, con el propósito de consolidar un campo teórico para la construcción de dicha relación y para la institucionalización de saberes en los estudiantes. Para este efecto, se identifica la opción de proponer la entrada a la relación pitagórica, mediante el registro figural, en tanto que se considera el figural como un registro más común a los estudiantes y menos complejo en su accesibilidad, frente a otros como el algebraico.

• Identificación de propósitos de aprendizaje para los talleres: Constituyen el horizonte del desarrollo del aprendizaje previsto en el diseño didáctico, articulan y secuencias tanto los momentos del aprendizaje como la evolución del producto aprendido y establecen el tipo de instrumentos y de relaciones entre ellos y las actividades de aprendizaje. Los propósitos de: i) elaborar sentido para la relación pitagórica desde el contexto euclidiano, ii) elaborar tramas argumentativas para la relación pitagórica en el contexto euclidiano, iii) desarrollar procesos inferenciales en el campo geométrico, complejizan la tarea, en términos de su orientación hacia la elaboración y justificación de relaciones matemáticas.

• Identificación de los requerimientos en el diseño didáctico: Los requerimientos didácticos considerados para el diseño establecen: La relación epistemológica- cognitiva que determina la jerarquía de los contenidos y La relación epistemológica- comunicativa que determina la jerarquía de las acciones y reglas de acción que orientan las tareas.

El taller como modo de organización de la interacción discursiva

Esta estrategia se constituye en una propuesta de acción organizada e intencionada, considerada como una técnica de trabajo grupa) (Calderón y Molina, 1999), que tiene asidero en la teoría de las dinámicas de grupo (Beal, 1970). Desde el punto de vista de su descripción, consiste en una actividad (realizada individual o grupalmente) diseñada para la discusión de un tema o de una situación o para el descubrimiento de relaciones, aplicaciones o factores asociados a un tema o cuestión. Desde el punto de vista comunicativo, exige centrar la interacción entre los talleristas y las actividades presentadas en el taller, con el fin de alcanzar los objetivos propuestos en el tiempo estipulado. Desde el punto de vista cognitivo, exige situar la relación de los sujetos participantes con el conocimiento en discusión. Desde los tres puntos de vista, opera bajo los criterios de aplicación del conocimiento previo y de verificación de los resultados obtenidos en la aplicación. Por esta razón, no constituye un espacio para la construcción inicial de conocimiento; es decir, se propone un taller, cuando se tiene un conocimiento previo sobre el que se quieren desarrollar aplicaciones, relaciones, proyecciones, entre otras. Además, como estrategia de trabajo, pone en juego la capacidad, de quien realiza el taller, de análisis, de síntesis y de sistematización de resultados. A la vez, al profesor le exige la capacidad de diseñar talleres: construir una estructura consistente y realizable que articule actividades con desarrollo de conocimiento; por ejemplo, establecer objetivos de aprendizaje alcanzables; proponer una metodología y unas actividades concordantes para el avance del conocimiento y el cumplimiento de tales objetivos, en un tiempo y en unas condiciones determinadas; explicitar criterios de evaluación para el desarrollo del taller, de tal manera que los talleristas tengan opción de regular sus propias actividades.

Desde el punto de vista del análisis discursivo, el diseño de la situación de enunciación en el aula, mediante la estrategia del taller, implica que la puesta en juego de los criterios y de las reglas que definen un taller, da como resultado la organización de la interacción (entre los interlocutores y entre ellos y el conocimiento). Aspecto éste que se refleja tanto en su propuestas textual: superestructura del taller (partes como indicaciones de tiempo, tema, objetivos, actividades, etc.) que instaura la situación de comunicación y proyecta las acciones que emprenderán los talleristas y las reglas y normas que regulan tales acciones; como en su propuesta discursiva:: macro estructura y microestructura que organiza la propuesta enunciativa (la solicitud general del profesor o del orientador del taller y que guía las reSpuestas del tallerista) y los enunciados que van orientando todo el procesó que há de réalizar el (los) tallerista (s) para responder a la solicitud géneral.

La intencionalidad, de formular una relación matemática

La opción por la formulación de una relación matemática, exige la selección de un tipo de relación que convoque diferentes camposde la matémática escolary precise el desarrollo de habilidades como la estimación geométrica y numérica, los procesos de medición a numérico y numéricos, la visualización, la argumentación matemática y la demostración: Esas dos exigencias llevaron a considerar la relación pitagórica como objeto de construcción para el taller, pues se identifican por lo menos tres sentidos posibles asociados a la relación pitagórica. La opCión de hacer la inserción en un curso avanzado (el último de la formación básica) se asoció con la exigencia de contar con una población que présentara.una experiencia previa de aplicación de la relacióh pitagórica. Se opta por un diseño que fortalece la experiencia de recupéración teórica de la relación.

Finalmente, como último aspecto del diseño metodológico del análisis a priori en su nivel macroestructural: se estructuró la secuencia de actividades definitiva, de acuerdo con los propósitos inveStigativoS y didácticos y con los aspectos metodológicos planteados anteriormente. En la siguiente tabla, se presenta una síntesis de esta secuencia.

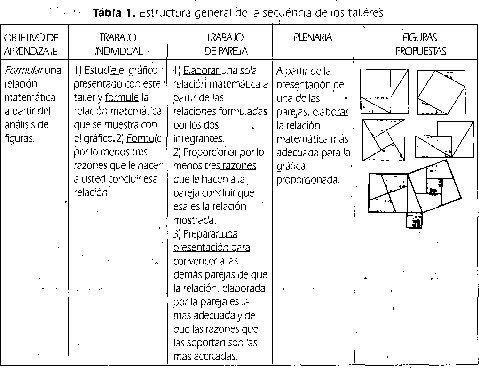
3.2 El desarrollo geométrico y sus variables microestructurales

Este segundo nivel corresponde a los aspectos relacionados con lo propuesto por la tarea y lo exigido por ella, a través de los enunciados que configuran cada uno de los talleres [3] . En este caso, el análisis identifica los elementos heurísticamente pertinentes para la formulación de la relación pitagórica, se realiza a partir de la propuesta textual manifiesta en los talleres diseñados y en los instructivos entregados a los estudiantes.

El componente matemático: La trama de relaciones

Interesa aquí el análisis al enunciado: «Estudie el gráfico presentado con este tallery formule la relación matemática que se muestra con el gráfico», que expresa la necesidad de buscar una relación matemática a partir de lo que las figuras muestran. El enunciado anterior, además de suponer una experiencia previa en cuanto al conocimiento de la relación pitagórica, exige que ella se realice a partir del estudio de una secuencia de gráficas. El análisis de la trama de relaciones asociadas a la formulación de la relación pitagórica en el contexto de la situación didáctica planteada considera las relaciones que cumplen una función heurística para la tarea.

• Relaciones de orden: Los elementos que se relacionan son de dos tipos: las figuras y las cantidades de área. Considerar uno u otro conjunto de elementos determina la manifestación de las siguientes relaciones.

Ser más grande que, aplicada a los tamaños de unidades figurales que conforman los grupos de gráficas. Esta relación es necesaria para obtener como parejas de la relación las siguientes:

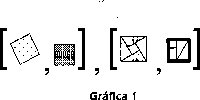
Tener más que. Los relacionandos son cantidades de magnitud; en este caso se consideran las unidades figuralés en tanto ellas aluden a cantidad de área. Este tipo de relación, además de identificar la magnitud geométrica evocada en la unidad figural, retorna la figura geométrica a la manera de Euclides: Una figura es lo contenido por uno o variós límites[4]. Aunque el criterio de comparación es el mismo anterior, ahora interesa la cantidad de magnitud presente, de ahí, el tipo de conclusión dada: hay más cantidad en. Esta relación es necesaria para la elaboración de la magnitud área. En el caso de la formulación de la relación pitagórica, ésta es la relación que consolida un sentido geométrico para ella.

• Relaciones de equivalencia: En este caso, aunque la relación se enuncie con Ser igual a, se manifiestan varias relaciones, por cuanto el criterio que determine juicio no es el mismo, como no lo son los relacionandos considerados. Se identific como necesarias para la formulación las siguientes relaciones de equivalencia que en la tradición euclidiana se han referido a la igualdad.

Ser igual en forma. Esta es una relación asociada a la relación de semejanza, se aplica cuando.distingue en dos grupos diferentes cuadrados y triángulos.

Ser igual en magnitud y forma. Esta relación corresponde a la relación de con g ruencia, se aplica a figuras geométricas. En este caso se requiere que las unidades figurales evoquen tanto las formas geométricas como la cantidad de área, la cantidad de longitud, o la cantidad de amplitud. Esta relación es la necesaria para establecer como premisa la igualdad entre los cuadrados externos del primer grupo de gráficos.

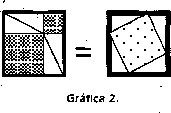
O como tercer enunciado en uno de los pasos de razonamiento, tanto del primer grupo de gráficas cómo del tercero:

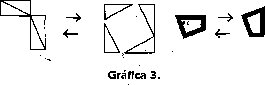
Este tipo de igualdad requiere del criterio establecido en la noción común 7: Y las cosas que coinciden entre si son iguales entre si, este criterio supone la acción previa de superposición [5] .

Ser igual en magnitud. Técnicamente es una relación de equiarealidad, o equilongitud, o equiamplitud, según la magnitud

considerada sea área, longitud o amplitud. Los relacionandos son cantidades de magnitud. En el caso de la relación pitagórica, esta relación se obtiene como conclusión de un paso de razonamiento cuando se razona, con las unidades figurales de los dos primeros grupos de gráficas, en ambos casos las figuras comparadas no son homogéneas en cuanto a su conexidad:

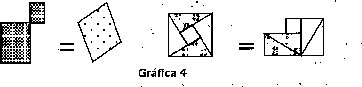
Relaciones de equicomplementariedad, corno la que se establece entre conjuntos de figuras de manera que dos figuras como las siguientes:

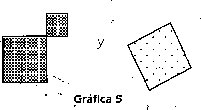
están en relación de equicompleMentarieda'd si existen dos conjuntos finitos de figuras congruentes dos a dos tal que al unirlas con las anteriores forman dos figuras congruentes

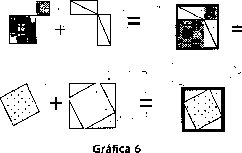
Relaciones de equidescomponibilidad, como las que se establecen entre las dos figuras siguientes:

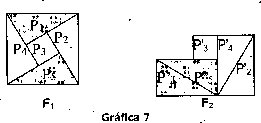
Dos figuras están en relación de equidescomponibilidad si ellas son la unión de figuras congruentes dos a dos. F₁ está en relación de equidescomponibilidad con F₂ Si P, es congruente con P', con 1≤i≤5. Esta relación es la que garantiza la conservación del área.[6]

• Relaciones aditivas: Relaciones ternarias de adición entreáreas de cuadrados. Esta relación surge de la operación adición aplicada a los cuadrados y a las magnitudes, en el primer caso se considera una operación que al aplicarla a dos cuadrados produce un tercer cuadrado, se observa que en este caso el triángulo rectángulo se convierte en un operador para la suma de cuadrados, de manera que se obtienen triplas de cuadrados como:

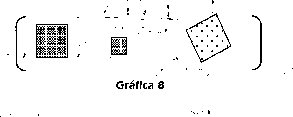
De manera que el tercer cuadrado es la suma de los dos primeros. En el segundo caso se obtienen triplas de cantidades de área como:

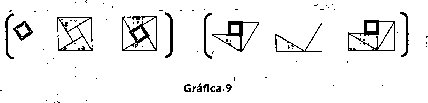
La petición de formular una relación matemática es de por sí compleja, por la diversidad de relaciones que tienen que articularse para formular la relación pitagórica. Se han mencionado las que son pertinentes para la'relación pretendida, sin considerar otras que puedan emerger por el tipo de aprehensión que se haga del sistema de unidades figurales. Hay una exigencia adicional para la formulación de la relación y es la de realizar una conversión del registro figura! al registro de la lengua natural.

El componente semiótico: La aprehensiones. Cie nc ias Bás icas y Educac ión

El análisis del registro figura) pretende identificar dos aspectos: Las aprehensiones del registro figural y los tratamientos heurísticamente pertinentes para la formulación de la relación pitagórica.

• Las aprehensiones perceptual y discursiva: Estas dos aprehensiones cumplen funciones muy importantes en los procesos de exploración heurística y formulación de la relación, desarrollados a partir del estudio de unidades figurales propuestas en la situación didáctica. El análisis siguiente expresa los elementos pertinentes para que de una parte la aprehensión perceptual determine una instanciación geométrica, y de otra parte la aprehensión discursiva, mediante las fuhciones de referencialidad y apofántica, constituya unidades apofánticas para los procesos de razonamiento. El análisis corresponde al grupo conformado por la siguiente pareja de figuras:

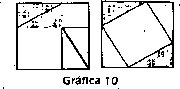
La siguiente tabla presenta las unidades que debe discriminar tanto la aprehensión perceptual como la aprehensión discursiva.

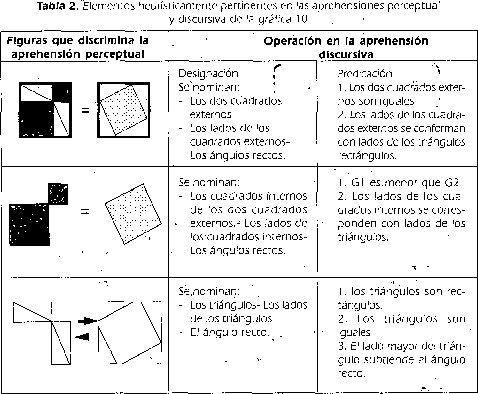
• La aprehensión operatoria: Este tipo de aprehensión modifica la figura de diferentes maneras y además, cumple una función heurística en los procesos de visualización de relaciones matemáticas. En el grupo de gráficos analizado, la aprensión operatoria requiere que se considere una de ellas como figura de partida y la otra como figura de llegada.

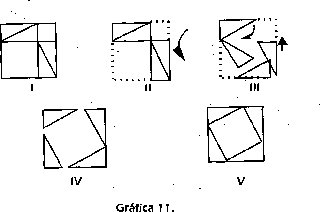
La aprehensión operatoria se convierte en un requisito implícito para garantizar la igualdad de área de los dos cuadrados internos de las figuras I y V.

El componente argumentativo: Las relaciones semánticas

En la tabla 3 se presentan los enunciados con su correspondiente consolidado del análisis, que identifica la forma de expansión requerida para enunciados dado y el tipo de similitud entre unidades apofánticas. En todos los casos se requiere dos tipos de estructura proposicional para la expansión:

Acumulativa. Desarrollo proposicional marcado por extensiones semánticas cuantitativas de tipo descriptivo, enumerativo, reiterativo. Privilegia formas de expansión lexical y natural.

Sustitución: Desarrollo proposicional por inferencias deductivas, y abductivas. Privilegia formas de expansión cognitiva y formal

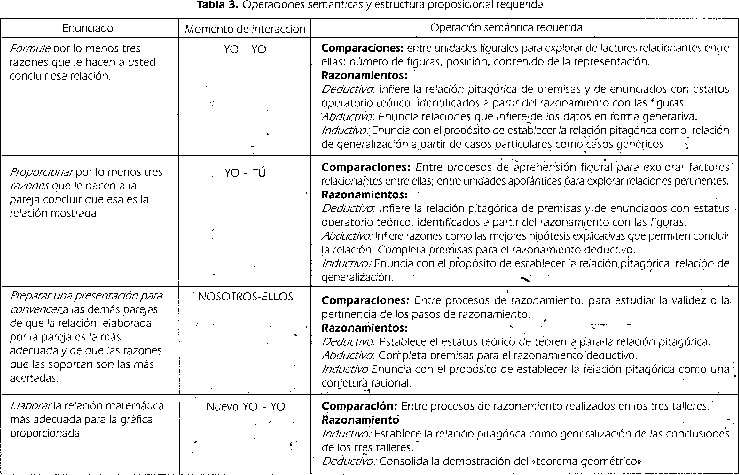
El componente argumentativo: Los razonamientos

Razonamientos deductivos que requieren como premisas la igualdad en forma y magnitud de las figuras y como tercer enunciado la noción común: Si a iguales se quita iguales, los restos son iguales o la relación de equicomplementariedad entre las figuras. Este tipo de razonamiento es el que se requiere para el primer grupo de gráficas:

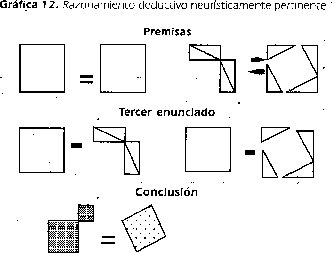
Razonamiento abductivos_a partir de los datos completan la hipótesis explicativa: Para cuadrados construidos sobre lados de triángulos rectángulos, la suma de las áreas de los cuadrados construidos sobre los catetos de los triángulos es igual al área del cuadrado construido sobre la hipotenusa. Se trata de establecer la relación haciendo explicito el triángulo rectángulo como factor que vincula los relacionandos:

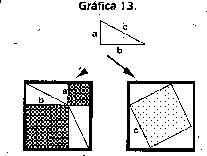
Razonamientos inductivos Sobre las conclusiones de los tres talleres y que formulen como una conjetura racional: Para cualquier triángulo rectángulo: la suma de los cuadrados constrúidos sobre los catetos es igual al cuadrado construido sobre la hipotenusa.

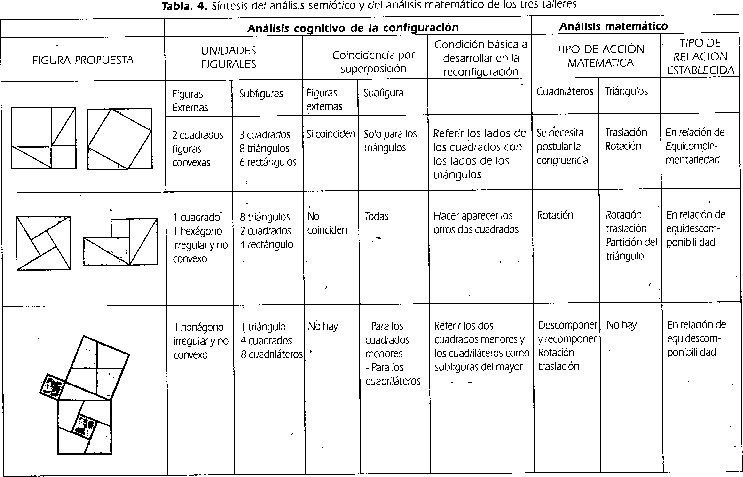
4. RESULTADOS DEL ANÁLISIS A POSTERIORI

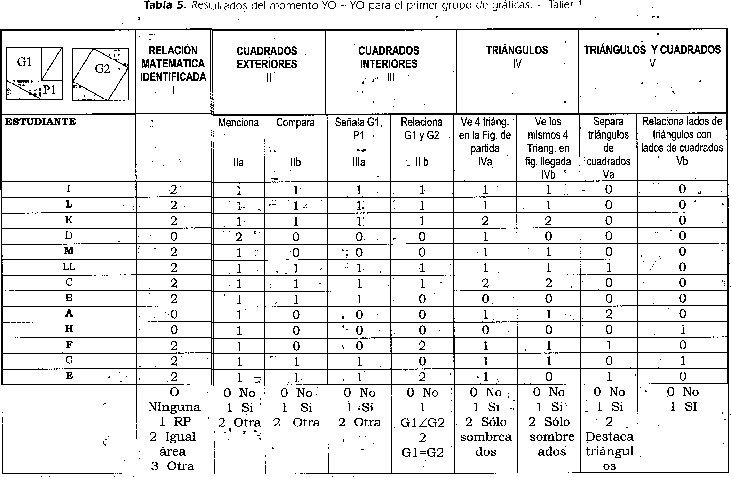
A partir de los resultados presentados en la tabla 5 se destacan los siguientes aspectos:

• La columna I, que presenta el resultado del componente matemático esperado, evidencia que ningún estudiante formula como relación matemática la relación pitagórica y que hay estudiantes que no formulan ninguna, relación matemática.

• Las columnas II a la IVb, que registran tanto la identificación de las unidades figurales bidimensionales pertinentes como la predicación necesaria para cada unidad figural pertinente, evidencian que sólo dos estudiantes (I,LL) realizan los comportamientos esperados para cada una de estas columnas.

• Las columnas Va y Vb, que registran los aspectos de tratamiento operatorio con las unidades figurales bidimensionales y de predicación con respecto a las unidades figurales unidimensionales, evidencian que ningún estudiante manifestó los comportamientos esperados en las dos columnas.

Como se puede observar, a partir de la , columna II , se disminuye la presencia de comportamientos a los que se les asigna una función heurística para la formulación de la relación pitágórica, de manera que ocho de los 12 estudiantes que manifiestán un comportamiento exitoso en la columna Ila atienden a las columnas Ilb y Illa; de éstos, cinco atienden al requisito de la columna IIIb; de los cuales tres cumplen con la de IVa y IVb; y ninguno de los tres cumple con la columnas Va y Vb. Es decir, ningún estudiante manifiesta todos los comportamientos requeridos para la formulación de la relación pitagórica.

Al observar que los aspectos que registran las columnas IIIb, Va y Vb refieren a operaciones cognitivas diferentes a la percepción de unidades figurales, es posible concluir aquí la manifestación de un privilegió por la aprehensión perceptual de las figuras y, en consecuencia, la evidencia de un bloqueo a nivel general en lo que concierne a la formulación de la relación pitagórica, a partir de lo que las figuras muestran. El anterior estado final del trabajo individual (designado como el mómento de interacción YO - YO'( se convierteen el estado inicial para el trabajo de parejas (designado como el momento YO - TÚ).

En los resultados de los momentos YO — TÚ y NOSOTROS ELLOS, aunque se avanza en las columnas II y IVa, en donde se répOrta un logro total y se avanza en la formulación de relaciones matemáticas, se mantienen las columnas V como las de menor nivel de logro. De los 13 estudiantes, nueve cumplen con III y IV; de éstos, ninguno cumple con las columnas Va y Vb, de manera que no es inmediata la formulación de la relación pitagórica a partir del estudio de las gráficas presentadas.

5. CONCLUSIONES

En lo que, concierne al componente semiótica la aprehensión perceptual determinó la emergencia y desarrollo de unidades apofánticas que por la función de referencia de la expansión discursiva se instanciaron en contextos geométricos. Se confirman los resultados de investigaciones anteriores (Duval, 1999) en cuanto al predominio de aprehensiones de formas bidimensionales sobre las unidimensionales, pero emerge un resultado complementario a estas investigaciones y es la escasa aprehensión de las unidades figurales bidimensionales abiertas (cómo los ángulos): Entre las figuras bidimensionales los triángulos y los cuadrados externos se toman como las figuras importantes.

La correspondencia entre los resultados que manifiestan poco uso de las aprehensiones operatorias de las figuras con la ausencia de los procesos de visualización necesarios para la formulación de la relación pitagórica, además de explicar la no formulación de la relación, déstaca la importancia de este tipo de operación semiótica en el desarrollo matemático, dada su incidencia directa en la manifestación de unidades apofánticas que no se enuncian desde la aprehensión perceptual. La no congruencia entre las unidades figurales del,registro y las unidades de la lengua natural que enuncian la relación pitagórica se evidencia domo un obstáculo para la formulación de la relación.

En lo que concierne al componente argu??entativo, las operaciones semánticas de comparación y razonamiento se desarrollaft a partir de las unidades apofánticas enunciadas en los procesos de aprehensión figural. La escasa presencia de pasos de razonamiento deductivo y la ausencia de los razonamientos heurísticamente pertinentes, no permiten la formulación de las unidades apofánticas necesarias para formular la relación pitagórica.

El predominio de la función de explicación sobre la de justificación, se asocia con la necesidad de entender la formulación de múltiples relaciones manifiestas en unidades apofánticas, que conforman diferentes contextos asociados al macro contexto escolar. La necesidad de convencer permanece primordialmente como un requerimiento instruccional.

La relación pitagórica es usada por los estudiantes como relación-formula-garante en el contexto aritmo-geométrico y no como relación-conclusión, en un contexto geométrico.

En lo que concierne al componente matemático. No se enuncia la relación pitagórica, pero las características evidenciadas en los procesos semióticos y argumentativos permiten la emergencia de relaciones de orden y de equivalencia de tipo congruencia,y semejanza, no emergen las de tipo equiarealidad equilongitud y equiamplitud, necesarias para la relación pitagórica. Como tampoco emergen las relaciones ternarias entre áreas de cuadrados.

El diseño didáctico fue pertinente para la investigación, por cuanto tanto su estructura de enunciados como su estructura de gráficas permitieron develar los factores que intervienen para que la formulación de una relación matemática se consolide como un paso en el desarrollo argumentativo de los estudiantes en matemáticas. Como propuesta didáctica, la secuencia de talleres propuesta no fue la adecuada para la población. Se pretendía la formulación de la relación pitagórica para su estructuración teórica, pero las condiciones de la población requerían más de un momento de elaboración que de consolidación; por lo tanto, hubiera sido más adecuado considerar la secuencia empezando por el grupo de gráficas más congruente con el enunciado de la relación pitagórica en lenguaje natural.

6. BIBLIOGRAFÍA

• BEAL, G.M. (1970) Conducción y acción dinámica del grupo. Buenos Aires: Kapeluz.
• CALDER&Oacuxte;N, D. y MOLINA, C. (1999). «Institución educativa y técnicas grupales» (1999). En: Módulo de Comunicación para la Especialización en Docencia Universitaria. Bogotá: Universidad Santo Tomás de Aquino.
• DUVAL, R. (1999). Semiosis y pensamiento Humano. Cali: UniverSidad del Valle, Peter La ng.
• DUVAL, R. (1999b). Representation, vision and visualization:cognitive functions in mathematical thinking, basic issues for learning. In: Proceedings of the Twenty First Annual Meeting North American Chapter of the International Group for the Psychology of Mathematics Education. Ohio: Clearinghouse for.Science, Mathematics, and Environmental Education Columbus, OH. Vol 1, 55-80. .
• DUVAL, R. (2004). Los problemas fundamentals en el aprendizaje de las matemáticas y las formas superiores en el desarrollo cognitivo. Cali: Universidad del Valle.
• EUCLIDES. (1991) Elementos I-IV. Madrid: Gredos.
• LEON, 0. (2005). Experiencia figura! y procesos semánticos para la argumentación en geometría. Tesis Doctoral Doctorado en Educación. Universidad del Valle.
• MARTÍNEZ, M. (2004). «La construcción de los sujetos discursivos, la orientación social de la argumentación en la dinámica enunciativa del discurso». Conferencia presentada en el 3er Coloquio Nacional de Estudios del Discurso. Medellín, septiembre 22 a 24 de 2004.
• MINISTERIO DE EDUCACI&Oacuxte;N NACIONAL( 2001) . Desarrollo histórico de los currículos generadós por el Ministerio de Educación Nacional . 1937-2001:Bogotá: MEN.
• PERELMAN, Ch. Y OLBRECHTS - TYTECA, L. (1989). Tratado de la argumentación. Madrid: Gredos.
• VASCO, C. E. (2005). Notas Seminario Doctoral. Bogotá: Universidad Distrital.

Notas

1. El diseño completo con su respectivo análisis se encuentra en el documento Tesis Doctoral: «Experiencia figural y procesos semánticos para la argumentación en geometría» de la autora.
2. Full design and analysis in the document Doctoral Thesis «Figural Experience and Semantic processes for the Argument in Geometry», by the author.
3. Las publicaciones corresponden a: «Requerimientos didácticos y competencias argumentativas en matemáticas» (2000) y «Argumentar y validár en matemáticas ¿una relación necesaria?» (2003).
4. Vale la pena señalar que en el artículo de la profesora Dora Inés Calderón en esta misma publicación se presenta el análisis desde la perspectiva discursiva. Los dos análisis constituyen la totalidad del análisis a priori de las tareas.
5. Definición 14 libro primero de los Elementos
6. En el capítulo 3 de la tesis doctoral de la autora, se establece que la acción de superposición está determinada bien por una experiencia mental, o bien por las herramientas de una teoría, entre las que se cuentan los sistemas de axiomas.
7. El teorema 51 de la Geometría de Hilbert establece: Dos poligonos equicomplernentables tienen lamisma área y dos polígonos con la misma área son equicomplementables.