DOI:
https://doi.org/10.14483/23448350.355Published:
11/30/2006Issue:
No. 9 (2007): Enero-diciembreSection:
Ciencias BásicasLa proporcionalidad como instrumento de matematización en Arquímedes: un análisis a Sobre cuerpos flotantes
The propórtionality as a mathematization instrument in Archimedes: an analisys to On floating bodies
Keywords:
Proporcionalidad, Arquímedes, matematización, flotación (es).Keywords:
Proportionality, Archimedes, mathematization, flotation. (en).Downloads
References
Archimedes, 287-212 (?). The Works of Archimedes, Edición inglesa de T. L. Heath, Nueva York Dover, 1952, pp. 397-596.
Boyer, C., Historia de la Matemática, Madrid, Alianza Editoria1,1986.
Euclid, 300 a. C (?). The Thirteen Books of Euclid. Edición inglesa de T.
L. Heath, Nueva York Dover, 1952, pp. 1-396
Guzmán, M., Matemáticas y estructura de la naturaleza, Universidad Complutense de España Madrid. 2001 [Versión electrónica] http://www.mat.ucm.es/deptos/am/guzman/matyest.htm
González, P., Las raíces del calculo infinitesimal en el siglo XVII, Madrid, Alianza Editorial, 1992
Heath, T., A History of Greek Mathematics, Vols. I y II, Nueva York, Dover, 1921.
Piaget, J.; García, R., Psicogénesis e historia de la ciencia, México, Siglo XXI, 1982.
Vera, E, Científicos griegos, México, Edición Aguilar, 1970.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ciencias Básicas
Revista Científica, 2007-08-00 nro:9 pág:143-158
La proporcionalidad como instrumento de matematización en Arquímedes: un análisis a Sobre cuerpos flotantes[1]
The proportionality as a mathematization instrument in Archimedes: an analisys to On floating bodies
Oriol Mora Valbuena
Investigador del grupo MESCUD y profesor de la Facultad de Ciencias y Educación de la Universidad Distrital Francisco José de Caldas. Av (Cra) 30 No 64 81 Piso 6. Especialización en Matemáticas. E-mail: orioledumat@udistrital.edu.co
Héctor Mauricio Becerra Galindo
Vianney Rocío Díaz Pérez
Cristhian Andrés Bello Rivera
Licenciados en Educación Básica con Énfasis en Matemáticas y coinvestigadores en términos de la Universidad Distrital Francisco José de Caldas.
En memoria de nuestra colega, compañera, y amiga Eugenia Castillo Echeverri.
Resumen
La proporcionalidad ha sido fundamental en el desarrollo histórico de las ciencias. Ante la evidencia de esto, en este artículo [4] se resalta el papel de la proporcionalidad en los procesos de matematización desarrollados por Arquímedes, específicamente en sus tratados Sobre cuerpos flotantes, que fueron tomados de la traducción de Heath al inglés (1952).
Particularmente, de estos libros destacaremos la aplicación de la proporcionalidad en el reposo, en la relación entre peso y volumen, y en cuerpos flotantes ideales como los paraboloides de revolución. Finalmente, concluimos que la proporcionalidad constituye lo que llamamos instrumento de matematización.
Palabras clave:
Proporcionalidad, Arquímedes, matematización, flotación.
Abstract
Proportionality has been fundamental in the historical development of sciences. This article stands out the role of proportionality in the processes of mathematization developed by Archimedes, specifically in his works On Floating Bodies, taken from the translation to English of Heath (1952).
Particularly, of these books we will highlight the application of the proportionality: in rest, in the relationship between weight and volume, and in ideal floating bodies as the paraboloid right of revolution. Finally, we conclude that proportionality constitutes what we call mathematization instrument.
Key words
Proportionality, Archimedes, mathematization, flotation.
EL REPOSO
Para los griegos, el mundo era considerado estático, como afirma Piaget y García (1982: 233):
Todo movimiento (excepto el movimiento de los astros sobre los cuales actúa un impulso divino) era considerado una "violencia" ejercida sobre un objeto. El movimiento, por consiguiente, requería una fuerza. Cuando cesaba la fuerza, el objeto volvía a su estado natural de reposo.
Esta concepción se evidencia aún más en el hecho de que axiomatizaron procesos físicos desde un estado ideal de reposo.
Desde este punto de vista, Arquímedes (desde concepciones aristotélicas) exploraba el mundo a través de un estado natural de.reposo. En el fluido lo postuló de la siguiente manera:
Supongamos que un fluido es de tal carácter que sus partes reposande igual forma y siendo continuas, la parte que está menos empujada es conducida por la que está más empujada; y cada una de sus partes es empujada por el fluido que está encima de ella en una dirección vertical, si el fluido está sumergido y comprimido por algo más [Arq., SCF I, Post. 1, p. 538,TN] [5].
Queremos resaltar en este postulado la relación entre reposo y proporcionalidad, dado que el reposo se puede interpretar como que la razón de la parte que comprime es a la parte comprimida igual que la razón de otra parte qu e comprime es a otra parte comprimida, siendo las dos partes comprimidas uniformes e iguales.
Por ejemplo, en la demostración de la proposición 2 de SFC I (figura 1): La razón entre la parte que comprime BQPE y la parte comprimida PQO es mayor que la razón entre la parte BGQR y la parte comprimida QRO. Esta desigualdad indica que el fluido no está en reposo. Esto permite considerar ,que Arquímedes describía el reposo como una relación de proporcionalidad en la que utilizó implícitamente las proposiciones 8 y 10 del libro V de Euclides [6], pues si se tienen dos razones con el mismo consecuente (en términos de Euclides), estas proposiciones establecen cuándo una razón es mayor que la otra.
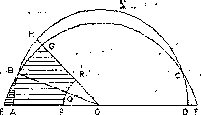
Arquímedes examinó en SFC I propiedades de los fluidos en reposo, en dos casos: la forma del fluido (Prop. 2) y el estudio de la localización de los objetos en el fluido (Prop. 3, 4 y 7).
Además en SFC II, Arquímedes determinó el estado de reposo de los cuerpos en el fluido (paraboloide de revolución o segmento de esfera) a través del estudio de la posición de su eje; para esto localizó los centros de gravedad de dichos cuerpos. Centros de gravedad' que había estudiado y relacionado proporcionalmente:
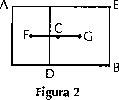
Si AB es una magnitud cuyo centro de gravedad es C y AD una parte de ésta cuyo centro de gravedad es F, entonces el centro de gravedad del resto de la magnitud será un punto G sobre la prolongación de FC, tal que GC : CF = (AD):(DE) [Arq, SEP I, Prop. 8, p. 504-505, TM. (Figura 2).
En SCF como en El Método y Sobre la cuadratura de la parábola, encontramos que Arquímedes establece relaciones de proporcionalidad a través del equilibrio usando como herramienta la ley de la palanca (demostrada en las proposiciones 6 y 7 de SEP I).
De lo anterior concluimos que lo definido por Euclides como proporción, Arquímedes lo aplica como equilibrio (con la ley de la palanca) y reposo (en el fluido).
HACIA LA NOCIÓN DE DENSIDAD
Una de las primeras aproximaciones a la noción de densidad ha sido caracterizada por Arquímedes en SCF, a partir del estudio de la localización de los objetos en el fluido.
En la modernidad, Stollberg y Hill (1968, p. 204) definen la densidad como La masa por unidad de volumen de una sustancia. En forma matemática:

Cuando Arquímedes se refiere a gravedad específica, se aproxima a la idea de densidad que actualmente conocemos; compara el peso [8] (no hemos encontrado en su obra una distinción entre masa y peso) [9] de los objetos a un mismo volumen. Inicialmente, no la denominó gravedad específica, pero la caracterizó a través de la siguiente proposición:
Los sólidos aquellos que, tamaño a tamaño, son de igual peso con el fluido, silos deja caer en el fluido, se sumergen de tal forma que no se proyectan sobre la superficie pero no se hunden más abajo [Arq., SCF I, Prop. 3, p. 539, TN] (cursivas nuestras)
Esta caracterización la llamó gravedad específica en la proposición 2 de SCF II. A partir de la proposición 4 de SCF II, Arquímedes puso en razón la gravedad específica del sólido con la gravedad específica del fluido[10]. Esto nos permite afirmar que la gravedad específica era tomada por Arquímedes como una magnitud[11], que le posibilitó relacionar pesos a un mismo volumen.
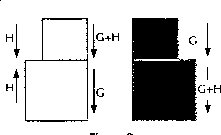
La gravedad específica en Arquímedes no estaba limitada a cuerpos uniformemente densos, hecho que evidenciamos en la demostración de la proposición 7 de SCF I[12], en la que para determinar la fuerza que pierde un objeto A (de mayor gravedad específica que el fluido), lo unió con un objeto B (de menor gravedad específica que el fluido) de manera que la composición de los dos objetos tenga la misma gravedad específica que el fluido (figura 3). Esto le permitió resolver "el problema de determinar la proporción de oro y plata en cierta corona... midiendo sucesivamente los volúmenes del fluido desplazado por los tres pesos, 1) la corona, 2) un sólido de igual peso de oro, 3) uno de igual peso de plata... " (Heath, 1921: 93-94, TN).
En la proposición 5 de SCF I: "Cualquier sólido más ligero que un fluido, si es colocado en el fluido, el peso del sólido será igual al peso del fluido desplazado", evidenciamos que Arquímedes pesaba objetos empleando el volumen del fluido. El volumen de fluido desplazado le indicaba el peso del objeto.
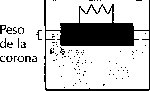
En el caso de los objetos más pesados que el fluido (como la corona, figura 4), los colocaba sobre otros objetos más ligeros que el fluido situados en él (para que la gravedad específica de los dos objetos juntos sea menor que la del fluido). El volumen desplazado por el sólido más pesado que el fluido representa su peso. Así el peso y el volumen, mediante este experimento, eran representados a través de magnitudes de la misma naturaleza (volumen del fluido).
Esta forma de pesar los objetos permitió a Arquímedes expresar la densidad como una razón, como se expresa en la proposición 1 de SCF II, en la que estableció: "Si un sólido más ligero que un fluido está en reposo dentro de éste, el peso del sólido es al peso del mismo volumen en fluido, como la porción sumergida del sólido es a todo el sólido" [Arq., SCF II, Prop. 1, p. 543, TN ], (cursivas nuestras).
La porción sumergida podría ser interpretada como el peso del objeto, debido a que experimentalmente el volumen de la porción sumergida (volumen desplazado) indica el peso de todo el sólido, como mostramos en el ejemplo de la corona.
De esta manera, Arquímedes se aproximó a la noción de densidad. Y no sólo la encontraba a un volumen específico del objeto, sino para cualquier cantidad de este, ya sea de un solo material uniformemente denso o no, como el caso de la corona.
Arquímedes no expresó la densidad como la relación masa/volumen respetando la definición de razón (expuesta en Elementos de Euclides), ya que esta no permite formar razones entre magnitudes de diferente naturaleza (masa es a volumen), pues una expresa fuerza :y la otra expresa tamaño. Arquímedes recurrió a relacionarlas a través del volumen del fluido (a partir de este, le era posible medir tanto el peso como el volumen de los cuerpos).
EL PARABOLOIDE DE REVOLUCIÓN: UN CUERPO EN EQUILIBRIO
En el estudio del equilibrio de los sólidos en el fluido, Arquímedes analizó en SFC I la posición del segmento de esfera (Prop. 8 y 9) y en SCF II analizó el paraboloide de revolución[13] (Prop. 2-10) de menor gravedad específica que el fluido como cuerpos de flotación.
Con respecto al segmento de esfera, únicamente dedicó dos proposiciones, y sólo se conserva la demostración de la posición de un segmento de esfera (mayor que el hemisferio) en la que su base está completamente sumergida en el fluido[14].
Arquímedes hizo énfasis en el paraboloide de revolución, y lo estudió teniendo en cuenta sus propiedades y las propiedades de la parábola [15] (un corte trasversal a través del eje). A partir de estas construyó una clasificación que le permitió analizar cuando un paraboloide de revolución encuentra el reposo en un fluido.
Para determinar cuándo alcanza el reposo, analizó el sentido de las fuerzas sobre los centros de gravedad del paraboloide, que dependen de las relaciones entre su eje, su base y una línea recta fija llamada parámetro.
Arquímedes concebía el parámetro como una línea recta p, fija, tal que la ordenada de la parábola BN es media proporcional entre el parámetro p y el eje AN (AN eje de la parábola desde la ordenada al vértice), es decir,  lo que permite representar a la parábola como una relación de proporcionalidad. Sin embargo, actualmente con la geometría analítica se ha llevado a presentarla sólo con la fórmula, y2 = 4px, dejando ocultas estas relaciones.
lo que permite representar a la parábola como una relación de proporcionalidad. Sin embargo, actualmente con la geometría analítica se ha llevado a presentarla sólo con la fórmula, y2 = 4px, dejando ocultas estas relaciones.
Luego de haber caracterizado el paraboloide y el parámetro, en lo que sigue presentaremos la clasificación de los paraboloides bajo distintos criterios (sección 3.1), y la posición de los centros de gravedad del paraboloide de revolución (sección 3.2), resaltando el papel de la proporcionalidad.
Clasificación de paraboloides
En la tabla 1, presentamos la clasificación de Arquímedes sobre los paraboloides de revolución; la organizamos teniendo en cuenta los siguientes criterios: los dos primeros (columna Eje) van referidos a la relación de tamaños entre el eje de la parábola (AN) y el parámetro (p); el tercer criterio (columna Gravedad específica) relaciona la gravedad específica del sólido (GES) con la gravedad específica del fluido (GEF). Arquímedes también tuvo en cuenta en este estudio la posición inicial del paraboloide colocado en el fluido (columna Base), y finalmente investiga su posición de reposo (columna Posición de reposo), así:
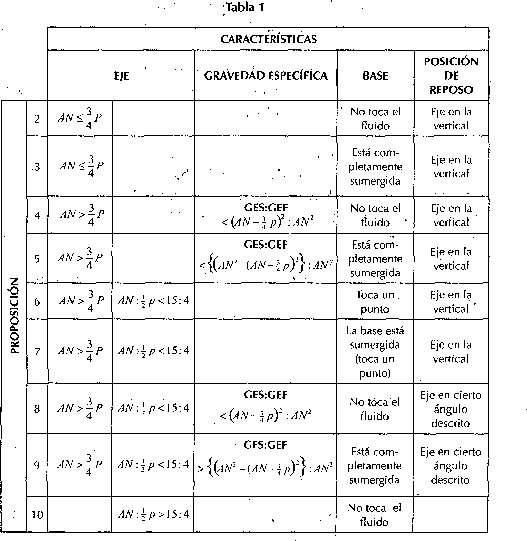
Podemos observar que todas las clasificaciones son expresadas a partir de relaciones entre razones "es más grande que" o "no es más grande que". Y en muchos casos, como en la proposición 8, la proporción indica la posición de reposo del objeto. Esto .nos lleva a concluir que la razón y la proporción no solo sirvieron a Arquímedes para dar soporte axiomático a las demostraciones, sino que se valió de estas para expresar las condiciones de flotación de los paraboloides de revolución.
Sobre el equilibrio y los centros de gravedad
Desde el postulado 2 evidenciamos la importancia de los centros de gravedad en el estudio del reposo de los sólidos en el fluido, así: "Los cuerpos que son impulsados hacia arriba en un fluido, son impulsados hacia arriba a lo largo de la perpendicular (de la superficie) que pasa a través de su centro de gravedad" (Arg., SCF 1, Post. 2, p 541, TN ].
A partir de este, Arquímedes determinó el sentido de las fuerzas, permitiéndole investigar la posición de reposo de objetos en el fluido. En el caso del paraboloide de revolución, planteó que el centro de gravedad de este se encuentra según la proporción 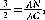 donde AN es el eje, A el vértice y C su centro de gravedad.
donde AN es el eje, A el vértice y C su centro de gravedad.
En la traducción de Vera (1970: 247) a SCF II, en la nota del traductor a la proposición 3, afirma que:
El siracusano da por sabido que el centro de gravedad de un conoide parabólico divide al eje en razón 2:3, propiedad que no se encuentra en ninguna de las obras que de él se conserva sin que pueda asegurarse, naturalmente, que tampoco estuviera en alguna de las pérdidas.
Sin embargo, esta propiedad se halla en la proposición 5 del Método[17], así:
El centro de gravedad de un segmento de un paraboloide recto de revolución, cortado por un plano perpendicular al eje, está sobre el eje del segmento y lo divide de tal manera que la porción adyacente al vértice es el doble de la porción restante. [Arq., El Método, Prop. 5, p. 577, TI\1].
Arquímedes, para demostrar esta proposición, inició la construcción realizando un corte perpendicular al eje del paraboloide en la parábola BAC, prolongó AD hasta H haciendo HD el doble del segmento AD. HD es la barra de equilibrio cuyo centro es A, luego inscribió un cono con la misma base del paraboloide y la misma altura, tal que los segmentos AB y AC son dos generadores del cono; después creó una doble ordenada OP intersecando el cono en Q y R, y al eje en S (figura 5).
A partir de la anterior, construcción, aplicó propiedades de la parábola a través de proporciones obteniendo HA: AS :: OP2 : QR2.
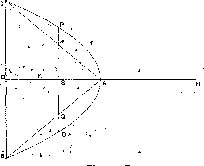
Así que se tiene:
HA : AS
:: (Círculo de diámetro OP): (Círculo del Diámetro QR)[18]
:: (Círculo del paraboloide): (Circulo del cono).
Luego, si el centro de gravedad del círculo del paraboloide es colocado en S y el centro de gravedad del circulo del cono es colocado en H, los dos juntos estarán en equilibrio sobre A. Esta proporción se cumple para los círculos del cono y del segmento de paraboloide en cualquier,ordenada de la parábola.
Por tanto, todos los círculos juntos del paraboloide y todos los círculos juntos del cono estarán en equilibrio de tal manera que A es el centro de gravedad de todo el sistema de equilibrio, y el punto H es el centro de gravedad del cono. Entonces el centro de gravedad del segmento de paraboloide estará sobre un punto K en la prolongación de HA tal que:
HA : AK (Segmento del paraboloide):(cono)
como[19] (segmento del paraboloide) = 3/2 (cono)
Entonces HA:AK:: 3 :2
Como acabamos de observar en la demostración del centro de gravedad del paraboloide, se relaciona el paraboloide con el cono, descomponiendo estos cuerpos en círculos para establecer relaciones proporcionales entre ellos, empleando el equilibrio como herramienta a través de la balanza con el fin de aplicar estas mismas propiedades a dichos cuerpos.
A partir de la integral, el proceso que se realiza es muy similar. Por ejemplo, en cualquier superficie, la concepción de la integral como la descomposición de una superficie en infinitos rectángulos cuyas bases son infinitamente pequeñas permite hallar el centro de gravedad de cada uno de estos rectángulos para determinar finalmente, con la ley de la palanca (tomada a partir de coordenadas cartesianas), el centro de gravedad de todo el sistema, el cual es conocido actualmente como centroide. Como afirma González (1992: 32):
En manos de Arquímedes, el método de exhausión, conjugado con su genial y heurístico método mecánico de descubrimiento (método de la palanca) se convierte en un poderoso instrumento infinitesimal rigurosamente lógico que le permite alumbrar y convalidar apodícticamente numerosos resultados sobre cuadraturas, cubaturas y centros de gravedad que hoy obtenemos con nuestros perfeccionados y rigurosos algoritmos infinitesimales.
Este proceso, en el caso de la parábola, se resume con la siguiente integral:
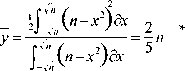
* Fórmula 1, donde n es la altura del eje de la parábola, (x, y) es el centroide del segmento de parábola y x = O por estar sobre el eje.
De igual forma sucede para los cuerpos, en este caso. Para encontrar el centro de gravedad del paraboloide de revolución, se utiliza actualmente la siguiente integral (figura 6, representación gráfica):
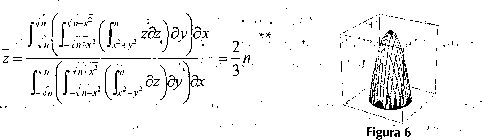
** Fórmula 2, donde n es la altura del eje del paraboloide de revolución, (x, y, z) es el centroide del segmento de parábola, x = O e y = O por estar el eje del paraboloide construido sobre los ejes x e y de la gráfica.
Comprobando de esta manera, que el centro de gravedad del paraboloide se encuentra en la siguiente proporción 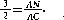
Los procesos para localizar los centros de gravedad en cuerpos y en figuras planas han hecho que la proporcionalidad haya sido simplificada, ya que para hallar el centro de gravedad de cualquier cuerpo sólo es necesario plantear una integral (como lo explicamos anteriormente) en que las relaciones proporcionales no son tan evidentes.
SOBRE EL PROCESO DE MATEMATIZACIÓN EN ARQUÍMEDES
A continuáción enfatizarémos en la próporcionalidad como instrumento de matematización en la construcción de la teoría de la flotación (estática de los fluidos) expuesta por Arquímedes [20].
Entendemos desde Piaget y García (1982: 18-19) que estos instrumentos no solo refieren a todos los conocimientos previos del sujeto, sino a aquellos que sirven como esquemas de acción en el proceso de adquisición de los conocimientos. En consecuencia, la proporcionalidad es un instrumento que permitió a Arquímedes matematizar fenómenos físicos como la flotación.
Anteriormente [Secciones 1, 2 y 3] evidenciamos que la proporcionalidad, tanto implícitamente (en el caso del reposo) como explícitamente (en el caso de la gravedad específica, los centros de gravedad, los paraboloides de revolución, entre otros), le sirvió paso para demostrar situaciones relacionadas con el fenómeno de la flotación dentro de un proceso de matematización.
De esta manera, el proceso de matematización del principio hidrostático, empezó desde lo experimental21 . A partir de allí Arquímedes encontró ciertos datos que la naturaleza le proveía, como afirma Piaget y García (1982: 10): " ... extrae informaciones de los objetos mismos" para luego establecer relaciones entre ellos, expresándolas generalmente a través de razones y proporciones, para componerlas como relaciones de relaciones con el fin de tematizarlas [22].
Ya tematizado el principio hidrostático, es devuelto al plano de la experiencia [23] y está listo para ser aplicado a nuevos dominios [24], convirtiéndose en un "no observable". Por ejemplo, en el caso de la flotación, permite determinar cuál es la posición de un paraboloide de revolución en un fluido; así mismo permite clasificarlos a través de relaciones entre razones [sección 3.1].
Se puede concluir que, en la flotación, los fenómenos del reposo y del equilibrio, que en un principio fueron únicamente observables [25], poco a poco fueron adquiriendo sentido para Arquímedes a través del proceso de matematización. Debido a este proceso, estos observables dejaron de ser simplemente parte del medio que rodeaba a Arquímedes para convertirse en hechos susceptibles de ser matematizados.
CONCLUSIONES
La proporcionalidad es un instrumento que permitió matematizar fenómenode la flotación, desde la acción de relacionar .y medir magnitudes, determinar centros de gravedad (y así la posición de reposo en cualquier cuerpo), expresar la densidad de los cuerpos y fijar parámetros de clasificación para el análisis del paraboloide, entre otros aspectos. Así, Arquímedes acudió a las razones y proporciones para matematizar observables, que se originaban situaciones y fenómenos del plano de la experiencia: "el matemático atiende a la realidad con ella como referencia construye los esquemas, que espera, se adapten mejor a ella y permanece abierto a la posibilidad de mejorar su forma de aproximación a esta misma realidad" (Guzmán, 2002: 8).
Desde este punto de vista, la proporción y la razón como elementos esenciales de la proporcionalidad, y el cimiento teórico de los trabajos de Arquímedes, que a su vez fueron un gran aporte a la humanidad.
AGRADECIMIENTOS
Agradecemos a los colegas del grupo MESCUD, en especial a Jaime Romero Cruz y a Pedro Javier Rojas, por su juiciosa lectura y correcciones realizadas a nuestro artículo.
BIBLIOGRAFÍA
- Archimedes, 287-212 (?). The Works of Archimedes, Edición inglesa de T. L. Heath, Nueva York Dover, 1952, pp. 397-596.
- Boyer, C., Historia de la Matemática, Madrid, Alianza Editoria1,1986.
- Euclid, 300 a. C (?). The Thirteen Books of Euclid. Edición inglesa de T.L. Heath, Nueva York Dover, 1952, pp. 1-396
- Guzmán, M., Matemáticas y estructura de la naturaleza, Universidad Complutense de España Madrid. 2001 [Versión electrónica] http://www.mat.ucm.es/deptos/am/guzman/matyest.htm
- González, P., Las raíces del calculo infinitesimal en el siglo XVII, Madrid,Alianza Editorial, 1992
- Heath, T., A History of Greek Mathematics, Vols. I y II, Nueva York, Dover, 1921.
- Piaget, J.; García, R., Psicogénesis e historia de la ciencia, México, Siglo XXI, 1982.
- Vera, E, Científicos griegos, México, Edición Aguilar, 1970.
NOTAS
- Este artículo se originó en el Seminario de Pensamiento Multiplicativo, en el marco de la investigación Pensamiento Multiplicativo: una mirada de su densidad y complejidad en el aula, que desarrolla el Grupo MESCUD, financiada por la Universidad Distrital Francisco José de Caldas, Colciencias y el IDEP.
- En este artículo utilizaremos las siguientes abreviaturas:
Arq. Arquímedes SCF Sobre Cuerpos Flotantes I y II
Euc. Euclides SCF 1 Sobre Cuerpos Flotantes I
Def. Definición SCF II Sobre Cuerpos Flotantes II
Prop.Proposición SEP I Sobre el Equilibrio de los Planos
Post.Postulado TN Traducción Nuestra - Las citas correspondientes a las abreviaturas encerradas en } son tomadas de Works ofArchimedes,traducido por Heath (1952: 397-592).
- "De magnitudes desiguales, la mayor guarda con una misma (magnitud) una razón mayor que la menor, y la misma (magnitud) guarda con la menor una razón mayor que con la mayor" [Euc., V, Prop. 8, p. 86,TN]. La proposición 10 del libro V de Euclides es la recíproca de la proposición 8 del mismo libro.
- El registro histórico mas cercano del pensamiento arquimediano esta en sus obras: Sobre el equilibrio de los planos I y II, Sobre conoides y esferoides, sobre la cuadratura de la parábola, El método, Sobre cuerpos flotantes entre otras.
- Arquímedes llamaba peso a la fuerza ejercida por un objeto dirigida al centro de la Tierra. Esto se evidencia de la siguiente manera: "Si un sólido es más ligero que un fluido y se sumerge fuertemente en él, el sólido será llevado hacia arriba por una fuerza igual a la diferencia entre su peso y el peso del fluido desplazado" [Arq., SCFI, Prop. 6, p. 540, TN ].Y como sólo se pueden sumar dos magnitudes del mismo tipo (homogéneas), afirmamos que Arquímedes admitió que la diferencia entre dos pesos es una fuerza.
- En este artículo no distinguimos entre peso, masa y gravedad, en parte porque masa y peso serían lo mismo desde la concepción estática del mundo para los griegos, y éstas sólo se diferenciaron varios siglos después con sir Isaac Newton (1642-1727).
- Con el fin de establecer en qué proporción está sumergido el paraboloide de revolución.
- Por la definición de razón: "Úna razón es determinada relación con respecto a su tamaño entre dos magnitudes homogéneas" [Euc., V, def. 3, p.81, TN.]
- "Cualquier sólido más pesado que un fluido y situado en él, se sumergirá hasta el fondo del fluido, y si se pesa dicho sólido dentro del fluido resultará más ligero que su verdadero peso, por el peso del fluido desplazado" [Arq., SCF I, Prop. 7, p. 541, TN.]
- Arquímedes definió paraboloide de revolución en la Carta dirigida a Dositeo en su tratado Sobre Conoides y Esferoides como: Lo concerniente al paraboloide de revolución digo lo siguiente: a) si una parábola gira alrededor de su diámetro fijo (eje) hasta regresar a la posición en la que partió, la figura comprendida por la parábola es llamada paraboloide en revolución, y el diámetro que permanece fijo es llamado su eje, mientras su vértice es el punto en que el eje encuentra la superficie del paraboloide. (Heath, 1921, p. 452, TN).
- Sobre esto comenta Heath (1952, p. 541) de la proposición 9 que: "La demostración de esta proposición ha sobrevivido solo de forma incompleta. Además con solo un caso de tres que son distinguidos desde el comienzo... se demuestra el caso en el que el segmento es más grande que el hemisferio".
- Arquímedes concebía la parábola, al igual que Menecmo, como "La sección producida por el corte de un plano a un cono circular recto, tal que el ángulo formado por dos generatrices coplanarias con el eje del cono es recto" (Vera, 1970, p. 100).
- Apolonio, en su libro The Conics, proposición 11, demuestra esta propiedad. En este libro también define el eje y el vértice de figuras.
- Vera (1971, p. 261 - 297) realizó una versión de la traducción al español de este tratado.
- "Los círculos están en razón uno al otro como los cuadrados de sus diámetros" [Euc., XII, Prop. 2,p. 339, TN].
- "El volumen de un segmento de un paraboloide recto de revolución, cortado por un plano perpendicular es al volumen de un cono que tiene la misma base y el mismo eje que el segmento como la razón 3:2" [Arg., El Método, Prop. 4, p. 576, TN 1.
- Debemos aclarar que este instrumento no fue el único que permitió el surgimiento de esta teoría,sino que intervinieron otros instrumentos teóricos como el uso de la ley de la palanca, del principio de exhaución, entre otros.
- Al realizar cualquier abstracción sobre la experiencia (entendiéndose experiencia no sólo lo tangible) "quisiera dejar claro que por realidad no quiero significar solamente el mundo externo...sino también el mundo mental que el mismo matemático va construyendo" (Guzmán, 2001, p. 10), donde esta se "abstrae, simplifica y modeliza, pero también hay que decirlo, mutila la realidad, para tratar de entenderla al menos parcialmente" (Guzmán, 2001, p. 12).
- El tematizar lo tomamos en el sentido de Piaget y García (1982, p. 103): "El pasaje del uso o aplicación implícita a la utilización conciente, a la conceptualización constituye lo que hemos convenido llamar tematización".
- Ver cita 21.
- Tomamos el término dominio como "subconjunto de objetos, eventos, etc., ya aceptados en las situaciones S que constituyen el punto de partida" (Piaget y García, 1982, p. 194).
- Observable desde Piaget y García (1982) es definido así: "cada teoría corresponde a un nivel determinado de abstracción con relación a la realidad física. En cada nivel se toman como punto de partida ciertas propiedades de los objetos a los cuales se le aplica a la teoría. Estas propiedades constituyen los observables para la teoría en cuestión".
Creation date:
License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.



