Ingeniería y Tecnología

Revista Científica, 2007-08-00 nro:9 pág:161-168

Didáctica de la programación lineal con el método gráfico

Didactic of linear programming with the graphic method (I)

Fernando León Parada

fleon@udistritaLedu.co

SOLUCIÓN GRÁFICA DE MODELOS DE PROGRAMACIÓN LINEAL C0N DOS VARIABLES

Resumen

El concepto de región factible, en programación lineal, cumple un papel similar al concepto de dominio en el estudio analítico de las funciones reales. Expresa la variabilidad del modelo matemático de un problema de optimización donde los valores de cada variable deben obedecer a un conjunto de restricciones establecido.

Palabras clave:
Programación lineal, optimización, región factible, modelo matemático.

Abstract

The graphic method is a good tool for solving mathematical models whose are related to optimization problems; with this method a typical problem of linear programming can be solved by simply evaluating the values of the objective function at the boundary vertices of the feasible region, this results of applying a special mathematical theorem for linear functions.

Key Words:
Linear Programming, optimization, feasible region, mathematical model.

Objetivo

Presentar la didáctica elemental del Método gráfico para solucionar modelos de optimización con dos variables de decisión; estas variables serán representadas con las letras x e y, pues se refieren al eje de abscisas (x) y al eje de ordenadas (y). La didáctica preliminar se dirige al estudio analítico de las funciones lineales, o de primer grado, de cualquiera de las formas siguientes:

Pendiente e intercepto vertical: y= mx + b
Simétrica de oblicuas: x/a + y/b =1
Pendiente y un punto (a,b): y= m(x—a)+ b
Dos puntos (a,b), (c,d): y= ((d—b)/(c—a))(x—a)+ b

La comprensión del Método gráfico emplea regiones convexas como los siguientes:

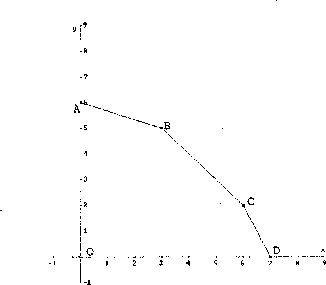
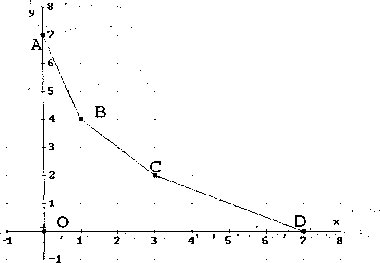
En la figura 1,1a región es acotada por la poligonal convexa cerrada de vértices O-A-B-C-D-O; mientras que en la figura 2, la región no es acotada superiormente, pues su frontera es eje vertical-A-B-C-D-eje horizontal.

Supuesto que se conocen las coordenadas de cada uno de los vértices, la expresión, analítica de cada región se logra mediante un sistema simultáneo de desigualdades lineales. Primero se establecen las ecuaciones de las rectas que contienen los segmentos que limitan la región. Para hallar cada ecuación de recta que pasa por dos puntos (a,b), (c,d) se aplica y = ((d—b)/(c—a)) (x — a) + b. Luego, cada ecuación se transforma en una desigualdad de la forma y≤ para representar los puntos de la región situados bajo cada segmento (la gráfica 1), o de la forma y≥ para los puntos situados arriba o a la derecha de cada segmento (figura 2). Las desigualdades forman un sistema simultáneo de inecuaciones que representan la intersección de semiplanos o región plana.

Estas nuevas inecuaciones también se establecen con las formas generales del tipo: a_il x + a_i2 y≤ b_i, o del tipo (a_il x + a_i2 y≥b_i donde la subvariable i sirve para indicar la ordenación de los segmentos o rectilíneas.

De modo inverso, dado el planteamiento de un sistema de desigualdades lineales se puede obtener la gráfica de la región. Basta resolver el sistema para hallar los puntos solución de corte entre las rectilíneas mediante las técnicas elementales del álgebra lineal; luego se consideran los casos de simultaneidad o de intersección entre los respectivos semiplanos que definen las desigualdades.

Cuando se trata de una ecuación de la forma a_il x + a_i2 y≤b. donde no sean nulos a_il y a_i2 la forma simétrica para recta oblicua, x/a + y/b =1, se aplica para identificar los cortes de la recta con los ejes coordenados.

La didáctica es reversible. Cada proceso se ilustra con un ejemplo que emplea alguno de los gráficos anteriores.

Ejemplo 1
Dada la figura 1, determinar la representación analítica de la región factible.

Solución
Con las coordenadas de los puntos se hallan la pendiente, la ecuación y la desigualdad del segmento:

A= (O,6), B= (3,5); AB tiene pendiente (5—6)/(3—0)= —1/3. La ecuación es y= (1/3)(x O )+ 6 = x/3 + 6: X +3 Y≤ 18

B= (3,5), C= (6,2); BC tiene pendiente (2—5)/(6—3)= — 1. La ecuación es y= 1(x-6)+2=-x+8: X + Y≤ 8

C= (6, 2), D= (7, 0); CD tiene pendiente (0—2)/(7—6)= - 2. La ecuación es y= 2(x 7) + O= 2x + 14: 2X + Y≤ 14

Como la región factible está en el primer cuadrante del plano, la abscisa y la ordenada son no negativas: X≥ O, Y≥ O.

De esta forma se representa la región factible de la figura 1 con el sistema simultáneo de desigualdades descritas anteriormente.

Ejemplo 2
Determinar la gráfica de la región factible que obedezca al siguiente sistema de desigualdades lineales:

X+2Y≥7, X+ Y≥5, 3X+Y≥7, X≥0, Y≥0.

Solución
Con la forma simétrica se determinan los cortes de las rectilíneas y los ejes coordenados:

X/7 + Y/(7/2) = 1, X/5 + Y/5 = 1, X/(7/3) + Y/7 = 1. En el primer cuadrante del plano, los vértices elementales son A = (0, 7) y D = (7, 0). Los otros vértices se determinan como soluciones de dos ecuaciones lineales, así:

{3X + Y = 7, X + Y = 5} = {2X = 2, X + Y = 5} = = 1, Y = 41: se obtiene el vértice B = (1,4).

{X + 2Y = 7, X + Y = 5} ={Y= 2, X + Y = 5} = {X = 3, Y = 2}: se obtiene el vértice C = (3,2).

Luego se representan los vértices en el plano y se trazan los segmentos. Con la condición de no negatividad de las variables, la intersección de los semiplanos se comprende sobre la figura 2, donde las condiciones del signo mayor o igual interpretan los puntos de ordenada mayor o igual que la de los puntos de todos los segmentos. Además, los puntos de la región permanecen arriba del eje horizontal de abscisas y a la derecha del eje vertical de ordenadas. Nótese que esta región no está acotada superiormente.

En algunos casos, las desigualdades lineales puede que no representen semiplanos oblicuos. Por ejemplo, si aparece una condición de variable respecto de constantes: h≤ X ≤ k, significa que la región traza una banda de plano limitada entre las líneas verticales X= h y X = k. Análogo si se trata de acotar la variable Y entre constantes.

En otros casos, la región puede resultar vacía cuando la intersección de los semiplanos así lo sea. La intersección también puede resultar reducida a un segmento de recta o a un solo punto; todo depende de su geometría.

Finalmente, una función bivariada cuyo dominio es el conjunto de puntos de la región se define por una fórmula algebráica que involucra las variables X e Y. Cuando la función es una combinación lineal de las variables, se afirma la función lineal y se expresa como Z(X,Y) = C₁ X + C₂ Y, donde C₁ y C₂ se denominan coeficientes respectivos de las variables. Ahora, el problema central de un modelo de programación lineal es hallar los puntos extremos de Z, es decir, los puntos de la región dominio donde Z alcanza sus valores máximos o mínimos. Cada modelo se expresa como maximizar (o minimizar) Z sujeta a la región factible.

La solución del problema consiste en evaluar Z sobre los vértices de la región, y comparar según el orden real.

Ejemplo 3
Maximizar Z = 2X + 3Y, sujeta a la región de la figura 1.

Solución
Basta evaluar Z en los vértices para conformar un conjunto finito del cual se obtenga su valor máximo.

En O = (0, 0), Z(0, 0) = 2(0) + 3(0) = 0.
En A = (0, 6), Z(0, 6) = 2(0) + 3(6) = 18.
En B = (3, 5), Z(3, 5) = 2(3) + 3(5) = 21.
En C = (6, 2), Z(6, 2) = 2(6) + 3(2) = 18.
En D = (7, O), Z(7, 0) = 2(7) + 3(0) = 14.

La comparación de estos valores indica que Z toma el máximo valor 21 en el punto óptimo B = (3,5).

Ejemplo 4
Maximizar Z = 2X + Y, sujeta a la región de la figura 1.

Solución
Análogo, al evaluar Z en los vértices resulta:

En O = (O, O), Z(0, 0) = 2(0) + (0) = 0.
En A = (0, 6), Z(0, 6) = 2(0) + (6) = 6.
En B = (3, 5), Z(3, 5) = 2(3) + (5) = 11.
En C = (6, 2), Z(6, 2) = 2(6) + (2) = 14.
En D = (7, 0), Z(7, 0) = 2(7) + (0) = 14.

La comparación de estos valores indica que Z toma el máximo valor 14,en los puntos óptimos C = (6, 2) y D = (7, 0).

Pero estos puntos forman un segmento que también pertenece a la región factible, y sus infinitos puntos también son óptimos pues en cada uno de ellos Z toma el valor máximo 14. Por tanto, la soluCión del modelo se brinda por el conjunto de puntos del segmento cuya forma paramétrica es (X, Y): 6≤ X≤ 7, Y = -2X + 141.

Ejemplo 5
Minimizar Z = 2X + Y, sujeta a la región de la figura 2.

Solución
Al evaluar Z en los vértices se conforma un conjunto finito del cual se obtiene su valor mínimo:

En A = (0, 7), Z(0, 7) = 2(0) + (7) = 7.
En B = (1, 4), Z(1, 4) = 2(1) + (4) = 6.
En C = (3, 2), Z(3, 2) = 2(3) + (2) = 8.
En D = (7, 0), Z(7, 0) = 2(7) + (0) = 14.

La comparación de esos valores indica que Z toma el mínimo 6 en el punto óptimo B = (1,4).

Ejemplo 6
Minimizar Z = X + Y , sujeta a la región de la figura 5.

Solución
Al evaluar Z en los vértices, resulta:

En A = (0, 7), Z(0, 7) = (0) + (7) = 7.
En B = (1, 4), Z(1, 4) = (1) + (4) = 5.
En C = (3, 2), Z(3, 2) = (3) + (2) = 5.
En D = (7, 0), Z(7, 0) = (7) + (0) = 7.

La comparación de valores indica que Z toma el mínimo valor 5 en los puntos óptimos B = (1, 4) y C = (3, 2).

Como estos puntos forman un segmento frontera de la región factible, los infinitos puntos de este segmento son óptimos pues Z toma el valor mínimo 5 en cada uno de ellos. Luego, la solución del modelo está dada por el conjunto de infinitos puntos del segmento óptimo que tiene forma paramétrica: {(X,Y): 1≤ X≤ 3, Y = 5 - X}.

El objetivo de la didáctica de la programación lineal con el método gráfico apenas inicia con los elementos aquí expuestos; siguen entonces las actividades de afianzamiento en el siguiente orden:

1. Hallar las expresiones analíticas de una región plana según sus fronteras poligonales

2. Graficar la región plana, dado un sistema simultáneo de relaciones lineales entre las variables.

3. Identificar regiones vacías o que se reducen a una recta (o a un solo punto) en el plano.

4. Determinar valores extremos (máximo o mínimo) de una función lineal definida sobre una región plana convexa (o no convexa), cuya solución no exista, o sea un solo punto o sea un segmento óptimo.

El método gráfico también es útil para comprender la variación de los coeficientes de la función objetivo de modo que la solución del modelo se mantenga en el mismo punto óptimo. Esto responde a las preguntas ¿qué márgenes pueden tener los coeficientes de la función objetivo de modo que la solución del modelo se mantenga en los puntos óptimos previamente obtenidos? y ¿cuáles serán las respectivas variaciones de los valores extremos de la función objetivo al modificar los coeficientes hasta esos márgenes?

También responde a las preguntas ¿qué variación aceptan las fronteras o bordes de la región para que ésta siga siendo factible?, ¿cuáles nuevos puntos óptimos y valores extremos resultan cuando se modifican paralelamente los bordes de la región original?