Ingeniería y Tecnología

Revista Científica, 2007-08-00 nro:9 pág:199-206

---

Topologías linealmente ordenadas

Linearly ordered topologies

Edilberto Sarmiento Sarmiento

Magíster en Matemáticas.
Profesor Universidad Distrital Francisco José de Caldas.
Proyecto Curricular de Tecnología en Topografía.

Resumen

En este artículo estudiamos las topologías linealmente ordenadas y para un conjunto finito X, encontramos el número de cadenas maximales en ℘ (X) y se hallan cotas superiores e inferiores para el número de topologías linealmente ordenadas sobre X.

Abstract

In this paper we study the linearly ordered topologies and for a finite set X, we find the number of maximal chains in ℘ (X), and find upper and lower bounds for the number of linearly ordered topologies:

---

ALGUNAS NOTACIONES

Sea α una colección de subconjuntos de un conjunto X. Se definen las siguientes colecciones, asociadas con α, por medio de la noción de complemento.

Complemento interno
αc= {A: X-A ∈ α }

Complemento externo
cα=℘(X)- α={B:B ∉ α}

Doble complemento
cαc =℘(X)- Ac = {B ∈℘ (X): cB ∉α}

El cardinal de un conjunto A se nota 1A1.

El conjunto ℘(X), denota la colección de subconjuntos no vacíos de X.

℘*(x) = {A: A ⊂ X}

La colección ℘*(X)_* denota a los subconjuntos de X distintos de ∅ y X. En símbolos:

℘*(X)_*=℘ (X)- {∅,X}

El conjunto ℘_k(X) denota la colección de subconjuntos de X que tienen k elementos:

℘k(X) = {A ⊆ X : lAl = k para 1 ≤ k≤ X

Si A es un subconjunto de X, se denota por Θ(A) a la colección de hiperconjuntos de A. En símbolos:

Θ(A) = {B∈℘(X): A ⊆ B}

Se denota por Θ(A), la colección de hiperconjuntos de A distintos de A. En símbolos:

Θ(A) = {3∈℘(X) :A⊆ B y B # A}

Se denota por S(X) al grupo de permutaciones de X.

Una colección a de subconjuntos de X es totalmente ordenada si (α, ⊆) es un conjunto totalmente ordenado

Por T(X) se denota la familia de todas las colecciones totalmente ordenadas sobre X:

T(X) = {α ∈℘²(X) : (A,⊆) es totalmente ordenada}

Proposición

La familia T(X) de todas las colecciones totalmente ordenadas satisface las hipótesis del lema de Zorn; luego en T(X) existen elementos Maximales. Estos elementos maximales se denominarán, en este artículo, cadenas maximales de ℘(X).

DEFINICIÓN Y EJEMPLOS DE TOPOLOGÍAS LINEALMENTE ORDENADAS

Definición

Una topología i es linealmente ordenada si el conjunto ordenado (t, ⊆) es un conjunto totalmente ordenado, es decir, si para cada par de elementos A,B ∈ T, se cumple A ⊆ B o B ⊆ A.

Se nota con TOPL(X) al conjunto de todas las topologías linealmente ordenadas

Observación
Las topologías linealmente ordenadas son conexas.

Ejemplos
Las siguientes son topologías linealmente ordenadas sobre, un conjunto arbitrario X.

1. {∅, X}

2. {∅, X, A}, donde A ∈ ℘*(X)_*, 1X1 2

3. -{∅, X, A_l, A₂}, tal que A_l ∈ ℘(X) y A₂ ∈ Θ (A₁)_*, 1X1 3

4. Las cadenas maximales de ℘(X) son topologías linealmente ordenadas.

Las siguientes son topologías linealmente ordenadas sobre intervalos de números reales R.

1. Sea T = {(-n,n) : n ∈ Z⁺} u {∅, R}. El espacio (R, r) no es compacto.

2. Si {a_n: n∈Z⁺} es una sucesión creciente y no acotada de números reales positivos,

T= {(-a_n, a_n): n∈Z⁺} u {∅, R}. El espacio (R, T) no es compacto.

3. Si {an: n∈Z⁺}} es una sucesión decreciente {bn:n∈Z+}} es una sucesión creciente de números reales tales que an < bn. para todo n,

τ= {(a_n, b_n): n ∈ Z⁺} ∪ {∅,X}, donde X= Ü(a_n, b_n). El espacio (X,τ) no es compacto.

4. Con las mismas condiciones del ejemplo 3, pero suponiendo además que las sucesiones son acotadas τ= {(a_n, b_n): n ∈ Z⁺} ∪ {∅,A,ℜ}, con A=Ü (a_n, b_n). El espacio (ℜ τ) es compacto.

5. Si {a_n: n ∈ Z⁺}} es una sucesión creciente y { b_n: n ∈ Z⁺}} es una sucesión decreciente de números reales tales que a_n < b_n para todo n,

τ= {(a_n, b_n): n ∈Z⁺} ∪ {∅, [a₁ ,b₁]}. El espacio ([a₁,b₁) es compacto.

Proposición
El conjunto ordenado (TOPL(X) ,⊆) satisface las siguientés condiciones:

1. Tiene elemento mínimo {∅, X} y maximales, que son precisamente las cadenas maximales de ℘(X).

2. La familia TOPL(X) es cerrada para intersecciones.

3. Si τ ∈ TOPL(X) y X es finito, entonces la colección de cerrados τc∈ TOPL(X).

Para un conjunto finito X, con |X|=n, notamos con TOPL_m (X) la colección de topologías linealmente ordenadas que tienen m elementos.

TOPL_m(X)= τ ∈ TOPL(X): |τ|= m}

Proposición
Sea X un conjunto finito, |X|= n.

1.TOPL(X)= {{∅, X }} ∪ Ü TOPL_m (X),

2.|TOPL(X)|= 1+∑ |TOPL_m(X)| es un número impar.

Demostración

1. Su demostración es inmediata.

2. Es suficiente probar que |TOPL_m(X)1 es un número par para m ≥ 3

Esto se sigue de que {{τ, τc} τ ∈ TOPL_m(X)} es una partición de TOPL_m (X).

NÚMERO DE CADENAS MAXIMALES EN ℘ (X)

Si X es un conjunto finito, una colección a es una cadena maximal de ℘ (X) si satisface:

(α,⊆) es un conjunto totalmente ordenado y |α ∩ ℘_k(X)|= 1 para todo k,0 ≤ k ≤ |k|

Ejemplo
Si X= {x₁, x₂,.... x_n}, la colección

α= {∅,{x₁}, {x₁,x₂}, {x₁, x₂, x₃},...,{x₁,x₂,.....x_n}}

es una cadena maximal en ℘ (X).

Se denotará por CM(X) al conjunto de todas las cadenas maximales de ℘ (X).

Teorema
Si X es un conjunto finito, hay exactamente |X|! cadenas maximales en ℘ (X)

Demostración

Supongamos que X = {x₁, x₂,...x_n}.

La función f: S(X)---> CM(X) tal que

f(σ) = {∅,σ,(x₁)} {σ(x₁),σ{σ(X₁),σ (x₂),} σ(x₃)},......, {σ(x₁), σ(x₂),..., σ(x_n)}} es biyectiva.

1. Es claro que f está bien definida.

2. f es inyectiva.

Si f(σ) = f(µ), entonces σ(x_j) = µ(x_j) 1 ≤ j ≤ n. y σ= µ

3. f es sobre.

Sea β= {∅, {m₁}, {m₁, m₂}, {m₁, m₂, m₃,....,m_n} ∈ CM(X), m_j ∈ X I ≤ j ≤ n

si π (x_i)= m_i 1 ≤ i ≤ n se tiene que π ∈ S(X) y f(π) =β

Nota. El resultado anterior sigue siendo válido para un conjunto X numerable. En este caso, se tiene que CM(X) es equipotente a S(X) mediante la biyección presentada en el teorema anterior.

SOBRE EL NÚMERO DE TOPOLOGÍAS LINEALMENTE ORDENADAS

Proposición
1. La función f:℘*(X)---> TOPL(X) tal que f(A) = {∅, X, A} está bien definida y es inyectiva.

2. n!+2^n-2+1≤ |TOPL(X)|.

Demostración

1. Se deduce de la definición de la función.

Se deduce de |TOPL₃(X)|= 2^n-2, TOPL,_n+i (X) = CM(X) y |TOPL_n+i (X)| = n!

Sea σ una permutación del conjunto finito X= {x1, x2,..., xn}

C_σ = {∅, {σ(x₁)}; σ{ (x₂), σ(x₃)},....,,{σ(x₁),σ(x₂)},(x_n) }}

Proposición

Si ℘(C_σ-{∅,X})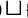 {{∅,X}} = {α ∪ {∅,X} : α ∈ ℘ (C_σ -{∅,X})}.

1. TOPL(X) ⊆ 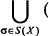(℘(C_σ- {∅,X})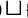{{∅,X}})

Proposición

Sea A ⊆ X, A # ∅ y CM(A) el conjunto de cadenas maximales de ℘ (A).Entonces:

1.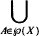 CM(A) ⊆ TOPL(X)

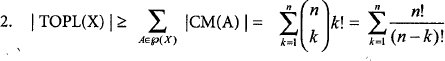
BIBLIOGRAFÍA

• [dyp] Davey y Priestley, Introduction to Latices and order, Cambridge University Press, Cambridge 1994.
• [em] Eisenberg, M., Axiomatic Theory of sets and classes, Holt, Rinhear and Winston, Inc. New York 1971.
• Graver, J.; WATKINS, M., Combinatories with emphasis on the Theory of Graphs, Springer Verlag, New York, 1977.
• Kopelberg, S. et al., Handbook of Bo,olean Algebras, Elsevier Science Publishers, Amsterdam, 1989.
• Muñoz, J., Introducción a la teoría de conjuntos, Bogotá, Universidad Nacional de Colombia, Bogotá 1993.
• Willard, S., General Topology, Addison Wesley, Alberta 1970.

---

Creation date: