Ingeniería y Tecnología

Revista Científica, 2007-08-00 nro:9 pág:261-276

Red Neuronal Artificial ART2 para la agrupación de datos

Artificial Neuronal Nerwork ART2 for Clustering Data

Jorge E. Rodríguez

Universidad Distrital Francisco José de Caldas,
Grupo de Investigación en Inteligencia Artificial.
jrodri@udistrital.edu.co

Resumen

Este artículo se presenta como un avance parcial del proyecto de investigación Desarrollo de Herramientas para Minería de Datos-UDMiner, en el que se muestra la implementación de una red neuronal tipo resonancia adaptativa, ART2, empleada para la agrupación de datos. Se compara la técnica implementada con el algoritmo EM y los mapas autoorganizativos de Kohonen.

Palabras clave
Minería de datos, grupo, red de resonanda adaptativa, mapasautoorganizativos, algoritmo EM.

Abstract

i In this paper, we present a partial advance of the project of development investigation of,tools for data mining, which consists on the implementa tion of Adaptative Resonance Network (ART2) for the clustering data. The implemented technique is compared with Self-Organizing Maps and the algorithm EM (Expectation Maximization) with the purpose of measuring the clustering effectiveness.

Key words
Data mining, cluster, adaptative resonance network, self-organizing maps, algorithm EM.

INTRODUCCIÓN

El objetivo de la agrupación de datos es obtener grupos o conjuntos de elementos entre los elementos de X, de manera que los elementos ,asignados al mismo grupo sean similares. Un grupo es una colección de datos semejantes a otros de un mismo grupo y diferentes a los objetos de otros grupos [1].

El análisis de agrupación es un conjunto de metodologías para clasificación automática de muestras entre un número de grupos usando medidas de asociación. Es decir, las muestras en un grupo son similares; las pertenecientes a otros grupos son diferentes [2].

El análisis de grupos, también llamado segmentación de datos, tiene gran variedad de metas, todas referidas a una colección de grupos o segmentos de objetos entre subconjuntos "grupos", de modo que los grupos de un mismo objeto están estrechamente relacionados entre sí, y difieren notablemente con grupos de otros objetos. Un objeto puede ser descrito por un conjunto de medidas o por sus relaciones con otros objetos [3].

El análisis de grupos puede ser una herramienta estándar para beneficiar la percepción en la de la distribución de los datos, para observar las características de cada grupo y para enfocarse en una colección particular de grupos con el fin de lograr mayor exploración. Alternativamente, puede servir cómo técnica para preprocesar datos, tal como caracterización y clasifiación, los cuales podrían operar sobre los grupos descubiertos.

La agrupación de datos contribuye a áreas de investigación, incluidos Minería de Datos, estadísticas, aprendizaje computacional, tecnología de bases de datos espaciales, biología, mercadeo, etc. Como consecuencia de la gran cantidad de información de las bases de datos, el análisis de grupos ha llegado a ser un tema importante en la investigación de Minería de Datos. Como una rama de la estadística, el análisis de grupos ha sido estudiado por varios años, concentrándose principalmente en la distancia basada en el análisis de grupos. Las herramientas basadas en K-means, K-medoids y otros métodos también han sido construidos dentro de varios paquetes o sistemas de software de análisis estadístico, como S-Plus, SPSS y SAS. En aprendizaje computacional, la agrupación es un ejemplo de aprendizaje no supervisado.

En Minería de Datos, algunos esfuerzos se han enfocado en encontrar métodos eficientes para el análisis de grupos en las grandes bases de datos. Recientes temas de investigación se están orientando en la escalabilidad de los métodos de agrupación, mayor eficiencia de los métodos para la agrupación de formas complejas y tipos de datos, técnicas de agrupación de alta dimensionalidad y métodos de agrupación para datos mixtos numéricos y categóricos en grandes bases de datos.

En el artículo se muestra el proceso de desarrollo y validación de una herramienta para la agrupación de datos, cuyo propósito es extraer conocimiento útil a partir de los datos. Se utiliza como técnica de agrupación una red neuronal artificial, llamada Red de Resonancia Adaptativa.

El artículo se encuentra estructurado en: 1) Requerimientos y métodos de agrupación de datos, donde se presenta una reseña referente a escalabilidad y capacidad para manejar diferentes tipos de datos. 2) Métodos de agrupación (basados en particionamiento, jerárquicos, basados en grid, basados en densidad, y basados en el modelo). 3) Red de resonancia adaptativa, aquí se presenta la teoría utilizada en la red ART2, juntó con su arquitectura, haciendo énfasis en el subsistema de orientación y de atención. 4) Análisis de resultados. Para tal fin se toman diferentes conjuntos de datos, provenientes de la WEB, y se hace la comparación con Mapas Autoorganizativos de Kohonen y el algoritmo EM (Maximización de la Esperanza). 5) Finalmente, se plantean las conclusiones obtenidas del avance parcial de investigación y se deja abierta la posibilidad realizar trabajos futuros.

REQUERIMIENTOS DE LA AGRUPACIÓN EN LA MINERÍA DE DATOS [1]

Escalabilidad
Existen algoritmos de agrupación que funcionan bien en pequeñas coleociones de datos (por ejemplo, 200 datos). Sin embargo, una gran base de datos contiene millones de objetos. La agrupación sobre un patrón en una gran colección de datos puede conducir a predisponer resultados, es decir, normalmente funcionan bien con pocos datos.

Capacidad para manejar diferentes tipos de datos
Diferentes algoritmos son diseñados para grupos de intervalos de datos numéricos; no obstante, las aplicaciones pueden requerir agrupación de otros tipos de datos, por ejemplo binarios, nominales, y ordinales, o mezclas de estos tipos de atributos.

Grupos de formas arbitrarias
Algunos algoritmos de agrupación están basados en las medidas de distancia euclidiana o Manhattan. Estos tienden a encontrar grupos esféricos con similar tamaño y densidad. Sin embargo, un conjunto de datos podría ser de cualquier forma. Es importante desarrollar algoritmos que puedan descubrir grupos de forma arbitraria.

Requerimientos mínimos para especificar parámetros
Un alto número de algoritmos de agrupación requieren especificar parámetros en el análisis de grupos (como el número de grupos deseados). La agrupación puede ser totalmente sensible a la especificación de parámetros. Los parámetros pueden ser, con frecuencia, difíciles de determinar, sobre todo con colecciones de datos contenidas en objetos de alta dimensionalidad.

Habilidad para tratar con datos ruidosos
La mayoría de bases de datos del mundo real contienen datos faltantes, datos sin conocer o datos erróneos. Algunos algoritmos de agrupación son sensibles a tales datos y pueden conducir a grupos de baja calidad.

Independencia en el orden de los registros
Existen algoritmos de. agrupación sensibles al orden de especificación de los datos; por ejemplo, la misma colección de datos, cuando se presenta con diferente disposición en un algoritmo, puede generar diferentes grupos.

Alta dimensionalidad
Una base de datos puede contener diversas dimensiones o atributos. La mayoría de los algoritmos de agrupación funcionan bien con datos de baja dimensionalidad, que involucran solo dos o tres dimensiones. Los humanos somos buenos para juzgar la calidad de agrupación por debajo de tres dimensiones. Esto está desafiando al análisis de grupos con alto espacio dimensional, en especial considerando que tales datos pueden ser escasos.

Interpretabilidad y usabilidad
Los que aplican la agrupación esperan que los resultados de ésta sean interpretables, comprensibles y usables.

MÉTODOS DE AGRUPACIÓN

Existe un gran número de algoritmos de agrupación en la literatura. Escoger uno depende del tipo de datos y del propósito mplicacióti del algoritmo. Si el análisis de agrupación se usa como herramienta descriptiva o explorativa, es posible probar diferentes algoritmos sobre el mismo dato para ver sus resultados. En general, los principales métodos de agrupación pueden ser clasificados en las siguientes categorías.

Métodos de particionamiento
Dada una base de datos de n objetos o registro de datos, un método de particionamiento construye K particiones sobre los datos, donde cada partición representa un grupo con k<=n, es decir, clasifica los datos dentro de K grupos, los cuales satisfacen los siguientes requerimientos:

1. Cada grupo podría contener al menos un objeto.
2. Cada objeto podría pertenecer exactamente a un grupo.

Dado K, el número de particiones por construir un método de particionamiento crea una partición inicial. Esta usa una técnica de relocalización iterativa que procura perfeccionarla partición por movimiento de objetos de un grupo a otro. El criterio general de un buen particionamiento es que los objetos del mismo grupo son "cercanos" o relacionados los unos con los otros, mientras que los objetos de diferentes grupos son "apartados" o muy diferentes.

Para llevar a cabo una buena agrupación basada en particionamiento, se podría requerir una numeración exhaustiva de las posibles particiones. En cambio, la mayoría de aplicaciones adoptan heurísticos: 1) el algoritmo k-means, en el que cada grupo es representado po'r el valor medio de los objetos en el grupo, y 2) el algoritmo k-medoids, en el que cada grupo es representado por uno de los objetos localizado cerca del centro del grupo. Estos métodos heurísticos funcionan bien con grupos esféricos y con bases de datos de pequeño y mediano tamaño. Si las bases de datos, forma compleja o son de gran tamaño, el método de particionamiento k-medoids necesita ser extendido [1].

Métodos jerárquicos
Un método jerárquico crea una descomposición jerárquica de una colección dada de datos. Considerando que los métodos basados en partición inician especificando un número de grupos y busan, a través de posibles asignaciones de grupos de puntos, encontrar una función que perfeccione el grupo, los métodos jerárquicos unen gradualmente puntos o dividen supergrupos [4].

Un método jerárquico puede ser clasificado en aglornerativo o divisivo, dependiendo de cómo se conforma la descomposición jerárquica. La forma aglomerativa también llamada fornia bottom-up, comienza formando un grupo separado. Con cada objeto. Este une sucesivamente los objetos o grupos cercanos a otros hasta que todos los grupos se unen en uno (el mayor nivel de la jerarquia) o hasta que se cumple determinada condición. El método divisivo, también llamado top-down;comienza con todos los objetos de un mismo conjunto. En cada iteración sucesiva, un grupo es dividido en pequeños grupos hasta que, eventualmente, cada objeto esté dentro de un grupo o hasta que se cumpla determinada condición.

Métodos basados en la densidad
La mayoría de los métodos de particionamiento agrupan objetos basados en la distancia entre éstos. Tales métodos pueden trabajar con grupos de formas esféricas y encontrar dificultades al descubrir grupos con formas arbitrarias: Otros métodos de agrupadón se han desarrollado basados en la noción de densidad. Su idea general es continuar extendiendo el grupo dado, tan extenso como la densidad (número de objetos o datos) en la "vecindad", excediendo algunos umbrales; es decir, por cada dato sin un grupo dado, la vecindad de un radio contiene un mínimo número de puntos. Tal método puede ser usado para filtrar ruido y descubrir grupos de formas arbitrarias.

Métodos basados en Grid.
Cuenta los espacios de objetos dentro de uri número infinito de celdas que forman una estructura grid. Todas las operaciones de agrupación son realizadas sobre la estructura del grid (ejemplo, la contabilización de los espacios). Las principales ventajas de esta forma es que este tiene un tiempo de procesamient o rápido, generalmente independiente del número de objetos, pues depende solo del número de celdas en cada dimensión de los espacios contabilizados.

Métodos basados en el modelo
Este método encuentra un modelo para cada grupo y los datos más adecuados para este modelo. Un algoritmo basado en el modelo puede localizar grupos para crear una función de densidad que refleje la distribución espacial de los datos puntuales. También puede determinar el número de grupos basados en una estadística estándar, tomando los objetos ruidosos dentro de un grupo para dar robustez a los métodos de agrupación.

RED DE RESONANCIA ADAPTATIVA (ART2)

Una de las características de la memoria humana consiste en su habilidad para aprender nuevos conceptos sin olvidar otros aprendidos en el pasado. Sería deseable que esta misma capacidad se pudiera conseguir en las redes neuronales artificiales. Sin embargo, muchas de éstas tienden a olvidar información pasada al tratar de enseñarle nueva. En respuesta Grossberg, Carpenter y otros desarrollaron la denominada teoría de la resonancia adaptativa--ART [5]. Este modelo se basa en la idea de hacer resonar la información de entrada con los prototipos o categorías que reconoce la red. Si entra en resonancia con alguno (es suficientemente similar), la red considera que pertenece a dicha categoría y se realiza una adaptación que incorpora algunas características de los nuevos datos a la categoría existente. Cuando no resuena con ninguno (no se parece a ninguna de las categorías existentes), la red se encarga de crear una nueva categoría con el dato de entrada como prototipo de la misma.

Esta teoría se aplica a sistemas competitivos (redes con aprendizaje competitivo) en los cuales, cuando se presenta cierta información de entrada solo se activa una de las neuronas de salida de la red (o una por cierto grupo de neuronas) alcanzando su valor de respuesta máximo después de competir con las otras. Esta neurona recibe el nombre de vencedora [5].

Existen tres elementos básicos para el aprendizaje competitivo [6] :

A. Un conjunto de neuronas iguales, excepto los pesos, definidos aleatoriamente, y que por consiguiente responde de manera diferente a cada de patrón de entrada.

B. Un límite impuesto a cada neurona.

C. Un mecanismo que permite a las neuronas competir para responder bien a un subconjunto dado de entradas, tal que solo se activa una neurona de salida o solo una neurona por grupo.

Una red ART2 consta de dos capas entre las que se establecen conexiones hacia adelante y hacia atrás (feedforward/feedback). La estructura general de una red ART2 se muestra en la figura 1.

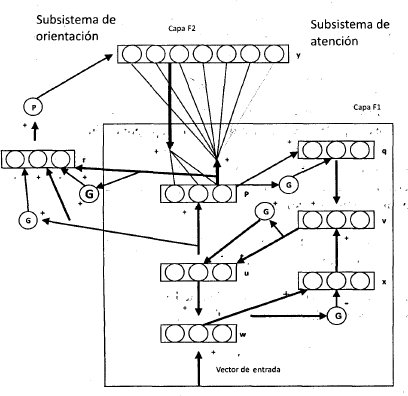
A continuación se hará un resumen del funcionamiento de la red ART2 [7].

La capa F1 se encuentra dividida en seis subcapas: w, x, u, v, p y q. Todos los nodos marcados con una G (llamadas unidades de control de ganancia) envían una señal inhibitoria no específica a todas las unidades de la capa a la que llegan. Todas las subcapas de F1, así como la capa r del subsistema de orientación, tienen el mismo número de unidades. Las subcapas individuales de Fl están conectadas de unidad a unidad; esto es, las capas no están completamente interconectadas, con la excepción de las conexiones ascendentes que llegan a F2 y de las conexiones descendéntes de F2.

El subsistema de orientación detecta la falta de coincidencia entre las tramas ascendentes y descendentes de la capa F 1 . Esta utiliza para determinar la coincidencia, una magnitud que recibe el nombre de parámetro de vigilancia y suele identificarse mediante el símbolo p. El valor del parámetro de vigilancia mide hasta qué grado discrimina el sistema entre distintas clases de tramas de entrada.

El control de ganancia se utiliza cuando se implementa una red ARt2 donde la capa F2 podría recibir entradas de otra capa por encima de ella (dentro de una jerarquía de redes pertenecientes a un sistema mayor), así corno de la capa Fl, situada más abajo. Este control impide que una trama que entre por encima de la capa F2, se cruce o se compare con otra trama que ha entrado al mismo tiempo por la capa F1.

El subsistema de atención está compuesto por las dos capas de elementos de procesamiento, Fl y F2, y un sistema de control de ganancia.

Procesamiento en F1. La actividad de las unidades de la subcapa F1 está gobernada por la ecuación de la forma

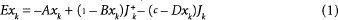
donde A, B, C, y D son constantes; eh y jk representan factores excitatorios e inhibitorios netos, respectivamente. Las actividades de cada una de las seis capas de F1 se pueden resumir mediante las siguientes ecuaciones:

Los factores de las ecuaciones para todas las capas de Fl y para la capa r son: I, es la i-ésima componente del vector de entrada. Los parámetros a, 17, c, d son constantes. La constante e recibe típicamente un valor positivo y considerablemente menor que 1, tiene el efecto de mantener finitas las activaciones cuando no está presente ninguna entradá en el sistema, y, es la actividad de la j-ésima unidad de la capa F2 y g(y) es la función de salida de F2.

Las tres unidades de control de ganancia de Fl inhiben de manera no especifica las subcapas x, u y q. La señal inhibitoria es igual al módulo del vector de entrada que llega a esas capas..

La forma de la función F(x) determina la naturaleza de mejoramiento de contraste que tiene lugar en F 1 . La elección lógica para esta función podría ser una sigmoide; aquí se presenta la opción de Carpenter:

donde ∅ es una constante positiva y menor que 1.

Del análisis de la capa F1, se puede concluir que esta lleva a cabo una normalización y una operación de mejoramiento de contraste. Antes de intentar buscar coincidencias en sí, se deben considerar los detalles del resto del sistema.

Procesamiento en F2. El procesamiento de F2 está dado por la siguiente ecuación:

La función de salida de F2 está dada por:

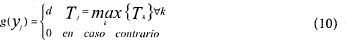
La ecuación 10 supone que el conjunto {T k} contiene únicamente aquellos nodos que no hayan sido restaurados recientemente por el subsistema dé orientación.

Ecuaciones de LTM (memoria a largo plazo). Tanto las ecuaciones ascendentes como las descendentes tienen la misma forma:

para los pesos ascendentes cksckv i al FI hasta v en F2, y

para los pesos descendentes que van desde vj en F2 hasta vj en F1.

De forma similar

El subsistema de orientación. La ecuación de las actividades de los nodos de la capa r tiene la forma

La condición para que produzca la restauración es

donde p es el parámetro de vigilancia. El valor del parámetro de vigilancia mide hasta qué grado discrimina el sistema entre distintas clases de tramas de entrada.

Iniciación de LTM (memoria a largo plazo) ascendente. Los valores iniciales para los vectores de pesos ascendentes están dados por la ecuación.

donde M es el número de unidades de cada subcapa de Fl.

El proceso también puede llevarse a cabo mediante la implementación de mapas autoorganizativos de Kohonen. Éste es un modelo aceptable para encontrar relaciones entre grupos complejos al basarse en el manejo de vecindad para agrupar; sin embargo, una limitante es el alto costo computacional que implica su ejecución [8]. Este modelo fue un desarrollo previo a la implementación de la red ART2, presentada como un avance parcial de investigación, del cual se muestran los resultados obtenidos para algunos conjuntos de datos en la tabla 1. Para mayor información acerca de este desarrollo, remítase a [8], donde encontrará la teoría empleada en los mapas autoorganizativos de Kohonen y las especificaciones de la implementación.

ANÁLISIS DE RESULTADOS

Para validar el software desarrollado, se utilizaron diferentes conjuntos de datos (tomados de http://www.ics.uci.edui --mlearn/MLRepository.html). Para cada uno se realizaron 10 pruebas con el fin de medir la efectividad del modelo neuronal ART2 en la agrupación de datos. Se hace una comparación del modelo implementado frente al modelo de mapas autoorganizativos de Kohonen y el algoritmo EM (Expectation Maximization). Para este último se utilizó la herramienta WEKA (Entorno para el Análisis de Conocimiento de la Universidad de Waikato). Ver tabla 1.

En cuanto a la configuración de la red ART2, luego de realizar las respectivas pruebas con cada uno de los conjuntos de datos; se obtiene: el valor medio para el parámetro de vigilancia es 0.4; para la constate e es 0.2: Para las demás constantes no se pudo establecer un valor medio.

En términos generales, la efectividad de agrupación de la red ART2 es superior a los mapas autoorganizativos de kohonen y al algoritmo EM al obtener una efectividad promedio del 69.12%.

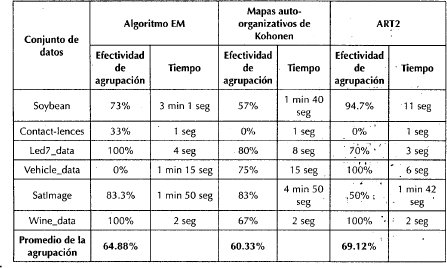
Existen casos particulares en los cuales no se logra obtener una buena agrupación, como el del conjunto de datos CONTACT-LENCES, en el cual el porcentaje de agrupación es del 0%. La razón está en que, para esteejemplo, no se logró determinar una configuración aceptable para la red ART2, siendo esta una limitante del modelo implementado.

Además, se observa que la calidad de agrupación obtenida con ART2 del conjunto de datos SATIMAGE es inferior a la obtenida con los otros dos modelos, alcanzándose solo un 50% de agrupación. La explicación radica en que el funcionamiento de la red ART2 tiende a degradarse cuando el volumen de instancias es alto (la degradación del funcionamiento se puede contrarrestar con una buena configuración de la red).

CONCLUSIONES

La red neuronal ART2 es una técnica viable para la agrupación de datos, dada su alta efectividad; sin embargo, la configuración del parámetro de vigilancia debe hacerse utilizando heurísticas o, en el peor de los casos, a través de la experimentación. Esto implica que si el parámetro empleado no es adecuado, la efectividad de agrupación es baja.

El modelo ART2 es una de las redes neuronales artificiales más poderosas debido a su capacidad de autoorganización, aprendizaje no supervisado y ONLINE, pero también es una de las más complejas en cuanto a su implementación. Además, al ser expuesta a una gran cantidad de datos puede degradarse su buen funcionamiento.

Con el presente desarrollo se observa que la red neuronal ART2 es eficiente para encontrar relaciones entre grupos. Esto se corrobora con la comparación hecha con otras técnicas de agrupación (algoritmo EM, mapas autoorganizativos), en los que con el modelo ART2 se obtuvo la mayor eficiencia (69.12%). Del mismo modo, se destaca que de las tres técnicas implementadas, ART2 es la que menor tiempo emplea para generar grupos.

TRABAJOS FUTUROS

Actualmente se está trabajando en un prototipo de software para la agrupación de datos a partir de la implementación del algoritmo GTM (Generative Topographic Mapping) y se tiene previsto la implementación de técnicas evolutivas con el fin de configurar automáticamente los parámetros de la red ART2.

BIBLIOGRAFÍA

[1] Han, J., y Kamber, M., Data Mining: Concepts and techniques; San Diego -- USA. Morgan Kaufmann, 2001, pp. 335-346.
[2] Kantardzic, M., Data Mining: Concepts, Models, Methods, and Algorithms, New Jersey -- USA. Wiley -- Interscience, 2001, p. 117.
[3] Hastie, T., TIBSHIRANI, R., and FRIEDMAN, J., The Elements of Statistical Learning. Heidelberg -- Canada. Springer, 2001, p. 453.
[4] Hand, D., Mannila, H., and SMYTH, P., Principies of Data Mining, London -- England. The MIT Press, 2001, p. 308.
[5] Hilera, J., y Martínez, V., Redes neuronales artificiales., Wilmington - USA. Addison Wesley Iberoamericana, 1995, pp. 219-220.
[6]Haykin, Neural Networks: "A comprehenSive foundation", New JereSr - USA. Prentice Hall, 1999, p. 58.
[7] Skapura, D. y Freeman, J., Redes noronales, algoritmos, aplicaciones y técnicas de progrdmación, Madrid --_Esparia. Díaz de Santos, 1993, pp.335-343.
[8] Bautista, S., Reyes, A., y Rodríguez, J., "Prototipo de software para la agrupación de datos con una red heuronal artificial con topología de Kohonen", Bogotá -- Colombia. Tecnura, Año 8, No. 15., 2004, p. 65.