DOI:
https://doi.org/10.14483/23448350.5596Publicado:
03/29/2014Número:
Vol. 18 Núm. 1 (2014): Enero-Abril 2014Sección:
Ingeniería y TecnologíaLinealización de sistemas VSC-HVDC para el diseño de un controlador PI vectorial
Linearization of VSC based HVDC systems for the design of vector PI controller
Palabras clave:
VSC, linealización, PI vectorial, realimentación de estados, potencia activa, potencia reactiva (es).Descargas
Referencias
Åstrom, K. and Murray, R. (2010). Feedback Systems: An Introduction for Scientists and Engineers. Princeton, New Jersey, United Estates of America: Princeton University Press. https://doi.org/10.2307/j.ctvcm4gdk
Bahrman, M. and Johnson, B. (2007, March-April). The ABCs of HVDC transmission technologies. Power and Energy Magazine, IEEE , 5(2), 32-44. https://doi.org/10.1109/MPAE.2007.329194
Chen, C.-T. (2006). Analog and Digital Control System Design: Transfer-Function, State-Space, and Algebraic Methods. Oxford University Press.
Diaz, N., Barbosa, F. and Trujillo, C. (septiembre, 2008). Implementation of Nonlinear power flow controllers to control a VSC. Power Electronics and Motion Control Conference, 2008. EPEPEMC 2008. 13th. Poznan, Poland.
https://doi.org/10.1109/EPEPEMC.2008.4635336
Diaz, N., Barbosa, F. and Trujillo, C. (septiembre, 2007). Analysis and Design of a Nonlinear Fuzzy Controller Applied to a VSC to Control the Active and Reactive Power Flow. Electronics, Robotics and Automotive Mechanics Conference, 2007. CERMA 2007. Cuernavaca. https://doi.org/10.1109/CERMA.2007.4367723
Dominguez-Garcia, J., Gomis-Bellmunt, O.and Bianchi, F. (septiembre, 2011). Power control of voltage source converter. Physcon 2011. Leon.
Forero, F., Molina, A., Guarnizo, J. and Chamorro, H. (2009). Implementation of Inverse Neural Control to VSC Converter for Active and Reactive Power Flow. The 15 th International Conference on Intelligent Systems Applications to Power Systems. ISAP 2009. Curitiba, Brasil. https://doi.org/10.1109/ISAP.2009.5352931
Forero, F., Molina, M. and Guarnizo, J. (2008). Design of a Inverse Neural Controller Applied to a VSC for the Control of the Active and Reactive Power Flow. XV Congreso internacional de Ingeniería Eléctrica, Electrónica y de Sistemas. Trujillo Perú: IEEE.
Hidalgo, C., Diaz, N., Trujillo, C. L. and Guarnizo, J. G. (2013). Design of Linear Controllers for VSC Based HVDC Systems. Las Conferencias Hispano Lusas de Ingeniería Eléctrica (CHLIE). Valencia.
Khalil, H. (2002). Nonlinear Systems (Third Edition ed.). Prentice Hall.
Latorre, H., Ghandhari, M. and Söder, L. (2008, October). Active and reactive power control of a VSC-HVdc. Electric Power Systems Research, 78(10), 1756-1763. https://doi.org/10.1016/j.epsr.2008.03.003
Meah, K.and Ula, S. (24-28 June 2007). Comparative Evaluation of HVDC and HVAC Transmission Systems". Power Engineering Society General Meeting, 2007. IEEE. Tampa, FL: IEEE. https://doi.org/10.1109/PES.2007.385993
Ruihua, S., Chao, Z., Ruomei, L.and Zhou, X. (2005). VSCs based HVDC and its control strategy. Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005 IEEE/PES. Dalian.
Song, R., Zheng, C., Ruomei, L. and Zhou, X. (2005). VSCs based HVDC and its control strategy. Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005 IEEE/PES. Dalian.
Sood, V. K. (2004). HVDC and FACTS Controllers. Applications of Static Converters in Power Systems. Kluwer Academic Publishers.
Trujillo, C., Velasco, D., Guarnizo, J. and Díaz, N. (2011, September). Design and implementation of a VSC for interconnection with power grids, using the method of identification the system through state space for the calculation of controllers. Applied Energy, 9(88), 3169-3175. https://doi.org/10.1016/j.apenergy.2011.02.038
Żak, S. (2003). Systems and Control. New York: Oxford University Press.
Zhang, G. and Zheng, X. (enero-febrero, 2001). Steady-state model for VSC based HVDC and its controller design. Power Engineering Society Winter Meeting, 2001. IEEE, 3, 1085-1090.Columbus, USA.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Linealización de sistemas VSC-HVDC para el diseño de un controlador PI vectorial1
Linearization of VSC based HVDC systems for the design of vector PI controller
Sistema HVDC VSC-linearização para projetar um Vector controlador PI
Nelson Díaz Aldana2
José Guillermo Guarnizo Marín3
César Leonardo Trujillo Rodríguez4
1Artículo dei investigación.
2Universidad Distrital Francisco José de Caldas. Correo: nldiaza@udistrital.edu.co
3Universidad Distrital Francisco José de Caldas. Correo: joguiguma@ieee.org
4Universidad Distrital Francisco José de Caldas. Correo: cltrujillo@udistrital.edu.co
Fecha de recepción:mayo de 2013, Fecha de aceptación: agosto de 2013
Resumen
Los sistemas VSC-HVDC son muy utilizados para la transmisión de energía en redes de interconexión eléctrica. Uno de los principales problemas que poseen estos sistemas es la complejidad de su modelo matemático, lo que conlleva grandes dificultades para el diseño de controladores que permitan la regulación de parámetros como la tensión DC de transmisión, así como la potencia activa y reactiva del sistema VSC-HVDC. En este artículo se presenta la linealización de un sistema VSC-HVDC y el posterior diseño de un controlador lineal PI vectorial a partir del modelo linealizado. Adicionalmente, se proponen dos estrategias para la validación de este tipo de controladores, la primera consiste en un único controlador PI para regular los estados del sistema para cada VSC, la segunda consiste en el diseño de controladores PI vectoriales independientes para la regulación de cada estado del VSC.
Palabras clave:VSC, linealización, PI vectorial, realimentación de estados, potencia activa, potencia reactiva.
Abstract
VSC-HVDC systems are highly used for energy transmission and interconnection of power grids with different features. However, the fact of obtaining an accurate mathematic model for designing controllers is not as straightforward as expected. Indeed, a VSC-HVDC is a multi-input multi-output system, for that reason the regulation of variables such as the common DC bus voltage, active and reactive power are complex tasks. In this paper, a new strategy for modelling and obtaining state space linear models of the VSC-HVDC system is explored. The linear models are used for obtaining vector PI controllers. Additionally, there are explored two different configurations for the state feedback controllers. The first one is based on a unique controller. Meanwhile, the second strategy is based on independent PI state feedback controllers for each variable controlled.
Keywords:VSC, linearization, PI vector, state feedback, active power, reactive power.
Resumo
Sistemas VSC- HVDC são amplamente utilizados para a transmissão de energia em redes de interligação eléctrica. Um dos principais problemas que têm esses sistemas é a complexidade do modelo matemático, que envolve grandes dificuldades na concepção de controladores que permitem a regulação de parâmetros, tais como a transmissão de tensão DC , bem como a energia activa e reactiva sistema VSC- HVDC . Este artigo apresenta a linearização de um sistema VSC- HVDC eo projeto subseqüente de um controlador linear do modelo PI vetor linear. Além disso, propõe duas estratégias para a validação desses controladores , a primeira composta de um único controlador PI para regular os estados do sistema para cada VSC , o segundo é o projeto de controladores PI para regular vetor independente de cada estado VSC.
Palavras-Chave:VSC, linearização , PI vetor , feedback estado , potência ativa , potência reativa.
Introducción
Los sistemas HVDC (High Voltage Direct Current por sus siglas en inglés) controlados mediante VSC (Voltage Source Converter por sus siglas en ingles) son, en el presente, muy utilizados para el transporte de energía en redes de transmisión eléctrica, ya que no tiene las restricciones para transmisión en largas distancias que sí poseen los sistemas HVAC (High Voltage Alternating Current por sus siglas en inglés) sin compensación reactiva, y que a su vez afecta la estabilidad de este tipo de sistema; este efecto adicionalmente produce menores pérdidas en los sistemas de transmisión HVDC. Otra ventaja que poseen los sistemas de transmisión de tensión continua son los costos económicos inferiores que los producidos por los sistemas HVAC (Meah y Ula, 2007). Adicionalmente, los sistemas HVDC-VSC se utilizan para la interconexión eléctrica con fuentes de energía renovables y micro redes (Bahrman y Johnson, 2007).
Particularmente, los sistemas HVDC-VSC son una técnica de mayor desarrollo en tiempos recientes, dado que los sistemas VSC son basados en interruptores transistorizados controlables, como son los el IGBT, el IGCT o el GTO (Ruihua, Chao, Ruomei, y Zhou, 2005), esto hace posible que se puedan trabajar señales sinusoidales de tensión con diferentes amplitudes y fases, y por consiguiente permite controlar de manera independiente la potencia activa y reactiva del sistema (Forero, Molina y Guarnizo, 2008).
Una línea de transmisión HVDC requiere de al menos dos estaciones de conversión eléctrica VSC, cada una de ellas está compuesta por un puente trifásico de dos niveles o tres niveles (Sood, 2004). En condiciones normales de trabajo para una línea HVDC, se tiene una estación encargada de la regulación de la tensión de transmisión DC, mientras que la otra estación se encarga del control de la potencia activa del sistema, adicionalmente cada estación puede controlar la potencia reactiva de manera independiente. Esto permite concluir que un sistema HVDC controlado mediante un VSC corresponde a un sistema de control de dos entradas, dos salidas, donde la potencia activa y reactiva pueden ser controladas ajustando respectivamente la fase y la amplitud de la onda de voltaje generada, y según proponen distintos autores, estas dos potencias pueden controlarse de manera independiente (Song, Zheng, Ruomei y Zhou, 2005). La principal dificultad para el diseño del controlador para el VSC es la obtención del modelo matemático que permita obtener un regulador lineal, dada la complejidad y las no linealidades presentes en el sistema. Algunos trabajos proponen el diseño de controladores no lineales, como por ejemplo controladores difusos para el control de la potencia activa y reactiva del VSC (Diaz, Barbosa y Trujillo, 2008), o controladores no lineales basados en funciones de Lyapunov, y análisis en pequeña ganancia (Latorre, Ghandhari y Söder, 2008), o el uso de redes neuronales para el control de la potencia activa y reactiva de manera independiente (Forero, Molina, Guarnizo y Chamorro, 2009).
En el presente artículo se propone la linealización del modelo matemático del VSC y su ajuste a un determinado nivel de potencia. Posteriormente se propone el uso de reguladores lineales PI vectoriales para el control de la potencia activa, potencia reactiva y la tensión DC de transmisión en el sistema HVDC-VSC. A partir de esto se exploran dos diferentes estrategias de control. La primera se basa en un único controlador MIMO para cada estación, la segunda estrategia consiste en un controlador lineal independiente para cada variable de control en cada estación. Las estrategias son validadas utilizando Simpower system de Matlab.
Modelo dinámico del sistema VSC conectado a la red
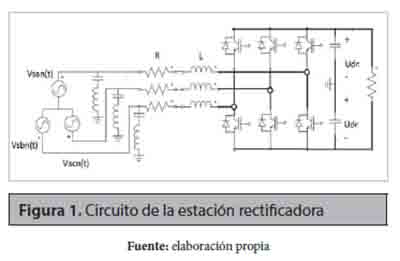
Para cada estación del sistema HVDC ha sido elegido un VSC de dos niveles; la primera estación del VSC actúa como rectificador y es, a su vez, responsable de la regulación de la tensión DC que es transmitida a lo largo de la red, el circuito esquemático de esta estación es presentado en la figura 1.
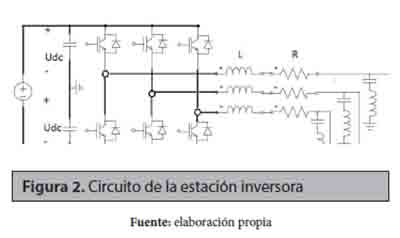
La segunda estación convierte la señal DC transmitida en una señal alterna, y es la encargada del control de la potencia activa del sistema, su circuito es presentado en la figura 2.
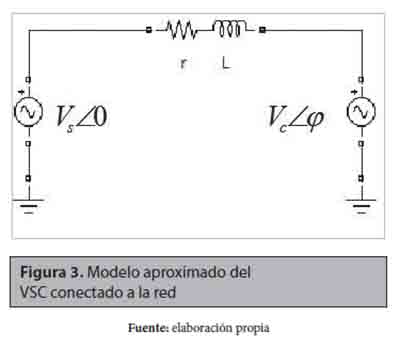
En la etapa inversora, una señal senosoidal de voltaje AC es generada con cualquier amplitud y ángulo de fase a partir de modulación senoidal de ancho de pulso SPWM (Diaz, Barbosa y Trujillo, 2007). Un modelo aproximado del VSC conectado a la red es presentado en la figura 3.
Basado en las leyes de voltajes y corrientes de Kirchhoff, se obtiene un modelo no lineal en variables de estado del sistema completo en la ecuación (1), de la estación rectificadora en la ecuación (2), y de la etapa inversora en las ecuaciones (3) y (4) (Trujillo, Velasco, Guarnizo y Díaz, 2011).


Donde r representa las pérdidas lineales de potencia, ia, ib e ic representan las corrientes de línea, Vsan, Vsbn, y Vscn es la tensión de la red por fase, Udc corresponde al voltaje DC de transmisión, R representa la carga nominal de la estación rectificadora, P es la potencia nominal en el inversor, (m) es el índice de modulación y θ=ωt+φ, donde φ es el ángulo de fase entre el voltaje del conversor y el voltaje de la red. La potencia activa y reactiva puede ser escrita de la siguiente forma:

Donde Vc corresponde al valor RMS de la componente fundamental del voltaje, Vs es el valor RMS de la componente fundamental de la red AC de voltaje, X=ωL. La resistencia de pérdidas r es despreciada en la ecuación (5) con el fin de simplificar el análisis (Zhang y Zheng, 2001). En la ecuación (5) muestra que la potencia activa P depende del ángulo de fase φ, mientras que Q depende de la amplitud de Vc=m*Udc principalmente. Dado eso, es posible controlar de manera independiente la potencia activa y reactiva del sistema, ajustando de manera independiente m y φ.
Para eliminar la dependencia en el tiempo del modelo, es aplicada la transformada de Park (Domínguez-García, Gomis-Bellmunt y Bianchi, 2011). Por consiguiente, el modelo transformado en un marco de referencia (dq0) para la estación rectificadora es presentado en la ecuación (6):

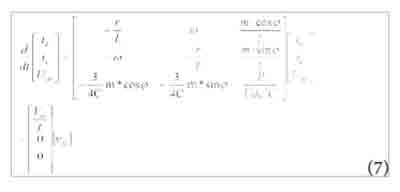
Y el modelo transformado en (dq0), para la estación inversora es presentado en la ecuación (7):
En el marco de referencia (dq0), la potencia activa y reactiva es expresada en la ecuación (8):
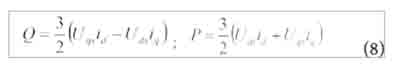
Para poder linealizar los modelos transformados de las estaciones presentados en (6) y (7), se deben encontrar los puntos de equilibro, para facilitar los cálculos inicialmente se hace vds=0, además se hace el término ≈ 0, a partir de esto es fácilmente calculable que el punto de equilibrio de las ecuaciones (6) y (7) es la solución trivial (Khalil, 2002).
Linealización del modelo matemático del sistema
Si la potencia activa y reactiva es medida en el punto donde el VSC se conecta a la red, entonces Uds=Vm y Uqs=0, donde Vm es el valor pico de la red de voltaje. Dado el modelo lineal del sistema, es realizada una linealización alrededor de un punto de equilibrio del sistema a partir de la expansión de series de Taylor (Åstrom y Murray, 2010). El modelo linealizado y representado en variables de estado de la estación rectificadora y la inversora se presenta en la ecuación (9) y (10) respectivamente:

Con el fin de obtener los puntos de equilibrio para las dos ecuaciones anteriores, se hacen las entradas del sistem a linealizado Δm=Δφ=0, manteniendo m y φ como valores constantes para el punto de operación del sistema. Es de recordar además que en el modelo linealizado se mantiene la condición ≈ 0, por lo que los puntos de equilibrio obtenidos a partir del modelo linealizado en la ecuación (9) y (10) corresponden igualmente a la solución trivial, como fue observado en las ecuaciones (6) y (7).
Teniendo en cuenta que todos los valores constantes de las ecuaciones (9) y (10) son mayores que cero, para determinar la clase de punto de equilibrio que se tiene, se obtiene el determinante de la matriz (λI -A)=0(Żak, 2003). Con el fin de simplificar estos cálculos, se han seleccionado los siguientes valores para las variables de las ecuaciones (9) y (10): L = 61*10-3 H, C = 10*10-6 F, m= 0.88, R = 253.5 Ω, φ = -0.1588 rad, w = 2*π*60 rad/seg, Uds =120*√2 V, Udc =195 V, Id = 1.1814 A, Iq = -1.2927*10-3 A.
(9) asociada a la estación rectificadora, se encuentra que los polos asociados a las variables de estado Δid y Δiq corresponden a polos complejos conjugados con parte real negativa, lo que significa que presentan un comportamiento estable, con algunas oscilaciones antes de llegar al estado estacionario, el tercer polo es un polo real negativo, que está asociado a la tensión Uds, lo cual significa que la tensión de transmisión es estable, dado que, desde esta estación, se controla la tensión de transmisión Uds y la potencia reactiva Q, se puede garantizar entonces que estos dos parámetros serán estables. Para el caso de la ecuación (10) asociada a la estación inversora, se encuentra que los dos primeros polos de la matriz A asociados a Δid y Δiq también son polos complejos conjugados con parte real negativa, lo que quiere decir que estas corrientes serán estables. No obstante el tercer polo perteneciente a Uds es un polo real inestable; no obstante, esta estación se encarga del control de P y Q, y estos dos parámetros dependen únicamente de las corrientes de transmisión y no de la tensión, por lo que no afecta la estabilidad de la potencia activa y reactiva del sistema. Adicionalmente, el modelo lineal obtenido en las ecuaciones (9) y (10) es un modelo observable y controlable.
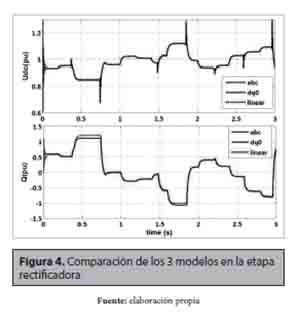
En la figura 4 se presenta una comparación de la respuesta de la estación rectificadora de los tresmodelos presentados hasta el momento, el modelo trifásico (abc), el modelo transformado al marco de referencia (dq0) y el modelo linealizado. Se puede observar un comportamiento similar para los tres modelos, presentando un error menor al 8% únicamente cuando Q≠±1 pu.
Diseño del controlador PI vectorial por realimentación de estados
Dado el modelo linealizado, se elige un control por realimentación de estado PI vectorial, ya que al adicionar un polo en el origen, se garantiza eliminación de errores de estado estacionario, adicionalmente, es un control sencillo de diseñar. Para el diseño del controlador se tienen en cuenta como variables de actuador (φ y m). Es de recordar que esta estrategia de control requiere por una continua monitorización de las variables de estado del sistema, además que el sistema por controlar sea tanto observable como controlable (Żak, 2003).
Para el diseño del controlador es necesario:
- Obtener las ecuaciones en variables de estado del sistema por controlar, en este caso las ecuaciones (9) y (10).
- Determinar la condición para la ubicación de los polos, que en este caso corresponde a un tiempo de establecimiento máximo permitido, y una sobre oscilación máxima admisible.
- Obtener la matriz de ganancia de realimentación del sistema.
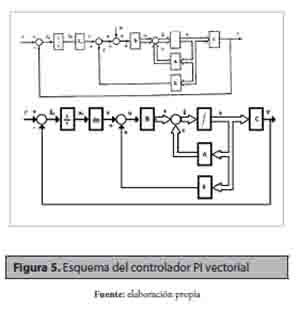
En la figura 5, se presenta un esquema del controlador utilizado, donde A, B C y D son obtenidas directamente a partir de las ecuaciones (9) y (10). La matriz de realimentación de estados K así como la ganancia del integrador Ka son calculadas utilizando MATLAB (Chen, 2006).
Resultados en simulación
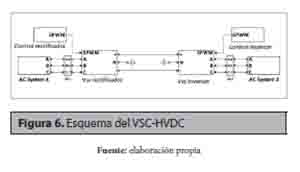
Las simulaciones fueron realizadas en un modelo conmutado para el sistema VSC-HVDC, construido a partir de un sistema Sympower de Simulink, la figura 6 presenta el esquema de este sistema, los valores de simulación utilizados fueron obtenidos a partir de (Hidalgo, Diaz, Trujillo y Guarnizo, 2013). En estas simulaciones son exploradas dos diferentes estrategias para implementar los controladores en realimentación de estados.
Simulación de un único controlador de realimentación de estados
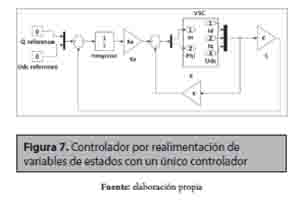
.La primera estrategia simulada está basada en un único controlador por realimentación de variables de estado. Estas ecuaciones utilizan los modelos de las ecuaciones (9) y (10) con el fin de obtener un único controlador. En la figura 7. Se presenta un esquema de este primer controlador propuesto para la estación rectificadora.
La figura 8, muestra la respuesta del sistema usando el controlador propuesto, donde diferentes referencias de potencia activa son presentadas para la estación inversora, los valores de la simulación son normalizados. En la figura 8 (a) se muestra la potencia activa P para las dos estaciones, la figura 8 (b) muestra la regulación de la tensión de transmisión DC y finalmente la figura 8 (c) muestra la regulación de la potencia reactiva.

Los resultados muestran que los resultados de control son alcanzados, aunque se mantiene un pequeño error de estado estacionario en la tensión de transmisión DC; además, no es fácil obtener una respuesta rápida del sistema dado que el control de la potencia reactiva depende de la tensión de transmisión DC, esto hace necesario que se requiera una respuesta de control Udc más rápida que la respuesta de control asociada a la potencia reactiva.
Independientes controladores por realimentación de estados
Basados en los resultados obtenidos en la sección anterior, es deseable ajustar la respuesta dinámica del sistema para cada variable de manera independiente. Por consiguiente, es propuesto controladores PI vectoriales independientes para cada variable a controlar.
Dado esto, en la ecuación (5) es posible ver que Udc y P pueden ser controladas ajustando el ángulo de fase φ en la estación rectificador a o inversora, respectivamente.
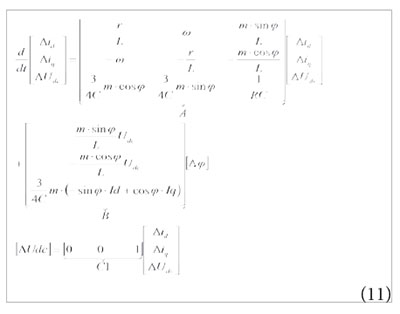
De forma similar, la potencia reactiva Q puede ser controlada ajustando el índice de modulación m. A partir de esto y utilizando la ecuación (9), es posible obtener las siguientes ecuaciones para cada variable del sistema en la estación rectificadora. Para controlar la tensión Udc en función de φ se tiene:
Para controlar la potencia reactiva Q en función del índice de modulación m, se tiene:
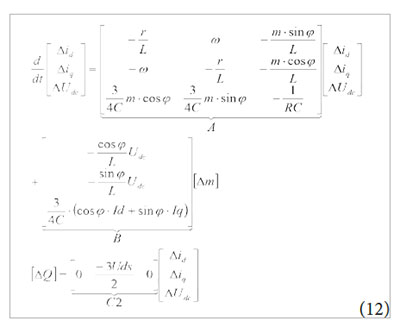
Donde se observa que la matriz A, que es la que determina la estabilidad del sistema, se mantiene igual que en la ecuación (9), lo que implica que el análisis acerca de la estabilidad del sistema realizados anteriormente no sufren modificación. Los cambios se ven reflejados en las matrices B y C; no obstante, los sistemas de las ecuaciones (11) y (12) siguen siendo observables y controlables (Hidalgo, Diaz, Trujillo y Guarnizo, 2013). Estos esquemas de control son presentados en la figura 9.
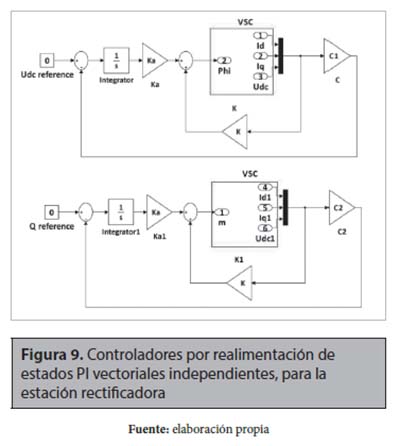
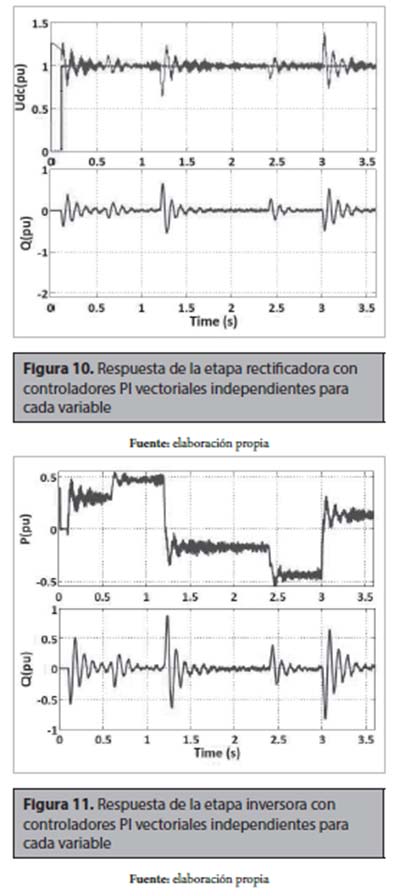
A partir de esto, en la figura 10 se muestra la respuesta de Udc y Q en la estación rectificadora, donde es posible observar una respuesta más rápida y sin error de estado estacionario en Udc, así como un sobrepaso menor que el observado en el caso donde se utilizaba un único controlador. En la figura 11 se presenta la respuesta de P y Q en la estación inversora.
Conclusiones
El análisis matemático presentado sobre el modelo no lineal del sistema VSC-HVDC permite obtener un modelo simple para el diseño de controladores. Esto permite un diseño sencillo de controladores lineales por realimentación de estado, junto a su posterior implementación, en este caso, se ha seleccionado un controlador PI vectorial. Adicionalmente, se ha observado que controladores lineales independientes aplicados en un sistema linealizado VSC-HVDC presentan un mejor desempeño que un único controlador por realimentación de estado que controle todas las variables del sistema, pues en este caso en particular, la respuesta dinámica del sistema puede ser ajustada de manera independiente para cada variable.
Referencias bibliográficas
Åstrom, K. and Murray, R. (2010). Feedback Systems: An Introduction for Scientists and Engineers. Princeton, New Jersey, United Estates of America: Princeton University Press.
Bahrman, M. and Johnson, B. (2007, March-April). The ABCs of HVDC transmission technologies. Power and Energy Magazine, IEEE , 5(2), 32-44. Chen, C.-T. (2006). Analog and Digital Control System Design: Transfer-Function, State-Space, and Algebraic Methods. Oxford University Press.
Diaz, N., Barbosa, F. and Trujillo, C. (septiembre, 2008). Implementation of Nonlinear power flow controllers to control a VSC. Power Electronics and Motion Control Conference, 2008. EPEPEMC 2008. 13th. Poznan, Poland.
Diaz, N., Barbosa, F. and Trujillo, C. (septiembre, 2007). Analysis and Design of a Nonlinear Fuzzy Controller Applied to a VSC to Control the Active and Reactive Power Flow. Electronics, Robotics and Automotive Mechanics Conference, 2007. CERMA 2007. Cuernavaca.
Dominguez-Garcia, J., Gomis-Bellmunt, O.and Bianchi, F. (septiembre, 2011). Power control of voltage source converter. Physcon 2011. Leon.
Forero, F., Molina, A., Guarnizo, J. and Chamorro, H. (2009). Implementation of Inverse Neural Control to VSC Converter for Active and Reactive Power Flow. The 15 th International Conference on Intelligent Systems Applications to Power Systems. ISAP 2009. Curitiba, Brasil.
Forero, F., Molina, M. and Guarnizo, J. (2008). Design of a Inverse Neural Controller Applied to a VSC for the Control of the Active and Reactive Power Flow. XV Congreso internacional de Ingeniería Eléctrica, Electrónica y de Sistemas. Trujillo Perú: IEEE.
Hidalgo, C., Diaz, N., Trujillo, C. L. and Guarnizo, J. G. (2013). Design of Linear Controllers for VSC Based HVDC Systems. Las Conferencias Hispano Lusas de Ingeniería Eléctrica (CHLIE). Valencia.
Khalil, H. (2002). Nonlinear Systems (Third Edition ed.). Prentice Hall.
Latorre, H., Ghandhari, M. and Söder, L. (2008, October). Active and reactive power control of a VSC-HVdc. Electric Power Systems Research, 78(10), 1756-1763.
Meah, K.and Ula, S. (24-28 June 2007). Comparative Evaluation of HVDC and HVAC Transmission Systems”. Power Engineering Society General Meeting, 2007. IEEE. Tampa, FL: IEEE.
Ruihua, S., Chao, Z., Ruomei, L.and Zhou, X. (2005). VSCs based HVDC and its control strategy. Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005 IEEE/PES. Dalian.
Song, R., Zheng, C., Ruomei, L. and Zhou, X. (2005). VSCs based HVDC and its control strategy. Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005 IEEE/PES. Dalian.
Sood, V. K. (2004). HVDC and FACTS Controllers. Applications of Static Converters in Power Systems. Kluwer Academic Publishers.
Trujillo, C., Velasco, D., Guarnizo, J. and Díaz, N. (2011, September). Design and implementation of a VSC for interconnection with power grids, using the method of identification the system through state space for the calculation of controllers. Applied Energy, 9(88), 3169-3175.
Żak, S. (2003). Systems and Control. New York: Oxford University Press.
Zhang, G. and Zheng, X. (enero-febrero, 2001). Steady-state model for VSC based HVDC and its controller design. Power Engineering Society Winter Meeting, 2001. IEEE, 3, 1085-1090. Columbus, USA.
Licencia
El (los) autor(es) al enviar su artículo a la Revista Científica certifica que su manuscrito no ha sido, ni será presentado ni publicado en ninguna otra revista científica.
Dentro de las políticas editoriales establecidas para la Revista Científica en ninguna etapa del proceso editorial se establecen costos, el envío de artículos, la edición, publicación y posterior descarga de los contenidos es de manera gratuita dado que la revista es una publicación académica sin ánimo de lucro.



