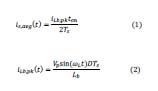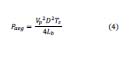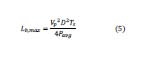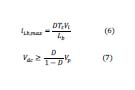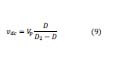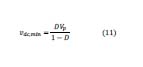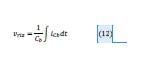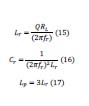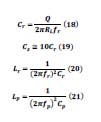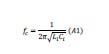DOI:
https://doi.org/10.14483/23448350.6489Published:
06/26/2014Issue:
Vol. 19 No. 2 (2014): May-August 2014Section:
Science and EngineeringDiseño y simulación de un balastro electrónico con corrección de factor de potencia con topología buck-boost e inversor alimentado por corriente-Design and simulation of an electronic ballast with power factor correction buck-boost topology and current-fed invertir
Keywords:
balastro electrónico, lámparas fluorescentes, factor de potencia, corrección del factor de potencia, balastro integrado. (es).Downloads
References
Blanco, A. y Parra, E. ( 2010). Effects of high penetration of CFLS and LEDS on the distribution networks. Harmonics and Quality of Power (ICHQP), 2010 14th International Conference on, 1-5.
Chuang, Y.-C. y Cheng, H.-L. (2006). Single-Stage Single-Switch High-Power-Factor Electronic Ballast for Fluorescent Lamps. Industrial and Commercial Power Systems Technical Conference, 1-7.
Díaz, A. R. (2000). Balastros electrónicos integrados con corrección activa de factor de potencia. Centro Nacional de Investigación y Desarrollo Tecnológico. Mexico
Electric Power Research Institute. (2009). Compact fluorescent lamps: harmonics analysis and distribution impact study. Electric Power Research Institute, Palo Alto, California
Garcia, J., Dalla-Costa, M., Andre Luis Kirsten, A., Gacio, D. y Calleja, A. (2011). A novel flyback-based input PFC stage for electronic ballasts in lighting applications. Industry Applications Society Annual Meeting (IAS), 1-6.
Grigore, V., Kyyra, J. y Rajamaki, J. (1999). Input filter design for power factor correction converters operating in discontinuous conduction mode. IEEE International Symposium on Electromagnetic Compatibility, 1, 145-150.
Lam, J. y Jain, P. K. (2007). A low cost single-stage electronic ballast with unity power factor using a novel single switch current fed resonant inverter topology. Power Electronics Specialists Conference, PESC 2007, 3106-3111.
Lam, J. y Jain, P. K. (2008). A dimmable electronic ballast with unity power factor based on a single-stage current-fed resonant inverter. IEEE Transactions on Power Electronics, 3103-3115.
Lam, J. y Jain, P. K. (2010). A high-power-factor single-stage single-switch electronic ballast for compact fluorescent lamps. IEEE Transactions on Power Electronics, 2045-2058.
Lam, J. y Jain, P. K. (2010). A novel high-power-factor single-switch electronic ballast. IEEE Transactions on Industry Applications, 2202-2211.
Lam, J. y Jain, P. K. (2011). A boost-type high power factor single switch electronic ballast for compact fluorescent lamps (energy-saving lamps). IECON 2011 - 37th Annual Conference on IEEE Industrial Electronics Society, 2854-2859.
Lin, R.-L., Liu, H.-Y. y Shih, H.-M. (2007). AC-Side CCM CS–CP–PFC Electronic Ballast. Power Electronics, IEEE Transactions on, 22(3) , 789-796.
Liu, K.-H. y Lin, Y.-L. (1989). Current waveform distortion in power factor correction circuits employing discontinuous-mode boost converters. Power Electronics Specialists Conference, PESC '89, 825-829.
Maamoun, A. (2000). An electronic ballast with power factor correction for fluorescent lamps. Electrical and Computer Engineering, 2000 Canadian Conference on, 385-389 .
Ponce, M., Martinez, A., Correa, J., Cotorogea, M. y Arau, J. (2006). High-efficient integrated electronic ballast for compact fluorescent lamps. Power Electronics, IEEE Transactions on, 532-542 .
Rashid, M. H. (2010). Power electronics handbook: devices, circuits and applications. Academic Press.
Sharma, H., Sunderman, W. G. y Gaikwad, A. (2011). Harmonic impacts of widespread use of CFL lamps on distribution systems. Power and Energy Society General Meeting, 1-5. IEEE.
Shrivastava, A. y Singh, B. (2010). PFC Cuk converter based electronic ballast for an 18 W compact fluorescent lamp. 2010 International Conference on Industrial and Information Systems (ICIIS), 393-397.
Vlatkovic, V., Borojevic, D. y Lee, F. C. (1996). Input filter design for power factor correction circuits. IEEE Transactions on Power Electronics, 199-205.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Diseño y simulación de un balastro electrónico con corrección de factor de potencia con topología buck-boost e inversor alimentado por corriente1
Design and simulation of an electronic ballast with power factor correction buck-boost topology and current-fed invertir
Projeto e simulação de um reator eletrênico com correção de fator de potência topologia buck-boost e inversor de corrente alimentada
Germán E. Melo2
Jonathan E. Cadena3
Nelson L. Díaz4
1Artículo de investigación
2Universidad Distrital Francisco Jóse de Caldas, Colombia, Contacto: eduarger123@gmail.com
3Universidad Distrital Francisco Jóse de Caldas, Colombia, Contacto: jecadenas@gmail.com
4Universidad Distrital Francisco Jóse de Caldas, Colombia, Contacto: nelson.diaz@gmail.com
Fecha de recepción: Octubre de 2013, Fecha de aceptación: Abril de 2014
Resumen
Las lámparas fluorescentes compactas o CFL (compact fluorescent lamp) se han convertido en uno de los tipos de iluminación más usados en la actualidad. Sin embargo, las CFL comerciales poseen en su mayoría balastros electrónicos de bajo factor de potencia. Esto genera un aumento en los niveles de distorsión del sistema de generación y distribución debido al uso masivo de estas lámparas. En el presente artículo se presenta el diseño y simulación de un balastro electrónico con corrección de factor de potencia para lámparas fluorescentes compactas. La propuesta busca evaluar la viabilidad de integrar el correcto funcionamiento, tamaño y costo de este dispositivo. La topología propuesta es una etapa buck-boost operando en modo de conducción discontinua integrada a un inversor alimentado por corriente. La alta factibilidad de implementación de esta topología es mostrada mediante simulaciones que logran un factor de potencia de 0.998 y una distorsión total armónica menor de 5%.
Palabras clave: balastro electrónico, lámparas fluorescentes, factor de potencia, corrección del factor de potencia, balastro integrado.
Abstract
Compact Flurconet Lamps (CFL’s) have became in one of kind of lighting widely used in nowadays. However, Commercial CFL’s uses electronic ballast of low power factor (LPF), that produces an increase in the system harmonic distortion levels in the generation and the distribution due the widespread use of this kind of lamps. The present paper presents the design and simulation of an Electronic Ballast with power factor correction for CFL’s. The proposal searches evaluate the feasibility of integrate the right operation. size and the costs of this device. The proposed topology consists in a Buck-Boost Stage operating in discontinuous conduction mode integrated with current fed inverter. The High feasibility of implementation Of this topology is showed through simulation that reached power factor of 0.998 and a Total Distortion Harmonics less than 5%
keywords: electronic ballast, florescent lamp, power factor, power factor correction, integrated ballast.
Introducción
Las lámparas fluorescentes son cada vez más usadas en aplicaciones para la iluminación en sectores residenciales, industriales y comerciales (Chuang Cheng, 2006). En especial, las lámparas fluorescentes compactas (CFL ‘compact fluorescent lamp’) se han convertido en una de las fuentes de luz artificial más populares debido a su alta eficiencia luminosa (lm/W) (Shrivastava y Singh, 2010).
Estos dispositivos pertenecen a las fuentes de luz por descarga. Poseen una característica tensión-corriente negativa consecuencia de la descarga que debe ser producida en el proceso de encendido de la lámpara. Además, para garantizar que la lámpara logre un buen rendimiento, la señal en estado estable deber ser de alta frecuencia. La lámpara también posee un comportamiento lineal a altas frecuencias como se muestra la figura 1. Debido a estas características, se utiliza un dispositivo llamado balastro o balasto que puede ser electrónico o electromagnético que permita estabilizar el proceso de encendido y mantener la señal de la lámpara a la frecuencia apropiada (Díaz, 2000).
En la actualidad, la tecnología de los balastros electrónicos de alta frecuencia para controlar las lámparas fluorescentes ha ido reemplazando a los balastros electromagnéticos. A pesar de que los balastros electromagnéticos son de bajo costo, presentan una serie de inconvenientes de los cuales se pueden destacar su gran tamaño (imposibilidad de ser utilizados en las CFL), el alto peso, baja frecuencia de operación, baja vida útil, parpadeos y zumbidos en la lámpara (Chuang y Cheng, 2006). Un balastro electrónico cumple la misma función del balastro electromagnético mejorando los aspectos mencionados.
Las CFL se clasifican en HPF (alto factor de potencia, 𝐹𝑃>0.9) y LPF (bajo factor de potencia, 𝐹𝑃 0.9). Las CFL de LPF son el tipo más usado de CFL debido a su menor costo. En estudios como el de Sharma, Sunderman y Gaikwad (2011) se citan varias investigaciones que analizan el incremento de la distorsión armónica en los sistemas de distribución a causa de las CFL. En el estudio de Electric Power Research Institute (2009) se determinó que individualmente las CFL no son una fuente importante de armónicos, pero el uso masivo de estas puede tener un impacto significativo en la contaminación armónica del sistema. En la figura 2 se presentan los datos medidos en laboratorios de pruebas de la distorsión armónica para 51 modelos de CFL disponibles en el mercado de 2009. Allí se observa que la mayoría de las CFL estudiadas corresponden a CFL LPF, ya que poseen una distorsión armónica total de la corriente de entrada 𝐼𝑇𝐻𝐷 superior a 120%.
Las etapas de un balastro electrónico de LPF son el rectificador (compuesto de diodos y condensador de filtrado). Este se encarga de la conversión AC-DC, seguido de aquel se encuentra un inversor, que se encarga de hacer la conversión de DC-AC de alta frecuencia, y por último se encuentra el tanque resonante que alimenta a la lámpara fluorescente, que se encarga de convertir la señal cuadrada de alta frecuencia del inversor en una señal sinusoidal de alta frecuencia. El rectificador posee un pico de corriente que trae como consecuencia un alto contenido armónico. Las soluciones más comunes es el uso de una etapa de corrección de factor de potencia entre el rectificador y el inversor, como lo muestra la figura 3.
Para dar solución a estos inconvenientes, se han propuesto prototipos de balastros electrónicos que implementen una etapa de corrección de factor de potencia. Estas propuestas van dirigidas tanto a lámparas tubulares (Maamoun, 2000; Lin, Liu y Shih, 2007; Garcia, Dalla-Costa, Kirsten, Gacio y Calleja, 2011) como a lámparas CFL (Ponce, Martinez, Correa, Cotorogea, Arau, 2006; Lamy Jain, 2010; Shrivastava y Singh, 2010), y presentan diferentes metodologías como balastros con etapa diferenciada de PFC, etapas de un solo interruptor que integran convertidor resonante y PFC y diferentes topologías como buck, boost, buck-boost, flyback, sepic o cuk (Rashid, 2010).
En este artículo se propone un balastro electrónico para una lámpara fluorescente de 20 W que integra la etapa de corrección de factor de potencia con las etapas del inversor y el tanque resonante. El prototipo es basado en un balastro propuesto en el trabajo de Lam y Jain (2007). El balastro implementa una etapa de corrección de factor de potencia con un conversor DC/DC buck-boost integrado a un inversor resonante alimentado por corriente, además de usar un solo interruptor. Se evaluará el rendimiento del balastro en torno a tres criterios: funcionamiento, potencial de integración y costo.
Materiales y Métodos
La propuesta consisten en la integración de la etapa de corrección de factor de potencia y el inversor resonante alimentado por corriente. Se expondrán los análisis de cada una forma independiente de cada una de las etapas para presentar posteriormente la del diseño integrado.
Etapa de corrección Buck-Boost
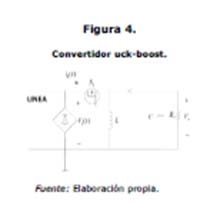
El convertidor Buck-Boost es presentado en la figura 4.Se eligió operar el convertidor buck-boost en modo de conducción discontinua (MCD), ya que si se emplea el MCD los convertidores se pueden usar sin un lazo de control para que logren la corrección de factor de potencia, ya que el pico de corriente en el inductor del convertidor sigue el voltaje de la señal rectificada de entrada (figura 5). En esta misma se muestran la relaciones ideales entre el voltaje de entrada y la corriente de salida. Vale la pena señalar que también hay propuestas de control del ciclo útil (D) en convertidores operando en el MCD.
Los convertidores en el MCD sin lazos de control, incluido el buck-boost, están limitados a aplicaciones de CFP a bajas o medias potencias, ya que en altas potencias estos poseen muchas pérdidas y sería muy ineficiente implementarlos (Rashid, 2010).
El convertidor buck-boost tiene dos desventajas en la práctica: 1) la polaridad del voltaje de salida (esta topología invierte el voltaje de entrada) y 2) necesita de un manejador de compuerta flotante para activar el interruptor.
Para el análisis del comportamiento del circuito, este se puede dividir en tres etapas de funcionamiento. La primera es cuando el interruptor está encendido, la segunda cuando el interruptor está apagado y en el diodo todavía circula corriente y la tercera ocurre cuando en el diodo no circula corriente y el interruptor sigue apagado.
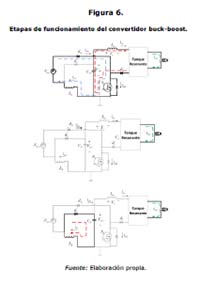
En la figura 4 se muestran las etapas de operación del circuito propuesto, de las cuales se obtienen las formas de onda presentadas en la figura 6. En estas, Vrect es el voltaje de salida del puente rectificador, VG hace referencia a la señal que conmuta el Mosfet (metal-oxide-semiconductor ‘metal-óxido-semiconductor inglés), iDinse refiere a la corriente que circula por el diodo Din, isn es la corriente de entrada al tanque resonante, la cual es la misma que circula por el inductor Lin, iDs1 es la corriente que circula a través del Mosfet S1, Vds es el voltaje entre el drain y source del interruptor, iLb es la corriente a través del inductor Lb y iout es la corriente de salida del tanque resonante, que es la misma corriente de la carga; en este caso, la lámpara.
Como se ve en la figura 6, la explicación del funcionamiento del circuito es válida indiferentemente al tanque resonante usado. La operación en las diferentes etapas se puede describir de la siguiente manera:
Etapa 1: Durante esta etapa, el Mosfet S1 se encuentra en estado de encendido, por lo tanto el diodo Din conduce y el inductor LB comienza a cargarse. La corriente iLB se incrementa linealmente. Al diodo D1 es forzado a encenderse ya que el S1 está encendido. Como resultado de esto, isn comienza a incrementarse debido a la presencia de Lin Por tanto, para minimizar las pérdidas causadas por la conmutación de encendido apagado en el interruptor se puede reducir el tamaño de la bobina Lin para que de esta manera isn retorne a 0 antes de que S1 se apague. En esta etapa, la corriente total del interruptor S1, iS1 es igual a la suma de iDin e isn.
Etapa 2: Esta etapa comienza cuando el Mosfet 𝑆1 es apagado por la señal de control 𝑉𝐺, lo cual fuerza al diodo 𝐷𝑖𝑛 también a apagarse. Como resultado de esto, 𝐷𝑏 comienza a conducir e 𝑖𝐿𝑏 decrece linealmente a través del lazo formado por el mismo 𝐷𝐵, 𝐶𝐵 y 𝐿𝐵. Debido a la capacitancia parásita del interruptor, 𝑣𝑑𝑠 se incrementa lentamente, lo que ayuda a reducir las pérdidas de la conmutación de encendido a apagado del Mosfet.
Etapa 3: Esta etapa comienza cuando 𝑖𝐿𝑏 llega a 0, lo que indica que el convertidor se encuentra en el MCD. 𝐷1 sigue apagado, y el circuito resonante continúa entregando la energía requerida por la lámpara.
De acuerdo con Lam y Jain (2007), Lam y Jain (2010) y Liu y Lin (1989) se expondrán las relaciones matemáticas de este convertidor, las cuales son útiles para su diseño.
La corriente promedio de línea de entrada será la primera en ser analizada. Si se parte de que el voltaje de línea es 𝒗𝒔(𝒕)=𝑽𝒑𝐬𝐢𝐧 (𝝎𝑳𝒕), donde 𝑽𝒑 y 𝝎𝑳 representan la amplitud del voltaje y la frecuencia angular de la linea 𝝎𝑳=𝟐𝝅𝟔𝟎𝑯𝒛, respectivamente. De forme ideal, el promedio de corriente después del rectificador es igual a la corriente promedio del Mosfet. Por lo tanto, la corriente de línea promedio, 𝒊𝒔,𝒂𝒗𝒈(𝒕) puede ser descrita mediante la ecuación 1, donde 𝒊𝑳𝒃,𝒑 es la corriente pico del inductor 𝑳𝑩, y puede ser expresada mediante la ecuación 2. 𝑫 es el ciclo útil de convertidor, 𝑻𝒔 el periodo de conmutación, 𝒕𝒐𝒏 es el tiempo durante el cual está encendido el Mosfet, el cual es equivalente a 𝒕𝒐𝒏=𝑫𝑻𝒔.
Por lo tanto, reemplazando la ecuación 1 en la ecuación 2 y reemplazando ton se obtiene que is,avg puede ser escrita como muestra la ecuación 3. Como se observa en esta última ecuación y como también se había expuesto anteriormente, la corriente promedio de línea se encuentra en fase con el voltaje. Además, en el convertidor buck-boost, a diferencia del convertidor boost operando en el MCD, el Mosfet no sufre estrés por alto voltaje para lograr la corrección de factor de potencia\citep{15_buck_boost2,buck_boost2}. La potencia promedio del convertidor 𝑃𝑎𝑣está dada por la ecuación 4:
La ecuación 4 es usada para asegurar la operación en el MCD del buck-boost. Es usual en las metodologías de diseño en \citep{buck_boost1, buck_boost2} que se escoja un ciclo útil 𝐷 fijo, de esta manera se calcula 𝐿𝑏,𝑚𝑎𝑥 (ecuación 5).
El valor calculado mediante la ecuación 5 es el valor máximo que puede tomar 𝐿𝑏 para garantizar que el convertidor esté operando en el MCD. El valor de 𝐿𝑏 no puede ser seleccionado arbitrariamente solo cumpliendo la condición expuesta en la ecuación 5, también habrá un límite mínimo del valor de 𝐿𝑏, el cual estará en función del rizado de la corriente.
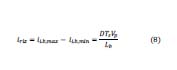
La operación en el MCD del convertidor no es del todo garantizada solo con el cumplimiento de la 𝐿𝑏,𝑚𝑎𝑥, además de esta condición también se tiene que cumplir que la corriente en la bobina se debe descargar completamente desde el valor máximo, el cual es dado por la ecuación 6, en 𝑡=𝐷∗𝑇𝑠 hasta antes de 𝑇𝑠, y como la corriente máxima tiene lugar en el máximo valor instantáneo del voltaje de entrada, por lo tanto para garantizar que el convertidor opere en el MCD se tiene que cumplir la relación expuesta en ecuación 7, donde 𝑣𝐷𝐶 es el voltaje entre los terminales del condensador, el cual a su vez es el voltaje de salida del convertidor.
Con la expresión de 𝑖𝐿𝑏,𝑚𝑎𝑥 se puede calcular la expresión del rizado de corriente, ya que el rizado es el voltaje máximo menos el voltaje mínimo, que para el caso MCD el voltaje mínimo es 0, por lo tanto la expresión que define esta relación es expuesta en la ecuación 8, la cual da como resultado la misma 𝑖𝐿𝑏,𝑚𝑎𝑥.
Por otro lado, el voltaje DC entre las terminales del condensador 𝐶𝐵, 𝑣𝑑𝑐 está dado por la ecuación 9, donde 𝐷2 es una constante que deber ser menor de 1. 𝐷2∗𝑇𝑠 es el tiempo en el cual se descarga la bobina, de esta manera cuando el convertidor opera en MCD 𝐷2<1.
También es importante conocer el voltaje DC mínimo del convertidor (ecuación 11).
Para asegurar el funcionamiento adecuado de la lámpara, 𝐶𝑏 tiene que ser diseñado de acuerdo con el rizado de voltaje 𝑉𝑟𝑖𝑧 que permitirá (se recuerda que este voltaje cae en el condensador 𝐶𝑏). El rizado del voltaje es provocado por la complemente AC del voltaje del condensador, por lo tanto este cumple la relación expuesta en la ecuación 12.
Desarrollando la integral de la ecuación 12tenemos que el voltaje de rizado 𝑉𝑟𝑖𝑧 está dado por la ecuación 13. Y partiendo de esta última, se puede obtener la relación donde 𝐶𝑏 es expresada en función del 𝑉𝑟𝑖𝑧. Esta última relación es mostrada en la ecuación 14.
Como se mostró en la figura 3, un bloque importante en este tipo de balastros es el filtro EMI. El análisis de las consideraciones de diseño de este filtro se basará en Vlatkovic, Borojevic y Lee (1996) y Grigore, Kyyra y Rajamaki (1999). El propósito del filtro EMI es obtener la corriente promedio de la corriente en el MCD que pasa por el inductor 𝐿𝑏, para que de esta manera se logre una corriente de entrada con bajo rizado de voltaje y con poca distorsión en la forma de onda, es decir que la corriente sea lo más parecido, en cuanto a forma de onda, a la señal sinusoidal de voltaje.
Inversor resonante alimentado por corriente
En la figura 7 se muestra una nueva topología de inversor resonante alimentado por corriente. Este inversor ha sido implementado en varias propuestas (Lam y Jain, 2010; Lam y Jain, 2007; Lam Jain, 2008), en las cuales son expuestas consideraciones de diseño.
De acuerdo a los resultados de Lam y Jain (2008), Lam y Jain (2010) y Lam y Jain (2010) la ventaja del inversor comparado con el inversor clase E se presenta cuando el interruptor está encendido; solo la corriente iin, que es la corriente de entrada del inversor (figura 7) fluye a través del interruptor. Lo anterior significa que las pérdidas de conducción en el Mosfet son reducidas significativamente (Lam y Jain, 2010).
Otra ventaja de este inversor es que el estrés de voltaje es mucho menor en comparación con el inversor clase E. Sin embargo, en el circuito propuesto, el voltaje en el Mosfet es función tanto de 𝑳𝒊𝒏 como de las características del inversor resonante, por lo tanto el voltaje en el Mosfet puede ser minimizado (Lam y Jain, 2010).
En la figura 7 se muestran dos topologías que han sido usadas y analizadas con el inversor de corriente propuesto. La primera topología mostrada, el esquemático de mostrado a la derecha, es una topología LLC (Lam y Jain, 2007; Lam y Jain, 2010; Lam y Jain, 2010; Lam y Jain, 2008). La segunda topología, mostrada en el esquemático de la izquierda, es un tanque resonante LCC (Lam y Jain, 2011), modificado para adaptarse a los requerimientos de este inversor.
Las ecuaciones de diseño del tanque LLC son mostradas en las ecuaciones 15, 16 y 17 , donde Q es el factor de calidad del tanque, fr es la frecuencia de resonancia del tanque resonante y RL es la resistencia equivalente de la lámpara fluroscente.
Las ecuaciones de diseño p y el tanque resonante LCC son mostrados en las ecuaciones 18, 19, 20 y 21, donde Q es el factor de calidad del tanque, fr es la frecuencia de resonancia del tanque resonante, RL es la resistencia equivalente de la lámpara fluroscente y fp es la frecuancia resonante en paralelo que tiene que ser menor de la frecuencia de resosnancia fr Cp es escogido como parámetro.
La resistencia equivalente de la lámpara fluorescente RL se puede obtener de la relación expuesta en la ecuación 22. Siendo VLamp,rm el voltaje RMS en estado estable de la lámpara y PLamp la potencia en estado estable.
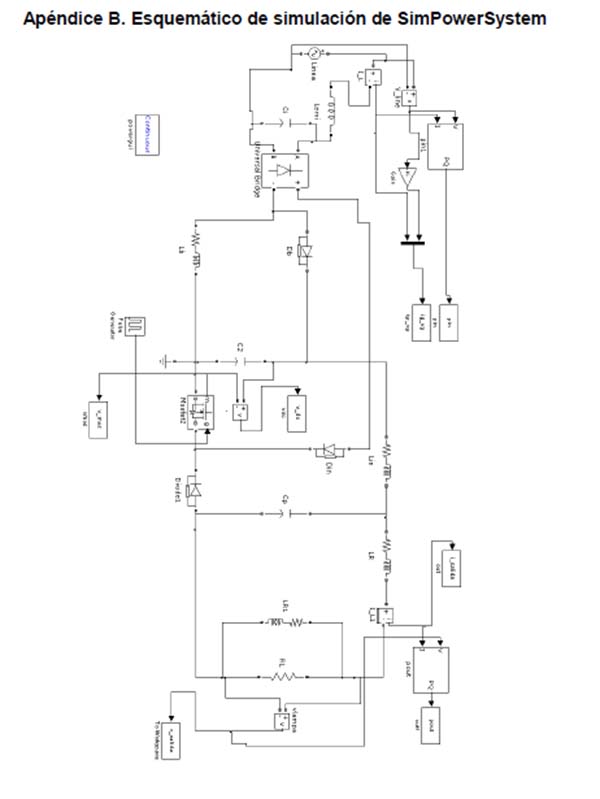
Finalmente, integrando las dos etapas y un filtro EMI para reducir la distorsión armónica total de la corriente de entrada, el esquemático de la propuesta queda definido (figura 8). El proceso de diseño del filtro EMI se presenta en el apéndice A.
Resultados y Discusión
Para el inversor alimentado por corriente se han hechos pocos estudios, por lo tanto se ejecutó un análisis en simulación de las los circuitos resonantes LLC y LCC para identificar diferencias entre factor de cresta y esfuerzos de voltaje de corriente y voltaje en estado de preencendido y estado estable. En la tabla 1 se muestran los resultados de los análisis ejecutados.
De acuerdo con lo expuesto en la tabla 1, se pueden concluir los siguientes aspectos:
- El tanque resonante LCC posee un mejor factor de cresta que el tanque LLC.
- El tanque resonante LCC posee una menor ganancia en el estado de encendido en el contexto analizado.
- El tanque resonante LLC posee menores esfuerzos de voltaje y corriente en el Mosfet en estado estable.
- El tanque resonante LLC posee mayores esfuerzos de voltaje y corriente en el Mosfet en estado de encendido, debido a la ganancia que resultó en el contexto analizado, pero estos esfuerzos se pueden mitigar diseñando más específicamente, por lo cual no se considera una total desventaja. >
- En el contexto aplicado del balastro analizado, el tanque resonante LLC es la topología de tanque resonante más adecuada para la topología de inversor de corriente analizada.
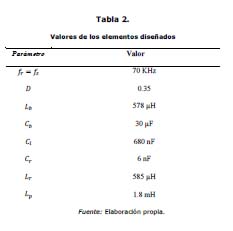
Con este análisis se diseñan los elementos del balastro con las dos etapas integradas. En la tabla 2 se presentan lo valores con los cuales se ejecuta la simulación posterior.
En el apéndice B se muestra el esquemático de simulación del diseño. En la figura 9 se presenta la comparación entre el voltaje de entrada (normalizado) y la corriente de entrada del balastro. Se observa que las dos señales están prácticamente en fase y la señal de la corriente es de forma sinusoidal.
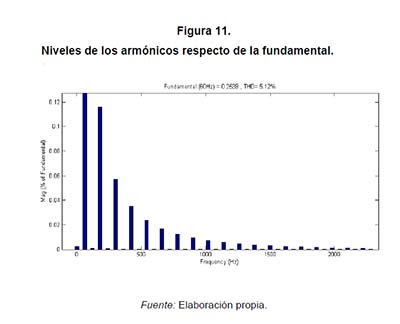
En la figura 10 se muestra la gráfica de potencia de entrada (azul) y de salida (roja) que se alcanza una eficiencia de 91%.En la figura 11 se muestran los niveles de los armónicos repecto del armónico de la fundamental. Se observa que se obtiene un THD = 5.72 %
Mediante los resultados de simulación se encontró un 𝐹𝑃=0.9780 con una 𝑇𝐻𝐷=5.72 %. Estos valores indican un alto 𝐹𝑃 con una baja 𝑇𝐻𝐷. Los niveles de los armónicos fueron comparados con los límites de la norma IEC-13002, observando que los armónicos generados por el balastro propuesto se encuentran bajo los límites de esta norma. La eficiencia obtenida es de 91 %, la cual es una eficiencia aceptable para este tipo de sistemas (se tiene en cuenta que los componentes implementados en la simulación fueron configurados presentando pérdidas). Se ha verificado que la propuesta también alimenta adecuadamente a la lámpara con bajo factor de cresta y en una alta frecuencia. De esto se concluye que desde el criterio de desempeño de funcionamiento la propuesta ha cumplido los requerimientos expuestos.
En cuanto al potencial de integración del circuito de la propuesta planteada, este sistema es concebido de tal manera que este criterio sea inherente a la propuesta. Tal circuito no necesita de circuito de control de realimentación, es decir, no necesita tampoco acondicionamiento de señales. Puede ser usado drivers de compuerta sencillos, en los que no haya que alimentarse con fuentes flotantes. Eso significa que con una adecuada selección de las bobinas en cuanto a tamaño y funcionalidad y un buen diseño de la PCB, que puede ser en dos capas, se puede implementar un modelo de tamaño de un balastro comercial. Esto significa que el potencial de integración de esta propuesta es alto.
De acuerdo con lo expuesto en la evaluación del potencial de integración, los costos solo subirán por los costos de las bobinas y de los drivers. Por lo tanto, se puede decir que una CFL con balastro como el presentado será cerca de dos veces más costosa que una CFL comercial. Pero este costo es justificable, ya que la propuesta supera fácilmente el 𝐹𝑃 y 𝑇𝐻𝐷 de un balastro comercial.
Agradecimientos
Los autores quieren expresar su agradecimiento al Centro de Investigación y Desarrollo Científico de la Universidad Distrital Francisco José de Caldas por su apoyo económico para la realización de este artículo y al proyecto de grado titulado Diseño e implementación de un prototipo de balastro electrónico para lámparas fluorescentes compactas (CFL) con corrección de factor de potencia, del cual se derivó el contenido expresado en el presente artículo. Los autores también quieren expresar especial agradecimiento al ingeniero Julián Camargo, profesor de planta de la Universidad Distrital por su apoyo ante el Centro de Investigación y Desarrollo Científico.
Referencias bibliográficas
Blanco, A. y Parra, E. ( 2010). Effects of high penetration of CFLS and LEDS on the distribution networks. Harmonics and Quality of Power (ICHQP), 2010 14th International Conference on, 1-5.
Chuang, Y.-C. y Cheng, H.-L. (2006). Single-Stage Single-Switch High-Power-Factor Electronic Ballast for Fluorescent Lamps. Industrial and Commercial Power Systems Technical Conference, 1-7.
Díaz, A. R. (2000). Balastros electrónicos integrados con corrección activa de factor de potencia. Centro Nacional de Investigación y Desarrollo Tecnológico.
Electric Power Research Institute. (2009). Compact fluorescent lamps: harmonics analysis and distribution impact study. Electric Power Research Institute.
Garcia, J., Dalla-Costa, M., Andre Luis Kirsten, A., Gacio, D. y Calleja, A. (2011). A novel flyback-based input PFC stage for electronic ballasts in lighting applications. Industry Applications Society Annual Meeting (IAS), 1-6.
Grigore, V., Kyyra, J. y Rajamaki, J. (1999). Input filter design for power factor correction converters operating in discontinuous conduction mode. IEEE International Symposium on Electromagnetic Compatibility, 1, 145-150.
Lam, J. y Jain, P. K. (2007). A low cost single-stage electronic ballast with unity power factor using a novel single switch current fed resonant inverter topology. Power Electronics Specialists Conference, PESC 2007, 3106-3111.
Lam, J. y Jain, P. K. (2008). A dimmable electronic ballast with unity power factor based on a single-stage current-fed resonant inverter. IEEE Transactions on Power Electronics,3103-3115.
Lam, J. y Jain, P. K. (2010). A high-power-factor single-stage single-switch electronic ballast for compact fluorescent lamps. IEEE Transactions on Power Electronics, 2045-2058.
Lam, J. y Jain, P. K. (2010). A novel high-power-factor single-switch electronic ballast. IEEE Transactions on Industry Applications, 2202-2211.
Lam, J. y Jain, P. K. (2011). A boost-type high power factor single switch electronic ballast for compact fluorescent lamps (energy-saving lamps). IECON 2011 - 37th Annual Conference on IEEE Industrial Electronics Society, 2854-2859.
Lin, R.-L., Liu, H.-Y. y Shih, H.-M. (2007). AC-Side CCM CS–CP–PFC Electronic Ballast. Power Electronics, IEEE Transactions on, 22(3) , 789-796.
Liu, K.-H. y Lin, Y.-L. (1989). Current waveform distortion in power factor correction circuits employing discontinuous-mode boost converters. Power Electronics Specialists Conference, PESC '89, 825-829.
Maamoun, A. (2000). An electronic ballast with power factor correction for fluorescent lamps. Electrical and Computer Engineering, 2000 Canadian Conference on, 385-389.
Ponce, M., Martinez, A., Correa, J., Cotorogea, M. y Arau, J. (2006). High-efficient integrated electronic ballast for compact fluorescent lamps. Power Electronics, IEEE Transactions on, 532-542.
Rashid, M. H. (2010). Power electronics handbook: devices, circuits and applications. Academic Press.
Sharma, H., Sunderman, W. G. y Gaikwad, A. (2011). Harmonic impacts of widespread use of CFL lamps on distribution systems. Power and Energy Society General Meeting, 1-5. IEEE.
Shrivastava, A. y Singh, B. (2010). PFC Cuk converter based electronic ballast for an 18 W compact fluorescent lamp. 2010 International Conference on Industrial and Information Systems (ICIIS), 393-397.
Vlatkovic, V., Borojevic, D. y Lee, F. C. (1996). Input filter design for power factor correction circuits. IEEE Transactions on Power Electronics, 199-205.

License
When submitting their article to the Scientific Journal, the author(s) certifies that their manuscript has not been, nor will it be, presented or published in any other scientific journal.
Within the editorial policies established for the Scientific Journal, costs are not established at any stage of the editorial process, the submission of articles, the editing, publication and subsequent downloading of the contents is free of charge, since the journal is a non-profit academic publication. profit.