Optimización topológica de un semirremolque tipo plataforma-Topological optimization of a platform semitrailer

Optimización topológica de un semirremolque tipo plataforma¹

Topological optimization of a platform semitrailer

Otimização topológica de um tipo semi reboque caixa aberta

Víctor Ruiz Rosas²

John Forero Casallas³

Carlos Bohórquez ávila⁴

¹Artí;culo de investigación

²Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, Grupo de Investigación en Ingeniería y Diseño Dising. Contacto: veruizr@udistrital.edu.co

³Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, Grupo de Investigación en Ingeniería y Diseño Dising. Contacto: jaforeroc@udistrital.edu.co

⁴Universidad Distrital Francisco José de Caldas, Bogotá, Colombia, Grupo de Investigación en Ingeniería y Diseño Dising. Contacto: cabohorqueza@udistrital.edu.co

Fecha de recepción: Octubre de 2013, Fecha de aceptación: Abril de 2014

Resumen

El artículo presenta los resultados de la optimización de un semirremolque tipo plataforma para vehículos de carga, buscando minimizar el peso en la estructura para aumentar la capacidad de carga. Mediante el uso de una estrategia de optimización topológica se redujo el peso de las vigas estructurales por ser estas las que más peso aportan al semirremolque. El diseño incluyó un análisis mediante elementos finitos del comportamiento estructural estático y dinámico para garantizar la funcionalidad del equipo. Se logró un diseño que reduce sustancialmente el peso del semirremolque sin perder resistencia estructural.

Palabras clave: optimización topológica, semirremolque, transporte de carga.

Abstract

The article presents the results of the optimization of a type semitrailer platform for freight vehicles, seeking to minimize weight in the structure to increase capacity. Using topology optimization strategy weight of the structural beams can be reduced by these that provide more weight to the semitrailer. The design included a finite element analysis of the static and dynamic functionality to ensure the structural performance of the team. A design that substantially reduces the weight of the semitrailer without losing structural strength is achieved.

Keywords: topological optimization, semitrailer, cargo transport.

Resumo

O artigo apresenta os resultados da otimização de uma plataforma semireboque tipo para veículos de carga, buscando minimizar o peso na estrutura para aumentar a capacidade. Usando topologia optimização peso estratégia das vigas estruturais pode ser reduzido por esses que proporcionam mais peso do semi-reboque. O projeto incluiu uma análise de elementos finitos da funcionalidade estática e dinâmica para garantir o desempenho estrutural da equipe. Um desenho que reduz substancialmente o peso do semi-reboque, sem perder a resistência estrutural é alcançado

Palavras-Chave: otimização topológica, semi reboque, transporte de carga.

Introducción

Los resultados presentados en el presente artículo corresponden al desarrollo del proyecto de investigación titulado Diseño óptimo de semirremolques para vehículos pesados apoyado en una plataforma colaborativa, financiado a través del Centro de Investigaciones y Desarrollo Científico de la Universidad Distrital Francisco José de Caldas.

En Colombia el transporte de carga pesada por carretera es uno de los sectores más dinámicos de la economía del país y se ha incrementado en los últimos años (Colfecar, 2010). A pesar de su crecimiento, los inconvenientes resultantes de una infraestructura limitada, los altos costos operativos y de combustibles y las políticas de regulación han llevado en varias ocasiones a poner en riesgo la estabilidad del sector. Los últimos gobiernos han planteado acciones orientadas a mitigar estas problemáticas a través de planes de mejoramiento de la infraestructura y regulación de la competencia; sin embargo, es necesario plantear estrategias alternativas que aporten en uno de los sectores clave del aparato productivo nacional (Colombia, Ministerio de Transporte, 2010).

Las plataformas y los tanques de transporte de fluidos especialmente de hidrocarburos son los semirremolques más comunes en Colombia, dada su versatilidad para el transporte de carga, especialmente los del tipo 3S2 y 3S3 que corresponden a semirremolques de dos y tres ejes para vehículos de tres ejes de hasta 52 000 kg de peso bruto vehicular, el cual se calcula a partir del peso del vehículo más la carga (Colombia, Ministerio del Transporte, 2004). En el caso de la plataforma, esta tiene una incidencia directa en el peso total, y por lo tanto en la cantidad de carga permisible por transportar; sus dimensiones máximas normalmente permiten llevar un contenedor de aproximadamente 35 t. Dada su configuración robusta, puede ser optimizado teniendo en cuenta que si el peso del semirremolque se reduce es posible mejorar la capacidad de carga; igualmente es posible disminuir los costos de operación por desgaste de ruedas y combustible. El estudio, entonces, se dedicó a mejorar las condiciones de diseño de este tipo de semirremolques, en particular los del tipo 2S3 y 3S3 (tres ejes en el semirremolque), que manejan las mayores capacidades de carga.

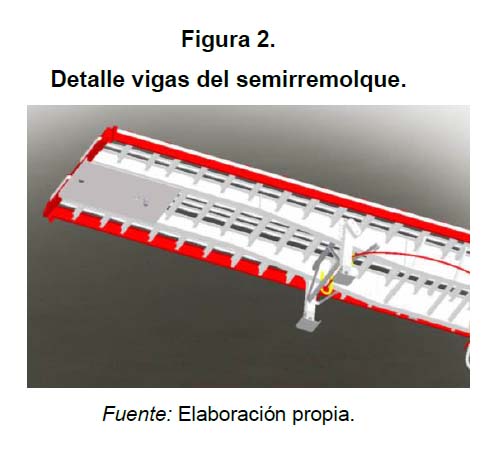
Estructuralmente, estos equipos cuentan con dos vigas longitudinales que soportan la carga. La plataforma la conforma un marco que se une a las vigas mediante puentes transversales que ayudan a distribuir mejor la carga (figura 1). Las vigas son de perfil en I , están conformadas por un patín superior, el alma y un patín inferior. La altura del alma varía teniendo en cuenta que se debe permitir un montaje apropiado sobre el tractocamión, por lo que en la zona del acople la viga es más corta que en el resto de la longitud del equipo. Esto es permisible dado que es una zona donde el camión ayuda a soportar en parte el peso del semirremolque (figura 2).

Las tareas de análisis del comportamiento mecánico y mejoramiento de este tipo de equipos han sido abordadas a partir del cambio y mejoramiento de los materiales y su distribución. En Ingrassia, Alaimo, Cappello, Mancuso y Nigrelli (2007), se plantea el uso de materiales compuestos utilizando fibra de vidrio reforzada (GPR) y en Farzad, Chien-Min y Kikuchi (s. d.) estructuras tipo panel las cuales mejoran la distribución del peso y hacen el remolque más liviano. El uso de técnicas de optimización topológica es planteado en Kim y Yoon (2010) —quienes se utilizan métodos de optimización robusta de Taguchi— y en Högberg (2001) y (Jang, Yoon y Park (2009). Por otro lado, se ha trabajado específicamente en la cabina y en la suspensión de vehículos de carga en Cole (2001) y Pang, Li, Fang y Shan (2010). Un análisis sobre los elementos estructurales de un remolque tipo volco se presenta en Gerardo, Bruno y Bruno (s. f.). Localmente no se presentan estudios de equipos optimizados, tal como se diagnostica en Ruiz y Guevara (2011).

Los grupos de investigación Dising y Metis de la Universidad Distrital junto con la colaboración de Talleres Torres S. A. reconociendo la problemática relacionada con el diseño y construcción de este tipo de equipos, especialmente en pequeños constructores, consideraron importante contribuir en el desarrollo de nuevas estrategias de diseño para este tipo de productos tecnológicos, con el fin de construir remolques para los cuales se disminuya su peso y aumentar la capacidad de carga como alternativa en el mejoramiento de los márgenes de utilidad para el sector transportador.

Metodología

El proceso de diseño óptimo incluyó en su fase inicial un contacto directo con usuarios del sector transportador y con algunos fabricantes, y sus requerimientos fueron resumidos en una matriz QFD presentada en Ruiz y Acero (2012). Posteriormente, se buscó hacer un análisis del comportamiento mecánico a partir del cual se pudieran encontrar las partes más susceptibles para ser optimizadas.

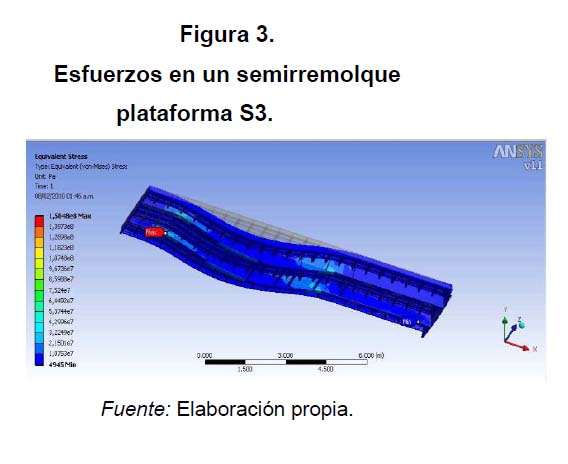
Se hizo una simulación utilizando ANSYS de un conjunto completo de semirremolque tipo S3 con una carga distribuida de 35 000 kg aplicada sobre los puentes transversales. El remolque se apoyó en el punto de acople o King Ping que corresponde al punto de unión con el tractocamión y en los puntos que se une en la parte posterior a la suspensión. El mallado utilizado fue de elementos tetraédricos sin controlar en un mallado no muy denso dada la longitud del equipo (12 500 mm). Los resultados de la simulación se muestran en las figuras 3. Los puntos de esfuerzo más crítico se ubicaron lógicamente en las vigas, cerca de los apoyos y en el cambio de altura del alma de las vigas. La magnitud del esfuerzo máximo es ubicada cerca del apoyo del acople y es un poco mayor de 50 % del límite de fluencia del material (acero A36, resistencia a fluencia Sy = 250 MPa). Sin embargo, se identifica que el conjunto soporta la carga de manera holgada, con factores de seguridad cercanos a 100 en buena parte de las vigas. Lo anterior permitió plantear una disminución de masa sin que se comprometa la resistencia estructural.

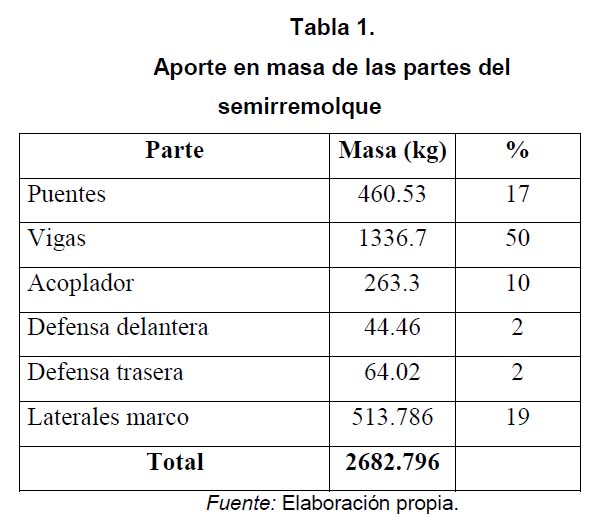
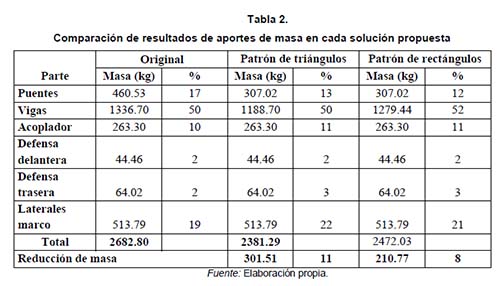
Posteriormente al análisis estructural se decidió establecer el aporte en masa que cada parte tiene en el semirremolque, y así decidir cuál de las partes sería el objeto de reducción. De esta manera, se estableció que las vigas aportan más de 50 % en masa de todo el conjunto (Ruiz y Acero, 2012) (tabla 1) . Teniendo en cuenta los resultados tanto de aporte en masa como de comportamiento mecánico, se decide reducir masa en las vigas buscando un impacto significativo en el peso total del remolque. El objetivo planteado por el grupo de investigación es disminuir de forma global 5 % del peso total minimizando la masa de las vigas y reduciendo el número de puentes transversales (Ruiz y Guevara, 2011).

Se requiere minimizar la masa de las vigas mediante técnicas de optimización, siendo la optimización topológica la estrategia más apropiada, dado que mediante ella es posible distribuir el material en las zonas donde se requiere una mayor densidad para tener en este caso resistencia a la carga de trabajo (Bendsoe y Sigmund, 2004; Huang y Xie, 2010). Para disminuir la cantidad de elementos en la optimización, se decide hacer el análisis en una viga bidimensional trabajando a 50 % de la carga total aplicada al remolque, teniendo en cuenta que del análisis estático se verificó que el comportamiento estructural de las dos vigas en conjunto es muy similar tanto en magnitud como en distribución del esfuerzo.

El problema de optimización que se plantea en este caso utilizando elementos finitos estará en buscar una distribución de material isotrópico para soportar cargas asociadas al peso del material transportado y ubicado en la plataforma. Como caso extremo, se considera el peso directamente soportado por las dos vigas, y asumiendo que cada una soportará la mitad de la carga completa, esto es 17 500 kg.

Con las simplificaciones necesarias para el caso, se plantea el siguiente problema de optimización estructural (ecuación (1)).

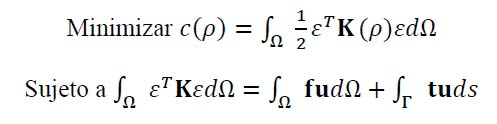
Donde:

K es la matriz de rigidez del modelo

F es el vector de cargas

t son las reacciones cercanas al apoyo

U es el vector de desplazamientos

ε es el vector de deformaciones

Ω es el dominio de Diseño

En el método SIMP, la matriz de rigidez se puede expresar de la forma (ecuación (2)).

Una vez se implementa la optimización, se require una etapa de refinamiento que permita adaptarse a un equipo real, y se verificará nuevamente su comportamiento mecánico-estructural.

Donde p corresponde a la variable de penalización y ρ(x) corresponde a la densidad como variable de control que estará definiendo dónde se debe adicionar material 1 y en dónde no 0. El valor de p varía de acuerdo con la relación de Poisson (Bendsoe y Sigmund, 2004).

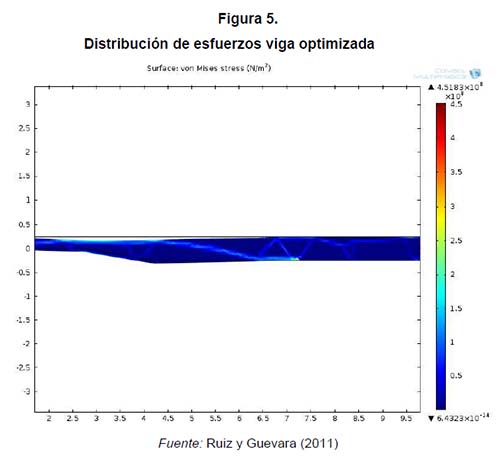
Implementado el modelo para diferentes valores de p, se obtuvieron los resultados presentados en la figura 4. Para valores cercanos a 3.0 se presentan distribuciones porosas que permiten percibir cómo sería la distribución de material; sin embargo, después de un valor de p cercano a 4.0 empieza a definirse la distribución en la figura cuando p = 4.5 se logra la mejor definición. Para valores mayores no hay cambios significativos en la distribución. En todos los casos, la distribución muestra un requerimiento completo de material en la zona del acople y cerca del cambio de altura del alma, mientras que en la parte media y cercana al apoyo trasero se logra una distribución que ahorra una gran cantidad de material. La distribución de esfuerzos para el último caso se presenta en la figura 5. Allí se encuentra un esfuerzo máximo de 198 MPa cerca del apoyo trasero muy próximo al límite de fluencia del material.

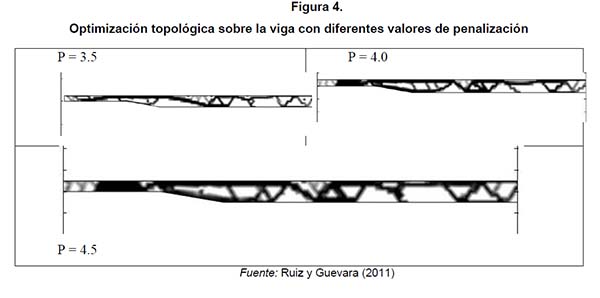
A partir de los resultados obtenidos en la distribución, se plantearon posibles modificaciones para las vigas. Estas fueron trabajadas entre el equipo de diseño del proyecto junto con expertos en diseño de vigas de la empresa Talleres Torres S. A.

Los criterios establecidos para el planteamiento de la solución utilizando la información obtenida fueron:

• Aligerar al máximo la viga y garantizar la resistencia de esta.

• No modificar sustancialmente la conformación de las demás partes del semirremolque que interactúan con la viga.

• No incurrir en gastos o procesos adicionales para la conformación.

De acuerdo con lo anterior, las soluciones propuestas buscaron retirar el material en la zonas seguras según la optimización. Teniendo en cuenta que la parte superior de las vigas viene atravesada por los puentes, no se previó retirar material allí, por lo que únicamente se hizo este proceso en la parte inferior de la viga donde la altura del alma es mayor.

Después de probar diferentes tamaños se escogieron cuadrados de 200 mm lado distribuidos cada 50 cm en un patrón de 9 repeticiones (figura 7).

El análisis del comportamiento mecánico estructural se realizó para las mismas condiciones de aplicación de carga y muestra que las dos tienen una buena capacidad para soportar las cargas aplicadas. Sin embargo, se identifican esfuerzos inducidos más altos en el patrón rectangular. En la aplicación que utiliza un patrón triangular, el esfuerzo máximo se ubica cerca de los 200 MPa, mientras que para la segunda alternativa este esfuerzo sobrepasa los 300 MPa. En la figura 7 se muestra la solución implementada en el semirremolque

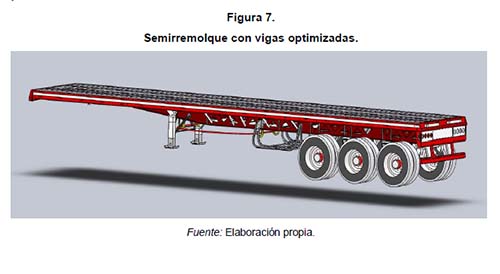
Fue posible llegar a un diseño que mejoró las condiciones de peso y que permite aumentar la capacidad de carga en un semirremolque de tipo plataforma multipropósito. La solución definida luego de los análisis respectivos ahorra masa en aproximadamente un 13 % que corresponde a 301.5 kg que pueden utilizarse para aumentar la capacidad de carga del semirremolque.

El uso del método SIMP es aún de gran utilidad para problemas de vigas convencionales, como las que se trabajaron en este proyecto, con la ventaja de ser más livianas computacionalmente con respecto a los algoritmos genéticos, que fue la otra técnica que se estudió para implementar la solución.

Teniendo en cuenta la magnitud de la aplicación, la simplificación de los modelos fue fundamental para poder llegar a resultados que pudieran validarse y utilizarse. El uso de aproximaciones bidimensionales a partir de asumir el caso crítico de las vigas como únicos elementos estructurales, dada su significancia en el equipo modelado, simplificó los cálculos significativamente, aunque se presume un error con respecto a un modelo tridimensional; sin embargo, las magnitudes tanto de esfuerzos como de deformaciones en las vigas en todo el conjunto tenderían a disminuir más que a aumentar por la rigidez que aportan los demás elementos que conforman el conjunto de soporte de carga.

La viabilidad económica de las soluciones está dentro del costo que normalmente un cliente pagaría por el semirremolque, el costo de la manufactura es el que fundamentalmente se tuvo en cuenta; para este proyecto no fueron calculados los costos asociados al diseño por ser una etapa puramente académica de generación de soluciones a problemáticas específicas.

Bendsoe, M. P. y Sigmund, O. (2004). Topology optimization (2ª ed.). Springer.

Cole, D. J. (2001). Fundamental issues in suspension design for heavy road vehicles. Vehicle System Dynamics, 35(4-5), 319-360.

Colfecar (2010). Comportamiento sectorial transporte y coyuntura 2010. Recuperado de www.colfecar.org Colombia, Ministerio del Transporte (2004). Resolución 4100 de diciembre 29 de 2004. Por la cual se adoptan los límites de pesos y dimensiones en los vehículos de transporte terrestre automotor de carga por carretera, para su operación normal en la red vial a nivel nacional.

Colombia, Ministerio de Transporte (2010). Diagnóstico del transporte 2010. Bogotá: Ministerio de Transporte/Oficina Asesora de Planeación/Grupo de Planificación Sectorial 2010.

Farzad R., Chien-Ming C. y Kikuchi N. (s. f.). Design analysis of composite laminate structures for light-weight armored vehicle by homogenization method. Elsevier Science-Computer and Structures, p.76.

Gerardo Franck, S. G., Bruno Lonardi, J. E. y Bruno, A. (s. f.). Análisis dinámico de un chasis de semirremolque de servicio pesado. Mecánica Computacional, Structural Dynamics (B), XXVIII(7), 503-517.

Högberg, D. (2001). Use of finite element method in trailer deck design. Journal of Materials Processing Technology, 117(1-2), 238-243.

Huang, X. y Xie, M. (2010). Evolutionary topology optimization of continuum structures: methods and applications. John Wiley y Sons. London, UK

Ingrassia, T., Alaimo, G., Cappello, F., Mancuso, A. y Nigrelli, V. (2007). A new design approach to the use of composite materials for heavy transport vehicles. International Journal of Vehicle Design, 44(3-4), 311-325.<

Jang, G.-W., Yoon, M.-S. y Park, J. H. (2009). Lightweight flatbed trailer design by using topology and thickness optimization. Structural and Multidisciplinary Optimization, 41(2), 295-307.

Kim, J.-G. y Yoon, M.-S. (2010). Optimal design of lightweight frame for heavy flat-bed trailer by using taguchi method. Transactions of the Korean Society of Mechanical Engineers A, 34(3), 353-359.

Pang, H., Li, H. Y., Fang, Z. D. y Shan, N. (2010). Ride comfort optimization and test research on an 8 × 4 heavy truck. Noise y Vibration Worldwide, 41(10), 6571.

Ruiz R., V. y Acero, E. (2012). Diseño óptimo de un semirremolque para vehículos de carga. Revista Tecnura, 16, 129-139.

Ruiz, V. y Guevara, J. C. (2011). Diseño óptimo de un semirremolque para vehículos pesados apoyado en una plataforma colaborativa (inédito). Bogotá: Universidad Distrital Francisco José de Caldas.