Estrategias didácticas para potenciar el pensamiento matemático a partir de situaciones del entorno métrico-Teaching strategies to enhance mathematical thinking from environmental situations metric

Estrategias didácticas para potenciar el pensamiento matemático a partir de situaciones del entorno métrico¹

Teaching strategies to enhance mathematical thinking from environmental situations metric

Ensinar estratégias para melhorar o pensamento matemático a partir de situações ambientais métrica

Alfonso Eduardo Chaucanés Jácome²

Jairo Escorcia Mercado³

Eugenio Therán Palacio⁴

Atilano Rafael Medrano Suarez⁵

¹Artículo de investigación

²Universidad de Sucre. Colombia. Contacto: chaucane@yahoo.com.mx

³Universidad de Sucre. Colombia. Contacto: escorciamercadojairo@yahoo.es

⁴Universidad de Sucre –Institución Educativa Sabaneta. Colombia. Contacto: eugeniotheran@gmail.com

⁵Universidad de Sucre – Institución Educativa Antonio Lenis. Colombia. Contacto: amedrasu@hotmail.com

Fecha de recepción: noviembre de 2013, Fecha de aceptación: julio de 2014

Resumen

En el presente artículo se comparten los frutos de una investigación sobre algunas estrategias tendientes a potenciar el pensamiento métrico en estudiantes de noveno grado de Educación Básica, a través de situaciones problema del contexto sociocultural y de las ciencias, bajo un diseño cualitativo. Se realizó un análisis didáctico, en relación con la comprensión de los conceptos, procedimientos y aplicaciones del pensamiento métrico, de los abordajes y soluciones de los estudiantes a las 15 situaciones de la prueba diagnóstica y de la prueba de contraste, diseñadas para reconocimiento de posibles dificultades de los estudiantes y para valorar el logro de las estrategias aplicadas, y algunas de la intervención en el aula usadas para superación de las dificultades detectadas.

Palabras clave: pensamiento matemático; resolución de problemas contextualizados; enseñanza; metodología de trabajo en el aula; estrategia didáctica; matemáticas escolares; medida.

Abstract

This article will share the fruits of research on some strategies to promote thinking metric freshmen Basic Education through sociocultural problem situations and science under a qualitative design. Training analyzes will be made in relation to the understanding of the concepts, procedures and applications of thinking metrically, approaches and solutions to the fifteen students diagnostic test situations and contrast test, designed to recognize possible difficulties of students and to assess the achievement of the strategies applied, and some of the classroom intervention used to overcome the difficulties encountered.

keywords: mathematical thinking, problem-solving situations, teaching, methodology of work in the classroom; teaching strategy; school mathematics; measure.

Resumo

Este artigo irá compartilhar os frutos da investigação sobre algumas estratégias para promover o pensamento calouros métricas educação básica por meio de situações-problema sócioculturais e de ciência em um projeto qualitativo. Formação análises serão feitas em relação à compreensão dos conceitos, procedimentos e aplicações de pensar metricamente, abordagens e soluções para os quinze estudantes situações de teste de diagnóstico e teste de contraste, destinadas a reconhecer possíveis dificuldades de estudantes e para avaliar o sucesso das estratégias aplicadas, e alguns de sala de aula da intervenção utilizada para ultrapassar as dificuldades encontradas.

Palavras-chave: pensamento matematico, situacoes de resolucao de problemas, ensino, metodologia de trabalho na estrategia de ensino em sala de aula, a matematica escolar; medida.

Introducción

En el primer semestre del año 2013 el grupo de investigación Pensamiento Matemático (PEMA) culminó el desarrollo de la
investigación Estrategias didácticas para potenciar el pensamiento matemático a partir de situaciones del entorno métrico en estudiantes de educación básica y media del municipio de Sincelejo, la cual contempló tres fases: diagnóstica, intervención y valoración de las estrategias y logros alcanzados por los estudiantes; se abordó la pregunta de investigación: ¿qué estrategias didácticas posibilitarían potenciar el pensamiento matemático en estudiantes de educación básica y media del municipio de Sincelejo, de tal manera que haya correspondencia entre los procesos de formación en la línea del pensamiento métrico con las competencias específicas de la matemática? La aplicación de la prueba diagnóstica permitió corroborar que a nivel general existe un bajo nivel de desarrollo del pensamiento métrico en los estudiantes. Frente a estas dificultades, en la etapa de intervención se implementó un trabajo de aula con la resolución de alrededor de 30 situaciones problema, teniendo en cuenta los indicadores de los estándares del pensamiento métrico, en un curso del grado noveno de la Institución Educativa Antonio Lenis de la ciudad de Sincelejo, Colombia. En la etapa de valoración de las estrategias se diseñó y aplicó, al mismo grupo que recibió el tratamiento, una prueba de contraste con categorías idénticas de la prueba diagnóstica, con el fin de validar la eficacia de las estrategias aplicadas. El contraste de los resultados evidenció que se lograron avances significativos en cuanto a la comprensión de los conceptos, procesos y aplicaciones ligados al pensamiento métrico, pero debe seguirse trabajando en el mejoramiento de estos logros.

De este acercamiento surgió una experiencia enriquecedora relacionada con los indicadores de los estándares sobre el pensamiento métrico, la cual se compartió con la comunidad de educadores de ASOCOLME en el ECME14 en la ciudad de Barranquilla, Colombia en el mes de octubre del año 2013, mediante el desarrollo de un curso corto, realizado en tres sesiones de 1.5 horas cada una. Con el desarrollo del curso se obtuvieron aportes de los participantes a las soluciones obtenidas con los estudiantes, pues a consideración del grupo PEMA merecen darse a conocer a la comunidad de educadores matemáticos, por su riqueza didáctica y como un ejemplo de la construcción social del conocimiento matemático, en tanto se dieron aportes en cadena en la siguiente dinámica: de la universidad a la escuela, de la escuela a la universidad, de ésta al ECME14 , del ECME14 a la universidad y de nuevo a la escuela, y viceversa , y en esta oportunidad nuevamente a la comunidad a través de este artículo. La misma dinámica o enfoque con el que se trabajó la resolución de las situaciones problema sobre el pensamiento métrico en la etapa de intervención, se utilizó en los diferentes escenarios universidad, escuela y ECME14, a saber: se proponen las situaciones problema, su abordaje, se obtienen las posibles soluciones según las interpretaciones de los estudiantes y socialización de éstas, conformándose así una cadena del proceso en otro escenario. Esta dinámica permite concluir que se obtendrán elaboraciones creativas cada vez tan amplias y ricas como el universo del pensamiento del ser humano.

Marco Teórico

Del marco conceptual de la investigación culminada, se extraen los siguientes fundamentos teóricos (Escorcia, Chaucanes, Theran y Medrano, 2013). Vasco et al (2006) definen los cinco tipos de pensamiento que hacen parte de la matemática, en especial el pensamiento métrico, el cual hace referencia a la comprensión general que tiene una persona sobre las magnitudes y las cantidades, su medición y el uso flexible de los sistemas métricos o de medidas en diferentes situaciones.

Según el Instituto Colombiano para el Fomento de la Educación Superior (ICFES) (2007), la competencia matemática de resolución de problemas se relaciona con la capacidad para formular problemas a partir de situaciones, dentro y fuera de la matemática, que implique traducir la realidad a una estructura matemática, desarrollar y aplicar diferentes estrategias y justificar la elección de métodos e instrumentos para la solución de problemas, justificar la pertinencia de un cálculo exacto o aproximado en la solución de un problema y lo razonable o no de una respuesta obtenida. Igualmente, verificar e interpretar resultados a la luz del problema original y generalizar soluciones y estrategias para dar solución a nuevas situaciones problema.

Para Freudhental (1991) el objetivo principal en la enseñanza de la matemática es matematizar la realidad cotidiana, en donde aprender matemáticas significa hacer matemáticas, una actividad mental reflexiva en torno a resolver problemas en contextos realistas. La resolución de problemas no es sólo uno de los fines de la enseñanza de las matemáticas, sino el medio esencial para lograr el aprendizaje. Los estudiantes deberán tener frecuentes oportunidades de plantear, explorar y resolver problemas que requieran un esfuerzo significativo. Los contextos de los problemas pueden referirse tanto a las experiencias familiares de los estudiantes, como a las aplicaciones en otras áreas.

Las estrategias en la solución de problemas se refieren a las operaciones mentales que los estudiantes utilizan para pensar sobre la representación de los datos, con el fin de transformar éstos en metas y alcanzar una solución. Las estrategias incluyen los métodos heurísticos, los algoritmos y los procesos de pensamiento divergente.

Descripción de las actividades

Las tres sesiones del curso fueron: una sesión de socialización de los resultados de la investigación y dos sesiones de trabajo práctico de resolución de situaciones problema sobre el pensamiento métrico, la última complementada con el uso del software cabrí.

Las actividades realizadas constaron del abordaje y solución, y de los análisis didácticos respectivos de las situaciones usadas por el grupo en las pruebas de diagnóstico y contraste, y las usadas en el proceso de intervención en el aula. Además de algunas ya diseñadas en la asignatura didáctica de las matemáticas en el Programa de Licenciatura en Matemáticas de la Universidad de Sucre (LIMA) en relación con el pensamiento métrico, y otras tomadas de olimpiadas internacionales de matemáticas. Las dos pruebas antes referidas, constan de ocho y siete situaciones respectivamente, y alrededor de 20 en la intervención, según los indicadores de los estándares del pensamiento métrico, relacionadas con los conceptos de magnitud y medida; los procesos de estimar, calcular, conservación de la cantidad y de aplicaciones en el contexto métrico.

A continuación se presentan, a modo de ejemplo, algunas de las situaciones que se trabajaron en el curso y se realiza la descripción del abordaje de ellas, poniendo de presente que la situación 1 se adaptó de su versión original de la Revista Unión No. 24 de diciembre de 2012 (p. 140)6 y las situaciones 2 y 3 se adaptaron de la Revista Olimpiada Matemática Estatal, Vitoria – Gastelz, de junio de 20l2, la cual es difundida por la Federación Española de Sociedades de Profesores de Matemáticas (FESPM).

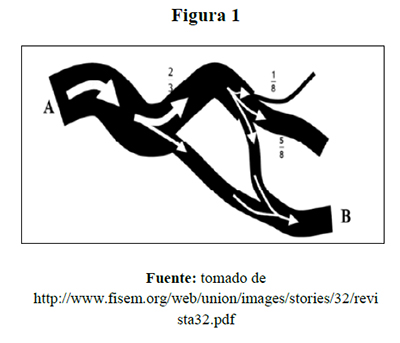
Situación 1. Un río empieza en el punto A; luego se divide en dos ramas, la primera se lleva 2/3 del agua y la otra el resto. Después la primera rama se divide en tres, una de ellas toma 1/8 del agua de esa rama, otra toma 5/8 y la otra rama, que lleva el sobrante, se une con la segunda rama original. ¿Qué proporción del río llega al punto B?

Situación 2. Ana quiere repartir una torta cuadrada de 30 cm de lado entre cinco personas de forma que reciban la misma cantidad de torta. El primer corte lo hace partiendo del centro del cuadrado hasta el borde de la torta, a 10 cm de una esquina. Si el resto de cortes los hace también en línea 6 Esta revista es un órgano de difusión de la Federación Iberoamericana de Educación Matemática (FISEM) recta y partiendo del centro, ¿cómo cortó la torta? Con la condición de que la longitud de cada trozo correspondiente al borde de la torta sea un número entero, indica entre cuántas personas podrían hacerse el reparto.

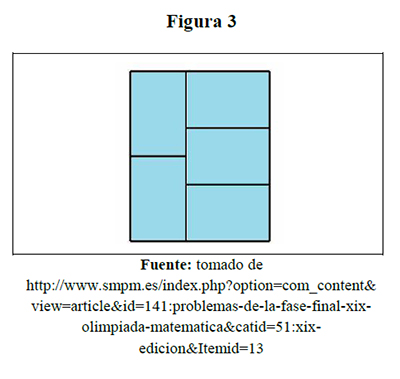
Situación 3. Si el perímetro de la plancha es de 880 cm y el precio del material es de 50 �/m2. ¿Cuánto pagaremos por las cinco ventanas?

Tres soluciones, que se destacaron, dadas por estudiantes que cursaron la asignatura Didáctica de las Matemáticas de la Universidad de Sucre en el semestre 01 de 2013 a la situación 3 son:

Solución 1. Desde el pensamiento numérico, un estudiante (Daniel) establece que se deben buscar dos números, correspondientes a la base y a la altura de cada uno de los cinco rectángulos y que estén en relación 2 a 3; obteniendo así 80 cm para altura y 120 cm para la base. Por tanto, la plancha es de 200 cm por 240 cm, es decir de 2 m por 2,4 m y así el pago de las cinco ventanas es de 240 euros.

Solución 2. Desde el pensamiento métrico, una estudiante (Alexandra) usa un cuadrado de lado ?? como unidad de medida, cuadriculando la plancha en 5 por 6 cuadros, de modo que el perímetro es 22 ??, que al igualar con 880 cm obtiene a ?? como 40 cm. Así la plancha es de 200 cm por 240 cm o de 2 m por 2,4 m, resultando que el pago de las cinco ventanas es de 240 euros.

Solución 3. Desde el pensamiento variacional, dos estudiantes (Carlos y Juan) establecen el sistema de ecuaciones lineales 4??+5??=880 y 2??=3?? , siendo a la altura y b la base de cada uno de los cinco rectángulos, que al resolver resulta que la plancha es de 200 cm por 240 cm, o de 4,8 metros cuadrados y así el pago de las cinco ventanas es de 240 euros.

Estas soluciones son un ejemplo de cómo una misma situación puede resolverse desde el dominio del pensamiento del estudiante y no necesariamente desde donde los docentes la proyectan. En cada una se mira la correspondencia con los conceptos, procesos y contextos del pensamiento métrico.

En el evento se les socializó alrededor de unas tres o cuatro soluciones más construidas para la tercera situación. La mayoría de los participantes en el curso resolvió la situación uno, sumando 1/3 con 2/8, lo cual deja entrever que no conservan la unidad, se les hizo las debidas aclaraciones, obteniendo la solución correcta de un medio. La solución dos no fue abordada, se dejó propuesta para los participantes.

Situación problema abordada con los estudiantes.

En este apartado se analiza cómo surgió el planteamiento de dos de las situaciones didácticas a trabajar con los participantes del curso en la sesión dos. A los estudiantes del primer semestre del programa de Licenciatura en Matemáticas (LIMA) periodo 01 de 2013 de la Universidad de Sucre, Colombia, se les presentó, en la asignatura matemática escolar, la situación problema que el profesor inicia comentando en un lenguaje coloquial de la siguiente manera:

Se tiene un cuadrado al que se le recortó en una esquina otro cuadrado pequeño. Teniendo otra figura igual a esta y ensamblándolas por las esquinas recortadas, hay que determinar el perímetro y el área de la figura resultante, si el lado del cuadrado “mayor” mide 10 cm y el del cuadrado “menor” es 2 cm. El profesor plantea, “bueno vamos a ver cómo redactamos el texto de la situación de la mejor forma para una mejor comprensión”.

Después de mirar posibilidades de comprensión e interpretación de lo que se solicitaba resolver, se elaboró con ellos diferentes redacciones del texto de la situación, convirtiéndose en un ejercicio interesante antes de proceder a resolver la situación:

R1: Se tienen dos cuadrados de lados 10 cm cada uno. Se recorta en cada uno de ellos un cuadrado de lado 2 cm en una de sus esquinas. Al ensamblar las figuras obtenidas por dichas esquinas, ¿Qué perímetro y que área tiene la figura que se forma?

R2: Dados dos cuadrados iguales de lados 10 cm, a los que se les recortó en una esquina un cuadrado de 2 cm de lado, ¿Qué perímetro y qué área tiene la figura que se forma al ensamblar los “cuadrados” por las esquinas recortadas?

R3: En dos cuadrados de lados 10 cm de lados se r

Después de cierto consenso de comprensión de la situación problema, los estudiantes elaboraron sus diseños y plantearon posibles estrategias de solución. Es de anotar que la situación se presentó en lenguaje verbal, aunque algunos estudiantes pidieron que, además del texto, se les dibujara la figura de o que se les estaba pidiendo resolver; se les aclaró que era importante mirar la interpretación que ellos hacían de la situación dada. Además, la situación se basa en el concepto no matemático de ensamblar.

Situaciones problema para analizar con los docentes.

A continuación se presenta una situación inicial trabajada con estudiantes de noveno grado en la fase de intervención de la investigación en la Institución Educativa Antonio Lenis de Sincelejo, Sucre, Colombia en noviembre de 2012.

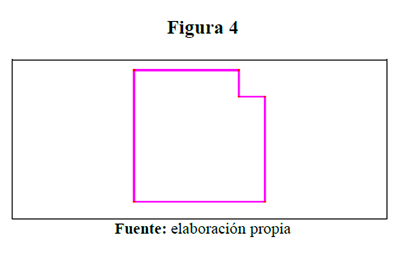
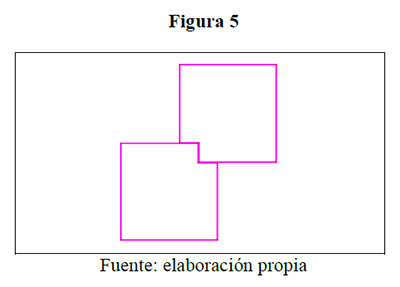
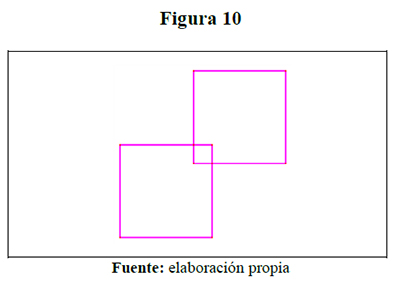
• En un cuadrado de lado 10 cm, se ha recortado en una de sus esquinas un cuadrado de 2 cm de lado (figura 4). Con otra figura igual a ella se obtiene la figura 5, ¿Qué perímetro tiene ella?

El rediseño de esta situación permitió desarrollar una clase en la asignatura Matemática Escolar en la línea de Didáctica de las Matemáticas, con los estudiantes de primer semestre del programa de Licenciatura en Matemáticas (LIMA) de la Universidad de Sucre (Colombia) en el periodo semestral 01 del año 2013. Se esperaba que los estudiantes dieran como respuesta la representación de la figura 5, y también otras que ellos lograsen construir creativamente.

Situación 1

A los estudiantes del primer semestre de LIMA período 01 de 2013, se les planteó resolver la siguiente situación problema:

• Dados dos cuadrados iguales de lados 10 cm, a los que se les recortó en una esquina un cuadrado de 2 cm de lado, ¿Qué perímetro y qué área tiene la figura que se forma al ensamblar los “cuadrados” por las esquinas recortadas?

Situación 2

Un estudiante representa la situación mediante la figura 4 para dar su solución.

A continuación se darán a conocer y se analizarán las soluciones que presentaron los docentes participantes frente a cada situación problema; posteriormente, se socializarán las soluciones que presentaron los estudiantes con el fin de buscar puntos de encuentro y el aporte de la situación en la potenciación del pensamiento métrico.

Un grupo representó la situación 1 de manera diferente a las dadas por los estudiantes: una figura encima de la otra apoyándose en la esquina recortada

Otras soluciones propuestas por los estudiantes.

A continuación se presentan las soluciones a la situación 1 propuestas por los estudiantes:

1. Los estudiantes colocan una enfrente de la otra y las unen encontrándose en las esquinas recortadas, tal como se muestra en la figura siguiente:

2. Los estudiantes unen las figuras de manera que se interceptan en dos puntos de las esquinas recortadas:

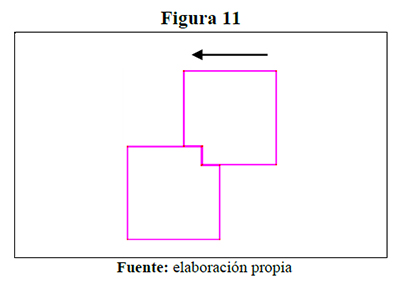
3. Los estudiantes deslizan una de las figuras sobre la otra como riel hasta recorrer la longitud del lado del cuadrado pequeño recortado:

4. Los estudiantes colocaron una figura frente a la otra y unieron introduciendo seis segmentos de ?? unidades cada uno, variable emergente en el planteamiento del problema, formando la figura tridimensional siguiente:

Es de notar que la solución planteada por el estudiante conduce al abordaje de expresiones algebraicas, al cálculo numérico de un polinomio cuando especifique un valor para ?? y a nuevos planteamientos, como por ejemplo el cálculo del volumen de la figura obtenida.

Análisis del desarrollo de las situaciones de aula.

Hay situaciones que, en su abstracción, producen una interpretación que conlleva a una solución, pero al trasladarlas a un modelo real pueden presentar otras vías o alternativas de interpretación y respuestas. También se puede ventilar la situación desde lo particular a la abstracción general, tal como lo señala el referente didáctico propuesto por Piaget, Van Hiele, Freudhental, entre otros. Frente a las variadas soluciones presentadas por los estudiantes, es pertinente preguntar ¿cuál es la correcta?, esto induce a establecer una negociación de significados, al diálogo e institucionalización del saber, para escudriñar la producción matemática del estudiante y sus actitudes metacognitivas.

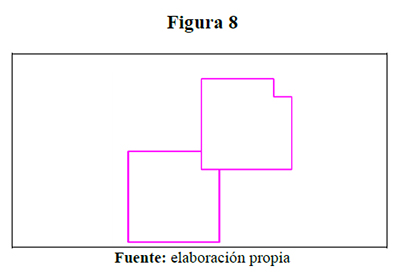
Usando la estrategia de un modelo de cuadrado en cartulina se presenta que los estudiantes ensamblan con o sin superposición de las figuras; en la figura 8 se presenta esta situación. Se entenderá como superposición la intersección de áreas entre las figuras, lo cual es una hipótesis nueva para el problema.

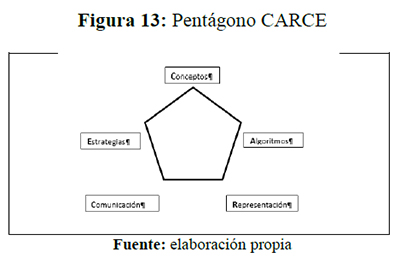
Se mostrarán algunos de los procesos seguidos con los estudiantes para obtener la solución del perímetro y del área en alguna de las figuras planteadas por ellos. Para este fin, en cada caso se iba mirando a qué tipo de elemento correspondía del pentágono CARCE, figura 13, la solución dada por el estudiante: redes conceptuales, estrategias varias, distintas formas de expresión, discursos, representaciones.

Además, se iba mirando a qué tipo de los cinco pensamientos correspondía o se enmarcaba la solución que estaban proponiendo. También se iba reconociendo a qué indicador correspondía de los estándares del pensamiento métrico, tal como se especifica en la siguiente tabla:

Explotación de la situación.

Consiste en hacer otros planteamientos o modificaciones a las condiciones de la situación dada, a fin de obtener procesos de generalización. Por ejemplo, realizar la situación cuando los cuadrados recortados son de lados diferentes; realizarla cuando varía el lado de los cuadrados a los que se le recorta el mismo cuadrado. Si en vez de dos cuadrados se cambia uno de los cuadrados por otra figura geométrica, o si en vez de recortar cuadrados se recortan otros tipos de figuras que sean semejantes.

Análisis de otras situaciones.

Con las situaciones 1 y 2 del inicio también se puede hacer exploración de contexto, es decir, buscar generalizaciones posibles como plantear el problema con otra forma diferente de la torta: circular, poligonal, entre otros, también con otras bifurcaciones de las corrientes de agua.

El curso se desarrolló con la misma metodología de trabajo, descrita anteriormente en el numeral 3.4. A continuación se presentan otras situaciones trabajadas: las situaciones del cubo de Gruyére, la del cubo perforado y la del diseño de una bandera nueva, las cuales fueron modeladas en cabrí y resueltas analíticamente.

Situación del cubo Gruyére.

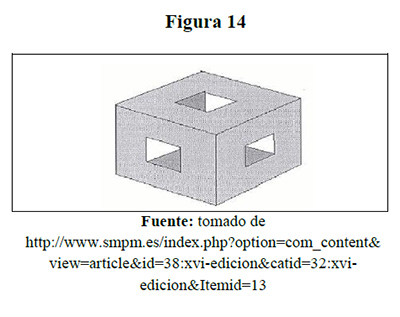
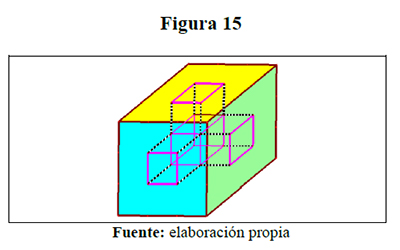
Un cubo de 3 por 3 tiene tres agujeros, cada uno con una sección de 1 por 1, que van desde el centro de cada cara en dirección a la cara opuesta, hasta que se encuentra y se une con otro agujero, ¿Cuál será la superficie total, en unidades cuadradas, del sólido que resulta?

Para ilustrar su solución, esta situación se modeló con el software cabrí así:

Una solución analítica consistió en mirar qué se conserva el área externa de las caras que es de 54 unidades cuadradas, pues las tres unidades de los orificios sólo se trasladaron hacia el interior del cubo, más 12 unidades cuadradas de las caras internas, para un total de 66 unidades cuadradas.

Situación del cubo perforado.

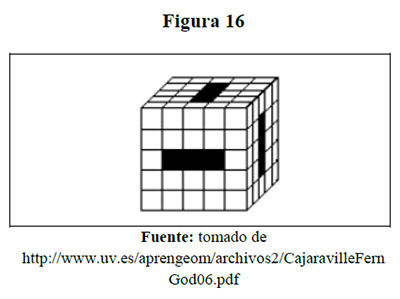
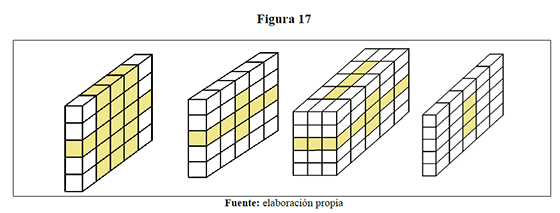
Se hacen túneles que atraviesan un cubo grande como se indica en la figura. ¿Cuántos cubos pequeños quedan?

a) 88 b) 80 c) 70 d) 96 e) 85

La solución se modeló en cabrí rebanando el cubo, obteniendo las capas que se muestran en la figura 17, lo que permite verificar un conteo directo de 88 cubitos blancos

Situación de la construcción de una bandera nueva.

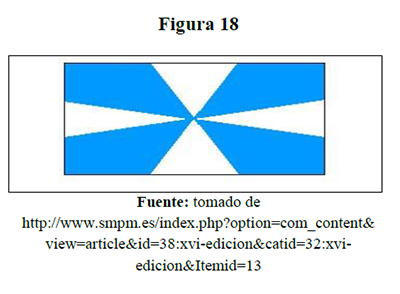
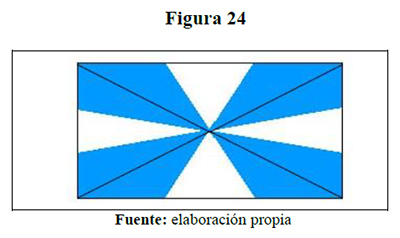
Un equipo de fútbol ha encargado su bandera bicolor a un prestigioso diseñador. �ste realizó el boceto a partir de un rectángulo en que dividió cada lado en tres segmentos de la misma longitud; uniendo los puntos obtenidos como se indica en la figura 18, ¿en qué proporción se encuentran los colores que tiene que utilizar para la confección de la bandera?

Una solución se verificó modelando con cabrí, así:

Construcción social del conocimiento matemático.

A continuación se presentan algunas soluciones en cadena, dada a la situación de la bandera, observándose que a partir de la socialización de la solución dada por Helen en el curso corto de ECME14, se generaron otras soluciones creativas. También se comparte una solución sorprendente suministrada por una profesora de química al proponerse resolver en una conferencia de la institución Madre Amalia de Sincelejo, dos semanas después de realizado el curso. De esta manera se pone de relieve la construcción de una red conceptual realizada sobre el pensamiento métrico.

Solución dada por Helen a la situación de la bandera.

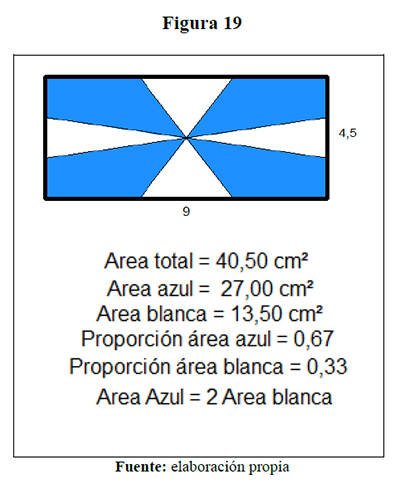
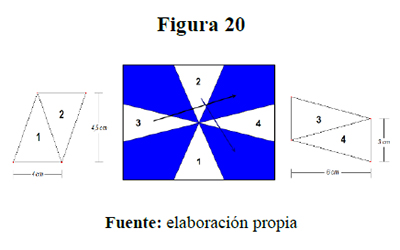
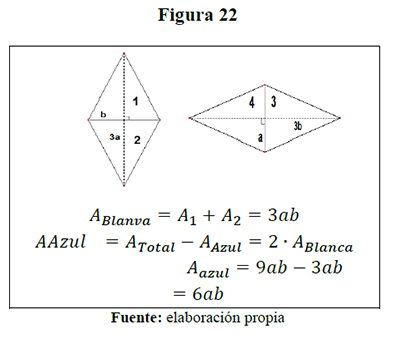
Helen consideró la bandera como un rectángulo de base 12 cm y altura 9 cm, resolviendo la situación de la manera siguiente: calcula el área blanca, para lo cual traslada el triángulo 2, contiguo al triángulo 1 y el triángulo 3 contiguo al triángulo 4, formando dos paralelogramos tal como se muestran en la figura siguiente:

Solución dada por estudiantes de primer semestre del Lima a la situación de la bandera.

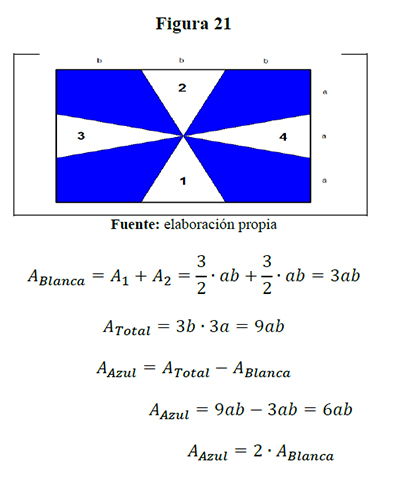
La solución dada por Helen se socializó a los estudiantes de I semestre de LIMA de la Universidad de Sucre una semana después de ECME 14 en la asignatura Matemática Escolar, donde también se observó, en forma general, que ??1 es el área del paralelogramo formado con los triángulos 1 y 2 y ??2 es el área del paralelogramo formado con los triángulos 3 y 4, a saber:

Finalizada la demostración, los estudiantes proponen otra solución, uniendo los triángulos por las bases y obteniendo dos rombos, ??1 es el área del rombo formado con los triángulos 1 y 2 , y ??2 es el área del rombo formado con los triángulos 3 y 4, a saber:

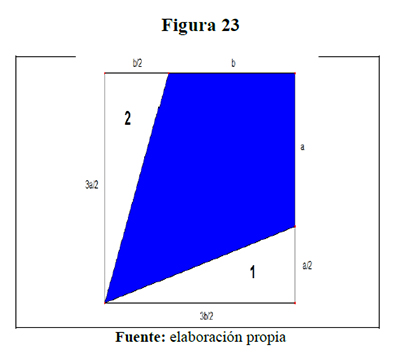
Otro estudiante plantea su solución, reduciendo el problema a encontrar una cuarta parte de la bandera, y lo resuelve de la siguiente forma:

Solución dada por la profesora de química a la situación de la bandera.

La profesora de química plantea su solución, manifestando que existe una relación dos a uno, por cuanto hay dos segmentos azules por uno blanco; bosquejando el problema así: ¿la proporcionalidad de los segmentos implica la de las áreas? Hecho que fue demostrado por un profesor del departamento de matemáticas de la Universidad de Sucre, Colombia de la manera siguiente: forma un triángulo con el trazo de dos segmentos desde el centro del rectángulo a los dos puntos extremos de la base del rectángulo, obteniéndose en definitiva tres triángulos de áreas congruentes que corrobora la relación de dos áreas azules por una blanca. De esta solución el profesor Jairo Escorcia Mercado presenta una solución que muestra una comprensión más sencilla de la relación de los colores de la bandera y de un uso claro del pensamiento métrico, por cuanto la bandera está formada por doce triángulos de áreas congruentes de los cuales el área azul tiene, al completar los trazos, ocho triángulos y la blanca tiene cuatro, apreciándose directamente que el área azul es el doble de la blanca.

Explotación de la situación de la situación de la bandera.

Se hacen los siguientes planteamientos:

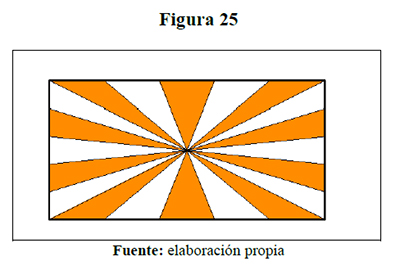
1. Si cambian las longitudes de los segmentos a y b, ¿cambia o se mantiene la relación Aazul =2 Ablanco? 2. Si en vez de dividir las longitudes de los lados de la bandera en tres segmentos, se dividen en 4, 5, 6, n segmentos respectivamente, ¿cuál es la relación en cada caso?, ¿cuántos colores necesitaría la bandera ahora? Por ejemplo, para la división de los lados de la bandera en 5 segmentos, se tendría que resolver la situación que se presenta en la figura 25.

CONCLUSIONES

Para el grupo PEMA compartir las bondades de esta experiencia con la comunidad académica tiene un significado trascendental por cuanto hubo variedad de logros didácticos del abordaje y solución de las situaciones problema en correspondencia con los indicadores de los estándares para el pensamiento métrico. Además, aunque las confusiones conceptuales y algunas dificultades fueron abordadas de manera satisfactoria en la intervención, aún persisten algunas que deben superarse. Los estudiantes presentaron, entre otras, confusión en los conceptos de magnitudes, perímetro con áreas, lado con altura, lado con una diagonal, lado con el perímetro del triángulo, existe confusión de las fórmulas del área del paralelogramo con la del triángulo y con la de perímetro; también en la conversión de las unidades de los sistemas de medidas.

Con esta dinámica de trabajo se muestra, en la práctica, que es posible potenciar en el aula los procesos para desarrollar el pensamiento matemático a través de la resolución de problemas relacionadas con el pensamiento métrico, donde intervienen diferentes actores, escenarios y momentos, apuntando a la construcción social del conocimiento. Esto evidencia que es posible cambiar el paradigma tradicional de enseñanza de la matemática, lo cual es el impacto que se espera lograr con la puesta en consideración ante la comunidad académica de educadores matemáticos de este artículo.

REFERENCIAS

Escorcia, J., Chaucanes, E. Therán, E. y Medrano, A.. (2013). “Estrategias didácticas para potenciar el pensamiento matemático a partir de situaciones del entorno métrico en estudiantes de educación básica y media del municipio de Sincelejo. Ciencia, Ingeniería y educación científica”. Revista Científica, (octubre), edición especial. Bogotá, D.C.

Freudenthal, H. (1991). Why to Teach Mathematics so as to Be Useful.Educational Studies in Mathematics, (s.d.)

Instituto Colombiano para el Fomento de la Educación Superior (ICFES). (2007). Fundamentación conceptual área de matemáticas. Bogotá: Grupo de evaluación de la educación superior.

Vasco, et al. (2006). Ministerio de Educación Nacional. Estándares Básicos de Competencias en Matemáticas, Potenciar el pensamiento matemático: �un reto escolar! Bogotá: Imprenta Nacional de Colombia.

Vitoria – Gastelz, (2012). XXIII Olimpiada Matemática Nacional para estudiantes de 2� ESO. Junio. Disponible en: http://www.fisem.org/web/union/images/stories/32/revista32.pdf